预测控制MATLAB仿真与设计

基于MATLAB控制系统的仿真与应用毕业设计论文目录一、内容概括 (2)1. 研究背景和意义 (3)2. 国内外研究现状 (4)3. 研究目的和内容 (5)二、MATLAB控制系统仿真基础 (7)三、控制系统建模 (8)1. 控制系统模型概述 (10)2. MATLAB建模方法 (11)3. 系统模型的验证与校正 (12)四、控制系统性能分析 (14)1. 稳定性分析 (14)2. 响应性能分析 (16)3. 误差性能分析 (17)五、基于MATLAB控制系统的设计与应用实例分析 (19)1. 控制系统设计要求与方案选择 (20)2. 基于MATLAB的控制系统设计流程 (22)3. 实例一 (23)4. 实例二 (25)六、优化算法在控制系统中的应用及MATLAB实现 (26)1. 优化算法概述及其在控制系统中的应用价值 (28)2. 优化算法介绍及MATLAB实现方法 (29)3. 基于MATLAB的优化算法在控制系统中的实践应用案例及分析对比研究31一、内容概括本论文旨在探讨基于MATLAB控制系统的仿真与应用，通过对控制系统进行深入的理论分析和实际应用研究，提出一种有效的控制系统设计方案，并通过实验验证其正确性和有效性。

本文对控制系统的基本理论进行了详细的阐述，包括控制系统的定义、分类、性能指标以及设计方法。

我们以一个具体的控制系统为例，对其进行分析和设计。

在这个过程中，我们运用MATLAB软件作为主要的仿真工具，对控制系统的稳定性、动态响应、鲁棒性等方面进行了全面的仿真分析。

在完成理论分析和实际设计之后，我们进一步研究了基于MATLAB 的控制系统仿真方法。

通过对仿真模型的建立、仿真参数的选择以及仿真结果的分析，我们提出了一种高效的仿真策略。

我们将所设计的控制系统应用于实际场景中，通过实验数据验证了所提出方案的有效性和可行性。

本论文通过理论与实践相结合的方法，深入探讨了基于MATLAB 控制系统的仿真与应用。

一、前言工业生产的过程是复杂的，建立起来的模型也是不完善的。

即使是理论非常复杂的现代控制理论，其效果也往往不尽人意，甚至在一些方面还不及传统的PID控制。

20世纪70年代，人们除了加强对生产过程的建模、系统辨识、自适应控制等方面的研究外，开始打破传统的控制思想，试图面向工业开发出一种对各种模型要求低、在线计算方便、控制综合效果好的新型算法。

在这样的背景下，预测控制的一种，也就是动态矩阵控制（DMC）首先在法国的工业控制中得到应用。

因此预测控制不是某种统一理论的产物，而是在工业实践中逐渐发展起来的。

预测控制中比较常见的三种算法是模型算法控制（MAC），动态矩阵控制（DMC）以及广义预测控制。

本篇所采用的是动态矩阵控制，其采用增量算法，因此在消除稳态余差方面非常有效。

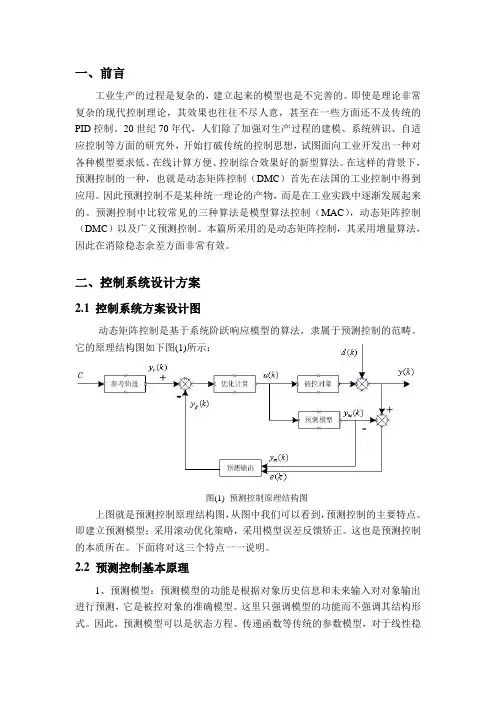
二、控制系统设计方案2.1 控制系统方案设计图动态矩阵控制是基于系统阶跃响应模型的算法，隶属于预测控制的范畴。

它的原理结构图如下图(1)所示：图(1) 预测控制原理结构图上图就是预测控制原理结构图，从图中我们可以看到，预测控制的主要特点。

即建立预测模型；采用滚动优化策略，采用模型误差反馈矫正。

这也是预测控制的本质所在。

下面将对这三个特点一一说明。

2.2 预测控制基本原理1、预测模型：预测模型的功能是根据对象历史信息和未来输入对对象输出进行预测，它是被控对象的准确模型。

这里只强调模型的功能而不强调其结构形式。

因此，预测模型可以是状态方程、传递函数等传统的参数模型，对于线性稳定对象，阶跃响应、脉冲响应这类非参数模型也可以作为预测模型使用。

预测模型具有展示系统未来动态行为的功能，这样，就可以利用预测模型来预测未来时刻被控对象的输出变化及被控变量与其给定值的偏差，作为控制作用的依据，使之适应动态系统所具有的因果性的特点，得到比常规控制更好的控制效果。

2、滚动优化：预测控制是一种优化控制算法，它是通过某一性能指标的最优来确定未来的控制作用。

这一性能指标涉及到系统未来的行为。

matlab控制系统仿真设计Matlab控制系统仿真设计控制系统是现代工业领域中的关键技术之一，用于实现对系统行为的预测和调节。

在控制系统设计中，仿真是一个重要的工具，可以帮助工程师和研究人员理解和评估系统的性能。

在本文中，我们将以Matlab的控制系统仿真设计为主题，介绍控制系统仿真的基本概念、方法和工具。

一、控制系统仿真基础1.1 什么是控制系统仿真？控制系统仿真是指通过计算机模拟系统的动态行为来评估和验证控制策略的一种方法。

仿真可以帮助工程师在构建实际系统之前，通过计算机模型对系统的运行过程进行预测和分析。

1.2 为什么要进行控制系统仿真？控制系统仿真可以帮助工程师在实际系统建造之前对系统进行评估和优化。

它可以提供系统的动态响应、稳定性、鲁棒性等信息，帮助工程师优化控制策略和设计参数。

此外，仿真还可以帮助工程师调试和验证控制算法，减少实际系统建造和测试的成本和风险。

1.3 Matlab在控制系统仿真中的作用Matlab是一款功能强大的科学计算软件，也是控制系统仿真的重要工具之一。

Matlab提供了丰富的控制系统设计和分析工具箱，使得控制系统仿真变得更加简单和高效。

二、Matlab控制系统仿真设计的步骤2.1 确定系统模型在进行控制系统仿真设计之前，首先需要确定系统的数学模型。

系统模型可以通过物理原理、实验数据或系统辨识方法得到。

在Matlab中，可以使用符号计算工具箱或数值计算工具箱来建立系统的数学模型。

2.2 设计控制器根据系统模型和性能要求，设计合适的控制器。

常用的控制器设计方法包括PID控制、根轨迹设计、频率响应设计等。

在Matlab中，可以使用Control System Toolbox来设计控制器，并进行性能分析和优化。

2.3 仿真系统响应利用Matlab的仿真工具，对系统进行动态仿真，观察系统的响应。

仿真可以根据预先设定的输入信号和初始条件，计算系统的状态和输出变量随时间的变化。

Mat1ab技术控制系统设计与仿真一、引言在现代科技领域中，控制系统是一个至关重要的概念。

在各种领域，如机械工程、电子工程、化工工程等，控制系统的设计和仿真是实现目标的关键。

而Mat1ab作为一种功能强大的数值计算软件，被广泛应用于控制系统设计和仿真。

本文将探讨MaHab技术在控制系统设计和仿真中的应用。

二、MatIab基础知识在开始探讨MatIab技术在控制系统设计和仿真中的应用之前，有必要先了解一些Mat1ab的基础知识。

Mat1ab是由MathWorks公司开发的一款用于数值计算和科学绘图的软件。

它提供了丰富的函数库和工具箱，能够满足各种数学和工程领域的需求。

Mauab的核心功能包括数值计算、数据分析、图形绘制和算法开发等。

通过Mat1ab,用户可以进行复杂的矩阵运算、符号计算、非线性优化和差分方程求解等操作。

此外，MaUab还具有强大的数据分析功能，能够进行统计分析、数据可视化和模型拟合等操作。

三、控制系统设计控制系统设计是指通过控制器和执行器对系统进行控制的过程。

Mat1ab提供了一系列用于控制系统设计的工具箱，如Contro1SystemToo1box和Simu1ink等。

Contro1SystemToo1box是Mat1ab中用于控制系统分析和设计的工具箱。

它包含了各种用于系统建模、控制器设计和仿真的函数和工具。

例如，用户可以使用TransferFunction对象来描述系统的传输函数，并使用该对象进行稳定性分析和控制器设计。

此外，COntrOISyStemTOOIbOX还提供了多种控制器设计方法，如根轨迹法、频域法和状态空间法等，可以满足不同系统的设计需求。

SimUIink是MatIab中的一个仿真工具，用于建立动态系统的模型和仿真。

通过Simu1ink,用户可以使用图形界面建立系统的模型，并使用各种模块来描述系统的构成和行为。

SimU1ink提供了广泛的预定义模块，包括传感器、执行器、控制器等。

MATLAB与控制系统的数字仿真及CAD课程设计引言MATLAB是一种高性能计算软件，广泛应用于科学计算、信号处理、图像处理、数据分析、控制工程等领域。

控制系统是MATLAB中应用广泛的一类工程实践。

数字仿真是利用计算机对各类物理、化学、机械、电气、通信等各类系统进行模拟，以求得对系统性能的认识和分析的一种有效方法。

此文档旨在介绍MATLAB与控制系统的数字仿真及CAD课程设计。

MATLAB数字仿真MATLAB数字仿真是一种基于MATLAB软件平台的模拟方法，可以有效模拟和分析电子系统、传感器、组装等各类系统的工作性能。

MATLAB软件有强大的数值计算和可视化工具，使得控制系统的数字仿真具有高精度的仿真结果和优秀的用户体验。

仿真工具箱MATLAB提供了很多工具箱，包括信号处理工具箱、图像处理工具箱等，控制系统仿真工具箱也是其中之一。

控制系统仿真工具箱提供了包括连续时间系统、离散时间系统、多变量系统、无线系统在内的多种控制系统模型，并提供了丰富的仿真方法，例如最小二乘法、维纳滤波等。

用户可以通过编写脚本或使用图形化界面操作控制系统仿真工具箱，实现自己想要的仿真结果。

建立仿真模型在进行数字仿真前，需要先建立仿真模型。

对于控制系统而言，建立仿真模型需要明确系统的输入、输出、各组件之间的关系以及系统的初始条件等。

建立好仿真模型后，可以对系统的工作过程进行仿真和分析。

以温度控制系统为例，建立仿真模型。

该温度控制系统包含温度感应器作为输入，控制器和加热器作为输出。

建立好模型后，系统可以对不同的工作条件下进行仿真和分析，例如调节感应器灵敏度、控制器输出功率等。

控制系统CAD设计控制系统的CAD设计是指利用计算机辅助设计软件（Computer-ded Design，简称CAD）进行控制系统的三维模型设计、仿真、优化等工作。

控制系统CAD设计可以有效降低设计成本，提高设计效率和质量。

CAD软件常用的CAD软件有AutoCAD和SolidWorks。

控制系统matlab仿真与设计
控制系统matlab仿真与设计
控制系统是现代工业领域中必不可少的一部分。

它能够控制各种
机械、电子及其他工程系统的工作，从而使其能够按照我们的意图去
运作。

控制系统matlab仿真与设计是控制系统中非常重要的一项工作，通过它我们能够更好的了解系统的性能、优化系统的控制方法，并减
少实际操作时的风险。

步骤一：模型建立
模型建立是控制系统matlab仿真与设计的重要步骤。

在这一步
骤中，我们需要根据系统的特征和数据建立一个合适的模型。

模型通
常是一个数学公式或者是一张流程图。

建立模型需要我们对系统非常
熟悉，有着一定的专业知识。

步骤二：仿真设计
在模型建立之后，我们需要进行仿真设计。

这一步是通过matlab 仿真软件对我们建立的模型进行仿真运行，并获得系统的反馈。

在仿
真设计的过程中，我们能够调整模型参数，使系统的工作效率更高、
更加稳定。

步骤三：系统控制
在控制系统matlab仿真与设计的最后一步，我们需要根据仿真
的结果对系统进行实际的控制。

这一步通常是对系统的运行进行调整
和优化。

我们可以通过改变控制系统中的参数，对系统进行优化来提
高系统的工作效率和稳定性。

控制系统matlab仿真与设计非常便于工程人员分析系统，优化
控制策略。

它可以帮助工程师们快速掌握系统的特性以及改进策略，
降低生产成本，提高工作效率。

Matlab模拟与仿真在控制系统设计中的应用引言：控制系统是现代科学技术中的重要组成部分，广泛应用于工业生产、交通运输、航空航天等领域。

控制系统的设计和优化对提高生产效率、降低能源消耗、保证安全性具有重要意义。

然而，真实系统的调试和优化需要大量的时间和成本，同时存在一定的风险。

为了克服这些困难，Matlab模拟与仿真成为了控制系统设计中不可或缺的工具。

本文将探讨Matlab模拟与仿真在控制系统设计中的应用，并深入探讨其优势和局限性。

一、Matlab在控制系统建模中的应用控制系统的建模是设计过程的关键一步，用于描述系统的物理特性和动态行为。

Matlab提供了强大的工具和函数库，可用于快速、准确地建立控制系统的数学模型。

其中最常用的是State Space（状态空间）模型和Transfer Function（传递函数）模型。

State Space模型是描述系统动态的一种方法，通过一组一阶微分方程表示系统的状态和输入输出关系。

利用Matlab，我们可以根据物理方程和参数创建State Space模型，并进行参数调整与优化。

Matlab提供了函数进行状态空间模型的系统响应分析和仿真，如step（阶跃响应）、impulse（冲击响应）等。

这使得我们能够快速评估系统的稳定性、性能和动态特性，为优化控制器提供依据。

Transfer Function模型是描述系统频率响应的一种方法，将输入和输出之间的关系表示为拉普拉斯变换的比值。

Matlab提供了一系列函数用于创建和分析传递函数模型，如tf（创建传递函数）、bode（频率响应）、nyquist（奈奎斯特图）等。

通过这些函数，我们能够快速分析系统的稳定性、频率响应和幅度相位特性，帮助我们理解系统的行为以及设计合适的控制器。

二、Matlab在控制系统仿真中的应用仿真是控制系统设计中必不可少的环节，用于模拟和验证设计的可行性和性能。

Matlab提供了完善的仿真工具，可进行开环仿真和闭环仿真。