第五章模拟信号的波形编码详解
- 格式:ppt
- 大小:2.04 MB
- 文档页数:105





第一部 各章重要习题及详细解答过程第1章 绪论1—1 设英文字母E 出现的概率为0.105,x 出现的概率为0.002。
试求E 及x 的信息量。
解:英文字母E 的信息量为105.01log 2=E I =3.25bit 英文字母x 的信息量为002.01log 2=x I =8.97bit 1—2 某信息源的符号集由A 、B 、C 、D 和E 组成,设每一符号独立出现,其出现概率分别为1/4、l/8、l/8/、3/16和5/16。
试求该信息源符号的平均信息量。
解:平均信息量,即信息源的熵为∑=-=ni i i x P x P H 12)(log )(=41log 412-81log 812-81log 812-163log 1632-165log 1652- =2.23bit/符号1—3 设有四个消息A 、BC 、D 分别以概率1/4、1/8、1/8和l/2传送,每一消息的出现是相互独立的,试计算其平均信息量。
解:平均信息量∑=-=ni i i x P x P H 12)(log )(=41log 412-81log 812-81log 812-21log 212-=1.75bit/符号1—4 一个由字母A 、B 、C 、D 组成的字。
对于传输的每一个字母用二进制脉冲编码,00代替A ,01代替B ,10代替C ,11代替D ,每个脉冲宽度为5ms 。
(1)不同的字母是等可能出现时,试计算传输的平均信息速率。
(2)若每个字母出现的可能性分别为P A =l/5,P B =1/4,P C =1/4,P D =3/10 试计算传输的平均信息速率。
解:(1)不同的字母是等可能出现,即出现概率均为1/4。
每个字母的平均信息量为∑=-=ni i i x P x P H 12)(log )(=41log 4142⨯-=2 bit/符号因为每个脉冲宽度为5ms ,所以每个字母所占用的时间为 2×5×10-3=10-2s每秒传送符号数为100符号/秒 (2)平均信息量为∑=-=ni i i x P x P H 12)(log )(=51log 512-41log 412-41log 412-103log 1032-=1.985 bit/符号平均信息速率为 198.5 比特/秒1—5 国际莫尔斯电码用点和划的序列发送英文字母,划用持续3单位的电流脉冲表示,点用持续1个单位的电流脉冲表示;且划出现的概率是点出现概率的l/3;(1)计算点和划的信息量;(2)计算点和划的平均信息量。

第五章 脉冲编码调制本章内容:● 引言● 脉冲编码调制(PCM)基本原理● 低通与带通抽样定理● 实际抽样● 模拟信号的量化● PCM编码原理引言模拟信号数字传输的步骤:(1) 把模拟信号数字化,即模数转换(A/D)(2) 数字传输(3) 把数字信号还原为模拟信号,即数模转换(D/A)。
说明:由于A/D,D/A变换的过程通常由信源编(译)码器实现,所以我们把发端的A/D变换称为信源编码,而收端的D/A变换称为信源译码,如语音信号的语音编码。
模拟信号数字化的方法:大致可划分为波形编码和参量编码两大类。
波形编码:直接把时域波形变换为数字序列,比特率通常在16kb/s~64kb/s;目前用的最普遍的Δ波形编码方法有PCM和M。
参量编码:利用信号处理技术,提高语音信号的特征参量,再变换为数字代码,起比特率在16kb/s 以下。
5.1 PCM基本原理PCM概念是1937年又法国工程师Alec Reeres最早提出来的。
脉冲编码调制简称脉码调制,是一种将模拟语音信号变换成数字信号的编码方式,主要包括:抽样、量化、编码。
图1 PCM 原理图抽样:把连续时间模拟信号转换成离散时间连续幅度的抽样信号。
量化:把离散时间连续幅度的抽样信号转换成离散时间离散幅度的数字信号。
编码:将量化后的信号编码形成一个二进制码输出。
国际标准化的PCM 码是一位码代表一个抽样值。
说明:(1)预滤波:把原始语音信号的频带(40~10000Hz 左右)限制在300~3400Hz 标准的长途模拟电话的频带内。
(2)在解调器过程中,一般采用抽样保持电路,所以LPF 均需要采用x/sinx 型频率响应以补偿抽样保持电路引入的频率失真sinx/x 。
(3)的失真主要来源于量化以及信道传输误码,通常用信号与量化噪声的功率比(S/N )来表示。
(4)PCM 编码过程是模拟信号调制一个二进制脉冲序列,载波是脉冲序列,调制改变脉冲序列的有无或“1”,“0”,所以PCM 称为脉冲编码调制。

模拟信号的基本原理和信号编码方案介绍-基础电子模拟信号是传播能量的一种形式,它指的是在时间上连续的(不间断),数值幅度大小也是连续不问断变化的信号(传统的音频信号、视频信号)。
如声波使它经过的媒体产生振动,可以以频率(以每秒的周期数或赫兹(Hz)为单位)测量声波。
通过将二进制数表示为电脉冲(其中每个脉冲是一个信号元素)使数字信号通过媒体传输。
线路上的电压在高低状态之间变化。
例如,可以采用高电平传输二进制的1,采用低电平传输二进制的0。
带宽是指每秒通过链路传输位数的术语。
图1描述了模拟和数字信号,其中模拟信号与数字信号等效。
在长距离传输时,信号由于衰减、噪声和导线束中其他导线的干扰而退化。
模拟信号可以周期性地加以放大,但是如果信号受到噪声破坏,则放大的是失真信号。
相比而言,由于可以很容易地从噪声中提取数字信号并重发,所以长距离传输数字信号更可靠。
信号编码方案数字数据传输利用PCM数字信道传输数据信号,首先要解决的问题是数据信号如何进入PCM话路的问题。
主要通过两种方式:同步方式和异步方式。
同步方式利用PCM数字信道传输数据,如果数据信号与数字端局的时钟是同步的,这时,数据终端输出的数据信号是受PCM 信道时钟控制的,因此只需对数据信号进行多路化处理即可。
这里数据终端设备处于受控制的从属地位,因此灵活性差。
如果数据信号与数据端局时钟是异步的,这时数据信号可采用填充方式复用到64kbit/s的集合信号,这就是异步方式。
如上所述,数字数据借助于电脉冲传输。
一一对应使用单脉冲表示一个位。
它的效率是非常低的,因此已经开发了多种编码方案以使用电脉冲更高效地传输数字数据。
结果大大提高了吞吐量。
这与使用旗语发送消息的情况相类似。
比如说“信号旗升起”表示1,“信号旗降下”表示O。
一种更有效的编码方案是“只在出现二进制1时升起或降下信号旗”。
例如,如果信号旗已经举起,则把它降下来。
不管信号旗是举起还是降下,它的运动才是指示器。

(第7讲)2011-04-121第五章模拟信号的数字编码25.1 概述通信系统中的编码技术:•通信系统中的编码技术-信源编码:提高通信系统的有效性;-信道编码:提高通信系统的可靠性。
•模拟信号的数字编码属于信源编码-波形编码:对统计特性分析后的信号进行编码;波形编码对统计特性分析后的信号进行编码-参量编码:直接提取信号的特征参量,对这些参量进行编码参量进行编码。
3图5.1.1模拟信号数字传输的系统框图5114图抽样与恢复5.2.168图5.2.2低通信号的抽样与恢复混叠失真:523<2时样值序列的频谱产生混叠失真图5.2.3当抽样频率w<2w m时,样值序列的频谱产生混叠失真s9从样值序列恢复原模拟信号:图5.2.1抽样与恢复10•非理想抽样和抽样保持13图5.2.4非理想抽样•实际中先用窄脉冲序列进行近似理想的的抽样,然后再经过展宽电路保持抽出的样值在脉宽内不变,从而形成平顶的样值序列,供其后的量化和编码。
图5.2.5抽样保持模型15图5.2.6平顶抽样信号的恢复带通型信号的抽样定理图5.2.8带通型信号的抽样定理18535.3幅度量化理论•量化的相关概念–量化的实质就是将连续的无限多种样值变为有限种取值,然后再用不同的数字序列表示,从而实现模/数变换。
量化级数图5.3.1量化器模型,,2,1)(1i s i m i x kT X x =<≤+若",,2,1)(is q mi y kT Y −==则:"21)()()(s s q q kT X kT Y k e =量化噪声:•量化特性–量化器的输入和输出关系就是量化器的量化特性;–均匀量化器:在整个量化范围(-V,+V)内,量化间隔都相等的量化器;–非均匀量化器:量化间隔不相等的量化器。
2321ii i x x y +=+24图5.3.2均匀量化器特性25图5.3.3均匀量化器特性2=x p 2)(图5.3.4语音信号幅度的概率密度),(m V V x −∈个均匀量化,其间有设语音信号的量化区为(第8讲)2011-04-12325.3.3 非均匀量化•均匀量化中,量化误差与被量化信号电平大小无关;量化均匀化中化差与被化信电大小关化误差的最大瞬时值等于量化间隔的一半;信号电平越低,信噪比越小。
图像编码是一项重要的技术,在数码摄影、视觉传感器、图像传输和存储等领域有着广泛的应用。
而波形编码是图像编码中常用的一种方法。
本文将详细讨论波形编码方法的原理和应用。
一、波形编码的原理波形编码是一种将图像数据转换为一系列波形的方法。
它利用图像的空间相关性,通过差分编码和熵编码来降低图像数据的冗余性,从而实现高效的数据压缩。
波形编码的第一步是差分编码。
这一步骤将图像中的每个像素与其周围像素进行比较,并记录他们之间的差异。
如果两个像素的差异很小,那么它们的波形将非常接近。
反之,如果差异很大,那么它们的波形将远离。
通过对图像中各个像素差异的记录,波形编码可以有效地减小图像数据的冗余性。
波形编码的第二步是熵编码。
它利用统计学原理对差分编码结果进行编码,实现对图像数据进一步的压缩。
常见的熵编码方法有哈夫曼编码和算术编码。
哈夫曼编码根据字符出现的概率来决定字符的编码长度,而算术编码通过将字符映射到概率区间来实现高效的编码。
熵编码可以根据差分编码的结果,生成可变长度的编码,进一步减少图像数据的冗余性。
二、波形编码的应用波形编码在图像编码中有着广泛的应用。
以下将介绍几个常见的应用场景。
1. 数码摄影在数码摄影中,波形编码被广泛用于将原始图像数据压缩为更小的文件大小。
通过差分编码和熵编码,波形编码可以实现高效的图像压缩,从而减少存储空间的使用和传输时间的消耗。
同时,波形编码可以在不影响图像质量的情况下,实现更好的图像还原效果。
2. 视觉传感器波形编码在视觉传感器中也得到了广泛的应用。
视觉传感器通常需要将捕捉到的图像数据进行传输或存储。
通过使用波形编码,可以将图像数据压缩为更小的文件,从而减少传输带宽和存储空间的使用。
这在无人机、机器人视觉和智能摄像头等领域有着重要的应用价值。
3. 图像传输和存储在图像传输和存储中,波形编码可以有效地降低图像文件的大小,减少对网络和存储介质的要求。
尤其在网络传输中,波形编码可以大大提高传输效率,从而实现更快速、更稳定的图像传输。
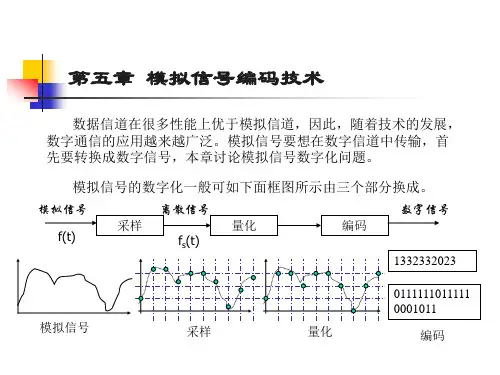
模拟信号数字化的基本原理及编码技术【实用版】目录一、引言二、模拟信号数字化的基本原理1.抽样2.量化3.编码三、模拟信号数字化的编码技术1.PCM 波形2.量化与编码示例四、模拟信号数字化的应用五、总结正文一、引言随着科技的发展,数字信号的应用已经越来越广泛。
数字信号的优势在于其抗干扰能力强,传输质量稳定,易于存储和处理。
然而,我们生活中所接触到的信号,如声音、图像等,大多都是模拟信号。
因此,如何将模拟信号转化为数字信号,已经成为了一个重要的研究课题。
模拟信号数字化的基本原理及编码技术就是为了解决这个问题。
二、模拟信号数字化的基本原理模拟信号数字化主要包括三个过程:抽样、量化和编码。
1.抽样:抽样是将连续的模拟信号在时间上离散化的过程。
抽样的目的是为了将模拟信号转化为数字信号,便于计算机处理。
抽样的间隔时间称为采样周期。
2.量化:量化是将抽样后的模拟信号在数值上离散化的过程。
量化的目的是将模拟信号的连续数值转化为有限的数字值,便于计算机存储和处理。
量化的过程通常使用 A/D 转换器来实现。
3.编码:编码是将量化后的数字信号用二进制代码表示的过程。
编码的目的是将量化后的数字信号转化为计算机能够识别和处理的二进制代码。
编码的方式有很多种,如努塞尔编码、韦弗编码等。
三、模拟信号数字化的编码技术模拟信号数字化的编码技术主要包括 PCM 波形和量化与编码示例。
1.PCM 波形:PCM 波形是一种用脉冲编码调制表示数字信号的方式。
PCM 波形可以根据不同的采样频率和量化位数来表示不同的音频、视频信号。
PCM 波形的主要优点是信号还原质量高,但是存储和传输所需的带宽较宽。
2.量化与编码示例:在实际应用中,为了节省存储空间和传输带宽,通常需要对模拟信号进行量化和编码。
例如,对于音频信号,可以使用 16 位或 24 位的量化位数来表示每个采样值,然后使用努塞尔编码或韦弗编码等方式来表示量化后的数字信号。
这样,可以大大节省存储和传输的带宽。
图像编码是一项重要的技术,它在电信、电视、多媒体等领域有着广泛应用。
而波形编码方法作为图像编码中的一种重要技术,具有独特的优势。
本文将详细介绍图像编码中的波形编码方法,探讨其原理和应用。
一、波形编码方法的原理波形编码方法是一种将图像信号转化为一系列连续波形的方法。
它充分利用了图像信号中存在的冗余信息,通过适当的压缩算法,将图像信号表示为较小的码字。
波形编码方法的核心原理是通过区分不同细节的波形形状来表达图像像素的信息,从而实现对图像的压缩和还原。
二、波形编码方法的分类波形编码方法可以分为无损压缩和有损压缩两种。
无损压缩是指通过波形编码的方式对图像信号进行压缩,同时保持图像质量不变。
无损编码方法常见的有霍夫曼编码、游程编码等。
而有损压缩则是在进行波形编码时,对图像信号的一些细节进行舍弃或者近似处理,从而达到更高的压缩比。
三、无损压缩中的波形编码方法1. 霍夫曼编码霍夫曼编码是一种经典的无损压缩方法,它通过将出现频率较高的像素值用较短的编码表示,而将出现频率较低的像素值用较长的编码表示,从而实现对图像信号的压缩。
这种方法在图像信号中存在频率较高的现象较为有效,可以获得较高的压缩比。
2. 游程编码游程编码也是一种常见的无损压缩方法,它将相同像素值连续出现的次数作为编码,从而实现对图像信号冗余信息的压缩。
游程编码方法适用于图像信号中存在大量重复像素值的情况,比如黑白图像中的背景。
四、有损压缩中的波形编码方法1. 离散余弦变换(DCT)DCT是一种常用的有损压缩方法,它通过将图像信号转化为频域信号,从而实现对图像的压缩。
离散余弦变换能够将图像信号的能量集中到少数高频系数上,而舍弃掉低频系数,从而实现更高的压缩比。
DCT广泛应用于JPEG图像压缩中。
2. 小波变换小波变换是一种具有多尺度分析能力的变换方法,它将原始图像信号分解成不同尺度的频域信号,从而实现图像的压缩。
小波变换通过将高频细节分离出来,对图像的压缩效果较好。
波形编码、参数编码和混合编码
波形编码、参数编码和混合编码是数字信号处理中常用的编码方式。
波形编码是将模拟信号离散化后,用离散的数值表示原信号波形的编码方式。
参数编码是将原信号的某些参数,如振幅、频率等,转换为数字信号的编码方式。
混合编码则是将波形编码和参数编码相结合,用于更准确地表达原信号。
波形编码有多种方式,常见的有脉冲编码调制(PCM)、$Delta$调制和$Sigma Delta$调制等。
PCM是将采样后的模拟信号用固定位数的二进制数表示,实现简单但精度有限。
$Delta$调制则是利用差分编码,将每个样本值与前一个样本值之差作为编码值,可提高精度。
$Sigma Delta$调制则是在$Delta$调制的基础上,增加了反馈环路,在时域和频域上都有优良的性能。
参数编码也有多种方式,如幅度调制(AM)、频率调制(FM)和相位调制(PM)等。
AM是将模拟信号的振幅转换为数字信号,FM是将模拟信号的频率转换为数字信号,PM则是将模拟信号的相位转换为数字信号。
这些编码方式在不同的应用场景中有着各自的优缺点。
混合编码将波形编码和参数编码相结合,可实现更准确地表达原信号。
例如$Sigma Delta$调制和FM编码结合起来,可以实现高精度、高分辨率的音频信号编码。
混合编码的实现较为复杂,但具有更高的性能和灵活性。
综上所述,波形编码、参数编码和混合编码是数字信号处理中常用的编码方式,它们各自适用于不同的信号特征和应用场景。
在实际
应用中,需根据具体情况灵活选用。
数字数据的模拟信号编码要在模拟信道上传输数字数据,首先数字信号要对相应的模拟信号进行调制,即用模拟信号作为载波运载要传送的数字数据。
载波信号可以表示为正弦波形式:f(t)=Asin(ωt+φ),其中幅度A、频率ω和相位φ的变化均影响信号波形。
因此,通过改变这三个参数可实现对模拟信号的编码。
相应的调制方式分别称为幅度调制ASK、频率调制FSK和相位调制PSK。
结合ASK、FSK和PSK可以实现高速调制,常见的组合是PSK和ASK 的结合。
1. 幅度调制幅度调制简称调幅,也称为幅移键控(ASK amplitude-shift keying)调制原理:用两个不同振幅的载波分别表示二进制值"0"和"1"。
图2-3-5 幅度调制2. 频率调制频率调制简称调频,也称为频移键控(FSK frequency-shift keying)调制原理:用两个不同频率的载波分别表示二进制值"0"和"1"。
图2-3-6 频移键控3. 相位调制(1) 绝对相移键控绝对相移键控用两个固定的不同相位表示数字“0”和“1”(见图2-3-7),用公式可表示为:U ( t ) = U m sin(ω t +π )数字“1”=U m sin(ω t + 0 )数字“0”图2-3-7 绝对相移键控(2) 相对相移键控法相对相移键控用载波在两位数字信号的交接处产生的相位偏移来表示载波所表示的数字信号。
最简单的相对调相方法是:与前一个信号同相表示数字“0”,相位偏移180度表示“1”,如图2-3-8所示。
这种方法具有较好的抗干扰性。
图2-3-8 相对相移键控数字数据的数字信号编码数字数据的数字信号编码,就是要解决数字数据的数字信号表示问题,即通过对数字信号进行编码来表示数据。
数字信号编码的工作由网络上的硬件完成,常用的编码方法有以下三种:1. 不归零码NRZ (non-return to zero )不归零码又可分为单极性不归零码和双极性不归零码。