数字图像处理第三版中文答案解析冈萨雷斯
- 格式:pdf
- 大小:4.04 MB
- 文档页数:35

23887-《数字图像处理(第3版)》习题解答(上传)(1)胡学龙编著《数字图像处理(第 3 版)》思考题与习题参考答案目录第1章概述 (1)第2章图像处理基本知识 (4)第3章图像的数字化与显示 (7)第4章图像变换与二维数字滤波 (10)第5章图像编码与压缩 (16)第6章图像增强 (20)第7章图像复原 (25)第8章图像分割 (27)第9章数学形态学及其应用 (31)第10章彩色图像处理 (32)第1章概述1.1连续图像和数字图像如何相互转换?答:数字图像将图像看成是许多大小相同、形状一致的像素组成。
这样,数字图像可以用二维矩阵表示。
将自然界的图像通过光学系统成像并由电子器件或系统转化为模拟图像(连续图像)信号,再由模拟/数字转化器(ADC)得到原始的数字图像信号。
图像的数字化包括离散和量化两个主要步骤。
在空间将连续坐标过程称为离散化,而进一步将图像的幅度值(可能是灰度或色彩)整数化的过程称为量化。
1.2采用数字图像处理有何优点?答:数字图像处理与光学等模拟方式相比具有以下鲜明的特点:1.具有数字信号处理技术共有的特点。
(1)处理精度高。
(2)重现性能好。
(3)灵活性高。
2.数字图像处理后的图像是供人观察和评价的,也可能作为机器视觉的预处理结果。
3.数字图像处理技术适用面宽。
4.数字图像处理技术综合性强。
1.3数字图像处理主要包括哪些研究内容?答:图像处理的任务是将客观世界的景象进行获取并转化为数字图像、进行增强、变换、编码、恢复、重建、编码和压缩、分割等处理,它将一幅图像转化为另一幅具有新的意义的图像。
1.4 说出图像、视频(video)、图形(drawing)及动画(animation)等视觉信息之间的联系和区别。
答:图像是用成像技术形成的静态画面;视频用摄像技术获取动态连续画面,每一帧可以看成是静态的图像。
图形是人工或计算机生成的图案,而动画则是通过把人物的表情、动作、变化等分解后画成许多动作瞬间的画幅,再用摄影机连续拍摄成一系列画面,给视觉造成连续变化的图画。

23887《数字图像处理(第3版)》习题解答(上传)(1)胡学龙编著《数字图像处理(第 3 版)》思考题与习题参考答案目录第1章概述 (1)第2章图像处理基本知识 (4)第3章图像的数字化与显示 (7)第4章图像变换与二维数字滤波 (10)第5章图像编码与压缩 (16)第6章图像增强 (20)第7章图像复原 (25)第8章图像分割 (27)第9章数学形态学及其应用 (31)第10章彩色图像处理 (32)第1章概述1.1连续图像和数字图像如何相互转换?答:数字图像将图像看成是许多大小相同、形状一致的像素组成。
这样,数字图像可以用二维矩阵表示。
将自然界的图像通过光学系统成像并由电子器件或系统转化为模拟图像(连续图像)信号,再由模拟/数字转化器(ADC)得到原始的数字图像信号。
图像的数字化包括离散和量化两个主要步骤。
在空间将连续坐标过程称为离散化,而进一步将图像的幅度值(可能是灰度或色彩)整数化的过程称为量化。
1.2采用数字图像处理有何优点?答:数字图像处理与光学等模拟方式相比具有以下鲜明的特点:1.具有数字信号处理技术共有的特点。
(1)处理精度高。
(2)重现性能好。
(3)灵活性高。
2.数字图像处理后的图像是供人观察和评价的,也可能作为机器视觉的预处理结果。
3.数字图像处理技术适用面宽。
4.数字图像处理技术综合性强。
1.3数字图像处理主要包括哪些研究内容?答:图像处理的任务是将客观世界的景象进行获取并转化为数字图像、进行增强、变换、编码、恢复、重建、编码和压缩、分割等处理,它将一幅图像转化为另一幅具有新的意义的图像。
1.4 说出图像、视频(video)、图形(drawing)及动画(animation)等视觉信息之间的联系和区别。
答:图像是用成像技术形成的静态画面;视频用摄像技术获取动态连续画面,每一帧可以看成是静态的图像。
图形是人工或计算机生成的图案,而动画则是通过把人物的表情、动作、变化等分解后画成许多动作瞬间的画幅,再用摄影机连续拍摄成一系列画面,给视觉造成连续变化的图画。

第六章6.1 给出用于产生图6.5中标为“日光”的点的红光、绿光、蓝光的百分比。
从图中可知,x=0.31,y=0.32,由x+y+z=1可得z=0.37,这是三色值系数。
我们感兴趣的是三色值XYZ。
由他们的变换公式:x = X/(X+Y+Z),y=Y/(X/Y/Z),z=Z/(X/Y/Z),可知他们的比例是相同的,故可得:X=0.31,Y=0.32,Y=0.376.2用c 表示给定的颜色,并且给出它的坐标,用(x0,y0)表示,c 和c1之间的距离以及c1和c2的距离分别为:c1占c的百分比表示为:c2的百分比用p2表示:p2=100-p1,由上面的等式我们知道,作为例子,当c=c1时,那么d(c,c1)=0,并且p1=100%,p2=0%,同样当d(c,c1)=d(c1,c2)时,p1=0%,p2=100%,从它们简单的关系中可以容易地得出它们的值。
6.5在中心点有R/2+ B/2+G= R+G+B /2 + G /2=midgray+G/2,由于增加了灰色分量和强度使人们看起来像纯绿色。
6.7 在每幅12比特图像中有4096212=种可能值。
对于灰度色彩,所有的RGB 分量必须相等,所以有4096种不同的灰度。
6.8(a )R 图像中的所有像素值都是255。
在G 图像中,第一列全是0,第二列全是1,最后一列全由255组成。
在B 图像中,第一行全为255,第二行全为254,直到最后一行全为0。
(b )(令坐标轴编号同书中图6.7(RGB 彩色立方体示意图)相同。
)则:(0,0,0)=白色,(1,1,1)=黑色,(1,0,0)=青色,(1,1,0)=蓝色,(1,0,1)=绿色,(0,1,1)=红色,(0,0,1)=黄色,(0,1,0)=深红色。
(c)不包括黑点和白点是饱和的。
在包含黑点或者白点时,饱和度会下降。
6.10 从式(6.5-5)的RGB 亮度映射函数推导出式(6.5-6)的CMY 亮度映射函数。

《数字图像处理_第三版_中_冈萨雷斯》第⼀章笔记
前⾔:没有做过系统性的学习,如何能对⼀个领域达到深究的地步。
《数字图像处理》——冈萨雷斯版只是零零碎碎的阅读过,未曾做过系统性的通读,故⽤博客记录,以便后续的巩固和温习,帖⼦只记录⼀些个⼈觉得⽐较有⽤的知识。
第⼀章笔记
数字图像处理领域
各种成像实例:伽马摄像成像、X射线成像、紫外波段成像、可见光及红外波段成像、微波波段成像、⽆线电波段成像。
超声图像成像步骤
数字图像处理的基本步骤
图像获取:图像起源
图像增强:对⼀幅图像进⾏某种操作。
图像复原:改进图像外观的处理领域,倾向于图像退化的数学或者概率模型为基础。
⼩波:不同分辨率描述图像的基础。
形态学处理:提取图像分量的⼯具,描述图像形状。
分割:将⼀幅图像划分它的组成部分或者⽬标。
图像处理系统的组成
趋势:⼤型图像处理系统朝着⼩型化和通⽤化的⼩型机并且带有专⽤图像处理硬件的混合系统的⽅向发展。

第二章2.1(第二版是0.2和1.5*1.5的矩形,第三版是0.3和1.5圆形)对应点的视网膜图像的直径x 可通过如下图题2.1所示的相似三角形几何关系得到,即()()01702302.x .d =解得x=0.06d 。
根据2.1 节内容,我们知道:如果把中央凹处想象为一个有337000 个成像单元的圆形传感器阵列,它转换成一个大小25327.⨯π成像单元的阵列。
假设成像单元之间的间距相等,这表明在总长为1.5 mm (直径) 的一条线上有655个成像单元和654个成像单元间隔。
则每个成像单元和成像单元间隔的大小为s=[(1.5 mm)/1309]=1.1×10-6 m 。
如果在中央凹处的成像点的大小是小于一个可分辨的成像单元,在我们可以认为改点对于眼睛来说不可见。
换句话说, 眼睛不能检测到以下直径的点:m .d .x 61011060-⨯<=,即m .d 610318-⨯<2.2 当我们在白天进入一家黑暗剧场时,在能看清并找到空座时要用一段时间适应。
2.1节描述的视觉过程在这种情况下起什么作用?亮度适应。
2.3 虽然图2.10中未显示,但交流电的却是电磁波谱的一部分。
美国的商用交流电频率是77HZ 。
问这一波谱分量的波长是多少?光速c=300000km/s ,频率为77Hz 。
因此λ=c/v=2.998 * 108(m/s)/77(1/s) = 3.894*106m = 3894 Km. 2.5根据图2.3得:设摄像机能看到物体的长度为x (mm),则有:500/x=35/14; 解得:x=200,所以相机的分辨率为:2048/200=10;所以能解析的线对为:10/2=5线对/mm. 2.7 假设中心在(x0,y0)的平坦区域被一个强度分布为:])0()0[(22),(y y x x Ke y x i -+--= 的光源照射。
为简单起见,假设区域的反射是恒定的,并等于1.0,令K=255。

word格式-可编辑-感谢下载支持胡学龙编著《数字图像处理(第 3 版)》思考题与习题参考答案目录第1章概述 (1)第2章图像处理基本知识 (4)第3章图像的数字化与显示 (7)第4章图像变换与二维数字滤波 (10)第5章图像编码与压缩 (16)第6章图像增强 (20)第7章图像复原 (25)第8章图像分割 (27)第9章数学形态学及其应用 (31)第10章彩色图像处理 (32)第1章概述1.1连续图像和数字图像如何相互转换?答:数字图像将图像看成是许多大小相同、形状一致的像素组成。
这样,数字图像可以用二维矩阵表示。
将自然界的图像通过光学系统成像并由电子器件或系统转化为模拟图像(连续图像)信号,再由模拟/数字转化器(ADC)得到原始的数字图像信号。
图像的数字化包括离散和量化两个主要步骤。
在空间将连续坐标过程称为离散化,而进一步将图像的幅度值(可能是灰度或色彩)整数化的过程称为量化。
1.2采用数字图像处理有何优点?答:数字图像处理与光学等模拟方式相比具有以下鲜明的特点:1.具有数字信号处理技术共有的特点。
(1)处理精度高。
(2)重现性能好。
(3)灵活性高。
2.数字图像处理后的图像是供人观察和评价的,也可能作为机器视觉的预处理结果。
3.数字图像处理技术适用面宽。
4.数字图像处理技术综合性强。
1.3数字图像处理主要包括哪些研究内容?答:图像处理的任务是将客观世界的景象进行获取并转化为数字图像、进行增强、变换、编码、恢复、重建、编码和压缩、分割等处理,它将一幅图像转化为另一幅具有新的意义的图像。
1.4 说出图像、视频(video)、图形(drawing)及动画(animation)等视觉信息之间的联系和区别。
答:图像是用成像技术形成的静态画面;视频用摄像技术获取动态连续画面,每一帧可以看成是静态的图像。
图形是人工或计算机生成的图案,而动画则是通过把人物的表情、动作、变化等分解后画成许多动作瞬间的画幅,再用摄影机连续拍摄成一系列画面,给视觉造成连续变化的图画。

第二章2.1(第二版是0.2和1.5*1.5的矩形,第三版是0.3和1.5圆形)对应点的视网膜图像的直径x 可通过如下图题2.1所示的相似三角形几何关系得到,即()()01702302.x .d =解得x=0.06d 。
根据2.1 节内容,我们知道:如果把中央凹处想象为一个有337000 个成像单元的圆形传感器阵列,它转换成一个大小25327.⨯π成像单元的阵列。
假设成像单元之间的间距相等,这表明在总长为1.5 mm (直径) 的一条线上有655个成像单元和654个成像单元间隔。
则每个成像单元和成像单元间隔的大小为s=[(1.5 mm)/1309]=1.1×10-6 m 。
如果在中央凹处的成像点的大小是小于一个可分辨的成像单元,在我们可以认为改点对于眼睛来说不可见。
换句话说, 眼睛不能检测到以下直径的点:m .d .x 61011060-⨯<=,即m .d 610318-⨯<2.2 当我们在白天进入一家黑暗剧场时,在能看清并找到空座时要用一段时间适应。
2.1节描述的视觉过程在这种情况下起什么作用?亮度适应。
2.3 虽然图2.10中未显示,但交流电的却是电磁波谱的一部分。
美国的商用交流电频率是77HZ 。
问这一波谱分量的波长是多少?光速c=300000km/s ,频率为77Hz 。
因此λ=c/v=2.998 * 108(m/s)/77(1/s) = 3.894*106m = 3894 Km. 2.5根据图2.3得:设摄像机能看到物体的长度为x (mm),则有:500/x=35/14; 解得:x=200,所以相机的分辨率为:2048/200=10;所以能解析的线对为:10/2=5线对/mm. 2.7 假设中心在(x0,y0)的平坦区域被一个强度分布为:])0()0[(22),(y y x x Ke y x i -+--= 的光源照射。
为简单起见,假设区域的反射是恒定的,并等于1.0,令K=255。

第二章(第二版是和* 的矩形,第三版是和圆形)对应点的视网膜图像的直径x 可通过如下图题所示的相似三角形几何关系得到,即d 2 x 20.30.017解得x=。
根据节内容,我们知道:如果把中央凹处想象为一个有337000 个成像单元的圆形传感器阵列,它转换成一个大小327.52 成像单元的阵列。
假设成像单元之间的间距相等,这表明在总长为 1.5 mm(直径)的一条线上有655 个成像单元和654 个成像单元间隔。
则每个成像单元和成像单元间隔的大小为s=[(1.5 mm)/1309]=× 10-6 m。
如果在中央凹处的成像点的大小是小于一个可分辨的成像单元,在我们可以认为改点对于眼睛来说不可见。
换句话说,眼睛不能检测到以下直径的点:x 0.06d 1.1 10 6 m ,即 d 18.3 10 6 m当我们在白天进入一家黑暗剧场时,在能看清并找到空座时要用一段时间适应。
节描述的视觉过程在这种情况下起什么作用亮度适应。
虽然图中未显示,但交流电的却是电磁波谱的一部分。
美国的商用交流电频率是 77HZ。
问这一波谱分量的波长是多少光速 c=300000km/s ,频率为 77Hz。
因此λ =c/v= * 10 8(m/s)/77(1/s) = *10 6m = 3894 Km.根据图得:设摄像机能看到物体的长度为x (mm),则有 :500/x=35/14; 解得: x=200 ,所以相机的分辨率为: 2048/200=10; 所以能解析的线对为:10/2=5 线对 /mm.假设中心在( x0,y0 )的平坦区域被一个强度分布为:i (x, y) Ke [( x x 0) 2 ( y y 0) 2 ] 的光源照射。
为简单起见,假设区域的反射是恒定的,并等于,令 K=255。
如果图像用 k 比特的强度分辨率进行数字化,并且眼睛可检测相邻像素间 8 种灰度的突变,那么 k 取什么值将导致可见的伪轮廓解:题中的图像是由:f x, y i x, y r x, y 255e x x02 y y0 2255ex x0 2 y y0 21.0一个截面图像见图(a)。
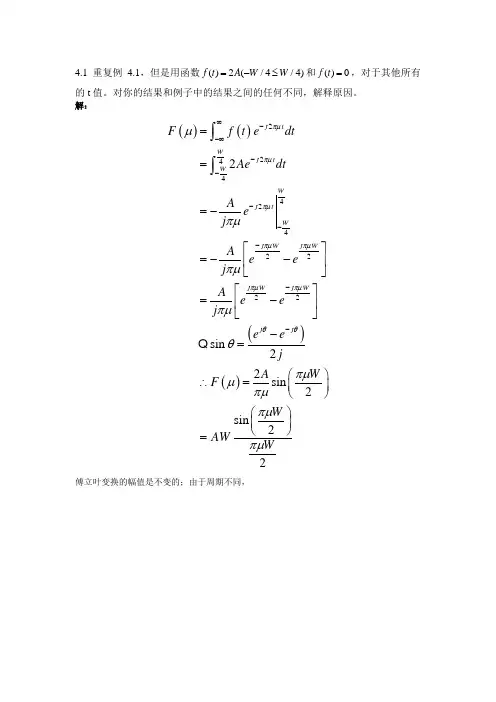
4.1 重复例4.1,但是用函数()2(/4/4)f t A W W =-≤和()0f t =,对于其他所有的t 值。
对你的结果和例子中的结果之间的任何不同,解释原因。
解:()()()()224442422222sin 22sin 2sin 22j tWj tW Wj tW j Wj W j W j Wj j F f t e dtA edtA ej A ee j A e ej ee jAW F W A WWπμπμπμπμπμπμπμθθμπμπμπμθπμμπμπμπμ∞--∞-------===-⎡⎤=--⎢⎥⎣⎦⎡⎤=-⎢⎥⎣⎦-=⎛⎫∴=⎪⎝⎭⎛⎫ ⎪⎝⎭=⎰⎰傅立叶变换的幅值是不变的;由于周期不同,4.2 证明式(4.4-2)()()()()()()~~2222j tj tn j tn j n Ttn n F f t edtf t t n T edt f t t n T edt f eπμπμπμπμμδδ∞--∞∞∞--∞=-∞∞∞--∞=-∞∞-∆=-∞==-∆=-∆=⎰∑⎰∑⎰∑中的()~F μ在两个方向上是无限周期的,周期为1/T ∆证明:(1) 要证明两个方向上是无限周期1/T ∆,只需证明根据如下式子:可得:其中上式第三行,由于k, n 是整数,且和的极限是关于原点对称。
(2) 同样的需要证明根据如下式子:()()()()()()~~2222j tj tn j tn j n Ttn n F f t edtf t t n T edt f t t n T edt f eπμπμπμπμμδδ∞--∞∞∞--∞=-∞∞∞--∞=-∞∞-∆=-∞==-∆=-∆=⎰∑⎰∑⎰∑可得:其中第三行由于k, n 都为整数,所以21j kneπ-=。
4.3 可以证明(Brancewell[2000])1()1()t t δδ⇔⇔和。
使用前一个性质和表4.3中的平移性质,证明连续函数()cos(2)f t nt π=的傅立叶变换是()()()()1/2F n n μδμδμ=++-⎡⎤⎣⎦,其中是一个实数。


1. 数字数据传输通常用波特率度量,其定义为每秒钟传输的比特数。
通常的传输是以一个开始比特,一个字节(8 比特)的信息和一个停止比特组成的包完成的。
基于这个概念回答以下问题:(a) 用56K 波特的调制解调器传输一幅1024×1024、256 级灰度的图像需要用几分钟?(b) 以750K 波特[这是典型的电话DSL(数字用户线)连接的速度]传输要用多少时间?解:(a)T=M/56000=(1024×1024)×(8+2)/56000=187.25s=3.1min(b) T=M/56000=(1024×1024)×(8+2)/750000=14s2.两个图像子集S1和S2图下图所示。
对于V={1},确定这两个子集是(a)4-邻接,(b)8-邻接,(c)m-邻接。
a) S1 和S2 不是4 连接,因为q 不在N4(p)集中。
(b) S1 和S2 是8 连接,因为q 在N8(p)集中。
(c) S1 和S2 是m 连接,因为q 在集合N D(p)中,且N4(p)∩ N4(q)没有V 值的像素3. 考虑如下所示的图像分割(a) 令V={0,1}并计算p 和q 间的4,8,m 通路的最短长度。
如果在这两点间不存在特殊通路,试解释原因。
(b) 对于V={1,2}重复上题。
解:(a) 当V={0,1}时,p 和q 之间不存在4 邻接路径,因为不同时存在从p 到q 像素的4 毗邻像素和具备V 的值,如图(a)p 不能到达q。
8 邻接最短路径如图(b),最短长度为4。
m邻接路径如图(b)虚线箭头所示,最短长度为5。
这两种最短长度路径在此例中均具有唯一性。
(b) 当V={1, 2}时,最短的4 邻接通路的一种情况如图(c)所示,其长度为6,另一种情况,其长度也为6;8 邻接通路的一种情况如图(d)实线箭头所示,其最短长度为4;m 邻接通路的一种情况如图(d)虚线箭头所示,其最短长度为6.或解: (1) 在V={0,1}时,p和q之间通路的D4距离为∞,D8距离为4,Dm距离为5。
胡学龙编著《数字图像处理(第 3 版)》思考题与习题参考答案目录第1章概述 (1)第2章图像处理基本知识 (4)第3章图像的数字化与显示 (7)第4章图像变换与二维数字滤波 (10)第5章图像编码与压缩 (16)第6章图像增强 (20)第7章图像复原 (25)第8章图像分割 (27)第9章数学形态学及其应用 (31)第10章彩色图像处理 (32)第1章概述1.1连续图像和数字图像如何相互转换?答:数字图像将图像看成是许多大小相同、形状一致的像素组成。
这样,数字图像可以用二维矩阵表示。
将自然界的图像通过光学系统成像并由电子器件或系统转化为模拟图像(连续图像)信号,再由模拟/数字转化器(ADC)得到原始的数字图像信号。
图像的数字化包括离散和量化两个主要步骤。
在空间将连续坐标过程称为离散化,而进一步将图像的幅度值(可能是灰度或色彩)整数化的过程称为量化。
1.2采用数字图像处理有何优点?答:数字图像处理与光学等模拟方式相比具有以下鲜明的特点:1.具有数字信号处理技术共有的特点。
(1)处理精度高。
(2)重现性能好。
(3)灵活性高。
2.数字图像处理后的图像是供人观察和评价的,也可能作为机器视觉的预处理结果。
3.数字图像处理技术适用面宽。
4.数字图像处理技术综合性强。
1.3数字图像处理主要包括哪些研究内容?答:图像处理的任务是将客观世界的景象进行获取并转化为数字图像、进行增强、变换、编码、恢复、重建、编码和压缩、分割等处理,它将一幅图像转化为另一幅具有新的意义的图像。
1.4 说出图像、视频(video)、图形(drawing)及动画(animati on)等视觉信息之间的联系和区别。
答:图像是用成像技术形成的静态画面;视频用摄像技术获取动态连续画面,每一帧可以看成是静态的图像。
图形是人工或计算机生成的图案,而动画则是通过把人物的表情、动作、变化等分解后画成许多动作瞬间的画幅,再用摄影机连续拍摄成一系列画面,给视觉造成连续变化的图画。
数字图像处理第三版中文答案解析引言《数字图像处理》是一本经典的图像处理教材,目前已经出版了第三版。
本文是对该书答案解析的总结,将分析和解释书中的问题和答案。
目录•第一章:绪论•第二章:数字图像基础•第三章:灰度变换•第四章:空间滤波•第五章:频域滤波•第六章:图像复原•第七章:几何校正•第八章:彩色图像处理•第九章:小波与多分辨率处理第一章:绪论本章主要介绍了数字图像处理的概念和基本步骤。
答案解析中包括对一些基本概念和术语的解释,以及相关的数学公式和图像处理方法的应用。
第二章:数字图像基础本章介绍了数字图像的表示和存储方法,以及图像的采样和量化过程。
答案解析中详细解释了图像的像素值和灰度级之间的关系,以及采样频率和量化步长对图像质量的影响。
第三章:灰度变换本章讲述了图像的灰度变换方法,包括线性和非线性变换。
答案解析中对不同灰度变换函数的作用和效果进行了解释,并给出了一些实例和应用。
第四章:空间滤波本章介绍了图像的空间滤波方法,包括平滑和锐化滤波。
答案解析中解释了不同滤波器的原理和效果,并给出了滤波器设计的步骤和实例。
第五章:频域滤波本章讲述了图像的频域滤波方法,包括傅里叶变换和滤波器设计。
答案解析中详细解释了傅里叶变换的原理和应用,以及频域滤波器的设计方法和实例。
第六章:图像复原本章介绍了图像的复原方法,包括退化模型和复原滤波。
答案解析中详细解释了退化模型的建立和复原滤波器的设计方法,以及如何根据退化模型进行图像复原的实例。
第七章:几何校正本章讲述了图像的几何校正方法,包括图像的旋转、缩放和平移等操作。
答案解析中给出了不同几何变换的矩阵表示和变换规则,以及几何校正的应用实例。
第八章:彩色图像处理本章介绍了彩色图像的表示和处理方法,包括RGB和HSV 等颜色模型的转换和处理。
答案解析中详细解释了不同颜色模型的表示和转换方法,以及彩色图像处理的实例和应用。
第九章:小波与多分辨率处理本章讲述了小波和多分辨率处理的方法和应用。
4.16 证明连续和离散二维傅里叶变换都是平移和旋转不变的。
首先列出平移和旋转性质:002(//)00(,)(,)j u x M v y N f x y e F u u v v π+⇔-- (4.6-3) 002(//)00(,)(,)j x r M y v N f x x y y F u v e π-+--⇔ (4.6-4)旋转性质:cos ,sin ,cos ,sin x r y r u v θθωϕωϕ====00(,)(,)f r F θθωϕϕ+⇔+ (4.6-5) 证明:由式(4.5-15)得:由式(4.5-16)得:依次类推证明其它项。
4.17 由习题4.3可以推出1(,)u v δ⇔和(,)1t z δ⇔。
使用前一个性质和表4.3中的平移性质证明连续函数00(,)cos(22)f t z A u t v z ππ=+的傅里叶变换是0000(,)[(,)(,)]2AF u v u u v v u u v v δδ=+++-- 证明:000000002()2()002()2()2()2()2()2()2((,)(,)cos(22)[]222j ut vz j ut vz j u t v z j u t v z j ut vz j u t v z j u t v z j ut vz j u F u v f t z e dtdzA u t v z e dtdzA e e e dtdzA A e e dtdz e e πππππππππππ∞∞-+-∞-∞∞∞-+-∞-∞∞∞+-+-+-∞-∞∞∞+-+-+--∞-∞==+=+=+⎰⎰⎰⎰⎰⎰⎰⎰)00000000(,)(,)22[(,)(,)]2t vz dtdz A Au u v v u u v v Au u v v u u v v δδδδ∞∞+-∞-∞=--+++=--+++⎰⎰ 4.18 证明离散函数(,)1f x y =的DFT 是1,0{1}(,)0,u v u v δ==⎧ℑ==⎨⎩其它证明:离散傅里叶变换112(//)00(,)(,)M N j ux M vy N x y F u v f x y e π---+===∑∑112(//)00112(//)00{1}M N j ux M vy N x y M N j ux M vy N x y e e ππ---+==---+==ℑ==∑∑∑∑如果0u v ==,{1}1ℑ=,否则:1100{1}{cos[2(//)]sin[2(//)]}M N x y ux M vy N j ux M vy N ππ--==ℑ=+-+∑∑考虑实部,1100{1}cos[2(//)]M N x y ux M vy N π--==ℑ=+∑∑,cos[2(//)]ux M vy N π+的值介于[-1, 1],可以想象,1100{1}cos[2(//)]0M N x y ux M vy N π--==ℑ=+=∑∑,虚部相同,所以1,0{1}(,)0,u v u v δ==⎧ℑ==⎨⎩其它4.19 证明离散函数00cos(22)u x v y ππ+的DFT 是00001(,)[(,)(,)]2F u v u Mu v Nv u Mu v Nv δδ=+++--证明:000000112(//)00112(//)0000112()2()2(//)00112()2(//)00(,)(,)cos(22)1[]21{2M N j ux M vy N x y M N j ux M vy N x y M N j u x v y j u x v y j ux M vy N x y M N j u x v y j ux M vy N x y F u v f x y e u x v y e e e e e e πππππππππ---+==---+==--+-+-+==--+-+====+=+=∑∑∑∑∑∑∑∑000000112()2(//)0011112(//)2(//)2(//)2(//)00000000}1{}21[(,)(,)]2M N j u x v y j ux M vy N x y M N M N j Mu x M Nv y N j Mu x M Nv y N j ux M vy N j ux M vy N x y x y e e e e e e u Mu v Nv u Mu v Nv ππππππδδ---+-+==----+-+-+-+====+=+=+++--∑∑∑∑∑∑4.20 下列问题与表4.1中的性质有关。
Al l t h d fo rs 2.5根据图2.3得:设摄像机能看到物体的长度为x (mm),则有:500/x=35/14; 解得:me an dAi nt he i rb ei n ga re go 包括起始比特和终止比特)为:N=n+m=10bits 。
对于一幅e an dAl l t h i ng si nt he i rb ei n ga re go od fo 特的图像。
又因为90min 为5400 秒,故储存90min 的电视节目所需的空间是:s.bits .byte 10001110062854003038192010801212⨯=⨯=⨯⨯⨯⨯⨯2.11解:p 和q 如图所示:(a) 和不是4 邻接,因为q 不在集中。
1S 2S ()p N 4 (b) 和是8 连接,因为q 在集。
1S 2S ()p N 8 (c) 和是m 连接,因为q 在集合中,且没有V 值的像素。
1S 2S ()p N D ()()q N p N 44 2.12 提出将一个像素宽度的8通路转换为4通路的一种算法。
解:找出一个像素点的所有邻接情况,将对角元素转化成相应的四邻接元素。
如下图所示:2.13 提出将一个像素宽度的m 通路转换为4通路的一种算法。
解:把m 通道转换成4 通道仅仅只需要将对角线通道转换成4 通道,由于m 通道是8 通道与4 通道的混合通道,4 通道的转换不变,将8 通道转换成4 通道即可。
如图所示:(1) 4 邻域关系不变(2) 8 领域关系变换如下图所示e an dAl l t h i ng si nt he i rb ei n ga re go od fo rs o 2.15 (没答案,自己做的,看对不对)(1) 在V ={0,1,2}时,p 和q 之间通路的D 4距离为8(两种情况均为8),D 8距离为4,D m 距离为6。
(2) 在V ={2,3,4}时,p 和q 之间通路的D 4距离为∞,D 8距离为4,D m 距离为5。
p 和q 之间不存在4 邻接路径,因为不同时存在从p 到q 像素的4 毗邻像素和具备V 的值,情况如图(a)所示。
p 不能到达q 。
2.16t he i rb ei n ge an dAl l t h i ng si nt he i rb ei n ga re go od fo rs o 范文范例 学习参考2.19(两个版本答案,一个意思)(1)中值ζ表示,数集的一半数值比它大,另一半比它小。
一个简单的例子能够表明,Eq.(2.6 - 1)的平均算子操作。
让 S1 = {1,-2,3}, S2 = {4,5, 6}, a = b = 1. 在这种情况下,H 是平均算子。
然后有H(S1 + S2)=中值{ 5,3,9 } = 5,S1 + S2是S1和S2的和。
接下来,计算H(S1)=中值{ 1、-2、3 } =1和H(S2)=中值{ 4、5、6 } = 5。
然后,从H(aS1 + bS2)≠aH(S1)+ bH(S2),因此,子图像区域S 中值的算子是非线性的。
(2)2.20e an dAl l th i ng si nt he i rb ei (a) 为A 的补集(b) CB A ()()C B B Ae an dAl l th i ng si nt he i rb ei n ga re go od fo rs o 答:使用三角区即三个约束点,所以我们可以解决以下的系数为6的线性方程组:654321c y c x c y c y c x c x ++='++='实施空间变换。
插值强度可使用2.4.4节的方法。
2.25(看看翻的对不对)傅里叶变换核是可分的,因为:()()()()()()v ,y r u ,x r e e e v ,u ,y ,x r N /vy j M /ux j N /vy M /ux j 21222===--+-πππ傅里叶变换核是对称的,因为:()()()()()v ,y r u ,x r e e e N /vy j M /ux j N /vy M /ux j 11222==--+-πππ2.26(看看翻的对不对)由可分离变换核的定义知其中:当x 值固定时,可看作f(x,y)某一行的一维变换,当x 从0变换到M-1时计算出整个数组T (x,v ),然后,通过替换这个数组的最后一行以前的方程我们可以得到T (x,v )按列的一维变换。
也就是说,当一个图像是内核可分的,我们可以计算图像沿行的一维变换,然后我们计算中间的一列得到最终的二维变换T(u,v).这和先计算列的一维变换再计算中间行得到二维变换最终结果是相同的。
从式(2.6-33),二维傅里叶变换是由:它很容易验证,傅立叶变换核是可分离的(参见题2.25),所以我们可以写这个方程:t h i ng si nt he i rb ei n ga re go od fo rs o 是沿着f(x,y)行的一维傅里叶变换,X= 0,1,……,M-1。
at e an dAl l t h i ng si nt he i rb ei n ga re go od fo rs o(a )由,得:,2)(Kr Ae r T s -==3/20A Ae KL =-)3/1ln(20=-KL 2/0986.1L K =2200986.1)(r L Aer T s -==(b )、由, 得:4/)1(20B eKL =--B ,)4/3ln(20=-KL 20/2877.0L K =)1()(2202877.0r L eB r T s --==(c )、3.4逐次查找像素值,如(x ,y )=(0,0)点的f (x ,y )值。
若该灰度值的4比特的第0位是1,则该位置的灰度值全部置1,变为15;否则全部置0,变为0。
因此第7位平面[0,7]置0,[7,15]置1,第6位平面[0,3],[4,7]置0,[8,11],[12,15]置15。
依次对图像的全部像素进行操作得到第0位平面,若是第i 位平面,则该位置的第i 位值是0还是1,若是1,则全置1,变为15,若是0,则全置0设像素的总数为n ,是输入图像的强度值,由,,所以,由和得由此得知,第二次直方图均衡化处理的结果与第一次t i me an Al l h i ng b ei n ga re go od fo rs ,dw w p z G v zz )()(0⎰==⎩⎨⎧=<<-5.00415.044)( w ww wz w p {5.00215.0221022)()(<<<<+-===⎰z z z z z zz dw w p z G v 令得v s =⎪⎧⎪⎧-<<+-±±5.01022r r r v (k=0,1,2,……K-1)成:(k=0,1,2,……K-1)(k=0,1,2,……K-1)。
变量是噪声的简单抽样,它i nt he i rb ei n ga re go od fo 的方差是。
因此并且我们可以得到。
上述过(A )中值是的最大值]2/)1[(2+=n ζ(B )一旦中值被找出,我们简单的删除邻域边缘的值,在合适的位置插入合适的值旋转前坐标的拉普拉斯定义为,旋转后坐标的拉普拉斯定义为22222y fx f f ∂∂+∂∂=∇,现在给出,其中指2'22'22yfx f f ∂∂+∂∂=∇θθθθcos sin sin cos ,,,,y x y y x x +=-=和θ轴旋转的角度,若想证明拉普拉斯变换是各向同性的,只需证明2222f f f f ∂∂∂∂ff y f x f f ∂∂∂∂∂∂∂t h i ng b ei n ga re go od f其中是预先确定的临域的平均数,更确切的说就是以为中心并且包),(_y x f ),(y x f ),(y xdAl l t h i ng si nt he i rb e4.2证明式(4.4-2)中的()()()()()()~~2222j t j t n j t n j n Ttn n F f t e dtf t t n T e dtf t t n T e dt f e πμπμπμπμμδδ∞--∞∞∞--∞=-∞∞∞--∞=-∞∞-∆=-∞==-∆=-∆=⎰∑⎰∑⎰∑在两个方向上是无限周期的,周期为()~F μ1/T∆证明:(1)要证明两个方向上是无限周期,只需证明1/T ∆根据如下式子:可得:其中上式第三行,由于k, n 是整数,且和的极限是关于原点对称。
Al l th i ng si nt he i rb ei n ga re go od fo rs o (2)同样的需要证明根据如下式子:()()()()()()~~2222j t j tn j t n j n Ttn n F f t e dtf t t n T edtf t t n T e dtf e πμπμπμπμμδδ∞--∞∞∞--∞=-∞∞∞--∞=-∞∞-∆=-∞==-∆=-∆=⎰∑⎰∑⎰∑可得:其中第三行由于k, n 都为整数,所以。
21j kneπ-=4.3可以证明(Brancewell[2000])。
1()1()t t δδ⇔⇔和使用前一个性质和表4.3中的平移性质,证明连续函数的傅立()cos(2)f t nt π=叶变换是,其中是一个实数。
()()()()1/2F n n μδμδμ=++-⎡⎤⎣⎦证明:根据一维傅里叶变换公式:h i ng si nt h可得:⎰⎰-∞∞--∞∞-==dte nt dte tf ut j ut j πππ22)2cos( )(F(u)an dAl l t h i ng si nt he i rb ei n ga re go od fo rs o 范文范例 学习参考滤器,将允许重建如果该正弦函数进行采样,采样定理满意)。
4.8解:(a)根据正交性,将式(4.4-5)直接代入式(4.4-4)得最后一步是根据问题的陈述中给出的正交条件,将式(4.4-4)代入式(4.6-5)应用同样的过程生成的相似特性。
n f (b)如上小题,根据正交性,将式(4.4-7)直接代入式(4.4-6)得最后一步是根据问题的陈述中给出的正交条件,将式(4.4-6)代入式(4.6-7)应用同样的过程生成的相似特性。
()f x 4.9证明式(4.4-8) 和式(4.4-9) 的正确性。
()()F u kM F u +=()()f x kM f x +=证明:(1)证明等式()()k 0,1, 2...F u kM F u +==±±将代入4.4.6式 :u u kM =+()12/0(),0,1,2,,1M j ux Mn F u f x eu M π--===-∑ ()12()/012/20() () F(u)M j u kM x M n M j ux M j kxn F u kM f x e f x e eπππ--+=---=+=⎡⎤=⎢⎥⎣⎦=∑∑e an dAl l t h i ng si nt 范文范例 学习参考()()()()1112/00112/0012/012/0()() () () ()() ()() M M j ux Mx m M M j ux M m x M j um Mm M j um Mm F u H u F m H t m eF m H t m e F m h x e h x f m e h x f x ππππ---==--==-=-=⎡⎤ℑ*=-⎡⎤⎣⎦⎢⎥⎣⎦⎡⎤=-⎢⎥⎣⎦===∑∑∑∑∑∑4.11 写出二维连续卷积的表达式对4.2.20式进行卷积运算得到:f(t,z)h(t,z)(,)(,)f h t z d d αβαβαβ∞∞-∞-∞*=--⎰⎰4.14 证明一维连续和离散傅里叶变换都是线性操作解:若连续傅里叶变换是线性的,只需证明:代入傅立叶变换定义其中第二步由于积分的分配率。