第6章 气象上常用小波及其应用
- 格式:doc
- 大小:800.50 KB
- 文档页数:11

小 波 分 析 及 应 用第一部分 引 言小波分析及应用傅立叶分析的有效性19世纪,傅立叶变换把时间域与频率域联系起来,用信号的频谱特性去分析时域内难以看清的问题,解决了很多物理和工程学方面的问题。
这个突破使得科学家们和工程师们开始考虑如何将傅立叶变换作为分析各种现象的最佳工具。
这种普遍性迫使人们开始进一步研究这种方法。
问题及大胆设想直到20世纪即将结束时,数学家、物理学家和工程师们才开始认识到傅立叶变换的缺点:它们在分析短时信号或突变信号时,效果并不理想。
在整个20世纪的过程中,各个领域的科学家们都试图突破上述这些障碍。
从本质上讲,科学家们往往想同时获取到低分辨率的森林——重复的背景信号;以及高分辨率的树——个体的、在背景上的局部变化。
他们提出了大胆的设想:也许通过将一个信号分割成并非纯正弦波的元素,就可以同时在时间和频率两方面对信息进行描述。
问题的解决小波变换是傅里叶变换的新发展,它既保留了傅里叶变换的优点,又弥补了傅里叶变换在信号分析上的一些不足。
原则上讲,小波变换适用于以往一切傅里叶变换应用的领域。
但小波变换并不是万能的,作为一种数学工具,小波变换(分析)有其特定的应用范围,即面向更能发挥小波分析优势的时间—频率局域性问题。
本课程的内容安排理论部分第二部分从傅里叶变换开始,沿着傅里叶变换→短时傅里叶变换→小波变换的发展轨迹,从物理直观的角度对其逐一进行介绍,引出小波变换的概念;然后对小波变换的基本理论进行了详细的讲解;第三部分首先介绍多分辨分析和多分辨率滤波器组的概念,在此基础上讲解由滤波器组系数构造小波基的方法,最后给出对信号和图像进行小波变换的Mallat算法;第四部分介绍小波理论的最新进展和发展方向:多小波;M带小波和提升框架等;应用部分第五部分在给出小波域滤波基本原理的基础上,介绍三种小波滤波方法——模极大值重构滤波、空域相关滤波和基于阈值的小波域滤波方法,并对这三种方法进行分析和比较;第六部分对经典小波滤波方法的改进、较新的进展及发展趋势进行介绍;第七部分对目前国内外小波分析软件应用领域的情况进行总结,着重介绍我们开发的小波分析领域通用信号处理软件系统——“小波软体”(Wavesoft),对其安装、运行、操作进行说明、演示;最后给出几个小波滤波方法的应用实例。



第6章 气象上常用小波及其应用实例(1)前面五章讲述了小波分析方法的由来和原理,这些基本知识为气象上实际应用奠定了基础。
本章将介绍气象上常用的几种小波,特别是Haar 小波和墨西哥帽(Mexihat )小波,以及小波分析的应用实例。
6.1 二进小波二进小波的产生基于第4章的“二分法”。
它的基本思路是把连续型函数)(t f 及其连续小波变换),(b a W f 离散化,以便于实际应用。
作为一种方便和常用的形式,是对小波参数中的放(伸)缩因子a 进行二进制离散。
若小波函数系的表达式{}Zm,n n t am∈-- ),(ψ(••) 中的放缩因子)(2Z j a j ∈=,则称)(t ψ为二进小波。
把经过这种离散化后的二进小波的变换,称为二进小波变换。
强调说明:在应用时所用的小波函数系(式(••))与前面第4章第3节的式(•)有所不同。
比照这两式:),()(),2(2)(,2/,b at a t k t t b a jj kj -=-=ψψψψ或(•)),()(,n t at mn m -=-ψψ(••) 可以看出,二者主要的不同点是t 的系数a 指数正负号恰好相反。
所以,用式(•)的小波作变换时,随着a (或者j )的增大,W 曲线变窄;而用式(••)的小波作变换时,随着a (或者j )的增大,W 曲线变宽。
定义6.1 函数)()(2R L t ∈ψ被称为二进小波,若存在两个常数∞<≤<B A 0,使得:∑∈-≤≤Zj j B A .)2(ˆ2ωψ(6.1)上述条件式(6.1)称为稳定性条件;若A =B ,则称最稳定条件。
而函数序列{}Zj j f W ∈2称为二进小波变换,其中,,d 2)(21)()(22b b t t f t f t f W Rjjjj ⎰⎪⎭⎫⎝⎛-=*=ψψ(6.2)这里j a 2=是放缩因子,b 是平移因子。
由卷积定理知:)2(ˆ)(ˆ)(ˆ2ωψωωj f f W j ⋅= (6.3) 据此,稳定性条件等价于:对任意)()(2R L t f ∈,有:∑∈≤≤Zj fB fW fA j 2020220(6.4)下面定理说明,二进小波一定是允许小波。

小波变换及其应用
小波变换是一种多尺度分析的信号处理技术,可以将信号分解为不同
频率和时间尺度的小波分量,从而提供了更全面的信息,具有很广泛的应用。
以下为小波变换的主要应用:
1.信号压缩:小波变换具有如同离散余弦变换(DCT)、小波重构等
变换可压缩性,可以通过选取一定的小波基,剔除高频噪声等方法将信号
压缩到较小的尺寸。
2.信号去噪:小波变换能够将信号分解为多个尺度和频段的小波系数,因而,小波变换可以应用于信号去噪。
在小波域中对噪声尺度和频段进行
分析和滤波,可有效地去除噪声,使信号更加真实。
3.图像处理:小波变换可以将图像分为低频和高频两个部分,分别表
示图像中大面积变化和微小变化的部分。
图像压缩往往采用这种特性进行
处理。
4.音频处理:小波变换也是音频处理领域中广泛应用的技术。
对语音
信号进行小波分析,可以提取其频率、语气、声调信息等,为音频处理提
供更多信息。
5.金融数据分析:小波变换也被广泛应用于金融领域中,用于对金融
数据进行分析和预测。
通过小波分解,可以提取出不同的时间尺度和频率
对应的信息,进一步了解金融市场的趋势和波动情况。
总之,小波变换在信号处理、图像处理、音频处理、金融领域等方面
都具有广泛的应用。

第六章 小波变换的几个典型应用6.1 小波变换与信号处理小波变换作为信号处理的一种手段,逐渐被越来越多领域的理论工作者和工程技术人员所重视和应用,并在许多应用中取得了显著的效果。
同传统的处理方法相比,小波变换取得了质的飞跃,在信号处理方面具有更大的优势。
比如小波变换可以用于电力负载信号的分析与处理,用于语音信号的分析、变换和综合,还可以检测噪声中的未知瞬态信号。
本部分将举例说明。
6.1.1 小波变换在信号分析中的应用[例6-1] 以含躁的三角波与正弦波的组合信号为例具体说如何利用小波分析来分析信号。
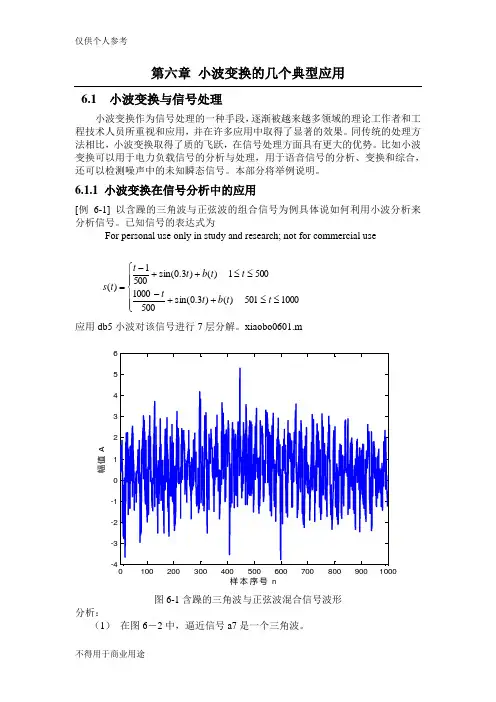
已知信号的表达式为For personal use only in study and research; not for commercial use⎪⎪⎩⎪⎪⎨⎧≤≤++-≤≤++-=1000501)()3.0sin(50010005001)()3.0sin(5001)(t t b t t t t b t t t s应用db5小波对该信号进行7层分解。
xiaobo0601.m1002003004005006007008009001000-4-3-2-10123456样本序号 n幅值 A图6-1含躁的三角波与正弦波混合信号波形分析:(1) 在图6-2中,逼近信号a7是一个三角波。
(2) 在图6-3中细节信号d1和d2是与噪声相关的,而d3(特别是d4)与正弦信号相关。
01002003004005006007008009001000-101a 701002003004005006007008009001000-202a 601002003004005006007008009001000-202a 501002003004005006007008009001000-202a 401002003004005006007008009001000-505a 301002003004005006007008009001000-505a 2010*******4005006007008009001000-505a 1样本序号 n图6-2 小波分解后各层逼近信号01002003004005006007008009001000-101d 701002003004005006007008009001000-101d 601002003004005006007008009001000-101d 501002003004005006007008009001000-202d 401002003004005006007008009001000-202d 301002003004005006007008009001000-202d 2010*******4005006007008009001000-505d 1样本序号 n图6-3 小波分解后各层细节信号6.1.2 小波变换在信号降躁和压缩中的应用一、信号降躁1.工程中,有用信号一般是一些比较平稳的信号,噪声通常表现为高频信号。

第六章寒潮天气过程第一节1、寒潮天气过程是一种大规模的冷空气活动过程。
寒潮天气的主要特点是剧烈降温和大风,有时还伴有雨、雪、雨凇或霜冻。
2、中央气象台的寒潮标准规定,以过程降温与温度负距平相结合来划定冷空气活动强度。
过程降温是指冷空气影响过程的始末,日平均气温的最高值与及最低值之差。
而温度负距平是指冷空气影响过程中最低日平均气温与该日所在旬的多年旬平均气温之差。
3、过程降温(℃)温度负距平绝对值(℃)冷空气强度等级≥10 ≥5 寒潮8—9 4 强冷空气5—7 ≦3 一般冷空气4、寒潮出现的时间,最早开始于9月下旬,结束最晚是第2年5月。
春季的3月和秋天10—11月是寒潮和强冷空气活动最频繁的季节,也是寒潮和强冷空气对生产活动可能造成危害最重的时期。
5、影响我国的冷空气的源地:第一个是在新地岛以西的洋面上,冷空气经巴伦支海、苏联欧洲地区进入我国。
它出现的次数最多,达到寒潮强度也最多。
第二个是在新地岛以东的洋面上,冷空气大多数经喀拉海、太梅尔半岛、苏联地区进入我国。
它的出现次数虽少,但是气温低,可达到寒潮强度。
第三个是在冰岛以南的洋而上,冷空气经苏联欧洲南部或地中海、黑海、里海进入我国。
它出现的次数较多,但是温度不很低,一般达不到寒潮强度。
6、西伯利亚中部(70。
—90。
E,43。
—65。
N)地区称为寒潮关键区。
冷空气从关键区入侵我国有四条路径:①西北路(中路)②西路③东路④东路加西路。
第二节1、极涡的移动路径主要有三种类型:①经向性运动②纬向性移动③转游性运动。
2、根据极涡中心的分布特点,按100百帕的环流分为四种类型:①绕极型,②偏心型,③偶极型,④多极型。
这四种极涡型在冬半年各月分布的频率并不相同,绕极型在10月份占绝对优势,频率占50%,11—12月偶极型频率占40—50%,到1—2月偶极型频率接近60%,其平均持续也最久可达11.8天。
3、中央气象局科学研究所普查了1962—1971年的历史天气图,发现所有中等以上强度的大范围持续低温都是出现在北半球对流层中、上部。

小波变换在风力发电预测中的应用引言:风力发电作为一种清洁能源的代表,正逐渐成为全球能源结构调整的重要组成部分。
然而,风力发电的稳定性和可预测性一直是制约其发展的关键因素之一。
为了提高风力发电的效率和可靠性,科学家们不断探索新的方法和技术。
其中,小波变换作为一种信号处理的有效工具,被广泛应用于风力发电的预测中。
本文将介绍小波变换的原理和在风力发电预测中的应用。
一、小波变换的原理小波变换是一种时频分析方法,可以将信号分解成不同频率的成分。
它通过将信号与一组基函数进行内积运算,得到不同频率的分量,从而实现对信号的分析。
小波变换具有局部性和多分辨率的特点,能够更好地捕捉信号的瞬时特征和频率特征。
二、小波变换在风力发电预测中的应用1. 数据预处理在进行风力发电预测之前,需要对原始数据进行预处理。
小波变换可以对原始数据进行去噪和平滑处理,去除噪声和异常值,提高数据的质量和准确性。
同时,小波变换还可以对数据进行降维处理,减少计算量和存储空间。
2. 特征提取风力发电预测需要提取一些有效的特征来描述风速和功率之间的关系。
小波变换可以通过分析信号的频域和时域特征,提取出频率、振幅、相位等重要信息。
这些特征可以用于建立预测模型,帮助预测风力发电的输出功率。
3. 预测建模小波变换可以将风力发电的时间序列信号分解成不同频率的子信号,对每个子信号进行独立的预测建模。
这样可以更好地捕捉不同频率成分的变化规律,提高预测的准确性。
同时,小波变换还可以根据实际需求选择合适的小波函数和尺度,从而适应不同的预测场景。
4. 预测评估小波变换可以对风力发电预测结果进行评估和优化。
通过将预测结果与实际观测值进行比较,可以计算出预测误差和准确率,评估预测模型的性能。
同时,小波变换还可以通过调整小波函数和尺度,优化预测模型的参数,提高预测的精度和稳定性。
三、小波变换在风力发电预测中的优势1. 高时频分辨率:小波变换能够在时域和频域上同时提供高分辨率的信息,可以更好地捕捉风力发电信号的瞬时变化和频率特征。

小波分析及其应用小波分析是一种时间-频率分析方法,是对时域信号在时间和频率上的特征进行分析的一种数学工具。
它不仅具有频域分析方法的优点,如傅立叶变换,可以提供信号的频率成分,而且还能提供信号的时间信息,即信号的局部特征。
小波分析在信号处理、图像处理、语音识别等领域有着广泛的应用。
小波分析的基本原理是通过对信号进行分解和重构,将信号转化为不同尺度和频率的小波基函数的叠加,然后通过分析小波系数的大小和位置,得到信号的频率和局部时间信息。
在信号处理领域,小波分析常用于信号压缩、去噪和特征提取。
由于小波函数具有时频局部化特性,可以更准确地描述信号的局部特征,所以在信号压缩方面有很好的应用。
小波压缩将信号分解为不同频率分量,然后根据各个频率分量的重要程度进行压缩,以达到减小数据量的目的。
在信号去噪方面,小波分析可以通过滤除小波系数的低能量分量来抑制信号中的噪声。
此外,小波变换还可应用于语音识别和图像处理中的特征提取,提取信号的频率特征和时间特征,以实现对语音和图像的处理和识别。
在图像处理领域,小波分析有着广泛的应用。
小波变换可以将图像分解为不同尺度和方向的频域信号,从而提供了更加精细的图像特征信息。
基于小波变换的图像处理技术包括图像压缩、边缘检测、纹理分析等。
通过对图像进行小波分解和重构,可以实现图像的压缩和去噪。
同时,小波变换还具有多尺度分析的优势,能够更好地捕捉图像中的局部细节和全局结构。
在金融领域,小波分析被用于金融时间序列的特征提取和预测。
金融市场的价格序列通常具有非线性、非平稳和非高斯分布的特点,传统的统计方法常常无法处理。
而小波分析可以更好地揭示金融时间序列的时间和频率特征,提供更准确的数据分析和预测。
通过分析小波系数的大小和位置,可以提取金融时间序列中的主要特征和周期,为金融决策提供参考。
此外,小波分析还在医学影像处理、地震信号处理、生物信号处理等领域有广泛的应用。
在医学影像处理中,小波分析能够提取出图像中的不同频率和方向的特征,从而实现对病变的检测和分析。

路漫漫其修远兮,吾将上下而求索- 百度文库上海大学2010~2011学年冬季学期研究生课程课程名称:信息采集与处理技术课程编号:091102910 论文题目: 小波分析理论及其应用研究生姓名: 刘金鼎学号: 11721228论文评语:成绩: 任课教师: 昝鹏评阅日期:小波分析理论及其应用刘金鼎(上海大学机电工程与自动化学院,上海 200072)摘要:小波分析的理论与方法是从Fourier分析的思想方法演变而来的。
就象Fourier分析分为积分Fourier变换和Fourier级数一样,小波分析也分为(积分)小波变换和小波级数两部分,(积分)小波变换的主体是连续小波变换,多尺度小波变换和s-进小波变换;而小波级数的主体部分是关于小波框架的理论。
小波分析理论深刻,应用广泛,并且仍在迅速发展之中。
本文作者作为初学者,单单就(积分)小波变换这一理论中比较基本和初步的东西所作的一点归纳和整理,介绍了小波变换的定义及特点,以及多分辨率分析的问题,最后以一些图像去噪应用来形象说明小波分析的作用。
关键词:傅里叶分析;小波分析;多分辨率PXI BusLIU Jin-ding(School of Mechatronics Engineering & Automation, Shanghai University, Shanghai 200072, China)Abstract: The theory and methods of wavelet analysis comes from Fourier analysis .Just as Fourieranalysis is divided into Fourier transform and Fourier series, wavelet analysis is divided into the wavelet transform and wavelet series. The main body of the wavelet transform is the continuous wavelettransform, multi-scale wavelet transform and s-dyadic wavelet transform, while the main part of thewavelet series is wavelet frame. Wavelet analysis is a kind of profound theory, which is used widely and develops rapidly. The author of the paper is a beginner of wavelet theory; he just summarized andorganized some fundamental theory of wavelet analysis. The paper introduced the definition andcharacteristics of wavelet analysis, and then talked about the theory of multi- resolution ratio. In the end,a few of image denoising abstract applications were used to explain the function of wavelet analysisvividly.Key words: Fourier analysis; wavelet analysis; multi- resolution ratio1 引言1.1 问题的提出Fourier变换只能告诉我们信号尺度的范围,而无法给出信号的结构以及它蕴含的大小不同尺度的串级过程,即Fourier变换在时空域中没有任何分辨率。
[实例2] 近百余年我国气温变化的突变点分析本例运用小波分析方法,利用近百年中国年平均气温序列进行小波变换和逆变换计算,分析我国气温变化的多时间尺度特征。
1. 我国气温变化的小波变换图6.20是墨西哥帽(Mexihat )小波变换图。
图a 、b 、c 分别是当放大因子a =32、16、8时所计算的结果。
从图6.20a 可以看出,小波变换系数由下而上的穿零点是在1917年附近,也就是说对墨西哥帽小波变换来讲,在a =32这个时间尺度上气温的突变点在1917年附近。
在1917年之前,温度偏低;在1917年之后,温度偏高。
从图6.20b 可以看出,小波变换系数的穿零点有3个,分别是在1920年、1955年和1985年附近,也就是说对墨西哥帽小波变换来讲,在a =16这个时间尺度上气温的突变点有3个,在1920年之前,温度偏低;在1920年到1955年间,温度偏高;在1955年到1985年间,温度偏低;在1985年到1999年间,温度偏高。
从图6.20c 可以看出,小波变换系数的穿零点有5个,即突变点有5个。
分别是在1892年、1900年、1920年、1952年和1990年附近,也就是说对墨西哥帽小波变换来讲,在a =8这个时间尺度上,在1892年之前,温度偏低;在1892年到1900年间,温度偏高;在1900年到1920年间,温度偏低;在1920年到1952年间,温度偏高。
在1952年到1990年间,温度偏低;在1990年之后,温度偏高。
图6.21 是取不同时间尺度时哈尔小波变换图。
图中a 、b 和c 是放大因子a =32、16、8时所取的时间尺度。
从图6.21a 可以看出,哈尔小波变换结果有两个峰一个谷。
对应于a =32这个时间尺度上气温的突变点也就是3个,即峰点和谷点的位置,分别在1920年、1953年和1985年附近。
哈尔小波变换图上,正值对应原序列上升区,负值对应原序列下降区,因此大约从1882年附近开始到1939年前后气温处于上升阶段,从1939年到1968年气温处于下降阶段,1968年到1999年气温处于上升阶段。
第6章 气象上常用小波及其应用实例(1)前面五章讲述了小波分析方法的由来和原理,这些基本知识为气象上实际应用奠定了基础。
本章将介绍气象上常用的几种小波,特别是Haar 小波和墨西哥帽(Mexihat )小波,以及小波分析的应用实例。
6.1 二进小波二进小波的产生基于第4章的“二分法”。
它的基本思路是把连续型函数)(t f 及其连续小波变换),(b a W f 离散化,以便于实际应用。
作为一种方便和常用的形式,是对小波参数中的放(伸)缩因子a 进行二进制离散。
若小波函数系的表达式{}Zm,n n t am∈-- ),(ψ(••) 中的放缩因子)(2Z j a j ∈=,则称)(t ψ为二进小波。
把经过这种离散化后的二进小波的变换,称为二进小波变换。
强调说明:在应用时所用的小波函数系(式(••))与前面第4章第3节的式(•)有所不同。
比照这两式:),()(),2(2)(,2/,b at a t k t t b a jj kj -=-=ψψψψ或(•)),()(,n t at mn m -=-ψψ(••) 可以看出,二者主要的不同点是t 的系数a 指数正负号恰好相反。
所以,用式(•)的小波作变换时,随着a (或者j )的增大,W 曲线变窄;而用式(••)的小波作变换时,随着a (或者j )的增大,W 曲线变宽。
定义6.1 函数)()(2R L t ∈ψ被称为二进小波,若存在两个常数∞<≤<B A 0,使得:∑∈-≤≤Zj j B A .)2(ˆ2ωψ(6.1)上述条件式(6.1)称为稳定性条件;若A =B ,则称最稳定条件。
而函数序列{}Zj j f W ∈2称为二进小波变换,其中,,d 2)(21)()(22b b t t f t f t f W Rjjjj ⎰⎪⎭⎫⎝⎛-=*=ψψ(6.2)这里j a 2=是放缩因子,b 是平移因子。
由卷积定理知:)2(ˆ)(ˆ)(ˆ2ωψωωj f f W j ⋅= (6.3) 据此,稳定性条件等价于:对任意)()(2R L t f ∈,有:∑∈≤≤Zj fB fW fA j 2020220(6.4)下面定理说明,二进小波一定是允许小波。
定理6.1 设)(t ψ是二进小波,则它一定是允许小波,且.2ln d )(ˆ,d )(ˆ2ln 022B A ≤-≤⎰⎰∞∞ωωωψωωωψ(6.5)若A =B ,则上式变成:.2ln 2d )(ˆ2A C ==⎰∞+∞-ωωωψψ (6.6)其中A 、B 的含义同式(6.1)。
式(6.5)的证明如下:用变量替换,可得ωωωψωωωψd )(ˆd )2(ˆ1222212⎰⎰+=j jj因此,用ω除式(6.1)中每一项并在区间(1,2)上对ω积分,有.2ln d )(ˆ2ln 02B A ≤≤⎰∞ωωωψ同样,用-ω除式(6.1)每一项并在区间(-2,-1)上对ω积分,得.2ln d )(ˆ2ln 02B A ≤-≤⎰∞+ωωωψ证毕。
定理6.1表明,当ψ使得式(6.1)成立时,由二进小波变换可完全重构原信号。
重构公式是:.d 2)(21)()()( 222b b t t f W t t f W t f R j jj jj ⎰⎪⎭⎫⎝⎛-⋅=*=ψψ(6.7)二进小波介于连续小波和离散小波之间,它只是对尺度参数进行离散化,而在时域上仍保持平移量(b )连续变化。
因此二进小波变换仍具有连续小波变换的平移不变性。
这是它有别于离散小波变换的独特优点,后者不具备平移不变性质。
6.2 正交小波中常用的Haar 小波正交小波是一种重要的小波型式,正交小波变换已在第4章讲过。
在正交小波中,Haar 小波是一种常用的型式。
Haar 小波型式简单,使用方便,计算快捷;然而它的缺点也很明显,即缺乏连续性。
本节将详细介绍Haar 小波,由此可以加深对正交小波的理解。
图6.1 Haar 小波(a) 三次样条函数)(t θ; (b) )(t θ的一阶导数,即小波函数t t d /d )(θψ=。
(b) 虚线是小波函数的“简化”,即Haar 小波。
图6.1(a)是作为光滑函数的三次样条函数)(t θ;(b )是由t d /d θ构成的小波函数,其中虚线意为实曲线的“简化”,即Haar 小波。
也可以从尺度函数与小波函数关系的角度来理解Haar 小波的构造,也就是该小波是如何构造出来的。
这时将信号序列{}4321,,,x x x x 看成单位区间上的一个函数:),()()()()()1,4/3[4)4/3,2/1[3)2/1,4/1[2)4/1,0[1t X x t X x t X x t X x t f +++= (6.8)其中)(),[t X b a 表示区间),[b a 上的特征函数。
)(t f 是一个分段常数函数,如图6.2所示。
).4/3()(),2/1()(),4/1()()4/1,0[)1,4/3[)4/1,0[)4/3,2/1[)4/1,0[)2/1,4/1[-=-=-=t X t X t X t X t X t X图6.2 序列{}4321,,,x x x x 对应的分段常数函数现分析)()4/1,0[t X 、)()2/1,4/1[t X 、)()4/3,2/1[t X 和)()1,4/3[t X 之间的关系。
由平移关系知:)4/1()()4/1,0[)2/1,4/1[-=t X t X ,)2/1()()4/1,0[)4/3,2/1[-=t X t X ,)4/3()()4/1,0[)1,4/3[-=t X t X .另一方面,)()4/1,0[t X 可以看成单位区间上的特征函数的伸缩,即)2()(2)1,0[)4/1,0[t X t X =于是,)()2/1,4/1[t X 、)()4/3,2/1[t X 和)()1,4/3[t X 都可看成)()1,0[t X 的伸缩和平移。
引入记号: ),()()1,0[t X t =ϕ(6.9)定义:)12,,1,0(),2()(,-=-=jj kj k k t t ϕϕ(6.10)则有 )()(0,0t t ϕϕ=⎩⎨⎧<≤==.0,1/2,t 0 ,1)2()(0,1其它t t ϕϕ⎩⎨⎧<≤=-=.0,1,t 1/2 ,1)12()(1,1其它t t ϕϕ这表明,)()(110,1t t ϕϕ和可以由)(0,0t ϕ的伸缩与平移得到。
如图6.3所示。
图6.3 尺度函数的图形称)(t ϕ为Haar 尺度函数。
于是,式(6.8)定义的函数)(t f 可以重新写成如下形式:).()()()()(3,242,231,220,21t x t x t x t x t f ϕϕϕϕ+++= (6.11)即函数f (t )可以用一个尺度函数)(t ϕ的伸缩和平移的线性组合表示。
k j ,ϕ在其上不为零的区间叫做该函数的支撑。
可以验证,k j ,ϕ的支撑为⎥⎦⎤⎢⎣⎡+j jk k 21,2,支撑的宽度j21随j 的增加而减小。
j 称为分辨率,j21称为尺度。
下面讨论用{}4321,,,x x x x 的小波变换{}1,10,10,00.0,,,d d d a 来表达式(6.11)定义的函数)(t f 。
把式(6.11)看成)(t f 最高分辨级的分解。
求平均如同把)(t f 进行较低分辨级的表示,这等价于用0,1ϕ和1,1ϕ来表示)(t f 。
在这种表示中,0,1ϕ的系数是0,1a ,它是式(6.11)中)(t f 的前两个系数的平均值;1,1ϕ的系数是1,1a ,它是)(t f 的后两个系数的平均值。
于是得到如下的函数:)()()(1,11,10,10,11t a t a t g ϕϕ+= (6.12)一般地,21x x ≠,所以由1)8/1(x f =及2/)()8/1(210,11x x a g +==知,1g 不等于1f ,即用1g 来表示f 时丢失了一些细节信息,因而需要一个函数来描述这种信息。
该函数称为小波函数。
基本小波函数定义如下:⎪⎩⎪⎨⎧<≤<≤=-=. 0,0,1/2 1,-1/2,0 ,1 )()()()1,2/1[)2/1,0[其它t t t X t X t ψ (6.13)于是,)12()2()(--=t t t ϕϕψ。
)(t ψ称为Haar 小波,如图6.4所示。
与尺度函数)(t ψ类似,定义小波函数的伸缩和平移如下:.12,,1,0),2()(,-=-=jj kj k k t t ψψ(6.14)于是有),()(0,0t t ψψ=⎪⎩⎪⎨⎧<≤<≤==. 0,1/2,1/4 1,-1/4,0 ,1 )2()(0,1其它t t t t ψψ⎪⎩⎪⎨⎧<≤<≤=-=. 0,1,3/4 1,-3/4,1/2 ,1 )12()(1,1其它t t t t ψψ图6.4 Haar 小波)(t ψ图6.5 )(0,1t ψ和)(1,1t ψ的图形表示)(0,1t ψ和)(1,1t ψ的图形如图6.5所示。
现在重新考虑利用{}1,10,10,00.0,,,d d d a 、尺度函数{}1,10,1,ϕϕ和小波函数{}1,10,1,ψψ表示)(t f 的问题。
由式(6.8)知,)(t f 的最高分辨率表示是在长度为1/4的子区间上。
下面就在每个子区间)1,4/3[)4/3,2/1[),2/1,4/1[),4/1,0[和上来看一下f g 和1的差别,以便利用小波函数捕捉丢失的细节信息。
在区间)4/1,0[上,);()()(0,10,110,10,111d a x d a x t g t f +=⇒=-=- 在区间)2/1,4/1[上,)()()(0,10,120,10,121d a x d a x t g t f -=⇒-=-=-。
这表明,在区间)2/1,0[上,)()()(0,10,10,10,1t d t a t f ψϕ+=。
类似地,在区间)1,2/1[上,有)()()(1,11,11,11,1t d t a t f ψϕ+=。
将区间)2/1,0[及)1,2/1[上两个)(t f 的表达式写在一起,可以得到区间)1,0[上)(t f 的一个新的表达形式:).()()()()(1,11,10,10,11,11,10,10,1t d t d t a t a t f ψψϕϕ+++= (6.15))(t f被表示成支撑宽度为1/2的尺度函数与小波函数的线性和。
其中,)(0,10,1t d ψ和)(1,11,1t d ψ用于捕捉用)(1t g 逼近)(t f 时丢失的细节信息。
现在根据对{}1,10.1,a a 求平均的原理,引入区间)1,0[上的平均函数)(0,00,0t a ϕ代替式(6.15)中的前两项,而细节项保持不变。