下载文档原格式
2．在现实生活中可视为牛顿流体的有水 和空气 等。
3．流体静压力和流体静压强都是压力的一种量度。
它们的区别在于：前者是作用在某一面积上的总压力；而后者是作用在某一面积上的平均压强或某一点的压强。
4．均匀流过流断面上压强分布服从于水静力学规律。
5．和液体相比，固体存在着抗拉、抗压和抗切三方面的能力。
7．流体受压，体积缩小，密度增大 的性质，称为流体的压缩性 ；流体受热，体积膨胀，密度减少 的性质，称为流体的热胀性 。
8．压缩系数β的倒数称为流体的弹性模量 ，以E 来表示12．液体静压强分布规律只适用于静止、同种、连续液体。
13．静止非均质流体的水平面是等压面，等密面和等温面。
14．测压管是一根玻璃直管或U 形管，一端连接在需要测定的容器孔口上，另一端开口，直接和大气相通。
16．作用于曲面上的水静压力P 的铅直分力z P 等于其压力体内的水重。
17．通过描述物理量在空间的分布来研究流体运动的方法称为欧拉法。
18． 流线不能相交（驻点处除外），也不能是折线，因为流场内任一固定点在同一瞬间只能有一个速度向量，流线只能是一条光滑的曲线或直线。
20．液体质点的运动是极不规则的，各部分流体相互剧烈掺混，这种流动状态称为紊流。
21．由紊流转变为层流的临界流速k v 小于 由层流转变为紊流的临界流速kv '，其中kv '称为上临界速度，k v 称为下临界速度。
23．圆管层流的沿程阻力系数仅与雷诺数有关，且成反比，而和管壁粗糙无关。
25．紊流过渡区的阿里特苏里公式为25.0)Re68(11.0+=d k λ。
26．速度的大小、方向或分布发生变化而引起的能量损失，称为局部损失。
29．湿周是指过流断面上流体和固体壁面接触的周界。
31．串联管路总的综合阻力系数S 等于各管段的阻抗叠加。
32．并联管路总的综合阻力系数S 与各分支管综合阻力系数的关系为3211111s s s s ++=。
管嘴与孔口比较,如果水头H 和直径d 相同，其流速比V 孔口/V 管嘴等于82.097.0,流量比Q 孔口/Q 管嘴等于82.060.0。
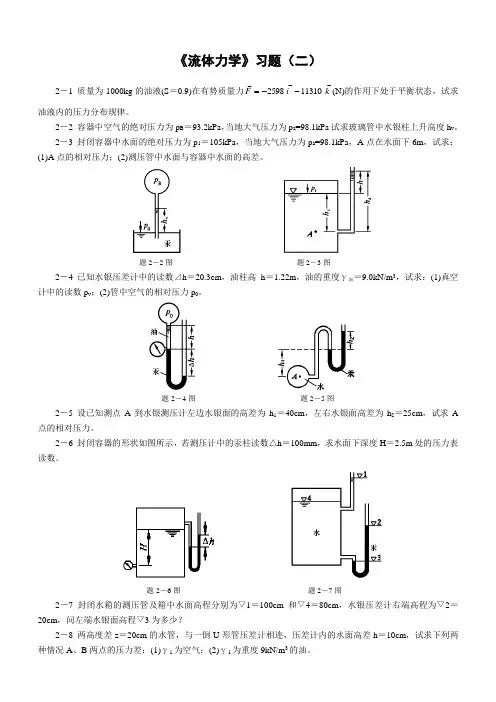
《流体力学》习题（二）2－1 质量为1000kg 的油液(S ＝0.9)在有势质量力k i F 113102598--=(N)的作用下处于平衡状态，试求油液内的压力分布规律。
2－2 容器中空气的绝对压力为p B ＝93.2kPa ，当地大气压力为p a =98.1kPa 试求玻璃管中水银柱上升高度h v 。
2－3 封闭容器中水面的绝对压力为p 1＝105kPa ，当地大气压力为p a =98.1kPa ，A 点在水面下6m ，试求：(1)A 点的相对压力；(2)测压管中水面与容器中水面的高差。
题2－2图 题2－3图 2－4 已知水银压差计中的读数⊿h ＝20.3cm ，油柱高h ＝1.22m ，油的重度γ油＝9.0kN/m 3，试求：(1)真空计中的读数p v ；(2)管中空气的相对压力p 0。
题2－4图 题2－5图 2－5 设已知测点A 到水银测压计左边水银面的高差为h 1＝40cm ，左右水银面高差为h 2＝25cm ，试求A 点的相对压力。
2－6 封闭容器的形状如图所示，若测压计中的汞柱读数△h ＝100mm ，求水面下深度H ＝2.5m 处的压力表读数。
题2－6图 题2－7图 2－7 封闭水箱的测压管及箱中水面高程分别为▽1＝100cm 和▽4＝80cm ，水银压差计右端高程为▽2＝20cm ，问左端水银面高程▽3为多少？2－8 两高度差z ＝20cm 的水管，与一倒U 形管压差计相连，压差计内的水面高差h ＝10cm ，试求下列两种情况A 、B 两点的压力差：(1)γ1为空气；(2)γ1为重度9kN/m 3的油。
题2－8图题2－9图2－9 有一半封闭容器，左边三格为水，右边一格为油(比重为0.9)。
试求A、B、C、D四点的相对压力。
2－10 一小封闭容器放在大封闭容器中，后者充满压缩空气。
测压表A、B的读数分别为8.28kPa和13.80kPa，已知当地大气压为100kPa，试求小容器内的绝对压力。
第二章例1：用复式水银压差计测量密封容器内水面的相对压强，如下列图。
：水面高程z 0=3m,压差计各水银面的高程分别为z 1=, z 2=, z 3=m, z 4=m, 水银密度 3/13600m kg ρ='，水的密度3/1000m kg ρ= 。
试求水面的相对压强p 0。
解：ap z z γz z γz z γp =-----+)(')(')(3412100)()('1034120z z γz z z z γp ---+-=∴例2：用如下列图的倾斜微压计测量两条同高程水管的压差。
该微压计是一个水平倾角为θ的Π形管。
测压计两侧斜液柱读数的差值为L=30mm ，倾角θ=30∘，试求压强差p 1 – p 2 。
解： 224131)()(p z z γz z γp =-+-- θL γz z γp p sin )(4321=-=-∴例3：用复式压差计测量两条气体管道的压差〔如下列图〕。
两个U 形管的工作液体为水银，密度为ρ2 ，其连接收充以酒精，密度为ρ1 。
如果水银面的高度读数为z 1 、 z 2 、 z 3、z 4 ，试求压强差p A – p B 。
解： 点1 的压强 ：p A )(21222z z γp p A --=的压强：点)()(33211223z z γz z γp p A -+--=的压强：点 B A p z z γz z γz z γp p =---+--=)()()(3423211224 )()(32134122z z γz z z z γp p B A ---+-=-∴例4：用离心铸造机铸造车轮。
求A-A 面上的液体总压力。
解： C gz r p +⎪⎭⎫ ⎝⎛-=2221ωρ a p gz r p +⎪⎭⎫ ⎝⎛-=∴2221ωρ在界面A-A 上：Z = - ha p gh r p +⎪⎭⎫⎝⎛+=∴2221ωρ⎪⎭⎫⎝⎛+=-=∴⎰2420218122)(ghR R rdr p p F a Rωπρπ例5：在一直径d= 300mm ，而高度H=500mm 的园柱形容器中注水至高度h 1 = 300mm ，使容器绕垂直轴作等角速度旋转。
第一章习题答案选择题（单选题）1.1 按连续介质的概念，流体质点是指：（d ）（a ）流体的分子；（b ）流体内的固体颗粒；（c ）几何的点；（d ）几何尺寸同流动空间相比是极小量，又含有大量分子的微元体。
1.2 作用于流体的质量力包括：（c ）（a ）压力；（b ）摩擦阻力；（c ）重力；（d ）表面张力。
1.3 单位质量力的国际单位是：（d ）（a ）N ；（b ）Pa ；（c ）kg N /；（d ）2/s m 。
1.4 与牛顿内摩擦定律直接有关的因素是：（b ）（a ）剪应力和压强；（b ）剪应力和剪应变率；（c ）剪应力和剪应变；（d ）剪应力和流速。
1.5 水的动力黏度μ随温度的升高：（b ）（a ）增大；（b ）减小；（c ）不变；（d ）不定。
1.6 流体运动黏度ν的国际单位是：（a ）（a ）2/s m ；（b ）2/m N ；（c ）m kg /；（d ）2/m s N ⋅。
1.7 无黏性流体的特征是：（c ）（a ）黏度是常数；（b ）不可压缩；（c ）无黏性；（d ）符合RT p=ρ。
1.8 当水的压强增加1个大气压时，水的密度增大约为：（a ）（a ）1/20000；（b ）1/10000；（c ）1/4000；（d ）1/2000。
1.9 水的密度为10003kg/m ，2L 水的质量和重量是多少？ 解：10000.0022m V ρ==⨯=（kg ）29.80719.614G mg ==⨯=（N ）答：2L 水的质量是2kg ，重量是19.614N 。
1.10 体积为0.53m 的油料，重量为4410N ，试求该油料的密度是多少？ 解：44109.807899.3580.5m G g V V ρ====（kg/m 3） 答：该油料的密度是899.358kg/m 3。
1.11某液体的动力黏度为0.005Pa s ⋅，其密度为8503/kg m ，试求其运动黏度。
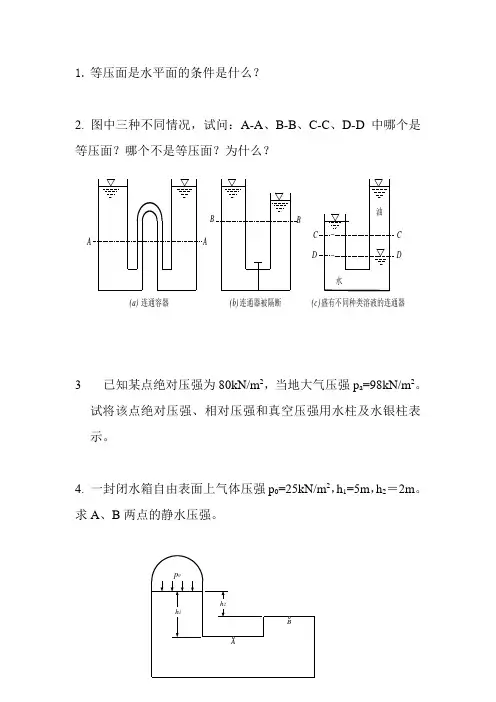
C (c) 盛有不同种类溶液的连通器DC D水油BB (b) 连通器被隔断AA(a) 连通容器1. 等压面是水平面的条件是什么？2. 图中三种不同情况，试问：A-A 、B-B 、C-C 、D-D 中哪个是等压面？哪个不是等压面？为什么？3 已知某点绝对压强为80kN/m 2，当地大气压强p a =98kN/m 2。
试将该点绝对压强、相对压强和真空压强用水柱及水银柱表示。
4. 一封闭水箱自由表面上气体压强p 0=25kN/m 2，h 1=5m ，h 2＝2m 。
求A 、B 两点的静水压强。
速？答：与流线正交的断面叫过流断面。
过流断面上点流速的平均值为断面平均流速。
引入断面平均流速的概念是为了在工程应用中简化计算。
8．如图所示，水流通过由两段等截面及一段变截面组成的管道，试问：(1)当阀门开度一定，上游水位保持不变，各段管中，是恒定流还是非恒定流？是均匀流还是非均匀流？(2)当阀门开度一定，上游水位随时间下降，这时管中是恒定流还是非恒定流？(3)恒定流情况下，当判别第II 段管中是渐变流还是急变流时，与该段管长有无关系？9 水流从水箱经管径分别为cmd cm d cm d 5.2,5,10321===的管道流出，出口流速sm V /13=，如图所示。
求流量及其它管道的断面平均流速。
解：应用连续性方程（1）流量：==33A v Q 4.91s l /103-⨯(2) 断面平均流速s m v /0625.01= , s m v /25.02= 。
10如图铅直放置的有压管道，已知d 1=200mm ，d 2=100mm ，断面1-1处的流速v 1=1m/s 。
求（1）输水流量Q ；（2）断面2-2处的平均流速v 2；（3）若此管水平放置，输水流量Q 及断面2-2处的速度v 2是否发生变化？（4）图a 中若水自下而上流动，Q 及v 2是否会发生变化？解：应用连续性方程 （1）4.31=Q s l / （2）s m v /42= （3）不变。
流体力学答案解析题目：一不可压缩流体在水平管道内作稳定流动，管道截面由圆形逐渐扩大为方形，入口直径为d，出口边长为a。
已知入口流速为v1，入口处的压力为p1，求出口处的流速v2和压力p2。
解析：首先，根据连续性方程，流体在管道内的流速和截面积之间存在以下关系：A1v1 = A2v2其中，A1和A2分别为入口和出口的截面积。
由于管道截面由圆形变为方形，我们可以分别计算两个截面的面积。
入口截面积A1 = π(d/2)^2出口截面积 A2 = a^2将上述面积代入连续性方程，得到：π(d/2)^2 v1 = a^2 v2解得：v2 = (π(d/2)^2 v1) / a^2接下来，我们应用伯努利方程，该方程描述了流体在流动过程中速度、压力和高度之间的关系。
在水平管道中，高度不变，因此伯努利方程简化为：p1/ρ + v1^2/2 = p2/ρ + v2^2/2其中，ρ为流体的密度。
将v2的表达式代入伯努利方程，得到：p1/ρ + v1^2/2 = p2/ρ + (π(d/2)^2 v1)^2 /(2a^2ρ)化简得到：p2 = p1 + ρ(v1^2 - v2^2)/2将v2的表达式代入上式，得到：p2 = p1 + ρ(v1^2 - (π(d/2)^2 v1)^2 /(2a^2ρ))/2化简得到：p2 = p1 + (ρ/2)(v1^2 - (π(d/2)^4 v1^2) / (2a^2))进一步化简得到：p2 = p1 + (ρ/2)(v1^2(1 - (π(d/2)^4) / (2a^2)))至此，我们已经求得了出口处的流速v2和压力p2。
以下是对解题过程的详细解析：1. 连续性方程的应用：连续性方程是流体力学中的一个基本原理，描述了流体在流动过程中质量守恒的关系。
在本题中，由于流体是不可压缩的，因此在流动过程中质量守恒。
根据连续性方程，我们可以求出出口处的流速v2。
2. 伯努利方程的应用：伯努利方程是流体力学中的一个重要方程，描述了流体在流动过程中速度、压力和高度之间的关系。
流体力学课程习题集含解析第1章流体力学的基本概念1-1.是非题(正确的打“√”，错误的打“⨯”)理想流体就是不考虑粘滞性的、实际不存在的，理想化的流体。
（√） 在连续介质假设的条件下，液体中各种物理量的变化是连续的。
（√） 粘滞性是引起流体运动能量损失的根本原因。
（√） 牛顿内摩擦定律适用于所有的流体。
（⨯） 牛顿内摩擦定律只适用于管道中的层流。
（⨯） 有旋运动就是流体作圆周运动。
（⨯） 温度升高时，空气的粘度减小。
（⨯）流体力学中用欧拉法研究每个质点的轨迹。
（⨯） 平衡流体不能抵抗剪切力。
（√） 静止流体不显示粘性。
（√） 速度梯度实质上是流体的粘性。
（√） 流体运动的速度梯度是剪切变形角速度。
（√） 恒定流一定是均匀流，层流也一定是均匀流。
（⨯）牛顿内摩擦定律中，粘度系数m 和v 均与压力和温度有关。
（⨯） 迹线与流线分别是Lagrange 和Euler 几何描述；它们是对同一事物的不同说法；因此迹线就是流线，流线就是迹线。
（⨯）如果流体的线变形速度θ=θx +θy +θz =0,则流体为不可压缩流体。
（√） 如果流体的角变形速度ω=ωx +ωy +ωz =0,则流体为无旋流动。
（√）流体的表面力不仅与作用的表面积的外力有关，而且还与作用面积的大小、体积和密度有关。
（⨯）对于平衡流体，其表面力就是压强。
（√）边界层就是流体的自由表明和容器壁的接触面。
（⨯）1-2已知作用在单位质量物体上的体积力分布为：，物体的密度，坐标量度单位为m ；其中，，，；，，。
试求：如图1-2所示区域的体积力、、各为多少？解：xy z f axf bf cz⎧=⎪=⎨⎪=⎩2lx ry nz ρπ=++0a =0.1b N kg =()0.5c N kg m =⋅52.0l kg m =0r =41.0n kg m =xF yF Fz V V V VVF f dV f dxdydz ρρ==⎰⎰⎰⎰00x x V VF f dV dxdydz ρρ∴==⋅=⎰⎰⎰⎰0x F N =答：各体积力为：、、1-3作用在物体上的单位质量力分布为：，物体的密度为，如图1-3所示，其中，，，；。
《流体力学》习题（五）5－1 水流经变截面管道，已知细管直径d1，粗管直径d2＝2d1，试问哪个截面的雷诺数大?两截面雷诺数的比值Re1/Re2是多少？5－2 水管直径d＝10cm，管中流速u＝1.0m/s，水温为10℃，试判别流态。
又流速u等于多少时，流态将发生变化？5－3 通风管道直径为250mm，输送的空气温度为20℃，试求保持层流的最大流量。
若输送空气的质量流量为200kg/h，其流态是层流还是紊流？5－4 有一矩形截面的小排水沟，水深15cm，底宽20cm，流速0.15m/s，水温10℃，试判别流态。
5－5 散热器由8×12mm2的矩形截面水管组成，水的运动粘性系数为0.0048cm2/s，要确保每根水管中的流态为紊流(取Re≥4000)以利散热，试问水管中的流量应为多少？5－6 输油管的直径d＝150mm，流量Q＝16.3m3/h，油的运动粘性系数ν＝0.2cm2/s，试求每公里管长的沿程压头损失。
5－7 应用细管式粘度计测定油的粘度，已知细管直径d＝6mm，测量段长l＝2m，实测油的流量Q＝77cm3/s，水银压差计读数h＝30cm，油的重度γ＝8.83kN/m3，试求油的运动粘性系数ν和动力粘性系数μ。
5－8 为了确定圆管内径，在管内通过ν为0.013cm2/s的水，实测流量为35cm3/s，长15m管段上的压头损失为2cm水柱，试求此圆管的内径。
5－9 要求用毕托管一次测出半径为r0的圆管层流的截面平均流速，试求毕托管测口应放置的位置。
题5－7图题5－9图题5－10图5－10 油管直径为75mm，已知油的重度为8.83kN/m3，运动粘性系数为0.9cm2/s，在管轴位置安放连接水银压差计的毕托管，水银面高差h＝20mm，水银重度为133.38kN/m3，试求油的流量。
5－11 铁皮风管直径d＝400mm，风量Q＝1.2m3/s，空气温度为20℃，试求沿程阻力系数，并指出所在阻力区。
第六章 粘性流体绕物体的流动6－1 已知粘性流体的速度场为k xz j xyz i y x u 22835 (m/s)。
流体的动力粘度μ＝0.144Pa·s ，在点(2，4，－6)处σyy ＝－100N/m 2，试求该点处其它的法向应力和切向应力。
已知：y x u 2x 5 ，z y x u 3y ，2z 8z x u ，μ＝0.144Pa·s ，σyy ＝－100N/m 2。
解析：在点(2，4，－6)处，有8010xxy x u ，363y z x yu ，19216z z x z u ；2052x x y u ，0x z u，723y z y x u ，243y y x zu ，28882z z x u ， 0z y u ；1zy x s 2361923680iv d zu y u x u u 由div 322yyyy u p ，可得 Pa 976.66100236144.032)36(144.02div 322yy yy u p ，则 Pa 592.66236144.03280144.02976.66div 322x xx u x u pPa 336.34236144.032192144.02976.66div 322z zz u z u pPa 488.7)2072(144.0)(xy yx xyyu xu Pa 456.3)240(144.0)(yz zy yz zu y u Pa 472.41)2880(144.0)(zx xz zx xu z u 6－2 两种流体在压力梯度为k xpd d 的情形下在两固定的平行平板间作稳定层流流动，试导出其速度分布式。
已知：k xpd d 。
解析：建立坐标系，将坐标原点放置在两种液体的分界面上，x 轴与流动方向相同，y 轴垂直于平行平板。
根据题意，两流体在y 轴和z 轴方向的速度分量都为零，即u y ＝u z ＝0。
由连续性方程知xu x＝0，即速度分量u x 与x 坐标无关。
另外，由式(6－6)可以看出，在质量力忽略不计时，有0 y p ，0 zp，因此，压力p 只是x 的函数，于是式(6－6)可简化为 )(1d d 2x 22x 2x z u y u x p u由于流体是在两无限大平行平板间作稳定层流流动，因此上式中2x 2z u 与2x2yu 项相比可以忽略不计，同时，由于x u ＝0，那么0d d xu ，于是上式可进一步简化为 x pyu d d 1d d 2x 2 对于第一种流体有 1121x 2d d 1d d kx p y u 对于第二种流体有 2222x 2d d 1d d kx p y u积分以上两式，得111x d d C y k y u ； 122x d d C y ky u 再次积分以上两式得21211x 2C y C y k u； 21222x 2C y C y k u 根据边界条件确定四个积分常数：① 当y ＝0时，x2x1u u ，得 22C C ； ② 当y ＝0时，21 ，即yuy u d d d d 2x 21x 1，得 2111 C C ；③ 当y ＝b 时，0x1 u ，得 b C b k C 11222 ；④ 当y ＝b 时，0x1 u ，得 b C b k C 12222 。
将以上所得各式联立，解得1212112 kb C ； 1212212 kb C ； 12222 kb C C于是得到两种流体的速度分布式分别为12212121211x 22kb y kb y k u ； 12212122222x 22kb y kb y ku 6－3 密度为ρ、动力粘度为μ的薄液层在重力的作用下沿倾斜平面向下作等速层流流动，试证明：(1) 流速分布为 )(2sin 22h H g u(2) 单位宽度流量为 33sin H g q已知：ρ，μ，H ，h ，θ。
解析：(1) 建立坐标系如图所示，液层厚度方向h 为自变量，由于液层的流动为不可压缩一维稳定层流流动，则N －S 方程可简化为0sin 22 hu g 将上式整理后，两次积分得212sin 2C h C h g u由边界条件：当h ＝0时，0 hu，得 01 C ； 当h ＝H 时，u ＝0，得sin 222H g C。
所以流速分布为 )(2sin 22h H g u(2) 单位宽度流量为3H22H3sin d )(2sin d H g h h H g h u q6－4 一平行于固定底面0－0的平板，面积为A ＝0.1m 2，以衡速u ＝0.4m/s 被拖曳移动，平板与底面间有上下两层油液，上层油液的深度为h 1＝0.8mm ，粘度μ1＝0.142N·s/m 2，下层油液的深度为h 2＝1.2mm ，粘度μ2＝0.235N·s/m 2，求所需要的拖曳力T 。
已知：A ＝0.1m 2，u ＝0.4m/s ，h 1＝0.8mm ，h 2＝1.2mm ，μ1＝0.142N·s/m 2，μ2＝0.235N·s/m 2。
解析一：建立坐标系如图所示，由于两层油液均作不可压缩一维稳定层流流动，则N －S 方程可简化为022 z u将上式两次积分后，得C z C u对两层油液的速度分布可分别写为222111C z C u C z C u 由边界条件：当z ＝0时，02 u ，得 02C ； 当z ＝h 2时，u 1＝u 2，得 22121h C C h C ； 当z ＝h 1＋h 2时，u 1＝u ，得 1211)(C h h C u ； 当z ＝h 2时，21 ，即zuz u 2211 ，得 2211C C 。
将以上四式联立，可解得 122121 h h u C； 12212211)( h h h u C ； 122112 h h u C ； 02C 代入上述速度分布式，得zh h u u h h h u z h h u u 1221121221221122121)(那么，拖曳平板所需要的力为 N 724.310)142.02.1235.08.0(4.01.0235.0142.0|31221211121 h h u A z u AT h h z解解析析二二：：设两油液分界面处的速度为*u ，由于在题设条件下，油液在z 方向的速度分布为线性分布，且在垂直于板面方向的粘性切应力为一常数，即0 。
因此有2*21*1h u h u u 所以 m/s 19.010)142.02.1235.08.0(102.1142.04.033122121* h h h u u那么，拖曳平板所需要的力为 N 724.3102.119.01.0235.032*2 h u AT 6－5 粘度μ＝0.05Pa·s 的油在正圆环缝中流动，已知环缝内外半径分别为r 1＝10mm ，r 2＝20mm ，若外壁的切应力为40N/m 2，试求(1)每米长环缝的压力降；(2)每秒流量；(3)流体作用在10m 长内壁上的轴向力。
已知：r 1＝10mm ，r 2＝20mm ，μ＝0.05Pa·s ，w2 ＝40N/m 2。
解析：建立坐标系，由于0θr u u ，由连续性方程可知，0xxu ；忽略质量力，N －S 方程可简化为)d d d d (d d x 2x 2r r u ru x p或写成 r x p r u r r d d 1)d d (d d x 对上式进行两次积分上式，得212x ln d d 41C r C r xp u根据边界条件确定积分常数： ① 当r ＝r 1时，0x u ，得 11212ln d d 41r C r xp C；② 当r ＝r 2时，0x u ，得 21222ln d d 41r C r xp C。
联立以上两式，得 )ln()(d d 411222211r r r r x p C ； )ln()ln ln (d d 41122211222r r r r r r x p C代入上述速度分布式，得)]ln()ln([4)]ln()ln([d d 412122122222m 2122122222x r r r r r r r r R r r r r r r r r x p u流量计算式为2121r r 2122122222r r x d 2)]ln()ln([d d 41d 2r r rr r r r r r r x p r r u Q])ln()([8])ln()([d d 812221224142m 12221224142r r r r r r R r r r r r r x p式中：xpR d d m，为单位体积流体在单位管长内流动时所造成的机械能损失，亦即单位管长上的压力损失或压力降，称为压力坡度或称比摩阻。
摩擦切应力分布式为]1)ln(2)([d d 211)ln()(d d 41d d 21d d 122221122221x r r r r r r x pr r r r r x p r x p r u(1) 当r ＝r 2时，w2 ＝40N/m 2，代入上式得到每米长环缝的压力降为Pa/m 8.8714]02.0)01.0/02.0ln(2/)02.001.0(02.0[402]1)ln(2)(/[2d d 2221222212m r r r r r r x pR (2) 每秒钟的流量为/sm 1038.1])01.0/02.0ln()01.002.0(01.002.0[05.088.871414.3])ln()([8332224412221224142m r r r r r r R Q(3) 流体作用在10m 长内壁上的轴向力为N85.311001.014.32]01.0)01.0/02.0ln(202.001.001.0[28.87142]1)ln(2)([d d 212211122221111w Lr r r r r r r xp A F6－6 设平行流流过平板时的附面层速度分布为2)2(y y u u，试导出附面层厚度δ与x的关系式，并求平板一面上的阻力。
平板长为L ，宽为B 。
流动为不可压缩稳定流动。
已知：L ，B ，2)2(y y u u。
解析：根据题意，对于层流附面层，由牛顿内摩擦定律得出平板板面上粘性摩擦应力为u y u y uy 2]4[2)(0y 20w ① 附面层的动量损失厚度δ2为152d ])2(1][)2([d )1(δ22δ02y y y y y y u u u u将以上两式代入动量积分方程(6－30)式，得到xu u d d 15222上式整理后为 x u d 51d对上式积分得C x u51212 由边界条件：x ＝0，δ＝0，得C ＝0。
