工程测量坐标系高程

建立工程坐标系的方案一、引言工程坐标系是工程测量中的重要组成部分，它是确保工程测量准确和可靠的基础。

建立工程坐标系最终目的是为了实现工程测量和工程施工的精准定位和方位的控制。

在现代工程中，常见的工程坐标系统有地理坐标系、平面坐标系和高程坐标系等。

建立工程坐标系的方案需要考虑到工程地质特征、地理环境以及测量技术等多方面因素，才能确保建立的工程坐标系满足实际工程需求。

二、确定建立工程坐标系的目标1. 确定工程测量的需要：首先需要明确工程测量的具体需要，比如工程地质调查、施工测量、工程监测等。

不同的测量需要可能对工程坐标系的要求不同，因此需要根据具体需求来确定建立工程坐标系的目标。

2. 确定测量精度要求：根据工程的实际情况和测量的精度要求，确定建立工程坐标系的精度标准。

比如，对于高精度测量，需要建立高精度的工程坐标系，而对于一般工程测量，可能只需要建立一般精度的工程坐标系。

3. 考虑工程地质和地理环境：工程坐标系的建立还需要考虑工程地质特征和地理环境因素，比如地表形态、地形地貌、地质构造等因素。

这些因素对工程坐标系的建立会产生一定的影响，需要进行综合分析和考虑。

三、工程坐标系的建立方案1. 工程坐标系的选取根据工程测量的需要和测量精度的要求，选取合适的工程坐标系。

常见的工程坐标系有直角坐标系、极坐标系等，需要根据具体情况选取合适的坐标系。

2. 坐标系原点的确定确定坐标系原点是建立工程坐标系的关键步骤。

原点的确定需要考虑到工程实际需求、测量精度和方便性等因素。

原点的选取应尽量符合工程测量和施工的实际需求，并且易于控制和使用。

3. 坐标系的坐标轴方向确定坐标系的坐标轴方向是建立工程坐标系的重要环节。

坐标轴方向的确定应符合工程测量的需要，比如工程方向、施工方位等。

同时，还需要考虑实际控制的便利性和测量的准确性等因素。

4. 坐标系统的缩放比例确定坐标系统的缩放比例是工程坐标系建立的重要步骤。

根据实际工程测量的需求和精度要求，确定合适的缩放比例。

机场工程测量坐标系统及换算关系摘要：重点阐述了我国测量坐标系和高程系的概念及分类,并结合重庆机场的工程建设对独立坐标系的建立方法进行了探讨,最后给出不同坐标系之间的坐标换算关系。

关键词：机场工程测量坐标换算关系Abstract: this paper focuses on measuring coordinate system and elevation in our country the concept and classification, and combined with the engineering construction of chongqing airport of establishing independent coordinate system methods are discussed, and finally gives the coordinate conversion between different coordinate relationship.Key words: the airport project coordinate conversion relation measurement1 概述坐标系指的是描述空间位置的表达形式,一个完整的坐标系统是由坐标系和基准两方面的要素所构成的。

而基准指的是为描述空间位置而定义的一系列点、线、面。

目前我国地形图使用最多的坐标系有地理坐标和高斯投影平面直角坐标系。

2，机场地区坐标系的建立机场辐射区域较大,一般选址远离中心城区20-50km,根据现行测量规范规定,机场地区控制网最好采用国家统一坐标系,即将所有地面观测成果归化到国家参考椭球面上,并按高斯正形投影坐标系计算其在3°带内的平面直角坐标值。

当长度投影变形比超过容许值,在日常的测图、用图工作中需要加入长度投影变形改正数,为避免进行繁琐的长度改正计算,同时出于机场地理参数保密的需要,可将任意高程面作为投影面,或者将任意子午线作为中央子午线建立机场局部坐标系统。

在我国的地理测量领域，1985年国家高程基准和西安80坐标系是两个非常重要的概念。

这两个概念不仅在地图制图、工程测量等领域有着广泛的应用，而且对于国家的基础设施建设和国土资源管理也具有重要意义。

本文将对1985年国家高程基准和西安80坐标系进行详细介绍，以便读者对这两个概念有一个清晰的了解。

1. 背景介绍1985年国家高程基准是我国规定的唯一高程基准。

1985年国家高程基准的确定，是为了逐步实现高程基准的统一。

1985年国家高程基准的制定，对于保证工程建设、地理信息系统建设、资源环境监测、国土资源管理等领域中的高程测量数据的质量和一致性，对于推动我国地球物理、天文地球测量、大地测量和测量科学技术的进步，提高地球物理领域的专业技术水平和地理信息科学的应用水平，都至关重要。

西安80坐标系是我国测绘界在1980年进行测量基准点计算平差和综合整体大地测量调查后确定的一个大地坐标系。

它是在1980年我国南北大地基础测量成果的基础上，由国家测绘局研究制定的山西省太原市偏正子午线为中央子午线的椭球面笛卡尔坐标系。

西安80坐标系被广泛应用于地理信息系统、全球定位系统、导航定位等领域。

2. 1985年国家高程基准的特点1985年国家高程基准具有以下特点：（1）高程基准标高采用广义正高。

（2）高程基准起算点采用测量学国际通用的高程起算点。

（3）高程基准点由国家测绘局认可的测绘单位实施。

3. 西安80坐标系的特点西安80坐标系的特点主要包括：（1）中央子午线经度：110度，相对于格林尼治子午线，东移73度7分，即东经110度。

（2）大地基准面：克拉索夫斯基椭球体。

（3）K0、K2有效位数： K0、K2检核记录不用特意列，必要现场计算核对。

（4）投影类型：高斯-克吕格投影。

4. 1985年国家高程基准和西安80坐标系的关系1985年国家高程基准和西安80坐标系是地理信息系统中两个非常重要的概念，它们之间存在着密切的联系。

2000坐标系高程转地方坐标系高程1.引言1.1 概述本文主要探讨的是2000坐标系高程转地方坐标系高程的问题。

在工程测量中，常常需要将以WGS84坐标系或者其他国家地理坐标系表达的地球高程转化为本地地方坐标系高程，以满足工程测绘的精确需求。

针对这个问题，本文将首先阐述2000坐标系高程转地方坐标系高程的基本原理，包括通过坐标系转换方法实现数据转化，以及各坐标系间的转换关系等。

其次，本文将详细介绍2000坐标系高程转地方坐标系高程的计算方法，包括高程基准转换、坐标转换以及相关参数的使用等。

通过研究和分析2000坐标系高程转地方坐标系高程的理论和计算方法，可以帮助工程测绘人员更准确地进行地球高程的测量和表达。

同时，本文也将总结研究结果，提出一些研究的启示，以期为相关领域的研究和应用提供参考和借鉴。

总之，本文将全面探讨2000坐标系高程转地方坐标系高程的原理和方法，并通过相关案例和实证分析来验证其有效性和准确性。

希望本文能够对相关领域的科研人员和工程测绘人员有所帮助，为工程测绘的高程测量提供有力的支持和指导。

1.2文章结构文章结构部分包括对整篇文章进行总体的呈现和组织。

本文主要介绍2000坐标系高程转地方坐标系高程的基本原理和计算方法，并得出结论和研究启示。

以下是本文的详细文章结构：1. 引言1.1 概述：介绍文章的背景和研究目的，说明2000坐标系高程转地方坐标系高程的重要性和应用场景。

1.2 文章结构：介绍本文的文章目录和主要章节内容，为读者提供整体阅读结构的概览。

1.3 目的：明确论文的目标和意义，指出本文的研究价值和实用性。

2. 正文2.1 2000坐标系高程转地方坐标系高程的基本原理：详细介绍2000坐标系高程和地方坐标系高程的概念和特点，解释二者之间的关联和转换原理。

2.2 2000坐标系高程转地方坐标系高程的计算方法：系统阐述了基于数学模型和算法推导的2000坐标系高程转地方坐标系高程的具体计算方法，包括重力异常的修正等相关步骤。

《工程施工测量》坐标计算工程施工测量是指在工程建设过程中对各种位置、尺寸、高程等进行测量和计算的工作。

其中，坐标计算是测量工作的重要内容之一、坐标计算旨在确定一些点的平面坐标或者空间坐标，并利用这些坐标进行工程设计、施工和验收等工作。

坐标计算的基本原理是通过测量获取各点的坐标数据，然后利用计算方法进行数学计算得出点的坐标。

常见的坐标计算方法有平差计算法、微分计算法和三角计算法。

平差计算法是通过观测数据的处理求解出未知点的坐标。

其基本思想是根据观测数据建立相关方程组，并通过最小二乘法求解。

平差计算法通常包括三个步骤：建立方程、求解方程组和检查与分析。

建立方程时，需要根据观测数据的类型确定方程的形式，如平面坐标观测通常采用距离方程，而空间坐标观测通常采用坐标方程。

求解方程组时，可以采用高斯消元法、逆平差法等方法进行计算。

检查与分析时，需要对计算结果进行检查，判断计算精度是否符合要求，并对计算误差进行分析。

微分计算法是通过已知点的坐标和测量数据，在测区域内进行坐标计算的方法。

其基本思想是通过观测数据的微分运算，计算出所需的未知点的坐标。

微分计算法通常包括两个步骤：设定原点和计算坐标。

设定原点是确定测区域中的一个已知点作为空间原点，然后在该点建立一套坐标系。

计算坐标时，通过测量数据的微分运算，计算出未知点的坐标。

具体的计算方法有高程分布的微分计算、立体观测的微分计算和等值线的微分计算等。

三角计算法是通过测量三角形的边长和角度来计算点的坐标。

其基本思想是根据三角函数的相关定理和公式，利用测量数据求解未知点的坐标。

三角计算法通常包括两个步骤：测量三角形和计算坐标。

测量三角形时，通过测量三角形的边长和角度，来获取所需的观测数据。

计算坐标时，利用测量数据和三角函数的关系，通过计算公式来求解未知点的坐标。

常用的三角计算法有正弦定理、余弦定理和正切定理等。

坐标计算在工程施工测量中具有重要的作用。

它可以提供工程设计和施工中所需的位置、尺寸和高程等参数，为工程建设提供基础数据。

在测量岗位工作已经有三个月到时间了，三个月的时间学习和收获了许多，现对这三个月的工作学习做一下总结。

测量工作容主要有以下两个方面：测量放线（坐标计算），高程控制。

一、测量放线测量放线到主要技术包括坐标计算和仪器使用。

坐标计算包括直线段坐标计算和曲线段坐标计算。

1、直线段坐标计算。

直线坐标计算分为中桩坐标计算和边桩坐标计算。

1）中桩坐标计算。

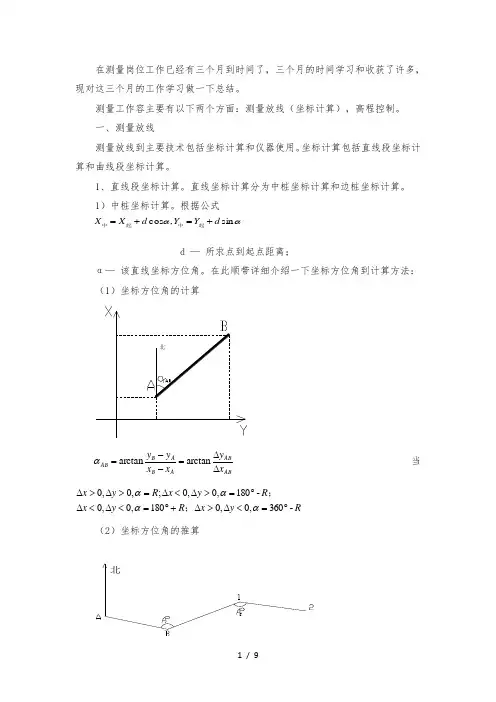
根据公式ααsin ,cos d Y Y d X X +=+=起中起中d — 所求点到起点距离；α— 该直线坐标方位角。

在此顺带详细介绍一下坐标方位角到计算方法： （1）坐标方位角的计算ABABA B A B AB x yx x y y ∆∆=--=arctan arctanα当Ry x R y x R y x R y x -360,0,0180,0,0-180,0,0;,0,0︒=<∆>∆+︒=<∆<∆︒=>∆<∆=>∆>∆αααα；；（2）坐标方位角的推算北，，218021*********βαβααβαβαα-︒+=-=+︒+=+=B B AB BA B 由此推出：βαα±︒+=180后前（“左”→“+”，“右”→“-”），计算中，若α值大于360°，应减去360°；若小于0°，则加上360°。

2）边桩坐标计算应用公式 )90sin(90cos(︒±+=︒±+=ααl y y l x x 中边中边）， 进行边桩坐标到计算。

北客站为直线车站，坐标计算较简单，现以位于机场线第二段底板的变电所夹层东北角C 点为例进行计算：以机场线右线为基准来计算中、边桩坐标。

已知起点坐标A （22264.4009，11553.2031），终点坐标B （22180.2655，11279.0739），起点里程为YDK0+255.275,C 点里程为YDK0+286.075,偏距为15.33m ，则由以上公式计算C 点坐标：α=arctan(（11279.0739-11553.2031）/（22180.2655-22264.4009）)+180°=252.938°，=中x 22264.4009+（286.075-255.275）*cos252.938°=22255.3640 =中y 11553.2031+（286.075-255.275）*sin252.938°=11523.7586 =c x 中x +15.33*cos （252.938°+90°）=22270.0193=c y 中y +15.33*sin （252.938°+90°）=11519.2606，则可求出C（22270.0193，11519.2606）。

《建筑工程测量》高斯坐标系一、高斯坐标系测量工作的基本任务是确定地面点的空间位置。

在工程测量中确定地面点的空间位置，通常需用三个量，即该点在一定坐标系下的三维坐标，或该点的二维球面坐标或投影到平面上的二维平面坐标，以及该点到大地水准面的铅垂距离（高程）。

为此，我们必须研究测量中所使用的坐标系。

地面点的坐标，可根据实际情况选用不同的坐标系，下面介绍几种用以确定地面点位的坐标系。

1.大地坐标系用大地经度L和大地纬度B表示地面点投影到旋转椭球面上位置的坐标，称为大地坐标系，亦称为大地地理坐标系。

该坐标系是以参考椭球面和法线作为基准面和基准线。

如图1-2所示，NS为椭球的旋转轴，N表示北极，S表示南极，O为椭球中心。

通过椭球心O与椭球旋转轴NS正交的平面称为赤道平面。

赤道平面与球面相交的纬线称为赤道。

过F点的法线（与旋转椭球面垂直的线）与赤道面的夹角，称为F点的大地纬度。

在赤道以北者为北纬或写成0°～90°N，在赤道以南者为南纬或写成0°～90°S。

过地面任一点与椭球旋转轴NS所组成的平面称为该点的子午面。

子午面与球面的交线称为子午线或经线。

国际公认通过英国格林尼治（Greenwich）天文台的子午面，是计算经度的起算面，称为首子午面。

过F点的子午面NFKSON与首子午面NGMSON所成的两面角，称为F点的大地经度。

它自首子午线向东或向西由0°起算至180°，在首子午线以东者为东经或写成0°～180°E，以西者为西经或写成0°～180°W。

大地坐标是由大地经度L、大地纬度B和大地高H三个量组成。

用以表示地面点的空间位置。

用大地坐标表示的地面点，统称大地点。

建国初期，我国采用的大地坐标系为“1954年北京坐标系”，亦称“北京—54坐标系”（简称P54。

该坐标系采用了原苏联的克拉索夫斯基椭球体，其参数是：长半轴a=6378.245km；扁率α=1/298.3；坐标原点位于原苏联的普尔科沃。

2000国家大地坐标系高程1. 介绍国家大地坐标系的背景国家大地坐标系是我国国家测绘局制定的一种地理坐标系统，用于描述地球表面上任一点的位置。

2000国家大地坐标系是在1980年国际地球参考系统（IGS）基础上制定的，它采用了全球大地测量系统（WGS 84）的椭球体参数，精度更高，适用范围更广。

2000国家大地坐标系的推出，标志着我国大地测量工作迈上了一个新的台阶，为国家的地理信息系统建设提供了更为准确的基础数据。

2. 2000国家大地坐标系的特点2000国家大地坐标系采用了椭球体和坐标系统的统一标准，其主要特点有：（1）高精度：2000国家大地坐标系采用了先进的大地测量技术和坐标转换方法，使得其精度比之前的坐标系有了大幅提高，能够更准确地描述地表上各个点的位置。

（2）全球适用：2000国家大地坐标系采用了WGS 84的椭球体参数，与国际通用的地理坐标系统兼容，使得其适用范围覆盖全球，为我国的地理信息数据与国际接轨提供了便利。

（3）标准统一：2000国家大地坐标系的推出，使得我国的地理信息数据统一了标准，为各行各业的数据交换和共享提供了良好的基础。

3. 高程数据在2000国家大地坐标系中的应用除了地理坐标数据外，高程数据也是地理信息系统中至关重要的数据之一。

在2000国家大地坐标系中，高程数据的应用主要有以下几个方面：（1）地形测绘：高程作为描述地表形态的重要数据，对地形的测绘和分析具有重要意义。

地图制图、地表变化分析等工作都需要高程数据的支持。

（2）工程建设：在道路、铁路、水利等工程建设中，高程数据是各种工程设计和施工的重要依据。

建设单位需要根据高程数据进行地形规划、路线选址等工作。

（3）资源调查：农林水利资源的规划开发，都需要高程数据进行资源定位和评估，高程数据对资源调查具有重要作用。

4. 2000国家大地坐标系高程数据的获取方法2000国家大地坐标系的高程数据可以通过多种手段进行获取，主要包括：（1）GPS测量：全球定位系统（GPS）是目前获取高程数据的常用手段，它能够实现对地表点位的准确测量，得出高程数据。

2000坐标系高程与85高程解释一、引言本文将对2000坐标系高程与85高程进行详细解释与比较。

首先，我们将介绍什么是2000坐标系高程以及85高程，并解释它们在地理测量和工程测量中的应用。

随后，我们将探讨二者之间的关系和差异，以及它们在实际应用中的使用建议。

二、2000坐标系高程2.1定义2000坐标系高程是一种用于描述地理位置高程的坐标系统。

它基于国际标准大地高系（In t er na ti on al Te rre s tr ia lR ef er en ceF r am e，简称I TR F）和国家大地基准系1985年高程修订二者结合而成。

2.2应用2000坐标系高程主要应用于全球定位系统（GP S）和地理信息系统（G IS）中，用于测量地球表面的高程。

由于其基于国际标准和修订，具有较高的精度和准确性，被广泛应用于地理测量、测绘、地质勘探等领域。

三、85高程3.1定义85高程是指根据大地水准面上某个点的高度与大地广义投影面（E ll ip so id al Pr oj e ct io nS ur fa ce）间的垂直距离而来的高程。

该高程使用的基准面是1985年提出的国家高程基准面。

3.2应用85高程主要应用于工程测量领域，如建筑物、道路、桥梁等工程的设计、施工和监测。

由于85高程直接与大地水准面相关，因此能够提供与地理位置具体相关的高程数据，满足工程测量的精度要求。

四、2000坐标系高程与85高程的关系2000坐标系高程与85高程是地理测量和工程测量中常用的高程描述方式。

它们之间存在一定的关系和差异。

4.1关系2000坐标系高程和85高程都是描述地理位置的高程，但它们使用的基准面和修订标准不同。

2000坐标系高程基于国际标准和修订，而85高程基于1985年的国家高程基准面。

4.2差异由于基准面和修订标准的不同，2000坐标系高程与85高程存在一定的差异。

在实际应用中，由于数据来源和处理方法的不同，两者之间可能存在一定的偏差。

工程测量坐标计算公式工程测量是工程建设的重要环节，准确的坐标计算是保证工程质量和施工安全的基础。

本文将介绍工程测量中常用的坐标计算公式，帮助读者更好地理解并应用于实践中。

一、坐标计算的基础知识在工程测量中，常用的坐标系统有直角坐标系和大地坐标系。

直角坐标系以某一点为原点，建立笛卡尔坐标系，用x、y、z三个轴线表示空间位置。

大地坐标系则以地球为基准，通过经度、纬度和高程来确定点的相对位置。

二、坐标计算公式1. 直角坐标系的坐标计算公式在直角坐标系中，常用的坐标计算公式有：- 两点间距离计算公式：设A点坐标为(x1, y1, z1)，B点坐标为(x2, y2, z2)。

则两点间的距离d计算公式如下：d = √((x2-x1)^2 + (y2-y1)^2 + (z2-z1)^2)- 点到直线距离计算公式：设点A的坐标为(x1, y1, z1)，直线方程为Ax + By + Cz + D = 0。

则A点到直线的距离d计算公式如下：d = |Ax1 + By1 + Cz1 + D| / √(A^2 + B^2 + C^2)- 点到平面距离计算公式：设点A的坐标为(x1, y1, z1)，平面方程为Ax + By + Cz + D = 0。

则A点到平面的距离d计算公式如下：d = |Ax1 + By1 + Cz1 + D| / √(A^2 + B^2 + C^2)2. 大地坐标系的坐标计算公式在大地坐标系中，常用的坐标计算公式有：- 两点间距离计算公式：根据两点的经纬度计算其球面距离，公式如下：d = R * arccos(sinφ1*sinφ2 + cosφ1*cosφ2*cos(λ2-λ1))其中，R为地球半径，φ为纬度，λ为经度。

- 两点间方位角计算公式：根据两点经纬度计算其中一点相对于另一点的方位角，公式如下：α = arctan((sinΔλ * cosφ2) / (cosφ1*sinφ2 -sinφ1*cosφ2*cosΔλ))其中，φ为纬度，λ为经度，Δλ为两点经度差。

工程测量中坐标系及投影面、投影带的选择摘要：在工程测量中，投影变形大地区工程坐标系的建立是一个敏感而困难的话题，建立坐标系的关键在于合理的选择投影面和投影带。

为了限制高斯投影长度变形，将椭球面按一定经度的子午线划分为不同的投影带或者为了抵偿长度变形选择某一个经度的子午线作为测区的中央子午线。

关键词：工程测量坐标系投影面投影带引言地面点空间位置描述需要选择一定的参照系和坐标系。

坐标系的建立是一切测量计算与地形测绘的基础。

本文主要介绍建立大地坐标系的基础和常用测量坐标系及其投影面的投影带的选择。

为了使工程控制网的网点坐标能不加改正的用于实际放样就必须限制投影后的边长变形。

当边长的综合变形较大而不能满足相应要求时可采用“抵偿高程面”或“任意带高斯正形投影”的方法来改善测区内边长经投影后的综合变形，通常根据工程测量的特点和要求,建立自己的区域坐标系。

而区域坐标系的建立,关键在于合理地选择投影带和投影面。

工程测量中几种可能采用的坐标系及选用方法选择坐标系的主要目的是解决长度变形问题,这种变形是由经过实测边长归化到椭球面上,再由椭球面化算到高斯平面上两次化算引起的。

1、坐标系1．1、坐标系的作用对于国家平面控制网而言，坐标系的主要任务和作用是满足我国各行各业基本建设和军事用途的需要。

为了对我国所有版图进行有效的测量和控制，全国必须布设一个统一的坐标系，以保证全国版图内坐标的统一、测绘资料管理和利用以及图纸的拼接。

1．2、常用坐标的表示形式1．2．1、空间直角坐标系坐标系原点位于参考椭球的中心，Z轴指向参考椭球的北极，X轴指向起始子午面与赤道的交点，Y轴位于赤道面上，且按右手系与X轴呈90°夹角。

某点在空间中的坐标可用该点在此坐标系的各个坐标轴上的投影来表示。

表示形式：X，Y，Z空间直角坐标系空间大地坐标系1．2．2、空间大地坐标系采用大地经度（L）、大地纬度（B）和大地高（H）来描述空间位置的。

纬度是空间的点与参考椭球面的法线与赤道面的夹角，经度是空间中的点与参考椭球自转轴所在的面与参考椭球的起始子午面的夹角，大地高是空间点沿参考椭球的法线方向到参考椭球面的距离。

⼯程测量坐标的问题第⼆节地⾯点位的表⽰⽅法⼀、地球的形状与⼤⼩(⼀) 地表状况：(⼆) 测量⼯作的基准线和基准⾯⼆、确定地⾯点位的⽅法1、地⾯点的⾼程2、地⾯点的坐标⼀、地球的形状与⼤⼩(⼀) 地表状况：1、地球(1) 地球是南北极稍扁，⾚道稍长，平均半径约为6371km的椭球.(2) 地球的⾃然表⾯有⾼⼭、丘陵、平原、盆地、湖泊、河流和海洋等，呈现⾼低起伏的形态，(3)珠峰8844.43m，马⾥亚那海沟11022m其中海洋⾯积约占71%，陆地⾯积约占29%.地球⾃然形体：是⼀个不规则的⼏何体，海洋⾯积约占地球表⾯的71%, 陆地⾯积约占29%。

2、地球的物理特性(1) 重⼒与铅垂线重⼒——地球上质点所受万有引⼒与离⼼⼒的合⼒。

铅垂线⽅向——重⼒⽅向。

(2) ⽔准⾯⾃由静⽌的⽔⾯，称为⽔准⾯。

理想的静⽌的封闭曲⾯即：受重⼒作⽤的海⽔分⼦呈静⽌状态⽽形成的重⼒等位⾯重⼒等位⾯：物体沿该⾯运动时,重⼒不做功(如⽔在这个⾯上不会流动)⽔准⾯的性质：①⽔准⾯处处与其相应的垂线垂直。

②潮汐影响，时刻不同⽔准⾯⾼度不同。

⽔准⾯有⽆穷个。

③同⼀⽔准⾯上各点重⼒位能相等。

⽔平⾯: 与⽔准⾯相切的平⾯(3）⼤地⽔准⾯：（是测量⼯作的基准⾯）将平均静⽌的海⽔⾯穿过岛屿、陆地所形成的闭合曲⾯。

它是特定的重⼒等位⾯，它是唯⼀的。

由于地表起伏以及地球内部质量分布不均匀，使铅垂线⽅向产⽣不规则变化，故⼤地⽔准⾯是⼀个复杂的曲⾯（全球有100多⽶的⾼低起伏）(4）⼤地体：⼤地⽔准⾯所包围的地球实体。

代表了地球的形状和⼤⼩。

由于其不规则，⽆法⽤数学公式表达。

提出问题：可否⽤⼀个形状和⼤⼩⾮常接近于⼤地体，并可⽤数学公式表⽰的⼏何形体来代替地球的形状3、参考椭球体：⾮常接近于⼤地体，并可⽤数学公式表⽰的⼏何形体（即旋转椭球）来代替地球的形状。

旋转椭球：它由⼀个椭圆NESW绕其短轴NS旋转⽽成的形体。

在图1-2中，O是椭球中⼼，NS是椭球的旋转轴，a是长半轴，b是短半轴。

《建筑工程测量》高斯坐标系一、高斯坐标系测量工作的基本任务是确定地而点的空间位置。

在工程测量中确定地而点的空间位置，通常需用三个量，即该点在一定坐标系下的三维坐标，或该点的二维球而坐标或投影到平而上的二维平而坐标，以及该点到大地水准面的铅垂距离（高程）。

为此，我们必须研究测量中所使用的坐标系。

地面点的坐标，可根据实际情况选用不同的坐标系，下而介绍几种用以确定地而点位的坐标系。

1.大地坐标系用大地经度L和大地纬度B表示地而点投影到旋转椭球面上位置的坐标，称为大地坐标系，亦称为大地地理坐标系。

该坐标系是以参考椭球面和法线作为基准而和基准线。

如图1-2所示，NS为椭球的旋转轴，N表示北极，S表示南极，0为椭球中心。

通过椭球心0与椭球旋转轴NS正交的平面称为赤道平面。

赤道平面与球而相交的纬线称为赤道。

过磧的法线（与旋转椭球面垂直的线）与赤道面的夹角，称为尸点的大地纬度。

在赤道以北者为北纬或写成0。

〜90。

N, 在赤道以南者为南纬或写成0°〜90° So过地面任一点与椭球旋转轴NS所组成的平面称为该点的子午面。

子午面与球面的交线称为子午线或经线。

国际公认通过英国格林尼治(Greenwich)天文台的子午面，是计算经度的起算面，称为首子午面。

过尸点的子午而NFKSON与首子午而NGMSON所成的两而角，称为F点的大地经度。

它自首子午线向东或向西由0。

起算至180。

，在首子午线以东者为东经或写成0°〜180° E,以西者为西经或写成0°〜180° Wo大地坐标是由大地经度L、大地纬度B和大地高H三个量组成。

用以表示地面点的空间位置。

用大地坐标表示的地面点，统称大地点。

建国初期，我国采用的大地坐标系为“1954年北京坐标系”，亦称“北京一54坐标系”(简称為。

该坐标系采用了原苏联的克拉索夫斯基椭球体, 其参数是：长半轴沪6378. 245km；扁率a =1/298. 3；坐标原点位于原苏联的普尔科沃。

2000坐标系对应的高程系统2000坐标系是一种用于描述地球表面特定位置的坐标系统，同时也包含了对应的高程系统。

它是国际上广泛使用的坐标系之一，可以用来标识和测量地球上的各种地理要素和现象。

在本文中，我们将探讨2000坐标系的定义、应用和在观测和测量中的指导意义。

首先，2000坐标系是以地球形状和轴向进行建模的数学模型。

它使用了世界地球坐标系统（WGS 84）作为基准，以实现地球表面的一致性和统一性。

这意味着无论我们身处地球的哪个角落，使用2000坐标系可以确保我们所测量和定位的地点都是准确无误的。

2000坐标系的高程系统是与地球表面上特定点的高度相关的数值定义。

它使用海平面作为参考基准，即将海平面设为零点，然后根据采样点的相对位置进行相应的测量和计算。

高程系统的应用非常广泛，它对于工程设计、地质勘探、水文学研究等领域都具有重要意义。

通过了解地球表面上各点的高程信息，我们可以更好地了解地理特征的分布和地形的复杂性。

在实际观测和测量中，2000坐标系的指导意义是不言而喻的。

首先，它提供了一个标准的坐标系统，使得地理空间信息可以更加方便、准确地进行采集和处理。

这对于地图绘制、导航和位置服务等应用至关重要。

其次，高程系统的引入使得我们可以更加准确地描述和分析地球表面的起伏和形态，从而为城市规划、土地利用和环境保护等工作提供了重要的参考依据。

此外，2000坐标系还具有良好的可兼容性和可扩展性，可以与其他坐标系和高程系统进行转换和整合，进一步提高数据的可用性和共享性。

综上所述，2000坐标系是一种全面、准确、可靠的地理信息标识系统，它在地理测量和观测中具有重要的指导意义。

通过使用2000坐标系，我们可以更好地理解和利用地球表面的地理资源，为各种应用提供有力支持。

随着技术的不断发展和应用的不断拓展，2000坐标系将继续发挥其重要作用，并为未来的地理信息科学做出更大的贡献。