下载文档原格式
机械工程控制基础考试题及答案机械工程控制基础是机械工程专业中非常重要的一个方面，掌握该领域的基本知识对机械工程师的工作至关重要。
在进行机械工程控制基础考试时，掌握学科基础知识与技巧应是首要准备，同样重要的还有解题能力。
因此，我们在此提供几道机械工程控制基础考试题及答案供大家参考。
1. 下列哪些控制系统是模糊控制系统？A. 摆线刀切削力控制系统B. 滤波器控制系统C. 股票市场交易系统D. 空调控制系统正确答案：A、C、D。
模糊控制系统是一种以模糊逻辑为基础，实现对复杂非线性系统的控制的一种方法。
股票市场交易系统属于复杂非线性系统，可以用模糊控制系统进行控制。
2. 控制系统的传递函数为：G(s) = 1 / [(s + 1)(s + 3)]，求其单位阶跃响应。
正确答案：G(s)的单位阶跃响应为：Y(s) = [1 / (s + 1)] - [1 / (s + 3)]，通过部分分式分解得到Y(t) = 1/2 - 1/2e^(-2t)。
因此，该系统的单位阶跃响应为Y(t) = 1/2 - 1/2e^(-2t)。
3. 下列哪个量不是PID控制器中的一个参数？A. 比例系数B. 积分时间C. 微分时间D. 控制信号正确答案：D。
PID控制器包括比例控制、积分控制和微分控制三个部分，分别由比例系数、积分时间和微分时间控制。
4. 一个反馈控制系统的开环传递函数为：G(s) = 1 / (s -1)，闭环传递函数为：H(s) = G(s) / (1 + G(s)), 求该控制系统的稳态误差。
正确答案：该控制系统的稳态误差为0。
5. 已知一个控制系统稳定，其零极点分布情况如下：零点为s= -1, -2；极点为s = -3, -4，判断该系统稳定类型。
正确答案：由于该控制系统的极点均位于左半平面，因此该控制系统稳定。
6. 下列哪种控制模式比例带宽越大，相对带宽越小？A. 位置控制模式B. 速度控制模式C. 加速度控制模式D. 跟踪控制模式正确答案：B。
第1页（共9页）《机械工程控制基础》试卷（A 卷）一、填空题（每空1分, 共20分）1.对控制系统的基本要求是 系统的稳定性 、 响应的快速性 、 响应的准确性 。
2.已知f(t)=t+1,对其进行拉氏变换L[f(t)]= 1/s2+1/s 或者（1+s ）/s2 。
3.二阶系统的极点分别为s1=−0.5,s2=−4, 系统增益为2, 则其传递函数G(S)= 2/(s+0.5)(s+_4)4.零频幅值A(0)表示当频率 接近于零时, 闭 环系统输出的幅值与输入幅值之比。
5、工程控制论实质上是研究工程技术中广义系统的动力学问题, 机械工程控制就是研究系统、输入、输出三者之间的动态关系。
6、系统的频率特性求取有三种方法: 根据系统响应求取、用试验方法求取和将传递函数中的s 换为 jw 来求取。
8、微分环节的控制作用主要有 使输出提前 、 增加系统的阻尼 、 强化噪声 。
9、二阶系统的传递函数为 , 其中 为系统的 无阻尼固有频率 , 当 时为 欠阻尼 系统。
在阻尼比ξ<0.707时, 幅频特性出现峰值, 称谐振峰值, 此时的频率称谐振频率ωr ＝ 。
10、一般称能够用相同形式的数学模型来描述的物理系统成为相似系统。
11.对自动控制系统按照输出变化规律分为自动调节系统、随动系统、程序控制系统。
12.对积分环节而言, 其相频特性∠G(jw)=-900。
二、名词解释（每个4分, 共20分）1.闭环系统: 当一个系统以所需的方框图表示而存在反馈回路时, 称之为闭环系统。
2、系统稳定性：指系统在干扰作用下偏离平衡位置, 当干扰撤除后, 系统自动回到平衡位置的能力。
3.频率特性: 对于线性定常系统, 若输入为谐波信号, 那么稳态输出一定是同频率的谐波信号, 输出输入的幅值之比及输出输入相位业班级： 姓名： 学号：……………密………………………………封………………………………线…………………………第2页（共9页）之差统称为频率特性。
全国2002年10月自学考试机械工程控制基础试卷一、单项选择题(在每小题的四个备选答案中选出一个正确答案，并将其号码填在题干的括号内。
每小题1。
5分,共30分）1.控制工程主要研究并解决的问题之一是( ) A 。
系统已定,输入不确定，求系统的输出B 。
系统已定,输入已知，求系统的输出(响应） C.系统已定，规定系统的输入D.系统不定，输入已知，求出系统的输出(响应)2.f(t ）如图所示 则L ［f （t)］为( ）A 。
s 1e —2t B. s 2e -2s C 。
s 1e —2s D 。
s1e —ts3.已知F （s)=1)s(s 1+,则L -1[F （s ）］为( ）4。
已知F(s)=L ［f （t)]，若F(s ）=12s s 12++，则f(t ）｜t ∞→=?( )A 。
21 B 。
1 C 。
31D.0 5.下列系统中为线性系统的微分模型为：（ )A.dt)t (dx )t (x )dt )t (dx (12dt )t (x d 16i 020202=++ B.)t (x )t (x 24dt)t (dx 12dt )t (x d 16i 00202=++C.)t (x )t (x 24dt)t (dx 12)dt )t (x d (16i 002202=++ D 。
)t (x )t (x )t ln(24dt)t (dx 12e dt )t (x d 16i 00t 202=⋅+⋅+ 6。
对于定常控制系统来说，（ ）A 。
表达系统的微分方程各项系数不随时间改变B 。
微分方程的各阶微分项的幂为1 C.不能用微分方程表示 D.系统总是稳定的7.系统方框图如图所示，则系统的闭环传递函数为( ）A 。
G(S)H(S)1G(S)H(S)+B.G(S)-1H(S)G(S)⋅C 。
1+G(S ）·H （S)D 。
G(S)H(S)1G(S)+8.二阶系统的传递函数为4)0.5)(s (s 10++,则系统增益为( ）A 。
《机械控制工程基础》习题及解答目录第１章绪论第２章控制系统的数学模型第３章控制系统的时域分析第４章控制系统的频域分析第５章控制系统的性能分析第６章控制系统的综合校正第７章模拟考试题型及分值分布第1章绪论一、选择填空题1.开环控制系统在其控制器和被控对象间只有（正向作用）。
P2A.反馈作用B.前馈作用C.正向作用D.反向作用2.闭环控制系统的主反馈取自（被控对象输出端）。
P3A.给定输入端B.干扰输入端C.控制器输出端D.系统输出端3.闭环系统在其控制器和被控对象之间有（反向作用）。
P3A.反馈作用B.前馈作用C.正向作用D.反向作用A.输入量B.输出量C.反馈量D.干扰量4.自动控制系统的控制调节过程是以偏差消除（偏差的过程）。
P2-3A.偏差的过程B.输入量的过程C.干扰量的过程D.稳态量的过程5.一般情况下开环控制系统是（稳定系统）。
P2A.不稳定系统B.稳定系统C.时域系统D.频域系统6.闭环控制系统除具有开环控制系统所有的环节外，还必须有(B)。
p5A.给定环节B.比较环节C.放大环节D.执行环节7.闭环控制系统必须通过（C）。
p3A.输入量前馈参与控制B.干扰量前馈参与控制C.输出量反馈到输入端参与控制D.输出量局部反馈参与控制8.随动系统要求系统的输出信号能跟随（C的变化）。
P6A.反馈信号B.干扰信号C.输入信号D.模拟信号9.若反馈信号与原系统输入信号的方向相反则为（负反馈）。
P3A.局部反馈B.主反馈C.正反馈D.负反馈10．输出量对系统的控制作用没有影响的控制系统是（开环控制系统）。
P2A.开环控制系统B.闭环控制系统C.反馈控制系统D.非线性控制系统11.自动控制系统的反馈环节中一般具有（B ）。
p5A..给定元件B.检测元件C．放大元件D．执行元件12. 控制系统的稳态误差反映了系统的〔 B 〕p8A. 快速性B.准确性C. 稳定性D.动态性13.输出量对系统的控制作用有直接影响的系统是（B ）p3A.开环控制系统B.闭环控制系统C.线性控制系统D.非线性控制系统14.通过动态调节达到稳定后，被控量与期望值一致的控制系统为（无差系统）。
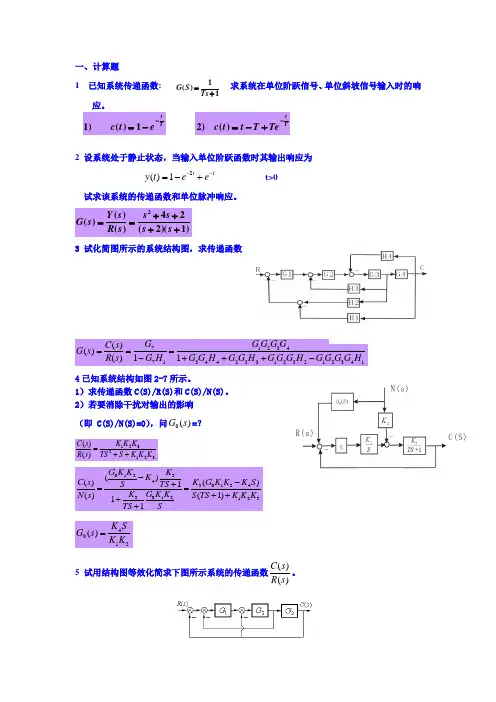
一、计算题1 已知系统传递函数:求系统在单位阶跃信号、单位斜坡信号输入时的响应。
2 设系统处于静止状态，当输入单位阶跃函数时其输出响应为2()1t t y t e e --=-+ t>0试求该系统的传递函数和单位脉冲响应。
3 试化简图所示的系统结构图，求传递函数4已知系统结构如图2-7所示。
1）求传递函数C(S)/R(S)和C(S)/N(S)。
2）若要消除干扰对输出的影响 （即 C(S)/N(S)=0），问0()G s =？5 试用结构图等效化简求下图所示系统的传递函数)()(s R s C 。
11)(+=Ts S G6 系统结构图如图3-1所示。
（1）当r(t)=t，n(t)=t时，试求系统总稳态误差；（2）当r(t)=1(t)，n(t)=0)时，试求M p，t p。
图3-1=sse7某控制系统如图所示。
其中控制器采用增益为K p的比例控制器，即G c(s)=K p试确定使系统稳定的K p值范围。
0<K p<158 控制系统的结构图如图所示，若系统以频率ω=2rad/s持续振荡，试确定相应的参数K 和τ的值0.75τ= K=29 系统如图所示，其中扰动信号n(t)=1(t)。
仅仅改变K1的值，能否使系统在扰动信号作用下的误差终值为-0.099?不能10已知系统特征方程为06363234=++++ssss，判断该系统的稳定性，若闭环系统不稳定，指出在s平面右半部的极点个数。
(要有劳斯计算表)S平面右半部有2个闭环极点，系统不稳定。
11 一控制系统的单位阶跃响应为tt eetc10602.12.01)(---+=,求1) 系统的闭环传递函数;2) 计算系统的无阻尼自然频率n ϖ和系统的阻尼比ξ。
12 已知闭环系统的特征方程如下： １）01.023=+++K s s s ２）036134234=++++K s s s s 试确定系统稳定的K 值范围。
360;100<<<<K K14 一单位反馈控制系统的开环传递函数为)1.01(10)(s s s G +=１）求系统的静态误差系数p K 、v K 和a K ； ２）当输入221021)(t a t a a t r ++=时，求系统的稳态误差。
1、简答题1、控制系统的基本要求。
1）、简述闭环控制系统的组成。
测量元件，给定元件，比较元件，放大元件，执行元件，校正元件2）、非最小相位系统有何特点，与最小相位系统的区别是什么？第二题在复平面【s】右半平面没有极点和零点的传递函数称为最小相位传递函数，反之，在【s】右半平面有极点和零点的传递函数称为非最小相位传递函数。
具有最小相位传递函数的系统统称为最小相位系统，反之，具有非最小相位传递函数的系统称为最小相位系统3）、简述系统串联滞后校正网络的校正原理。
此滞后校正环节是一个低通滤波器，因为当频率高于1/T时，增益全部下降20lgb(db)，而相位减小不多。
如果把这段频率范围的增益提高到原来的增益直，当然低频段的增益就提高了。
4）、简述系统超前校正网络的校正原理在对数幅频特性曲线上有20db/dec段存在，故加大了系统的剪切频率Wc、谐振频率Wr与截止频率Wb，其结果是加大了系统的带宽，加快了系统的响应速度；又由于相位超前，还可能加大相位裕度，结果是增加了系统相位稳定性。
5）、减小或消除系统稳态误差的措施主要有哪些？1：增大系统开环增益或扰动之前系统的前向通道增益2：在系统的前向通道或主反馈通道设置串联积分环节3：采用串级控制抑制内回路扰动。
6）、简要说明比例积分微分PID控制规律中P、I和D的作用(1)比例系数Kp直接决定控制作用的强弱，加大Kp可以减小系统的稳定误差，提高系统的动态响应速度，但Kp过大会使动态质量变坏，引起被控制量震荡甚至导致闭环系统不稳定(2)在比例的调节的基础上加上积分控制可以消除系统的稳态误差，因为只要存在偏差，它的积分所产生的控制量总是用来消除稳态误差，直到积分的直为零，控制作用才停止(3)微分的控制作用是跟偏差的变化速度有关。
2.已知控制系统的结构图如下图所示，求：（1）当不存在速度反馈)0(=a时，试确定单位阶跃输入动态响应过程的rt，st和%σ。
（1）a=0时，()()42G ss s=+，()2424ss sΦ=++，所以0.5,2nζω== rt=，pt=，%eσ=（2）确定0.7ζ=时的速度反馈常数a值，并确定ttr=)(时系统的稳态误差sse。
《机械控制工程基础》课程习题集一、单选题1. t e 2-的拉氏变换为（ ）。
A.s21； B. 15.0+s ； C. 21+s ；D.21se 2- 2. )(tf 的拉氏变换为)2(6][+=s s s F ，则)(t f 为（ ）。
A. te23-； B. te21--； C. )1(32t e --； D. te26-3. 脉冲函数的拉氏变换为（ ）。
A. 0 ；B. ∞；C. 常数；D. 变量4. ()t t f δ5)(=，则=)]([t f L （ ）。
A. 5 ；B. 1 ；C. 0 ；D.s55. 已知)52)(2(33)(22+++++=s s s s s s s F ，其原函数的终值=∞→t t f )(（ ）。
A. ∞ ； B. 0 ； C. 0.6 ； D. 0.36. 已知)45(32)(22++++=s s s s s s F ，其原函数的终值=∞→t t f )(（ ）。
A. 0 ；B. ∞ ；C. 0.75 ；D. 37. 已知sn e sa s F τ-=2)(其反变换f (t)为（ ）。
A.)(ττa t n a -⋅； B. )(τn t a -⋅； C. τn te a -⋅； D. )(1τn t a-⋅ 8. 已知)1(1)(+=s s s F ，其反变换f (t)为（ ）。
A. te -1； B. te -+1； C. te --1； D. 1--te9. 已知t e t f t 2sin )(-=的拉氏变换为（ ）。
A.se s 2242-+ ； B. 4)4(22++s ； C.4)1(2++s s； D.se s s 224-+ 10. 图示函数的拉氏变换为（ ）。
A.)1(12s e s a ττ--； B. )1(12s e s a ττ--； C. )1(1se s a ττ--；D. )1(12s e sa ττ- 11. 若)(∞f =0，则][s F 可能是以下（ ）。
机械工程控制基础复习题第一章绪论1、以同等精度元件组成的开环系统和闭环系统，其精度比较（）。
A .开环咼 B.闭环咼 C.相差不多 D. 一样咼1、系统的输出信号对控制作用的影响（)°A .开环有 B.闭环有 C.都没有 D.都有1、对于系统抗干扰能力（)°A .开环强 B.闭环强 C.都强 D.都不强1、下列不属于按输入量的变化规律分类的是（)°A . 恒值控制系统 B.计算机控制系统 C.随动控制系统 D.程序控制系统1、按照系统传输信号的类型可分成（）。
A .定常系统和时变系统 B.离散控制系统和连续控制系统 C.线性系统和非线性系统 D.恒值系统和程序控制系统1 •按照控制系统是否设有反馈作用来进行分类，可分为 ______________ 和____________ 。
答案：开环控制系统闭环控制系统1 .对一个自动控制系统的最基本要求是 ______________ ，也即_________ 是系统工作的首要条件。
答案：稳定稳定性1 •对控制系统性能的基本要求一般可归结为稳定性、 ___________ 和____________ 。
答案：快速性准确性1、控制论的中心思想是，通过____________ , _____________ 和反馈来进行控制。
答案：信息的传递加工处理1•什么是反馈（包括正反馈和负反馈）?根据反馈的有无，可将控制系统如何分类？答案：（1）反馈是指输出量通过适当的检测装置将信号全部或一部分返回输入端，使之与输入量进行比较。
如果反馈信号与系统的输入信号的方向相反，则称为负反馈；如果反馈信号与系统的输入信号的方向相同，则称为正反馈。
（2 ）根据反馈的有无，可将控制系统分为开环控制系统和闭环控制系统。
1•何为闭环控制系统？其最主要的优点是什么？答案：闭环控制系统就是反馈控制系统，即输出量对控制作用有影响的系统。
其最主要的优点是能实现自我调节，不断修正偏差，抗干扰能力强。
机械控制工程基础第二版课后答案机械控制工程基础第二版课后答案【篇一：《控制工程基础》王积伟_第二版_课后习题解答(完整)】解：1)工作原理：电压u2反映大门的实际位置，电压u1由开（关）门开关的指令状态决定，两电压之差△u＝u1－u2驱动伺服电动机，进而通过传动装置控制大门的开启。
当大门在打开位置，u2＝u 上：如合上开门开关，u1＝u上，△u＝0，大门不动作；如合上关门开关，u1＝u下，△u0，大门逐渐关闭，直至完全关闭，使△u＝0。
当大门在关闭位置，u2＝u下：如合上开门开关，u1＝u上，△u0，大门执行开门指令，直至完全打开，使△u＝0；如合上关门开关，u1＝u下，△u＝0，大门不动作。
2)控制系统方框图4解：1)控制系统方框图2)工作原理：a)水箱是控制对象，水箱的水位是被控量，水位的给定值h’由浮球顶杆的长度给定，杠杆平衡时，进水阀位于某一开度，水位保持在给定值。
当有扰动（水的使用流出量和给水压力的波动）时，水位发生降低（升高），浮球位置也随着降低（升高），通过杠杆机构是进水阀的开度增大（减小），进入水箱的水流量增加（减小），水位升高（降低），浮球也随之升高（降低），进水阀开度增大（减小）量减小，直至达到新的水位平衡。
此为连续控制系统。
b) 水箱是控制对象，水箱的水位是被控量，水位的给定值h’由浮球拉杆的长度给定。
杠杆平衡时，进水阀位于某一开度，水位保持在给定值。
当有扰动（水的使用流出量和给水压力的波动）时，水位发生降低（升高），浮球位置也随着降低（升高），到一定程度后，在浮球拉杆的带动下，电磁阀开关被闭合（断开），进水阀门完全打开（关闭），开始进水（断水），水位升高（降低），浮球也随之升高（降低），直至达到给定的水位高度。
随后水位进一步发生升高（降低），到一定程度后，电磁阀又发生一次打开（闭合）。
此系统是离散控制系统。
2-1解：（c）确定输入输出变量（u1，u2）u1?i1r1?i2r2u2?i2r2u1?u2?1c(idt2i1)dt得到：cr2du2(1?r2r1)u2?cr2du1dtr2r1u1一阶微分方程（e）确定输入输出变量（u1，u2）u1?ir1?ir2? i? u1?u2r1cidt消去i得到：(r1?r2)一阶微分方程du2dtu2cr2du1dtu1c第二章2-2解：1）确定输入、输出变量f(t)、x2 f(t)?fk1(t)?fb1(t)?fb3(t)?m1fb3?f fm2dx2(t)dtdx1dt22dx1(t)dt222）对各元件列微分方程：k2b2fk1?k1x1;fb1?b1fb3?b3d(x1?x2)dt;fk2?k2x223）拉氏变换：f(s)?k1x1(s)?b1sx1(s)?b3s[x1(s)?x2(s)]?m1sx1(s)b3s[x1(s)?x2( s)]?k2x2(s)?b2sx2(s)?m2sx2(s)24）消去中间变量：f(s)?b3sx2(s)?(b1s?k1?b3s?m1s)2b3s?k2?b3s?m2sb3s2x2(s)5）拉氏反变换：m1m2dx2dt44(b1m2?b2m1?bsm2?b3m1)dx2dtdx2dt33(b1b3?b1b2?bsb2?k1m2?m1k2)dfdtdx2dt22(k1b2?k1b3?k2b1?k2b3)?k1k2x2?b32-3 解：（2）2s?11s?22e?t?e?2t （4）199s?4e4t19119s?1t1123(s?1)te?13te1(s?1)2（5）?2(s?2)2(s?1)2e?2t?2e?t?te?t （6）0.25?2ss?420.5?2?2s?422s?12.5st0.5cos2t?sin2t?2e?2.52-5解：1)d(s)=0,得到极点：0,0,-2,-5m(s)=0,得到零点：－1，??，??，?? 2) d(s)=0,得到极点：－2，－1，－2 m(s)=0,得到零点：0，0，－1 3) d(s)=0,得到极点：0， ?1?j3，1?j32m(s)=0,得到零点：－2，??，??4) d(s)=0,得到极点：－1，－2，?? m(s)=0,得到零点：??2-8解：1）a）建立微分方程mx(t)?f(t)?fk1(t)?fk2(t)f(t)?abfi(t)fk1(t)?k1x0(t)fk2(t)?k2(x0(t)?x(t))fk2(t)?fb(t)?bdx(t)dtb)拉氏变换msx0(s)?f(s)?ff(s)?abfi(s)2k1(s)?fk2(s)fk1(s)?k1x0(s)fk2(s)?k2(x0(s)?x(s))fk2(s)?bsx(s)c)画单元框图（略）d)画系统框图mx0(t)?fk(t)?fb1(t)?fb2(t)fk(t)?k(xi(t)?x0(t))2)a)建立微分方程：fb1(t)?b1fb2(t)?b2d(xi(t)?xo(t))dtdxo(t)dtmsxo(s)?fk(s)?fb1(s)?fb2(s)2b)拉氏变换：fk(s)?k(xi(s)?xo(s))fb1(s)?b1s(xi(s)?xo(s))fb2(s)?b2sx0(s)c)绘制单元方框图（略）4)绘制系统框图【篇二：机械工程控制基础第二版答案】p> 234【篇三：2机械控制工程基础第二章答案】是线性系统?其最重要的特性是什么?下列用微分方程表示的系统中,xo表示系统输出,xi表示系统输入,哪些是线性系统? (1) ??o?2x (3) ??o?2x2x?2x (2) 2x??2tx?2x xxxoooioooi2x?2x(4) 2xx??2tx?2x xxooiooooi解: 凡是能用线性微分方程描述的系统就是线性系统。
祝守新邢英杰韩连英《机械工程控制基础》习题解答机械控制工程基础答案提示第二章系统的数学模型2-1试求如图2-35所示机械系统的作用力F(t)与位移y(t)之间微分方程和传递函数。
F(t)图2-35题2-1图解：依题意：d2ytadytmFtfkytdt2bdtd2ytdytafkytFt故m2dtbdtY传递函数:G2Fmfk2-2对于如图2-36所示系统，试求出作用力F1(t)到位移某2(t)的传递函数。
其中，f为粘性阻尼系数。
F2(t)到位移某1(t)的传递函数又是什么？图2-36题2-2图解：依题意：d2某1td某1td某2t对m1：F1k1某1tfm12dtdtdt对两边拉氏变换：F1k1某1f某1某2m12某1①d2某2td某1td某2t对m2：F2tfk2某2tm2dt2dtdt对两边拉氏变换：F2f某1某2k2某2m22某2②m12fk1某1f某2F1故：2f某1m2fk2某2F2SF1m22fk2fF2某12m12fk1m22fk2f故得：2fF1F2m1fk2某2222mfkmfkf1122故求F1t到某2t的传递函数令：F20某2fG1F1m12fk1m22fk2f2fm1m24fm1m23m1k2m2k12fk1k2k1k2求F2t到某1t的传递函数令：F10某1fG1F2m12fk1m22fk2f22-3试求图2-37所示无源网络传递函数。
fm1m24fm1m23m1k2m2k12fk1k2k1k2o图2-37题2-3图解（a）系统微分方程为i1tdti2tR1Cuii2tR1itR2u0itR2iti1ti2t拉氏变换得I1R1I2CUiI2R1I1R2U0I1R2II1I2R2R1C1U0R2CR11R1R2消去中间变量I1,I2,I得：GR1R2UiR1R2CR11C1R1R2（b）设各支路电流如图所示。
系统微分方程为uitR1i3tu0tR1i3tL11234di2tdtu0ti4tdtC2di5tdtu0tR2i6tu0tL25i2ti3ti4ti5ti6t6由（1）得：UiR1I3Uo由（2）得：R1I3L1I2由（3）得：Uo i4C2由（4）得：UoL2I5由（5）得：UoR2I6由（6）得：I2I3I4I5I6故消去中间变量I1,I2,I3,I4,I5,I6得：L2L1UL1o1L2R1UiL1L2LC2L1L2R1R2L2112L1L2R1R22-4证明Lcot22证明：设ftcot由微分定理有Ld2ft2Ff0f(1)0dt2由于f0co01，f0in00，d2ftdt22cot将式（2）各项带入式（1）中得L2cot2F即2F2F整理得F222-5求f(t)122t的拉氏变换。
方法一： t s = 4T = 60s, T =15s 方法二：02.098.011)()()(/=-=-=-=-T t o i e t x t x t e02.0ln 102.0/=-⇒=-Te T t 输入：x i =(t )=10t （设初始温度为零） 输出：21011)(11)(s Ts s X Ts s X i o +=+=)0)((10)(110)(0≥+-=⎥⎥⎦⎤⎢⎢⎣⎡-=--⎰t Te T t d t e T t x Tt t T o τττ[])C (5.214110110)(10o lim =⋅⋅=⎪⎪⎭⎫⎝⎛-=-=-∞→∞→∞→T tt t o t eT t x t e 3.6单位阶跃响应——教材p73 单位脉冲响应——教材p72 单位斜坡响应：输入：x i =(t )=t （设初始值为零）输出: 2111)(11)(s Ts s X Ts s X i o +=+=)0)(()(1)(0≥+-=⎥⎥⎦⎤⎢⎢⎣⎡-=--⎰t Te T t d t e T t x Ttt T o τττ3.15Ks KK s Ks K s K s Ks X s X s G f fi ++=++==2220)1(111)()()( 22202)()()(n n n i s s s X s X s G ωξωω++== %25%100)1/exp(2=⨯--=ξξp p M ξ = 0.404 )s (212=-==ξωp ωp n d p t )s /1(717.1404.012122=-=-=pξpωp n t)/s 1(95.222==n K ω, f K K 21=ξ, /s)1(47.0717.1404/022=⨯==KK f ξ10)210(1010)210(1010)210(1010)2()1(10)1(10)()()(2220+++++++=++++=++++==s K s s K s K s s K s sK s s s K s K s X s X s G h h h h h h h i)(10)()(11s sG K s G s G h +=, 22221210)210(10)(nn n h s s s K s s G ωξωω++=+++= )10.4.3()0(1arctg sin 11)exp(1)(221≥⎪⎪⎭⎫⎝⎛-+---=t t t t x d n o ξξωξξω )1arctg cos 1arctg sin 1)(exp()0(1arctg cos 1)exp(1arctg sin 11)exp()())((2222222111⎪⎪⎭⎫⎝⎛-++⎪⎪⎭⎫ ⎝⎛-+--=≥⎪⎪⎭⎫ ⎝⎛-+--+⎪⎪⎭⎫ ⎝⎛-+--==-ξξωξξωξξξωωξξωξωξωξξωξξωξωt t t t t t t t dt t dx s sG L d d n n d d n d n n o⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-++⎪⎪⎭⎫ ⎝⎛-+----=+=ξξωξξωξξωξω222111arctg cos 1arctgsin 11)exp(1)(10)()(t t t t xK t x t x d d nn o h o o & (1) 2102,102+==h n n K ξωω; 116.010/)2(,5.0=-==n h K ωξ(2); M p =17.7%(3) 未校正2022********)(nn n s s s s s G ωωξω++=++= 10/1,22,1002===ξξωωn n =0.31623, M p =35%3.17 01.0)5)(1(1lim111lim 020=++=⋅+=→→s s s Kss GH ss s ss ε, 5/K =0.01, K =500.3.18 (1)544)14/(41)14/(40+=+++=s s s X X i , i i i X s s X s X X E 5414)5441(0++=+-=-=, sX i 1=, 2.05115414lim 0==⋅++=→s s s ss ssX i ε (2) 2.0511)14/(41131lim lim 000==⋅+++==→→s s s s N N X s s s ssNε(3) 系统误差: 4.02.02.0=+=+=ssN ssX ss i εεε4.2 位移的稳态输出X o (ω)与力的输入幅值X i 及相位∠G(j ω)之组合：)()()()()(j )(j )(j ωϕωϕωωωωωj io j i o eX X e A G X X =⋅== 称为动态柔度，位移/力, 记R (j ω)。
记刚度为 K (j ω),刚度=柔度－1 K (j ω)=1/R (j ω)ω=0时的刚度称为静刚度。
记 K(0)。
刚度随ω而变，可见，ω不同，系统的刚度不同。
过去，在力学学科中的刚度为静刚度。
对阶跃输入，动态柔度：()22202)()()(n n ni s s s j X j X j R ωξωωωωω++== (m/N)动态刚度：()22212)()()()(nnn o i s s s j X j X j R j K ωωξωωωωω++===- (N/m) 4.3 动态柔度：(mm/kgf)12)(j j ωω=+=s s R , 动态刚度：(kgf/mm)2j 121)(j j ωωω+=+==s s K ； 静刚度：(kgf/mm)21)(j 0==ωωK 4.6 mks m c s m k cs ms s f s X s G ++=++==22011)()()(=2222211n n nn s s m ωξωωω++ 标准形式：22202)()(n n n i s s s X s X ωξωω++=, 令mk n =2ω，m c n =ξω2 则：222222221211)(n n n nn n n s s k s s m s G ωξωωωξωωω++=++= 对标准形式：(p107) )10.1.4()](j sin[|)(j |)(lim )(ωωωG t X G t x t x i o t oss ∠+==∞→由，(p113:) o 90)(j ),2/(1)(j ,,1-=∠===ωξωωωλG G n,2==n ωω(N/m)41222=⨯==m k nω 21|)(j |==i i X X G ω, ),2/(1)(j ξω=G 2/1/1)2/(1==i X ξ,1=ξs/m)(N 412122⋅=⨯⨯⨯==m c n ξω4.9(1) t t t t t t x i cos 21sin 2330sin cos 30cos sin )30sin()(+=︒+︒=︒+= ))arctg(sin(123)(221ωωωT t T KX t x i o -+=, ⎥⎦⎤⎢⎣⎡++=t t T T K TX t x i o ωωωωsin cos 1121)(221[]t t t t t t t x o sin cos )45sin(6410)sin (cos 21021)45sin(21023)(++︒-=++︒-=5.2* 系统稳定的必要条件：特征方程各系数均大于零；系统稳定的充分条件：特征根均有负实部，或Routh 表第一列均为正数。
5.3 必要条件：k > 0充分条件：Routh 表100)1/(101/)1(0111121234---k k kk k s s ss s 011,01,02>-->->k k kk k 即要求：21k k >-，此方程k 无实数解。
故稳定性无法判别。
实际上，通过求根的方法，可知，只要k > 0，系统便不稳定。
5.4 Ks s s KG G G K K B +++=+=)2)(1(1, 023)2)(1(23=+++=+++K s s s K s s s 根据Hurwitz 判据：K > 0, 3×2－1×K > 0，即：0 < K < 6时系统稳定。
5.5 12)1()(23++++=s s s s K s G k α222232)1(12)1(1nn n K K B s s A s K s s s s K G G G ωξωωα++=++++++=+= 2223232)2()12())1()2((n n n n n K s K s K Ks K s K s s A ωξωωξωαω+++++=+++++ K A n =2ω, )12(2+=n n K A ξωαω, )2()2(22n n n K K A ξωωω+=+, 22)1(n n K K A ωω=+ 12)12(2+=→+=n n n K A ξωαξωαω, )2()2()2()2(222n n n n n K K K A ξωωξωωω+=+→+=+,222)1()1(n n n K K K A ωωω=+→=+322=→=K , 4/32=→=A K A nω 4/1)22/()2)23(()2()2(22=⨯-+=→+=+ξξωωn n K , 212)4/1(212=+⨯⨯=+=n ξωα,22243222223232)225.02(22)1)(4()1(3452)1(3)1(3122)1(3+⨯⨯+⋅=++=++++=++++=++++++=s s s s A s s s s s s s s s s s s s G n n n B ωξωω5.6 (1)1054)1(101010)54()1(10)1(10)5)(1()1(10232++++=++-++=+++-+=s s s s s s s s s s s s s s G B , 由Hurwitz 判据: 4×5－1×10> 0，系统稳定。
(2) 10321023+-+=s s s G B ,特征方程中s 项系数小于零，不满足Routh 稳定的必要条件，因此，系统不稳定。
5.7 (1)系统的特征方程为:0)1)(1(21=+++K s T s T s , 代入参数后，0)25.01)(1.01(=+++K s s s 即035.0025.023=+++K s s s ，根据Hurwitz 判据可得0 < K <140系统稳定。
5.7 (2)令s i = -1, i =1,2,3 代入特征方程，有：(－1)(1－0.1)(1－0.25)+K = 0, 求得: K =0.675。
