53解析函数在无穷远点的性质.

解析函数在无穷远点的性质摘要:无穷远点作为解析函数的奇点的分类及其判定方法,给出含无穷远点的区域的柯西积分定理、积分公式,为下一步讨论函数在无穷远点处的留数计算做准备.关键词:解析函数无穷远点奇点1问题的提出无穷远点是解析函数的孤立奇点时,它的分类及其类型判定为函数在无穷远点处的留数计算提供了理论依据,而无穷远点处的留数计算及其相关定理是解决复变函数“大范围”的积分计算的有力工具。

所以,本文研究解析函数在无穷远点的性质及其分类。

2解析函数的定义2.1 解析函数的定义定义2.1[1]如果函数在区域内可微,则称为区域内的解析函数,或称在区域内解析.2.2 奇点的定义定义2.2[2]若函数在点不解析,但在的任一邻域内总有的解析点,则称为函数的奇点.奇点分为孤立奇点和非孤立奇点两类,而孤立奇点根据函数在奇点去心邻域内洛朗展式主要部分的项数又可以分为三类:可去奇点(主要部分为0);极点(主要部分为有限多项);本质奇点(主要部分为无限多项).例2.1判定函数的奇点及其类型.解在平面上只有为孤立奇点,在其去心邻域内的洛朗展式为,因其主要部分为0,故为的可去奇点.3 解析函数在无穷远点的性质3.1 无穷远点的引入在复分析中,我们讨论的函数在自变量趋于一个定点时,函数值可能趋于无穷大.为了讨论这种情况,我们在复数域中引入符号表示无穷大,并且约定.同时规定它和有限数的运算关系如下:(加减法) ,(乘法) ,(除法),,在此定义下无意义.由于在复平面上没有对应无穷远点的位置,因此在复平面上引入一个“理想点”与无穷大对应,称之为无穷远点,仍记为,且把复平面加上点后称为扩充复平面,常记作.另外扩充复平面的几何模型是复球面,且北极与复平面上的无穷远点相对应.性质: 的实部﹑虚部及辐角都无意义, ;复平面上每一条直线都通过点,同时没有一个半平面包含点.3.2 无穷远点作为奇点的分类由于任一函数在处无意义,所以点总是的奇点.定义3.1 [3] 设函数在无穷远点的去心邻域内解析,则称为的一个孤立奇点,否则为非孤立奇点.若在平面上有一列趋于无穷远点的奇点,则为的非孤立奇点.例3.1讨论的奇点的类型.解:此函数因分母不能为0,故有奇点和.由于有限奇点(它们各为一阶极点)以为极限,故为此函数的非孤立奇点.设为的孤立奇点, 在无穷远点的去心邻域内的洛朗展式为,在式中正幂部分称为在的主要部分,非正幂部分称为在的正则部分.定义3.2设为函数的孤立奇点.若在点的主要部分为零,则称为的可去奇点;若在点的主要部分为有限多项,设为,则称为的阶极点;若在点的主要部分有无限多项,则称为的本质奇点.注: 若为的可去奇点,我们定义,则在处解析.3.3 解析函数在无穷远点的性质根据定义3.2,不难得到定理3.1函数的孤立奇点为可去奇点的充要条件是下列条件之一成立: ;令, 为的可去奇点;在的某去心邻域内有界.例如, ,所以为函数的可去奇点.定理3.2函数的孤立奇点为阶极点的充要条件是下列条件之一成立: 令, 为的阶极点;在的某去心邻域内能表成,其中在的邻域内解析,且;以为阶零点(只要令).注:为的极点的充要条件是.例3.2试确定函数的奇点的类型.解:由,设,因在的邻域内解析且,所以为阶极点.定理3.3函数的孤立奇点为本质奇点的充要条件是下列条件之一成立:不存在;令, 为的本质奇点.例3.3试确定函数的奇点的类型.解:令,其在的空心邻域内的展式为,它的主要部分为无穷多项,故为的本质奇点.定理 3.4 (含点的区域的柯西积分定理)设是一条周线,区域是的外部(含点), 在内解析且连续到;又设,则,这里及是在无穷远点去心邻域内的洛朗展式的系数.证明:由已知有在解析,又,所以为可去奇点;设充分大,使及其内部全含于圆周的内部(图1),则得点的去心邻域: 在其内展成洛朗级数,设为( 可为0).因,所以.再就复围线(图1)应用柯西积分定理有:,,.定理3.5 (含点的区域的柯西积分公式)假设条件同定理3.4,则这里表示的方向,含点的区域恰在一人沿它前进的方向.证明:1)设,以为心作充分大的圆周,使及其内部全含于的内部(图2), 构成一复围线.则应用有界区域的柯西积分公式,.在(这里以为中心的点的去心邻域)内的洛朗展式可设为( 可为0),由此可得.当,有,所以.2) (即在图2中的阴影部分),有,所以.参考文献:[1]钟玉泉.复变函数论[M].北京:高等教育出版社,2005年版.[2]陈广锋.无穷远点作为解析函数奇点时的讨论[J].西安教育学院学报,2000(3).。

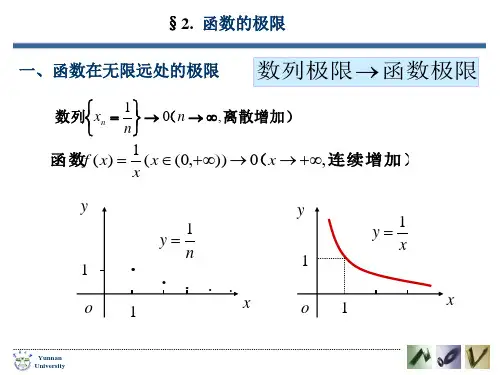
函数的无穷值点
函数的无穷值点是指函数在特定点处取得，或接近于无穷大的值。

无穷值点可以用来分析函数的行为及其应用。

无穷值点的主要内容可以归纳为三部分：
一、无穷值点的概念。

无穷值点是指函数在某一点处取得，或接近于无穷大的值，也称之为函数的极值点。

无穷值点是指函数在某一特定点处，显然函数取得了或接近于无穷大的值。

在这里，函数本身的值可能小于1，也可能大于1，但是它们都
接近于或取得了无穷大的值，就形式而言，可以描述为f(x) = ∞。

二、无穷值点的解法。

无穷值点的解法通常需要根据函数的特性和表示形式来考虑，可以使用微分法或其他方法来求解。

微分法：如果令函数的导数为零，即f'(x) = 0，那么将会得到
函数的无穷值点。

由于此处导数为零，因此无穷值点对应的函数值应该极大或极小，因此可以将其看作一个极值点。

其他方法：无穷值点的求解也可以根据函数的其他特性来考虑。

例如，函数可能存在一些特定的参数，通过调整参数，就可以得到函数的无穷值点。

三、无穷值点的应用。

无穷值点的求解有助于我们理解函数的行为，例如函数的单调性、函数有没有极值点等。

无穷值点的另一个重要应用是可以使用它来确定函数的最大值或最小值，这有助于我们确定函数中极值点的位置。

此外，无穷值点也有
被用作物理和工程中的数学解析方法，它可以用来简化繁琐的性能分析等问题。

解析函数的主要性质综述作者：安辉燕来源：《科学导报》2017年第75期一、导引解析函数是一类具有某种特性的可微函数，它将我们所熟悉的数学分析中的一些内容推广到复数域上并研究其性质。

本文通过搜集材料，系统总结了解析函数的几个主要性质：解析函数的唯一性、零点的孤立性、零点的分布问题、解析函数在无穷远点的性质、解析变换的特征及解析函数、共轭解析函数和复调和函数之间的关系，并通过举例进行了深入、详细的分析。

二、预备知识1.定义如果函数在区域D内是可微的，则称为区域D内的解析函数。

复变函数中解析函数的充要条件有多种形式，最常见的有以下几种。

2.定理函数在区域D内解析的充要条件：A（1）二元函数在区域D内可微；（2）在D内满足方程。

B（3）在D内连续；（4）在D内满足方程。

C 在D内任意一点的邻域内可以展成的幂级数，也就是泰勒级数。

D C为D内任意一条周线，则。

三、解析函数的主要性质1.解析函数的唯一性定理（解析函数的唯一性）如果函数在区域D内解析，是D内彼此不同的点，并且点列的极限点，若有，则在D内必有。

根据定理我们可得到以下结论：推论1 如果函数在区域D内解析，且在区域内某点的邻域内有，则在D内必有。

推论2 如果函数在区域D内解析，且在区域D内某一曲线上有，则在内必有。

2.解析函数零点的孤立性定理如果在内的解析函数不恒为零，是的一个零点，则必存在的一个邻域使得在其中无其他零点。

（即：不恒为零的解析函数的零点具有孤立性）此性质是解析函数的特殊性质，实函数不具有此性质。

3. 解析函数零点的分布问题解析函数的零点的分布问题是复变函数论中的一个重要问题，一下就复多项式的零点可以全部分布在一个指定的区域内这个问题进行讨论。

定理1若复平面上多项式在虚轴上无零点，则它的零点全分布在右半平面上的充要条件为。

定理2若复平面上多项式在实轴上无零点，则它的零点全分布在上半平面的充要条件为。

四、解析变换的特性解析函数的特性是从几何的角度对解析函数的性质和应用进行讨论。

第四章 级 数第三节 洛朗展式1、整函数与亚纯函数的概念：如果f (z )在有限复平面C 上解析，那么它就称为一个整函数。

显然无穷远点是整函数的孤立奇点。

在C 上，f (z )围绕无穷远点的洛朗展式也就是其泰勒展式：,)(0∑+∞==n n n z z f α当f (z )恒等于一个常数时，无穷远点是它的可去奇点；当f (z )是)1(≥n 次多项式时，无穷远点是它的n 阶极点；在其它情况下，无穷远点是f (z )的本性奇点，而这时称f (z )为一个超越整函数。

例如z z e z cos ,sin ,等都是超越整函数，无穷远点是它们的本性奇点。

由刘维尔定理，我们有代数基本定理：任何)1(≥n 次代数方程至少有一个根。

证明：设)0(...)(011≠+++=--n n n n n z z z P αααα是一个这样的代数方程。

我们要证明整函数P (z )至少有一个零点。

反证之，假定P (z )没有零点，那么)(1z P 也是一个整函数，因为 |)...(||)(|01nn n n zzz z P ααα+++=-)0(|)||||...|||||(|||01≠---≥-z z z z n n n n ααα 所以我们有,0)(1lim,|)(|lim =+∞=∞→∞→z P z P z z因而)(1z P 在全平面上有界，于是根据刘维尔定理，)(1z P 恒等于0，与所设矛盾，因此P (z )至少有一个零点。

定理1 设f (z )是一个整函数，按照∞=z 是可去奇点、)1(≥n 阶极点或本性奇点，必须而且只需f (z )是恒等于常数、)1(≥n 次多项式或超越整函数。

证明：设∞=z 是f (z )的可去奇点，那么)(lim z f z ∞→为有限复数，从而f (z )有界，由刘维尔定理，f (z )恒等于一个常数。

设∞=z 是f (z )的极点或本性奇点时，设f (z )在∞=z 的主要部分是∑∑+∞===11)(k k k nk kk z z z g αα或那么∞=z 是f (z )-g (z )的可去奇点。