在统计出本次比赛的分数之后

2024年四年级数学下册计算比赛活动总结在2024年的四年级数学下册计算比赛活动中，我们组织了一场生动、有趣且富有挑战性的比赛。

活动由学校主办，吸引了全年级的学生积极参与。

首先，为了确保比赛的公平性和规范性，我们制定了严格的规则和流程。

参赛学生必须提前报名，并按照年级进行分组。

比赛分为个人赛和团体赛两个环节，并设立了不同的题目类型和难度等级。

在个人赛中，学生们根据抽签确定了自己的参赛顺序。

每位学生必须在规定的时间内回答一系列数学计算题目，包括加法、减法、乘法和除法等。

这其中不乏一些复杂的应用题，以及需要推理和思考的问题，旨在考察学生的计算能力、速度和逻辑思维能力。

而团体赛则是以小组为单位进行，每个小组有三名成员。

小组成员共同合作解答一些更加复杂的问题，并制定解题策略。

这一环节更加强调学生之间的合作和团队精神，培养学生们的协作能力和沟通能力。

本次比赛活动的结果表明，学生们在数学计算方面的能力得到了较好的提升。

许多同学在比赛中表现出色，解题速度和准确率高，对于不同类型的题目能够灵活运用所学知识和方法。

同时，比赛也暴露出一些问题和不足，例如有些学生在时间紧迫的情况下可能会出现疏忽和忽略一些细节的情况。

为了进一步提高学生们的数学计算能力，接下来，我们将组织更多的训练和竞赛活动，例如数学奥赛，以及加强个别学生的辅导和指导。

通过这些努力，我们相信学生们在数学方面的成绩和自信心都会有所提高。

总的来说，2024年四年级数学下册计算比赛活动是一次成功的活动。

通过比赛，学生们不仅提高了数学计算能力，还培养了团队合作和竞争意识。

我们将持续关注学生们的学习情况，为他们提供更多的学习机会和挑战，帮助他们在数学学科中取得更好的成绩。

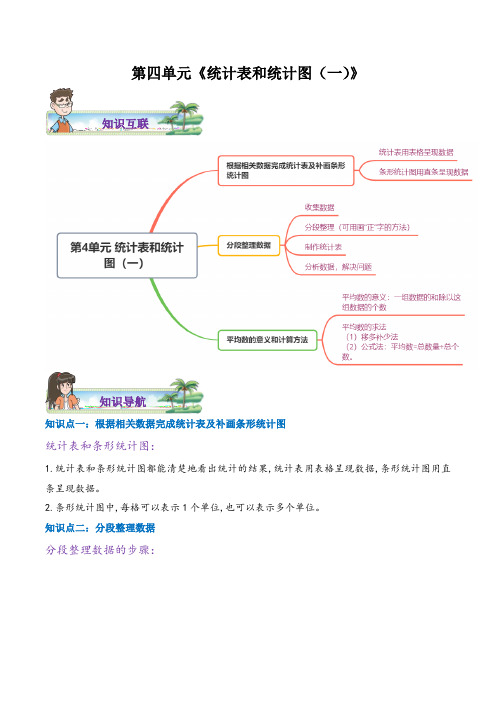
第四单元《统计表和统计图（一）》知识互联知识导航知识点一：根据相关数据完成统计表及补画条形统计图统计表和条形统计图：1.统计表和条形统计图都能清楚地看出统计的结果,统计表用表格呈现数据,条形统计图用直条呈现数据。

2.条形统计图中,每格可以表示1个单位,也可以表示多个单位。

知识点二：分段整理数据分段整理数据的步骤：1.收集数据；2.分段整理（可用画“正”字的方法）；3.制作统计表；4.分析数据,解决问题。

知识点三：平均数的意义和计算方法1.平均数的意义：一组数据的和除以这组数据的个数,所得的数就是平均数。

2.平均数的求法：（1）移多补少法：在总量不变的前提下,在几个（或若干个）不相同的数中,从多的数中拿出一部分给少的数,使它们变成相同的数,这个相同的数就是这组数据的平均数。

（2）公式法：平均数=总数量÷总个数。

夯实基础一、精挑细选（共5题；每题2分,共10分）1．（2020·江苏溧阳·四年级期中）笑笑要了解本班同学最喜欢的电视节目,应选用调查表（）。

A．你喜欢看什么类节目？动画类科普类体育类综艺类B．你喜欢看动画片吗？喜欢不喜欢C．你每天看多长时间电视节目？10分钟 20－40分钟 40分钟以上2．（2020·江苏溧阳·四年级期中）小华在3个笔筒里放了一些铅笔,平均每个笔筒25支,前面两个笔筒里的铅笔都比25支多,那么第三个笔筒里有的铅笔（）。

A．比25支多B．比25支少C．正好25支3．（2020·江苏邳州·四年级期中）三年级女生做仰卧起坐。

1分钟做40个以上（含40个）为优秀,21～39个为及格,21个以下为不及格。

三（1）班女生1分钟仰卧起坐成绩统计如下：等第优秀及格不及格人数9 14 3芳芳的成绩在三（1）班女生中排名第7。

她可能做了多少个？（）A．38个B．27个C．43个（2021·山西临汾·四年级期中）小明是某公司员工,公司员工月平均工资是4200元,小明的月工资（）4．4200元。

羽毛球赛策划书主办方：xxx承办方：xxx一、大赛概况（一）大赛背景万物复苏，春意盎然，值此美丽的季节我社团特此举办本届羽毛球大赛，为了增强大学生体育锻炼意识，使羽毛球运动更加普及，并且吸引羽毛球爱好者参加到我社团活动中来。

并希望此次活动能达到丰富同学们的课余生活的目的，给爱好者一个广阔交友的平台和一个展示自我的空间。

（二）大赛特色1.专业性：本次大赛是由青羽羽毛球协会协办，具有很强的专业性。

2.公正性：本次大赛由动机院社团联合会成员担当裁判员，青羽协会成员负责担任副裁。

在比赛的过程中，做到公正、公开。

3.趣味性：本次大赛设有男单、女单、男双、混双4个项目。

既有自我能力的挑战，也有自由组合的乐趣。

除此以外，更可以以球会友，认识更多志同道合的同学。

(三)大赛宗旨本次大赛旨在让同学们在竞技比赛活动的过程中，提高自己的羽毛球水平，增强身体素质，意识到锻炼身体的重要性，领会运动精神，扩大自身的社交范围，实现“我实践，我成长”的目的。

二、大赛介绍“丰羽杯”羽毛球赛是社团联合会、青羽协会倾心打造的精品活动。

本次大赛将秉承公开、公平、公正原则，比赛以素质、技能为主，理论知识为辅，努力为参赛选手提供一个规范化、专业化的竞赛平台和自我展现的舞台。

三、参赛对象、方式、时间、地点及赛程安排（一）参赛对象：本次大赛面向学院全体学生。

参赛选手须自备球拍（大会提供羽毛球）。

要求参赛选手态度端正、认真、负责，无特殊理由不得中途退赛，以影响比赛进程。

（二）参赛报名方式要求学生以个人或组队（双打）形式报名参赛，参赛选手于截止日期前到各报名点报名参赛。

报名时请写明参赛项目、联系方式、专业、学号。

报名时间：xxx报名地点： xxx（三）参赛方式（1）男单(2) 女单（3）男双（4）混双（四）大赛时间：xxx（五）比赛地点：xxx（六）比赛环节如下：大赛主要由初赛和决赛两个主体。

初赛采用淘汰赛制，实行单局11分，3局2胜制。

由参赛选手之间按照大会安排的顺序进行对战。

【学习内容】百分数的认识（人教版教材六年级上册）。

【学习目标】1.学生能在真实的情境中体会百分数产生的必要性，了解百分数与日常生活的密切联系，理解百分数的意义。

2.学生在经历整理、分析数据并做出判断的过程中，初步感悟数据的随机性，感悟百分数的统计意义，逐步形成数据意识，发展应用意识。

【课堂实录】一、激活经验，理解倍数关系的表达师：（出示表1）两个选手进行投篮比赛，如果我们选一个投篮水平高的选手代表班级去参加比赛，你选几号？表1编号1号2号投中次数95生：（异口同声）1号。

师：不急，都同意吗？（在静静的思考中，学生陆陆续续举起手来）生：不能确定，没有投篮的总次数就不好进行比较。

假如1号投100次，只中了9次；而2号投了5次，中了5次，百发百中呢。

所以只比较两个选手的投中次数不公平。

师：有道理。

我把投篮的总次数带来了（在表1中补充一列——投篮次数），1号选手投了20次，2号选手投了10次，你们选几号？生：我把920和510通分，920小于1020,所以2号选手成绩比较好。

生：我是这样做的，920=9÷20=0.45，510=5÷10=0.5，0.5大于0.45，说明2号选手成绩比较好。

师：通过比较我们都选择了2号。

1020表达的是什么意思呢？生：2号选手共投篮20次，命中了10次。

师：510表达什么意思？生：2号选手共投了10次，投中了5次。

生：我认为它还表达一半的意思。

师：谁是谁的一半？生：投中的次数是投篮总数的一半，反过来投篮总数是投中次数的2倍。

师：感觉越来越好了，510表达了哪两个数在统计视角下建构百分数的意义——“百分数的认识”课堂教学实录134之间的什么关系？生：2号选手投中次数与投篮总数的倍数关系。

师：那1020呢？生：也表达了2号选手投中次数与投篮总数的倍数关系。

师：我特别欣赏他说的这个“也”，这个倍数关系的表达可以叫作投篮的“命中率”。

你们能说说两位选手的“命中率”分别是多少吗？生：2号选手的“命中率”是510，也可以说是1020。

2022-2023学年度第一学期第二次阶段性反馈初三数学一．选择题（本大题共6小题，共12分）1.学校组织才艺表演比赛，前5名获奖，有11位同学参加比赛且他们所得的分数互不相等，某同学知道自己的比赛分数后，要判断自己能否获奖，在这11名同学成绩的统计量中只需知道一个量，它是（ ） A ．众数B ．方差C ．中位数D ．平均数2.如图O 的半径为6，圆心到一条直线的距离为3，则这条直线可能是（ ） A ．1lB ．2lC ．3lD ．4l3.若关于x 的一元二次方程()2210a x a x a -+-=有一个根是1x =，则a 的值为（ ） A ．-1B ．0C ．1D ．-1或14. 参加一次活动的每个人都和其他人各握了一次手，所有人共握手10次，有多少人参加活动？设有x 人参加活动，可列方程为( ) A ．1(1)102x x -=B ．(1)10x x -=C ．1(1)102x x +=D ．2(1)10x x -=5. 如图，下列条件中不能判定ACD ABC ∆∆∽的是( )A ．AB ADBC CD=B ．ADC ACB ∠=∠ C ．ACD B ∠=∠ D ．2AC AD AB =⋅6. 点1(,)A m y ，2(,)B n y 均在抛物线2()7y x h =-+上，若||||m h n h ->-，则下列说法正确的是( ) A ．120y y +=B ．120y y -=C ．120y y -<D ．120y y ->二.填空题（本大题共10小题，共20分） 7. 一组数据1，6，3，4-，5的极差是 ．8. 在比例尺为1:100000的工程图上，五峰山长江大桥全长约6.4厘米，那么它的实际长度约为 米．9. 在平面直角坐标系中，将抛物线22y x =-先向右平移2个单位，再向上平移3个单位，得到的抛物线的解析式是 ．10. 如图，一个转盘，转盘上共有红、白两种不同的颜色，已知红色区域的圆心角为80︒，自由转动转盘，指针落在白色区域的概率是 ．11. 如图，PA 、PB 分别切O 于点AB ，点E 是O 上一点，且50E ∠=︒，则P ∠的度数为 ．12. 如图所示，一个宽为2cm 的刻度尺在圆形光盘上移动，当刻度尺的一边与光盘相切时，另一边与光盘边缘两个交点处的读数恰好是“2”和“10”（单位：)cm ，那么该光盘的直径是 cm ．13. 《九章算术》是中国古代的数学专著，书中记载了这样一个问题：“今有勾五步，股十二步．问勾中容方几何．”其大意是：如图，Rt ABC ∆的两条直角边的长分别为5和12，则它的内接正方形CDEF 的边长为 ．14. 发射一枚炮弹，经x 秒后的高度为y 米，且时间与高度的关系为2(0)y ax bx a =+≠．若此炮弹在第7秒与第15秒时的高度相等，则第 秒时，炮弹位置达到最高． 15. 设a ，b 分别是方程220220x x +-=的两个实数根，则22a a b ++的值是 ．16. 如图，四边形ABCD 内接于以BD 为直径的O ，CA 平分BCD ∠，若四边形ABCD 的面积是230cm ，则AC = cm ．三．解答题（本大题共11小题，共88分） 17. 解下列方程（1）()255x x -=-（2）212270x x ++=18. 甲、乙两人在5次打靶测试中命中的环数如下： 甲：8，8，7，8，9 乙：5，9，7，10，9 （1）填写下表：平均数 众数 中位数 方差 甲 8 8 8 0.4 乙93.2（2）教练根据这5次成绩，选择甲参加射击比赛，教练的理由是什么？（3）如果乙再射击1次，命中8环，那么乙的射击成绩的方差 ．（填“变大”、“变小”或“不变” )．19. “共和国勋章”获得者钟南山院士说：按照疫苗保护率达到70%计算，中国的新冠疫苗覆盖率需要达到近80%，才有可能形成群体免疫．本着自愿的原则，18至60周岁符合身体条件的中国公民均可免费接种新冠疫苗．居民甲、乙准备接种疫苗，其居住地及工作单位附近有两个大型医院和两个社区卫生服务中心均可免费接种疫苗，提供疫苗种类如下表：接种地点疫苗种类医院A 新冠病毒灭活疫苗 B重组新冠病毒疫苗(CHO细胞）社区卫生服务中心 C 新冠病毒灭活疫苗 D重组新冠病毒疫苗(CHO细胞）若居民甲、乙均在A 、B 、C 、D 中随机独立选取一个接种点接种疫苗，且选择每个接种点的机会均等．（提示：用A 、B 、C 、D 表示选取结果） （1）居民甲接种的是新冠病毒灭活疫苗的概率为 ；（2）请用列表或画树状图的方法求居民甲、乙接种的是相同种类疫苗的概率．20. 如图，已知二次函数23y ax bx =++的图象经过点(1,0)A ，(2,3)B -． （1）求该二次函数的表达式；（2）用无刻度直尺画出抛物线的对称轴l ；（用虚线表示画图过程，实线表示画图结果） （3）结合图象，直接写出当3y >时，x 的取值范围是 20x -<< ．21. 如图，四边形ABCD 中，//AD BC ，90BAD ∠=︒，CB CD =，连接BD ，以点B 为圆心，BA 长为半径作B ，交BD 于点E ． （1）试判断CD 与B 的位置关系，并说明理由； （2）若4AD =，60BCD ∠=︒，求图中阴影部分的面积．22. 如图，在ABC ∆中，90B ∠=︒，22AB =，2BC =，以AC 为边作ACE ∆，90ACE ∠=︒，AC CE =，延长BC 至点D ，使32CD =，连接DE ．求DE 的长．23. 某商店销售一种进价50元/件的商品，经市场调查发现：该商品的每天销售量y （件)是售价x （元/件）的一次函数，其售价、销售量的二组对应值如表： 售价x （元/件） 55 65 销售量y （件/天）9070（1）直接写出y 关于售价x 的函数关系式： 2200y x =-+ ； （2）若某天销售利润为800元，求该天的售价为多少元/件？（3）设商店销售该商品每天获得的利润为W （元)，求W 与x 之间的函数关系式，并求出当销售单价定为多少时，该商店销售这种商品每天获得的利润最大？24. 如图，点A 、B 在O 上，点P 为O 外一点．（1）请用直尺和圆规在优弧AmB 上求一点C ，使CP 平分ACB ∠（不写作法，保留作图痕迹）；（2）在（1）中，若AC 恰好是O 的直径，设PC 交O 于点D ，过点D 作DE AC ⊥，垂足为E ．若4OE =，求弦BC 的长．25. 已知：如图，AB 为O 的直径，AB AC ⊥，BC 交O 于D ，E 是AC 的中点，ED 与AB 的延长线相交于点F ．（1）求证：DE 为O 的切线； （2）求证：AB DF AC BF ⋅=⋅．26. 已知二次函数222(y x mx m m =-++是常数）的图象是抛物线． （1）若抛物线与x 轴只有一个公共点，求m 的值； （2）求证：抛物线顶点在函数22y x x =-++的图象上；（3）若点(2,)B a ，(5,)C b 在抛物线上，且a b >，则m 的取值范围是27. 圆心到弦的距离叫做该弦的弦心距．【数学理解】如图①，在O 中，AB 是弦，OP AB ⊥，垂足为P ，则OP 的长是弦AB 的弦心距．（1）若O 的半径为5，弦AB 的弦心距为3，则AB 的长为 8 ．（2）若O 的半径确定，下列关于AB 的长随着OP 的长的变化而变化的结论：①AB的长随着OP的长的增大而增大；②AB的长随着OP的长的增大而减小；③AB的长与OP的长无关．其中所有正确结论的序号是．（3）【问题解决】若弦心距等于该弦长的一半，则这条弦所对的圆心角的度数为︒．（4）已知如图②给定的线段EF和O，点Q是O内一定点．过点Q作弦AB，满足=，请问这样的弦可以作条．AB EF2022-2023学年度第一学期第二次阶段性反馈初三数学答案一．选择题（本大题共6小题，共12分）1.学校组织才艺表演比赛，前5名获奖，有11位同学参加比赛且他们所得的分数互不相等，某同学知道自己的比赛分数后，要判断自己能否获奖，在这11名同学成绩的统计量中只需知道一个量，它是（ ） A ．众数B ．方差C ．中位数D ．平均数【解答】因为5名获奖肯定是11位同学中最高的，而且11位同学的分数按从小到大排序后，中位数及中位数之后的共有5个数，故只要知道自己的分数和中位数就可以知道是够获奖了.故选C ．2.如图O 的半径为6，圆心到一条直线的距离为3，则这条直线可能是（ ） A ．1lB ．2lC ．3lD ．4l【解答】由于O 的半径为6，圆心到一条直线的距离为3，6>3，所以直线与O 相交 顾选B ．3.若关于x 的一元二次方程()2210a x a x a -+-=有一个根是1x =，则a 的值为（ ） A ．-1B ．0C ．1D ．-1或1【解答】把1x =带入方程中，得到21a =，又因为10a -≠是，所以1a =-，故选A ．4. 参加一次活动的每个人都和其他人各握了一次手，所有人共握手10次，有多少人参加活动？设有x 人参加活动，可列方程为( ) A ．1(1)102x x -=B ．(1)10x x -=C ．1(1)102x x +=D ．2(1)10x x -=【解答】解：设x 人参加这次聚会，则每个人需握手：(1)x -（次)； 依题意，可列方程为：(1)102x x -=．故选：A ．5. 如图，下列条件中不能判定ACD ABC ∆∆∽的是( )A ．AB ADBC CD=B ．ADC ACB ∠=∠ C ．ACD B ∠=∠ D ．2AC AD AB =⋅【解答】解：若AB AD BC CD =，不能判定ACD ∆与ABC ∆相似，当AB ACBC CD=，结合A A ∠=∠可判定ACD ∆与ABC ∆相似，故A 选项符合题意；若ADC ACB ∠=∠，结合A A ∠=∠可得ACD ABC ∆∆∽，故B 选项不符合题意； 若ACD B ∠=∠，结合A A ∠=∠可得ACD ABC ∆∆∽；故C 选项不符合题意； 若2AC AD AB =⋅，即AC ABAD AC=，结合A A ∠=∠可得ACD ABC ∆∆∽；故D 选项不符合题意； 故选：A ．6. 点1(,)A m y ，2(,)B n y 均在抛物线2()7y x h =-+上，若||||m h n h ->-，则下列说法正确的是( ) A ．120y y += B ．120y y -=C ．120y y -<D ．120y y ->【解答】解：2()7y x h =-+，∴抛物线开口向上，对称轴为直线x h =，若||||m h n h ->-，则点A 与对称轴距离大于点B ， 12y y ∴>，即120y y ->，故选：D ．二.填空题（本大题共10小题，共20分） 7. 一组数据1，6，3，4-，5的极差是 10 ． 【解答】解：由题意可知，极差为6(4)10--=． 故答案为：10．8. 在比例尺为1:100000的工程图上，五峰山长江大桥全长约6.4厘米，那么它的实际长度约为 6400 米．【解答】解：设这两城市的实际距离是x 厘米，由题意，得 1:100000 6.4:x =，解得：640000x =， 640000厘米6400=米．答：它的实际长度约为6400米， 故答案为：6400．9. 在平面直角坐标系中，将抛物线22y x =-先向右平移2个单位，再向上平移3个单位，得到的抛物线的解析式是 2(2)1y x =-+ ．【解答】解：将抛物线22y x =-先向右平移2个单位，再向上平移3个单位，得到的抛物线的解析式是2(2)23y x =--+，即2(2)1y x =-+． 故答案为：2(2)1y x =-+．10. 如图，一个转盘，转盘上共有红、白两种不同的颜色，已知红色区域的圆心角为80︒，自由转动转盘，指针落在白色区域的概率是79．【解答】解：P （指针落在白色区域）3608073609-==， 故答案为：79．11. 如图，PA 、PB 分别切O 于点AB ，点E 是O 上一点，且50E ∠=︒，则P ∠的度数为 80︒ ．【解答】解：连接OA ，BO ； 2100AOB E ∠=∠=︒， 90OAP OBP ∴∠=∠=︒， 18080P AOB ∴∠=︒-∠=︒．故答案为：80︒．12. 如图所示，一个宽为2cm 的刻度尺在圆形光盘上移动，当刻度尺的一边与光盘相切时，另一边与光盘边缘两个交点处的读数恰好是“2”和“10”（单位：)cm ，那么该光盘的直径是 10 cm ．【解答】解：如图，设圆心为O ，弦为AB ，切点为C ．如图所示．则8AB cm =，2CD cm =． 连接OC ，交AB 于D 点．连接OA ． 尺的对边平行，光盘与外边缘相切， OC AB ∴⊥． 4AD cm ∴=．设半径为Rcm ，则2224(2)R R =+-， 解得5R =，∴该光盘的直径是10cm ．故答案为：1013. 《九章算术》是中国古代的数学专著，书中记载了这样一个问题：“今有勾五步，股十二步．问勾中容方几何．”其大意是：如图，Rt ABC ∆的两条直角边的长分别为5和12，则它的内接正方形CDEF 的边长为6017．【解答】解：设正方形CDEF 边长为x ，则CD DE x ==，由Rt ABC ∆的两条直角边的长分别为5和12可知5AC =，5AD x =-，12BC =， 正方形CDEF ， //DE BC ∴， ADE ACB ∴∠=∠，又A A ∠=∠， ADE ACB ∴∆∆∽，∴DE ADBC AC =， ∴5125x x-=， 解得6017x =． 故答案为：6017．14. 发射一枚炮弹，经x 秒后的高度为y 米，且时间与高度的关系为2(0)y ax bx a =+≠．若此炮弹在第7秒与第15秒时的高度相等，则第 11 秒时，炮弹位置达到最高． 【解答】解：此炮弹在第7秒与第15秒时的高度相等，∴抛物线的对称轴是直线715112x +==， ∴炮弹位置达到最高时，时间是第11秒．故答案为：11．15. 设a ，b 分别是方程220220x x +-=的两个实数根，则22a a b ++的值是 2021 ． 【解答】解：a ，b 分别是方程220220x x +-=的两个实数根，1a b ∴+=-，220220a a +-=，22022a a ∴+=，故222()202212021a a b a a a b ++=+++=-=， 故答案为2021．16. 如图，四边形ABCD 内接于以BD 为直径的O ，CA 平分BCD ∠，若四边形ABCD 的面积是230cm ，则AC = 215 cm ．【解答】解：如图，过点A 作AE AC ⊥，交CD 的延长线于点E ，BD 为O 的直径，90BCD BAD ∴∠=∠=︒， CA 平分BCD ∠， 45ACB ACD ∴∠=∠=︒， 45ABD ADB ∴∠=∠=︒，AB AD ∴=，四边形ABCD 内接于O ， 180ABC ADC ∴∠+∠=︒，又180ADE ADC ∠+∠=︒， ABC ADE ∴∠=∠． AE AC ⊥， 90CAE ∴∠=︒，又45ACE ∠=︒ AC AE ∴=90BAD ∠=︒，90CAE ∠=︒， BAC DAE ∴∠=∠．在ABC ∆与ADE ∆中，BAC DAE AB ADABC ADE ∠=∠⎧⎪=⎨⎪∠=∠⎩， ()ABC ADE ASA ∴∆≅∆， ABC ADE S S ∆∆∴=， 30ACE ABCD S S ∆∴==，∴21302AC =， ∴215AC =．故答案为：215．三．解答题（本大题共11小题，共88分） 17. 解下列方程（1）()255x x -=-（2）212270x x ++=【解答】（1）()()2550x x ---= （2）()()390x x ++=()()560x x --= 123,9x x =-=-125,6x x ==18. 甲、乙两人在5次打靶测试中命中的环数如下： 甲：8，8，7，8，9 乙：5，9，7，10，9 （1）填写下表：平均数 众数 中位数 方差 甲 8 8 8 0.4 乙93.2（2）教练根据这5次成绩，选择甲参加射击比赛，教练的理由是什么？（3）如果乙再射击1次，命中8环，那么乙的射击成绩的方差．（填“变大”、“变小”或“不变”)．【解答】解：（1）甲的众数为8，乙的平均数1(597109)85=⨯++++=，乙的中位数为9；（2）因为他们的平均数相等，而甲的方差小，发挥比较稳定，所以选择甲参加射击比赛；（3）如果乙再射击1次，命中8环，那么乙的射击成绩的方差变小．故答案为：8，8，9；变小．19. “共和国勋章”获得者钟南山院士说：按照疫苗保护率达到70%计算，中国的新冠疫苗覆盖率需要达到近80%，才有可能形成群体免疫．本着自愿的原则，18至60周岁符合身体条件的中国公民均可免费接种新冠疫苗．居民甲、乙准备接种疫苗，其居住地及工作单位附近有两个大型医院和两个社区卫生服务中心均可免费接种疫苗，提供疫苗种类如下表：若居民甲、乙均在A、B、C、D中随机独立选取一个接种点接种疫苗，且选择每个接种点的机会均等．（提示：用A、B、C、D表示选取结果）（1）居民甲接种的是新冠病毒灭活疫苗的概率为12；（2）请用列表或画树状图的方法求居民甲、乙接种的是相同种类疫苗的概率．【解答】解：（1）居民甲接种的是新冠病毒灭活疫苗的概率为21 42 =，故答案为：12；（2）画树状图如下：共有16种等可能的结果，居民甲、乙接种的是相同种类疫苗的结果有8种，∴居民甲、乙接种的是相同种类疫苗的概率为81162=．20. 如图，已知二次函数23y ax bx =++的图象经过点(1,0)A ，(2,3)B -． （1）求该二次函数的表达式；（2）用无刻度直尺画出抛物线的对称轴l ；（用虚线表示画图过程，实线表示画图结果） （3）结合图象，直接写出当3y >时，x 的取值范围是 20x -<< ．【解答】解：（1）将(1,0)A ，(2,3)B -代入二次函数23y ax bx =++， 得03,342 3.a b a b =++⎧⎨=-+⎩解得1,2.a b =-⎧⎨=-⎩该二次函数的表达式为223y x x =--+； （2）如图，直线l 为所求对称轴；由（1）得二次函数的解析式为223y x x =--+， 变换形式得2(1)4y x =-++，所以可以得出顶点D 的坐标为(1,4)-，对称轴为1x =-． （3）令0y =，则2230y x x =--+=， 解得：0x =或2-，结合图形得20x -<<时，3y >． 故答案为：20x -<<．21. 如图，四边形ABCD 中，//AD BC ，90BAD ∠=︒，CB CD =，连接BD ，以点B 为圆心，BA 长为半径作B ，交BD 于点E ． （1）试判断CD 与B 的位置关系，并说明理由； （2）若4AD =，60BCD ∠=︒，求图中阴影部分的面积．【解答】解：（1）CD 与B 相切， 理由：过点B 作BF CD ⊥，垂足为F ， //AD BC ， ADB CBD ∴∠=∠， CB CD =， CBD CDB ∴∠=∠， ADB CDB ∴∠=∠．在ABD ∆和FBD ∆中， ADB FDB BAD BFD BD BD ∠=∠⎧⎪∠=∠⎨⎪=⎩，()ABD FBD AAS ∴∆≅∆，BF BA ∴=，则点F 在圆B 上，CD ∴与B 相切；（2）60BCD ∠=︒，CB CD =， BCD ∴∆是等边三角形， 60CBD ∴∠=︒BF CD ⊥，30ABD DBF CBF ∴∠=∠=∠=︒， 60ABF ∴∠=︒，4AD =，43AB ∴=，∴阴影部分的面积ABD ABE S S ∆=-扇形2130(43)4342360π⋅⨯=⨯⨯-834π=-．22. 如图，在ABC ∆中，90B ∠=︒，22AB =，2BC =，以AC 为边作ACE ∆，90ACE ∠=︒，AC CE =，延长BC 至点D ，使32CD =，连接DE ．求DE 的长．【解答】解：90B ∠=︒，AB =2BC =，AC ∴ CE AC =，∴CE =∴AB CE =-，AC CD ==， ∴AB ACCE CD=， 90B ∠=︒，90ACE ∠=︒，90BAC BCA ∴∠+∠=︒，90BCA DCE ∠+∠=︒， BAC DCE ∴∠=∠， ABC CED ∴∆∆∽，∴AB BC CE DE ==，DE ∴==23. 某商店销售一种进价50元/件的商品，经市场调查发现：该商品的每天销售量y （件)是售价x （元/件）的一次函数，其售价、销售量的二组对应值如表：（1）直接写出y 关于售价x 的函数关系式： 2200y x =-+ ； （2）若某天销售利润为800元，求该天的售价为多少元/件？（3）设商店销售该商品每天获得的利润为W （元)，求W 与x 之间的函数关系式，并求出当销售单价定为多少时，该商店销售这种商品每天获得的利润最大？ 【解答】解：（1）设关系式为y kx b =+，把(55，99)(65，70)代入得： 55996570k b k b +=⎧⎨+=⎩， ∴2200k b =-⎧⎨=⎩，y ∴与x 的之间的函数关系式为2200y x =-+，故答案为：2200y x=-+；（2）若某天销售利润为800元，则(50)(2200)800x x--+=，解得：160x=，290x=，答：该天的售价为60元或者90元；（3）设总利润为w，根据题意得，22(50)(2200)2300100002(75)1250w x x x x x=--+=-+-=--+，20a=-<，∴当75x=时，w有最大值，答：当销售单价定为75元时利润最大．24. 如图，点A、B在O上，点P为O外一点．（1）请用直尺和圆规在优弧AmB上求一点C，使CP平分ACB∠（不写作法，保留作图痕迹）；（2）在（1）中，若AC恰好是O的直径，设PC交O于点D，过点D作DE AC⊥，垂足为E．若4OE=，求弦BC的长．【解答】解：（1）如图，点C即为所求；（2）如图，连接OD交AB于点F．∠=∠，PCA PCB=，∴BD AD∴⊥，OD AB⊥，DE OA∴∠=∠=︒，90OFA OED∠=∠，OA OD=，FOA EOD∴∆≅∆，OFA OED AAS()∴==，4OE OF⊥，OD AB∴=，BF AFOC OA=，∴==．BC OF2825. 已知：如图，AB为O的直径，AB AC⊥，BC交O于D，E是AC的中点，ED与AB的延长线相交于点F．（1）求证：DE为O的切线；（2）求证：AB DF AC BF⋅=⋅．【解答】证明：（1）连AD，OD，AB 为O 的直径，90ADB ADC ∴∠=∠=︒， E 是AC 的中点，EA ED ∴=，EDA EAD ∴∠=∠，OD OA =，ODA OAD ∴∠=∠，EDO EAO ∴∠=∠，AB AC ⊥90EAO ∴∠=︒，90EDO ∴∠=︒，DE ∴为O 的切线；（2）90BAC ADC ∠=∠=︒，C BAD ∴∠=∠，ABD CBA ∠=∠，ABD CBA ∴∆∆∽， ∴AB BD AC AD=， 90FDB BDO BDO ADO ∠+∠=∠+∠=︒，FDB ADO OAD ∴∠=∠=∠，F F ∠=∠，FDB FAD ∴∆∆∽， ∴BD BF AD DF =， ∴AB BF AC DF=，AB DF AC BF ∴⋅=⋅．26. 已知二次函数222(y x mx m m =-++是常数）的图象是抛物线．（1）若抛物线与x 轴只有一个公共点，求m 的值；（2）求证：抛物线顶点在函数22y x x =-++的图象上；（3）若点(2,)B a ，(5,)C b 在抛物线上，且a b >，则m 的取值范围是 72m >． 【解答】解：（1）1a =，2b m =-，2c m =+，∴△2224(2)41(2)4(2)b ac m m m m =-=--⨯⨯+=--． 抛物线与x 轴只有一个公共点，2244(2)0b ac m m ∴-=--=，解得12m =，21m =-．（2）22222()2y x mx m x m m m =-++=--++，∴顶点坐标为2(,2)m m m -++，令x m =时，函数2222y x x m m =-++=-++，∴抛物线顶点在函数22y x x =-++的图象上．（3）抛物线开口向上，对称轴为直线x m =，∴当a b >时，|2||5|m m ->-，当20m ->时，2m <，50m ->，25m m ∴->-，不符合题意，当20m -<，50m ->时可得25m m ->-， 解得72m >． 当20m -<，50m -<时，5m >，25m m ∴-<-，符合题意， 故答案为：72m >． 27. 圆心到弦的距离叫做该弦的弦心距．【数学理解】如图①，在O 中，AB 是弦，OP AB ⊥，垂足为P ，则OP 的长是弦AB 的弦心距．（1）若O 的半径为5，弦AB 的弦心距为3，则AB 的长为 8 ．（2）若O 的半径确定，下列关于AB 的长随着OP 的长的变化而变化的结论： ①AB 的长随着OP 的长的增大而增大；②AB 的长随着OP 的长的增大而减小；③AB 的长与OP 的长无关．其中所有正确结论的序号是 ．（3）【问题解决】若弦心距等于该弦长的一半，则这条弦所对的圆心角的度数为 ︒．（4）已知如图②给定的线段EF 和O ，点Q 是O 内一定点．过点Q 作弦AB ，满足AB EF =，请问这样的弦可以作 条．【解答】解：（1）连接OA ，如图，OP AB ⊥，12AP BP AB ∴==， 在Rt OAP ∆中，由勾股定理得224AP OA OP -，28AB AP ∴==，故答案为：8；（2）设O 的半径为(0)r r >（点值），(0)OP x x =>，由（1）知，2AB AP =，22=-，AP OA OP222AB AP AP∴==(2)422=-OA OP4()22=-4()r x22=-+，44x r二次项2-的系数为404x-<，AB随x的增大而减小，∴>时，2xOP>，2∴随x的增大而减小，AB∴也随x的增大而矩形，AB即AB的长随OP的增大而减小，故正确结论的序号是②，故答案为：②；（3）连接OA，弦心距等于该弦长的一半，∴=，OP APAOP∴∠=︒，45AOB AOP∴∠=∠=︒，290故答案为：90；（4）根据圆的轴对称性质可知，这样的弦可以作2条，故答案为：2．。

公司趣味运动会主持词3篇公司职工运动会是是增强企业活力，汇聚全体员工凝聚力和进行企业文化建设的重要途径;同时也是发展体育运动，增强人民体质的关键环节，是“健康重庆”的重要内容，是惠及广大人民群众的民生工程，本文是店铺为大家整理的公司趣味运动会主持词，仅供参考。

公司趣味运动会主持词篇一：各位领导，各位来宾，亲爱的运动员们：大家下午好!追逐十月的和风，沐浴金秋的阳光，很高兴与xx科技有限公司的各位相聚在南海湿地公园。

运动使人快乐，团结令人兴奋。

为了丰富公司企业文化生活,促进员工之间的友谊与合作,提高团队精神,增强公司凝聚力，今日的趣味运动会应运而生。

现在，我宣布，xx趣味运动会正式开始。

艳艳骄阳好似我们的如火热情，看着大家都整装待发，咱们每个队伍是不是都给自己起好了队名，想好了口号呢?先给自己队伍一点掌声好不好。

那么现在，我们从左到右，依次喊一遍自己的队名和口号，鼓舞一下士气吧!从左边第一个队伍开始，这样喊“我们是xx队，我们的口号是xx”。

那么第一个队伍准备好，我要喊开始了哦。

1/2/3开始..... 谢谢大家，队名都非常的有趣，不知道大家觉得哪个队伍能得到今天的冠军呢?()都很自信呀!那么言归正传，下面我来宣布接下来的游戏评分规则：比赛采取积分模式，每个游戏中第一名：10分，第二名：8分，第三名：6分，第四名：4分，第五名：2分，其他名次：1分;会有专门的工作人员为大家计分。

所有比赛项目结束后，将得分累计，评选出冠、亚、季军;同时呢，我们也会在活动过程中根据各队伍的表现评选出最佳趣味奖、最佳团队奖、最佳体育精神奖。

大家有没有信心拿奖啊?还是那句老话：友谊第一，比赛第二。

希望大家都能在趣味运动会的过程中得到享受，在运动中展现不一样的风采! 本次趣味运动会一共准备了10个趣味运动项目，前五个项目为必须比赛项目：分别是【袋鼠接龙、无敌风火轮、海底捞月、托球平衡、四人五足】(都是非常炫酷的名字哦)。

后五个项目为备选项目【集体跳绳、集体拔河、双人背部顶球接力、夹球接力、背“老婆”大赛(这个老婆是打着引号的哈，大家不要误会)】。

备考2023年中考数学二轮复习-统计与概率_数据收集与处理_用样本估计总体-综合题专训及答案用样本估计总体综合题专训1、(2015本溪.中考真卷) 某中学为开拓学生视野，开展“课外读书周”活动，活动后期随机调查了九年级部分学生一周的课外阅读时间，并将结果绘制成两幅不完整的统计图，请你根据统计图的信息回答下列问题：（1）本次调查的学生总数为____人，被调查学生的课外阅读时间的中位数是___小时，众数是___小时；（2）请你补全条形统计图；（3）在扇形统计图中，课外阅读时间为5小时的扇形的圆心角度数是；（4）若全校九年级共有学生700人，估计九年级一周课外阅读时间为6小时的学生有多少人？2、(2019朝阳.中考模拟) 某校举行全体学生“汉字听写”比赛，每位学生听写汉字39个.随机抽取了部分学生的听写结果，绘制成如下的图表.组别正确字数x 人数A 0≤x＜8 10B 8≤x＜16 15C 16≤x＜24 25D 24≤x＜32 mE 32≤x＜40 n根据以上信息完成下列问题：（1）统计表中的m＝，n＝，并补全条形统计图；（2）扇形统计图中“C组”所对应的圆心角的度数是；（3）已知该校共有900名学生，如果听写正确的字的个数少于24个定为不合格，请你估计该校本次听写比赛不合格的学生人数.3、(2017丹东.中考模拟) 某中学对全校1200名学生进行“校园安全知识”的教育活动，从1200名学生中随机抽取部分学生进行测试，成绩评定按从高分到低分排列分为A、B、C、D四个等级，绘制了图①、图②两幅不完整的统计图，请结合图中所给信息解答下列问题：（1）求本次被抽查的学生共有多少人？（2）将条形统计图和扇形统计图补充完整；（3）求扇形统计图中“A”所在扇形圆心角的度数；（4）估计全校“D”等级的学生有多少人？4、(2016高邮.中考模拟) 为了解高邮市6000名九年级学生英语口语考试成绩的情况，从中随机抽取了部分学生的成绩（满分30分，得分均为整数），制成下表：分数段（x分）x≤1011≤x≤1516≤x≤2021≤x≤2526≤x≤30人数10 15 35 112 128 （1）本次抽样调查共抽取了名学生；（2）若用扇形统计图表示统计结果，则分数段为x≤10的人数所对应扇形的圆心角为°；（3）学生英语口语考试成绩的众数落在11≤x≤15的分数段内；（填“会”或“不会”）（4）若将26分以上（含26）定为优秀，请估计该区九年级考生成绩为优秀的人数．5、(2019瑞安.中考模拟) 共享单车是一种新型环保的交通工具，为市民的出行带来了极大的方便.某市中学生对市民共享单车的使用情况进行了问卷调查，并将这次调查情况整理、绘制成如图两幅统计图（部分信息未给出）.根据图中的信息，解答下列问题：（1）这次活动中接受问卷调查的市民共有名；（2）补全条形统计图，并计算扇形统计图中的D类的扇形圆心角为度；（3）根据统计结果，若该市市区有80万市民，请估算利用单车“外出游玩“的人数.6、(2017宁波.中考模拟) 宁波轨道交通4号线已开工建设，计划2020年通车试运营．为了了解镇民对4号线地铁票的定价意向，某镇某校数学兴趣小组开展了“你认为宁波4号地铁起步价定为多少合适”的问卷调查，并将调查结果整理后制成了如下统计图，根据图中所给出的信息解答下列问题：（1）求本次调查中该兴趣小组随机调查的人数；（2）请你把条形统计图补充完整；（3）如果在该镇随机咨询一位居民，那么该居民支持“起步价为2元或3元”的概率是（4）假设该镇有3万人，请估计该镇支持“起步价为3元”的居民大约有多少人？7、(2017临沂.中考模拟) 某市为提倡节约用水，准备实行自来水“阶梯计费”方式，用户用水不超出基本用水量的部分享受基本价格，超出基本用水量的部分实行超价收费．为更好地决策，自来水公司的随机抽取了部分用户的用水量数据，并绘制了如图不完整的统计图（每组数据包括在右端点但不包括左端点），请你根据统计图解答下列问题：（1）此次抽样调查的样本容量是．（2）补全频数分布直方图，并求扇形图中“15吨～20吨”部分的圆心角的度数．（3）如果自来水公司将基本用水量定位每户25吨，那么该地区6万用户中约有多少用户的用水全部享受基本价格？8、(2017濮阳.中考模拟) 中华文明，源远流长；中华汉字，寓意深广，为了传承优秀传统文化，某校团委组织了一次全校3000名学生参加的“汉字听写”大赛，赛后发现所有参赛学生的成绩均不低于50分，为了更好地了解本次大赛的成绩分布情况，随机抽取了其中200名学生的成绩（成绩x取整数，总分100分）作成绩x/分频数频率50≤x＜60 10 0.0560≤x＜70 30 0.1570≤x＜80 40 n80≤x＜90 m 0.3590≤x≤10050 0.25请根据所给信息，解答下列问题：（1） m=，n=；（2）请补全频数分布直方图；（3）这次比赛成绩的中位数会落在分数段；（4）若成绩在90分以上（包括90分）的为“优”等，则该校参加这次比赛的3000名学生中成绩“优”等约有多少人？9、(2014河南.中考真卷) 某兴趣小组为了了解本校男生参加课外体育锻炼情况，随机抽取本校300名男生进行了问卷调查，统计整理并绘制了如下两幅尚不完整的统计图．请根据以上信息解答下列问题：（1）课外体育锻炼情况扇形统计图中，“经常参加”所对应的圆心角的度数为；（2）请补全条形统计图；（3）该校共有1200名男生，请估计全校男生中经常参加课外体育锻炼并且最喜欢的项目是篮球的人数；（4）小明认为“全校所有男生中，课外最喜欢参加的运动项目是乒乓球的人数约为1200× =108”，请你判断这种说法是否正确，并说明理由．10、(2017广东.中考模拟) 为了解本校九年级学生期末数学考试情况，小亮在九年级随机抽取了一部分学生的期末数学成绩为样本，分为A（100﹣90分）、B（89～80分）、C（79～60分）、D（59～0分）四个等级进行统计，并将统计结果绘制成如下统计图，请你根据统计图解答以下问题：（1）这次随机抽取的学生共有多少人？（2）请补全条形统计图；（3）这个学校九年级共有学生1200人，若分数为80分（含80分）以上为优秀，请估计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少？11、(2016海南.中考真卷) 在太空种子种植体验实践活动中，为了解“宇番2号”番茄，某校科技小组随机调查60株番茄的挂果数量x（单位：个），并绘制如下不完整的统计图表：“宇番2号”番茄挂果数量统计表挂果数量x（个）频数（株）频率25≤x＜35 6 0.135≤x＜45 12 0.245≤x＜55 a 0.2555≤x＜65 18 b65≤x＜75 9 0.15请结合图表中的信息解答下列问题：（1）统计表中，a=，b=；（2）将频数分布直方图补充完整；（3）若绘制“番茄挂果数量扇形统计图”，则挂果数量在“35≤x＜45”所对应扇形的圆心角度数为°；（4）若所种植的“宇番2号”番茄有1000株，则可以估计挂果数量在“55≤x＜65”范围的番茄有株．12、(2020武汉.中考模拟) 中华文明，源远流长，中华汉字，寓意深广。

大学生比赛活动策划方案(学生竞赛活动方案)下面是我收集的大学生比赛活动策划方案(学生竞赛活动方案)，供大家品鉴。

要展开一场活动，除了要精心准备以外，一份好的策划书更是少不了。

下面就是我给大家带来的大学生比赛活动策划方案，欢迎大家阅读参考!大学生比赛活动策划方案1比赛目的：本次ELAA短文诗歌朗诵大赛意在锻炼和战线我外国语学院新生英语和风采。

加深同学对英语国家文化的理解，丰富大学新生的课余生活。

让同学们更快地融入到精彩的大学生活中。

比赛时间：20_年10月19日、20日6：30p。

m。

比赛地点：外语楼106、411活动对象：外国语学院_级同学。

主办方：外国语学院英语语言艺术团(ELAA)比赛流程：预赛阶段：所有报名同学将在外语楼参加预赛，选手被要求富有感情地朗诵一篇英语短文或者英语诗歌，题材不限，时间必须控制在2分钟以内。

ELAA还将邀请在相关英语大赛获奖的同学来担任评委。

在预赛结束后，后有40%的的同学有机会晋级决赛。

决赛阶段：在预赛表现出色的同学，将参加更加精彩的决赛。

接塞的赛制将发生改变，每位选手将要朗诵两篇材料，分别为自选材料和待选材料。

待选材料将由ELAA的人员负责挑选提供，材料难度适中，时间控制在2分钟以内。

ELAA还将要求外教担任评委。

如果选手准备了原创的短文或者诗歌，评委将会有额外加分。

评分标准：选手分数将有朗诵的流畅程度(4分)，语音语调(4分)，比赛台风(2分)三个部分组成，评委将对选手事物进行相应扣分。

奖项设置：比赛将设一等奖1名，二等奖2名，三等奖2名，另有人气奖和台风奖。

获奖者将获得ELAA颁发的荣誉奖状。

活动方案：—、主办单位：博雅外文协会二、活动时间：初赛4月29日，决赛5月13日三、活动地点：校内。

四、参加人员：全校英文诗歌爱好者，文学爱好者。

五、报名形式：以个人或小组为单位。

六、比赛形式：比赛由初赛和决赛两部分组成。

七、奖项设置：一、二、三等奖各一名，台风奖，魅力奖各一名。

人教版四年级数学下册第八单元《平均数与条形统计图》考试卷（含答案）一、选择题1．小华看一本故事书，前3天每天看10页，后2天共看了30页，小华平均每天看多少页？下列算式中正确的是（）。

A．（10＋30）÷5B．（3×10＋2×30）÷5C．（3×10＋30）÷52．小明所在组的同学的体重最轻31千克，最重40千克，他们这个组的同学的平均体重可能是（）。

A．41千克B．30千克C．35千克3．如果知道几个人的平均体重，一定能知道每个人的体重吗？( )A．能B．不能C．不能确定4．一个小球由静止开始,在斜坡上向下滚动滚到底部后,在平地上减速,最后停下．下示小球运动情况的是( )．A．B．C．5．为了统计五年级各班男、女生的人数情况，选择（）统计图能够帮助我们更好地分析和判断。

A．条形B．折线C．复式条形D．复式折线6．在第31届奥运会上，美国、英国、中国代表团分别夺得金牌46枚、27枚、26枚，平均每个代表团夺得金牌（）枚。

A．32B．33C．347．平城小学教职工的平均年龄是31岁，张老师今年54岁，他（）是这个学校的教职工。

A．不可能B．可能C．一定8．一位战士在打靶考核中前9枪成绩环数如图，问：不管这位战士最后一枪打几环，一定不会变的是（）A．中位数B．平均数C．众数D．无法确定9．一个三角形中，其中两个角的平均度数是45度，这是一个（）三角形。

A．钝角B．锐角C．直角10．开心所在班级学生的平均身高是142厘米，果果所在班级学生的平均身高是145厘米，比较两人身高，结果是（）。

A．开心高B．果果高C．无法比较二、其他计算11．求下列数据的平均数、中位数和众数：89，77，82，93，92，96，82，88，75．三、填空题12．有一列数：142，143，140，154，145，144，168，这列数的平均数是________．13．在运动会中，五（1）有6个同学参加了跳绳比赛，每分钟跳的个数如下：其中，中位数是，众数是，平均数是．王芳李雨张小琳邹蝶杨婷婷杨倩13514213511712416314．下图是兴华小学2014—2017年购买图书情况统计图。