立体几何求体积

立体几何中的体积与表面积计算立体几何是数学中的一个重要分支，涉及到了体积与表面积的计算。

在现实生活中，我们经常会遇到需要计算物体的体积与表面积的情况，比如建筑设计、工程测量等。

本文将探讨立体几何中的体积与表面积计算的方法和应用。

一、体积的计算体积是描述一个物体所占空间的大小，常用单位有立方米、立方厘米等。

在立体几何中，常见的物体包括立方体、长方体、圆柱体、圆锥体等。

1.1 立方体的体积计算立方体是最简单的几何体之一，它的六个面都是正方形。

立方体的体积计算公式为：体积 = 边长的立方。

例如，一个边长为5cm的立方体的体积为5^3 =125cm^3。

1.2 长方体的体积计算长方体是另一种常见的几何体，它的六个面中有两个是相等的长方形。

长方体的体积计算公式为：体积 = 长 ×宽 ×高。

例如，一个长为6cm、宽为4cm、高为3cm的长方体的体积为6 × 4 × 3 = 72cm^3。

1.3 圆柱体的体积计算圆柱体是一个由两个平行圆底和一个侧面围成的几何体。

圆柱体的体积计算公式为：体积= π × 半径^2 ×高。

其中，π取近似值3.14。

例如，一个半径为2cm、高为5cm的圆柱体的体积为3.14 × 2^2 × 5 = 62.8cm^3。

1.4 圆锥体的体积计算圆锥体是一个由一个圆锥底和一个侧面围成的几何体。

圆锥体的体积计算公式为：体积= 1/3 × π × 半径^2 ×高。

例如，一个半径为3cm、高为8cm的圆锥体的体积为1/3 × 3.14 × 3^2 × 8 = 75.36cm^3。

二、表面积的计算表面积是描述一个物体外部所占面积的大小，常用单位有平方米、平方厘米等。

在立体几何中，常见的物体的表面积计算方法有所不同。

2.1 立方体的表面积计算立方体的表面积计算公式为：表面积 = 6 ×边长^2。

立体几何求体积一、求体积的方法常见有如下三种：1、公式法：利用公式求出简单几何体体积。

2、等体积转化法：从不同的角度看待原几何体，通过改变顶点和底面，利用体积不变的原理，求原几何体的体积。

（一般指三棱锥，找高优先）3、割补法：对于给出的一个不规则的几何体，不能直接套用公式，常常需要通过“割”或“补”化复杂图形为已熟知的简单几何体，并作体积的加、减法，从而较快地找到解决问题的突破口。

（注：“一找二证三求”的顺序和原则。

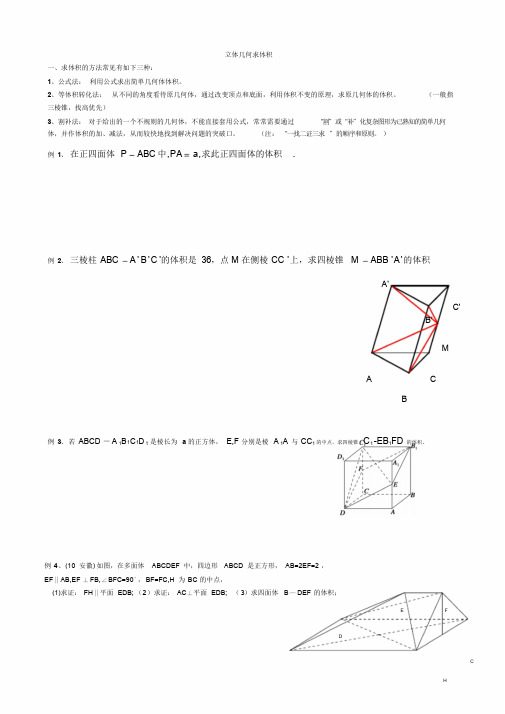
）例1、在正四面体P ABC中,PA a,求此正四面体的体积.例2、三棱柱ABC A'B'C'的体积是36，点M 在侧棱CC '上，求四棱锥M ABB 'A'的体积A'C'B'MA CB例3、若ABCD －A 1B1C1D1 是棱长为a的正方体，E,F 分别是棱 A 1A 与CC1 的中点，求四棱锥C1-EB1FD 的体积。

例4、(10 安徽) 如图，在多面体ABCDEF 中，四边形ABCD 是正方形，AB=2EF=2 ，EF∥AB,EF ⊥FB,∠BFC=90°，BF=FC,H 为BC 的中点，(1)求证：FH∥平面EDB; （2）求证：AC⊥平面EDB; （3）求四面体B—DEF 的体积；E FDCHA B 1ABCDEFG 为多面体，平面ABED 与平面AGFD 垂直，点O在线段AD 上，例5、(11 安徽) 如图，OA 1,OD 2, VOAB , △O AC，△ODE ，△O DF 都是正三角形。

（1）证明直线BC ∥EF ；（2）求棱锥F-OBED的体积。

例6、(13·安徽)如图，四棱锥P－ABCD 的底面ABCD 是边长为 2 的菱形，∠BAD ＝60°.已知PB＝PD＝2，PA＝ 6.(1)证明：PC⊥BD；(2)若E 为P A的中点，求三棱锥P－BCE 的体积．例7、(辽宁卷)已知点P，A，B，C，D 是球O 表面上的点，PA⊥平面ABCD，四边形ABCD 是边长为 2 3的正方形．若PA＝2 6，求△OAB 的面积．例8、(13·广东)如图1，在边长为 1 的等边三角形ABC 中，D，E 分别是AB，AC 上的点，AD＝AE，F 是BC 的中点，AF 与DE 交于点G.将△ABF 沿AF 折起，得到如图 2 所示的三棱锥A－BCF，其中BC＝ 2.22时，求三棱锥F－DEG 的体积V(1)证明：DE∥平面BCF；(2)证明：CF⊥平面ABF；(3)当AD＝F-DEG.32练习：1、求侧棱长为2，底面边长为 3 的正三棱锥的体积。

高中数学公式大全立体几何与空间向量高中数学公式大全：立体几何与空间向量一、立体几何立体几何是数学中研究三维空间中的几何图形及其性质的分支，对于高中生来说，常见的立体几何包括了体积、表面积等方面的内容。

下面是一些常用的立体几何公式：1. 立方体体积公式立方体是一种边长相等的六个正方形围成的立体。

其体积公式为：V = 边长³。

2. 正方体体积公式正方体是一种六个面都是正方形的立体。

其体积公式为：V = 底面积 ×高。

3. 长方体体积公式长方体是一种六个面都是矩形的立体。

其体积公式为：V = 长 ×宽×高。

4. 圆柱体积公式圆柱体是一种底面为圆形的立体。

其体积公式为：V = π × 半径² ×高。

5. 圆锥体积公式圆锥体是一种底面为圆形，顶点和底面中心连线垂直于底面的立体。

其体积公式为：V = 1/3 × π × 半径² ×高。

6. 球体积公式球体是一种所有点到球心的距离都相等的立体。

其体积公式为：V= 4/3 × π × 半径³。

7. 棱柱表面积公式棱柱是一种顶面和底面是平行的多边形，侧面是平行四边形的立体。

其表面积公式为：S = 底面积 + 侧面积。

8. 棱锥表面积公式棱锥是一种底面为多边形，侧面是由底面上的点和顶点连线形成的三角形的立体。

其表面积公式为：S = 底面积 + 侧面积。

二、空间向量空间向量是指具有大小和方向的箭头，可以表示空间中的位移、速度、加速度等物理量。

在高中数学中，空间向量常用于解决线性相关、平面垂直、平面平行等问题。

下面是一些常用的空间向量公式：1. 两点之间的距离公式设空间中的两点为A(x₁, y₁, z₁)和B(x₂, y₂, z₂)，则两点之间的距离公式为：AB = √((x₂ - x₁)² + (y₂ - y₁)² + (z₂ - z₁)²)。

高中数学立体几何体积和表面积计算技巧在高中数学中，立体几何是一个重要的内容，其中计算几何体的体积和表面积是必不可少的技巧。

本文将介绍一些常见的计算技巧，并通过具体的题目来说明这些技巧的应用。

一、立体几何体的体积计算技巧1. 直接计算法对于常见的几何体，如长方体、正方体、圆柱体、圆锥体和球体，可以直接使用相应的公式进行计算。

举例来说，如果要计算一个长方体的体积，可以使用公式 V = lwh，其中 l、w 和 h 分别表示长方体的长、宽和高。

如果已知长方体的长为 6 cm，宽为 4 cm，高为 3 cm，则可以直接代入公式计算得到体积 V = 6 × 4 × 3 = 72 cm³。

2. 分割法对于复杂的几何体，可以通过将其分割成若干简单的几何体来计算体积。

这种方法常用于计算不规则体的体积。

举例来说，如果要计算一个由三棱锥和一个正方体组成的复合体的体积，可以先计算三棱锥的体积，再计算正方体的体积，最后将两者相加。

3. 单位体积法对于一些特殊的几何体，可以利用单位体积的性质来计算体积。

这种方法常用于计算球台、球冠等几何体的体积。

举例来说，如果要计算一个球台的体积，可以先计算整个球的体积，再减去球冠的体积。

具体计算步骤如下：步骤一：计算整个球的体积，使用公式V = (4/3)πr³，其中 r 表示球的半径。

步骤二：计算球冠的体积，使用公式V = (1/3)πh²(3r - h)，其中 h 表示球台的高度。

步骤三：将步骤一的结果减去步骤二的结果，即可得到球台的体积。

二、立体几何体的表面积计算技巧1. 直接计算法对于常见的几何体，可以直接使用相应的公式进行表面积的计算。

举例来说，如果要计算一个长方体的表面积，可以使用公式 S = 2lw + 2lh +2wh，其中 l、w 和 h 分别表示长方体的长、宽和高。

如果已知长方体的长为 6 cm，宽为 4 cm，高为 3 cm，则可以直接代入公式计算得到表面积 S = 2(6×4) + 2(6×3) +2(4×3) = 108 cm²。

立体几何中的体积问题立体几何中求解体积问题的技巧求解体积是立体几何的重要教学内容，也是数学竞赛的常见考查内容之一。

在解决这类问题时，除了要记住公式，还需要巧妙思考，根据具体条件灵活选择计算体积的方法。

一、公式法举例来说，对于一个四面体ABCD，已知AB=AC=AD=DB=5，BC=3，CD=4，求该四面体的体积。

根据题意，可知BC=3，CD=4，DB=5，因此∠BCD=90°。

我们可以取BD的中点E，连结AE、CE，由直角三角形的性质可知BE=CE=DE，而AB=AC=AD=5，因此△ABE≌△ACE≌△ADE。

由此可得AE⊥BD，AE⊥EC，因此AE⊥平面BCD，即AE为平面BCD上的高。

计算可知V(ABCD)=1/3×S(BCD)×AE=1/3×6×4=8/3.变式1：对于一个三棱锥P-ABC，已知PA=1，AB=AC=2，∠PAB=∠PAC=∠BAC=60°，求三棱锥A-PBC的体积。

在△PAB中，有PB²=PA²+AB²-2PA×AB×cos∠PAB=1²+2²-2×1×2×cos60°=3.同理可得PA⊥PB，PA⊥PC，因此PA⊥平面PBC。

又因为AB=AC=2，∠BAC=60°，所以△ABC为正三角形，BC=2.取BC的中点D，连结PD，则PD²=PB²-BD²=3-1=2.因此S(△PBC)=1/2×BC×PD=2.故V(A-PBC)=1/3×S(△PBC)×PA=2/3.二、分割法对于一个正四棱锥P-ABCD的体积为1，已知E、F、G、H分别是线段AB、CD、PB、PC的中点，求多面体BEG-CFH的体积。

为了求解该问题，需要将多面体BEG-CFH切割成常见的几何体。

高中数学立体几何体积解题技巧立体几何是高中数学中的一个重要内容，其中涉及到的体积计算问题常常让学生感到困惑。

本文将介绍一些解题技巧，帮助高中学生更好地理解和解决立体几何体积问题。

一、直角三棱柱的体积计算直角三棱柱是指底面为直角三角形的三棱柱。

计算其体积时，可以利用底面积与高的乘积来求解。

例如，已知直角三棱柱的底面是一个直角边长为3cm和4cm 的直角三角形，高为5cm，求其体积。

解答：首先计算底面积，底面积=1/2 × 3cm × 4cm = 6cm²。

然后将底面积与高相乘，体积=6cm² × 5cm = 30cm³。

因此，该直角三棱柱的体积为30cm³。

通过这个例子可以看出，直角三棱柱的体积计算可以通过底面积与高的乘积来求解，这是一个常用的解题方法。

二、棱柱的体积计算棱柱是指底面为多边形的柱体。

计算其体积时，可以利用底面积与高的乘积来求解。

例如，已知一个棱柱的底面是一个边长为6cm的正六边形，高为8cm，求其体积。

解答：首先计算底面积，正六边形的面积可以通过将其分割为六个等边三角形来计算。

每个三角形的面积为1/2 × 6cm × 6cm × sin(60°) = 9√3 cm²。

因此，正六边形的面积为6 × 9√3 cm² = 54√3 cm²。

然后将底面积与高相乘，体积=54√3 cm² ×8cm = 432√3 cm³。

所以，该棱柱的体积为432√3 cm³。

通过这个例子可以看出，对于底面为多边形的棱柱，可以将其分割为若干个三角形来计算底面积，然后再与高相乘求解体积。

三、圆柱的体积计算圆柱是指底面为圆形的柱体。

计算其体积时，可以利用底面积与高的乘积来求解。

例如，已知一个圆柱的底面半径为5cm，高为10cm，求其体积。

研究立体几何中的体积问题立体几何是数学中的一个重要分支，主要研究的是空间中的各种立体图形，其中体积问题是立体几何中的基本内容之一。

本文将围绕研究立体几何中的体积问题展开详细的讨论。

一、立体几何中的体积概念在立体几何中，体积是指一个立体图形所占据的物理空间大小。

常见的立体图形包括球体、长方体、圆柱体、圆锥体等。

计算这些图形的体积，需要根据其不同的性质和特点使用相应的公式和方法。

二、球体的体积计算球体是一种所有点到某一固定点的距离都相等的几何图形。

球体的体积计算可以通过以下公式得到：V = (4/3)πr³其中，V表示球体的体积，π是一个数学常数，约等于3.14159，r 表示球体的半径长度。

利用这个公式，我们可以便捷地计算出球体的体积。

三、长方体的体积计算长方体是一种具有矩形底面的立体图形，其体积计算公式如下：V = lwh其中，V表示长方体的体积，l表示长方体的长度，w表示长方体的宽度，h表示长方体的高度。

通过这个公式，我们可以直接求解出长方体的体积。

四、圆柱体的体积计算圆柱体是由两个平行圆面和一个连接两个底面的侧面组成的立体图形。

计算圆柱体的体积需要使用下面的公式：V = πr²h其中，V表示圆柱体的体积，π是一个常数，r表示圆柱体底面的半径，h表示圆柱体的高度。

五、圆锥体的体积计算圆锥体是由一个圆锥面和一个底面为圆的侧面组成的立体图形。

计算圆锥体的体积需要使用下面的公式：V = (1/3)πr²h其中，V表示圆锥体的体积，π是一个常数，r表示圆锥体底面的半径，h表示圆锥体的高度。

六、其他立体图形的体积计算除了上述常见的立体图形，还存在其他复杂形状的立体图形，如棱柱、棱锥、正多面体等。

对于这些立体图形，体积的计算需要根据具体的特点使用相应的公式和方法。

七、应用实例立体几何中的体积问题常常涉及到实际生活和工程中的应用。

例如，我们可以根据房屋的长、宽、高计算出房屋的体积，以评估其空间大小。

立体几何体的表面积与体积计算立体几何体是指具有三个尺寸（长度、宽度和高度）的物体。

在几何学中，了解如何计算立体几何体的表面积和体积是非常重要的。

本文将介绍几种常见立体几何体的表面积和体积计算方法。

一、立方体的表面积与体积计算立方体是最简单的一种立体几何体，其所有边长相等。

要计算立方体的表面积，只需将六个面的面积相加。

假设一个立方体的边长为a，则其表面积S可以通过公式S = 6a^2求得。

另外，立方体的体积V可以通过公式V = a^3计算得到。

二、长方体的表面积与体积计算长方体是另一种常见的立体几何体，它拥有两个不同的边长和一个高度。

要计算长方体的表面积，可以将其面分为六个矩形，然后分别计算每个矩形的面积并相加。

假设长方体的长、宽、高分别为a、b和c，则其表面积S可以通过公式S = 2(ab + ac + bc)求得。

长方体的体积V可以通过公式V = abc计算得到。

三、圆柱体的表面积与体积计算圆柱体由一个圆柱体和两个平行于圆底的圆锥体组成。

要计算圆柱体的表面积，可以先计算圆柱的侧面积和两个底面积，然后相加。

假设圆柱体的半径为r，高度为h，则其侧面积Sl可以通过公式Sl = 2πrh 求得，底面积St可以通过公式St = πr^2求得。

因此，圆柱体的表面积S = 2πrh + 2πr^2。

圆柱体的体积V可以通过公式V = πr^2h计算得到。

四、金字塔的表面积与体积计算金字塔是由一个底面为多边形、侧面为三角形的立体几何体。

要计算金字塔的表面积，首先计算底面的面积，然后计算侧面的面积并相加。

假设金字塔的底面积为B，侧面的面积之和为Ss，则金字塔的表面积S = B + Ss。

金字塔的体积V可以通过公式V = (1/3)Bh计算得到，其中h为金字塔的高度。

五、球体的表面积与体积计算球体是唯一一个没有平面面积的立体几何体。

要计算球体的表面积，可以使用球体的半径r来计算。

球体的表面积S可以通过公式S =4πr^2求得。

立体几何体积与表面积公式一、棱柱。

1. 长方体。

- 设长方体的长、宽、高分别为a、b、c。

- 体积V = abc。

- 表面积S=2(ab + bc+ac)。

2. 正方体（特殊的长方体，a = b = c）- 设棱长为a。

- 体积V=a^3。

- 表面积S = 6a^2。

3. 棱柱（底面积为S_底，高为h）- 体积V=S_底h。

- 表面积S = S_侧+2S_底，其中直棱柱的侧面积S_侧=Ch（C为底面多边形的周长）。

二、棱锥。

1. 三棱锥（四面体）- 设三棱锥的底面积为S_底，高为h。

- 体积V=(1)/(3)S_底h。

- 表面积S = S_侧+S_底，三棱锥的侧面是三个三角形，S_侧为三个侧面三角形面积之和。

2. 棱锥（底面积为S_底，高为h）- 体积V=(1)/(3)S_底h。

- 表面积S = S_侧+S_底，其中正棱锥的侧面积S_侧=(1)/(2)Ch^′（C为底面多边形的周长，h^′为斜高）。

三、圆柱。

1. 设圆柱底面半径为r，高为h- 体积V=π r^2h。

- 表面积S = 2π r^2+2π rh（两个底面圆的面积2π r^2加上侧面展开矩形的面积2π rh）。

四、圆锥。

1. 设圆锥底面半径为r，母线长为l，高为h（h=√(l^2)-r^{2}）- 体积V=(1)/(3)π r^2h=(1)/(3)π r^2√(l^2)-r^{2}。

- 表面积S=π r^2+π rl（底面圆面积π r^2加上侧面展开扇形的面积π rl）。

五、球。

1. 设球的半径为R- 体积V=(4)/(3)π R^3。

- 表面积S = 4π R^2。

立体几何中的体积与表面积在立体几何中，体积和表面积是两个重要的概念。

体积指的是三维物体所占据的空间大小，表面积则是三维物体外部的表面总面积。

本文将介绍立体几何中的体积与表面积的计算公式以及应用。

一、体积的计算体积是衡量一个物体所占空间大小的量度。

不同的立体形状有不同的计算方法。

1.1 直线体的体积立方体是最简单的直线体，其体积计算公式为立方体的边长的三次方，即V=a³，其中V表示体积，a表示边长。

长方体也属于直线体的一种，其体积计算方法与立方体相同，即V=lwh，其中V表示体积，l表示长度，w表示宽度，h表示高度。

其他直线体如正方体、长方体变形以及长方体切割等形状的体积计算方法也遵循以上原则。

1.2 曲面体的体积曲面体的体积计算略显复杂，需要采用数学方法进行求解。

例如，球体的体积计算公式为V=4/3πr³，其中V表示体积，r表示球的半径。

圆柱体的体积计算公式为V=πr²h，其中V表示体积，r表示底面半径，h表示高度。

其他曲面体如圆锥体、棱柱体、棱锥体等也有相应的体积计算公式。

二、表面积的计算表面积是指一个物体外部所有面的总面积。

同样，不同形状的立体有不同的表面积计算方法。

2.1 直线体的表面积直线体的表面积计算公式与体积的计算方法相似，只是多了一些需要计算的面的面积。

例如，立方体的表面积计算公式为S=6a²，其中S表示表面积，a表示边长。

因为立方体有六个面，所以要乘以6。

长方体的表面积计算公式为S=2lw + 2lh + 2wh，其中S表示表面积，l表示长度，w表示宽度，h表示高度。

同样，因为长方体有六个面，所以每个面的面积都需要计算并累加起来。

其他直线体如正方体、长方体变形以及长方体切割等形状的表面积计算方法也遵循以上原则。

2.2 曲面体的表面积曲面体的表面积计算同样需要采用数学方法。

例如，球体的表面积计算公式为S=4πr²，其中S表示表面积，r表示球的半径。