基于图论的语义Web服务聚类方法
- 格式:pdf
- 大小:211.16 KB
- 文档页数:2

搜索引擎结果聚类(web网页自动分类)简介搜索引擎结果聚类(搜索引擎结果中的web网页自动分类)算法简介一、搜索结果中的web网页聚类基本流程和框架这里引用的是Carrot2的一个框架, 这跟我研究的web网页自动分类是一致的。
通过各种大型搜索引擎API获得源数据(一般至少包括一个唯一的URL地址,网页标题), 通过网页清洗,分词,提取特征项(降维作用),建立VSM, 构造STC进行聚类(如果你采用STC作为聚类算法), 聚类后就到了怎样把聚类结果展现给用户了, 这里有个很关键的问题是,如果让用户一看分类目录的标题,就知道这个类里包含那方面的内容.这里要补充说一下的是, Carrot2并没有中文分词功能,其默认的分词功能往往不能尽如人意.本人打算以后用中科院的ICTCLAS分词组件进行分词.二、搜索引擎结果聚类基本概念解释1、TF:(term frequency)用关键词的次数除以网页的总字数(在一篇特定网页中)-------词权值, 用于建立VSM2、IDF(Inverse document frequency):它的公式为log(D/Dw)其中D是全部网页数(假定一个关键词w 在 Dw 个网页中出现过)-------词权值, 用于建立VSM3、TF/IDF(可以有改进,见论文TFRDF---词频相对文本频率): 在 VSM中文档被映射成由一组规范化特征项权值矢量 ,其中特征项权值常见的量化加权模型有:布尔模型、词频模型、TF IDF模型 ,我们使用效果较好的 TF IDF 模型。
这种模型认为特征词条在某文档中的重要性与其在该文档中出现的频率成正比 ,与其在其他文档中出现的频率成反比。
因此它主要考虑两个因素: ①词语频率 TF TermFrequency ,即词语在(文档中出现次数; ②词语倒排文档频率IDF InverseDocumentFrequency ,即词语在文档集合中分布的一种量化。

基于聚类与二分图匹配的语义web服务发现摘要:为高效准确地查找语义web服务,引入聚类与二分图匹配技术,提出一种新的语义web服务发现方法。
根据服务描述信息将相似服务聚集到一起,采用空间向量模型表示服务,针对标准K-Means算法的缺陷设计基于k值优化和粒子群优化的K-Means聚类算法对服务进行聚类。
借鉴了带权二分图最优匹配思想对服务的功能属性进行匹配,设计基于WordNet 的概念间语义相似度计算方法用于计算二分图的权值,并针对如何构建满足最优匹配条件的带权二分图问题给出解决方案。
实验结果表明,该方法在查全率和匹配效率上均优于OWLS-MX方法。
关键词:服务发现;k值优化;粒子群优化算法;K-Means算法;概念相似度;二分图匹配Semantic Web Service Discovery Based on Clustering and Bipartite Graph Matching[Abstract] Inorder to efficiently and accurately locate semantic Web service, a new semantic Web service discovery method is proposed based on clustering and bipartite graph matching. In this method, services are clustered according to the service description information, in which Vector Space Model (VSM) is adopted to indicate the service. The K-Means algorithm based on k value optimization and Particle Swarm Optimization (PSO) optimization is proposed to resolve thetwo major defects of standard K-Means algorithm. Then the attributes of serv ices’ functions are matched by optimal matching of weighted bipartite graph, and a method based on WordNet is proposed to calculate the similarity between concepts which is the weight of bipartite graphs. A new solution is proposed to build the weighted bipartite graph whichmeets the optimal matching criteria. Experimental results show that the proposed method is superior to OWLS-MXmethod on the recall and matching efficiency[Keywords] service discovery;k value optimization;Particle Swarm Optimization(PSO)algorithm;K-Means algorithm; concept similarity; bipartite graph matching1.概述随着Internet的快速发展,Web服务的数量和种类也得到了快速增长,如何准确、快速地搜索到满足用户需求的Web服务已经成为当前研究的重点。

2008,44(23)ComputerEngineeringandApplications计算机工程与应用随着互联网的发展和网络用户的增加,如何根据用户喜好的不同提供页面过滤、网页推荐等个性化服务,不但有助于提高信息搜索效率缓解网络拥塞,而且也是Internet向智能化发展的方向[1-2]。
在Internet上,用户按照自己的兴趣进行访问,这种兴趣度可以通过用户在Web站点上的浏览行为体现出来,通过对具有相似访问兴趣的用户群进行聚类,发现用户的类属模式,利用这些聚类知识可以为站点结构改进,网页推荐服务以及电子商务中发掘潜在客户等应用提供决策依据。
本文提出基于概率潜在语义分析PLSA(ProbabilisticLa-tentSemanticAnalysis)的Web用户聚类算法,首先对Web日志进行数据预处理,将日志记录处理成用户会话形式;然后根据用户会话构建会话-页面矩阵SP;利用概率潜在语义分析将独立隐式变量Z与共现数据对———如页面P在用户会话S中的出现———联系成概率统计模型的特点,将隐式变量Z对页面P的条件概率转换为隐式变量Z对会话S的条件概率,以此为依据进行聚类分析。
在计算过程中,根据信息论的原理设计矩阵权值计算方法,权值由局部权值和全局权值组成。
计算方法着重考虑了页面对会话的类别区分能力;聚类方法采用了基于距离的k-medoids算法,以进一步改善聚类精度。
1相关概念1.1概率潜在语义分析概率潜在语义分析起源于自然语言处理研究,用于分析文档的潜在语义[3-4]。
它的基本思想是对于给定文档集D={d1,d2,…,dm}和词集W={w1,w2,…,wn}以及文档和词的共现矩阵A=|aij|n×m,其中aij代表不同词wj在文档di中的权值。
使用Z={z1,z2,…,zk}表示潜在语义的集合,k为指定的一个常数。
概率潜在语义分析假设词-文档对之间是条件独立的,并且潜在语义在文档或词上分布也是条件独立的。

基于聚类的语义分割方法在计算机视觉领域,语义分割是一项重要的任务,旨在将图像中的每个像素分配给特定的语义类别,如人、车、树等。
近年来,基于聚类的语义分割方法在这一领域引起了广泛关注。
传统的语义分割方法通常依赖于深度学习和卷积神经网络(CNN),这些方法需要大量标记的训练数据,并且计算量较大。
相比之下,基于聚类的语义分割方法具有更低的计算复杂度和更少的标记数据需求。
基于聚类的语义分割方法通常包括以下步骤:1. 特征提取,首先,从图像中提取特征。
这些特征可以是颜色、纹理、形状等。
常用的特征提取方法包括HOG、LBP、SIFT等。
2. 聚类,接下来,使用聚类算法对提取的特征进行聚类。
常用的聚类算法包括K均值聚类、DBSCAN、谱聚类等。
通过聚类,相似的像素将被分配到同一类别中。
3. 后处理,最后,对聚类结果进行后处理,如边界平滑、像素分类等,以获得更准确的语义分割结果。
基于聚类的语义分割方法具有一些优点。
首先,它们可以在不需要大量标记数据的情况下进行训练,因为聚类算法可以自动发现图像中的相似区域。
其次,这些方法通常具有较低的计算复杂度,可以在资源受限的设备上运行,如嵌入式系统和移动设备。
然而,基于聚类的语义分割方法也存在一些挑战。
例如,聚类算法的选择和参数设置可能会影响最终的分割结果。
此外,对于复杂的场景和图像,聚类方法可能无法捕捉到所有的语义信息。
总的来说,基于聚类的语义分割方法为解决语义分割问题提供了一种新的思路,它们在一定程度上克服了传统方法的一些限制。
随着技术的不断发展,相信这一领域的研究和应用将会取得更多的进展。

图论在数据分类与聚类中的应用图论是数学中的一个分支,研究的是图形以及图形中各个元素之间的关系。
图论在计算机科学领域有着广泛的应用,其中之一就是在数据分类与聚类中的应用。
本文将介绍图论在数据分类与聚类中的应用,并探讨其优势和应用场景。
一、图论介绍图论是一种模型,它将事物之间的关系用图形来表示。
一个图形由节点和边组成,节点表示事物,而边则表示事物之间的关系。
图论中有两种常见的图形模型,分别是有向图和无向图。
有向图中的边有方向,而无向图中的边没有方向。
图论不仅可以用于描述事物之间的关系,还可以通过图的算法进行数据分析和分类。
二、数据分类和聚类数据分类是将数据根据一定的特征划分为多个类别的过程,而聚类是将数据根据相似度进行自动分组的过程。
数据分类和聚类是数据挖掘中常见的任务,它们能够帮助我们从大量的数据中获取有用的信息。
三、图论在数据分类中的应用在数据分类中,图论可以帮助我们分析数据之间的关系,并将相似的数据划分到同一个类别中。
图论中一些常用的算法,如最短路径算法和最小生成树算法,在数据分类中也有很大的作用。
这些算法可以帮助我们计算数据之间的相似度,从而进行分类。
四、图论在数据聚类中的应用在数据聚类中,图论可以帮助我们度量数据之间的相似性,并将相似的数据聚集到一起。
图论中的聚类算法,如谱聚类算法和模块度最大化算法,可以帮助我们发现数据中的子群组。
这些算法通过计算数据之间的相似度,将相似的数据聚类在一起,从而形成聚类结果。
五、图论在社交网络分析中的应用社交网络是一种特殊的图结构,其中节点表示个体,边表示个体之间的关系。
图论可以帮助我们分析社交网络中的群组、关键人物以及信息传播等问题。
通过图论分析,我们可以发现社交网络中的隐含模式,从而为社交网络的管理和优化提供有效的策略。
六、图论在网络安全中的应用网络安全是图论在实际应用中的一个重要领域。
图论可以帮助我们分析网络中的攻击路径,识别网络中的异常行为,并进行网络流量分析。
2009,45(34)Web服务在Internet上的广泛应用使Web服务发现这一领域成为研究热点。
现今的工业标准UDDI和WSDL可以满足服务发现的需要,但由于它们的架构并不支持对于Web服务基于语义的搜索和匹配,UDDI和WSDL的功能有较大的局限性。
由于WSDL缺乏语义描述及UDDI不提供语义支持,注册中心返回的搜索结果不够精确,很多返回的服务并不符合用户的请求。
鉴于UDDI及WSDL不能支持语义的缺陷,研究者将语义Web技术引入Web服务,使用OWL-S对Web服务描述增加语义信息。
采用OWL-S描述Web服务,同时,为了提高服务发现效率,根据Web服务描述术语的语义相似度将Web服务聚类。
由于在Web服务发现过程中采用语义和聚类策略,UDDI 注册中心能返回更精确的结果。
1基本概念1.1面向Web服务的本体描述OWL-SOWL-S[1]是基于OWL语言的Web服务本体,其前身为DAML-S,它基于Web服务和语义Web。
OWL-S提供了一套标记语言,从而将Web服务的属性和功能以精确和机器可读的形式进行描述,这样就可以实现服务的自动发现、执行、组合、互操作及执行监控。
OWL-S主要定义了Web服务三个方面的语义,如图1所示:一个Web服务由presents,describedby和supports三个属性进行描述,服务概要(ServiceProfile)、服务模型(ServiceModel)和服务绑定(ServiceGrounding)分别为其属性取值。
这三个属性分别描述了服务可以做什么、如何进行工作和如何使用服务等信息。
ServiceProfile提供信息供服务查找代理确定服务是否符合查找要求。
ServiceProfile提供服务及服务提供者的高层描述,可以利用ServiceProfile在服务注册库中进行服务发布或服务发现。
ServiceProfile包含三个方面的信息:供人读取的服务描述信息;关于服务所提供的功能信息;关于服务的一个额外的信息。
ISSN 1000-9825, CODEN RUXUEW E-mail: jos@Journal of Software, Vol.21, No.7, July 2010, pp.1561−1575 doi: 10.3724/SP.J.1001.2010.03704 Tel/Fax: +86-10-62562563© by Institute of Software, the Chinese Academy of Sciences. All rights reserved.∗图像-文本相关性挖掘的Web图像聚类方法吴飞+, 韩亚洪, 庄越挺, 邵健(浙江大学计算机科学与技术学院,浙江杭州 310027)Clustering Web Images by Correlation Mining of Image-TextWU Fei+, HAN Ya-Hong, ZHUANG Yue-Ting, SHAO Jian(College of Computer Science and Technology, Zhejiang University, Hangzhou 310027, China)+ Corresponding author: E-mail: wufei@Wu F, Han YH, Zhuang YT, Shao J. Clustering Web images by correlation mining of image-text. Journal ofSoftware, 2010,21(7):1561−1575. /1000-9825/3704.htmAbstract: To cluster the retrieval results of Web image, a framework for the clustering is proposed in this paper. Itexplores the surrounding text to mine the correlations between words and images and therefore the correlations areused to improve clustering results. Two kinds of correlations, namely word to image and word to word correlations,are mainly considered. As a standard text process technique, tf-idf method cannot measure the correlation of word toimage directly. Therefore, this paper proposes to combine tf-idf method with a feature of word, namely visibility, toinfer the correlation of word to image. Through LDA model, it defines a topic relevance function to compute theweights of word to word correlations. Finally, complex graph clustering and spectral co-clustering algorithms areused to testify the effect of introducing visibility and topic relevance into image clustering. Encouragingexperimental results are reported in this paper.Key words: graph clustering; complex graph; visibility; latent Dirichlet allocation; spectral clustering摘要: 为了实现Web图像检索结果的聚类,提出了一种Web图像的图聚类方法.首先定义了两种类型关联:单词与图像结点之间的异构链接以及单词结点之间的同构链接.为了克服传统的TF-IDF方法不能直接反映单词与图像之间的语义关联局限性,提出并定义了单词可见度(visibility)这一属性,并将其集成到传统的tf-idf模型中以挖掘单词-图像之间关联的权重.根据LDA(latent Dirichlet allocation)模型,单词-单词之间关联权重通过一个定义的主题相关度函数来计算.最后,应用复杂图聚类和二部图协同谱聚类等算法验证了在图模型上引入两种相关性关联的有效性,达到了改进了Web图像聚类性能的目的.关键词: 图聚类;复杂图;可见度;LDA(latent Dirichlet allocation);谱聚类中图法分类号: TP311文献标识码: A∗ Supported by the National Natural Science Foundation of China under Grant Nos.60603096, 60533090 (国家自然科学基金); theNational High-Tech Research and Development Plan of China under Grant No.2006AA010107 (国家高技术研究发展计划(863)); theProgram for Changjiang Scholars and Innovative Research Team in University of China under Grant Nos.IRT0652, PCSIRT (长江学者和创新团队发展计划)Received 2009-02-27; Revised 2009-05-21; Accepted 2009-07-23; Published online 2010-04-121562 Journal of Software软件学报 V ol.21, No.7, July 2010在Web上,使用关键字搜索图像仍然是有效的常用检索手段.在Web图像检索中,用户提交的查询关键字往往是视觉多义词(visually polysemous word)[1],这类单词包含多个不同视觉含义.例如,单词mouse可表示“computer mouse”,“mouse animal”和“Mickey mouse”等多个主题.因此,用这些视觉多义词查询图像,所返回的图像检索结果会包含多个主题,并且不同主题的图像混合在一起.这就需要在得到初始检索结果后对表达不同主题的图像进行归类等处理.近年来,研究者提出了若干Web图像聚类方法[2−8]来解决这个问题.由于图像的底层特征和高层语义之间存在“语义鸿沟”,这些聚类方法往往同时利用了被聚类图像集合所包含的视觉、文本和链接等多模态信息.属于不同特征空间的多模态信息是相互关联的,在模态信息融合学习中挖掘和利用这些相关性关联以正确理解多媒体隐含语义是近期机器学习研究的重点课题,代表性工作有多视角学习(multi-view learning)[9]和迁移学习(transfer learning)[10,11].前者同时利用同一数据的多种特征空间表示进行学习,而后者研究训练数据和测试数据有不同分布或属于不同特征空间的学习问题.本文挖掘文本与图像两种模态信息之间相关性关联,通过图模型对该关联关系进行建模,并利用图聚类算法对Web图像进行聚类.Web图像通常与其伴随文本共存于HTML页面之中,伴随文本以及一些文本标签(textual tags)描述了图像的语义内容.在Web图像检索和标注领域,很多研究利用了图像和文本之间的相关性关联.文献[12]中的实验表明:利用图像伴随文本和一些HTML标记中的文本对图像检索结果进行重排序可以提高图像检索性能.在图像自动标注领域,文献[13]研究从图像伴随文本中提取关键短语(salient term)来对图像进行标注,文献[14,15]研究如何将文本中的单词关联到图像某个区域,从而对图像进行更准确标注.但是,伴随文本中不同单词对图像语义描述所做贡献不同.对于文本中多个单词,有的单词能够找到合适的图像来形象地描述该单词的含义,例如chairs;有的单词比较抽象,则很难找到一个合适图像来形象地描述该单词的含义,例如statistics.从形象思维的角度,这种差异反映了单词和其指代图像之间存在或弱或强的关联,也反映单词具有可见度(visibility)属性.可见度定义为某个单词可以被视觉感知的概率.文献[16]中提出了一个单词可见度模型,并将之应用到文本-图片合成系统(TTP).另外一些研究者[17,18]则将单词可见度属性引入到图像标注领域,以改善图像标注结果.本文提出一种新的更合理的单词可见度模型,并将该模型与传统的tf-idf方法结合来定义单词-图像相关性关联.另一方面,对于包含多个主题的Web图像集合,其伴随文本中的隐含主题(latent topic)信息间接地反映了图像间的主题相关性.文献[1,19]通过LDA(latent Dirichlet allocation)学习发现图像伴随文本中的隐含主题,并依据单词上的隐含主题分布对图像进行聚类和排序.本文引入LDA模型挖掘图像伴随文本中的隐含主题,并通过其在各个单词上的边缘概率分布定义单词-单词的主题相关性关联.因此,本文考虑两种关联关系:单词-图像相关性关联和单词-单词主题相关性关联.这种交叉关联可用图模型进行建模.近来,研究者已开始将图模型引入到Web图像聚类研究中.文献[2]利用三部图(tripartite graph)对图像-图像同构底层特征以及图像-文本异构结点间异构链接(heterogeneous links)关系进行建模,并基于图分割(graph cut)方法对Web图像进行聚类.与文献[2]模型不同,本文定义的关联关系不仅包含图像-文本间异构链接,也包含单词-单词间同构链接(homogeneous links).因此,本文用更一般的复杂图模型[20,21]对其进行建模,并应用复杂图聚类算法[20]对Web图像进行聚类.基于图像-文本相关性挖掘,本文提出一种新的Web图像聚类框架.如图1所示,图模型中包含两类结点:图像结点和单词结点.本例中图像是将关键字jaguar作为查询提交给Google的图像搜索引擎返回结果,这些返回图像主要包含3个语义主题:jaguar animal,jaguar car和jaguar plane.图中单词来自图像所在网页中伴随文本.实线和虚线分别代表单词-图像以及单词-单词相关性关联.通过单词可见度模型与tf-idf方法的结合,高可见度单词与图像间的链接得到加强.在聚类过程中,高可见度单词结点将向与之关联的图像结点传递更多的主题相关性信息,从而提高Web图像的聚类性能.本文第1节介绍图像-文本相关性挖掘.第2节介绍图聚类方法.第3节给出实验,对可见度计算模型进行分析,并对将单词可见度和主题相关度引入Web图像聚类的有效性进行验证.第4节总结全文.吴飞 等:图像-文本相关性挖掘的Web 图像聚类方法 1563Fig.1 Graph model (two types of nodes: Image nodes & word nodes; two types of links: Heterogeneous linksbetween image and word; homogeneous links (dashed) between words)图1 图模型(两种结点:图像结点和单词结点;两种链接:同构链接(虚线)和异构连接(实线))1 图像-文本相关性挖掘如图1所示,本聚类框架的核心是定义单词-图像和单词-单词这两种相关性关联,前者通过将单词可见度与tf-idf 方法结合予以实现,后者通过LDA 学习获得. 1.1 单词的可见度本节讨论如何挖掘图像伴随文本中的单词和图像之间的相关性,即得到单词和图像两种不同类型结点之间的链接权重.不同的单词对图像语义描述所起到的贡献不同,本文用单词和图像的相关性来衡量这种差别.传统的通过tf-idf 方法衡量单词对图像的重要性,在一定程度上忽略了图像本身具有的视觉特性,本节所定义的可见度模型弥补了这一不足. 1.1.1 传统方法:tf-idf基于文本的图像检索方法[12]用查询单词与图像伴随文本之间的相关性代替单词与图像之间的相关性.根据向量空间模型(vector space model),单词在伴随文本中的重要性用该单词的tf-idf 值来度量.假设单词w 来自第i 个图像的伴随文本d i 中,单词w 的tf-idf 值tfidf (w )计算如下:1()(,)log()Ni i Ntfidf w freq w d num w ==⋅∑ (1)其中,freq (w ,d i )是单词w 在文档d i 中的词频,N 是图像的总数,num (w )是伴随文本中含有单词w 的图像的总数.由于tf-idf 方法来源于文本处理领域,tfidf (w )并不能直接地度量单词和图像之间的相关性.因此,需要进一步挖掘单词和图像之间语义联系.1.1.2 可见度计算模型单词的可见度(visibility)体现了单词(尤其是名词)所蕴含语义可用图像来描述的程度.从认知心理学和形象思维的角度,高可见度的单词(如banana)要比低可见度的单词(如Bayesian)更易在人脑中形成直接视觉形象.近期一些研究[16−18]已将可见度作为单词一种新的属性,用来表达单词与图像之间的语义关联.在Web 页面中,图像周围每个单词具有不同程度的可见度,高可见度单词对图像的语义有更强的描述能力.文献[16−18]分别提出了不同单词的可见度模型,但文献[16]中的可见度模型更加直接和简单,并运用到文本到图像(text-to-picture,简称TTP)合成系统之中.TTP 系统研究如何自动地为文本寻找语义相关的图像,并将找到的图像自动合成一幅图画来形象地描述文本的语义内容.为了计算文本中单词可见度,文献[16]提出的可见度模型如下:1564 Journal of Software 软件学报 V ol.21, No.7, July 20101()1exp(( 2.7815.40))P w x =+−−+ (2)其中,P (w )表示单词w 的可见度,x =log((C 1+10−9)/(C 2+10−9)),C 1是将单词w 作为查询提交给Google 图像搜索引擎返回的搜索结果数目,C 2是将单词w 作为查询提交给Google 文本搜索引擎返回的搜索结果数目.根据式(2),P (w )是x 的增函数.所以对于单词w ,如果在Google 上得到的C 1/C 2值比较大,则w 可见度就比较高.通过实验发现,公式(2)给出的可见度计算模型对于某些主题宽泛的词会失效.如图2所示,该图像是用关键字bass 作为查询,由Google 图像搜索引擎返回的前5个结果中的一个.伴随文本中名词的C 1和C 2值见表1.如图3所示,legend,record,scale 等词C 1/C 2值大于largemouth 和fishermen.但是根据可见度定义,因为largemouth 和fishermen 是这幅图像中两个主要对象,它们应有更高可见度.造成这种结果的原因是,record 等主题较宽泛单词大量地出现在Web 页面上,同时也大量地出现在图像伴随文本中,从而提高了它们C 1/C 2值.因此,有必要对式(2)给出的可见度模型进行改进.由于主题宽泛单词的C 2值往往很大,因此可以用逆文档词频来对其可见度进行抑制.Fig.2 Image and surrounding text Fig.3 Visibility scores comparison for nouns in Fig.2(the italic words are nouns)图2 图像和伴随文本(斜体字是名词) 图3 图2的伴随文本中名词的可见度对比Table 1 Google image hit counts C 1 and Google Web hit C 2 counts for the nounsin the surrounding text in Fig.1 (retrieved from Google on Apr. 24, 2009)表1 图1的伴随文本中名词的C 1和C 2值(从Google 上检索得到,2009年4月24日)WordC 1 C 2 Largemouth 88 800 1 560 000 Fishermen 690 000 9 900 000 Pound 16 000 000 77 300 000 Legend 50 000 000 198 000 000 Scale 35 100 000 223 000 000 Record 110 000 000 606 000 000 Questions 79 400 000 869 000 000 Friend 114 000 000 1 310 000 000 Number88 700 0001 660 000 000基于上述分析,本文提出了式(3)所示的一个可见度模型:Google ()919210()10IDF w C vis w C −−−⎛⎞+=⎜⎟+⎝⎠(3)其中,IDF Google (w )定义如下:Google 2||()logIDF w C =D (4) Could this be it? The new number 1 for largemouth bass fishermen ? Mike Winn is holding a 25.1-pound bass caught on Dixon Lake in southern California Monday by his friend Mac Weakley. By all accounts it smashes the standing record , but questions (as always) loom. Jed Dickerson, a bass fishing legend and friend of Weakley’s, weighed the big’un with a digital scale and then released it.L a r g e m o u t hF i s h e r m e nP o u n dL e g e n dS c a l eR e c o r dQ u e s t i o n sF r i e n dM e m b e rvis (w )C 1/C 2P (w )吴飞 等:图像-文本相关性挖掘的Web 图像聚类方法1565其中,D 是Google 索引的所有Web 页面集合.图2中名词的vis (w )值如图3所示.largemouth 和fishermen 的vis (w )值最大,且不同单词可见度存在明显区分度.可见,改进的可见度模型更加合理.为了进一步验证本模型的合理性和性能,本文将在第3.1节对该模型进行详细定量分析.我们提出将可见度模型集成到传统的tf-idf 方法中来定义单词-图像的相关性,即单词w 与图像之间的关联度为tfidf (w )⋅vis (w ).这样,高可见度单词与图像的相关性得到加强,低可见度单词与图像的相关性减弱. 1.2 单词间的主题相关度本节介绍如何挖掘单词间的主题相关性,得到单词-单词之间的关联.这里提出通过LDA 对图像伴随文本进行学习,发现分布在各个单词上的隐含主题,并利用这个概率分布对图像伴随文本中任意两个单词之间的主题相关性进行度量.1.2.1 LDA 基本理论给定一个文档集合,LDA 模型[22,23]假设每个文档是多个隐含主题z ∈{1,…,K }的混合.假设文档集合中有M 个文档,每个文档包含N d 个词,d ∈{1,…,M }.根据LDA 模型,文档中多个单词由以下生成过程产生[22]:1) 对于每一个隐含主题j =1,…,K ,根据一个狄利克雷(Dirichlet)先验分布Dir (β)选择一个分布在单词上的参数为ξj 的多项分布(multinomial distribution);2) 对于每一个文档d ,根据一个Dirichlet 先验分布Dir (α)选择一个分布在隐含主题上的参数为ψ的Multinomial 分布;3)对于产生第i 个单词,首先根据Multinomial 分布ψ确定一个主题z =j ,然后根据Multinomial 分布ξj 产生单词w i .根据以上生成模型,生成一个文档1,...,d N d w w =的概率定义为111(,...,|,)(|,)(|)d d N KN i z i P w w P w z P z ξψξψ===∑∏ (5)根据贝叶斯(Bayes)定理,隐含主题z =j 分布在文档1,...,d N d w w =上的概率P (z =j |d )可计算如下:11(|)()(|)(|)()ddN N i i i i i P z j w P z j P z j d P z j w P w ========∑∑(6)1.2.2 主题相关度函数在式(6)中,P (z =j |w i )是隐含主题z =j 在文档1,...,d N d w w =中各个单词w i 上边缘分布,可以看作该隐含主题在 各个单词上分配的份额.如果某一个单词对于某个隐含主题比较重要,那么该主题在这个单词上的边缘分布就相对比较大.因此,我们可以根据LDA 模型定义主题相关度函数来计算文档集合中任意两个单词同时属于某一个主题的概率,这个概率值可以衡量两个单词的主题相关度.定义1(单词的主题相关度函数). 文档集合中任意两个单词w s 和w t 之间的主题相关度函数Topic _r (w s ,w t )定义为_(,)max (|)(|)(|)()(|)()max()()(|)(|)()maxs t s t js t js t s t jTopic r w w P z j w P z j w p w z j P z j p w z j P z j P w P w p w z j p w z j P z j σ========⋅==== (7)在定义1中,由于乘积P (w s )⋅P (w t )与某个隐含主题z =j 无关,我们选择常数σ作为归一化(normalized)常数.2 图聚类方法传统的图聚类方法大多处理仅包含单一类型结点的同构结点图(homogeneous-node graph).但是,反映现实世界中对象之间复杂关系的图模型一般是异构结点图(heterogeneous-node graph),即图中包含多种类型结点,例1566 Journal of Software 软件学报 V ol.21, No.7, July 2010如科技著作网中包含作者和论文两种类型结点.异构结点图同时包含两种类型的链接关系:同类型结点之间的同构链接(homogeneous links)和不同类型结点之间的异构链接(heterogeneous links).例如,作者之间的合作关系以及论文之间的引用关系是同构链接;作者和论文之间的创作关系是异构链接.显然,同构结点图是异构结点图的一种特例.如图1所示,本聚类框架中的图模型包含两种不同类型结点:图像结点和单词结点以及两种类型链接关系:单词-图像间的异构链接和单词-单词间的同构链接.文献[20]将这种更具一般性的异构结点图定义为复杂图(complex graph).利用复杂图聚类(complex graph clustering)[20]算法可对图像结点进行聚类.如果忽略单词-单词间的同构链接(如图1中虚线所示),该图模型简化为二部图(bipartite graph),可利用二部图协同谱聚类(spectralco-clustering)算法[24]对图像进行聚类. 2.1 复杂图聚类定义1(复杂图(complex graph )). 给定一个(无向的)复杂图1({},)m i i G V E ==,其中,1{}mi i V =代表m 个不同类型结点集合,E 代表图中边的集合,G 可以表示为一个相关矩阵的集合[20]:()()1,1{{},{}}i j i i n n n n i mij mi i j S R A R ××+=+=∈∈ (8)其中,S (i )表示结点集合V i 中同构结点之间的同构链接(边)的权重矩阵,A (ij )表示结点集合V i 和V j 之间的异构链接(边)的权重矩阵.结点集合V i 中的结点个数|V i |=n i . 2.1.1 复杂图聚类框架文献[20]提出了一个复杂图聚类框架,该框架可以利用复杂图中的同构和异构链接信息对多种类型的结点分别聚类.在聚类过程中,不同类型结点之间的聚类结构可互相传递最终完成聚类.假定k i 表示结点集合V i 聚类个数,()i i n k i C R ×+∈表示结点集合V i 中结点的类属关系指示矩阵,矩阵元素()i pqC 表示V i 中的第p 个结点隶属于第q 类的类属权重,()i i k k iD R ×+∈代表V i 内结点的聚类模式,矩阵元素()i pq D 表示V i中第p 类和第q 类之间的链接强度,()ijk k ij B R ×+∈代表V i 和V j 内结点之间的聚类模式,矩阵元素()ij pq B 表示V i 中第p 类和V j 中的第q 类之间的链接强度.复杂图聚类框架可以描述为如下优化问题[20]:()(),()()()()()()()()()()11()()arg min (,())(,()).. {0,1},i j i i C C m mi i i i i T ij ij i ij j T i ij n k i i L L S C D C A C B C s t C C ωω==×⎡⎤⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥∈=⎢⎥⎣⎦∑∑11D D (9) 其中,向量1的每个分量都为1,D 代表给定的距离函数,ω(i )和ω(ij )分别代表同构链接和异构链接的权重系数(ω(i )和ω(ij )由用户根据具体问题求取).式(9)中并未指定距离函数D ,因此,这个复杂图聚类框架有很好的推广性.从不同的现实系统中抽象得到的复杂图模型有不同的统计特性,要根据复杂图边权重的统计分布特性选择合适的距离函数.文献[20]中讨论了两种边权重分布及其对应的距离函数:1) 正态分布(normal distribution).这时,距离函数D 应选用欧氏距离(Euclidean distance);2)指数分布族(exponential family distribution),这是1)的推广.欧氏距离、扩展的I-散度(generalizedI-divergence)距离、KL 散度(KL divergence)距离都可以推广为Bregman 散度(Bregman divergences)距离,与之对应的是一系列指数分布.2.1.2 复杂图聚类算法常用的复杂图模型构建在两种类型的结点集合之上.如图1所示.在复杂图G 1=(V 1,V 2,E )中,同构链接来自V 1中的结点之间,异构链接来自V 1和V 2中的结点之间.根据定义1,G 1可表示为1112{,}n n n n S R A R ××++∈∈.如果忽略权重系数ω,式(9)中目标函数L 简化为 L =D (S ,C (1)D (C (1))T )+D (A ,C (1)B (C (2))T ) (10)如果D 选用欧氏距离,则复杂图G 1的聚类任务可以表示为如下的优化问题[20]:吴飞 等:图像-文本相关性挖掘的Web 图像聚类方法 1567(1)(2)1122(1)(1)2(1)(2)2,,,(1)(2)(1)(2)min ||()||||()||s.t. {0,1},{0,1},,T T C C D B n k n k S C D C A C B C C C C C ××⎡⎤−+−⎢⎥⎢⎥∈∈==⎣⎦1111 (11) 定理1. 如果11221112(1)(2){0,1},{0,1},,n k n k k k k k C C D R B R ××××++∈∈∈∈是优化问题(11)的最优解,那么有(1)(1)1(1)(1)(1)(1)1(())()())T T T D C C C SC C C −−= (12)(1)(1)1(1)(2)(2)(2)1(())()())T T T B C C C AC C C −−= (13)文献[20]给出了定理1的证明.根据定理1,复杂图G 1的聚类算法如下: 算法1. 复杂图G 1的聚类算法CGC.输入:矩阵S 和A ,结点集合V 1的聚类个数k 1,V 2的聚类个数k 2; 输出:类属关系指示矩阵C (1)和C (2). 步骤1. 重复迭代步骤2~步骤5直到收敛; 步骤2. 根据式(12)计算D ; 步骤3. 根据式(13)计算B ;步骤4. 固定D ,B 和C (2),逐行更新C (1),使得最小化(1)(1)2(1)(2)2||()||||()||T T L S C D C A C B C =−+−; 步骤5. 固定D ,B 和C (1),逐行更新C (2),使得最小化(1)(1)2(1)(2)2||()||||()||T T L S C D C A C B C =−+−.本文中,对称矩阵i i n n S R ×+∈为单词-单词相关性矩阵,n i 是词典(vocabulary)中单词的个数,矩阵元素S ij (i ≠j )表示单词w i 和w j 之间的主题相关度,S ij =Topic _r (w i ,w j ).矩阵ijn n A R ×+∈为单词-图像相关性矩阵,n j 是图像集合中图像的个数,矩阵元素A ij 表示单词w i 和第j 个图像之间的相关度,A ij =tfidf (w i )⋅vis (w i ).2.2 基于二部图的协同谱聚类定义2(二部图(bipartite graph )). 给定一个(无向的)二部图G =(V 1,V 2,E ),其中,V 1={d 1,…,d n }和V 2={w 1,…, w m }代表两个不同类型结点集合,12{{,}:,}i j i j E d w d V w V =∈∈代表图中边的集合.定义3(图G 的分割(cut )). 给定图G 的邻接矩阵M ,图G 中边(d i ,w j )的权重为E ij ,则M 定义为,{,}0, ij i j ij E d w M ⎧=⎨⎩如果存在边否则 (14)如果图G 的一个分割将结点集V 分成两个子集V 1和V 2,则图G 的分割定义为1212,(,)i j ij d V w V cut V V M ∈∈=∑(15)如果推广到k 个子集,则图G 的k -分割(k -cut)定义为12-(,,...,)(,)k i j i jk cut V V V cut V V <=∑ (16)根据定义3,二部图聚类框架可以描述为式(17)所示优化问题:1111,...,-(,...,)min -(,...,)kk k k V V k cut W D W D k cut V V ∪∪= (17)文献[24]中的协同谱聚类(spectral co-clustering)算法Multipartition(k )给出了以上优化问题的解.将单词-图 像相关性矩阵ijn n A R ×+∈作为算法Multipartition(k )的输入可对图像进行聚类.3 实 验3.1 可见度计算模型分析本节将在5个单词集合上对本文提出的单词可见度计算模型进行定量分析,以验证其合理性和性能.第3.1.2节通过对可见度计算模型在5个单词集合上的总体性能进行分析,表明该模型的合理性.第3.1.3节进一步验证了本模型对主题宽泛单词可见度有抑制能力.1568 Journal of Software软件学报 V ol.21, No.7, July 20103.1.1 单词集合可见度用来度量单词语义可被视觉感知的能力,为了验证本文提出的可见度计算模型的合理性,我们选取了下述5个单词集合进行定量分析和对比实验:(1) Columbia374[25].该集合选自LSCOM本体[26],包含374个单词,分别对应374个视觉概念(visualconcepts),它们由研究者定义并用来对视频语义内容进行标注;(2) Flickr Hot Tags.该集合选自Flickr(/photos/tags),包含144个单词,是Flickr上用户最常用的图像标签;(3) IAPR Annotations.该集合选自开放数据集IAPR TC-12 Benchmark[27]中的图像标注数据.我们选取了IAPR TC-12的一个子集,包含2 000个图像,并提取了其标注文本中的名词,共包含约500个单词;(4) Surrounding Words.该集合由我们构建,首先将视觉多义词apples作为查询提交给Google的图像搜索引擎,对返回结果中的每个图像,我们下载了图像文件以及该图像所在的Web页面,并提取了图像伴随文本中的名词构成单词集合,共包含约1 200个单词;(5) NIPS BOWs.该集合选自Topic Modeling Toolbox[28]中的数据集“NIPS proceedings papers (bag ofwords)”,该数据集包含9 244个NIPS会议论文集中的单词,我们随机选取了其中的500个名词构成单词集合.3.1.2 可见度模型总体性能应用公式(3),我们计算了5个数据集中每个单词的可见度.见表2,对每个数据集,从可见度最高的单词开始,每个可见度数值区间选取一个单词,列出了20个代表单词.每个数据集的平均可见度如图4所示.实验结果表明:(1) 数据集Colimbia374,Surrounding Words,Flickr Hot Tags和IAPR Annotations中单词是图像标注所用标签或视觉概念,见表2中的football和oceans,其语义可被视觉感知的能力普遍较强,应用可见度计算模型其单词有较高vis(w)值;(2) 数据集NIPS BOWs中单词多数属于机器学习领域的抽象概念,见表2中的statistics和probability,其语义可被视觉感知的能力较弱,因此平均vis(w)值较低;(3) 在图像标签或视觉概念中,描述图像中特定对象的单词,见表2中的pavilions和railings,往往获得更高vis(w)值,这和图3中的单词fishermen和largemouth的高可见度一致.Table 220 representative words and corresponding vis(w) values from each of the 5 word sets(values of C1 and C2 are retrieved from Google on May 27, 2009)表25个数据集中20个代表单词及其vis(w)值(C1和C2值来自Google,2009年5月27日)NIPS BOWs Columbia374 Surr. words Flickr hot tags IAPR annotationsFields 0.930 6 Pavilions 0.986 5Fuji 0.952 1Museum 0.925 5Football 0.991 2 Dimension 0.889 2 Harbors 0.977 0Statue 0.947 3Urban 0.919 9Foreground 0.987 43 Oceans 0.965 0Oranges 0.934 2Autumn 0.906 6Railings 0.978 3Feature 0.874Pattern 0.855 7 Microphones 0.959 6Bananas 0.927 1Portrait 0.897 3Pavement 0.969 9Kernel 0.845 3 Suburban 0.944 8Apples 0.913 1Mountains0.890 7Pillows 0.955 6Distance 0.830 3 Supermarket 0.935 0Spices 0.904 9Landscape0.878 8Chairs 0.946 9Output 0.808 4 Farms 0.923 1Fruits 0.897 9Festival 0.868 5Cliff 0.938 1Detection 0.796 5 Flood 0.917 0Orchard 0.880 2 Ireland 0.856 5Fountain 0.923 0 Properties 0.792 1 Clouds 0.909 6Downtown0.879 6Holiday 0.845 5Sunrise 0.914 6Abstract 0.784 8 Flags 0.896 4Bush 0.862 4Florida 0.836 6Lamp 0.900 5Weight 0.773 9 Laundry 0.886 1Ridge 0.858 2Island 0.823 6Desk 0.899 1Statistics 0.752 9 Desert 0.875 2Wine 0.844 6Christmas0.813 4Peak 0.886 1Variable 0.740 3 Politics 0.867 3Temperature0.833 2Wedding 0.800 4Bathroom 0.870 9System 0.727 4 Traffic 0.858 0Wood 0.829 3Food 0.796 1Mirror 0.864 4 Information 0.622 3 Block 0.847 7Storage 0.814 6Fashion 0.784 0Stone 0.856 5 Probability 0.601 9 Oil 0.830 4Ground 0.801 4Birthday 0.774 2Areas 0.841 8 Size 0.585 9 Hand 0.820 3Settings 0.794 2Family 0.765 8Plant 0.836 4Results 0.551 2 Frame 0.813 8Format 0.785 4Green 0.737 3Town 0.825 0Type 0.512 4 Party 0.804 1 Firm 0.777 0Art 0.717 0Night 0.818 0Search 0.352 8 Driver 0.797 0Point 0.768 7Black 0.700 7Border 0.802 2吴飞 等:图像-文本相关性挖掘的Web 图像聚类方法 1569Fig.4 Average of vis (w ) for each datasets图4 5个数据集的平均可见度3.1.3 可见度与NOS文献[1]利用WordNet(/)得到视觉多义词的不同含义(sense),然后通过伴随文本检索某个特定含义的图像.基于此方法,我们提出利用NOS(number of senses in WordNet),即单词在WordNet 中不同含义(sense)的个数这一指标来度量单词的主题宽泛程度.例如,名词place 和desk 的NOS 值分别为16和1,则单词place 比desk 更宽泛.为了考察式(3)对主题宽泛单词可见度的抑制效果,本实验对比不同可见度单词的NOS 值.如图5所示,分3个vis (w )值区间对比相应单词的平均NOS 值.高可见度单词(vis (w )∈[0.9,1])的平均NOS 值约为2.5,而低可见度单词(vis (w )≤0.8)的平均NOS 值约为6.Fig.5 Average of NOS for each datasets 图5 不同vis (w )值区间的平均NOS 值为了进一步考察可见度与NOS 的关系,我们将单词可见度vis (w )与其NOS 值进行了二维可视化表示.如图6所示,大部分高vis (w )值单词其NOS 值很小,而随着vis (w )值的减小,相应单词的NOS 值逐渐增加.以上实验结果表明:(1) 整体上,式(3)对主题宽泛单词可见度的抑制效果是明显的.(2) 通过对5个数据集中单词NOS 值分析发现,描述图像中特定对象的标签或视觉概念,其单词的NOS 较小,如desk,pavilion,railings,pillows,largemouth 和fishermen 等单词的NOS 值为1,而这些单词通过单词可见度模型计算得到的vis (w )值较高.因此,本文所提出的单词可见度计算模型在抑制主题宽泛单词可见度的同时,进一步提升了描述图像中特定对象单词的可见度,从而使得这些单词和图像的链接权重在本文提出的单词-图像相关性定义下得到增强.vis (w )∈[0.9,1)vis (w )∈[0.8,0.9)vis (w )∈[0,0.8)N I P SC o l u m b i a 374S u r r . w o r d sF l i c k rI A P R。
基于图论的语义Web 服务聚类方法黎 英(哈尔滨工程大学经济管理学院,哈尔滨 150001)摘 要:提出一种基于图论的聚类方法,用于在语义Web 服务类别数量未知的情况下实现领域服务分类。
通过计算待分类服务的相似度矩阵,得到相似度阈值,将相似度矩阵中超过该阈值的元素置为1,其余元素置为0,由此得到服务连接矩阵,再以该矩阵为图,逐个提取其中的最大完全子图,每个子图的节点服务就是一个服务类。
理论分析与实验结果证明,该方法可以通过一次聚类得到服务的自然分群,聚类时间较短。
关键词关键词::语义;Web 服务;聚类;本体;图论Semantic Web Service Clustering Method Based on Graph TheoryLI Ying(School of Economy and Management, Harbin Engineering University, Harbin 150001, China)【Abstract 】This paper proposes a semantic Web service clustering method wihtout knowing the number of kinds of services. The similarity matrix of the services is calculated, and the threshold value of similarity is calculated based on the matrix. Those elements which are greater than the threshold value are set 1, and the other elements are 0 in the similarity matrix, so that the connecting matrix of services based on the threshold is formed. Regarding the connecting matrix as a graph, it abstracts the biggest complete sub-graphs from this graph one by one. The services in each sub-graph are a kind of services. Theory analysis and experiments verify that the method can acquire nature clusters by one time of clustering in acceptable time.【Key words 】semantic; Web service; clustering; ontology; graph theory DOI: 10.3969/j.issn.1000-3428.2011.22.014计 算 机 工 程 Computer Engineering 第37卷 第22期V ol.37 No.22 2011年11月November 2011·软件技术与数据库软件技术与数据库·· 文章编号文章编号::1000—3428(2011)22—0051—02 文献标识码文献标识码::A中图分中图分类号类号类号::TP301.61 概述随着UDDI 服务注册中心的关闭,在因特网上发布服务更趋于领域化和专业化,因此,如何组织领域服务成为服务发现的一个重要问题。
例如,文献[1-2]针对语义Web 服务分类进行了研究,但这些服务聚类方法只适用于服务类别数量已知的情况,而服务的类别数量往往不能事先知道,因此,需要研究更为实用的服务聚类方法。
本文综合考虑了输入和输出参数,提出了一种基于图论的服务聚类方法,其适用于服务类别数量未知的情况,能对同类型组织所提供的领域服务进行准确分类。
2 语义Web 服务描述首先给出服务聚类方法的2个前提:(1)服务提供者属于某种组织类型,例如银行、学校、政府机构。
(2)服务是基于本体的。
同类组织拥有自己的领域本体,由实体及实体之间的联系组成。
实体包含一个或多个属性。
基于OWL-S 模型的语义Web 服务用IOPE(Input/Output/ Precondition/Effect)参数来表示服务能力。
由于I/O 参数更能体现服务能力,因此本文算法主要考虑这2个参数的表示方法。
本文使用一个二元组集合来表示I/O 参数,其形式为{<e i , {a ji }>| i =1,2,…,n ;1≤j ≤m },其中,e i 表示领域本体的第i 个实体;a ji 表示该实体的第j 个属性;n 是领域本体实体的数量;m 是实体的最大属性值。
3 基于图论的基于图论的服务聚类服务聚类服务聚类方法方法聚类分析的重要环节是寻找数据中客观存在的类别,这些类别即自然分群。
由于同类型的组织具有很多相似业务,因此实现相似业务的服务可以组成一个服务类,从而形成自然分群。
3.1 相关计算(1)I/O 参数转换成矩阵的方法 设计一个矩阵M ,令其每一列对应领域本体的一个实体,每个元素对应实体的一个属性。
把一个I/O 参数集合映射成该矩阵,那么<e i , {a ji }>中的e i 对应矩阵的第i 列,a ji 则对应该列的第j 个元素,将该列的第j 个元素置为1,其他元素置为0。
输入(I)参数集合对应的矩阵为M I ,输出(O)参数集合对应的矩阵为M O 。
(2)2个服务的I/O 参数相似度计算方法[3]T (,')'/(||||||'||)S = X X X X X X其中,X 和'X 分别是2个服务I/O 参数对应的矩阵;T 'X X 表示X 和'X 同时拥有的共享属性个数;||||||'|| X X =T T 1/2('')X XX X 代表X 和'X 分别拥有属性个数的几何均值。
(3)2个服务的综合相似度计算方法当前实用性较强的综合服务相似度是对I/O 参数相似度进行加权计算,文献[4-5]采用了这种方法。
本文的综合相似度计算公式为S (w 1, w 2)=(1-α)S (w 1.I , w 2.I )+αS (w 1.O , w 2.O ),其中,w 1.I 和w 2.I 分别表示服务w 1和w 2的I 参数集合对应的M I ;w 1.O 和w 2.O 分别表示w 1和w 2的O 参数集合对应的M O 。
下文所提到的相似度均指综合相似度。
(4)服务相似度矩阵计算方法给定服务集合{w i |i =1, 2,…, n },以w i 为行和列标识,以作者简介作者简介::黎 英(1973-),女,博士,主研方向:语义Web 服务,电子商务,信息共享技术收稿日期收稿日期::2011-05-20 E-mail :ling.ly@52 计 算 机 工 程 2011年11月20日2个服务相似度S (w i , w j )为元素,并规定对角线元素全为0,这样的矩阵称为服务相似度矩阵。
(5)服务连接矩阵计算方法服务连接矩阵用来表示服务之间是否相连。
给定服务相似度矩阵和一个相似度阈值s 0,把相似度矩阵中大于s 0的元素值置为1,而其余元素置为0,由此得到服务连接矩阵。
(6)误差平方和准则函数误差平方和准则函数[3]为:J e =21||||i ci i x D m =∈−∑∑X ,其中,1ii x Di m n ∈=∑X ,i m 为第i 个服务类的平均相似度;X 为第i 类中某对服务的相似度;c 表示服务类的数量;J e 表示所有服务类的相似度的误差平方和。
3.2 方法方法思路思路 3.2.1 相关概念定义 1 一个服务类中任意2个服务的相似度称为类内相似度;而来自不同服务类的2个服务的相似度称为类间相似度。
定义2 核心服务是一个服务类的代表服务,是虚拟服务,其I/O 参数是它代表的服务类中所有服务的I/O 参数所共享的实体的属性。
服务集合在自然分群状态下的最小类内相似度用s in 表示,而最大类间相似度用s out 表示。
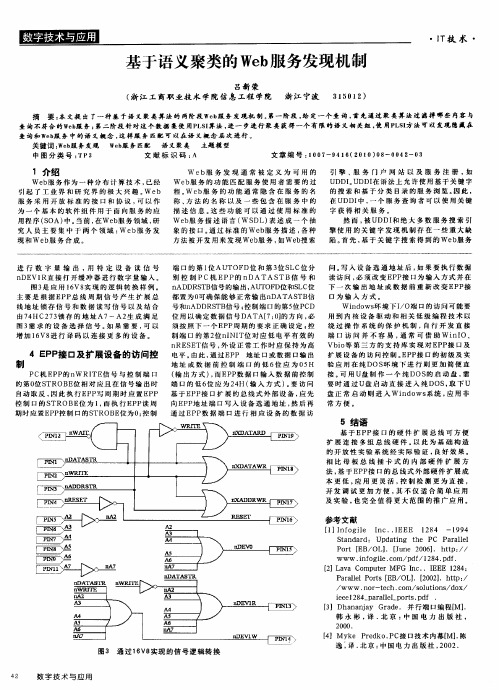
3.2.2 基于图论的一次聚类方法若把服务看作节点,2个服务的相似度超过某个相似度阈值,则把它们连接起来,那么,服务集合中的服务及其连线就是一个服务图。
自然分群中的每一个群都应该看作是一个完全图,否则,如果某几个服务之间是单连通,就不能保证第一个服务和最后一个服务都具有超过指定阈值的相似度,从而无法保证服务能够形成自然分群。
对服务进行聚类可以转变成从服务图中逐个提取所有最大完全子图。
聚类过程如下:计算服务集合的相似度矩阵,然后根据某个相似度阈值计算相应的连接矩阵,它表示服务图。
从该图中可以提取所有最大完全子图。
从服务图中提取一个最大完全子图后,要把图中该子图所包含的节点删除,然后再提取下一个最大完全子图,直到该图中只存在孤立节点。
所提取的最大完全子图就是各服务群。
这就完成了一次聚类。
根据相似度阈值s 0进行的一次聚类也是基于s 0的分群。
3.2.3 自然分群的寻找方法利用变化的相似度阈值进行多次聚类基于以下定理: 定理 给定服务集合及其自然分群状态下的s in 、s out 和相似度阈值s 0,那么:(1)∀s 0∈(s out , s in ),基于s 0的服务分群是自然分群。
(2)∀s 0>s in ,基于s 0的服务分群不是自然分群。
证明:(1)用反证法。
当s out <s 0<s in 时,假设基于s 0的服务分类不是自然分群,那么有2种可能性:至少存在一个自然群被包含在某个群中;至少存在某个自然群被分成至少2个群。
1)至少存在一个自然群(设为C )被包含在某个群(设为 C 0)中。
∀w 1∈C , w 2∈(C 0-C ),因为C 0⊃C ,所以(w 1∈C 0)∧ (w 2∈C 0),S (w 1, w 2)>s 0,又因为(w 1∈C )∧(w 2∉C ),所以S (w 1, w 2)≤s out <s 0,这与S (w 1, w 2)>s 0矛盾,因此,不可能至少存在一个自然群被包含在某个群中。
2)至少存在一个自然群(设为C )被分成至少2个群(设为C 1和C 2)。
因为C 被分成2个群C 1和C 2,所以∃w 1∈C 1,w 2∈C 2,且S (w 1, w 2)<s 0,又因为C =C 1∪C 2,所以S (w 1, w 2)≥s in >s 0,这与S (w 1, w 2)<s 0矛盾,因此,不可能至少存在某个自然群被分成至少2个群。