信号时频分析理论共121页
- 格式：ppt
- 大小：8.93 MB
- 文档页数：121
文档推荐
-
跳频信号的参数估计和调制识别页数:2
-
跳频信号的侦察技术研究页数:3
-
基于稀疏重构的跳频信号时频分析方法页数:6
下载文档原格式
合集下载
信号时频分析
离散STFT变换的定义
•分析信号 x(n),n0~ •分析窗 w (n),n0~Nw1
•STFT变换
S T F T (n , )x (m )w (n m )e j m S T F T ( n ,k ) m x ( n m ) w ( m ) e j2 N k m ,k 0 ,1 ,...,N 1 ,n ~
✓STFT变换
S T F T (t, ) x ()w * ( t) e j d
G (n ,k) S T F T (n T 0 ,k 0)
Gabor变换等效对连续STFT变换在时域和频域进行二维抽样
C
QJ
Digital Signal Processing
二次型时频分布
▪当信号具有很强的非平稳性时，采用短时傅里叶变换分析方法时， 必须选用很短的分析窗。而短分析窗的频率分辨率很差，会影响平 稳时段的信号分析
瞬时频率和复信号
✓瞬时频率的定义
▪复解析信号 s (t) s r(t) js i(t) A (t)e j(t)
d(t)
dt
s(t)
2
dt
i (t)
d(t)
dt
'(t)
✓实数信号频谱分析
▪关于X轴对称
▪平均频率等于零
▪频谱的负频率轴并没有新息
C
QJ
Digital Signal Processing
✓解析信号
N w (m )k0
C
QJ
Digital Signal Processing
✓加窗区间的选择
▪n0时刻的短时序列 xn0(m ),m0,1,...,N w1 n0~n0Nw1 ▪n0时刻的离散短时傅里叶变换 S T F T (n 0 ,k ) D T F [x n 0 (m )]
信号时频分析-讲义.
- -从Fourier 分析到小波分析1 Fourier 分析所有客观存在的事物都包含着大量标志其本身所存的时间空间特征的数据，这就是该事物的信息。
当人们要了解事物某方面的情况时，通常要以各种手段把所需的信息表达出来，供人们观测和分析，这种对信息的表达形式称之为“信号”，所以信号是信息的载体。
信号是无处不在的。
如我们随时可听到的语音信号，随时可看到的视频图像信号，发电机组运行时的温度信号和振动信号等。
对一个给定的信号或过程，如)(t x ，我们可以用众多的方法来描述它，如)(t x 的函数表达式，通过Fourier 变换所得到的)(t x 的频谱，即)(ˆωx，再如)(t x 的相关函数，其能量谱或功率谱等。
在这些众多的描述方法中，有两个最基本的物理量，即时间和频率。
Fourier 变换和反Fourier 变换作为桥梁建立了信号)(t x 与其频谱)(ˆωx之间的一对一映射关系，从时域到频域的映射关系为Fourier 变换：⎰∞∞--=dt e t x x t j ωω)()( (1-1) 反过来，从频域到时域的映射关系为反Fourier 变换：⎰∞∞-=ωωπωd e x t x t j )(21)( (1-2) Fourier 变换的本质思想是用一些简单的基本函数的加权和来近似和表示一个复杂的函数，这样的近似和表示有很多优点，它给我们分析和认识复杂现象提供了一种有效的途径，一些在时域内难以观察的现象和规律，在频域内往往能十分清楚地显示出来。
Fourier 变换和反Fourier 变换属于整体或全局变换，即只能从整体信号的时域表示得到其频谱，或者只能从整体信号的频域表示得到信号的时域表示。
也就是说频谱)(ˆωx的任一频点值都是由时间过程)(t x 在整个时域(-∞,∞)上的贡献所决定；反之，过程)(t x 在某一时刻的状态也是由其频谱)(ˆωx在整个频域(-∞,∞)上的贡献所决定。
也就是说，)(t x 在任何时刻的微小变化都会牵动整个频谱，而任何有限频段上的信息都不足确定任意小时间范围内的过程)(tx。
时频信号分析课件
2020/3/28
6
2020/3/28
7
2020/3/28
8
2、傅里叶变换对于非平稳信号的局限性
平稳信号 工程上 频率不随时间变化的信号（时
不变信号）
非平稳信号 工程上 频率随时间变化的信号（时
变信号）
定义上有别与平稳随机信号——均值（一阶矩）和 相关（二阶矩）函数不随时间变化。
非平稳信号——频率随时间变换不合适 X ( j)
2020/3/28
4
傅里叶变换建立了一个域到另一个域的通道，但它
并没有将时域和频域组合成一个域。在上述傅里叶
变换中，x和t 这两个变量是互相排斥的。即若想知
道在某一频率处 的X (j) ，需要知道x(t)在 t
所有值，反之亦然：
X
(
jΩ0
)
x(t)e jΩ0tdt
x(t
0
)
1 2π
2020/3/28
2
时间和频率是描述信号的两个最基本的物理量 频率 ------ 具有明确的物理意义 （1）波形源 （2）波的传播 （3）简化对波形理解 （4）FT数学工具
时域 （傅里叶变换） 频域
X
(
j
பைடு நூலகம்
)
x(t)e jtdt
x(t)
1
X ( j )e jtd
2π
x(t) dt
2020/3/28
13
但是受实际上不确定原理的制约，时间分辨率和频率 分辨率不能同时达到最好（即分辨间隔最小）。因此 在实际信号分析中，应根据信号的特点及信号处理任 务的需求选取不同的时间分辨率和频率分辨率。
时域突变信号——高的时域分辨率，降低频率分辨率 要求
信号理论讲义6(时频分析)
频域位移不变性
若
s( ) s( 0 )
则 P(t , ) P(t , 0 )
若 则
s (t ) e
j0t
s (t t0 )
P(t , ) P(t t0 , 0 )
线性尺度变换：
若 则
s (t ) as (at ) P (t , ) P ( at , / a )
特点：
原理简单明确 有合理的物理意义 计算容易。
特性分析：
总能量
E＝ Psp (t , )dtd | st ( ) |2 dtd ˆ | s( t ) |2 | g ( ) |2 dtd ˆ ( | g ( ) |2 | s ( t ) |2 dt )d ˆ | g ( ) |2 d s
1.将信号和窗函数离散化。 s (t ) {s (n)} g (t ) {g (n)} 2.将s (n)与g (n－m)相乘，得到{s (n) g (n－m)}。 3.对{s (n) g (n－m)}作离散傅立叶变换。 DSTFT ( s )(m, l ) s (n) g (n－m)e
？
二次型时频分布：
信号项
若 则
z (t ) c1 x(t ) c2 y (t ) Pz (t , ) | c1 |2 Px (t , ) | c2 |2 Py (t , )
* * c1c2 Px , y (t , ) c2c1 Py , x (t , )
交叉项
3.对函数st ( )作傅立叶变换 1 ˆ st ( ) st ( )e j d 2 1 s ( ) g ( t )e j d 2 因此，在t时刻信号的能量密度频谱是 ˆ Psp (t , )＝|st ( ) |2
信号时频分析理论
2
g 0 (t ) 4 2e t
—— 凝聚态
窗函数的数学定义
wt L1 R , 且twt L2 R 如果函数
,
则 wt 被称为窗函数.它的中心和半径分别 定义为： 1 2 t wt dt 中心： t 0 2
w
2
半径：
1 2 2 w (t t 0 ) wt dt w 2
Teff Beff
1 2
不相容原理
例如：g (t ) (t ) Teff 0 Beff 理想的时间分辨率 理想的频率分辨率 时宽－带宽乘积 Teff Beff 频率分辨率的丧失 时间分辨率的丧失
G( f ) ( f ) Beff 0 Teff
1 的窗函数： 2
(3) Wavelet transform (4) Time-Variant Basis Expansion
(5) Hilbert-Huang Transform (唯一逃脱Fourier transform 的架构)
局域变换
<信号取局部，核函数取全局>
<信号取全局，核函数取局部>
信号取局部,核函数取全局的两个典型例子 例1: 短时Fourier变换 Short-time Fourier Transform
1 f (t ) 2
ˆ ( )e i t d , R f
信号的 Fourier 变换能给出信号的频率特性, 即其频谱分析。由于Fourier变换和逆变换具有很好
的对称性, 使得信号的重构很容易进行. 特别是后来
离散Fourier变换(DFT)的发展,
ˆ X m xn e
g 0 (t ) 4 2e t
—— 凝聚态
窗函数的数学定义
wt L1 R , 且twt L2 R 如果函数
,
则 wt 被称为窗函数.它的中心和半径分别 定义为： 1 2 t wt dt 中心： t 0 2
w
2
半径：
1 2 2 w (t t 0 ) wt dt w 2
Teff Beff
1 2
不相容原理
例如：g (t ) (t ) Teff 0 Beff 理想的时间分辨率 理想的频率分辨率 时宽－带宽乘积 Teff Beff 频率分辨率的丧失 时间分辨率的丧失
G( f ) ( f ) Beff 0 Teff
1 的窗函数： 2
(3) Wavelet transform (4) Time-Variant Basis Expansion
(5) Hilbert-Huang Transform (唯一逃脱Fourier transform 的架构)
局域变换
<信号取局部，核函数取全局>
<信号取全局，核函数取局部>
信号取局部,核函数取全局的两个典型例子 例1: 短时Fourier变换 Short-time Fourier Transform
1 f (t ) 2
ˆ ( )e i t d , R f
信号的 Fourier 变换能给出信号的频率特性, 即其频谱分析。由于Fourier变换和逆变换具有很好
的对称性, 使得信号的重构很容易进行. 特别是后来
离散Fourier变换(DFT)的发展,
ˆ X m xn e
信号的时频分析与小波分析PPT
(2) 离散小波变换函数dwt实现一维信号单级离散小波变换。 小波名称以及DWT延拓模式都可以设定。
其调用格式为： [cA,cD] = dwt(x, 'wname') [cA,cD] = dwt(x, 'wname', 'mode', MODE) 返回变量cA：信号DWT对应的近似(Approximation)展开系数 cJ [k ] 返回变量cD：信号离散小波变换对应的细节(Detail)展开系数 d J [k] 调用参数x：表示信号序列，相当于 cJ1[k] 调用参数wname：表示小波名称，参见函数wfilters 调用参数MODE：表示信号DWT延拓模式。
[CXD, LXD] = wavedec(XD, N, ‘wname’) 调用参数TPTR：表示阈值规则，主要有'rigrsure', 'heursure', 'sqtwolog', 'minimaxi'规则 调用参数SORH：表示是soft阈值(‘s’)还是hard阈值(‘h’) 调用参数SCAL：表示是否需要设置多重阈值 调用参数N：表示信号离散小波变换的级数，为正整数。
8
实验六 信号的时频分析与小波分析
(6) 函数wden实现一维信号的去噪，小波名称以及阈值都可以设定。 调用格式为
[XD, CXD, LXD] = wden(x, TPTR, SORH, SCAL, N, 'wname') [XD, CXD, LXD] = wden(C, L, TPTR, SORH, SCAL, N, 'wname') 返回变量XD：表示由噪声信号x的DWT经过阈值去噪后得到的信号； 返回变量CXD与LXD：表示信号XD的小波变换，即
其调用格式为： [cA,cD] = dwt(x, 'wname') [cA,cD] = dwt(x, 'wname', 'mode', MODE) 返回变量cA：信号DWT对应的近似(Approximation)展开系数 cJ [k ] 返回变量cD：信号离散小波变换对应的细节(Detail)展开系数 d J [k] 调用参数x：表示信号序列，相当于 cJ1[k] 调用参数wname：表示小波名称，参见函数wfilters 调用参数MODE：表示信号DWT延拓模式。
[CXD, LXD] = wavedec(XD, N, ‘wname’) 调用参数TPTR：表示阈值规则，主要有'rigrsure', 'heursure', 'sqtwolog', 'minimaxi'规则 调用参数SORH：表示是soft阈值(‘s’)还是hard阈值(‘h’) 调用参数SCAL：表示是否需要设置多重阈值 调用参数N：表示信号离散小波变换的级数，为正整数。
8
实验六 信号的时频分析与小波分析
(6) 函数wden实现一维信号的去噪，小波名称以及阈值都可以设定。 调用格式为
[XD, CXD, LXD] = wden(x, TPTR, SORH, SCAL, N, 'wname') [XD, CXD, LXD] = wden(C, L, TPTR, SORH, SCAL, N, 'wname') 返回变量XD：表示由噪声信号x的DWT经过阈值去噪后得到的信号； 返回变量CXD与LXD：表示信号XD的小波变换，即
第十章 信号的时频分析
x(t ) x(t )e j 2 f0t STFTx( ) (t , f )
及
STFTx( ) (t , f f 0 ) x(t ) x (t t0 ) STFTx( ) (t , f )
STFTx( ) (t t0 , f )e j 2 t0 f
和δ(k)=0 (k≠0)
这个离散STFT综合关系式只有在下列条件下才是正确的，即采样周期T和F、 δ 函 数 ， 即 δ(0)=1 分析窗以及综合窗g(t)应满足所谓的“完全重构条件”：
1 1 g (t k F nT ) (t nT ) (k ) (对所有t) F n
对短时傅里叶变换系数取平方，可得到信号的短时功率谱估计STPx(γ)(t, f)。 它反映了信号在时频相平面上的功率谱密度分布情况，从中可看出信号的时 变特征：
第十章 信号的时域分析
青岛大学机电工程学院
第一节
短时傅里叶变换
一、短时傅里叶变换（STFT）的基本原理
1、基本原理 目的：为了克服FT没有时间分辨率的缺陷。通常采用两种方法来适应分析 非平稳信号的需要。方法一：在FT中引入时间相关性而又保持线性不变。其 思想是引入一个“局部频率”参数（在某时间内局部）。这样，“局部”FT 便是通过一个窗口来观察信号，在这个窗口内信号接近平稳，见下图。通过 移动时窗进行分段取样，将整个信号化为若干个局部“平稳”的信号；对这 “平稳”信号进行FT，可得到一组原信号的“局部”频谱。方法二：将FT 中所用的正弦基函数改为在时间上更集中而在频率上较分散的基函数。 2、定义与性质 信号x(t’)的短时傅里叶变换或 短时谱定义为
如果x(t’)和 (t -t) 的FT为X(f’)和 ( f ' f )，则可得到STFT的另一种表示式
时频信号分析
非平稳信号——频率随时间变换不合适 X ( j)
2020/4/3
与时间无关
9
EX: 线性频率调制信号
x(t) ejt2
Energy spectral density
Linear scale
Real part
1 0.5
0 -0.5
Signal in time WV, lin. scale, contour, Threshold=5%
0.4 0.3 0.2 0.1
0 365 182 0
Frequency [Hz]
20
40
60
80
100 120
Time [s]
2020/4/3
10
2020/4/3
11
从上例可见，傅里叶变换反映不出信号频率随时间 变换的行为。因此，它只适合于分析平稳信号，而 对频率随时间变换的非平稳信号，即时变信号，它 只能给出一个总的平均效果。
整个频率轴，相反也一样，X (j) 某个局部的变换也 将传遍整个时间轴。
2020/4/3
6
2020/4/3
7
2020/4/3
8
2、傅里叶变换对于非平稳信号的局限性
平稳信号 工程上 频率不随时间变化的信号（时
不变信号）
非平稳信号 工程上 频率随时间变化的信号（时
变信号）
定义上有别与平稳随机信号——均值（一阶矩）和 相关（二阶矩）函数不随时间变化。
2020/4/3
16
1.2 克服傅里叶变换不足的一些主要方法
1、短时傅里叶变换
STFTx (t, )
x( )g*(t )ej d
g(t) 窗函数
意义：用 g(t) 沿着t滑动，不断地截取一段一段的信
时频信号分析 PPT课件
即 X (j) jsgn(-)µX(j)
由此可以得到Hilbert反变换的公式
x(t) 1 x$(t) 1 x$( ) d
πt
π t
设 x$(t) 为信号x(t)的Hilbert变换，定义
z(t) x(t) jx$(t)
为信号x(t)的解析信号。 对实信号x(t)引入解析信号z(t)的理由： （1） x(t) ——实，X(j Ω) ——共轭对称，即
这样，我们无法从局部频率处 ( 0或1 2 ) 的 X (j) 来得到某一局部时刻 (t t0或t1 t t2 ) 的 x(t)，反过来也是如此的。这就是说，通过傅里叶变 换建立起来时域——频率关系无“定位”功能。换 句话说，时间信号x(t)某个局部的改变将传遍（影响） 整个频率轴，相反也一样，X (j) 某个局部的变换也 将传遍整个时间轴。
但是受实际上不确定原理的制约，时间分辨率和频率 分辨率不能同时达到最好（即分辨间隔最小）。因此 在实际信号分析中，应根据信号的特点及信号处理任 务的需求选取不同的时间分辨率和频率分辨率。
时域突变信号——高的时域分辨率，降低频率分辨率 要求
时域慢变信号——降低时间分辨率，高的频率分辨率 一个“好”的方法，除了能够选择不同的时间分辨率 和频率分辨率外，还应能适应信号特点自动调节时域 的分辨率和频域的分辨率。
2、傅里叶变换对于非平稳信号的局限性
平稳信号 工程上 频率不随时间变化的信号（时
不变信号）
非平稳信号 工程上 频率随时间变化的信号（时
变信号） 定义上有别与平稳随机信号——均值（一阶矩）和 相关（二阶矩）函数不随时间变化。 非平稳信号——频率随时间变换不合适 X ( j)
与时间无关
EX: 线性频率调制信号
X ( j） x(t)e jtdt
由此可以得到Hilbert反变换的公式
x(t) 1 x$(t) 1 x$( ) d
πt
π t
设 x$(t) 为信号x(t)的Hilbert变换，定义
z(t) x(t) jx$(t)
为信号x(t)的解析信号。 对实信号x(t)引入解析信号z(t)的理由： （1） x(t) ——实，X(j Ω) ——共轭对称，即
这样，我们无法从局部频率处 ( 0或1 2 ) 的 X (j) 来得到某一局部时刻 (t t0或t1 t t2 ) 的 x(t)，反过来也是如此的。这就是说，通过傅里叶变 换建立起来时域——频率关系无“定位”功能。换 句话说，时间信号x(t)某个局部的改变将传遍（影响） 整个频率轴，相反也一样，X (j) 某个局部的变换也 将传遍整个时间轴。
但是受实际上不确定原理的制约，时间分辨率和频率 分辨率不能同时达到最好（即分辨间隔最小）。因此 在实际信号分析中，应根据信号的特点及信号处理任 务的需求选取不同的时间分辨率和频率分辨率。
时域突变信号——高的时域分辨率，降低频率分辨率 要求
时域慢变信号——降低时间分辨率，高的频率分辨率 一个“好”的方法，除了能够选择不同的时间分辨率 和频率分辨率外，还应能适应信号特点自动调节时域 的分辨率和频域的分辨率。
2、傅里叶变换对于非平稳信号的局限性
平稳信号 工程上 频率不随时间变化的信号（时
不变信号）
非平稳信号 工程上 频率随时间变化的信号（时
变信号） 定义上有别与平稳随机信号——均值（一阶矩）和 相关（二阶矩）函数不随时间变化。 非平稳信号——频率随时间变换不合适 X ( j)
与时间无关
EX: 线性频率调制信号
X ( j） x(t)e jtdt
信号时频分析-讲义-WVD
Wigner-Ville 分布Wigner-Ville 分布可以看作是一大类分布的原型，它们和短时傅立叶变换谱有着本质的不同。
它首先由Wigner 提出，用于量子力学领域问题的研究，后由Ville 引入到信号分析。
因为在计算中，信号需要用到两次，因此Wigner-Ville 分布被称为一种二次型分布。
基本定义及计算Wigner-Ville 分布可由信号x (t )本身或它的频谱)(ωX 定义为如下两种等价方式ττ+τ-=ωτω-+∞∞-⎰d )e 21()21(π21)(i t x t x ,t WVD *x , (2.1.1)τθ+ωθ-ω=ωθ+∞∞-⎰d )e 21()21(π21)(i t *x X X ,t WVD . (2.1.2) 其中*表示复数共轭。
要证明上面两式是等价的，只需将信号写成它的频谱形式，然后将其代入到(2.1.1)式，即可得到(2.1.2)式。
式(2.1.1)中，)2/()2/(*ττ+-t x t x 称为信号的瞬时相关函数，因此Wigner-Ville 分布实质上是对信号的瞬时相关函数的傅立叶变换，它的结果能够反映信号的时频特征。
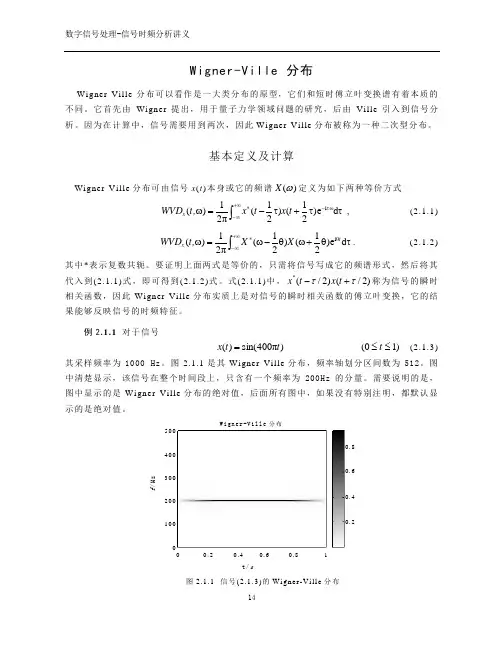
例2.1.1 对于信号)π400sin()(t t x = )10(≤≤t (2.1.3)其采样频率为1000 Hz 。
图2.1.1是其Wigner-Ville 分布，频率轴划分区间数为512。
图中清楚显示，该信号在整个时间段上，只含有一个频率为200Hz 的分量。
需要说明的是，图中显示的是Wigner-Ville 分布的绝对值，后面所有图中，如果没有特别注明，都默认显示的是绝对值。
图2.1.1 信号(2.1.3)的Wi gn er-Vi ll e 分布t /sf /H zW i g n e r -V il l e 分布50040030020010000.2 0.4 0.6 0.8 10.20.40.60.8例2.1.2)π50π100sin()(2t t t x += )20(≤≤t , (2.1.4)这是一个线性调频信号。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
谢谢！
121
26、要使整个人生都过得舒适、愉快，这是不可能的，因为人类必须具备一种能应付逆境的态度。——卢梭
▪
27、只有把抱怨环境的心情，化为上进的力量பைடு நூலகம்才是成功的保证。——罗曼·罗兰
▪
28、知之者不如好之者，好之者不如乐之者。——孔子
▪
29、勇猛、大胆和坚定的决心能够抵得上武器的精良。——达·芬奇
▪
30、意志是一个强壮的盲人，倚靠在明眼的跛子肩上。——叔本华
信号时频分析理论
31、园日涉以成趣，门虽设而常关。 32、鼓腹无所思。朝起暮归眠。 33、倾壶绝余沥，窥灶不见烟。
34、春秋满四泽，夏云多奇峰，秋月 扬明辉 ，冬岭 秀孤松 。 35、丈夫志四海，我愿不知老。
▪