下载文档原格式
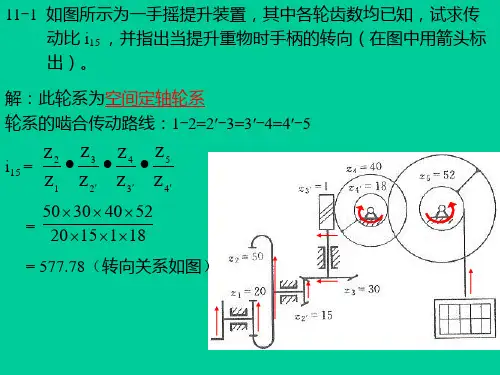
一、解：（1）判断方向，蜗杆左旋用左手右旋用右手，四指握向蜗杆转动方向，拇指指向的反方向即为涡轮转向。
由此逆向判断图中蜗杆、涡轮和齿轮旋转方向如图中箭头所示。
手柄转向如图所示。
4001
601836186056341265432116=××=••=••=z z z z z z w w w w w w i 二、解：该轮系为周转轮系，由反转法对整个轮系加一个反向旋转角速度H w −，
由于齿轮4为定齿轮，角速度为零，即04=w ，所以H H i i 14
11−=； 又有 2.2)1(3423123
14−=•••−=z z z z z z i H
所以 2.32.211=+=H i
三、解：此轮系中假设轮1的方向向下，则行星轮2、2'和太阳轮4的转向都是
向下。
行星轮2、2'和行星架的角速度相同 在左边行星轮系中,1
3
1H 130z z H H −=−−=ωωωω 在右边行星轮系中,'2
444'2z z H ==ωωωω ∴4114ωω=i ==+4'2131z z z z z 25416
四、解：该轮系可以分为两部分，如图中虚线所分的左右两部分，左边为周转轮系，右边为定轴轮系；
分别求出两个轮系的传动比如下：
周转轮系：=H i 1414
1556601441===++z z n n n n H H ； 定轴轮系：7
63530566556====z z n n i ； 两轮系的关系是：
45n n =； 联立方程组求得min 9.741r n ≈； 转向与齿轮6转向相反。
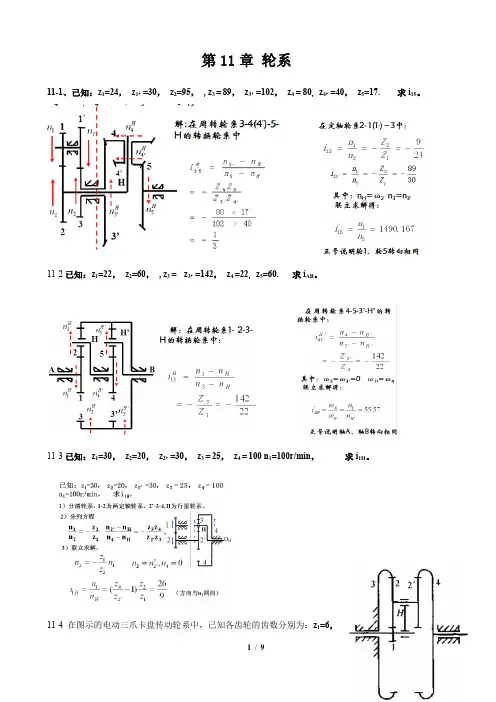
第11章轮系11-1、已知：z1=24，z1’=30，z2=95，, z3 =89，z3’=102，z4 = 80，z4’=40，z5=17.求i15。
11-2已知：z1=22，z2=60，, z3 =z3’=142，z4 =22，z5=60.求i AB。
11-3已知：z1=30，z2=20，z2’=30，z3 =25，z4 =100 n1=100r/min，求i1H。
11-4 在图示的电动三爪卡盘传动轮系中，已知各齿轮的齿数分别为：z1=6，z2=z2’=25，z3 =57，z4 =56，求传动比i1411-5 图示轮系，已经各齿轮齿数为：z1=24，z1’=34，z2=40，z2’=40，z3 =18，z3’=38，z4 =36，z4’=22，求该轮系传动比i AH,11-6 图示轮系，已经各齿轮齿数为：z1=22，z3 =z5，求该轮系传动比i1511-7 .图 示 轮 系 中， 已 知z z z z 134420===='，z 280=，z 560=。
若n A =1000 r/min, 求n B 的 大小 及 方 向。
(1) n z z n 212120801000250=-=-⨯=-r/min n n 23= (2) i n n n n n z z z z H H H H 3533453401206020203=--=-=-=-⨯⨯=-'(3)n n H34=11-8 .图 示 轮 系 中， 已 知 各轮 齿 数， 试 求 轮 系 的 传 动 比 i AB 。
（ 写 成 齿 数 比 的 形 式〕(1)(2)11-9 .在 图 示 轮 系 中， 已 知 各 轮 的 齿 数z z 1380=='，z z 3520==, 及 齿 轮1 的 转 速n 170= r/min, 方 向 如 图 示。
试 求 齿 轮5 的 转 速n 5 的 大 小 及 方 向。
(1) 1、2、3 为 定 轴 轮 系。
mnmn 第十一章的课后答案11-1 在计算行星轮系的传动比时，式i= 1- i H 只有在什么情况下才是正确的？mHmn答：在行星轮系，设固定轮为 n ，即ξ = 0 时， i= 1- i H 公式才是正确的。
nmHmn11-2 在计算周转轮系的传动比时，式i mH = (n m - n H )/ (n n - n H ) 中的i mH 是什么传动比，如何确定其大小和“ ± ”号？答：i mH 是在根据相对运动原理，设给原周转轮系加上一个公共角速度“ -ξH ”，使之绕 行星架的固定轴线回转，这时各构件之间的相对运动仍将保持不变。
而行星架的角速度为 0， 即行星架“静止不动”，于是周转轮系转化成了定轴轮系，这个转化轮系的传动比。
其大小可以用i mH = (n m - n H ) / (n n - n H ) 公式计算；方向由“ ± ”号确定，但注意，它由在转化轮系中m ，n两轮的转向关系来确定。
11-3 用转化轮系法计算行星轮系效率的理论基础是什么?为什么说当行星轮系为高速时，用它来计算行星轮系的效率会带来较大的误差？答：用转化轮系法计算行星轮系效率的理论基础是行星轮系的转化轮系和原行星轮系的差别，仅在于给整个行星轮系附加了一个公共角速度“ -ξH ”。
经过这样的转化之后，各构 件之间的相对运动没有改变，而轮系各运动副中的作用力（当不考虑构件回转的离心惯性力时）以及摩擦因数也不会改变。
因而行星轮系与其转化轮系中的摩擦损失功率应相等。
用转化轮系法计算行行轮系效率没有考虑由于加工、安装和使用情况等的不同，以及还有一些影响因素如搅油损失、行星轮在公转中的离心惯性力等，因此理论计算的结果并不能完全正确地反映传动装置的实际效率。
11-4 何谓正号机构、负号机均，各有何特点？各适用什么场合？答：行星轮系的转化轮系中当传动比i H > 0 ，称为正号机构；当传动比i H < 0 ，称为负号机构。
第11章作业11-1在给定轮系主动轮的转向后，可用什么方法来确定定轴轮系从动轮的转向？周转轮系中主、从动件的转向关系又用什么方法来确定?答：参考教材216~218页。
11-2如何划分一个复合轮系的定轴轮系部分和各基本周转轮系部分?在图示的轮系中，既然构件5作为行星架被划归在周转轮系部分中，在计算周转轮系部分的传动比时，是否应把齿轮5的齿数,Z5计入?答：划分一个复合轮系的定轴轮系部分和各基本周转轮系部分关键是要把其中的周转轮系部分划出来，周转轮糸的特点是具有行星轮和行星架，所以要先找到轮系中的行星轮，然后找出行星架。
每一行星架，连同行星架上的行星轮和与行星轮相啮合的太阳轮就组成一个基本周转轮糸。
在一个复合轮系中可能包括有几个基本周转轮系（一般每一个行星架就对应一个基本周转轮系)，当将这些周转轮一一找出之后．剩下的便是定轴轮糸部分了。
在图示的轮系中．虽然构件5作为行星架被划归在周转轮系部分中，但在计算周转轮系部分的传动比时．不应把齿轮5的齿数计入。
11-3在计算行星轮系的传动比时，式i mH=1-i H mn只有在什么情况下才是正确的?答在行星轮系，设固定轮为n, 即ωn=0时, i mH=1-i H mn公式才是正确的。
11-4在计算周转轮系的传动比时，式i H mn=(n m-n H)／(n n-n H)中的i H mn是什么传动比，如何确定其大小和“±”号?答: i H mn是在根据相对运动原理，设给原周转轮系加上一个公共角速度“-ωH”。
使之绕行星架的固定轴线回转，这时各构件之间的相对运动仍将保持不变，而行星架的角速度为0，即行星架“静止不动”了．于是周转轮系转化成了定轴轮系，这个转化轮系的传动比，其大小可以用i H mn=(n m-n H)／(n n-n H)中的i H mn公式计算；方向由“±”号确定，但注意，它由在转化轮系中m. n两轮的转向关系来确定。
11-5用转化轮系法计算行星轮系效率的理论基础是什么?为什么说当行星轮系为高速时，用它来计算行星轮系的效率会带来较大的误差?答: 用转化轮系法计算行星轮系效率的理论基础是行星轮系的转化轮系和原行星轮系的差别，仅在于给整个行星轮系附加了一个公共角速度“-ωH”。
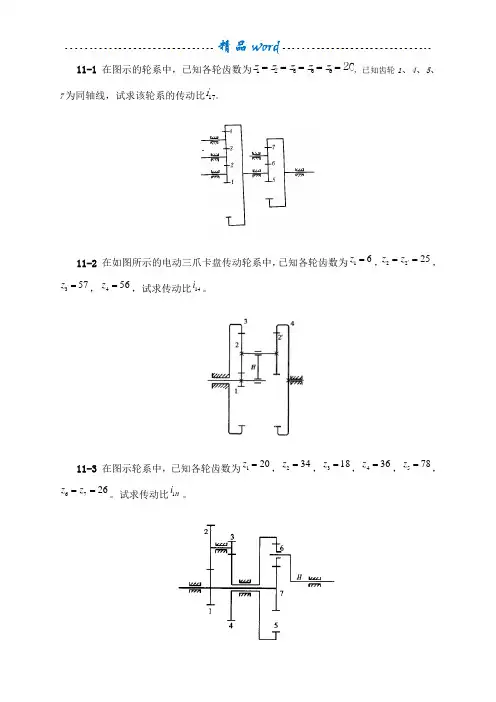
11-1 在图示的轮系中，已知各轮齿数为z z z z z 1235620=====，已知齿轮1、4、5、7为同轴线，试求该轮系的传动比i 17。
11-2 在如图所示的电动三爪卡盘传动轮系中，已知各轮齿数为16z =，2225z z '==，357z =，456z =，试求传动比14i 。
11-3 在图示轮系中，已知各轮齿数为120z =，234z =，318z =，436z =，578z =，6726z z ==。
试求传动比1H i 。
11-6 在图示的轮系中，已知各轮齿数为122z =，388z =，46z z =，试求传动比16i 。
11-8 求图示卷扬机减速器的传动比1H i 。
若各轮的齿数为124z =，248z =，230z '=，360z =，320z '=，440z =，4100z '=。
11-10 在图示的轮系中，已知各轮齿数：11z =，240z =，224z '=，372z =，318z '=，4114z =，蜗杆左旋，转向如图示。
求轮系的传动比1H i ，并确定输出杆H 的转向。
11-11 在图示轮系中，各轮模数相同，均为标准齿轮，各轮齿数如下，z z 123050==,,z z z z 4678100303050====,,,,z z 10550120==,。
试求轴Ⅰ、Ⅱ之间的传动比I,IIi 。
第十一章 轮系习题答案11-1（1）z z z z z 41231225520100=++==⨯=z z z z 75612332060=+==⨯=（2）i z z z z z z z z z z 17323467123561=-()=-⨯⨯=-1006020201511-2（1）三爪卡盘传动轮系是一个行星轮系，它可以看作由两个简单的行星轮系组成。
第一个行星轮系由齿轮1、2、3和行星架H 所组成；第二个行星轮系由齿轮3、2、2'、4和行星架H 组成。
一、填空题：1．轮系可以分为：定轴轮系和 周转轮系 。
2．定轴轮系是指：当轮系运动时，各轮轴线位置固定不动的轮系；周转轮系是指：轮系运动时，凡至少有一个齿轮的轴线是绕另一齿轮的轴线转动的轮系。
3．周转轮系的组成部分包括：太阳轮 、 行星轮 和 行星架 。
4．行星轮系具有1个自由度，差动轮系有 2自由度。
5、行星轮系的同心条件是指：要使行星轮系能正常运转，其基本构件的回转线必须在同一直线上。
6、确定行星轮系中各轮齿数的条件包括：传动比条件、同心条件、均布条件、邻接条件。
7、正号机构和负号机构分别是指：转化轮系的传动比H 1n i 为正号或者负号的周转轮系。
动力传动中多采用 负号 机构。
二、分析计算题1、在图示的车床变速箱中，移动三联齿轮a 使3’和4’啮合。
双移动双联齿轮b 使齿轮5’和6’啮合。
已知各轮的齿数为z 1=42，582=z ,38'3=z ,42'4=z ,48'5=z ,48'6=z 电动机的转速为n 1=1445r/min ，求带轮转速的大小和方向。
解：3858483842484258'5'31'6'426116-=⨯⨯⨯⨯=-==z z z z z z n n i min /9466r n -=(与电动机转动方向相反)2、在图示的轮系中，已知各轮齿数为20z z z z z 65321=====,已知齿轮1、4、5、7为同轴线，试求该轮系的传动比17i 。
（1）z z z z z 41231225520100=++==⨯= z z z z 75612332060=+==⨯=（2）iz z z z zz z z z z17323467123561=-()=-⨯⨯=-100602020153、在图示轮系中，已知：蜗杆为单头且右旋，转速n11440= r/min，转动方向如图示，其余各轮齿数为：402=z，20'2=z，303=z，18'3=z，544=z，试：（1）说明轮系属于何种类型；（2）计算齿轮4得转速n4；（3）在图中标出齿轮4的转动方向。
一、填空题：1．轮系可以分为：定轴轮系和 周转轮系 。
2．定轴轮系是指：当轮系运动时，各轮轴线位置固定不动的轮系；周转轮系是指：轮系运动时，凡至少有一个齿轮的轴线是绕另一齿轮的轴线转动的轮系。
3．周转轮系的组成部分包括： 太阳轮 、 行星轮 和 行星架 。
4．行星轮系具有 1个自由度，差动轮系有 2自由度。
5、行星轮系的同心条件是指：要使行星轮系能正常运转，其基本构件的回转线必须在同一直线上。
6、确定行星轮系中各轮齿数的条件包括：传动比条件、同心条件、均布条件、邻接条件。
7、正号机构和负号机构分别是指：转化轮系的传动比H 1n i 为正号或者负号的周转轮系。
动力传动中多采用 负号 机构。
—二、分析计算题 1、在图示的车床变速箱中，移动三联齿轮a 使3’和4’啮合。
双移动双联齿轮b 使齿轮5’和6’啮合。
已知各轮的齿数为z 1=42，582=z ,38'3=z ,42'4=z ,48'5=z ,48'6=z 电动机的转速为n 1=1445r/min ，求带轮转速的大小和方向。
解：3858483842484258'5'31'6'426116-=⨯⨯⨯⨯=-==z z z z z z n n i min /9466r n -=(与电动机转动方向相反)2、在图示的轮系中，已知各轮齿数为20z z z z z 65321=====, 已知齿轮1、4、5、7为同轴线，试求该轮系的传动比17i 。
（1）z z z z z 41231225520100=++==⨯=z z z z 75612332060=+==⨯=:（2）iz z z z zz z z z z17323467123561=-()=-⨯⨯=-100602020153、在图示轮系中，已知：蜗杆为单头且右旋，转速n11440= r/min，转动方向如图示，其余各轮齿数为：402=z，20'2=z，303=z，18'3=z，544=z，试：（1）说明轮系属于何种类型；（2）计算齿轮4得转速n4；（3）在图中标出齿轮4的转动方向。
（1）定轴轮系（2）nz z z nz z z412312341201840305414408=⋅⋅⋅⋅⋅=⨯⨯⨯⨯⨯=''r/min（3）n4方向←。
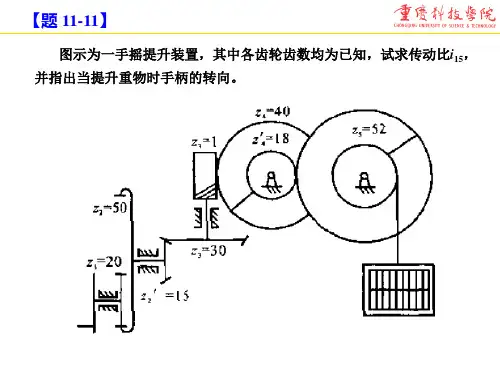
…4、如图所示为一手摇提升装置，其中各轮齿数均已知，试求传动比15i，并指出当提升重物时手柄的转向（从左往右看时的转向）解：方向判断用画箭头的方法完成，从左往右看时的转向为逆时针方向。
2345115''5123420304052'2015118577.7z z z znin z z z z⨯⨯⨯===⨯⨯⨯=5、在图示周转轮系中，已知各齿轮的齿数60,20,25,153'221====z z z z ，齿轮1的转速m in /2001r n =，齿轮3的转速min /503r n =,其转向相反。
（1） 求行星架H 的转速n H 的大小和方向； （2） 当轮3固定不动时，求n H 的大小和方向。
解 ⑴图示为一差动轮系。
其转化机构的传动比为520156025'21323113-=⨯⨯-=⨯⨯-=--=z z z z n n n n i H H H设齿轮1的转速为正值，则齿轮3的转速为负值，将已知值代入得;min /33.86506)50(52006531r n n n H -=-=-+=+=转向与齿轮3的转向相同。
（2）当轮3固定不动时，Hi i 13131-==6，H n =min ，方向与n 1的方向相同6、在图示自动化照明灯具的传动装置中，已知输入轴的转速n 1=min ，各齿轮的齿数为z 1=60，z 2=z 3=30，z 4=z 5=40，z 6=120，求箱体B 的转速n B 。
解：将该传动装置反转(B n -)，转化后的轮系为定轴轮系，其传动比为：23060120305316426116-=⨯⨯-=⨯⨯⨯⨯-=--=z z z z z z n n n n i B B B31161=-=BB i i所以，m in /5.6r n B =,方向与n 1的方向相同~7、已知轮系中,20,15,60'221===z z z 各轮模数均相等，求H i z 13及。
解⑴图示为一行星轮系。
⑵由同心条件得|()()'232122z z m z z m-=- 所以651520602'213=-+=-+=z z z z⑶0,3'21323113==--=n z z zz n n n n i H H H1631613120606515111'2132131=-=⨯⨯-=-=-=z z z z i i HH 齿轮1与行星架H 的转向相同。
8、在图示轮系中，各齿轮均是模数相等的标准齿轮，并已知,22,3421==z z 184=z ，886=z 。
试求齿数3z 及5z ，并计算传动比AB i 。
解：根据同心条件：78222342213=⨯+=+=z z z@1-2-3-4组成行星轮系(4为系杆)21324341413z z zz n n n n i -=--=2941.311213241314=+=-=z z z z i i 4-5-6-B 组成行星轮系0,6466446=-=--=n z zn n n n i B B B8889.518/1061146464==+=-=z z i i BB3987.1944=⨯=B A AB i i i (A 和B 的转向一致)9、在图示轮系中，单头右旋蜗杆1的回转方向如图，各轮齿数分别为372=z ,15'2 =z ,253=z ，20'3 =z ，604=z ，蜗杆1的转速14501=n r/min,方向如图。
试求轴B 的转速n B 的大小及方向（标明从右往左看时的旋向）。
解：1、2为定轴轮系n n z z n n 12212137137=== 方向。
2'、3、3'、4、B 为周转轮系。
3 243B 4B 2B4 2z z zz n n n n i -=--=：3 24321z z z z n n B +=， n n 22'=。
r/min 53.643 3 23 2B =+=z z z z z z n 转向同n 2'。
10、在图示的复合轮系中，设已知n 1=3549r/min ，又各轮齿数为z 1=36，z 2=60，z 3=23，z 4=49，z 4’=69，z 6=131，z 7=94，z 8=36，z 9=167，试求行星架H 的转速H n (大小及转向)解：转向用画箭头的方法表示 1-2-3-4组成定轴轮系55.331424114===z z z z n n i 4’-5-6-7组成行星轮系(7为行星架)0,6'46767'4764'=-=--=n z zn n n n i8986.2'114676'47'4=+=-=z z i i 7-8-9-H 组成行星轮系^0,9799779=-=--=n z zn n n n i H H H=+=-==79797711z z i n n i HH H571.28747141=⨯⨯=H H i i i i ，min /2.12411r i n n HH ==行星架转动方向与齿轮4的回转方向相同11、在图示双螺旋桨飞机的减速器中，已知18,30,20,265421====z z z z ，及1n =15000r/min ，试求Q P n n 和的大小和方向。
（提示：先根据同心，求得3z 和6z 后再求解。
）解：根据同心条件：66202262213=⨯+=+=z z z 66182205246=⨯+=+=z z z4-5-6-Q 组成行星轮系 Q Q Q Qi z z n n n n i 44664461-=-=--=(1) 1-2-3-P 组成行星轮系 P pp Pi z z n n n n i 11331131-=-=--=(2) —轮系之间的关联：4P n n =(3)323.11.4141==Q Q i i i ，min /737.1324r n Q =（与n 1同向）5385.311314=-=Pi i ,m in /4329r n P =（与n 1同向）12、如图所示轮系，已知25'21==z z ，100=H z ，20432===z z z 。
求传动比41i 。
解 （1）图示为一复合轮系。
（2）1-2-2’-3-H 组成行星轮系，其传动比为H H H Hi z z zz n n n n i 1'213231131-=⨯⨯=--=()25925252020111'213221=⨯⨯-=⨯⨯--=z z z z i H（3）由齿轮4和行星架H 组成定轴轮系，}5110020444-=-=-==H H H z z n n i（4）125951259414114-=⎪⎭⎫ ⎝⎛-⨯=•==H H i i n n i 41i =9125-齿轮1和齿轮4的转向相反。
13、在图示轮系中，已知各轮齿数分别为381=z ，,202=z ,18z '14==z 19'4=z ，38z 5=，88' 5=z ，,336=z 36'6=z ，907=z ，188=z 。
试问：齿轮7转一圈，齿轮8转多少圈两者转向是否相同2-1-1’-3-4-4’-5组成定轴轮系519191820381838'43'1254315225-=⨯⨯⨯⨯-=-==z z z z z z z z n n i (1) 5’-6-6’-7(8)组成差动轮系163'6 '586H 8H '5H 8'5-=-=--=z z z z n n n n i (2)1615'6 '576H 7H '5H 7'5==--=z z z z n n n n i (3)关联：25'5,n n n n H == (4)联立解以上方程得到584.29n n -= 5732.1n n = 7827.22n n -=也就是说，当齿轮7转动一圈时，齿轮8要反方向专动圈，二者的方向相反。
