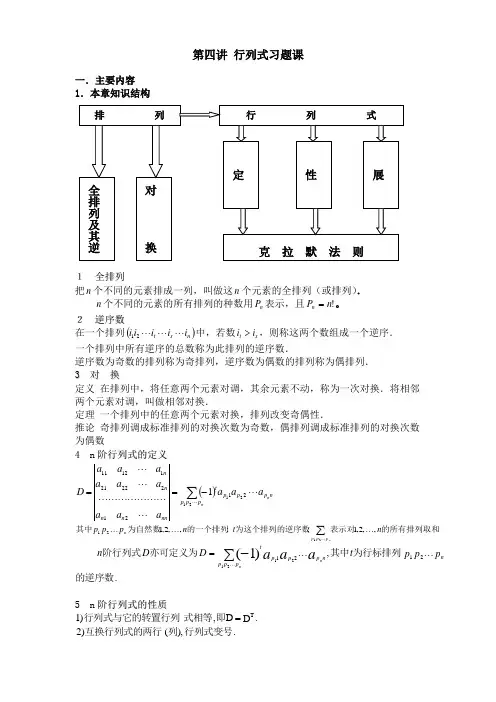
第四讲 行列式习题课一．主要内容 1．本章知识结构１ 全排列把n 个不同的元素排成一列，叫做这n 个元素的全排列（或排列）． n 个不同的元素的所有排列的种数用n P 表示，且!n P n =。
２ 逆序数在一个排列()n s t i i i i i 21中，若数s t i i >，则称这两个数组成一个逆序． 一个排列中所有逆序的总数称为此排列的逆序数．逆序数为奇数的排列称为奇排列，逆序数为偶数的排列称为偶排列． 3 对 换定义 在排列中，将任意两个元素对调，其余元素不动，称为一次对换．将相邻两个元素对调，叫做相邻对换．定理 一个排列中的任意两个元素对换，排列改变奇偶性．推论 奇排列调成标准排列的对换次数为奇数，偶排列调成标准排列的对换次数为偶数4 n 阶行列式的定义()np p p p p p tnnn n n nn n a a a a a a a a a a a a D 2121222211121121211∑-==.,,2,1;;,,2,12121的所有排列取和表示对为这个排列的逆序数的一个排列为自然数其中n t n p p p p p p n n∑.,21212121)1(的逆序数为行标排列其中亦可定义为阶行列式p p p t D D n nn p p p p p p ta aa nn∑-=5 n 阶行列式的性质.D D ,1)T =即式相等行列式与它的转置行列 .),()2行列式变号列互换行列式的两行.,)()3则此行列式等于零完全相同列如果行列式有两行. ,)()4乘此行列式等于用数一数中所有的元素都乘以同列行列式的某一行k k . )( )5面以提到行列式符号的外的所有元素的公因子可列行列式中某一行 ., )( )6则此行列式为零元素成比例列行列式中如果有两行., )( )7列式之和则此行列式等于两个行的元素都是两数之和行若行列式的某一列 ., )( , )( )8行列式的值不变对应的元素上去行然后加到另一列的各元素乘以同一数行把行列式的某一列6 行列式按行（列）展开 １） 余子式与代数余子式.,1 )1(的代数余子式叫做元素；记的余子式，记作阶行列式叫做元素列划去后，留下来的行和第所在的第阶行列式中，把元素在a A M A M a a ijijijji ijij ijij n j i n -+=-２）关于代数余子式的重要性质⎩⎨⎧≠==⎩⎨⎧≠===⎩⎨⎧≠===∑∑==.,0;,1.,0;,.,0;,11j i j i j i j i D D j i j i D D ij ijjk nk ik ij ki nk ki A a A a 当当其中 当当或当当δδδ８ 克拉默法则如果线性方程组⎪⎪⎩⎪⎪⎨⎧=+++=+++=+++.,,22112222212111212111b x a x a x a b x a x a x a b x a x a x a n n nn n n n n n n 那么它有唯一解的系数行列式,0 ≠D.,,2,1,n j DD jj x ==., ,,2,11的行列式所得到，列换成常数项中第）是把系数行列式（其中２b b b n j j D n j D =二．典型例题1．计算排列的逆序数例1()()()()()., 132******** 并讨论奇偶性的逆序数求排列k k k k k k +--- 。
