常见噪声

常见的几种噪声
一、交通噪声：主要指各种机动车辆、飞机、火车、轮船等在行驶过程中的振动和喇叭声产生的噪声。

它的特点是流动性和不稳定性。

对交通干道两侧以及港口、机场附近的居民影响最大。

飞机的噪声污染汽车等交通工具的噪声污染
二、工业噪声：指工厂的机器在运转时产生的噪声和建筑工地施工时的噪声。

它的特点是具有稳定的噪声源。

在工厂和工地工作的人是直接的受害者，在其附近的居民也深受其害。

工业噪声是主要声污染施工噪声
三、社会生活噪声：主要产生在商业区。

另外，娱乐、体育场所，游行、集会、宣传等社会活动也会产生噪声。

其他如家用电器的运转声，宠物的叫声，上楼下楼的脚步声，喧哗声，打闹声等等，都属于社会生活噪声。

家庭噪声
繁华的闹市手机是新的声污染源
耳机成为年轻一代的健康杀手。

噪声分类标准四类
噪声可以按照其产生原因和特征进行分类，常见的噪声分类标准有以下四类：
1. 机械噪声：机械噪声主要产生于机械设备运行过程中，如发动机噪声、电机噪声、空调噪声等。

机械噪声的特点是频率较低、能量较高、持续时间较长。

2. 环境噪声：环境噪声是指自然界和人类活动所产生的噪声，如交通噪声、工业噪声、建筑施工噪声等。

环境噪声的特点是频率较高、能量较低、持续时间较短。

3. 社会噪声：社会噪声是指人们在生活中产生的各种噪声，如人声噪声、音乐噪声、广告噪声等。

社会噪声的特点是频率较高、能量较低、持续时间不确定。

4. 电磁噪声：电磁噪声是指来自电子设备或无线通信系统等的噪声。

电磁噪声的特点是频率范围较宽、能量较低、对电子设备或通信系统的正常工作产生干扰。

三类噪声标准值
在信号处理中，常见的三类噪声标准值有以下三种：
1. 高斯白噪声（Gaussian white noise）：高斯白噪声是一种常
见的噪声类型，其统计特性为平均值为0，方差为常数，且满
足高斯分布。

它的功率谱密度为常数，且在所有频率上具有相同的能量。

高斯白噪声经常用于模拟实际环境下的噪声，如电子器件的热噪声、大气电波的噪声等。

2. 色噪声（Colored noise）：色噪声是指在不同频率上具有不
同能量分布的噪声。

常见的色噪声包括红色噪声、蓝色噪声和粉色噪声等。

红色噪声在低频部分的能量高于高频部分，蓝色噪声则相反，而粉色噪声在频率上具有-3dB/oct的功率下降特性。

色噪声常用于模拟某些实际系统中存在的噪声，如电路中的1/f噪声。

3. 脉冲噪声（Impulse noise）：脉冲噪声是指在信号中出现的
突发式干扰，通常表现为短暂的高能量脉冲或突变。

脉冲噪声往往来自于信号传输过程中的不完美，如电力线上的突发电压变化、信号传输通道中的插入噪声等。

脉冲噪声的幅值、持续时间以及出现的频率等特性可以根据具体应用进行调整和描述。

值得注意的是，噪声标准值通常是指噪声的统计特性，如均值、方差、功率谱密度等。

这些值的具体大小会因不同的应用和系统而有所变化，无法一概而论。

电子设计中常见的噪声问题及解决方法在电子设计中，噪声是一个常见且影响深远的问题。

它会对系统性能造成严重影响，因此必须采取有效的方式进行解决。

在本文中，我们将讨论电子设计中常见的噪声问题以及相应的解决方法。

首先，让我们了解什么是噪声。

在电子设备中，噪声是指系统中出现的不希望的干扰信号，会导致输出信号的失真或降低信噪比。

电子设备中的噪声通常可以分为两类：外部噪声和内部噪声。

外部噪声是来自环境中的干扰，比如电源线上的电磁干扰、无线电信号等；内部噪声则是电子设备本身产生的信号干扰，比如器件本身的热噪声、晶体管的噪声等。

常见的电子设计中的噪声问题包括：热噪声、1/f 噪声、射频干扰以及电源干扰等。

热噪声是由于电阻器、晶体管等器件的热运动引起的，通常可以通过降低工作温度或选择低噪声器件来减小；1/f 噪声是一种与频率成反比的噪声，通常可以通过滤波器进行抑制；射频干扰是来自无线电频段的干扰信号，通常可以通过屏蔽、滤波等技术进行减小；电源干扰则是由电源波动等因素引入的干扰信号，可以通过滤波器、稳压器等措施进行消除。

为了解决这些噪声问题，我们可以采取一系列有效的解决方法。

首先，选择低噪声器件是很关键的，因为器件本身的噪声会影响整个系统的性能。

其次，合理布局电路板是很重要的，可以避免信号叠加引入额外的干扰。

此外，使用合适的滤波器、隔离器等器件也是很有效的方法，可以将不需要的干扰信号滤除。

在面对射频干扰时，可以采用屏蔽罩、隔离器件等技术来隔离干扰信号，保证系统的正常工作。

除了以上方法外，还可以利用数字信号处理技术来进行噪声消除。

通过滤波、降噪算法等方法，可以有效地去除信号中的噪声成分，提高系统的信噪比。

此外，还可以采用差分信号传输、差分输入放大器等技术来减小信号传输过程中的干扰，提高系统的抗干扰能力。

总的来说，电子设计中的噪声问题是一个不可忽视的挑战，但是只要采取适当的解决方法，就可以有效地减小噪声对系统性能的影响。

电子电路中常见的电路噪声问题解析电子设备中的电路噪声问题一直以来都是工程师们在设计和优化电子电路时必须面对的挑战。

电路噪声是指在电子设备中产生的无意识的、随机的、或者非期望的信号，它会影响电路的性能和稳定性。

本文将对电子电路中常见的电路噪声问题进行解析，帮助读者更好地了解和应对这些问题。

一、噪声来源在电子电路中，噪声可以来自多个方面。

以下是一些常见的噪声来源：1. 热噪声：也称为约瑟夫森噪声，是由于电子元件（如电阻）受到温度变化的影响产生的噪声。

2. 互感噪声：由于电子元件之间的互感效应引起的噪声。

3. 混频噪声：当多个频率信号在电路中混合时，会产生混频噪声。

4. 开关噪声：由于电子开关的不完美导致的噪声。

5. 自激噪声：在电路中形成自激振荡时产生的噪声。

二、常见的电路噪声问题1. 热噪声：热噪声是电子设备中常见的一种噪声问题。

在放大器电路中，热噪声会对信号的增益和精度产生负面影响。

为了降低热噪声，可以采用降低电阻温度、增加电阻阻值等措施。

2. 交叉耦合噪声：交叉耦合噪声是电子电路中常见的问题，尤其是在高频电路中更加明显。

交叉耦合噪声是由于不同电路之间互相干扰引起的，例如一个信号线上的噪声会通过电磁感应传递到其他信号线上。

3. 开关噪声：开关噪声是数字电路中常见的问题，特别是CMOS电路。

由于开关器件的非线性特性，会产生开关噪声。

为了降低开关噪声，可以采用滤波器、电源中的抗噪声电容等方法。

4. 振荡噪声：当电子电路中出现自激振荡时，会产生振荡噪声。

振荡噪声会使电路不稳定，影响电路的正常工作。

为了解决这个问题，可以采用增加阻尼、提高负反馈等方法。

三、噪声分析与处理方法在电子电路中，对于不同的噪声问题，我们可以采取不同的分析和处理方法。

以下是一些常见的方法：1. 噪声频谱分析：通过对电子电路中的噪声进行频谱分析，可以确定噪声的频率成分和幅值。

这有助于工程师们找出噪声的来源，进而采取相应的措施降低噪声。

噪声分贝等级划分
噪声分贝（dB）是用来表示声音强度级别的单位，它是对声音的相对强度进行测
量和比较的标准。

以下是常见的噪声分贝等级划分：
1. 30 dB以下：非常安静的环境，比如林中的静谧。

2. 30-40 dB：安静的住宅区、夜晚的室内正常交谈声。

3. 40-50 dB：普通住宅内部、图书馆的安静环境。

4. 50-60 dB：普通室内对话声、办公室中的轻声交谈。

5. 60-70 dB：普通城市街道旁边的交通噪声、普通办公室的工作环境。

6. 70-80 dB：繁忙的城市交通声、餐厅中的人声。

7. 80-90 dB：摩托车、机械设备或工厂噪声。

8. 90-100 dB：汽车喇叭声、摇滚音乐会的音量。

9. 100-120 dB：飞机起飞或降落的轰鸣声、摇滚音乐会的高分贝噪音。

10. 120 dB以上：喷气发动机噪声、爆炸声等极高噪声水平。

这只是一些常见的噪声分贝等级划分，具体的噪声水平还要考虑测量方法和环境刺激等因素。

请注意，长时间暴露于高分贝噪声下可能会对听力和健康产生负面影响，因此保护耳朵和寻求安静的环境非常重要。

通信中的常见噪声几种噪声，它们在通信系统的理论分析中常常用到，实际统计与分析研究证明，这些噪声的特性是符合具体信道特性的白噪声在通信系统中，经常碰到的噪声之一就是白噪声。

所谓噪声是指它的功率谱密度函数在整个频域 卜⑷.0匚十可内是常数,即服从均匀分布。

之所以称它为 白”噪声，是因为它类似于光学中包括全部可见光频率在内的白光。

凡是不符合上述条件的噪声就称为有色噪声。

白噪声的功率谱密度函通常被定义为而在任意两个不同时刻上的随机取值都是不相关的。

白噪声的功率谱密度及其自相关函数，如图2-11所示。

式中, 一个常数，单位为 W/Hz 。

若采用单边频谱，即频率在（(2-22)_____ ）的范围内，白噪声的功率谱密度函数又常写成(2-23)由信号分析的有关理论可知，功率信号的功率谱密度与其自相关函数里卫］互为傅氏变换对，即=；■••订（2-24）因此，白噪声的自相关函数•为_________ JJ ______________________________ ( 2-25)式（2-25）表明，白噪声的自相关函数是一个位于 ______________ 处的冲激函数，它的强度为。

这说明，白噪声只有在1J/2时才相关,实际上完全理想的白噪声是不存在的，通常只要噪声功率谱密度函数均匀分布的频率范围远远超过通信系统工作频率范围时, 就可近似认为是白噪声。

例如，热噪声的频率可以高到 看作白噪声。

高斯噪声在实际信道中，另一种常见噪声是高斯噪声。

所谓 高斯噪声|是指它的概率密度函数服从高斯分布（即正态分布）的一类噪声。

其一 维概率密度函数可用数学表达式表示为通常，通信信道中噪声的均值 匡］=0。

由此，我们可得到一个 重要的结论：在噪声均值为零时，噪声的平均功率等于噪声的方差。

证明如下:因为噪声的平均功率而噪声的方差为口— D ［琲）2站［喊）-总（毗））了 ；=&齡（0 I-［%◎））『=凤Q ）-疋=MEJ HZ ,且功率谱密度函数在 0〜心'I Hz 内基本均匀分布，因此可以将它式中，"I 为噪声的数学期望值，也就是均值;_为噪声的方差。

水声测量原理五种典型噪声
水声测量是利用声波在水中传播的特性来获取相关信息的一种技术方法。

以下是水声测量中常见的五种典型噪声：
1. 海底地震噪声：由于地球内部的地震活动产生的地震波向水体传播引起的噪声，频率范围广泛，能够遍及整个水柱。

2. 海洋动力噪声：由于海洋水体的风浪、潮汐等运动引起的噪声，频率范围通常在几十赫兹到几千赫兹之间。

3. 海洋生物噪声：由于海洋中生物活动产生的声音引起的噪声，如鱼类的鳞片摩擦、鲸鱼的歌声等。

频率范围较低，通常在几十赫兹到几千赫兹之间。

4. 人为噪声：由于船只、渔船、潜水器等人为活动引起的噪声，频率范围较宽，通常在几十赫兹到几千赫兹之间。

5. 水声仪器本身的噪声：由于水声仪器及其传感器本身的电子噪声引起的噪声，可以通过合理的设计和隔离来降低。

以上是水声测量中的五种典型噪声，根据噪声的特点和频率范围的不同，科研人员在测量过程中会采取相应的去噪处理措施，以减小噪声对测量结果的干扰。

工业噪声分类标准一、机械性噪声机械性噪声是指由于机械的摩擦、振动、冲击等引起的噪声。

其中，常见的机械性噪声包括：1.轴承和轴在运转中发生撞击、振动，或者由于不平衡而产生的振动。

2.机器设备部件的周期性振动，如活塞泵、锻造设备等。

3.运转的机器设备与材料之间的摩擦、撞击，如轧钢机、碎石机等。

4.风机的喘振、旋转体的不平衡等。

二、空气动力性噪声空气动力性噪声是由于气体状态的改变而产生的噪声。

它包括：1.空气流动产生的噪声，如风扇、空调和通风设备等。

2.空气的压缩和膨胀产生的噪声，如喷气发动机、汽笛等。

3.空气射流产生的噪声，如高速气流动的管道口、喷雾器等。

三、电磁性噪声电磁性噪声是由于电磁场的作用而产生的噪声。

它包括：1.变压器的噪声，如电源变压器、音频变压器等。

2.电流的脉冲噪声，如电源的开关操作、电火花加工等。

3.电磁铁的噪声，如电机的电磁部分、磁悬浮列车等。

四、流体动力性噪声流体动力性噪声是由于液体的流动或气体的流动而产生的噪声。

它包括：1.液体流动产生的噪声，如水泵、液压马达、冷却塔等。

2.气体流动产生的噪声，如通风管道、气缸阀等。

3.喷射流产生的噪声，如喷泉、喷气发动机等。

五、燃烧爆炸性噪声燃烧爆炸性噪声是由于燃烧或爆炸而产生的噪声。

它包括：1.锅炉、窑炉等燃烧设备在燃烧时产生的噪声。

2.火药爆炸、化学反应爆炸等爆炸时产生的噪声。

3.燃气轮机、喷气发动机等高速燃烧设备在燃烧时产生的噪声。

六、建筑结构噪声建筑结构噪声是由于建筑物本身的结构和振动而产生的噪声。

它包括：1.建筑物的振动，如地震、机械振动等引起的建筑物振动。

2.建筑物的风致振动，如高层建筑的风振等。

3.建筑物的撞击振动，如设备振动传递到建筑物上引起的振动。

4.建筑物的声波传播，如建筑物的回声、混响等引起的声音传播。

T[五种常见的电路内部噪声｀． 、f ＿｀-＝ ，．点击上方蓝字关注我们！FOLLOW US ,. ,. 噪声重要与否，取决于它对目标电路工作的影响程度。

例如，—个开关电源在3MHz时具有显著的输出电压纹波，如果它为之供电的电路仅有几Hz 的带宽，如温度传感器等，则该纹波可能不会产生任何影响。

但是，如果该开关电源为RF锁相环(PLL)供电，结果可能大不相同。

为了成功设计—个鲁棒的系统，了解噪声源至关重要。

就低压差(LDO)调节器而言或者说任何电路，噪声源都可以分为两大类：内部噪声和外部噪声。

•内部噪声好比是您头脑中的噪声·外部噪声则好比是来自喷气式飞机的噪声对于电子电路，内部噪声是指任何电子器件内部产生的噪声，外部噪声则是指从电路外部传到电路中的噪声。

D C +SOURCE -（ 唱EXTERNAL AC N O I SE �1' ＿＿EE UT s p UT OI O US N C L C ID P A 上工一＝＿l l l l l l l I l l l l l l I I I I ­} ＿ ＿ 竺＿ El N Nl ­O l ­耍)D -­ll _＿ 一～D 一IIE l ＿ IF ­L 一P l ­M l ＿ SI -－ ＿ ＿ l ＿ ＿ ＿ ＿ ．一-="' + ... REFERENCE 壬V OLTAGE ... ,k表示波尔兹曼常数(1.38-23J/K)T表示绝对温度(K= 273°()R表示电阻（单位0)B表示观察到噪声的带宽（单位Hz,电阻上测得的均方根电压也是进行测星的带宽的函数）粉红浪漫?NO, 这里只有1/f噪声1/f噪声来源千半导体的表面缺陷，声功率与器件的偏置电流成正比，并且与频率成反比，这一点与热噪声不同。

即使频率非常低，该反比特性也成立，然而，当频率高千数kHz时，关系曲线几乎是平坦的。

电⼦系统中的常见噪声锁相放⼤器最基本功能就是在噪声环境中提取出⽬标信号，在所有的电⼦系统中，噪声都是⽆处不在的。

根据噪声的起因可以⼤致分为两类，分别是系统的内部噪声（本征噪声）和外部环境噪声。

从微观上讲，产⽣内部噪声的原因，是载流⼦的瞬时运动具有随机性，这种随机性会导致我们⽆法准确地预知未来任意时刻的瞬时值，即引⼊了系统噪声；对于外部噪声⽽⾔，系统外环境⼀些不可预知的⼲扰会引起系统内部的响应，从⽽引起系统的误差。

从主观⾓度看的话，凡是不希望得到的亦或是有碍于准确测量结果的信号均可认为是噪声。

虽然噪声具有瞬时值不可预知性的特点，但这样的随机性也并不是完全的杂乱⽆章，它们具有⼀定的统计规律。

⼀、电⼦系统常见噪声源1.1 热噪声不论系统是否在⼯作状态下，热噪声都存在于任何电⼦系统中，即使系统没有上电，电⼦器件都会对外呈现出噪声特性。

热噪声最早由J.B.Johnson于1928年发现，因此热噪声⼜被称为Johnson噪声。

热噪声的噪声电压值可由以下公式计算给出：V noise (rms)=(4kTR△f)1/2上式中， k为Boltzmann常数，其值为1.38×10-23J⁄K ； T为开尔⽂温度；R 为电阻的阻值，其单位为欧姆Ω；△f是测量设定的带宽。

由上式可以看出，热噪声的功率谱密度函数与频率⽆关，当温度与阻值⼀定时，该功率谱密度函数即为⼀条直线，说明热噪声拥有⽩噪声的性质。

1.2 散弹噪声散弹噪声⼀般存在于PN结中，⼜被称为散粒噪声（Shot Noise），其微观机理为PN结中载流⼦随机发射与湮灭导致流过势垒的电流随机涨落。

散弹噪声⾸先由W.Schottky于1918年在热阴极电⼦管的研究中发现，并从理论上证明了散弹噪声是⼀种⽩噪声。

散弹噪声可以在电流测量中以噪声电流值的形式出现，由以下公式计算给出：I noise (rms)=(2qI△f)1/2上式中， q为电⼦元电荷量，其值为1.62×10-19C；I 为PN结交流电流有效值或直流电流平均值；△f是测量设定的带宽。

常见音频噪声及其产生原因作者:钟方源(FanyChong)转载请注明出处。

咔嗒声：由于设备故障或数字同步处理误差而产生的瞬态声音，其包含有明显的高频，声音在时间上表现得十分短促。

产生的原因包括模拟设备故障，接线插接操作，断掉模拟信号操作，或数字设备互相连接时作同步运法出现误差。

由模拟设备故障产生的咔嗒声通常以随机和零星的现象出现。

应对此问题的解决方法可以是采用仪表来指示咔嗒声的通道情况，尤其是在没有节目信号时出现咔嗒声的情况上最为有效。

由设备之间互相连接数字信号而产生的咔嗒声，首先要检查所有互相连接的设备的采样率是否一致。

其次要检查时钟信号源的稳定性。

如果在数字音频里选用的时钟信号源不正确，那么咔嗒声会每隔一段时间出现一次，一般来说这个时间是几秒钟，而且该咔嗒声的音量一般来说会比较小。

喷口气流声：由于歌唱时爆破音而产生的一种声音，听上去类似“砰”声的低频瞬态声音。

一般是由在录音设备正面的人发出的爆破音产生的。

爆破音十分常见，一般是辅音，如字母p,b,d等的声音。

发生爆破音时通常会伴随短促气流的产生，这些气流到达录音设备振膜时，就会产生出类似重击发生的“砰”声。

喷口气流声会分散听音人的注意力。

因此，在录制音频的时候，音频工程师一般都要在录制者面前设置一个由薄纤维构成的防喷网。

通常情况下，音频工程师可以插接高通滤波器过滤喷口气流声，并且该滤波器只在出现喷口气流声的瞬间才发生作用。

接地哼鸣声：由于不正确的接地系统产生的声音，与交流电功率源频率有关。

如北美电源频率是60Hz,西欧是50Hz。

接地哼鸣声一般是由基频等于交流电频率以及其整数倍的谐波而构成的声音。

因此，既有低次谐波，也有高次谐波。

由于接地哼鸣声包括的谐波一般在50Hz或60Hz（注意逻辑词是“或”，不是“至”），所以可以使用窄带陷波器将其调节至各次谐波频率上，但在后期处理上相对麻烦。

因此最简单的办法就是调整设备接地系统。

接地哼鸣声一般在基础录音监听时并不明显，但是会在后期处理，一般如压缩增益补偿或者提高监听等级时暴露出来。

夜间噪声标准
夜间噪声标准是指在夜间时段针对不同居住区域、不同类型的建筑和不同场所所设定的环境噪声标准。

下面是一些常见的夜间噪声标准的相关参考内容。

1. 住宅区夜间噪声标准：根据不同国家和地区的规定和标准，住宅区夜间噪声通常不应超过以下范围：在室外核心区域（如卧室窗户），噪声水平不得超过40分贝(A-weighted decibels, dBA)；在室外次核心区（如客厅、厨房窗户），噪声水平不得超过45分贝；在室外边缘区域（如院子、花园），噪声水平不得超过50分贝。

2. 商业区夜间噪声标准：商业区夜间噪声标准通常相对较高，以适应商业活动的需求。

典型的商业区夜间噪声标准通常为在室外核心区域噪声水平不得超过55-60分贝；在室外次核心区域，噪声水平不得超过60-65分贝；在室外边缘区域，噪声水平不得超过65-70分贝。

3. 工业区夜间噪声标准：工业区夜间噪声标准通常较高，以适应工业生产过程中产生的噪声。

工业区夜间噪声标准通常为在室外核心区域，噪声水平不得超过65分贝；在室外次核心区域，噪声水平不得超过70分贝；在室外边缘区域，噪声水平不得超过75分贝。

4. 教育区夜间噪声标准：教育区夜间噪声标准通常比较严格，以提供良好的学习环境。

教育区夜间噪声标准通常为在室外核心区域，噪声水平不得超过35-40分贝；在室外次核心区域，
噪声水平不得超过40-45分贝；在室外边缘区域，噪声水平不得超过45-50分贝。

需要注意的是，这些噪声标准只是一般性的参考内容，具体的夜间噪声标准可能会因不同地区、不同类型的建筑和不同场所而有所不同。

此外，还需要结合当地的法规、政策和实际情况来制定具体的夜间噪声控制措施。

通信中常见噪声通信中的常见噪声几种噪声,它们在通信系统的理论分析中常常用到,实际统计与分析研究证明,这些噪声的特性就是符合具体信道特性的。

2、5、1 白噪声在通信系统中,经常碰到的噪声之一就就是白噪声。

所谓就是指它的功率谱密度函数在整个频域内就是常数,即服从均匀分布。

之所以称它为“白”噪声,就是因为它类似于光学中包括全部可见光频率在内的白光。

凡就是不符合上述条件的噪声 就称为有色噪声。

通常被定义为( 2-22)式中, 就是一个常数,单位为 W/Hz。

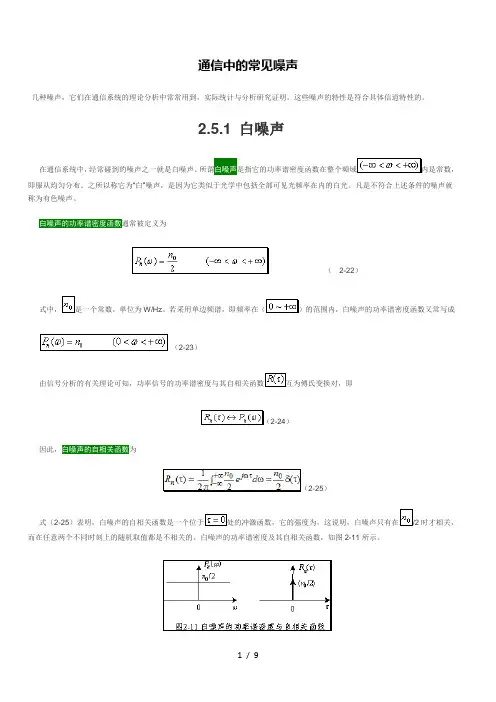
若采用单边频谱,即频率在()的范围内,白噪声的功率谱密度函数又常写成(2-23)由信号分析的有关理论可知,功率信号的功率谱密度与其自相关函数互为傅氏变换对,即因此,为(2-24)(2-25)式(2-25)表明,白噪声的自相关函数就是一个位于处的冲激函数,它的强度为。

这说明,白噪声只有在意两个不同时刻上的随机取值都就是不相关的。

白噪声的功率谱密度及其自相关函数,如图 2-11 所示。

/2 时才相关,而在任实际上完全理想的白噪声就是不存在的,通常只要噪声功率谱密度函数均匀分布的频率范围远远超过通信系统工作频率范围时,通信中常见噪声就可近似认为就是白噪声。

例如,热噪声的频率可以高到 作白噪声。

Hz,且功率谱密度函数在 0～Hz 内基本均匀分布,因此可以将它瞧2、5、2 高斯噪声在实际信道中,另一种常见噪声就是高斯噪声。

所谓就是指它的概率密度函数服从高斯分布(即正态分布)的一类噪声。

其一维概率密 度函数可用数学表达式表示为(2-26)式中, 为噪声的数学期望值,也就就是均值; 为噪声的方差。

通常,通信信道中噪声的均值 =0。

由此,我们可得到一个:在噪声均值为零时,噪声的平均功率等于噪声的方差。

证明如下:因为噪声的平均功率而噪声的方差为(2-27)所以,有(2-28)通信中常见噪声上述结论非常有用,在通信系统的性能分析中,常常通过求自相关函数或方差的方法来计算噪声的功率。

噪声分类自然界中不存在绝对静止的事物，一切事物必定随时间或空间的推移而发生变化，我们将某个物理量在宏观平均值附近的随机变化称为“波动”。

波动现象随处可见：有直观的，如风速的快慢变化、声音的节奏和强弱变化；也有抽象的，如人的情绪变化。

自然界存在着许多波动，可以按功率谱密度与频率的对应关系对其进行分类。

有三种典型噪声的波动特性。

白噪声是一种完全无规律的令人烦躁不安的噪声，该噪声的功率谱密度平行于横轴，是与频率无关的量，我们称之为1/f0 波动；布朗噪声是一种相关性很强，使人感到单调乏味的噪声，该噪声的功率谱密度与f2 成反比，我们称之为1/f2 波动；介于上述两种形式之间的噪声是一种在局部呈无序状态，而在宏观上具有一定相关性的噪声，是一种使人感到舒服的波动。

由于该噪声的功率谱密度与频率是成反比的，我们称之为1/f 波动。

事实证明：“1/f 波动”与人在安静时的α脑波及心拍周期等生物体信号的变化节奏相吻合并与人的情感、感觉有着密切联系，使人能感到舒适。

人的感觉千差万别造成对美的感受各有不同，我们缺少一个客观评估的标准。

而“1/f 波动”理论的提出使我们有了这样一个准则。

常见的随机噪声可分为三类:1 单频噪声2 脉冲噪声3 起伏噪声白噪声定义定义:白噪声是指功率谱密度在整个频域内均匀分布的噪声。

严格地说，白噪声只是一种理想化模型，因为实际噪声的功率谱密度不可能具有无限宽的带宽，否则它的平均功率将是无限大，是物理上不可实现的。

信道中加性噪声的来源，一般可以分为三方面：1 人为噪声人为噪声来源于无关的其它信号源，例如：外台信号、开关接触噪声、工业的点火辐射等；2 自然噪声自然噪声是指自然界存在的各种电磁波源，例如：闪电、雷击、大气中的电暴和各种宇宙噪声等；3 内部噪声内部噪声是系统设备本身产生的各种噪声，例如：电阻中自由电子的热运动和半导体中载流子的起伏变化等。

某些类型的噪声是确知的。

虽然消除这些噪声不一定很容易，但至少在原理上可消除或基本消除。