八年级数学培优专题(一) 直角三角形

北京四中八年级培优班数学全等三角形复习题1．如图1，已知在等边△ABC 中，BD ＝CE ，AD 与BE 相交于P ，则∠APE 的度数是 。

图1B 图2BA图32．如图2，点E 在AB 上，AC ＝AD ，BC ＝BD ，图中有 对全等三角形。

3．如图3，OA ＝OB ，OC ＝OD ，∠O ＝60°，∠C ＝25°，则∠BED 等于 度。

4．如图4所示的2×2方格中，连接AB 、AC ，则∠1＋∠2＝ 度。

图4B图5AB图6CB5．如图5，下面四个条件中，请你以其中两个为已知条件，第三个为结论，推出一个正确的命题。

（ ）①AE ＝AD ；②AB ＝AC ；③OB ＝OC ；④∠B ＝∠C 。

6．如图6，在△ABC 中，∠BAC ＝90°，延长BA 到点D ，使AD ＝21AB ，点E 、F 分别为边BC 、AC 的中点。

（1）求证：DF ＝BE ；（2）过点A 作AG ∥BC ，交DF 于点G ，求证：AG ＝DG 。

7．如图7，在四边形ABCD 中，对角线AC 平分∠BAD ，AB ＞AD ，下列结论正确的是（ ）A. AB －AD ＞CB －CDB. AB －AD ＝CB －CDC. AB －AD ＜CB －CDD. AB －AD 与CB －CD 的大小关系不确定图7BD图8CB8．In Fig. 8, Let △ABC be an equilateral triangle, D and E be points on edges AB and AC respectively, F be intersection of segments BE and CD, and ∠BFC=120°, then the magnitude relation between AD and CE is ( )A. AD>CEB. AD<CEC. AD=CED. indefinite（英汉小词典：equilateral 等边的；intersection 交点；indefinite 不确定的；magnitude 大小，量） 9．如图9，在△ABC 中，AC ＝BC ＝5，∠ACB ＝80°，O 为△ABC 中一点，∠OAB ＝10°，∠OBA ＝30°，则线段AO 的长是 。

初中数学《直角三角形》培优、拔高（奥数）专题讲义阅读与思考直角三角形是一类特殊三角形，有以下丰富的性质： 角的关系：两锐角互余；边的关系：斜边的平方等于两直角边的平方和；边角关系：30所对的直角边等于斜边的一半.这些性质广泛应用于线段计算、证明线段倍分关系、证明线段平方关系等方面.在现阶段，勾股定理是求线段的长度的主要方法，若图形缺少条件直角条件，则可通过作辅助垂线的方法，构造直角三角形为勾股定理的应用创造必要条件；运用勾股定理的逆定理，通过代数方法计算，也是证明两直线垂直的一种方法.熟悉以下基本图形基本结论：例题与求解【例l 】（1）直角△ABC 三边的长分别是x ，1x 和5，则△ABC 的周长＝_____________.△ABC 的面积＝_____________.（2）如图，已知Rt △ABC 的两直角边AC ＝5，BC ＝12，D 是BC 上一点，当AD 是∠A 的平分线时，则CD ＝_____________.DC（太原市竞赛试题）解题思路：对于（1），应分类讨论；对于（2），能在Rt △ACD 中求出CD 吗？从角平分线性质入手.【例2】如图所示的方格纸中，点A ，B ，C ，都在方格线的交点，则∠ACB ＝（ ） A.120° B.135° C.150° D.165°（“希望杯”邀请赛试题）解题思路：方格纸有许多隐含条件，这是解本例的基础.【例3】如图，P为△ABC边BC上的一点，且PC＝2PB，已知∠ABC＝45°，∠APC ＝60°，求∠ACB的度数.B C（“祖冲之杯”邀请赛试题）解题思路：不能简单地由角的关系推出∠ACB的度数，综合运用条件PC＝2PB及∠APC ＝60°，构造出含30°的直角三角形是解本例的关键.【例4】如图，在△ABC中，∠C＝90°，∠A＝30°，分别以AB，AC为边在△ABC的外侧作等边△ABE和等边△ACD，DE与AB交于F，求证：EF＝FD.BA C（上海市竞赛试题）解题思路：已知FD为Rt△FAD的斜边，因此需作辅助线，构造以EF为斜边的直角三角形，通过全等三角形证明.【例5】如图，在四边形ABCD中，∠ABC＝30°，∠ADC＝60°，AD＝CD，求证：222+=BD AB BCBC（北京市竞赛试题）解题思路：由待证结论易联想到勾股定理，因此，三条线段可构成直角三角形，应设法将这三条线段集中在同一三角形中.【例6】斯特瓦尔特定理：如图，设D 为△ABC 的边BC 上任意一点，a ，b ，c 为△ABC 三边长，则222b BDc DC AD BD DC a+=-⋅.请证明结论成立.B解题思路：本题充分体现了勾股定理运用中的数形结合思想.能力训练A 级1.如图，D 为△ABC 的边BC 上一点，已知AB ＝13，AD ＝12，AC ＝15，BD ＝5，则BC ＝_____________.第1题2.如图，在Rt △ABC 中∠C ＝90°，BE 平分∠ABC 交AC 于E ，DE 是斜边AB 的垂直平分线，且DE ＝1cm ，则AC ＝_____________cm.第2题3.如图，四边形ABCD 中，已知AB ∶BC ∶CD ∶DA ＝2∶2∶3∶1，且∠B ＝90°，则∠DAB ＝_____________.第3题ABC（上海市竞赛试题）4.如图，在△ABC 中，AB ＝5，AC ＝13，边BC 上的中线AD ＝6，则BC 的长为_____________.第4题D B（湖北省预赛试题）5.如果一个三角形的一条边是另一条边的2倍，并且有一个角是30 º，那么这个三角形的形状是（ ）A.直角三角形B. 钝角三角形C. 锐角三角形D.不能确定（山东省竞赛试题）6.如图，小正方形边长为1，连结小正方形的三个顶点可得△ABC ，则AC 边上的高为（ ）B.C.D. 第6题CB（福州市中考试题）7.如图，一个长为25分米的梯子，斜立在一竖直的墙上，这时梯足距墙底端7分米，如果梯子的顶端沿墙下滑4分米，那么梯足将滑（ ）A. 15分米B. 9分米C. 8分米D. 5分米第7题8.如图，在四边形ABCD 中，∠B ＝∠D ＝90°，∠A ＝60°，AB ＝4，AD ＝5，那么BCCD等于（ ） A.1 B. 2C.D.54第8题A9. 如图，△ABC 中，AB ＝BC ＝CA ，AE ＝CD ，AD ，BE 相交于P ，BQ ⊥AD 于Q ，求证：BP ＝2PQ.DC（北京市竞赛试题）10. 如图，△ABC 中，AB ＝AC.（1）若P 是BC 边上中点，连结AP ，求证：22BP CP AB AP ⋅=-（2）P 是BC 边上任意一点，上面的结论还成立吗？若成立，请证明；若不成立，请说明理由；（3）若P 是BC 边延长线上一点，线段AB ，AP ，BP ，CP 之间有什么样的关系？请证明你的结论.BP11.如图，直线OB 是一次函数2y x =图象，点A 的坐标为（0，2），在直线OB 上找点C ，使得△ACO 为等腰三角形，求点C 的坐标.12.已知：如图，将矩形ABCD 沿对角线BD 折叠，使点C 落在C '处，BC '交AD 于E ，AD ＝8，AB ＝4，求△BED 的面积.D（山西省中考试题）B 级1.若△ABC 的三边a,b,c 满足条件：222338102426a b c a b c +++=++，则这个三角形最长边上的高为_____________.2.如图，在等腰Rt △ABC 中，∠A ＝90°，P 是△ABC 内的一点，PA ＝1，PB＝3，PC ，则∠CPA ＝_____________.第2题A3. 在△ABC 中，AB ＝15，AC ＝13，高AD ＝12，则△ABC 的周长为_____________.4.如图，在Rt △ABC 中，∠ACB ＝90°，CD ⊥AB 于D ，AF 平分∠CAB 交CD 于E ，交CB 于F ，且EG ∥AB 交CB 于G ，则CF 与GB 的大小关系是（ ）A. CF ＞GBB. CF ＝GBC. CF ＜GBD. 无法确定第4题AB5. 在△ABC 中，∠B 是钝角，AB ＝6，CB ＝8，则AD 的范围是（ ） A. 8＜AC ＜10 B. 8＜AC ＜14 C. 2＜AC ＜14 D. 10＜AC ＜14（江苏省竞赛试题）6.满足两条直角边长均为整数，且周长恰好等于面积的整数倍的直角三角形的个数有（ ）A. 1个B. 2个C. 3个D.4个（浙江省竞赛试题）7.如图，△ABC 是等腰直角三角形，AB ＝AC ，D 是斜边BC 的中点，E ，F 分别是AB ，AC 边上的点，且DE ⊥DF ，若BE ＝12，CF ＝5，求△DEF 的面积.DBC（四川省联赛试题）8.如图，在Rt △ABC 中，∠A ＝90°，D 为斜边BC 中点，DE ⊥DF ，求证：222EF BE CF =+B（江苏省竞赛试题）9.周长为6，面积为整数的直角三角形是否存在？若不存在，请给出证明；若存在，请证明有几个.（全国联赛试题）10.如图，在△ABC 中，∠B AC ＝45°，AD ⊥BC 于D ，BD ＝3，CD ＝2，求△ABC 面积.BC（天津市竞赛试题）11.如图，在△ABC 中，∠B AC ＝90°，AB ＝AC ，E ，F 分别是BC 上两点，若∠EAF＝45°，试推断BE ，CF ，EF 之间数量关系，并说明理由.A C12.已知在Rt △ABC 中，∠ACB ＝90°，AC ＝BC ，∠MCN ＝45°. （1）如图1，当M ，N 在AB 上时，求证：222MN AM BN =+（2）如图2，将∠MCN 绕点C 旋转，当M 在BA 的延长线上时，上述结论是否成立？若成立，请证明；若不成立，请说明理由.图1NAB M图2N BM（天津市中考试题）。

八年级下册第一章《直角三角形》培优习题一、知识要点填空：1、直角三角形的性质：（1）直角三角形的两个锐角_________（2）直角三角形斜边上的中线等于斜边的_________;（3）直角三角形30°角所对的直角边是______的一半；（4）直角三角形中，如果有一条直角边是斜边的一半，那么这条直角边所对的角是30°.2、直角三角形的判定方法：（1）有一个角是直角的三角形是直角三角形；（2）有两个角______的三角形是直角三角形；（3）如果一条边上的中线等于这边的一半，那么这个三角形是直角三角形。

3、等腰直角三角形是特殊的直角三角形，它的两个底角都是_____,且两条直角边相等。

等腰直角三角形具有等腰三角形和直角三角形的所有性质，是很常见的特殊三角形。

二、练习题1、如图，已知△ABC为直角三角形，∠C=90°，若沿图中虚线剪去∠C，则则∠1+∠2等于__________.2、设M表示直角三角形，N表示等腰三角形，P表示等边三角形，Q表示等腰直角三角形，则下列四个图中，能表示它们之间关系的是（）A. B.C. D.3、如图，Rt△ABC中，AB⊥AC，AD⊥BC，BE平分∠ABC，交AD于E，EF∥AC，下列结论一定成立的是（）A.AB=BF B．AE=ED C．AD=DC D．∠ABE=∠DFE4、如图，在△ABC中，∠C=90°，AC=3，∠B=30°，点P是BC边上的动点，则AP的长不可能的是（）A．3.5 B．4.2 C．5.8 D．75、如图，在Rt△ABC中，∠ACB=90°，AB的垂直平分线DE交于BC的延长线于F，若∠F=30°，DE=1，则EF的长是（） A．3 B．2 C．3 D．16、已知等腰△ABC 中，AD ⊥BC 于点D ，且AD=21BC ，则△ABC 底角的度数为___________________.7、四边形ABCD 由一个∠ACB=30°的Rt △ABC 与等腰Rt △ACD 拼成，E 为斜边AC 的中点，则∠BDE=__________．8、已知：在△ABC 中，∠BAC=90°，AD ⊥BC 于点D ，∠ABC 的平分线BE 交AD 于点F ，试说明AE=AF.9、在△ABC 中，∠A=90°，AB=AC ，∠ABC 的平分线BD 交AC 于D ，CE ⊥BD 的延长线于点E ．求证：CE ＝21BD10、一根长2a 的木棍（AB ），斜靠在与地面（OM ）垂直的墙（ON ）上，设木棍的中点为P ．若木棍A 端沿墙下滑，且B 端沿地面向右滑行．木棍滑动的过程中，点P 到点0的距离不变化，在木棍滑动的过程中，△AOB 的面积最大为______________.11、如图在Rt △ABC 中，∠ACB=90°，CD 、CE 分别是斜边AB 边上的高与中线，CF 是∠ACB 的平分线，则∠1与∠2的大小关系是（ ）A ．∠1>∠2 B. ∠1=∠2 C. ∠1<∠2 D.不能确定12、如图，在Rt △ABC 中，∠ACB=90°，AB=2BC ，在直线BC 或AC 上取一点P ，使得△PAB 为等腰三角形，则符合条件的点P 共有（ ）A ．4个B ．5个C ．6个D ．7个13、如图，在直角三角形ABC 中，CM 是斜边AB 上的中线，MN ⊥AB ，∠ACB 的平分线CN 交MN 于N ，求证：CM=MN ．14、如图，在斜边长为1的等腰直角三角形OAB 中，作内接正方形A 1B 1D 1C 1；在等腰直角三角形OA 1B 1中作内接正方形A 2B 2D 2C 2；在等腰直角三角形OA 2B 2中作内接正方形A3B3D3C3；…；依次做下去，则第n个正方形A nB n D nC n的边长是_______________.15、下面的方格图案中的正方形顶点叫做格点，图1中以格点为顶点的等腰直角三角形共有4个，图2中以格点为顶点的等腰直角三角形共有________个，图3中以格点为顶点的等腰直角三角形共有_________个，图4中以格点为顶点的等腰直角三角形共有_________个．16、如图，在△ABC中，∠B=90°，∠BAC=78°，过C作CF∥AB,连接AF于BC相交于G，若GF=2AC，则∠BAG=17、如图，在等腰Rt△ABC中，∠C=90°，AC=8，F是AB边上的中点，点D、E分别在AC、BC边上运动，且保持AD=CE．连接DE、DF、EF．在此运动变化的过程中，下列结论：①△DFE是等腰直角三角形；②DE长度的最小值为4；③四边形CDFE的面积保持不变；④△CDE面积的最大值为8．其中正确的结论是（）A．①②③B．①③ C．①③④D．②③④18、如图，已知OA=a，P是射线ON上一动点（即P可以在射线ON上运动），∠AON=60°，填空：（1）当OP=_________时，△AOP为等边三角形；（2）当OP=__________时，△AOP为直角三角形；（3）当OP满足___________时，△AOP为钝角三角形．GF CB A。

第1讲三角形知识点1 三角形的三边关系1、三角形三条边之间的关系：三角形任意两边之和大于第三边，三角形任意两边之差小于第三边．2、解题技巧：“当三条线段中最长的线段小于另两条线段之和时，或当三条线段中最短的线段大于另两条线段之差时，即可组成三角形”【典例】1.已知a、b、c为△ABC的三边，化简：|a+b﹣c|﹣|a﹣b﹣c|+|a﹣b+2c|=________．【方法总结】本题是三角形三边关系与绝对值的性质的综合问题：1、怎样判断绝对值内三边运算值的正负：①当绝对值内有一个减号时，三边运算值是正，例如|a+b﹣c|= a+b﹣c②有绝对值内有两个或三个减号时，三边运算值是负，例如|a﹣b﹣c|=-（a﹣b﹣c）2、注意“-|a﹣b﹣c|”在去绝对值符号的时候，为避免错误，可写成-[-（a﹣b﹣c）]的形式，再去括号。

a ﹣b+2c 可看做（a ﹣b+c ）+c ，再判断正负。

【随堂练习】1．（2018•杭州二模）四根长度分别为3，4，6，x （x 为正整数）的木棒，从中任取三根，首尾顺次相接都能组成一个三角形，则（ ）A ．组成的三角形中周长最小为9B ．组成的三角形中周长最小为10C ．组成的三角形中周长最大为19D ．组成的三角形中周长最大为162．（2018•芦淞区一模）已知关于x 的不等等式组至少有两个整数解，且存在以3，a ，7为边的三角形，则a 的整数解有（ ）A ．4个B ．5个C ．6个D ．7个知识点2 三角形的中线 三角形的中线：在三角形中，连结一个顶点与它的对边中点的线段，叫做三角形的中线． 三角形的中线将三角形分成两个等底同高的三角形，这两个三角形的面积相等。

【典例】1.如图，A 、B 、C 分别是线段A 1B 、B 1C 、C 1A 的中点，若的面积是14，求△ABC 的面积？111A B C【方法总结】本题已知：A 、B 、C 分别是线段A 1B 、B 1C 、C 1A 的中点，所以我们连接AB 1，BC 1，CA 1，使A 1B 、B 1C 、C 1A 成为三角形的中线，寻找三角形面积的关系，从而得到与△ABC 面积的关系。

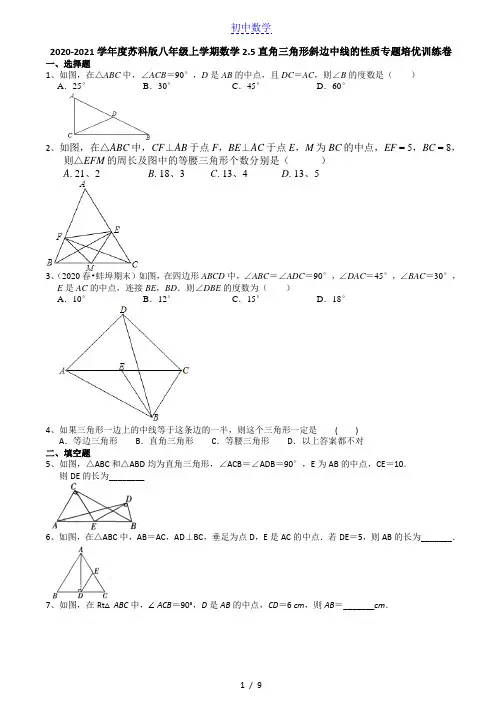
2020-2021学年度苏科版八年级上学期数学2.5直角三角形斜边中线的性质专题培优训练卷一、选择题1、如图，在△ABC中，∠ACB＝90°，D是AB的中点，且DC＝AC，则∠B的度数是（）A．25°B．30°C．45°D．60°2、如图，在△ABC中，CF⊥AB于点F，BE⊥AC于点E，M为BC的中点，EF = 5，BC = 8，则△EFM的周长及图中的等腰三角形个数分别是（）A.21、2B.18、3C.13、4D.13、53、（2020春•蚌埠期末）如图，在四边形ABCD中，∠ABC＝∠ADC＝90°，∠DAC＝45°，∠BAC＝30°，E是AC的中点，连接BE，BD．则∠DBE的度数为（）A．10°B．12°C．15°D．18°4、如果三角形一边上的中线等于这条边的一半，则这个三角形一定是( )A．等边三角形B．直角三角形C．等腰三角形D．以上答案都不对二、填空题5、如图，△ABC和△ABD均为直角三角形，∠ACB＝∠ADB＝90°，E为AB的中点，CE＝10．则DE的长为________6、如图，在△ABC中，AB＝AC，AD⊥BC，垂足为点D，E是AC的中点．若DE＝5，则AB的长为_______．7、如图，在Rt△ABC中，∠ACB＝90°，D是AB的中点，CD＝6 cm，则AB＝_______cm．8、若直角三角形斜边上的高和中线分别为10 cm 、12 cm ，则它的面积为_________cm 2．9、如图，三位同学分别站在一个直角三角形的三个直角顶点处做投圈游戏，目标物放在斜边AC 的中点O 处，已知AC ＝6m ，则点B 到目标物的距离是 m ．10、（2019秋•沭阳县期中）已知：如图，四边形ABCD 中，∠ABC ＝∠ADC ＝90°，AC 与BD 相交于点O ，E 、F 分别是AC 、BD 的中点．则∠EFO ＝ ．11、（2020春•包河区期末）如图，已知△ABC 中，∠ACB ＝90°，O 为AB 的中点，点E 在BC 上，且CE＝AC ，∠BAE ＝15°，则∠COE ＝ 度．12、如图，在ABC ∆中，AD 平分BAC ∠，AD BD ⊥于点D ，//DE AC 交AB 于点E ，若8AB =，则DE = ．13、如图，已知ABC ∆中，90ACB ∠=︒，O 为AB 的中点，点E 在BC 上，且CE AC =，15BAE ∠=︒，则COE ∠= 度．三、解答题14、已知：如图∠ABC ＝∠ADC ＝90°，M 、N 分别是AC 、BD 的中点．求证：MN ⊥BD ．15、（2019秋•余姚市期末）如图，AD 是△ABC 的高线，且BD =21AC ，E 是AC 的中点，连结BE ，取BE 的中点F ，连结DF ，求证：DF ⊥BE ．16、如图，点B 在线段AC 上，点E 在线段BD 上，∠ABD ＝∠DBC ，AB ＝DB ，EB ＝CB ，M 、N 分别是AE 、CD 的中点．（1）求证：△ABE ≌△DBC ；（2）判定△BMN 的形状，并证明你的结论．17、（2020春•重庆期末）如图（1），已知锐角△ABC 中，CD 、BE 分别是AB 、AC 边上的高，M 、N 分别是线段BC 、DE 的中点．（1）求证：MN ⊥DE ．（2）连结DM ，ME ，猜想∠A 与∠DME 之间的关系，并证明猜想．（3）当∠A 变为钝角时，如图（2），上述（1）（2）中的结论是否都成立，若结论成立，直接回答，不需证明；若结论不成立，说明理由．2020-2021学年度苏科版八年级上学期数学2.5直角三角形斜边中线的性质专题培优训练卷（答案）一、选择题1、如图，在△ABC中，∠ACB＝90°，D是AB的中点，且DC＝AC，则∠B的度数是（）A．25°B．30°C．45°D．60°解：∵在△ABC中，∠ACB＝90°，D是AB的中点，∴AD＝CD，∵DC＝AC，∴AD＝CD＝AC，∴△ACD是等边三角形，∴∠A＝60°，∴∠B＝180°﹣90°﹣60°＝30°，故选：B．2、如图，在△ABC中，CF⊥AB于点F，BE⊥AC于点E，M为BC的中点，EF = 5，BC = 8，则△EFM的周长及图中的等腰三角形个数分别是（ D ）A.21、2B.18、3C.13、4D.13、53、（2020春•蚌埠期末）如图，在四边形ABCD中，∠ABC＝∠ADC＝90°，∠DAC＝45°，∠BAC＝30°，E是AC的中点，连接BE，BD．则∠DBE的度数为（）A．10°B．12°C．15°D．18°【解答】解：连接DE，∵∠ADC＝90°，E是AC的中点，∴DE AC＝AE，∴∠EDA＝∠DAC＝45°，∴∠DEC＝∠EDA+∠DAC＝90°，同理，∠BEC＝60°，∴∠DEB＝90°+60°＝150°，∵DE AC，BE AC，∴DE＝BE，∴∠DBE（180°﹣150°）＝15°，故选：C．4、如果三角形一边上的中线等于这条边的一半，则这个三角形一定是( B)A．等边三角形B．直角三角形C．等腰三角形D．以上答案都不对二、填空题5、如图，△ABC和△ABD均为直角三角形，∠ACB＝∠ADB＝90°，E为AB的中点，CE＝10．则DE的长为___10_____6、如图，在△ABC中，AB＝AC，AD⊥BC，垂足为点D，E是AC的中点．若DE＝5，则AB的长为___10____．7、如图，在Rt△ABC中，∠ACB＝90°，D是AB的中点，CD＝6 cm，则AB＝__12______cm．8、若直角三角形斜边上的高和中线分别为10 cm、12 cm，则它的面积为___120_______cm2．9、如图，三位同学分别站在一个直角三角形的三个直角顶点处做投圈游戏，目标物放在斜边AC的中点O处，已知AC＝6m，则点B到目标物的距离是m．解：∵∠ABC＝90°，点O是斜边AC的中点，∴BO＝AC＝3m，故答案为：3．10、（2019秋•沭阳县期中）已知：如图，四边形ABCD中，∠ABC＝∠ADC＝90°，AC与BD相交于点O，E、F分别是AC、BD的中点．则∠EFO＝．【分析】连接EB 、ED ，根据直角三角形的性质得到EB ＝ED ，根据等腰三角形的性质得到答案．【答案】解：连接EB 、ED ，∵∠ABC ＝90°，E 是AC 的中点，∴BE AC ，同理，DE AC ，∴EB ＝ED ，又F 是BD 的中点，∴EF ⊥BD ，∴∠EFO ＝90°，故答案为：90°．11、（2020春•包河区期末）如图，已知△ABC 中，∠ACB ＝90°，O 为AB 的中点，点E 在BC 上，且CE ＝AC ，∠BAE ＝15°，则∠COE ＝ 度．【解答】解：∵∠ACB ＝90°，CE ＝AC ，∴∠CAE ＝∠AEC ＝45°，∵∠BAE ＝15°，∴∠CAB ＝60°，∴∠B ＝30°，∵∠ACB ＝90°，O 为AB 的中点，∴CO ＝BO ＝AO AB ，∴△AOC 是等边三角形，∠OCB ＝∠B ＝30°，∴AC ＝OC ＝CE ，∴∠COE ＝∠CEO （180°﹣30°）＝75°， 故答案为：75．12、如图，在ABC ∆中，AD 平分BAC ∠，AD BD ⊥于点D ，//DE AC 交AB 于点E ，若8AB =，则DE = ．【解答】AD 是BAC ∠的平分线，CAD BAD ∴∠=∠，//DE AC ，CAD ADE ∴∠=∠，ADE BAD ∴∠=∠，AE DE ∴=，BD AD ⊥，90ADE BDE BAD ABD ∴∠+∠=∠+∠=︒，ABD BDE ∴∠=∠，DE BE ∴=，12DE AB ∴=， 8AB =，1842DE ∴=⨯=．故答案为：4．13、如图，已知ABC ∆中，90ACB ∠=︒，O 为AB 的中点，点E 在BC 上，且CE AC =，15BAE ∠=︒，则COE ∠= 75 度．【解答】90ACB ∠=︒，CE AC =，45CAE AEC ∴∠=∠=︒，15BAE ∠=︒，60CAB ∴∠=︒，30B ∴∠=︒，90ACB ∠=︒，O 为AB 的中点，12CO BO AO AB ∴===， AOC ∴∆是等边三角形，30OCB B ∠=∠=︒，AC OC CE ∴==，1(18030)752COE CEO ∴∠=∠=︒-︒=︒，故答案为：75． 三、解答题14、已知：如图∠ABC ＝∠ADC ＝90°，M 、N 分别是AC 、BD 的中点．求证：MN ⊥BD ．证明：如图，连接BM 、DM ，∵∠ABC ＝∠ADC ＝90°，M 是AC 的中点，∴BM ＝DM ＝12AC ， ∵点N 是BD 的中点，∴MN ⊥BD ． (10分）15、（2019秋•余姚市期末）如图，AD是△ABC的高线，且BD AC，E是AC的中点，连结BE，取BE的中点F，连结DF，求证：DF⊥BE．【解答】证明：连结DE，∵AD是△ABC的高线，E是AC的中点，∴，又∵，∴DE＝BD．又∵F是BE的中点，∴DF⊥BE．16、如图，点B在线段AC上，点E在线段BD上，∠ABD＝∠DBC，AB＝DB，EB＝CB，M、N分别是AE、CD的中点．（1）求证：△ABE≌△DBC；（2）判定△BMN的形状，并证明你的结论．【答案】解：（1）在△ABE和△DBC中，∵AB DBABD DBCEB CB=⎧⎪∠=∠⎨⎪=⎩，∴△ABE≌△DBC(SAS)（2）△MBN是等腰直角三角形证明如下：∵△ABE≌△DBC∴AE＝CD，∠BAM＝∠BDN∵M，N分别是AE，CD的中点，∴AM＝12AE，CN＝12CD，∴AM＝CN在△ABM和△DBN中，∵AM CNBAM BDNAB BD=⎧⎪∠=∠⎨⎪=⎩∴ABM≌△DBN(SAS)∴BM＝BN，∠ABM＝∠DBN∵∠ABD＝∠DBC，∠ABD＋∠DBC＝180°，∴∠ABD＝∠ABM＋∠DBM＝90°∴∠DBN＋∠DBM＝∠MBN＝90°，∴△MBN是等腰直角三角形17、（2020春•重庆期末）如图（1），已知锐角△ABC中，CD、BE分别是AB、AC边上的高，M、N分别是线段BC、DE的中点．（1）求证：MN⊥DE．（2）连结DM，ME，猜想∠A与∠DME 之间的关系，并证明猜想．（3）当∠A变为钝角时，如图（2），上述（1）（2）中的结论是否都成立，若结论成立，直接回答，不需证明；若结论不成立，说明理由．【解答】（1）证明：如图（1），连接DM，ME，∵CD、BE分别是AB、AC边上的高，M是BC的中点，∴DM BC，ME BC，∴DM＝ME，又∵N为DE中点，∴MN⊥DE；（2）在△ABC中，∠ABC+∠ACB＝180°﹣∠A，∵DM＝ME＝BM＝MC，∴∠BMD+∠CME＝（180°﹣2∠ABC）+（180°﹣2∠ACB）＝360°﹣2（∠ABC+∠ACB），＝360°﹣2（180°﹣∠A）＝2∠A，∴∠DME＝180°﹣2∠A；（3）结论（1）成立，结论（2）不成立，理由如下：连结DM，ME，在△ABC中，∠ABC+∠ACB＝180°﹣∠BAC，∵DM＝ME＝BM＝MC，∴∠BME+∠CMD＝2∠ACB+2∠ABC＝2（180°﹣∠BAC）＝360°﹣2∠BAC，∴∠DME＝180°﹣（360°﹣2∠BAC）＝2∠BAC﹣180°．。

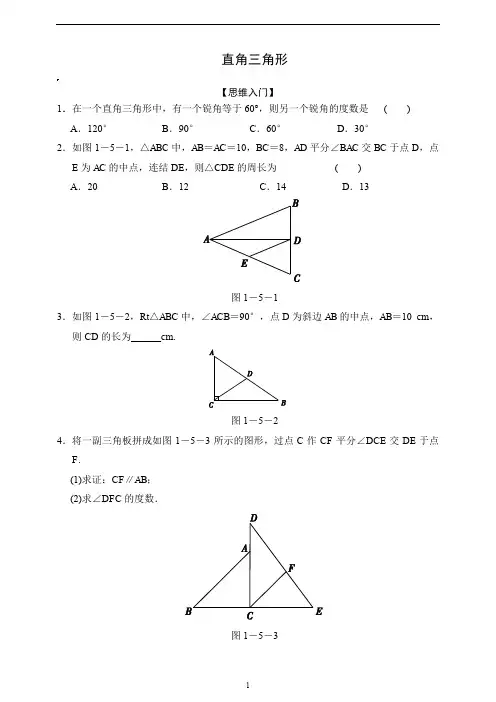
直角三角形【思维入门】1．在一个直角三角形中，有一个锐角等于60°，则另一个锐角的度数是() A．120°B．90°C．60°D．30°2．如图1－5－1，△ABC中，AB＝AC＝10，BC＝8，AD平分∠BAC交BC于点D，点E为AC的中点，连结DE，则△CDE的周长为()A．20 B．12 C．14 D．13图1－5－13．如图1－5－2，Rt△ABC中，∠ACB＝90°，点D为斜边AB的中点，AB＝10 cm，则CD的长为______cm.图1－5－24．将一副三角板拼成如图1－5－3所示的图形，过点C作CF平分∠DCE交DE于点F.(1)求证：CF∥AB；(2)求∠DFC的度数．图1－5－35．如图1－5－4，在△ABC 中，AB ＝CB ，∠ABC ＝90°，D 为AB 延长线上一点，点E 在BC 边上，且BE ＝BD ，连结AE ，DE ，DC . (1)求证：△ABE ≌△CBD ；(2)若∠CAE ＝30°，求∠BDC 的度数．【思维拓展】6．如图1－5－5，在Rt △ABC 中，D ，E 为斜边AB 上的两个点，且BD ＝BC ，AE ＝AC ，则∠DCE 的大小为____°.图1－5－57．如图1－5－6，△ABC 中，AB ＝AC ，DE 垂直平分AB ，BE ⊥AC ，AF ⊥BC ，则∠EFC ＝______．图1－5－68．如图1－5－7，∠ABC ＝90°，D ，E 分别在BC ，AC 上，AD ⊥DE ，且AD ＝DE ，点F 是AE 的中点，FD 与AB 延长线相交于点M . (1)求证：∠FMC ＝∠FCM ； (2)AD 与MC 垂直吗？并说明理由．图1－5－79．如图1－5－8，在△ABC中，∠ACB＝90°，AC＝BC，E为AC边的中点，过点A作AD⊥AB交BE的延长线于点图1－5－8D．CG平分∠ACB交BD于点G，F为AB边上一点，连结CF，且∠ACF＝∠CBG.求证：(1)AF＝CG；(2)CF＝2DE.【思维升华】10．如图1－5－9，有一块直角三角板XYZ放置在△ABC上，恰好三角板XYZ的两条直角边XY，XZ分别经过点B，C，若∠A＝40°，则∠ABX＋∠ACX＝()图1－5－9A．25°B．30°C．45°D．50°11．如图1－5－10，直线l平行于射线AM，要在直线l与射线AM上各找一点B和C，使得以A，B，C为顶点的三角形是等腰直角三角形，这样的三角形最多能画____个．图1－5－1012．如图1－5－11，点P在△ABC的BC边上，且PC＝2PB，若∠ABC＝45°，∠APC ＝60°，则∠ACB的度数是____．图1－5－1113．如图1－5－12，在△ABC中，AC＝BC，且∠ACB＝90°，点D是AC上一点，AE⊥BD，交BD的延长线于点E，且AE＝12BD，则∠ABD＝____．图1－5－1214．如图1－5－13，在△ABC中，∠ACB＝90°，M是∠CAB的平分线AL的中点，延长CM交AB于K，BK＝BC，则∠CAB＝____，∠ACK∠KCB＝____．图1－5－1315．如图1－5－14，已知△BAD和△BCE均为等腰直角三角形，∠BAD＝∠BCE＝90°，点M为DE的中点．过点E与AD平行的直线交射线AM于点N.(1)当A，B，C三点在同一直线上时(如图1－5－14①)，求证：M为AN的中点；(2)将图1－5－14①中△BCE绕点B旋转，当A，B，E三点在同一直线上时(如图1－5－14②)，求证：△CAN为等腰直角三角形；(3)将图1－5－14①中△BCE绕点B旋转到图③的位置时，(2)中的结论是否仍然成立？若成立，试证明之；若不成立，请说明理由．图1－5－14第5讲直角三角形【思维入门】1．在一个直角三角形中，有一个锐角等于60°，则另一个锐角的度数是(D) A．120°B．90°C．60°D．30°2．如图1－5－1，△ABC中，AB＝AC＝10，BC＝8，AD平分∠BAC交BC于点D，点E为AC的中点，连结DE，则△CDE的周长为(C) A．20 B．12 C．14 D．13图1－5－1【解析】∵AB＝AC，AD平分∠BAC，BC＝8，∴AD⊥BC，CD＝BD＝12BC＝4，∵点E为AC的中点，∴DE＝CE＝12AC＝5，∴△CDE的周长＝CD＋DE＋CE＝4＋5＋5＝14.3．如图1－5－2，Rt△ABC中，∠ACB＝90°，点D为斜边AB的中点，AB＝10 cm，则CD的长为__5____cm.图1－5－24．将一副三角板拼成如图1－5－3所示的图形，过点C作CF平分∠DCE交DE于点F.(1)求证：CF∥AB；(2)求∠DFC的度数．图1－5－3解：(1)证明：∵∠DCE＝90°，CF平分∠DCE，∴∠DCF ＝45°，∵△ABC 是等腰直角三角形，∴∠BAC ＝45°，∴∠BAC ＝∠DCF ，∴CF ∥AB ； (2)∵∠D ＝30°，∴∠DFC ＝180°－30°－45°＝105°.5．如图1－5－4，在△ABC 中，AB ＝CB ，∠ABC ＝90°，D 为AB 延长线上一点，点E 在BC 边上，且BE ＝BD ，连结AE ，DE ，DC . (1)求证：△ABE ≌△CBD ；(2)若∠CAE ＝30°，求∠BDC 的度数． 解：(1)证明：∵∠ABC ＝90°，∴∠DBE ＝180°－∠ABC ＝180°－90°＝90°， ∴∠ABE ＝∠CBD .在△ABE 和△CBD 中，∵⎩⎨⎧AB ＝CB ，∠ABE ＝∠CBD ，EB ＝DB ，∴△ABE ≌△CBD ；(2)∵AB ＝CB ，∠ABC ＝90°， ∴△ABC 是等腰直角三角形， ∴∠ECA ＝45°.∵∠CAE ＝30°，∠BEA ＝∠ECA ＋∠EAC ， ∴∠BEA ＝45°＋30°＝75°. 由①知∠BDC ＝∠BEA . ∴∠BDC ＝75°.【思维拓展】6．如图1－5－5，在Rt △ABC 中，D ，E 为斜边AB 上的两个点，且BD ＝BC ，AE ＝AC ，则∠DCE 的大小为__45__°.图1－5－5【解析】设∠DCE＝x，∠ACD＝y，则∠ACE＝x＋y，∠BCE＝90°－∠ACE＝90°－x－y.∵AE＝AC，∴∠ACE＝∠AEC＝x＋y，∵BD＝BC，∴∠BDC＝∠BCD＝∠BCE＋∠DCE＝90°－x－y＋x＝90°－y.在△DCE中，∵∠DCE＋∠CDE＋∠DEC＝180°，∴x＋(90°－y)＋(x＋y)＝180°，解得x＝45°，∴∠DCE＝45°.7．如图1－5－6，△ABC中，AB＝AC，DE垂直平分AB，BE⊥AC，AF⊥BC，则∠EFC ＝__45°____．图1－5－68．如图1－5－7，∠ABC＝90°，D，E分别在BC，AC上，AD⊥DE，且AD＝DE，点F是AE的中点，FD与AB延长线相交于点M.(1)求证：∠FMC＝∠FCM；(2)AD与MC垂直吗？并说明理由．图1－5－7解：(1)证明：∵△ADE是等腰直角三角形，F是AE的中点，∴DF⊥AE，DF＝AF＝EF.又∵∠ABC＝90°，∠DCF，∠AMF都与∠MAC互余，∴∠DCF＝∠AMF.又∵∠DFC＝∠AFM＝90°，∴△DFC≌△AFM.∴CF＝MF.∴∠FMC＝∠FCM；(2)AD⊥MC.由(1)知∠MFC＝90°，FD＝FE，FM＝FC，∴∠FDE＝∠FMC＝45°，∴DE∥CM，∴AD⊥MC.9．如图1－5－8，在△ABC中，∠ACB＝90°，AC＝BC，E为AC边的中点，过点A作AD⊥AB交BE的延长线于点图1－5－8D．CG平分∠ACB交BD于点G，F为AB边上一点，连结CF，且∠ACF＝∠CBG.求证：(1)AF＝CG；(2)CF＝2DE.证明：(1)∵∠ACB＝90°，CG平分∠ACB，AC＝BC.∴∠BCG＝∠CAB＝45°，又∵∠ACF＝∠CBG，AC＝BC，∴△ACF≌△CBG(ASA)，∴AF＝CG；(2)如答图，延长CG交AB于点H.∵AC＝BC，CG平分∠ACB，∴CH⊥AB，H为AB的中点，又∵AD⊥AB，∴CH∥AD，∴G为BD的中点，∠D＝∠EGC，∵E为AC的中点，∴AE＝EC，又∵∠AED＝∠CEG，∴△AED≌△CEG，∴DE＝EG，∴DG＝2DE，∴BG＝DG＝2DE，由(1)得CF＝BG，∴CF＝2DE.第9题答图【思维升华】10．如图1－5－9，有一块直角三角板XYZ放置在△ABC上，恰好三角板XYZ的两条直角边XY，XZ分别经过点B，C，若∠A＝40°，则∠ABX＋∠ACX＝(D)图1－5－9A．25°B．30°C．45°D．50°11．如图1－5－10，直线l平行于射线AM，要在直线l与射线AM上各找一点B和C，使得以A，B，C为顶点的三角形是等腰直角三角形，这样的三角形最多能画__3__个．图1－5－10【解析】如答图．①AC为直角边时，符合的等腰直角三角形有2个，一个是以∠BAC为直角，一个是以∠ACB为直角；②AC为斜边时，符合的等腰直角三角形有1个．∴这样的三角形最多能画3个，12．如图1－5－11，点P在△ABC的BC边上，且PC＝2PB，若∠ABC＝45°，∠APC＝60°，则∠ACB的度数是__75°__．图1－5－11【解析】过C作AP的垂线CD，垂足为点D，连结BD.∵△PCD中，∠APC＝60°，∴∠DCP＝30°，PC＝2PD，∵PC＝2PB，∴BP＝PD，∴△BPD是等腰三角形，∠BDP＝∠DBP＝30°，∵∠ABP＝45°，∴∠ABD＝15°，∵∠BAP＝∠APC－∠ABC＝60°－45°＝15°，∴∠ABD＝∠BAD＝15°，∴BD＝AD，∵∠DBP＝∠DCP＝30°，∴BD＝DC，∴△BDC是等腰三角形，∵BD＝AD，∴AD＝DC，∵∠CDA＝90°，∴∠ACD＝45°，∴∠ACB＝∠DCP＋∠ACD＝75°.13．如图1－5－12，在△ABC中，AC＝BC，且∠ACB＝90°，点D是AC上一点，AE⊥BD，交BD的延长线于点E，且AE＝12BD，则∠ABD＝__22.5°__．第11题答图图1－5－12 第13题答图【解析】 延长AE ，BC 交于点F .∵AE ⊥BE ， ∴∠BEF ＝90°，又∵∠ACF ＝∠ACB ＝90°， ∴∠DBC ＋∠AFC ＝∠F AC ＋∠AFC ＝90°， ∴∠DBC ＝∠F AC ， 在△ACF 和△BCD 中，⎩⎨⎧∠ACF ＝∠BCD ＝90°，AC ＝BC ，∠F AC ＝∠DBC ，∴△ACF ≌△BCD (ASA )， ∴AF ＝BD . 又∵AE ＝12BD ，∴AE ＝EF ，即点E 是AF 的中点． ∴AB ＝BF ，∴BD 是∠ABC 的角平分线． ∴∠ABD ＝22.5°.14．如图1－5－13，在△ABC 中，∠ACB ＝90°，M 是∠CAB 的平分线AL 的中点，延长CM 交AB 于K ，BK ＝BC ，则∠CAB ＝__45°__，∠ACK ∠KCB＝__13__．图1－5－13【解析】 设∠CAB ＝2α.∵AM ＝ML ，且∠ACB ＝90°，∴CM ＝MA ， ∴∠ACM ＝∠MAC ＝α.∴∠CKB ＝∠CAK ＋∠ACM ＝3α， ∠KCB ＝90°－∠ACM ＝90°－α. ∵BK ＝BC ， ∴∠CKB ＝∠KCB .∴3α＝90°－α，即α＝22.5°. ∴∠CAB ＝45°，∠ACK ∠KCB ＝22.5°67.5°＝13.15．如图1－5－14，已知△BAD 和△BCE 均为等腰直角三角形，∠BAD ＝∠BCE ＝90°，点M 为DE 的中点．过点E 与AD 平行的直线交射线AM 于点N .(1)当A ，B ，C 三点在同一直线上时(如图1－5－14①)，求证：M 为AN 的中点； (2)将图1－5－14①中△BCE 绕点B 旋转，当A ，B ，E 三点在同一直线上时(如图1－5－14②)，求证：△CAN 为等腰直角三角形；(3)将图1－5－14①中△BCE 绕点B 旋转到图③的位置时，(2)中的结论是否仍然成立？若成立，试证明之；若不成立，请说明理由．图1－5－14证明：(1)∵点M 为DE 的中点，∴DM ＝ME . ∵AD ∥EN ，∴∠ADM ＝∠NEM ，又∵∠DMA＝∠EMN，∴△DMA≌△EMN，∴AM＝MN，即M为AN的中点；(2)由(1)中△DMA≌△EMN可知DA＝EN，又∵DA＝AB，∴AB＝NE，∵∠ABC＝∠NEC＝135°，BC＝CE，∴△ABC≌△NEC，∴AC＝CN，∠ACB＝∠NCE，∵∠BCE＝∠BCN＋∠NCE＝90°，∴∠BCN＋∠ACB＝90°，∴∠ACN＝90°，∴△CAN为等腰直角三角形．(3)由(2)可知AB＝NE，BC＝CE.又∵∠ABC＝360°－45°－45°－∠DBE＝270°－∠DBE＝270°－(180°－∠BDE－∠BED)＝90°＋∠BDE＋∠BED＝90°＋∠ADM－45°＋∠BED＝45°＋∠MEN＋∠BED ＝∠CEN，∴△ABC≌△NEC，再同(2)可证△CAN为等腰直角三角形，∴(2)中的结论仍然成立.。

学科教师辅导讲义学员编号：年级：八年级(下)课时数：3学员姓名：辅导科目：数学学科教师：授课主题第02讲-直角三角形授课类型T同步课堂P实战演练S归纳总结教学目标①掌握直角三角形的性质与判定方法；②进一步掌握推理证明的方法，培养演绎推理能力；授课日期及时段T（Textbook-Based）——同步课堂一、知识梳理1、直角三角形的性质和判定方法定理：直角三角形的两个锐角互余。

定理：有两个角互余的三角形是直角三角形。

2、勾股定理勾股定理：直角三角形两条直角边的平方和等于斜边的平方。

3、勾股定理的逆定理如果三角形两边的平方和等于第三边的平方，那么这个三角形是直角三角形。

4、逆命题、逆定理互逆命题：在两个命题中，如果一个命题的条件和结论分别是另一个命题的结论和条件，那么这两个体系搭建命题称为互逆命题，其中一个命题称为另一个命题的逆命题。

互逆定理：如果一个定理的逆命题经过证明是真命题，那么它也是一个定理，其中一个定理称为另一个定理的逆命题。

5、斜边、直角边定理定理：斜边和一条直角边分别相等的两个直角三角形全等。

简述为“斜边、直角边定理”或“HL”定理。

考点一：直角三角形全等的判定例1、在如图中，AB=AC，BE⊥AC于E，CF⊥AB于F，BE、CF交于点D，则下列结论中不正确的是（）A．△ABE≌△ACF B．点D在∠BAC的平分线上C．△BDF≌△CDE D．点D是BE的中点【解析】选D．例2、如图，AB=12，CA⊥AB于A，DB⊥AB于B，且AC=4m，P点从B向A运动，每分钟走1m，Q点从B向D运动，每分钟走2m，P、Q两点同时出发，运动4分钟后△CAP与△PQB全等．【解析】∵CA⊥AB于A，DB⊥AB于B，∴∠A=∠B=90°，设运动x分钟后△CAP与△PQB全等；则BP=xm，BQ=2xm，则AP=（12﹣x）m，分两种情况：①若BP=AC，则x=4，AP=12﹣4=8，BQ=8，AP=BQ，∴△CAP≌△PBQ；②若BP=AP，则12﹣x=x，解得：x=6，BQ=12≠AC，此时△CAP与△PQB不全等；综上所述：运动4分钟后△CAP与△PQB全等；故答案为：4．例3、如图，∠A=∠B=90°，E是AB上的一点，且AE=BC，∠1=∠2．（1）Rt△ADE与Rt△BEC全等吗？并说明理由；（2）△CDE是不是直角三角形？并说明理由．【解析】（1）全等，理由是：∵∠1=∠2，∴DE=CE，∵∠A=∠B=90°，AE=BC，∴Rt△ADE≌Rt△BEC；P(Practice-Oriented)——实战演练实战演练➢课堂狙击1、下列条件中，能判定两个直角三角形全等的是（）A．一锐角对应相等B．两锐角对应相等C．一条边对应相等D．两条直角边对应相等【解析】选：D．2、如图，若要用“HL”证明Rt△ABC≌Rt△ABD，则还需补充条件（）A．∠BAC=∠BAD B．AC=AD或BC=BDC．AC=AD且BC=BD D．以上都不正确【解析】从图中可知AB为Rt△ABC和Rt△ABD的斜边，也是公共边．跟据“HL”定理，证明Rt△ABC≌Rt△ABD，还需补充一对直角边相等，即AC=AD或BC=BD，故选B．3、如图，BD平分∠ABC，CD⊥BD，D为垂足，∠C=55°，则∠ABC的度数是（）A．35°B．55°C．60°D．70°【解析】∵CD⊥BD，∠C=55°，∴∠CBD=90°﹣55°=35°，∵BD平分∠ABC，∴∠ABC=2∠CBD=2×35°=70°．故选D．4、如图，△ABC中，CD⊥AB于D，且E是AC的中点．若AD=6，DE=5，则CD的长等于（）A．5 B．6C．7 D．8【解析】∵△ABC中，CD⊥AB于D，∴∠ADC=90°．∵E是AC的中点，DE=5，∴AC=2DE=10．∵AD=6，∴CD===8．故选D．5、如图，AC⊥BC，AD⊥DB，要使△ABC≌△BAD，还需添加条件AC=BD或BC=AD或∠DAB=∠CBA或∠CAB=∠DBA．（只需写出符合条件一种情况）【解析】∵AC⊥BC，AD⊥DB，∴∠C=∠D=90°∵AB为公共边，要使△ABC≌△BAD∴添加AC=BD或BC=AD或∠DAB=∠CBA或∠CAB=∠DBA后可分别根据HL、HL、AAS、AAS判定△ABC≌△BAD．6、如图，已知点P是射线ON上一动点（即P可在射线ON上运动），∠AON=30°，当∠A=60°或90°时，△AOP为直角三角形．【解析】若∠APO是直角，则∠A=90°﹣∠AON=90°﹣30°=60°，若∠APO是锐角，∵∠AON=30°是锐角，∴∠A=90°，综上所述，∠A=60°或90°．故答案为：60°或90°．7、如图，在直角三角形ABC中，斜边上的中线CD=AC，则∠B等于30°．【解析】∵CD是斜边AB上的中线，∴CD=AD，又CD=AC，∴△ADC是等边三角形，∴∠A=60°，∴∠B=90°﹣∠A=30°．故答案为：30°．8、底角为30°，腰长为a的等腰三角形的面积是a2．【解析】如图，过点A作AD⊥BC于D，∵△ABC是等腰三角形，∴BC=2BD，∵底角∠B=30°，∴AD=AB=a，由勾股定理得，BD==a，∴BC=2BD=a，∴三角形的面积=×a×a=a2．故答案为a2．9、如图，在△ACB中，∠ACB=90゜，CD⊥AB于D．（1）求证：∠ACD=∠B；（2）若AF平分∠CAB分别交CD、BC于E、F，求证：∠CEF=∠CFE．【解析】证明：（1）∵∠ACB=90゜，CD⊥AB于D，∴∠ACD+∠BCD=90°，∠B+∠BCD=90°，∴∠ACD=∠B；（2）在Rt△AFC中，∠CFA=90°﹣∠CAF，同理在Rt△AED中，∠AED=90°﹣∠DAE．又∵AF平分∠CAB，∴∠CAF=∠DAE，∴∠AED=∠CFE，又∵∠CEF=∠AED，∴∠CEF=∠CFE．10、已知：如图，在△ABC中，AB=AC=2，∠B=15°．过点C作CD⊥BA，交BA的延长线于点D，求△ACD的周长．【解析】如图，在△ABC中，AB=AC=2，∠B=15°，∴∠B=∠ACB=15°，∴∠DAC=2∠B=30°．又∵CD⊥BA，∴CD=AC=1，∴根据勾股定理得到AD==，∴△ACD的周长=AD+CD+AC=+1+2=+3．答：△ACD的周长是+3．➢课后反击1、要判定两个直角三角形全等，下列说法正确的有（）①有两条直角边对应相等；②有两个锐角对应相等；③有斜边和一条直角边对应相等；④有一条直角边和一个锐角相等；⑤有斜边和一个锐角对应相等；⑥有两条边相等．A．6个B．5个C．4个D．3个【解析】故选B2、如图，O是∠BAC内一点，且点O到AB，AC的距离OE=OF，则△AEO≌△AFO的依据是（）A．HL B．AASC．SSS D．ASA【解析】∵OE⊥AB，OF⊥AC，∴∠AEO=∠AFO=90°，又∵OE=OF，AO为公共边，∴△AEO≌△AFO．故选A．3、直角三角形两个锐角平分线相交所成的钝角的度数为（）A．90°B．135°C．120°D．45°或135°【解析】如图：∵AE、BD是直角三角形中两锐角平分线，∴∠OAB+∠OBA=90°÷2=45°，两角平分线组成的角有两个：∠BOE与∠EOD这两个角互补，根据三角形外角和定理，∠BOE=∠OAB+∠OBA=45°，∴∠EOD=180°﹣45°=135°，故选B．4、如图，在Rt△ABC中，∠ACB=90°，∠A=60°，过点C的直线与AB交于点D，且将△ABC的面积分成相等的两部分，则∠CDA=（）A．30°B．45°C．60°D．75°【解析】如图，∵在Rt△ABC中，∠ACB=90°，∠A=60°，∴AC=AB，又∵过点C的直线与AB交于点D，且将△ABC的面积分成相等的两部分，∴AD=BD∴AC=AD，∵∠A=60°，∴△ADC是等边三角形，∴∠CDA=60°．5、如图，△ABC中，AB=AC=10，AD平分∠BAC交BC于点D，点E为AC的中点，连接DE，则DE 的长为（）A．10 B．6C．8 D．5【解析】∵AB=AC=10，AD平分∠BAC，∴BD=DC，∵E为AC的中点，∴DE=AB=×10=5，故选D．6、如图，已知AB⊥CD，垂足为B，BC=BE，若直接应用“HL”判定△ABC≌△DBE，则需要添加的一个条件是AC=DE．【解析】AC=DE，理由是：∵AB⊥DC，∴∠ABC=∠DBE=90°，在Rt△ABC和Rt△DBE中，，∴Rt△ABC≌Rt△DBE（HL）．故答案为：AC=DE．7、如图，在Rt△ABC中，∠ACB=90°，将边BC沿斜边上的中线CD折叠到CB′，若∠B=50°，则∠ACB′= 10°．【解析】∵∠ACB=90°，∠B=50°，∴∠A=40°，∵∠ACB=90°，CD是斜边上的中线，∴CD=BD，CD=AD，∴∠BCD=∠B=50°，∠DCA=∠A=40°，由翻折变换的性质可知，∠B′CD=∠BCD=50°，∴∠ACB′=∠B′CD﹣∠DCA=10°，故答案为：10°．8、如图，在△ABC中，∠C=90°，∠B=30°，AB的垂直平分线ED交AB于点E，交BC于点D，若CD=3，则BD的长为6．【解析】∵DE是AB的垂直平分线，∴AD=BD，∴∠DAE=∠B=30°，∴∠ADC=60°，∴∠CAD=30°，∴AD为∠BAC的角平分线，∵∠C=90°，DE⊥AB，∴DE=CD=3，∵∠B=30°，∴BD=2DE=6，故答案为：6．9、如图所示，AB⊥BC，DC⊥AC，垂足分别为B，C，过D点作BC的垂线交BC于F，交AC于E，AB=EC，试判断AC和ED的长度有什么关系并说明理由．【解析】AC=ED，理由如下：∵AB⊥BC，DC⊥AC，ED⊥BC，∴∠B=∠EFC=∠DCE=90°．∴∠A+∠ACB=90°，∠CEF+∠ACB=90°．∴∠A=∠CEF．在△ABC和△ECD中，∴△ABC≌△ECD（ASA）．∴AC=ED（全等三角形的对应边相等）．10、在直角△ABC中，∠ACB=90°，∠B=30°，CD⊥AB于D，CE是△ABC的角平分线．（1）求∠DCE的度数．（2）若∠CEF=135°，求证：EF∥BC．【解析】∵∠B=30°，CD⊥AB于D，∴∠DCB=90°﹣∠B=60°．S(Summary-Embedded)——归纳总结重点回顾1、直角三角形的性质和判定方法定理：直角三角形的两个锐角互余。

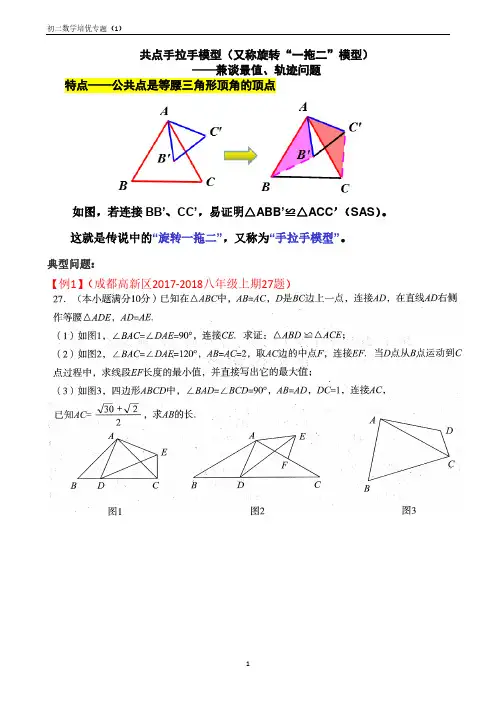
共点手拉手模型（又称旋转“一拖二”模型）——兼谈最值、轨迹问题特点——公共点是等腰三角形顶角的顶点如图，若连接BB’、CC’，易证明△ABB’≌△ACC’（SAS）。

这就是传说中的“旋转一拖二”，又称为“手拉手模型”。

典型问题：【例1】（成都高新区2017-2018八年级上期27题）【例2】（成都金牛区2017-2018八年上期27题）如图，在△ABC中,∠B=45°，AB=22，2=BC，等腰直角∆ADE中，∠DAE=90°，2+3且点D是边BC上一点。

(1)（3 分）求AC的长；(2)（4 分）如图1，当点E恰在AC上时,求点E到BC的距离；(3)（3 分）如图2, 当点D从点B向点C运动时，求点E到BC的距离的最大值。

图1【例3】（2017届初二上期七中联盟半期）已知：ABC △是等腰直角三角形，动点P 在斜边AB 所在的直线上，以PC 为直角边作等腰直角三角形PCQ ，其中90PCQ =∠，探究并解决下列问题：（1）如图①，若点P 在线段AB上，且AC =，12PA =，则： ①线段PB =________，PC =________；②猜想：222,,PQ PA PB 三者之间的数量关系为_______________________；（2）如图②，若点P 在AB 的延长线上，在（1）中所猜想的结论仍然成立，请你利用图②给出证明过程； （3）若动点P 满足4PA PB =,求PQAC的值．（提示：请利用备用图进行探求）图① 图② 备用图QCBPAQCB ACBA【例4】如图,已知30MON ∠=︒ ,B 为OM 上一点,BA ON ⊥ 于A ,四边形ABCD 为正方形,P 为射线BM 上一动点,连结CP ,将CP 绕点C 顺时针方向旋转90︒ 得CE ,连结BE ,若 4AB = ,则BE 的最小值为【例5】（成都武侯区2016-2017八年上期27题）如图，已知直线x y =过点A ，y AB ⊥轴于点B ，x AC ⊥轴于点C ，点P 是y 轴上的一动点，连接AP 交直线BC 于点E .点N 在直线BC 上，连接AN 且︒=∠90PAN ，在射线AN 上截取AE AD =，连接DE .（1）求证：2222AE EC BE =+；（2）若点A 的坐标是（6，m ），点P 的坐标是（0，m 32），求线段AD 的长； （3）当31=EC BE 时，求BPDE的值.27题【例6】（成都青羊区2016-2017八上期27题）在Rt ACB ∆中，90ACB ∠=︒，AC=BC ，D 为AB 上一点，连结CD ，将CD 绕C 点逆时针旋转90︒至CE ，连结DE ，过C 作CF ⊥DE 交AB 于F ，连结BE.（1）求证：AD=BE ；（2）求证：222AD BF DF +=； （3）若15ACD ∠=︒，1CD =+，求BF.【例7】（1）问题发现：如图1，△ACB 和△DCE 均为等边三角形，当△DCE 旋转至点A ，D ，E 在同一直线上，连接BE ，易证△BCE ≌△ACD ．则 ①∠BEC ＝；②线段AD 、BE 之间的数量关系是 ． （2）拓展研究：如图2，△ACB 和△DCE 均为等腰三角形，且∠ACB ＝∠DCE ＝90°，点A 、D 、E 在同一直线上，若AE ＝15，DE ＝7，求AB 的长度．（3）探究发现：如图3，P 为等边△ABC 内一点，且∠APC ＝150°，且∠APD ＝30°，AP ＝5，CP ＝4，DP ＝8，求BD 的长．E答案典型问题：【例1】（2017-2018上期成都高新区27题）解：（1）∵∠BAC=∠DAE=︒90 ∴∠BAD=∠CAE∵AB=AC ，AD=AE ∴△ABD ≌△ACE （SAS ）（2）取AB 的中点G ，连接DG（I ）∵∠BAC=∠DAE=︒120且点D是边BC上一点。

第1讲三角形的初步知识1（认识三角形、定义与命题、证明）一、知识建构1. 三角形按角分类：（1）锐角三角形：三角形的，这样的三角形称之为锐角三角形（2）直角三角形：三角形有，这样的三角形称之为直角三角形（3）钝角三角形：三角形有，这样的三角形称之为钝角三角形2. 三角形的角平分线：在三角形中，，这个角的顶点与交点之间的线段叫做三角形的角平分线。

3.三角形的中线：在三角形中，，叫做这个三角形的中线。

（1）三角形的中线的形状也是一条；（2）三角形的三条角中线.4.三角形高的定义：从三角形的一个顶点线，的线段叫做三角形的高。

5.三角形三边之间的关系为：6.能清楚地规定某一名称或术语的句子叫做该名称或术语的______．7．对某一件事情作出_______判断的句子叫做命题．•每个命题都是由______•和______两部分组成的．8.思考下列命题的条件和结论分别是什么？并判断那些命题正确? 那些命题不正确?(1)相等的角是对顶角。

(2)直角三角形两锐角互余。

(3)同位角相等。

(4)一个角的补角一定大于这个角的余角。

9. 阅读教材内容后请回答：(1)怎样判断一个命题是真命题还是假命题？(1)真命题、公理、定理三者的区别与联系各是什么？10.判断下列命题是真命题还是假命题？如果是假命题，请说明理由；如果是真命题，请用推理的方法来说明.（1）如果ab=0，那么a=b=0；（2）如图，若AC∥DE，∠1=∠2，则AB∥CD.二、经典例题例1．对于同一平面内的三条直线a，b，c，给出下列5个判断：①a∥b②b∥c；•③a⊥b；④a∥c；⑤a⊥c．请以其中两个论断为条件，一个论断为结论，组成一个你认为正确的命题（至少写两个命题）．例2.如图，△ABC中，∠ACB=90°，沿CD折叠△CBD，使点B恰好落在AC边上的点E处．若∠A=22°，则∠BDC等于（）A．44°B．60°C．67°D．77°例3. 如图，已知∠AOB=α，在射线OA、OB上分别取点OA1=OB1，连接A1B1，在B1A1、B1B上分别取点A2、B2，使B1B2=B1A2，连接A2B2…按此规律下去，记∠A2B1B2=θ1，∠A3B2B3=θ2，…，∠A n+1B n B n+1=θn，则（1）θ1= , （2）θn= .例4．如图，在Rt△ABC中，∠ACB=90°，∠A=α，将△ABC绕点C按顺时针方向旋转后得到△EDC，此时点D在AB边上，则旋转角的大小为．图1图2DC EA B例5. 一个三角形的三条边长分别为1、2、x ，则x 的取值范围是（ ）A ．1≤x ≤3B ．1＜x ≤3C ．1≤x ＜3D ．1＜x ＜3例6. 已知实数x ，y 满足，则以x ，y 的值为两边长的等腰三角形的周长是 ．例7. 两个大小不同的等腰直角三角形三角板如图1所示放置，图2是由它抽象出的几何图形，B C E ，，在同一条直线上，连结DC ．（1）请找出图2中的全等三角形，并给予证明（说明：结论中不得含有未标识的字母）； （2）证明：DC BE ．例8.如图，已知AB ∥CD ，直线EF 分别截AB 、CD 于 点M 、N ，MG 、NH 分别是∠EMB 与∠END 的平分线.求证：MG ∥NH . 请根据分析思路，写出证明过程.三、基础演练1.在△ABC 中，若∠A +∠B =88°，则∠C =_______，这个三角形是______ 三角形.∠EMG=12∠∠ENH=12∠END可证∠EMG=∠MNH要证MG ∥NH 只需证：∠EMB=∠END已知AB ∥CDABCDE FHMN2.直角三角形的一个锐角为42°，则另一个锐角为_________.3.在△ABC 中，若∠A =35°，∠B =68°，则与∠C 相邻的外角等于_______ °.4．若5条线段长分别为1cm ，2cm ，3cm , 4cm ，5cm ，则以其中3条线段为边长可以构成三角形的个数是___________ .5．一木工师傅有两根70，100长的木条，他要选择第三根木条，将它们钉成三角形木架，则第三根木条取值范围_____________ ，木架周长的取值范围_____________ . 6. 如图所示，下面的推理中正确的是 ( ) A ．∵∠1＝∠2，∴AB ∥CDB ．∵∠ABC ＋∠BCD ＝180°，∴AD ∥BC C ．∵AD ∥BC ，∴∠3＝∠4D ．∵∠ABC ＋∠DAB ＝180°，∴AD ∥BC 7.命题“若a b >，则1ab>”是真命题还是假命题？请说明理由.8．若等腰三角形腰长为6,则底边x 的取值范围是 （ ） A . 6<x <12 B . 0<x <6 C . 0<x <12 D . 无法确定9. 如果一个三角形的三条高的交点恰是三角形的一个顶点，那么这个三角形是（ ）A .锐角三角形B .直角三角形C .钝角三角形D .锐角三角形 10.如图所示，在△ABC 中，∠C ＝90°，BD 平分∠ABC 交AC 于点D ，过点D 作DE ∥BC •交AB 于点E ，过点D 作DF ⊥AB 于点F .求证：BC ＝DE ＋EF .四、直击中考1. （2013广西）一个三角形的周长是36cm ，则以这个三角形各边中点为顶点的三角形的周长是（ ）A ．6cmB ．12cmC ．18cmD ．36cm2．（2013衡阳）如图，∠1=100°，∠C =70°，则∠A 的大小是（ ）A ．10°B ．20°C ．30°D ．80°3241D CBA B CE DF A3．（2013鄂州）一副三角板有两个直角三角形，如图叠放在一起，则∠α的度数是（ ）A ．165°B ．120°C ．150°D ．135°4.（2013黔东南州）在△ABC 中，三个内角∠A 、∠B 、∠C 满足∠B ﹣∠A =∠C ﹣∠B ，则∠B = 度．5.（2013温州）如图，直线a ，b 被直线c 所截，若a ∥b ，∠1=40°，∠2=70°，则∠3= 度．6.（2013雅安）若（a ﹣1）2+|b ﹣2|=0，则以a 、b 为边长的等腰三角形的周长为 ．7．（2013东城）.如图，∠ACD 是△ABC 的外角，ABC ∠的平分线与ACD ∠的平分线交于点1A ，1A BC ∠的平分线与1A CD ∠的平分线交于点2A ，…，1n A BC -∠的平分线与1n A CD -∠的平分线交于点n A . 设A θ∠=,则1A ∠＝ ；n A ∠＝ 8.(2014杭州)下列命题中，正确的是（ ）A .梯形的对角线相等B . 菱形的对角线不相等C . 矩形的对角线不能互相垂直D . 平行四边想的对角线可以互相垂直五、能力拓展1.如图，OB 、OC 是∠AOD 的任意两条射线，OM 平分∠AOB ，ON 平分∠DOC ，若∠MON =α，∠BOC =β，则∠AOD 可表示为（ ）A . 2α－βB . α－βC . α+βD . 2α2.如图，在锐角△ABC中，CD、BE分别是AB、AC上的高，•且CD、BE交于一点P，若∠A=50°，则∠BPC的度数是（）A．150°B．130°C．120°D．1003.已知等腰三角形的周长为14cm，底边与腰的比为3：2，求各边长.4. 已知a,b,c是一个三角形的三条边长,则化简|a+b－c|－|b－a－c|的结果是多少?5.如图所示，已知等腰直角三角形ABC中，∠ACB=90°，直线L经过点C，•AD•⊥L，BE⊥L，垂足分别为D，E．（1）证明：△ACD≌△CBE；（2）求证：DE=AD+BE；（3）当直线L经过△ABC内部时，其他条件不变，（2）中的结论还成立吗？如果成立，请给出证明；如果不成立，猜想这时DE，AD，BE有什么关系？证明你的猜想．六、挑战竞赛1. 在△ABC中,∠A= 50°, 高BE，CF所在的直线相交于点Ｏ，求∠BOC.FEC AB2.△ABC 中,已知∠ABC = 74°, ∠A = 56°, BE 是AC 边上的高,CF 是△ ABC 的角平分线,求∠ACF 和∠BFC .4.如图，在△ABC 中，D 、E 分别是BC 、AD 的中点，S △ABC =4cm 2，求S △ABE ．5．如图，45AOB ∠=，过OA 上到点O 的距离分别为1，4，7，10，13，16，…的点作OA 的垂线与OB 相交，得到并标出一组黑色梯形，它们的面积分别为,,,321s s s …，观察图中的规律，第4个黑色梯形的面积=4S ，第n (n 为正整数)个黑色梯形的面积=n S ．6.在△ABC 中，AC AB =,D 是底边BC 上一点，E 是线段AD 上一点,且∠BAC CED BED ∠=∠=2．(1) 如图1,若∠︒=90BAC ,猜想DB 与DC 的数量关系为 ； (2) 如图2,若∠︒=60BAC ，猜想DB 与DC 的数量关系，并证明你的结论； （3）若∠︒=αBAC ，请直接写出DB 与DC 的数量关系.OA BCDEA EBCD图1 图2。

八年级数学竞赛培优专题讲义----- 直角三角形知识精讲勾股定理揭示了直角三角形三边之间的关系，在公元前110多年前，商高已经证明了普遍意义下的勾股定理，国外把勾股定理称为“毕达哥拉斯定理”。

勾股定理是平面几何中一个重要定理，其广泛的应用体现在：勾股定理是现阶段线段计算、证明线段平方关系的主要方法；运用勾股定理的逆定理，通过计算也是证明两直线垂直位置关系的一种有效手段。

直角三角形是一类特殊三角形，有着丰富的性质：两锐角互余（角的关系）、勾股定理（边的关系）、300角所对的直角边等于斜边的一半（边角关系），这些性质在求线段的长度、证明线段倍分关系、证明线段平方关系等方面有广泛的应用。

例题精析例1、如图，四边形ABCD 中，DC//AB ，BC=1，AB=AC=AD=2，则BD 的长为（ ） A.14 B.15 C.23 D.32例2、如图，在△ABC 中，AC=BC ，∠ACB=90°，D 、E 是边AB 上的两点，AD=3，BE=4， ∠DCE=45°，求△ABC 的面积。

ABCD E图-184例3、如图，在凸四边形ABCD 中，∠ABC=30°，∠ADC=60°，AD=DC. 证明：BD 2=AB 2+BC 2例4、一个直角三角形的边长都是整数，它的面积和周长的数值相等，这样的直角三角形是否存在？若存在，确定它三边的长；若不存在，说明理由。

例5、 如图，设正△ABC 的边长为2，M 是AB 边上的中点，P 是BC 边上的任意一点，PA+PM 的最大值和最小值分别记作S 和T ，求22S T 的值。

186M PBAC例6、设A 是给定的正有理数（1）若A 是一个三边长都是有理数的直角三角形的面积，求证：一定存在3个正有理数x 、y 、z ，使得2222x y y z A -=-=；（2）若存在3个正有理数x 、y 、z ，满足2222x y y z A -=-=，求证：存在一个三边长都是有理数的直角三角形，它的面积等于A 。