物体转动惯量的测定

转动惯量的测定实验报告转动惯量的测定实验报告引言：转动惯量是物体在转动过程中抵抗改变其转动状态的性质。

在物理学中，转动惯量是描述物体转动惯性大小的物理量。

本实验旨在通过测量不同物体的转动惯量，探究物体的形状、质量分布对转动惯量的影响，并验证转动惯量的计算公式。

实验装置和方法：1. 实验装置：转动惯量测量装置、计时器、质量秤、直尺、物体样品。

2. 实验方法：a. 将转动惯量测量装置固定在水平台上。

b. 选择不同形状的物体样品，如圆柱体、长方体和球体，并测量其质量和尺寸。

c. 将物体样品放置在转动惯量测量装置的转轴上，并使其旋转。

d. 通过计时器测量物体样品旋转一定圈数所需的时间。

e. 根据测量结果计算物体样品的转动惯量。

实验结果与分析：1. 圆柱体样品：a. 质量：m = 100gb. 高度：h = 10cmc. 半径：r = 3cmd. 转动惯量：I = 1/2 * m * r^2 = 1/2 * 0.1kg * (0.03m)^2 = 4.5 * 10^-5kg·m^22. 长方体样品：a. 质量：m = 150gb. 长度：l = 15cmc. 宽度：w = 5cmd. 高度：h = 2cme. 转动惯量：I = 1/12 * m * (l^2 + w^2) = 1/12 * 0.15kg * ((0.15m)^2 +(0.05m)^2) = 4.375 * 10^-4 kg·m^23. 球体样品：a. 质量：m = 200gb. 半径：r = 4cmc. 转动惯量：I = 2/5 * m * r^2 = 2/5 * 0.2kg * (0.04m)^2 = 2.56 * 10^-4 kg·m^2通过实验测量得到的转动惯量结果显示，不同形状的物体样品具有不同的转动惯量。

圆柱体样品的转动惯量最小，长方体样品的转动惯量次之，球体样品的转动惯量最大。

这是因为转动惯量与物体的质量分布和形状有关。

测定物体转动惯量的实验步骤为了测定物体的转动惯量，我们可以进行以下实验步骤：实验器材：- 转动惯量测量装置（如转动台）- 不同形状和质量的物体（如圆盘、长方体等）- 测量工具（如尺子、天平等）- 装置固定工具（如螺丝刀、夹具等）- 实验记录表格实验步骤：1. 准备工作：- 将转动台放在平坦的实验台上，并确保转动台能够自由旋转。

- 根据实验的需要，选择不同形状和质量的物体进行测量，并确保它们被清洁干净以消除外部因素的影响。

- 使用天平测量物体的质量，并记录在实验记录表格上。

2. 测量转动惯量：a. 将选定的物体放在转动台上，并用装置固定工具将其稳定固定在转动台上，以确保其不会滑动。

b. 根据实验要求，给物体施加一个力矩以使其开始自由旋转。

可以通过给物体施加一个外力矩（如推动）或者施加一个震动力矩（如敲击）来实现。

c. 测量物体的转动加速度。

可以通过计时物体旋转某段距离所需要的时间，并结合物体的几何参数（如半径、长宽等）来计算得到。

3. 多次测量：a. 为了提高实验结果的准确性，建议进行多次重复测量。

b. 对于每次测量，必须确保物体被置于相同的初始条件下（如力矩的大小和方向、物体的位置等），以消除不确定性因素的影响。

c. 对于每次测量，都需要记录物体的质量、几何参数、施加的力矩大小和方向以及得到的转动加速度。

4. 数据分析：a. 将所得的所有测量结果整理并计算平均值。

b. 根据所使用的力矩和转动加速度的关系，应用转动惯量的定义公式（转动惯量=力矩/转动加速度）计算物体的转动惯量。

c. 对不同形状和质量的物体进行转动惯量的比较分析。

5. 讨论和结论：a. 根据实验结果的分析，讨论物体的转动惯量与其形状和质量之间的关系。

比较不同形状和质量的物体的转动惯量差异。

b. 分析实验中可能存在的误差来源，并提出减小误差的改进方法。

c. 根据实验结果和讨论得出结论，总结整个实验的目的和意义。

6. 结束实验：- 清洁和整理实验器材，确保实验台的干净和整洁。

测定物体转动惯量的实验步骤实验目的：本实验旨在通过测定物体转动惯量，帮助学生更好地理解和掌握力矩和转动惯量的概念，并通过实验数据计算物体的转动惯量。

实验器材：1. 轴心固定装置2. 离心定标器3. 钢球或圆盘样品4. 测量尺5. 偏心块6. 电子天平7. 实验台实验步骤：1. 准备工作：a. 将轴心固定装置安装在实验台上，并确保稳固。

b. 将离心定标器安装在轴心固定装置上。

c. 用测量尺测量离心定标器的半径，并记录下来。

2. 测量样品的质量：a. 使用电子天平准确测量钢球或圆盘样品的质量，记录下来。

3. 安装样品：a. 将钢球或圆盘样品与轴心连接，确保连接牢固。

b. 若要增加转动惯量，可以添加偏心块到样品上。

根据需要添加适量的偏心块，确保安装均匀。

4. 进行实验：a. 将离心定标器转动起来，使样品旋转。

b. 通过逐渐增加离心定标器的转速，逐步增加样品的转动速度。

c. 记录离心定标器的转速，并记录下每个转速对应的样品转动时间。

5. 数据处理和计算：a. 根据测量的数据绘制样品转速和转动时间的图表。

b. 使用线性拟合方法，在图表上找到转速和转动时间之间的线性关系，并计算出斜率。

c. 利用转动时间与离心定标器转速的线性关系，计算样品的转动惯量。

d. 如果使用了偏心块，还需计算偏心块的贡献转动惯量，并将其加到样品转动惯量上。

实验注意事项：1. 在进行实验前，务必保证实验器材和安装固定装置的稳定性，以避免安全事故发生。

2. 在进行实验时，遵守实验室规范，注意个人防护，避免发生意外伤害。

3. 在测量样品质量时，尽量保持准确性，避免误差对实验结果的影响。

4. 在进行数据处理和计算时，需要仔细分析和处理数据，确保计算结果的准确性和可靠性。

5. 如果使用了偏心块，请确保偏心块的安装均匀，并将其转动惯量计算在最终的转动惯量结果中。

总结：通过以上实验步骤，我们可以测定物体的转动惯量，并更好地理解力矩和转动惯量的概念。

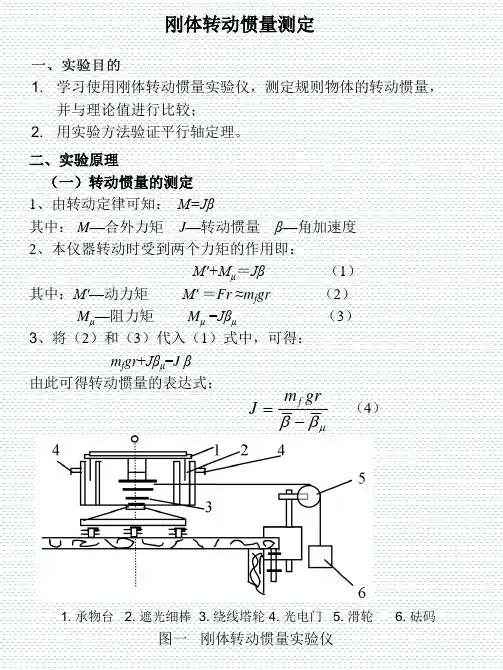
篇一：大学物理实验报告测量刚体的转动惯量测量刚体的转动惯量实验目的：1．用实验方法验证刚体转动定律，并求其转动惯量；2．观察刚体的转动惯量与质量分布的关系3．学习作图的曲线改直法，并由作图法处理实验数据。

二.实验原理:1．刚体的转动定律具有确定转轴的刚体，在外力矩的作用下，将获得角加速度β，其值与外力矩成正比，与刚体的转动惯量成反比，即有刚体的转动定律：m = iβ (1)利用转动定律，通过实验的方法，可求得难以用计算方法得到的转动惯量。

2．应用转动定律求转动惯量图片已关闭显示，点此查看如图所示，待测刚体由塔轮，伸杆及杆上的配重物组成。

刚体将在砝码的拖动下绕竖直轴转动。

设细线不可伸长，砝码受到重力和细线的张力作用，从静止开始以加速度a下落，其运动方程为mg – t=ma，在t时间内下落的高度为h=at/2。

刚体受到张力的力矩为tr和轴摩擦力力矩mf。

由转动定律可得到刚体的转动运动方程：tr - mf = iβ。

绳与塔轮间无相对滑动时有a = rβ，上述四个方程得到：22m(g - a)r - mf = 2hi/rt (2)mf与张力矩相比可以忽略，砝码质量m比刚体的质量小的多时有a<<g，所以可得到近似表达式：2mgr = 2hi/ rt (3)式中r、h、t可直接测量到，m是试验中任意选定的。

因此可根据（3）用实验的方法求得转动惯量i。

3．验证转动定律，求转动惯量从（3）出发，考虑用以下两种方法：2a．作m – 1/t图法：伸杆上配重物位置不变，即选定一个刚体，取固定力臂r和砝码下落高度h，（3）式变为：2m = k1/ t (4)2式中k1 = 2hi/ gr为常量。

上式表明：所用砝码的质量与下落时间t的平方成反比。

实验中选用一系列的砝码质量，可测得一组m与1/t的数据，将其在直角坐标系上作图，应是直线。

即若所作的图是直线，便验证了转动定律。

222从m – 1/t图中测得斜率k1，并用已知的h、r、g值，由k1 = 2hi/ gr求得刚体的i。

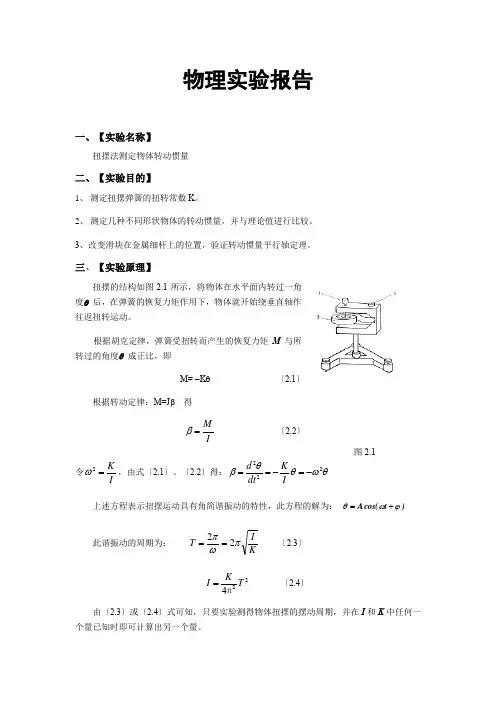
物理实验报告一、【实验名称】扭摆法测定物体转动惯量二、【实验目的】1、 测定扭摆弹簧的扭转常数K 。

2、 测定几种不同形状物体的转动惯量，并与理论值进行比较。

3、改变滑块在金属细杆上的位置，验证转动惯量平行轴定理。

三、【实验原理】扭摆的结构如图2.1所示，将物体在水平面内转过一角度θ 后，在弹簧的恢复力矩作用下，物体就开始绕垂直轴作往返扭转运动。

根据胡克定律，弹簧受扭转而产生的恢复力矩M 与所转过的角度θ 成正比，即M= -K θ 〔2.1〕根据转动定律：M=J β 得IM=β 〔2.2〕 令IK=2ω，由式〔2.1〕、〔2.2〕得：θωθθβ222-=-==I K dt d 上述方程表示扭摆运动具有角简谐振动的特性，此方程的解为： )t cos(A ϕωθ+=此谐振动的周期为： KIT πωπ22==〔2.3〕 224T K I π=〔2.4〕 由〔2.3〕或〔2.4〕式可知，只要实验测得物体扭摆的摆动周期，并在I 和K 中任何一个量已知时即可计算出另一个量。

图2.1本实验用一个已知形状规则的物体，它的转动惯量可以根据它的质量和几何尺寸用理论公式直接计算得到，再算出仪器弹簧的K 值。

如先测载物盘转动的周期T 0，有T=2KI 0π(4-5〕 再测载物盘加塑料圆柱〔大〕的转动周期T 1，有KI I T 1012'+=π(4-6) 1I '为塑料圆柱转动惯量理论计算值1I '=221mr 〔4-7〕由式〔4-5〕和式〔4-6〕可得K=422112T T I -'π(4-8) 假设要测定其它形状物体的转动惯量，只需将待测物体安放在本仪器顶部的各种夹具上，测定其摆动周期，由公式〔2.3〕即可算出该物体绕转动轴的转动惯量。

理论分析证明，假设质量为m 的物体绕通过质心轴的转动惯量为I 0，当转轴平行移动距离x 时，则此物体对新轴线的转动惯量变为I 0+mx 2。

称为转动惯量的平行轴定理。

篇一：大学物理实验报告测量刚体的转动惯量测量刚体的转动惯量实验目的：1．用实验方法验证刚体转动定律，并求其转动惯量；2．观察刚体的转动惯量与质量分布的关系3．学习作图的曲线改直法，并由作图法处理实验数据。

二.实验原理:1．刚体的转动定律具有确定转轴的刚体，在外力矩的作用下，将获得角加速度β，其值与外力矩成正比，与刚体的转动惯量成反比，即有刚体的转动定律：m = iβ (1)利用转动定律，通过实验的方法，可求得难以用计算方法得到的转动惯量。

2．应用转动定律求转动惯量图片已关闭显示，点此查看如图所示，待测刚体由塔轮，伸杆及杆上的配重物组成。

刚体将在砝码的拖动下绕竖直轴转动。

设细线不可伸长，砝码受到重力和细线的张力作用，从静止开始以加速度a下落，其运动方程为mg – t=ma，在t时间内下落的高度为h=at/2。

刚体受到张力的力矩为tr和轴摩擦力力矩mf。

由转动定律可得到刚体的转动运动方程：tr - mf = iβ。

绳与塔轮间无相对滑动时有a = rβ，上述四个方程得到：22m(g - a)r - mf = 2hi/rt (2)mf与张力矩相比可以忽略，砝码质量m比刚体的质量小的多时有a<<g，所以可得到近似表达式：2mgr = 2hi/ rt (3)式中r、h、t可直接测量到，m是试验中任意选定的。

因此可根据（3）用实验的方法求得转动惯量i。

3．验证转动定律，求转动惯量从（3）出发，考虑用以下两种方法：2a．作m – 1/t图法：伸杆上配重物位置不变，即选定一个刚体，取固定力臂r和砝码下落高度h，（3）式变为：2m = k1/ t (4)2式中k1 = 2hi/ gr为常量。

上式表明：所用砝码的质量与下落时间t的平方成反比。

实验中选用一系列的砝码质量，可测得一组m与1/t的数据，将其在直角坐标系上作图，应是直线。

即若所作的图是直线，便验证了转动定律。

222从m – 1/t图中测得斜率k1，并用已知的h、r、g值，由k1 = 2hi/ gr求得刚体的i。

理论力学转动惯量实验报告【实验目的】1.了解多功能计数计时毫秒仪实时测量（时间）的基本方法2.用刚体转动法测定物体的转动惯量3.验证刚体转动的平行轴定理4.验证刚体的转动惯量与外力矩无关【实验原理】1.转动力矩、转动惯量和角加速度关系系统在外力矩作用下的运动方程T×r+Mμ=Jβ2（1）由牛顿第二定律可知，砝码下落时的运动方程为：mg-T=ma即绳子的张力T=m(g-rβ2)砝码与系统脱离后的运动方程Mμ=Jβ1（2）由方程（1）（2）可得J=mr(g-rβ2)/(β2-β1) （3）2.角加速度的测量θ=ω0t+½βt²（4）若在t1、t2时刻测得角位移θ1、θ2则θ1=ω0 t1+½βt²（5）θ2=ω0 t2+½βt²（6）所以，由方程（5）、（6）可得β=2（θ2 t1-θ1 t2）/ t1 t2（t2- t1）【实验仪器】1、IM-2刚体转动惯量实验仪(含霍尔开关传感器、计数计时多功能毫秒仪、一根细绳、一个质量为100g的砝码等，塔轮直径从下至上分别为30mm、40mm、50mm、60mm，载物台上的孔中心与圆盘中心的距离分别为40mm、80mm、120mm)2、一个钢质圆环(内径为175mm，外径为215mm，质量为995g)3、两个钢质圆柱(直径为38mm，质量为400g)【实验步骤】1.实验准备在桌面上放置IM-2转动惯量实验仪，并利用基座上的三颗调平螺钉，将仪器调平。

将滑轮支架固定在实验台面边缘，调整滑轮高度及方位，使滑轮槽与选取的绕线塔轮槽等高，且其方位相互垂直。

通用电脑计时器上光电门的开关应接通，另一路断开作备用。

当用于本实验时，设置1个光电脉冲记数1次，1次测量记录大约20组数。

2.测量并计算实验台的转动惯量1)放置仪器，滑轮置于实验台外3-4cm处，调节仪器水平。

设置毫秒仪计数次数为20。

2)连接传感器与计数计时毫秒仪，调节霍尔开关与磁钢间距为0.4-0.6cm，转离磁钢，复位毫秒仪，转动到磁钢与霍尔开关相对时，毫秒仪低电平指示灯亮，开始计时和计数。

转动惯量测量方法
转动惯量的测量方法有多种，以下是一些常用的方法：
1.扭摆法：利用扭摆的自由振动周期与转动惯量之间的关系，通
过测量扭摆的自由振动周期，可以推算出转动惯量。

2.复摆法：利用复摆的摆动周期与转动惯量之间的关系，通过测
量复摆的摆动周期，可以推算出转动惯量。

3.旋转盘法：利用旋转盘的转动惯量与转速之间的关系，通过测
量旋转盘的转速和转动惯量，可以推算出转动惯量。

4.振动法：利用物体的振动频率与转动惯量之间的关系，通过测
量物体的振动频率，可以推算出转动惯量。

5.电子式扭矩仪法：利用电子式扭矩仪测量扭矩和转速，结合角
动量守恒定律推算转动惯量。

6.刚体转动实验台法：将待测刚体放置在刚体转动实验台上，通
过测量实验台的运动状态和刚体的转速，结合角动量守恒定律
推算转动惯量。

这些方法各有优缺点，可以根据具体的情况选择适合的方法进行测量。

王皓平 6100411063 电III112班 S07716 00 十 一 16 T004实验名称： 扭摆法测定物体转动惯量一、引言：转动惯量是刚体转动时惯性的量度，其量值取决于物体的形状、质量分布及转轴的位置。

刚体的转动惯量有着重要的物理意义，在科学实验、工程技术、航天、电力、机械、仪表等工业领域也是一个重要参量。

二、实验目的：1. 用扭摆测定几种不同形状物体的转动惯量和弹簧的扭动常数，并与理论值进行比较。

2. 验证转动惯量平行轴定理。

三、实验原理：物体装在一螺旋弹簧上，当物体在水平面内转过θ 角后弹簧产生恢复力矩 M =−Kθ, 在此力矩作用下物体转动，由转动定律M =Iβ,得T =2πω=2π√I K不放物体时，仍有转动惯量，因此：T 0=2π√I 0KT 1=2π√I 0+I 1KK =4π2T 12−T 02I 1 四、实验仪器：转动惯量测定仪 电子天平 游标卡尺五、实验内容：1. 测出各种待测物体的内外径，长度等。

2. 调节仪器。

3. 测定T0。

4. 测定T1 。

5. 更换物体重复测量。

王皓平6100411063 电III112班S07716 00 十一16 T004六、实验记录：王皓平6100411063 电III112班S07716 00 十一16 T004七、数据处理：10.052=0.000445K=4π2T12−T02I1=4π20.9892−0.72020.5×0.356×0.052=0.038I0=0.72020.9892−0.72020.000445=5.02×10−4I塑料筒大=KT24π2−I0=8.86×10−4 I′塑料筒大=18mD2=8.9×10−4 E=0.45%I金属筒=KT24π2−I0=1.60×10−3 I′塑料筒大=18m（D12+D22）=1.53×10−3 E=4.58%I塑料球=KT24π2−I支座=1.67×10−3 I′塑料筒大=110mD2=1.7956×10−3 E=7.16%I细杆=KT24π2−I夹具=4.20×10−3 I′细杆=112mL2=4.02×10−3 E=4.48%I5=KT24π2=5.50×10−3 I′5=I′细杆+I夹具+2mx2+I=5.29×10−3 E=3.97%I25=KT24π2=3.43×10−2 I′25=I′细杆+I夹具+2mx2+I=3.02×10−2 E=13.58%八、实验结果：I塑料筒大=8.86×10−4E=0.45%I金属筒=1.60×10−3E=4.58%I塑料球=1.67×10−3 E=7.16%I细杆=4.20×10−3E=4.48%王皓平6100411063 电III112班S07716 00 十一16 T004I5=5.50×10−3E=3.97%I25=3.43×10−2E=13.58%九、误差分析：1. 实验中，仪器未保持完全水平。

实验七用三线摆法测定物体的转动惯量摆法测定物体转动惯量是物理学中常见的实验之一，该实验可以帮助学生加深对物体转动惯量的理解，掌握机械学的基础原理和实验操作技能。

在本实验中我们将采用三线摆法来测定物体的转动惯量。

1.实验原理物体绕固定轴线旋转时，具有旋转惯量，即转动惯量。

对于一根固定轴线，围绕其转动的平面内的点质量越分散，它的转动惯量越大。

绕固定轴旋转的物体，平面内距轴线最远的点的到轴线距离原则上可以任选一个点来计算，但固定点的选取会使计算过程变得简单。

黄铜丝由于具有一定的弹性，所以作为固定轴的黄铜丝实验延长杆，必须修正其转动惯量，而加入之修正电子秤的质量必须加入考虑范围内以保证测量数据的准确性。

在实验过程中，需要通过三线摆法来测定固体圆柱的转动惯量，我们可以利用固定轴线到重心的距离、摆的周期和摆长等参数来计算转动惯量，转动惯量的计算公式如下：I = (mD² + m(L/2)²)T²/4π²其中，I为转动惯量，m为物体质量，D为固定轴线到重心点的距离，L为黄铜丝的总长度，T为摆的周期。

2.实验器材Ⅰ) 数字示波器Ⅱ) 固定轴线的黄铜丝Ⅲ) 固体圆柱Ⅳ) 科学计时器Ⅴ) 数据采集卡Ⅵ) 实验立杆3.操作步骤（一）实验前的准备将立杆装到三脚架上，将黄铜丝固定在立杆上，使其垂直于桌面，用超额重量调整器进行平衡调整后验重，保证黄铜丝处于稳定竖直状态。

（二）测量黄铜丝的直径和长度使用量规和卷尺测量黄铜丝的直径和长度，将测得的数据记录下来。

（三）固体圆柱质量的测定使用精密天平，测量固体圆柱的质量。

用卷尺测量固体圆柱的半径，并记录下来。

将固体圆柱放在平衡台上，测量固体圆柱的质心距离固定轴线的距离，记录下测量值。

（六）测量摆杆的长度（七）测量黄铜丝的弹性系数在执行实验时，要记录黄铜丝的弹性系数，即黄铜丝的直径。

悬挂固体圆柱后，通过小往复角的周期性转动，测量摆的周期，而后进行多次测量记录。

实验一 三线摆法测定物体的转动惯量转动惯量是刚体转动惯性大小的量度，是表征刚体特性的一个物理量。

转动惯量的大小除与物体质量有关外，还与转轴的位置和质量分布（即形状、大小和密度）有关。

如果刚体形状简单，且质量分布均匀，可直接计算出它绕特定轴的转动惯量。

但在工程实践中，我们常碰到大量形状复杂、且质量分布不均匀刚体，理论计算将极为复杂，通常采用实验方法来测定。

转动惯量的测量，一般都是使刚体以一定的形式运动。

通过表征这种运动特征的物理量与转动惯量之间的关系，进行转换测量。

测量刚体转动惯量的方法有多种，三线摆法是具有较好物理思想的实验方法，它具有设备简单、直观、测试方便等优点。

【实验目的】1、学会用三线摆测定物体的转动惯量。

2、学会用秒表测量周期运动的周期。

3、验证转动惯量的平行轴定理。

【实验器材】三线摆，米尺，游标卡尺，待测圆环，待测圆柱和秒表【实验原理】图1-1是三线摆实验装置的示意图。

上、下圆盘均处于水平，悬挂在横梁上。

三个对称分布的等长悬线将两圆盘相连。

上圆盘固定，下圆盘可绕中心轴O O '作扭摆运动。

当下盘转动角度很小，且略去空气阻力时，扭摆的运动可近似看作简谐运动。

根据能量守恒定律和刚体转动定律均可以导出物体绕中心轴O O '的转动惯量(推导过程见本实验附录)。

2002004T H gRr m I π=（1-1） 式中各物理量的意义如下：0m 为下盘的质量；r 、R 分别为上下悬点离各自圆盘中心的距离；0H 为平衡时上下盘间的垂直距离；T 0为下盘作简谐运动的周期，g 为重力加速度（桂林地区g =9.797m/s 2）。

将质量为m 的待测物体放在下盘上，并使待测刚体的转轴与O O '轴重合。

测图1 三线摆实验装置图出此时下盘运动周期1T 和上下圆盘间的垂直距离H 。

同理可求得待测刚体和下圆盘对中心转轴O O '轴的总转动惯量为：212014)(T HgRr m m I π+=（1-2）如不计因重量变化而引起的悬线伸长， 则有0H H ≈。

一、实验名称：扭摆法测定物体的转动惯量二、实验目的：1、测定扭摆的仪器常数（弹簧的扭转常数）K。

2、测定熟料圆柱体、金属圆筒、木球与金属细长杆的转动惯量。

3、验证转动惯量的平行轴定理。

三、实验器材：扭摆、转动惯量测试仪、金属圆筒、实心塑料圆柱体、木球、验证转动惯量平行轴定理用的金属细杆（杆上有两块可以自由移动的金属滑块）、游标卡尺、米尺、托盘天平。

四、实验原理：1、测量物体转动惯量的构思与原理将物体在水平面内转过以角度θ后，在弹簧的恢复力矩作用下物体就开始绕垂直轴作往返扭转运动。

更具胡克定律，弹簧受扭转而产生的恢复力矩M与所转过的角度θ成正比，即式中K为弹簧的扭转常数。

若使I为物体绕转轴的转动惯量，β为角加速度，由转动定律可得令，忽略轴承的磨察阻力距，得上式表示扭摆运动具有角简谐振动的特性，角加速度与角位移成正比，且方向相反。

方程的解为式中A为简谐振动的角振幅，为初相位角，为角速度。

谐振动的周期为由上式可知，只要通过实验测得物体扭摆的摆动周期，并在I和K中任何一个量已知时即可计算出另外一个量。

本实验使用一个几何形状规则的小塑料圆柱，它的转动惯量可以根据质量和几何尺寸用理论公式直接计算得到，将其放在扭摆的金属载物盘上，通过测定其在扭摆仪上摆动时的周期，可算出仪器弹簧的K值。

若要测定其他形状物体的转动惯量，只需将待测物体安放在同一扭摆仪顶部的各种夹具上，测定其摆动周期，即可算出该物体绕转动轴的转动惯量。

假设扭摆上只放置金属载物圆盘时的转动惯量为，周期为，则若在载物圆盘上放置已知转动惯量为的小塑料圆柱后，周期为，由转动惯量的可加性，总的转动惯量为，则解得以及若要测量任何一种物体的转动惯量，可将其放在金属载物盘上，测出摆动周期T，就可算出其转动惯量I，即本实验测量木球和金属细杆的转动惯量时，没有用金属载物盘，分别用了支架和夹具，则计算转动惯量时需要扣除支架和夹具的转动惯量。

1、验证物体转动惯量的平行轴定理本实验利用金属细杆和两个对称放置在细杆两边凹槽内的滑块来验证平行轴定理。

实验02 扭摆法测定物体转动惯量实验02扭摆法测定物体转动惯量实验2用扭摆法测量物体的转动惯量转动惯量是刚体转动时惯性大小的量度，是表明刚体特性的一个物理量。

刚体转动惯量除了与物体质量有关外，还与转轴的位置和质量分布（即形状、大小和密度分布）有关。

如果刚体形状简单，且质量分布均匀，可以直接计算出其绕特定转轴转动的转动惯量。

对于形状复杂，质量分布不均匀的刚体，其转动惯量计算极为复杂，必须通常采用实验方法来测定，例如机械部件，电动机转子和枪炮的弹丸等。

惯性矩的测量通常是使刚体以某种形式运动。

转换测量通过表征运动的物理量与惯性矩之间的关系进行。

在本实验中，将物体制成扭摆，通过测量摆动周期和其他参数来计算物体的惯性矩。

【实验目的】1.2.3.4.5.加深对刚体转动知识、胡克定律、谐振方程的理解。

了解光电门的工作原理。

掌握游标卡尺的使用方法。

学习使用扭摆法测量不同形状物体的惯性矩。

验证转动惯量平行轴定理（实验设计项目、选做）。

[文书]th-2型智能转动惯量实验仪、游标卡尺、电子天平[实验原理]根据胡克定律，弹簧受扭转而产生的恢复力矩m与所转过的角度?成正比，即MK（2-1）式中，k为弹簧的扭转常数，根据转动定律M我（2-2）式中I是物体绕旋转轴的惯性矩，？是角加速度吗，？是角速度。

角加速度？角速度和角度是多少？这种关系是：d?d22（2-3）Dtdt由方程式（2-1）和方程式（2-2）得出ik?（2-4）i令?02?k，忽略轴承的摩擦阻力矩，由式（2-3）、式（2-4）得d2？k2？？2.0 （2-5）idt即d2？2.（2-6）0dt2方程（2-5）表明，扭摆运动具有角简谐振动的特征，角加速度与角位移成正比，方向相反。

这个方程的解是：acos(?0t)（2-7）式中，a为谐振动的角振幅，?为初相位角，?0为谐振动的圆频率，根据圆频率?0与周期t的关系（t?2?）和式（2-5）的关系有0吨？2.0 2? I（2-8）k由等式（2-8）表示kt2（2-9）i1?24?由式（2-9）可知，只要测得物体扭摆的摆动周期t和弹簧的扭转常数k即可计算出夹具与待测物体一起旋转的惯性矩I。

实验五物体转动惯量的测定刚体转动的一个重要物理量是转动惯量，它是表征物体转动惯性大小的量度，在许多研究领域和工业设计中都要考虑物体转动惯量的大小，因此，测定物体的转动惯量具有重要的实际意义。

对于形状比较规则的物体，可用数学方法计算出它的转动惯量。

但对于形状比较复杂的物体，一般需用实验的方法进行测定，如机械零件、电动机转子和枪炮的弹丸等。

测量刚体转动惯量的方法很多，本实验介绍两种测定给定物体的转动惯量，并由此验证转动定理和平行轴定理。

1 用转动惯量仪测量物体的转动惯量【实验目的】【实验仪器】【实验原理】【实验内容】【数据处理】【分析与讨论】【实验目的】1．通过实验验证刚体的转动定理；2．研究刚体绕定轴转动时，转动惯量随质量分布而改变的规律；3．用作图法处理数据。

【实验仪器】BDF1型刚体转动惯量仪自由落体仪SSM-5C计时-计数-计频仪⑴BDF1型刚体转动惯量仪转动体塔轮，两边各伸出一根具有等分刻度的均匀细杆B、B ′。

在B、B′上各有一可移动的圆柱形重物（称重锤），它们构成一个可定轴OO′转动的刚体系。

塔轮上绕一根细线，通过滑轮C与砝码相连，从而通过细线对刚体系施以力矩。

滑轮C 的位置可用固定螺钉D调节，以保证绕线的塔轮不同位置时都能与转轴OO′保持垂直。

固定架E上有指针标记F，此标记为砝码落下时的起始位置，H是固定螺杆。

实验前，通过底脚螺钉S 装置如图。

A是有不同半径R（15、25、30、20、10mm）的1、S2和S3可调转轴OO′的竖直状态。

⑵SSM-5C计时-计数-计频仪和自由落体仪的使用请参照重力加速度测定的仪器介绍。

【实验原理】当刚体绕定轴转动时，根据转动定律有 βI M =⑴式中M 为刚体所受合外力矩，I 为刚体对该轴的转动惯量（单位：KG ·M 2），β为角加速度。

在转动惯量仪装置图中，刚体所受的力矩M 为绳子所施力矩Tr M T =和磨擦力矩的合力矩，即μM M =Tr —⑵μM 式中T 为绳子的张力且与OO ′垂直。