垂线段最短

利用垂线段最短求解几何最值问题
垂线段被定义为从一点开始链接另一点，以一条把两点分开的直线段为基础。

垂线段经常被用来解决几何最值问题，其中一种最值拥有独特的特性，即在两点中总是能够找到最短的垂线段。

然而，这种方法并不总是对每一个问题都有用。

在给定一组几何形状时，垂线段法可以帮助求解几何最值问题，而无需进行复
杂的计算。

例如，许多几何形状的最长垂线段长度可以很容易地被求解。

比如，给定一个三角形，可以确定三角形最长垂线段长度取决于最长边和与该边成夹角的最长垂线段。

使用垂线段法，就可以容易地计算出该垂线段的最短长度。

此外，垂线段法还可以帮助求解另一类几何最值问题，即求解两点之间的最短
距离。

例如，求解一个圆的最近距离，即求解两个圆之间的最短距离。

一般来说，最近距离可以取决于两个圆心之间的距离以及这两个圆的半径。

通过使用垂线段法，我们可以容易地求解出两个圆之间的最短距离。

综上所述，垂线段法可以帮助我们求解各种几何最值问题，有效地减少计算量，从而提高处理效率。

这种有效的方法，可以说是对几何最值问题的有益尝试，是一种可靠的解决方案。

1．如图，计划把河水引到水池A中，先作AB⊥CD，垂足为B，然后沿AB开渠，能使所开的渠道最短，这样设计的依据是连接直线外一点与直线上所有点的连线中，垂线段最短．考点：垂线段最短。

专题：应用题。

分析：过直线外一点作直线的垂线，这一点与垂足之间的线段就是垂线段，且垂线段最短．解答：解：根据垂线段定理，连接直线外一点与直线上所有点的连线中，垂线段最短，∴沿AB开渠，能使所开的渠道最短．点评：本题是垂线段最短在实际生活中的应用，体现了数学的实际运用价值．2．如图，要从小河引水到村庄A，请设计并作出一最佳路线，理由是垂线段最短．考点：垂线段最短。

专题：应用题。

分析：过直线外一点作直线的垂线，这一点与垂足之间的线段就是垂线段，且垂线段最短．据此作答．解答：解：根据垂线段定理，连接直线外一点与直线上所有点的连线中，垂线段最短，∴过点A作河岸的垂线段，理由是垂线段最短．点评：本题主要考查了从直线外一点到这条直线上各点所连的线段中，垂线段最短在生活中的应用．3．如图，AB⊥BC，则AB ＜AC（填“＞”或“=”或“＜”），其理由是垂线段最短．考点：垂线段最短。

分析：把BC看作直线，点A为直线BC外一点，根据垂线段定理进行判断．解答：解：根据从直线外一点到这条直线上各点所连的线段中，垂线段最短，可知AB＜AC，其理由是垂线段最短．点评：本题主要考查了从直线外一点到这条直线上各点所连的线段中，垂线段最短的性质．4．如图，计划把河AB中的水引到水池C中，可以先作CD⊥AB，垂足为D，然后沿CD开渠，则能使所打开的水渠最短，这种方案的设计根据是连接直线外一点与直线上各点的所有线段中，垂线段最短．考点：垂线段最短。

专题：应用题。

分析：过直线外一点作直线的垂线，这一点与垂足之间的线段就是垂线段，且垂线段最短．据此作答．解答：解：这种方案的设计根据是：连接直线外一点与直线上各点的所有线段中，垂线段最短．点评：本题考查了垂线的性质在实际生活中的运用．5．如图，现有一条高压线路沿公路l旁边建立，某村庄A需进行农网改造，必须要从这条高压线上架接一条线路去村庄A，为了节省费用，请你帮他们规划一下，并说明理由．理由是从直线外一点到这条直线上各点所连的线段中，垂线段最短．考点：垂线段最短。

垂线段一、知识互动1、垂线段的定义：从直线外一点引一条直线的垂线，这点和垂足之间的线段叫做垂线段。

2、垂线段的性质：连接直线外一点与直线上各点的所有线段中，垂线段最短。

简单说成：垂线段最短。

3、点到直线的距离定义：直线外一点到这条直线的垂线段的长度，叫做点到直线的距离。

【注】区别垂线、垂线段和点到直线的距离：是三个不同的概念，垂线是直线；垂线段是线段，都是图形。

点到直线的距离是垂线段的长度，是一个数量，不能说垂线段是点到直线的距离。

二、例题讲解例1 已知钝角△ABC中，∠BAC为钝角。

（1）画出点C到AB的垂线段；（2）过点A画BC的垂线；（3）量出点B到AC的距离。

例2 如图所示，污水处理厂要从A处把处理过的水引入排水沟PQ，应如何铺设排水管道，才能使用料最省？试画出铺设管道的路线，并说明理由。

三、课堂反馈1、如图１所示，ON⊥l，OM⊥l，则ＯＭ与ON重合的理由是（）Ａ、过两点只有一条直线B、经过一点只有一条直线垂直于已知直线C、平面内，过一点只能作一条已知直线的垂线D、垂线段最短图１图２2、点到直线的距离是指（）A、从直线外一点到这条直线的垂线B、从直线外一点到这条直线的垂线段C、从直线外一点到这条直线的垂线的长D、从直线外一点到这条直线的垂线段的长3、如图２，ＢＣ⊥ＡＣ，CB=8cm，ＡＣ＝６ｃｍ，AB=10cm，那么点Ｂ到ＡＣ的距离是；点Ａ到ＢＣ的距离是；A、B两点间的距离是。

4、如图３所示，AC⊥BC，CD⊥AB于D，图中有个直角，线段的长表示点C到AB的距离，线段的长表示点A到BC的距离。

图３图４5、如图４所示，ＡＢ⊥ＢＣ于B，ＡＢ＝４，ＡＣ＝５，则点A到ＢＣ的距离是。

６、直线ａ上一点Ａ与ａ外一点Ｂ的距离是２，与ａ外一点Ｃ的距离为３，则点Ｂ到直线ａ的距离1d 与点Ｃ到直线ａ的距离2d 的关系是（ Ｄ ） Ａ、21d d < Ｂ、21d d = Ｃ、21d d > Ｄ、以上都有可能７、填空并在（ ）处填写理由，完成下列题目的解答。

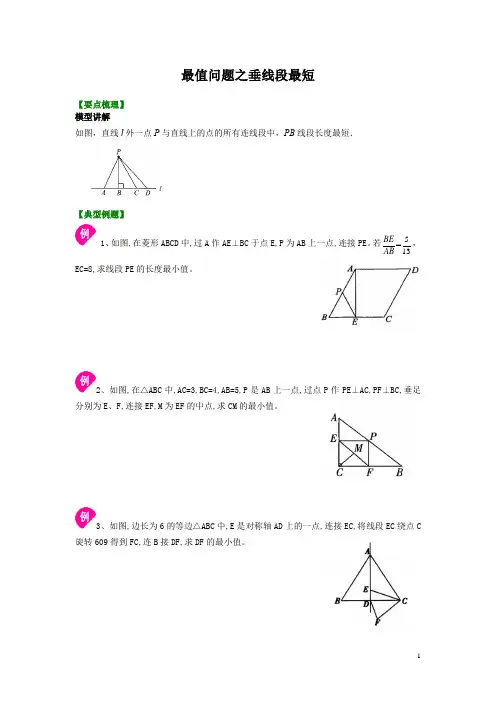
1最值问题之垂线段最短【要点梳理】模型讲解如图，直线l 外一点P 与直线上的点的所有连线段中，PB 线段长度最短．【典型例题】1、如图,在菱形ABCD 中,过A 作AE ⊥BC 于点E,P 为AB 上一点,连接PE 。

若5=13BE AB ，EC=8,求线段PE 的长度最小值。

2、如图,在△ABC 中,AC=3,BC=4,AB=5,P 是AB 上一点,过点P 作PE ⊥AC,PF ⊥BC,垂足分别为E 、F,连接EF,M 为EF 的中点,求CM 的最小值。

3、如图,边长为6的等边△ABC 中,E 是对称轴AD 上的一点,连接EC,将线段EC 绕点C 旋转609得到FC,连B 接DF,求DF 的最小值。

4、如图，线段AB的长为10，C为AB上的一个动点，分别以AC、BC为斜边在AB 的同侧作两个等腰直角△ACD和△BCE，求DE长的最小值。

5、已知点D与点A(8，0)，B(0，6)，C(a，－a)是一平行四边形的四个顶点，求CD 长的最小值。

【巩固练习】1、如图，在Rt△ABC中，∠BAC＝90°，AB＝5，AC＝12，P为边BC上一动点，PE⊥AB 于E，PF⊥AC于F，M为EF中点，则AM 的取值范围是．2、如图，已知平行四边形OABC的顶点A、C分别在直线x＝1和x＝4上，O是坐标原点，则对角线OB长的最小值为．23 3、在平面直角坐标系中，己知平行四边形ABCD 的点A (0，－2)、点B (3m ，4m ＋1)(m ≠－1)，点C (6，2)，则对角线BD 的最小值是 ．4、如图，等边△ABC 的边长是2cm ，将边AC 沿射线BC 的方向平移2cm ，得到线段DE ，连接AD 、CE ．(1)求证：四边形ACED 是菱形；(2)将△ABC 绕点C 旋转，当CA ′与DE 交于一点M ，CB ′与AD 交于一点N 时，点M 、N 和点D 构成△DMN ，试探究△DMN 的周长是否存在最小值？如果存在，求出该最小值；如果不存在，请说明理由．A'B'N M A B C D E。

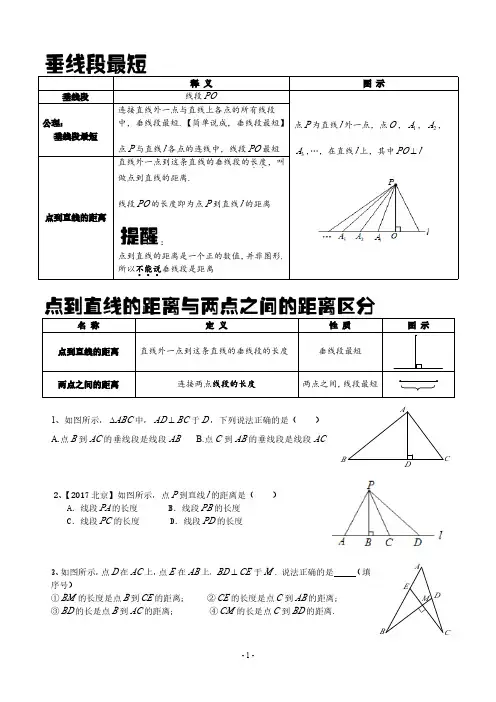
释义图示垂线段线段PO点P 为直线l 外一点，点O ，1A ，2A ，3A ，…，在直线l 上，其中l PO ⊥公理：垂线段最短连接直线外一点与直线上各点的所有线段中，垂线段最短.【简单说成，垂线段最短】点P 与直线l 各点的连线中，线段PO 最短点到直线的距离直线外一点到这条直线的垂线段的长度．．，叫做点到直线的距离.线段PO 的长度即为点P 到直线l 的距离：点到直线的距离是一个正的数值，并非图形，所以不能说．．．垂线段是距离名称定义性质图示点到直线的距离直线外一点到这条直线的垂线段的长度垂线段最短两点之间的距离连接两点线段的长度两点之间，线段最短ii1、如图所示，ABC ∆中，BC AD ⊥于D ，下列说法正确的是（）A.点B 到AC 的垂线段是线段ABB.点C 到AB 的垂线段是线段ACCABD2、【2017北京】如图所示，点P 到直线l 的距离是（）A．线段PA 的长度B．线段PB 的长度C．线段PC 的长度D．线段PD 的长度3、如图所示，点D 在AC 上，点E 在AB 上，CE BD ⊥于M .说法正确的是（填序号）①BM 的长度是点B 到CE 的距离；②CE 的长度是点C 到AB 的距离；③BD 的长是点B 到AC 的距离；④CM 的长是点C 到BD 的距离.CEM A BD4、点到直线的距离是（）A 、点到直线上一点的连线B 、点到直线的垂线C 、点到直线的垂线段D 、点到直线的垂线段的长度5、如图所示，︒=∠90AOB （1）、AB BO （填“>”，“<”或“=”），判断理由是（2）、若m OA 2=，cm OB 3=，则点A 到OB 的距离是cm ；点B 到OA 的距离是cm ；ABO6、如图，△ABC 中，∠C =90°，AC =3，点P 是边BC 上的动点，则AP 长不可能．．．是()A ．2.5B ．3C ．4D ．5P7、点P 为直线l 外一点，A 、B 、C 为直线l 上三点，cm PA 4=，cm PB 5=，cm PC 2=，则P 到直线l 的距离（）A．不小于2cm B．小于2cm C．不大于2cm D．不小于5cm 8、如图，点M ，N 分别在直线1l ，2l 上，画出三条线段，使它们的长分别是：（1）、M ，N 两点间的距离；（2）、点M 到直线2l 的距离；（3）、点N 到直线1l 的距离.∙MN∙1l 2l 9、如图，计划把河水引到水池A 中，先引CD AB ⊥，垂足为B ，然后沿AB 开渠，能使所开的渠道最短，这样设计的依据是_______________________________________.10、如图，修一条公路将村庄A ，B 与公路MN 连接起来，怎样修才能使所修的公路最短？画出线路图，并说明理由.A BM N∙∙答案：1、D 2、B ；3、①④4、D 5、（1）、>；垂线段最短；（2）、2；36、A7、C8、EF ∙M N∙1l 2l 答案：（1）、图中线段MN 为所求（2）、图中线段ME 为所求（3）、图中线段NF 为所求9、垂线段最短10、连接AB ，作MN BC ⊥于C ，沿AB ，BC 修公路长度最短.理由：①两点之间，线段最短；②垂线段最短A BCMN∙∙。

垂线段最短问题是一个经典的几何问题，也是数学中的重要知
识点之一。

下面是一个关于垂线段最短的压轴题，供您参考：
题目：在直角三角形ABC中，∠ACB=90°，CD⊥AB于D点，E
为CD的中点，延长BE交AC的延长线于点F。

求证：CF=CE。

证明：
第一步，由题意知，CD⊥AB于D点，E为CD的中点，所以
CE=ED。

第二步，因为∠ACB=90°，所以∠ACD+∠BCD=90°。

又因为
CD⊥AB，所以∠B+∠BCD=90°。

所以∠ACD=∠B。

第三步，由于∠ACD=∠B，并且∠ACF=∠BCD=90°，所以
△ACF∽△BCD。

因此，有CD/AF=BD/CF。

第四步，由于E是CD的中点，所以CE=ED=1/2CD。

又因为
BD=ED-BE=1/2CD-BE。

根据第二步得出的∠ACD=∠B和第三步的结论，我们有：CF=2BE。

综上，CF=2BE，且E是CD的中点，所以CF=CE。

垂线段最短的说理
垂线段最短，是说当从直线外一点到这条直线所画的线段中，垂线段是最短的。

这是因为垂线段是连接直线外一点与直线上各点的所有线段中最短的一条。

根据垂线段的性质，当两条线段都与同一条直线垂直时，较短的线段长度一定小于较长的线段长度。

因此，垂线段是最短的。

为了证明这个性质，我们可以考虑以下步骤：
第一步，设点A是直线L外一点，点B是直线L上的一点，从点A到直线L可以作无数条线段，其中垂线段AB是最短的。

第二步，假设存在另一条线段AC（AC>AB），且AC垂直于直线L于点C。

现在我们需要证明线段AB的长度小于或等于线段AC 的长度。

第三步，根据勾股定理，在直角三角形ABC中，有AB² = BC² + AC²。

如果AC>AB，那么AC² > AB²，进而BC² < AC² - AB²。

第四步，由于点C位于直线L上，所以BC的长度至少为d（d 为点B到直线L的最短距离），因此有BC² ≥ d²。

结合第三步的结论，我们得到d² < AC² - AB²，这意味着d < AC - AB。

第五步，由于d是点B到直线L的最短距离，所以d是所有点到直线L距离中最短的。

因此，我们有AB + d < AC。

第六步，由于AB是垂线段的长度，而AB + d < AC证明了垂线段的长度是最短的，所以我们可以得出结论：垂线段是最短的。

垂线段最短的生活实例垂线段是几何中的重要概念之一，它是指从一个点到一条直线之间的垂直线段。

垂线段最短的生活实例可以通过以下方式重新表述，以帮助我们更好地理解这个概念。

在我们日常生活中，可以将垂线段最短的实例应用到建筑和设计领域。

想象一下，你有一个长方形的房间需要安装一面镜子，你想确保镜子与墙壁之间的距离尽可能地短。

通过绘制与墙壁垂直的垂线段，你可以找到镜子和墙壁之间最短的距离，从而使设计看起来更加美观和整洁。

另一个生活中的实例是在农业中。

假设你是一个土地规划师，负责设计一片农田的种植布局。

为了最大程度地利用空间并提高农作物的产量，你需要找到每个农作物之间最短的距离。

通过绘制垂直于各条行与列的垂线段，你可以确定最短的距离，并合理安排农作物的种植。

此外，垂线段的概念也可以应用于交通规划中。

想象一下，在一个繁忙的路口，你想设计一个行人过街的最短路径。

通过在每个道路中心点绘制垂直线段，你可以找到行人从一条道路走到另一条道路的最短距离，从而优化交通流量和保证行人安全。

垂线段最短的生活实例还可以在地图定位和导航系统中应用。

当你使用或设计一个导航应用程序时，你希望找到从一个位置到另一个位置的最短路径。

通过绘制垂直于道路的垂线段，你可以找到导航的最短路径，选择最优路线并节省时间和成本。

总之，垂线段最短的生活实例在建筑、农业、交通规划和导航系统等领域都有重要的应用。

通过理解和应用垂线段的概念，我们可以优化设计和规划，提高效率，并最大程度地利用可用的资源。

所以，在我们日常生活中，垂线段最短的实例不仅是一个几何概念，而且是一个实用而有价值的工具。

利用垂线段最短解决最值问题模型一垂线段最短如图，已知直线l 外一定点A 和直线l 上一动点B，求A、B 之间距离的最小值 .通常过点A 作直线l 的垂线AB，利用垂线段最短解决问题，即连接直线外一点和直线上各点的所有线段中，垂线段最短．【典型例题】1.如图，在Rt△ABC 中，∠C＝90°，AD 是∠BAC 的平分线，点E 是AB 上任意一点．若AD＝5，AC＝4，则DE 的最小值为( )A. 3B. 4C. 5D. 6答案：A .当DE⊥AB 时，DE 最小，此时DE = CD，在Rt△ACD 中，根据勾股定理易得CD = 3 .2. 如图，在△ABC 中，AB＝AC＝5，BC 边上高AD＝4，若点P 在边AC 上( 不含端点) 移动，则BP 长的最小值为________．答案：24/5 .如图，延长CA，过点B 作BP'⊥CA 于点P'，此时BP' 的长最小 .在等腰△ABC 中根据“三线合一”的性质可知BD = CD = 3 ,S△ABC = 1/2 ×BP' ×AC = 1/2 ×AD ×BC，可得BP' = 24/5 . （等积求距）3. 如图，点A 坐标为(－2，0)，点B 在直线y＝x－4 上运动，当线段AB 最短时，点B 坐标为________．答案：（1，-3）.如图，当AB'⊥直线y＝x－4 时，此时线段AB 最短 .设直线AB' 的解析式为y = kx + b （k ≠0）,∵AB'⊥BB'，K BB' = 1，（KBB' 为直线y＝x－4 的斜率）∴K AB' ×K BB' = - 1 ，（两条直线垂直斜率乘积为-1）∴K AB' = - 1 ，即k = -1 ,∴直线AB' 的解析式为y = -x + b ,∵点A（-2,0）在直线AB' 上，∴0 = 2 + b , 解得b = -2 ,∴直线AB' 的解析式为y = -x - 2 .联立直线y = x - 4 , 解方程可得B'（1，-3）.模型二胡不归问题“胡不归”问题即点P 在直线l 上运动时的“PA＋k·PB ( 0 < k < 1 ) ”型最值问题 .问题：如图①，已知sin∠MBN＝k，点P 为∠MBN 其中一边BM 上的一个动点，点A 在射线BM、BN 的同侧，连接AP，则当“PA＋k·PB ”的值最小时，点P 的位置如何确定？解题思路：本题的关键在于如何确定“k·PB ”的大小 .过点P 作PQ⊥BN 于点Q，则k·PB＝PB·sin∠MBN＝PQ，∴可将求“PA＋k·PB ”的最小值转化为求“PA＋PQ ”的最小值( 如图②)，∴当A、Q、P 三点共线时，PA＋PQ 的值最小( 如图③)，此时AQ⊥BN .【典型例题】1. 如图，四边形ABCD 是菱形，AB＝6，且∠ABC＝60°，M 为对角线BD ( 不与点B 重合) 上任意一点，则AM＋1/2 BM 的最小值为________．答案：3√3 .如图，过A 点作AE⊥BC 于点E，交AB 于点M' ，则AM＋1/2 BM 的最小值为AE .在Rt△AEB 中，AB = 6，∠ABC = 60°，∴AE = AB ▪sin∠ABC = 6 ×√3 / 2 = 3√3 .拓展应用：对于求“m·PA＋k·PB”的最值，若m > k ≥1，可转化为“m ( PA + k/m ·PB ) ”的最值, 此时0< k/m < 1.(1) 本题若要求“2AM＋BM ”的最小值，你会吗？请求解．答案：6√3 .(2) 本题若要求“AM＋BM＋CM”的最小值，你会吗？请求解．答案：6√3 .AM＋BM＋CM 最小时，此时点M 为△ABC 的“费马点”，所以AM＋BM＋CM = BD = 2 ×√3 / 2 ×6 = 6√3 .2. 如图，在平面直角坐标系中，二次函数y＝ax2 + bx＋c 的图象经过点A(－1，0)、B(0，－√3 )、C(2，0)，其对称轴与x 轴交于点D .若P 为y 轴上的一个动点，连接PD，则1/2 PB＋PD 的最小值为_______．答案：3√3 / 4 .如图1/2 PB＋PD = PD + 1/2 PB 的最小值为DE，则∠PBE = 30°，可解得DE = 3√3 / 4 .。

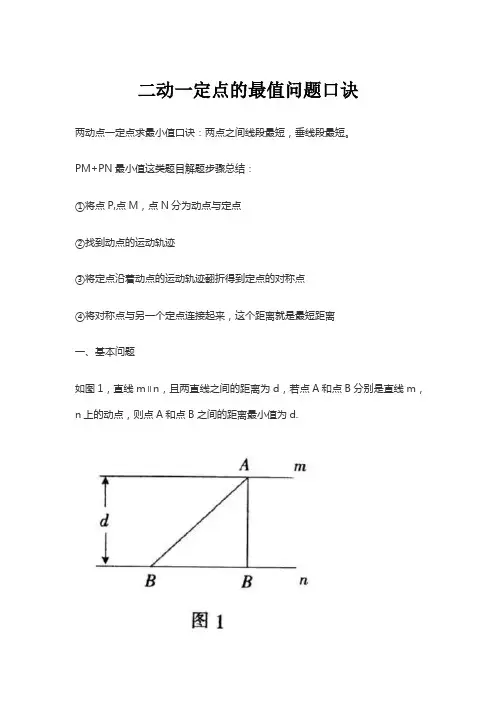
二动一定点的最值问题口诀
两动点一定点求最小值口诀：两点之间线段最短，垂线段最短。

PM+PN最小值这类题目解题步骤总结：
①将点P,点M，点N分为动点与定点
②找到动点的运动轨迹
③将定点沿着动点的运动轨迹翻折得到定点的对称点
④将对称点与另一个定点连接起来，这个距离就是最短距离
一、基本问题
如图1，直线m∥n，且两直线之间的距离为d，若点A和点B分别是直线m，n上的动点，则点A和点B之间的距离最小值为d.
解析：根据运动的相对性，不妨固定点A，则问题就变成了直线n外有一定点A到直线n上一动点B的距离最短问题.根据“垂线段最短”可知，当AB⊥直线n时，线段AB最短，此时，点A
和点B之间的距离最小值即为直线m和直线n之间的距离，即d.
二、应用
例1 如图2，在RT⊿ABC中，∠B=90°,AB=4,BC＞AB，点D在BC边上，在以AC
为对角线的平行四边形ADCE中，试求DE长的最小值.
解析由四边形ADCE为平行四功形可知，AE∥BC，且两平行线间的距离为AB 的长，即点D
和点E可看作两平行线上的各一动点，因此，当DE垂直于BC时，DE的长取得最小值，其最小值为4。

方法一：利用几何性质解决问题知识点1：垂线段最短（点到直线的距离，垂线段最短）知识点2：两点之间线段最短（即“将军饮马”问题）知识点3：利用“画圆”来确定动点问题解决最值问题运用画圆解决问题有两种情况：情况1：动点到某一定点的距离是定值（圆上的点到圆心的距离恒等于半径）情况2：动点为90°固定角的顶点（直径所对的圆周角恒定为90°）在中考中最常用的是“知识点2”、“知识点3”方法二：利用代数法直接证明知识点1：利用配方法求三次二项式的最值知识点2：运用二次函数中顶点求最值代数方法较为常见，所以我们本篇暂时不会涉及.接下来，我们来简单看一下每个几何知识点对应的问题知识点1：垂线段最短常出现几何图形问题中，通常在初二会见到，中考中不会涉及。

例：如图，在△ABC中有一点D在AC上移动，若AB=AC=5，BC=6则AD+BD+CD的最小值为_______.分析:题目中问“AD+BD+CD”的最小值，通过图形我们可以知道“AD+CD”是定值，所以问题可以转换为求BD的最小值.那么求BD的最小值即为求一点B到某一直线AC上的最小值，所以可以利用“垂线段最短”的性质来求解.过点B作AC垂线即可解决问题.知识点2：两点之间线段最短这类问题常出现在函数的大题中，考生如果函数知识不过关也不能拿到满分，因为仅作出图形别不能得出答案，还需要利用函数知识进行求点坐标.解题思路：通常做定点关于动点所在直线的对称点（两个动点所在直线就做两个对称点），然后连接对称点与另一点与动点所在直线的交点即为动点位置。

例1.如图，在直角坐标系中，点A、B的坐标分别为（1，3）和（2，0），点C是y轴上的一个动点，且A、B、C三点不在同一条直线上，当△ABC的周长最小时，点C的坐标是______.分析：典型的“将军饮马”问题。

通过作点B关于y轴的对称点即可解决问题.例2：如图所示，直线y=x+2与两坐标轴分别交于A、B两点，点C 是OB的中点，D、E分别是直线AB、y轴上的动点，则△CDE周长的最小值是_______.分析：本题中存在两个动点，分别是点D、点E所以我们只需要做点C关于直线AB、关于y轴的对称点即可解决问题.知识点3：利用“画圆”来确定动点问题解决最值问题例1：如图，在Rt△ABC中，∠ACB=90°，AC=4，BC=6，点D是边BC的中点，点E是边AB上的任意一点（点E不与点B重合），沿DE翻折△DBE使点B落在点F处，连接AF，则线段AF长的最小值是________.分析：由翻折得到，DF=DB=3.所以点F在以点D为圆心以3为半径的圆上.连接A与圆心D，AD与圆的交点即为F'所以AF的最小值是AD-DF'=5-3=2.例2：如图，E，F是正方形ABCD的边AD上两个动点，满足AE=DF．连接CF交BD于点G，连接BE交AG于点H．若正方形的边长为2，则线段DH长度的最小值是________.分析：根据正方形的性质可得AB=AD=CD，∠BAD=∠CDA，∠ADG=∠CDG，然后利用“边角边”证明△ABE和△DCF全等，根据全等三角形对应角相等可得∠1=∠2，利用“SAS”证明△ADG和△CDG 全等，根据全等三角形对应角相等可得∠2=∠3，从而得到∠1=∠3，然后求出∠AHB=90°.所以点H在以AB为直径的圆上，所以以AB中点为圆心，以AB长的一半为半径画圆，连接D与圆心交点即为点H.所以DH'=OD-OH'中考中常见的求最值方法就是上面所提到的这些。

垂线段最短的生活实例
一个常见的生活实例是人们在建筑和设计中使用垂线段来确定墙壁或其他垂直结构的最短距离。

考虑以下情况：
假设有一块矩形的土地，上面有一栋建筑物和一棵高大的树。

你想要在土地上建造一堵围墙，使建筑物和树都位于围墙内部。

但是你希望围墙离建筑物和树的最近距离尽可能短。

在这种情况下，你可以使用垂线段来找到围墙与建筑物和树之间的最短距离。

首先，在建筑物和树的底部各设置一个垂直线。

然后，通过将围墙的一端连接到这两个垂直线上，使围墙与建筑物和树相接。

围墙与建筑物和树之间的连接线就是垂线段。

因为垂线段是垂直于建筑物和树的，所以它代表了围墙离这两个物体的最短距离。

这样设计的围墙可以最大限度地减少占地面积，同时确保建筑物和树都位于围墙内部。

通过使用垂线段来确定围墙与建筑物和树之间的最短距离，你可以在建筑和设计中实际应用几何原理，达到最优的空间利用效果。

这是一个生活中常见的例子，展示了垂线段最短的应用。

1/ 1。

四年级数学垂线段最短的练习题垂线段是数学中的一个重要概念，它在几何图形中起着重要的作用。

在本篇文章中，我将为大家带来一些关于垂线段最短的练习题。

通过解决这些题目，可以加深对垂线段概念的理解，并提高解决问题的能力。

一、直角三角形的垂线段问题1. 题目描述：在一个直角三角形ABC中，已知AB=3cm，AC=4cm。

请你求出从点B到AC边的垂线段BD的最短长度。

解题思路：在直角三角形中，垂线段的最短长度恰好是从顶点到斜边的垂直距离。

根据勾股定理，我们可以计算出斜边的长度。

然后，利用面积公式和底边长度，求出垂线段的最短长度。

解答：首先，根据勾股定理，可以计算出斜边BC的长度：BC² = AB² + AC²BC² = 3² + 4²BC² = 9 + 16BC² = 25BC = √25BC = 5cm然后，利用三角形面积公式计算出三角形ABC的面积：S = 1/2 × AB × ACS = 1/2 × 3 × 4S = 6cm²最后，根据面积公式和底边长度，求出垂线段BD的最短长度：BD = 2 × S / BCBD = 2 × 6 / 5BD = 12 / 5BD = 2.4cm所以，从点B到AC边的垂线段BD的最短长度为2.4cm。

二、等边三角形的垂线段问题2. 题目描述：在一个边长为6cm的等边三角形ABC中，点D是边AC的中点，请你求出从点D到BC边的垂线段DE的最短长度。

解题思路：在等边三角形中，垂线段的最短长度恰好是从顶点到底边的垂直距离。

由于等边三角形的底边是边长为6cm，而且点D是边AC的中点，垂线段DE的最短长度可以通过简单计算得到。

解答：由于等边三角形的三条边长度相等，所以边BC的长度也为6cm。

由于点D是边AC的中点，所以垂线段DE的长度等于边BC的一半。