图形的轴对称与中心对称

轴对称图形与中心对称图形一、轴对称1.轴对称图形定义：如果一个图形沿着一条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形。

折痕所在的直线叫做对称轴。

2.两个图形成轴对称：对于两个图形来说，如果沿一条直线对折后，它们能完全重合，那么称这两个图形成轴对称，这条直线就是对称轴。

3.关键知识点：①轴对称是说两个图形的位置关系；而轴对称图形是说一个具有特殊形状的图形。

②成轴对称的两个图形，必定是全等图形。

4.轴对称的性质：对应点所连的线段被对称轴垂直平分；对应线段相等；对应角相等。

5.简单的轴对称作图：求作一个几何图形关于某条直线对称的图形，可以转化为求作这个图形上的特征点关于这条直线对称的点。

后依次连结各特征点即可。

二、中心对称图形1.定义：把一个图形绕着某一点旋转180°，如果它能与另一个图形重合，那么就说这两个图形关于这个点对称或中心对称。

2.中心对称和中心对称图形中心对称：如果把一个图形绕某一点旋转180度后能与另一个图形重合，这两个图形成中心对称。

中心对称图形：如果把一个图形绕某一点旋转180度后能与自身重合，这个图形是中心对称图形。

3.性质a.关于中心对称的两个图形是全等形。

b.关于中心对称的两个图形，对称点连线都经过对称中心，并且被对称中心平分。

c.关于中心对称的两个图形，对应线段平行（或者在同一直线上）且相等。

三、图案的分析与设计① 首先找到基本图案，然后分析其他图案与它的关系，即由它作何种运动变换而形成。

② 图案设计的基本手段主要有：轴对称、平移、旋转三种方法。

专项练习轴对称与中心对称图形的概念：轴对称是指在平面内，如果一个图形沿一条直线折叠，直线两旁的部分能够完全重合，这样的图形叫做轴对称图形。

中心对称图形是指平面内，如果把一个图形绕某个点旋转180°后，能与自身重合，那么就说这两个图形关于这个点成中心对称。

1、（2013年潍坊市）下面的图形是天气预报中的图标，其中既是轴对称图形又是中心对称图形的是（ ）.A.B.C.D. BA ．B ．C ．D ．4、（2013四川南充，7，3分）有五张卡片（形状、大小、质地都相同），上面分别画有下列图形：①线段；②正三角形；③平行四边形；④等腰梯形；⑤圆。

轴对称与中心对称图形图形在数学中扮演着重要的角色，我们常常通过图形来进行分析和研究。

其中，轴对称和中心对称是两种常见的图形特征，本文将对这两种特征进行深入探讨。

一、轴对称图形轴对称图形是指具有轴对称特点的图形。

轴对称意味着图形可以通过一个轴进行镜像对称，即图形和其镜像重合。

简单来说，轴对称图形是左右完全对称的，即使折叠图形，两边也完全相同。

轴对称图形具有以下特点：1. 存在轴线：轴对称图形一定存在轴线，该轴线可以是垂直、水平或倾斜的。

2. 镜像关系：图形沿轴线进行折叠后，两侧完全对称。

3. 完全对称：图形的任意一点关于轴线，其对应点均重合于图形上。

常见的轴对称图形有正方形、长方形、圆形等。

这些图形的特点是左右对称，通过图形中的轴线可以轻松确定这些图形是否轴对称。

例如，对于一个正方形，通过从中心点绘制两条垂直、水平的轴线，可以发现图形可以完全折叠。

二、中心对称图形中心对称图形是指图形具有中心对称性质的图形。

中心对称意味着图形可以通过一个中心点进行旋转180度，使得旋转后的图形与原图形完全一致。

中心对称图形具有以下特点：1. 存在中心点：中心对称图形一定存在中心点，该中心点可以位于图形内部或边界上。

2. 旋转180度：图形绕中心点旋转180度后，与原图形完全一致。

3. 完全一致：图形的任意一点关于中心点，其对应点均重合于图形上。

常见的中心对称图形有正五边形、正六边形等。

这些图形的特点是任意一点到中心点的距离相等，并且旋转180度后的图形与原图形完全相同。

总结：轴对称和中心对称是图形的重要特征，通过观察和分析图形的对称性质，可以更好地理解图形的形态和结构。

轴对称图形以左右对称为主要特点，而中心对称图形以中心旋转180度为主要特点。

研究和了解这些对称性质，有助于我们更深入地理解数学中的图形学知识。

通过对轴对称和中心对称图形的介绍，我们可以更好地理解图形的形态和特点。

图形学是数学中的重要分支，通过研究图形的特征和性质，我们可以将其应用于各个领域，如几何学、计算机图形学等。

什么是中心对称图形中心对称：在平面内，把一个图形绕着某个点旋转 180° ,如果旋转后的图形与另一个图形重合，那么就说明这两个图形的形状关于这个点成中心对称 (Central of symmetrygraph)，这个点叫做它的 对称中心(Center of symmetry )，旋转180°后重合的两个点叫做 对 称点(corresponding points )。

理解中心对称的定义要抓住以下三个要素： (1 )有一个对称中心 一一点； (2 )图形绕中心旋转 180° ； (3)旋转后两图形重合. 中心对称的性质：连接中心对称图形上每一对对称点的线段都经过对称中心，且被对称中心平分 中心对称图形：在平面内，把一个图形绕着某个点旋转 180。

，如果旋转后的图形能与原来的图形重合，那么这个图形叫做 中心对称图形，这个点叫做它的 对称中心.旋转180°后重合的两个点叫做对应点(corresp onding poi nts)。

① 对称中心平分中心对称图形内通过该点的任意线段且使中心对称图形的面积被平分 (对称点在中心对称图形中)。

② 成中心对称的两个图形全等。

③ 中心对称图形上每一对对称点所连成的线段都被对称中心平分。

区分：中心对称是两个图形间的位置关系，而中心对称图形是一种具有独特特征的图 形。

中心对称图形常见图形常见的中心对称图形有：线段，矩形，菱形，正方形，平行四边形，圆，边数为偶数的正多边形，某些不规则图形等。

正偶边形是中心对称图形正奇数边形不是中心对称图形※正六角形是中心对称图形，等腰梯形不是中心对称图形，等边三角形(正三角形)，至少需旋转120度，而不是180度，所以它不是中心对称图形。

反比例函数的图像双曲线是以原点为对称中心的中心对称图形什么是轴对称图形如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形(axial symmetric figure)，这条直线叫做对称轴(axis of symetric);这时，我们也说这个图形关于这条直线对称。

轴对称图形、中心对称图形的基本概念轴对称图形的定义如果一个图形沿着一条直线对折，两侧的图形能完全重合，这个图形就是轴对称图形。

轴对称图形的性质1）如果沿某条直线对折，对折的两部分是完全重合的，那么就称这样的图形为轴对称图形，这条直线叫做这个图形的对称轴。

（对于一个图形来说）（2）把一格图形沿着某一条直线翻折过去，如果它能够与另一个图形重合，那么就说这两个图形成轴对称。

这条直线就是对称轴。

两个图形中的对应点（即两个图形重合时互相重合的点）叫做对称点。

（对于两个图形来说）（3）轴对称图形（或关于某条直线对称的两个图形）的对应线段相等，对应角相等。

中心对称的定义：把一个图形绕着某一点旋转180°，如果它能与另一个图形重合，那么就说这两个图形关于这个点对称或中心对称（central symmetry），这个点叫做对称中心，这两个图形的对应点叫做关于中心的对称点。

中心对称的性质：①于中心对称的两个图形是全等形。

②关于中心对称的两个图形，对称点连线都经过对称中心，并且被对称中心平分。

③关于中心对称的两个图形，对应线段平行（或者在同一直线上）且相等。

识别一个图形是否是中心对称图形就是看是否存在一点，使图形绕着这个点旋转180°后能与原图形重合。

中心对称是指两个图形绕某一个点旋转180°后，能够完全重合，这两个图形关于该点对称，该点称为对称中心.二者相辅相成，两图形成中心对称，必有对称中点，而点只有能使两个图形旋转180°后完全重合才称为对称中点。

既是轴对称图形又是中心对称图形的有：直线，线段，两条相交直线，矩形，菱形，正方形，圆等．只是轴对称图形的有：射线，角等腰三角形，等边三角形，等腰梯形等．只是中心对称图形的有：平行四边形等．既不是轴对称图形又不是中心对称图形有：不等边三角形，非等腰梯形等．。

轴对称与中心对称轴对称和中心对称是几何学中常用的概念，用来描述图形的对称性质。

它们在数学、物理、工程等领域中都有广泛的应用。

本文将介绍轴对称和中心对称的定义、性质以及一些实际应用。

轴对称的概念是指图形相对于某一条线对称，即图形绕某条线旋转180度后，仍能与原来的图形完全重合。

这条线被称为对称轴。

举个例子，我们可以想象一张纸上画了一个直角三角形，如果我们将纸沿着三角形的斜边对折，那么对折后的纸与原来的纸完全重合，这说明三角形是关于对称轴对称的。

中心对称是指图形相对于某一点对称，即图形绕某一点旋转180度后，仍能与原来的图形完全重合。

这个点被称为对称中心。

一个简单的例子是正方形，当我们将正方形绕着其中心旋转180度后，它仍然与原来的正方形完全一样。

轴对称和中心对称在几何学中有一些重要的性质。

首先，它们都是自反的，即一个图形关于对称轴或对称中心对称的话，它自身也是对称的。

其次，轴对称和中心对称都是可传递的，即如果图形A关于对称轴或对称中心对称，图形B关于同样的轴或中心对称，那么图形A 和图形B之间也是对称的。

轴对称和中心对称的应用非常广泛。

在艺术和设计领域，许多作品都利用了对称的美感。

建筑设计中，对称结构可以使建筑更加稳定和美观。

在化学领域，分子的对称性对于分子的性质和反应有着重要的影响。

在物理学中，对称性是研究物理定律和现象的基础。

总结起来，轴对称和中心对称是几何学中常用的概念，用来描述图形的对称性质。

它们有着自反性和传递性的特点，广泛应用于各个领域。

通过研究轴对称和中心对称，我们可以更深入地理解和应用几何学的知识。

什么是中心对称图形中心对称:在平面内，把一个图形绕着某个点旋转180°，如果旋转后的图形与另一个图形重合,那么就说明这两个图形的形状关于这个点成中心对称（Central of symmetry graph），这个点叫做它的对称中心(Center of symmetry）,旋转180°后重合的两个点叫做对称点（corresponding points)。

理解中心对称的定义要抓住以下三个要素：（1)有一个对称中心——点；(2）图形绕中心旋转180°；(3）旋转后两图形重合．中心对称的性质：连接中心对称图形上每一对对称点的线段都经过对称中心，且被对称中心平分中心对称图形：在平面内，把一个图形绕着某个点旋转180°，如果旋转后的图形能与原来的图形重合，那么这个图形叫做中心对称图形，这个点叫做它的对称中心。

旋转180°后重合的两个点叫做对应点(corresponding points）.中心对称图形性质①对称中心平分中心对称图形内通过该点的任意线段且使中心对称图形的面积被平分（对称点在中心对称图形中）。

②成中心对称的两个图形全等。

③中心对称图形上每一对对称点所连成的线段都被对称中心平分。

区分：中心对称是两个图形间的位置关系,而中心对称图形是一种具有独特特征的图形。

常见图形常见的中心对称图形有：线段,矩形，菱形，正方形，平行四边形，圆,边数为偶数的正多边形，某些不规则图形等.正偶边形是中心对称图形正奇数边形不是中心对称图形※正六角形是中心对称图形,等腰梯形不是中心对称图形,等边三角形（正三角形），至少需旋转120度,而不是180度，所以它不是中心对称图形.反比例函数的图像双曲线是以原点为对称中心的中心对称图形什么是轴对称图形如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形（axial symmetric figure），这条直线叫做对称轴(axis of symetric);这时,我们也说这个图形关于这条直线对称。

初中数学知识归纳中心对称与轴对称初中数学知识归纳：中心对称与轴对称中心对称（Symmetry with a Center）是几何学中的重要概念之一，也是初中数学中需要重点掌握的知识之一。

它描述了一个图形在某个点上：关于这个点对称时，图形的两侧完全一致。

而轴对称（Symmetry with an Axis）是另一个重要的概念，描述了一个图形以某条线为对称轴时，图形的两侧完全一致。

下面将对中心对称与轴对称进行详细的归纳。

一、中心对称中心对称是指图形关于一个点对称时，图形的两侧完全相同。

具体来说，对于一个点O，如果图形上的每个点P，都能找到另一个点P'，使得OP与OP'重合，并且P'在点O的对称位置上，那么图形就是关于点O中心对称的。

中心对称的特点有：1. 对称中心是唯一的。

2. 关于中心对称的图形的每个点到中心的距离相等。

3. 对称中心是图形的一个内部点。

常见的中心对称图形有：1. 圆形：圆是一种最简单的中心对称图形。

它的所有点到圆心的距离相等，因此每个点都能找到另一个点，使得它们关于圆心对称。

2. 正方形：正方形是一个有四条等长边和四个直角的图形。

它的中心即为正方形的对称中心。

3. 六边形：同样是一个有六条边的图形，如果可以找到合适的点作为对称中心，使得六边形的两侧完全一致，那么它就是中心对称的。

中心对称在现实生活中有广泛应用。

例如，许多雪花的形状都是中心对称的，许多建筑物的外观也采用了中心对称的设计。

二、轴对称轴对称是指图形关于一条直线对称时，图形的两侧完全相同。

具体来说，对于一条直线l，如果图形上的每个点P，都能找到另一个点P'，使得P'在l上，并且P和P'关于l对称，那么图形就是关于直线l轴对称的。

轴对称的特点有：1. 对称轴是唯一的。

2. 关于轴对称的图形的每个点到直线的距离相等。

3. 对称轴是图形的一个内部线。

常见的轴对称图形有：1. 正圆：正圆是一个最简单的轴对称图形。

轴对称图形在平面内，如果一个图形沿一条直线折叠，直线两旁的部分能够完全重合，这样的图形叫做轴对称图形（axial symmetric figure)，这条直线叫做对称轴(axis of symmetric)，并且对称轴用点画线表示；这时，我们也说这个图形关于这条直线对称。

比如圆、正方形、等腰三角形、等边三角形、等腰梯形等。

例如等腰三角形、正方形、等边三角形、等腰梯形和圆和正多边形都是轴对轴对称图形2 示例称图形.圆有无数条对称轴，都是经过圆心的直线。

要特别注意的是线段，它有两条对称轴，一条是这条线段所在的直线,另一条是这条线段的中垂线。

大写字母A、B、C、D、E、H等等性质编辑1.对称轴是一条直线。

2.在轴对称图形中，对称轴两侧的对应点到对称轴两侧的距离相等。

3.在轴对称图形中，沿对称轴将它对折，左右两边完全重合。

4.如果两个图形关于某条直线对称，那么这条直线就是对称轴且对称轴垂直平分对称点所连线段。

5.图形对称。

定理定理1：关于某条直线对称的两个图形是全等形。

定理2：如果两个图形关于某条直线对称，那么对称轴是对应点连线的垂直平分线。

定理3：两个图形关于某条直线对称，如果对称轴和某两条对称线段的延长线相交，那么交点在对称轴上。

定理3的逆定理：如果两个图形的对应点连线被同一条直线垂直平分，那么这两个图形关于这条直线对称。

生活作用1、为了美观。

比如天安门，对称就显的美观漂亮。

2、保持平衡。

比如飞机的两翼。

3、特殊工作的需要。

比如五角星，剪纸。

对称方法编辑方法1、找出所给图形的关键点。

2、找出图形关键点到对称轴的距离。

3、找关键点的对称点。

4、按照所给图形的顺序连接各点。

画法1、找出图形的一对对称点。

2、连接对称点。

3、过这条线段的中点作这条线段的垂线。

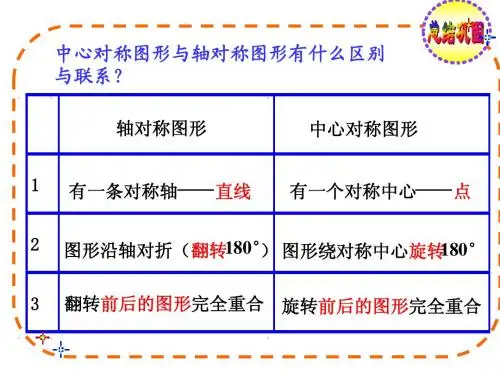
区别区分这两个概念要注意：轴对称图形一定要沿某直线折叠后直线两旁的部分互相重合，关键抓两点：一是沿某直线折叠，二是两部分互相重合；中心对称图形是图形绕某一点旋转180°后与原来的图形重合，关键也是抓两点：一是绕某一点旋转，二是与原图形重合。

轴对称与中心对称轴对称和中心对称是几何学中常见的两种对称性形态。

它们在不同的对象和场景中都有广泛的应用，无论是在数学中的几何学还是在现实生活中的设计中，都扮演着重要的角色。

本文将介绍轴对称和中心对称的概念、特点以及应用，并通过实例展示其在实际生活中的具体应用。

一、轴对称轴对称就是以某条直线为轴，对称图形的一种对称形态。

在轴对称中，图形的一部分与其余部分关于轴线对称，即对称图形的每一点在轴线上的投影到对称图形的另一侧都保持相等距离。

轴对称的特点是对称形态关于中心轴线对称，具有镜像对称性。

这种对称形态常见于图形的设计中，尤其是时钟面、树叶、汽车对称等。

轴对称能够给人以和谐、稳定、平衡的感觉，因此在设计中被广泛应用。

例如，时钟面上的数字通常被设计成轴对称的形态，这样一来无论是数字“6”还是数字“9”，只需要沿着钟面的某条轴线翻折即可得到对称的结果。

这种设计不仅美观，还使得人们在观看时能够迅速辨认出时间。

二、中心对称中心对称即以某一点为中心，对称图形的一种对称形态。

在中心对称中，对称图形的每一点都对称于以中心点为对称中心的另一点，即对称位置上的点到中心点的距离保持相等。

中心对称的特点是对称形态关于中心点对称，具有旋转对称性。

这种对称形态常见于自然界中的一些对象，如花朵、雪花、生物身体结构等。

中心对称能够给人以和谐、优美、自然的感觉，因此在艺术和设计中被广泛运用。

例如，花朵的形态通常呈现出中心对称的特点。

以玫瑰花为例，花瓣的排列呈现出以花心为中心的旋转对称，使得整个花朵看起来美丽而有序。

这种对称性不仅使花朵具有视觉上的吸引力，还让人们在欣赏花朵时感受到一种和谐与平衡。

三、轴对称与中心对称的应用轴对称和中心对称的应用非常广泛，涉及到多个领域和行业。

以下将分别介绍它们在数学、艺术和设计、自然界以及日常生活中的应用。

1. 数学领域轴对称和中心对称是数学几何学中的重要概念，常被用于分析和描述图形的形态特征。

通过研究轴对称和中心对称的性质，可以进一步深入理解几何学的基本原理，并应用于解决实际问题。