当前位置：文档之家 › 高中数学人教版必修课件：§圆与圆的位置关系

高中数学人教版必修课件：§圆与圆的位置关系

  • 格式：pptx
  • 大小：697.62 KB
  • 文档页数：33

下载文档原格式

  / 33

合集下载

高中数学课件-2 2圆与圆的位置关系(共25张PPT)

高中数学课件-2 2圆与圆的位置关系(共25张PPT)
解法一：把圆C1和圆C2的方程化为标准方程：
C1 : ( x 1)2 ( y 4)2 52 C1的圆心(1,4), 半径为r1 5 C2 : (x 2)2 ( y 2)2 ( 10)2 C2的圆心(2, 2),半径为r2 10
连心线长为 (1 2)2 (4 2)2 3 5
r O2
R
r
O
O
1
2
外离 O1O2>R+r
外切 O1O2=R+r
相交 │R-r│<O1O2<R+r
O
1
R
Or
2
R
O
1
Or
2
R
O Or
12
内切
内含
同心圆 (一种特殊的内含)
O1O2=│R-r│ 0≤O1O2<│R-r│ O1O2=0
圆与圆的位置关系转化为圆心距d与R+r、|R-r|关系
圆与圆的位置关系的判定方法二（代数法）：
弦长公式为| AB | 2 r2 d2
例题(变式）：已知圆 C1 : x2 y2 2x 8y 8 0 与圆 C2 : x2 y 2 4x 4 y 2 0
试求两圆公共弦长
解：联立两圆方程得方程组源自x2 y2 2x 8y 8 0 ①
x
2
y2
4x
4
y
2
0
②
①-②得
x 2y 1 0 ③
把上式代入① x2 2x 3 0 解得x1 1, x2 3
x1 y1
1 ,
1
x2 y2
3 1
所以交点A,B坐标分别为（-1,1），（3，-1)
思考3:
已知两圆C1：x2+y2+D1x+E1y+F1=0 和C2：x2+y2+D2x+E2y+F2=0相交，

2-5-2圆与圆的位置关系课件-高中数学人教A版选择性必修第一册

2-5-2圆与圆的位置关系课件-高中数学人教A版选择性必修第一册
第二章直线和圆的方程
2.5 直线与圆、圆与圆的位置关系 2.5.2 圆与圆的位置关系
数学
学习指点 1.能根据给定圆的方程，判断圆与圆 的位置关系.
2.能用直线和圆的方程解决一些简单 的问题，体会用代数方法处理几何问 题的思想.
核心素养
1.数学抽象、数学运算：圆与 圆的位置关系的判断. 2.直观想象、数学运算：两圆 相交及相切的问题.
1. 圆O₁ :x²+y²-4y+3=0 与圆O₂ :x²+y²—16y=0 的位置关系是( )
A. 相离
B. 相交
C. 相 切
D . 内含
解析：因 为O₁ (0,2),r₁=1,O₂ (0,8),r₂=8,|O₁O₂I=
(0 — 0)²+(2 - 8)²=6,则 |O₁O₂I<r₂—r₁, 所以两圆内含.
即两圆的公共弦长 ●
(1)两圆相交时，公共弦所在的直线方程
若圆C₁:x²+y²+D₁x+E₁y+F₁=0
与圆C₂:x²+y²+D₂x+E₂y+F₂=0 相
交，则两圆公共弦所在直线的方程为(D₁-D₂)x+ (E₁ 一E₂)y+F₁-F₂=0.
(2)圆系方程
一般地过圆C₁:x²+y²+D₁x+E₁y+F₁=0 与圆C₂:x²+y²+D₂x+E₂y+ F₂=0 交点的圆的方程可设为：x²+y²+D₁x+E₁y+F₁+λ(x²+y²+D₂x+
探究点1 圆与圆位置关系的判断 [问题探究] 根据代数法确定两个圆的位置关系时，能否准确得出两圆的位置关系? 提示：不能，如两圆方程组成的方程组有一组解，两圆外切或内切.

人教版新课标高中数学圆和圆的位置关系 (共30张PPT)教育课件

人教版新课标高中数学圆和圆的位置关系 (共30张PPT)教育课件

: 其实兴趣真的那么重要吗？很多事情我 们提不 起兴趣 可能就 是运维 我们没 有做好 。想想 看，如 果一件 事情你 能做好 ，至少 做到比 大多数 人好， 你可能 没有办 法岁那 件事情 没有兴 趣。再 想想看 ，一个 刚来到 人世的 小孩， 白纸一 张，开 始什么 都不会 ，当然 对事情 开始的 时候也 没有 兴趣这 一说了 ，随着 年龄的 增长， 慢慢的 开始做 一些事 情，也 逐渐开 始对一 些事情 有兴趣 。通过 观察小 孩的兴 趣，我 们可以 发现一 个规律 ，往往 不是有 了兴趣 才能做 好，而 是做好 了才有 了兴趣 。人们 总是搞 错顺序 ，并对 错误豪 布知晓 。尽管 并不绝 对是这 样，但 大多数 事情都 需要熟 能生巧 。做得 多了， 自然就 擅长了 ；擅长 了，就 自然比 别人做 得好； 做得比 别人好 ，兴趣 就大起 来，而 后就更 喜欢做 ，更擅 长，更 。。更 良性循 环。教 育小孩 也是如 此，并 不是说 买来一 架钢琴 ，或者 买本书 给孩子 就可以 。事实 上，要 花更多 的时间 根据孩 子的情 况，选 出孩子 最可能 比别人 做得好 的事情 ，然后 挤破脑 袋想出 来怎样 能让孩 子学会 并做到 很好， 比一般 人更好 ，做到 比谁都 好，然 后兴趣 就自然 出现了 。
线是两圆公共弦 AB所在的直线
①-②得
y
x2y10 ③
探究：画出圆C1与圆 C2以及直线方程③ ， 你发现了什么？
A
O
C2 Bx
C1
题型 与两圆公共弦有关的问题 例3:已知圆C1:x2+y2+2x-6y+1=0,圆C2:x2+y2-
4x+2y-11=0.求两圆的公共弦所在的直线方程 及公共弦长.

2.5圆与圆的位置关系课件-人教A版高中数学选择性必修第一册

2.5圆与圆的位置关系课件-人教A版高中数学选择性必修第一册
因为d=r₁+r₂,所以两圆外切. ②将两圆的方程化为标准方程，得(x+3)²+y²=16,x²+(y+3)²=36, 故两圆的半径分别为r₁=4和r₂=6. 两圆的圆心距 d=J[o-(-3)]²+(-3-O)²=3√Z,因为Ir1-r₂I<d<ri+r2,所以两圆相交
新教材新高 考
典例解析
新教材 新
解得 故圆心为
,半径为
故圆的方程为
即x²+y²-x+7y-32=0.
(方法2)设所求圆的方程为x²+y²+6x-4+λ(x²+y²+6y-28)=0(λ≠-1),
其圆心为
,代入x-y-4=0,解得λ=-7.
故所求圆的方程为x²+y²-x+7y-32=0.
新教材新高
归纳总结
新教材 新 高
相交弦及圆系方程问题的解决 1.求两圆的公共弦所在直线的方程的方法：将两圆方程相减即得两圆公共弦 所在直线方程，但必须注意只有当两圆方程中二次项系数相同时，才能如此求
.m+c=5-2=3.
答案：3
典例解析
例 3求与圆x²+y²-2x=0外切且与直线x+ √3y=0相切于点M(3,-√3) 的圆的方程.
新教材新
思路分析：设圆的方程，利用两圆外切和直线与圆相切建立方程组求得.
解：设所求圆的方程为(x-a)²+(y-b)²=r² (r>0),
由题知所求圆与圆x²+y²-2x=0外切，
解析：:x²+y²=a表示一个圆， .∴a>0. 两圆的圆心、半径长分别为(0,0), √a与(-3,4),6. 由于两圆内切，则

人教A版 必修二 第4章 2 42 圆与圆的位置关系 公开课一等奖课件

人教A版 必修二 第4章 2 42 圆与圆的位置关系 公开课一等奖课件
2 2 x ＋y －6x－6＝0 得 2 2 x ＋y －4y－6＝0
① ， ② ③，
3 ①－②并整理得，y＝2x
将③代入①式整理得 13x2－24x－24＝0.
高中数学人教版必修2课件
∵Δ＝(－24)2－4×13×(－24)>0，故此方程有两个不等实 根， ∴圆 C1 与圆 C2 有两个不同的交点，
思维突破：可用方程思想和几何法两种方法，几何法更为
简便：先求出公共弦所在直线方程，再通过直角三角形求解． 解法一：由题意，列出方程组
2 2 x ＋y －4＝0 2 2 x ＋y －4x＋4y－12＝0
，消去二次项，得 y＝x＋2.
把 y＝x＋2 代入 x2＋y2－4＝0， 得 x2＋2x＝0，重点
圆与圆的位置关系及判定方法
圆 C1：(x－a1)2＋(y－b1)2＝R2， 圆 C2：(x－a2)2＋(y－b2)2＝r2(R>r)． 两圆的位置关系如下表：
两圆的位 图示 置关系 几何法 代数法
相离
|C1C2|>R＋r
Δ<0
高中数学人教版必修2课件
续表
两圆的位
置关系
图示
几何法
代数法
外切
|C1C2|＝R＋r
Δ＝0
内切
|C1C2|＝R－r
Δ＝0
相交
R－r<|C1C2|<R＋r
Δ>0
内含
|C1C2|<R－r
Δ<0
高中数学人教版必修2课件
难点
两圆的公切线
和两个圆都相切的直线称为两圆的公切线，公切线条数如 下表：
两圆位 相离 置关系 公切线 外切 内切 相交 内含
4条
∴圆 C1 与圆 C2 相交．

新课标高中数学人教A版必修二全册课件4.2.2圆与圆的位置关系

新课标高中数学人教A版必修二全册课件4.2.2圆与圆的位置关系
设两圆的圆心距为d，两圆半径 分别为R、r. 当d＞R＋r时，两圆 ， 当d＝R＋r时，两圆 ， 当|R－r|＜d＜R＋r时，两圆 ， 当d＝|R－r|时，两圆 ， 当d＜|R－r|时，两圆 .
第四页，编辑于星期日：十三点 十六分。
讲授新课
例1. 已知圆C1: x2＋y2＋2x＋8y－8＝0， 圆C2: x2＋y2－4x－4y－2＝0，试判断 圆C1与圆C2的位置关系.
第五页，编辑于星期日：十三点 十六分。
探讨: 问题如何根据圆的方程，判断
两圆之间的位置关系？
第六页，编辑于星期日：十三点 十六分。
探讨: 问题如何根据圆的方程，判断
两圆之间的位置关系？
方法：通常是通过解方程或不等式
等方法加以解决.
第七页，编辑于星期日：十三点 十六分。
例2.圆C1的方程是: x2＋y2－2mx＋4y＋m2 －5＝0， 圆C2的方程是: x2＋y2＋2x－2my＋m2 －3＝0，
4.2.2圆与圆 的位置关系
第一页，编辑于星期日：十三点 十六分。
复习引入
1. 两圆的位置关系有哪几种？
第二页，编辑于星期日：十三点 十六分。
复习引入
2. 如何利用半径与圆心距之间的关系 来判断两圆的位置关系？
第三页，编辑于星期日：十三点 十六分。
复习引入
2. 如何利用半径与圆心距之间的关系 来判断两圆的位置关系？
第十三页，编辑于星期日：十三点 十六分。
2. 已知圆C与圆x2 y2 2x 0相外切, 并 且与直线x 3 y 0相切于点Q(3, 3), 求圆C的方程 .
3. 求两圆x2＋y2＝1和(x－3)2＋y2＝4的外 公切线方程.
第十二页，编辑于星期日：十三点 .129到P.130； 2. 《习案》二十八.

高一数学人教版A版必修二课件：4.2.2 圆与圆的位置关系


思考2 已知两圆C1：x2＋y2＋D1x＋E1y＋F1＝0和C2：x2＋y2＋D2x＋ E2y＋F2＝0，如何通过代数的方法判断两圆的位置关系？ 答案 联立两圆的方程，消去y后得到一个关于x的一元二次方程， 当判别式Δ>0时，两圆相交，当Δ＝0时，两圆外切或内切， 当Δ<0时，两圆外离或内含.
答案
解析答案
1 23 4
2.圆C1：x2＋y2＝1与圆C2：x2＋(y－3)2＝1的内公切线有且仅有( B )
A.1条
B.2条
C.3条
D.4条
解析 圆心距为3，半径之和为2，故两圆外离，内公切线条数为2.
解析答案
1 23 4
3.若圆C1：x2＋y2＝16与圆C2：(x－a)2＋y2＝1相切，则a的值为( D )
解析 由题意知：直线AB与直线x－y＋c＝0垂直， ∴kAB×1＝－1， 3－－1
1－m ＝－1，得 m＝5， AB的中点坐标为(3,1)， AB的中点在直线x－y＋c＝0上. ∴3－1＋c＝0，∴c＝－2， ∴m＋c＝5－2＝3.
解析答案
(2)求圆C1：x2＋y2＝1与圆C2：x2＋y2－2x－2y＋1＝0的公共弦所在直线
为啥总是听懂了， 但不会做，做不好？
高效学习模型-内外脑模型
2
内脑-思考内化
思 维 导 图 &超 级 记 忆 法 &费 曼 学 习 法
1
外脑-体系优化
知 识 体 系 &笔 记 体 系
内外脑高效学习模型
超级记忆法
超级记忆法-记忆规律
记忆前
选择记忆的黄金时段 前摄抑制：可以理解为先进入大脑的信息抑制了后进 入大脑的信息
返回
题型探究
重点难点 个个击破

高中数学 4.2圆与圆的位置关系课件1 理 新人教A版必修2


精选ppt
1
6.圆系方程：
②设圆C∶x2+y2+Dx+Ey+F=0与直线l： Ax+By+C=0，若直线与圆相交，则过交点的圆 系方程为x2+y2+Dx+Ey+F+λ(Ax+By+C)=0 (λ为参 数)．
精选ppt
2
例1.求以圆C1∶x2+y2-12x-2y-13=0和 圆C2：x2+y2+12x+16y-25=0的公共弦为直径的圆方程．
∵圆心C应在公共弦AB所在直线上，
∴ 所求圆的方程为x2+y2-4精x选+pp4t y-17=0．
4
• 完成圆系题单：例题2，7 作业： • 圆系题单剩下的
精选ppt
6
6.圆系方程：
①设圆C1∶x2+y2+D1x+E1y+F1=0和 圆C2∶x2+y2+D2x+E2y+F2=0．
若两圆相交，则过交点的圆系方程为 x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0(λ为 参数，圆系中不包括圆C2，λ=-1为两圆的公共弦 所在直线方程)．
若两圆相切呢？
解法
相减得公共弦所在直线方程为4x+3y-2=0．
∵所求圆以AB为直径，
于是圆的方程为(x-2)2+(y+2)2=25 .
精选ppt
3
例1.求以圆C1∶x2+y2-12x-2y-13=0和 圆C2：x2+y2+12x+16y-25=0的公共弦为直径的圆方程． 解法二： 设所求圆的方程为： x2+y2-12x-2y-13+λ(x2+y2+12x+16y-25)=0(λ为参数)

人教A2019最新版教材高中数学选择性必修第一册2.5.2圆与圆的位置关系课件

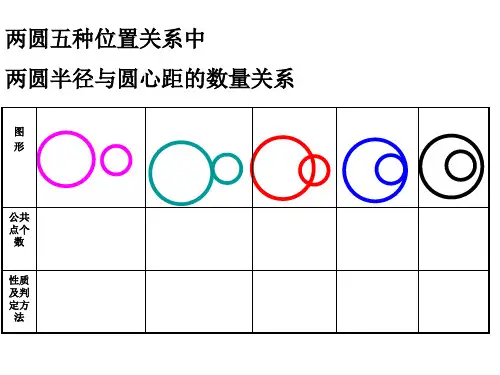
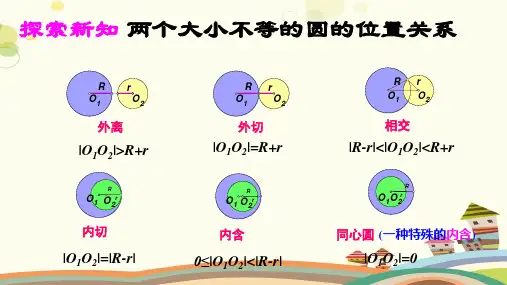
如图所示，将直线方程与圆的方程联立，设直线与圆的两交点分别是
A(xi,yi),B(x₂,y2), 则AB|=√(x₁-x₂)² +(v₁-y₂)²=√ 1+k²|x₁-x₂l
直线l 的斜率k 存在且不为0). 3.几何法：如图，直线与圆C 交于A,B 两点，设弦心距为d, 圆的半径为r, 弦长为
AB|, 则有
则P 在直线1上且MP 与直线l垂直.
则有
则有b=2a,
又由P 在直线l 上，则有一a+2b—3=0, 可解得a=1,b=2, 则直线l 的方程为x+2y-3=0.
(2)由直线y=x+1 上任一点向圆(x—3)²+y²=1 引切线，则该切线长的最小 值为( )
A.1
B.2√
C
D.3
C 解析：圆心C(3,0)到y=x+1 的距离 所以切线的最小值为
题型三直线与圆相交 例3(1)求直线l:3x+y-6=0 被圆C:x²+y²-2y-4=0 截得的弦长|AB|.
(2)过点(一4,0)作直线l 与 圆x²+y²+2x-4y-20=0
交 于A,B 两点，如果 A|B
= 8 , 求 直 线l的方程 .
解：(1)联立直线l与 圆C 的方程，
事
解
事
事
所以交点为A(1,3),B(2,0). 故直线l:3x+y-6=0 被 圆C:x²+y²-2y-4=0
2.5 直线与圆、圆与圆的位置关系 2.5.1 直线与圆的位置关系
学习目标
素养 目标
1.掌握直线与圆的三种位置关系：相交、相切、 相离.(重点)
2.会用代数法和几何法来判断直线与圆的三种位 置关系.(难点)

高中数学必修二教学课件圆与圆的位置关系共9张PPT

两圆五种位置关系中 两圆半径与圆心距的数量关系
图 形
公共 点个
数
性质 及判 定方
法
例题讲解
例1：判断下列两圆的位置关系
（1） x2 y2 4x 4 y 7 0
与 x2 y2 4x 10 y 13 0
（2）
x2
y2
4
与
x y
3 2cos 1 2cos
判断两圆位置关系的方法：
1.几何方法
小结：
1、圆和圆的五种位置关系、判断及应用。 2、相交两圆的有关计算。 3、圆的几何性质及运用。
A
O
Bx
6. 过两圆 x2 + y2 + 6x – 4 = 0
和 x2 + y2 + 6y – 28 = 0 的交点 且圆心在直线 x - y - 4 = 0上的圆方程是( ) (A)x2+y2+x-5y+2=0 (B)x2+y2-x-5y-2=0 (C)x2+y2-x+7y-32=0 (D)x2+y2+x+7y+32=0
的公切线有且仅有
条。
3. 求与点A(1,2)的距离为1，且与 点B(3,1)之距离为2的直线共有 条。
4.已知以C(- 4,3)为圆心的圆
与圆 x2 y2 1相切，求圆C的方程。
5.过圆 x2 + y2 = 4外一点 P( 3 , 4 )
作圆的两条切线，切点分别为数方法
例题讲解
例1：判断下列两圆的位置关系
（1） x2 y2 4x 4 y 7 0 与 x2 y2 4x 10 y 13 0
（2）
x2 y2 4
与
x y
32 1
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
圆与圆的位置关系 : 设两圆圆心距离为d,半径
分别为r1，r2 交点个数
圆和圆外离 d r1 r2
圆和圆外切
d r1 r2
圆和圆相交
| r1 r2 | d r1 r2
圆和圆内切 圆和圆内含
2019年高中数学人教版必修2课件：§4 .2.2圆 与圆的 位置关 系(共3 4张PPT )
d | r1 r2 | 0≤d<|r1-r2|
|r1－r2|<d<r1＋r2⇔两圆__相___交__； d＝|r1－r2|⇔两圆__内___切__； 0<d<|r1－r2|⇔两圆_内___含___， d＝0 时为同心圆．
2．两圆的公切线条数：
当两圆内切时有__一___条__公切线；当两圆外切时有 _三__条____公切线；相交时有__两___条__公切线；相离时有 _四__条____公切线；内含时_无___公切线．
求圆心坐标及半径r （配方法）
圆心到直线的距离d （点到直线的距离公式）
消去y
1．圆与圆的位置关系：
新知预习
两圆(x－a1)2＋(y－b1)2＝r21(r1>0)与(x－a2)2＋(y－b2)2＝r22(r2>0)
圆心距 d＝ a1－a22＋b1－b22，
d>r1＋r2⇔两圆外___离____；d＝r1＋r2⇔两圆_外___切___；
2019年高中数学人教版必修2课件：§4 .2.2圆 与圆的 位置关 系(共3 4张PPT )
说明:1．相切（外切、内切）两圆的性质 相切两圆的连心线必经过__切__点． 2．相交两圆的性质 相交两圆的连心线__垂__直__平__分____两圆的公共弦． 3．两圆的公切线 和两个圆都相切的直线称为两圆的公切线，当两圆在公切线的同 侧时，公切线为_外__公切线；当两圆在公切线的两侧时，公切线 为__内_公切线．
2019年高中数学人教版必修2课件：§4 .2.2圆 与圆的 位置关 系(共3 4张PPT )
它方法的优缺点；
几何方法直观，但不能求出交点； 代数方法能求出交点，但Δ=0，Δ<0 时， 不能准确判断圆的位置关系.
2019年高中数学人教版必修2课件：§4 .2.2圆 与圆的 位置关 系(共3 4张PPT )
方法二，代数法． 由两者方程组成方程组，由方程组解的情况决定.
2019年高中数学人教版必修2课件：§4 .2.2圆 与圆的 位置关 系(共3 4张PPT )
2019年高中数学人教版必修2课件：§4 .2.2圆 与圆的 位置关 系(共3 4张PPT )
解法一：把圆的方程都化成标准形式,为
C1 : (x 1)2 ( y 4)2 25
学习目标
1.能根据圆的方程判断圆与圆的位置关系（重点）。
2.了解几何法与代数法判断圆与圆位置时的优缺点。
3.学习了圆与圆的位置关系，并应用于解决实际问题，体验 感受并应用了数形结合的思想方法，在直观想象、数学运算、 数学建模等核心素养方面有所提高。
知识回顾 判断直线和圆的位置关系
几何方法
代数方法
用Δ判断两 圆的位置
关系
2019年高中数学人教版必修2课件：§4 .2.2圆 与圆的 位置关 系(共3 4张PPT )
2019年高中数学人教版必修2课件：§4 .2.2圆 与圆的 位置关 系(共3 4张PPT )
规律总结：利用几何法判断两圆的位置关系，直观，容 易理解，但不能求出交点坐标；利用代数法判断两圆的位置 关系，不能准确地判断位置关系(如Δ＝0仅能说明两圆只有一 个公共点，但确定不了是内切还是外切；Δ<0仅能说明两圆没 有公共点，但确定不了是外离还是内含，所以必须借助于图 形)．
x2 y2 2x 8y 8 0,
①
x
2
y2
4x
4y
2
0.
②
联立方程组
① ②，得 x 2y 1 0 ③
消去二次项
由③得y 1 x 2
把上式代入①，并整理得 x2 2x 3 0 ④
方程④根的判别式 △=(2)2 41 (3) 16 0
所以方程④有两个不等实数根， 方程组有两解； 故两圆相交．
比较、 判断
. C2(2,2) O
x
. C1（-1,-4）
所以两圆相交.
C1
2019年高中数学人教版必修2课件：§4 .2.2圆 与圆的 位置关 系(共3 4张PPT )
2019年高中数学人教版必修2课件：§4 .2.2圆 与圆的 位置关 系(共3 4张PPT )
解法二：将两个圆方程联立,得方程组
2019年高中数学人教版必修2课件：§4 .2.2圆 与圆的 位置关 系(共3 4张PPT )
圆与圆的位置关系的判定：
几何方法
代数方法
圆心距d (两点间距离公式)
比较d和r1，r2的 大小，下结论
2019年高中数学人教版必修2课件：§4 .2.2圆 与圆的 位置关 系(共3 4张PPT )
两圆的方程组成 的方程组的实数 解的情况
2019年高中数学人教版必修2课件：§4 .2.2圆 与圆的 位置关 系(共3 4张PPT )
例1：已知圆C1 : x2 y2 2x 8y 8 0， 圆 C2 : x2 y2 4x 4 y 2 0，
试判断圆C1与圆C2的位置关系.
分析：方法一，几何法． 判断圆心距与两圆半径的和与差的绝对值的大小关系.
课堂导入
思考: 圆与圆有哪几种位置关系呢？
你能从生活中举几个圆和圆的位置 关系的例子吗？
问题探究
探究 圆与圆的位置关系？
1.相离（没有公共点） 2.相切（一个公共点）
外离 内含 内切 外切
3.相交（两个公共点）
2019年高中数学人教版必修2课件：§4 .2.2圆 与圆的 位置关 系(共3 4张PPT )
C1 的圆心坐标是 (1, 4,半) 径长 r1 5; C2 的圆心坐标是 (2, 2,)半径长 r2 10;
所以圆心距 C1C2 (1 2)2 (4 2)2 3 5 y
两圆半径的和与差
r1 r2 5 10, r1 r2 5 10
而 5 10 3 5 5 10
即 r1 r2 3 5 r2 r1
总结评述：如何判断两圆公切线的条数 首先判断两圆的位置关系，然后判断公切线的条数： (1)两圆相离，有四条公切线； (2)两圆外切，有三条公切线，其中一条是内公切线，两条是外公 切线； (3)两圆相交，有两条外公切线，没有内公切线； (4)两圆内切，有一条公切线； (5)两圆内含，没有公切线．
2019年高中数学人教版必修2课件：§4 .2.2圆 与圆的 位置关 系(共3 4张PPT )