logistic回归分析案例

第18章 Logistic 回归 案例辨析及参考答案案例18-1 一项前瞻性队列研究中，欲研究某疾病与甲、乙两因素的关系，数据见教材表18-13。

教材表18-13 某前瞻性队列研究中疾病与甲、乙两因素的关系 乙 因 素 甲 因 素 发 病 未发病 合计（2X ）（1X ） （Y =1） （Y =0） 暴露（2X =1）暴露（1X =1）150250400未暴露（1X =0） 250 150 400 未暴露（2X =0）暴露（1X =1）400150550未暴露（1X =0）200450650疾病发病与否是因变量Y （发病赋值1，未发病赋值0），甲、乙两个因素为两个自变量1X 和2X ，采用logistic 回归研究疾病与甲、乙两个因素的关系。

（1） 单变量模型 分析结果提示：疾病与甲因素有联系（回归系数Wald 检验2χ＝44.766，P <0.001）；疾病与乙因素没有联系（回归系数Wald 检验2χ＝0.000，P ＝1.000）。

（2）主效应模型 将甲、乙两个因素同时纳入模型，拟合结果见教材表18-14。

提示疾病与甲因素有联系，与乙因素的联系仍然没有统计学意义。

与单变量拟合结果比较，纳入乙因素后，甲因素的优势比只有微小改变。

研究者据此得出结论：疾病与甲因素有联系，疾病与乙因素没有联系，乙因素也不是混杂因素。

教材表18-14 按照模型22110it log X X βββπ++=拟合结果变 量 b SE Wald df Pexp(b ) 1X 0.607 0.091 44.838 1 ＜0.001 1.835 2X -0.026 0.092 0.077 1 0.781 0.975 Constant-0.2780.07215.0761＜0.0010.757（3）有交互效应的模型 根据专业知识判断，甲、乙两因素间可能存在交互效应，选用有交互效应的全模型，拟合结果见教材表18-15。

结果提示：疾病与甲因素有联系，疾病与乙因素也有联系，甲、乙两因素间还有交互效应。

Logistic回归分析报告范文结果解读分析Logitic回归常用于分析二分类因变量(如存活和死亡、患病和未患病等)与多个自变量的关系。

比较常用的情形是分析危险因素与是否发生某疾病相关联。

例如，若探讨胃癌的危险因素，可以选择两组人群，一组是胃癌组，一组是非胃癌组，两组人群有不同的临床表现和生活方式等，因变量就为有或无胃癌，即“是”或“否”，为二分类变量，自变量包括年龄、性别、饮食习惯、是否幽门螺杆菌感染等。

自变量既可以是连续变量，也可以为分类变量。

通过Logitic回归分析，就可以大致了解胃癌的危险因素。

Logitic回归与多元线性回归有很多相同之处，但最大的区别就在于他们的因变量不同。

多元线性回归的因变量为连续变量；Logitic回归的因变量为二分类变量或多分类变量，但二分类变量更常用，也更加容易解释。

1.Logitic回归的用法一般而言，Logitic回归有两大用途，首先是寻找危险因素，如上文的例子，找出与胃癌相关的危险因素；其次是用于预测，我们可以根据建立的Logitic回归模型，预测在不同的自变量情况下，发生某病或某种情况的概率(包括风险评分的建立)。

2.用Logitic回归估计危险度所谓相对危险度(rikratio，RR)是用来描述某一因素不同状态发生疾病(或其它结局)危险程度的比值。

Logitic回归给出的OR(oddratio)值与相对危险度类似，常用来表示相对于某一人群，另一人群发生终点事件的风险超出或减少的程度。

如不同性别的胃癌发生危险不同，通过Logitic回归可以求出危险度的具体数值，例如1.7，这样就表示，男性发生胃癌的风险是女性的1.7倍。

这里要注意估计的方向问题，以女性作为参照，男性患胃癌的OR是1.7。

如果以男性作为参照，算出的OR将会是0.588(1/1.7)，表示女性发生胃癌的风险是男性的0.588倍，或者说，是男性的58.8％。

撇开了参照组，相对危险度就没有意义了。

logistic回归分析案例Logistic回归分析案例。

Logistic回归分析是一种常用的统计分析方法，主要用于预测二分类或多分类的结果。

在实际应用中，Logistic回归分析可以帮助我们理解影响某一事件发生的因素，以及对事件发生的概率进行预测。

本文将通过一个实际的案例来介绍Logistic回归分析的应用。

案例背景。

假设我们是一家电商公司的数据分析师，现在我们需要分析用户的购买行为，并预测用户是否会购买某一产品。

我们收集了一些用户的个人信息和他们最近一次购买的产品，希望通过这些数据来预测用户是否会购买新产品。

数据准备。

首先，我们需要收集用户的个人信息和购买行为数据。

个人信息包括年龄、性别、职业等；购买行为数据包括购买的产品类型、购买时间等。

在收集完数据后，我们需要对数据进行清洗和预处理，包括缺失值处理、异常值处理等。

模型建立。

在数据准备完成后，我们可以开始建立Logistic回归模型。

首先，我们需要将数据划分为训练集和测试集，以便对模型进行验证。

然后，我们可以利用训练集来拟合Logistic回归模型，并利用测试集来评估模型的预测效果。

模型评估。

在模型建立完成后，我们需要对模型进行评估。

常用的评估指标包括准确率、精确率、召回率等。

这些指标可以帮助我们判断模型的预测效果，并对模型进行调优。

模型应用。

最后，我们可以利用建立好的Logistic回归模型来预测用户是否会购买新产品。

通过输入用户的个人信息和购买行为数据，模型可以给出用户购买新产品的概率，从而帮助我们进行精准营销和推广。

结论。

通过以上实例，我们可以看到Logistic回归分析在预测用户购买行为方面具有很好的应用价值。

通过收集用户数据、建立模型、评估模型和应用模型，我们可以更好地理解用户行为，并做出更精准的预测和决策。

总结。

Logistic回归分析是一种强大的统计工具，可以帮助我们预测二分类或多分类的结果。

在实际应用中，我们可以根据具体情况收集数据、建立模型，并利用模型进行预测和决策。

logistic回归医学案例
逻辑回归在医学中有广泛的应用，尤其是在预测疾病风险和诊断疾病方面。

以下是一个逻辑回归在医学中的实际案例：
案例：预测糖尿病风险
背景：糖尿病是一种常见的慢性疾病，预测糖尿病风险对于预防和控制疾病非常重要。

通过逻辑回归模型，可以基于患者的特征预测其患糖尿病的风险。

数据集：数据集中包含患者的年龄、性别、体重指数（BMI）、家族病史、饮食习惯等特征以及是否患有糖尿病的标签（0表示无糖尿病，1表示有糖
尿病）。

模型训练：使用逻辑回归模型训练数据集，将特征作为输入，标签作为输出。

通过训练模型，可以学习到特征与糖尿病风险之间的关系。

模型评估：使用测试集评估模型的准确性和预测能力。

可以通过计算准确率、灵敏度、特异度等指标来评估模型的性能。

应用：基于训练好的逻辑回归模型，对于具有不同特征的患者，可以预测其患糖尿病的风险，并提供相应的预防和治疗建议。

总结：逻辑回归是一种强大的预测模型，在医学领域中具有广泛的应用。

通过逻辑回归模型，可以根据患者的特征预测其患病风险，并提供针对性的预防和治疗建议，有助于提高疾病的预防和控制效果。

二分类logistic回归案例
以下是一个二分类Logistic回归的案例：
假设我们正在研究肺癌的危险因素。

在这个案例中，因变量是是否患有肺癌（是或否），自变量可能包括性别、体重指数（BMI）、是否吸烟、年龄以及是否有慢性阻塞性肺病（COPD）病史等。

首先，我们需要收集数据，包括所有可能的影响因素以及是否患有肺癌的结果。

然后，我们进行数据清理和预处理，包括处理缺失值、异常值和编码问题。

接下来，我们进行单变量分析，单独考察每个自变量与因变量之间的关系。

例如，我们可以使用卡方检验来分析性别、吸烟状况、COPD病史等分类变量与肺癌的关系，使用t检验来分析年龄和BMI等连续变量与肺癌的关系。

根据单变量分析的结果，我们筛选出与肺癌有显著关系的变量，然后进行多因素分析。

在这个案例中，我们可以使用二分类Logistic回归模型来分析这些变量与肺癌的关系。

我们可以通过逐步回归、向前选择或向后删除等方法选择自变量进入模型。

在Logistic回归分析中，我们可以通过估计回归系数、似然比检验和AIC 等信息准则来评估模型的拟合优度和预测能力。

我们还可以使用交叉验证等技术来评估模型的泛化能力。

最后，我们解释结果并撰写研究报告或论文。

在解释结果时，我们需要考虑自变量之间的相互作用和多重共线性问题。

如果存在多重共线性问题，我们需要采取措施解决它，例如使用主成分分析或岭回归等方法。

总之，二分类Logistic回归是一种强大的统计工具，可以帮助我们了解分类结果与一组影响因素之间的关系，并预测新数据点的分类概率。

在案例研究中，我们需要注意数据预处理、变量选择和结果解释等方面的问题。

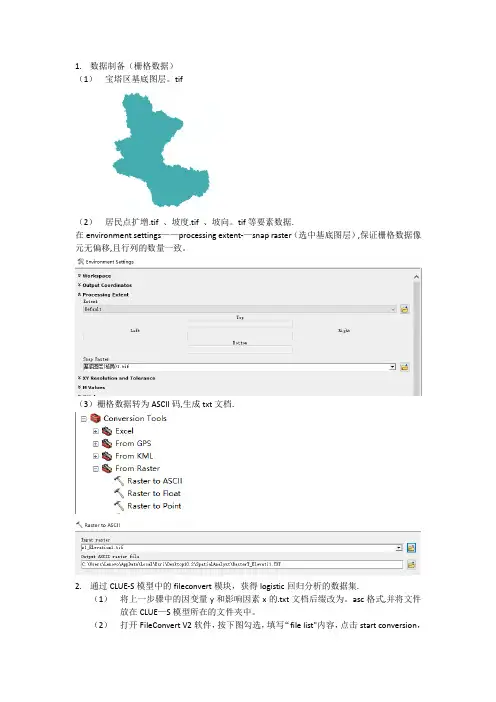
1.数据制备（栅格数据）
（1）宝塔区基底图层。

tif
（2）居民点扩增.tif 、坡度.tif 、坡向。

tif等要素数据.
在environment settings——processing extent-—snap raster（选中基底图层）,保证栅格数据像元无偏移,且行列的数量一致。

（3）栅格数据转为ASCII码,生成txt文档.
2.通过CLUE-S模型中的fileconvert模块，获得logistic回归分析的数据集.
（1）将上一步骤中的因变量y和影响因素x的.txt文档后缀改为。

asc格式,并将文件放在CLUE—S模型所在的文件夹中。

（2）打开FileConvert V2软件，按下图勾选，填写“file list"内容，点击start conversion，
生成stat.txt 文档。

3．Spss软件中logistic二元回归分析
（1)数据标准化处理，加载数据——描述统计——描述，勾选“将标准化得分另存为变量”
(2）logistic回归分析
按图设置参数因变量、自变量；由于x3属于分类变量，点击分类按钮，按图设置参数。

点击“选项”按钮，按图进行勾选，继续.点击“保存"按钮，勾选“概率”. ROC曲线检测。

logistic回归例题Logistic回归是一种线性分类器，针对的是线性可分问题。

以下是使用Logistic 回归进行分类的一个简单例子：假设我们有一个数据集，其中包含一个人的年龄、收入和信用评分。

我们的目标是预测这个人是否会违约。

首先，我们需要收集数据。

假设我们有100个人的数据，其中50人违约，50人没有违约。

我们可以将这些数据分为训练集和测试集，例如80%的数据用于训练集，20%的数据用于测试集。

接下来，我们需要将数据转换为数值形式，以便在计算机中处理。

我们可以将年龄和收入作为特征，将是否违约作为目标变量。

我们可以将年龄和收入的值标准化或归一化，以便它们在同一尺度上。

然后，我们可以使用Logistic回归模型来拟合数据。

在这个例子中，Logistic 回归模型的公式如下：\(\ln\frac{P}{1 - P} = \alpha + \beta_1 \cdot X_1 + \beta_2 \cdot X_2\)其中\(P\)表示这个人违约的概率，\(\alpha\)和\(\beta_1\)和\(\beta_2\)是待估计的参数，\(X_1\)和\(X_2\)分别是年龄和收入的值。

通过最大似然估计等优化方法，我们可以估计出\(\alpha\)、\(\beta_1\)和\(\beta_2\)的值。

一旦我们得到了这些值，我们就可以使用它们来预测新数据点的违约概率。

最后，我们可以使用测试集来评估模型的性能。

我们可以计算模型的准确率、召回率、F1得分等指标，以评估模型的分类性能。

这个例子仅仅是一个简单的Logistic回归应用，实际上它可以应用于更复杂的问题，例如医学诊断、金融欺诈检测、推荐系统等。

转载⼏个R语⾔中实现Logistic回归模型的案例案例⼀：本⽂⽤例来⾃于John Maindonald所著的《Data Analysis and Graphics Using R》⼀书，其中所⽤的数据集是anesthetic，数据集来⾃于⼀组医学数据，其中变量conc表⽰⿇醉剂的⽤量，move则表⽰⼿术病⼈是否有所移动，⽽我们⽤nomove做为因变量，因为研究的重点在于conc的增加是否会使nomove的概率增加。

⾸先载⼊数据集并读取部分⽂件，为了观察两个变量之间关系，我们可以利cdplot函数来绘制条件密度图install.packages('DAAG')library(lattice)library(DAAG)head(anesthetic)move conc logconc nomove1 0 1.0 0.0000000 12 1 1.2 0.1823216 03 0 1.4 0.3364722 14 1 1.4 0.3364722 05 1 1.2 0.1823216 06 0 2.5 0.9162907 1cdplot(factor(nomove)~conc,data=anesthetic,main='条件密度图',ylab='病⼈移动',xlab='⿇醉剂量')从图中可见，随着⿇醉剂量加⼤，⼿术病⼈倾向于静⽌。

下⾯利⽤logistic回归进⾏建模，得到intercept和conc的系数为-6.47和5.57，由此可见⿇醉剂量超过1.16(6.47/5.57)时，病⼈静⽌概率超过50%。

anes1=glm(nomove~conc,family=binomial(link='logit'),data=anesthetic)summary(anes1)结果显⽰：Call:glm(formula = nomove ~ conc, family = binomial(link = 'logit'),data = anesthetic)Deviance Residuals:Min 1Q Median 3Q Max-1.76666 -0.74407 0.03413 0.68666 2.06900Coefficients:Estimate Std. Error z value Pr(>|z|)(Intercept) -6.469 2.418 -2.675 0.00748 **conc 5.567 2.044 2.724 0.00645 **---Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1(Dispersion parameter for binomial family taken to be 1)Null deviance: 41.455 on 29 degrees of freedomResidual deviance: 27.754 on 28 degrees of freedomAIC: 31.754Number of Fisher Scoring iterations: 5下⾯做出模型的ROC曲线anes1=glm(nomove~conc,family=binomial(link='logit'),data=anesthetic)对模型做出预测结果pre=predict(anes1,type='response')将预测概率pre和实际结果放在⼀个数据框中data=data.frame(prob=pre,obs=anesthetic$nomove)将预测概率按照从低到⾼排序data=data[order(data$prob),]n=nrow(data)tpr=fpr=rep(0,n)根据不同的临界值threshold来计算TPR和FPR，之后绘制成图for (i in 1:n){threshold=data$prob[i]tp=sum(data$prob>threshold&data$obs==1)fp=sum(data$prob>threshold&data$obs==0)tn=sum(data$probfn=sum(data$probtpr[i]=tp/(tp+fn) #真正率fpr[i]=fp/(tn+fp) #假正率}plot(fpr,tpr,type='l')abline(a=0,b=1)R中也有专门绘制ROC曲线的包，如常见的ROCR包，它不仅可以⽤来画图，还能计算ROC曲线下⾯⾯积AUC,以评价分类器的综合性能，该数值取0-1之间，越⼤越好。