四种滤波器的幅频特性

第一章习题：一、填空题1、电量分为和，如电流、电压、电场强度和电功率属于；而描述电路和波形的参数，如电阻、电容、电感、频率、相位则属于。

2、传感器输出的经过加工处理后，才能进—步输送到记录装置和分析仪器中。

3、现代科学认为，、、是物质世界的三大支柱。

4、与三大支柱相对应，现代科技形成了三大基本技术，即、、。

5、传感技术是人的的扩展和延伸；通信技术是人的的扩展和延伸；计算机技术是人的的延伸。

6、、、技术构成了信息技术的核心。

二、简答题1、举例说明信号测试系统的组成结构和系统框图。

2、举例说明传感技术与信息技术的关系。

3、分析计算机技术的发展对传感测控技术发展的作用。

4、分析说明信号检测与信号处理的相互关系。

三、参考答案（－）填空题1、电能量、电参量、电能量、电参量2、电信号、信号调理电路3、物质、能量、信息4、新材料技术、新能源技术和信息技术5、感官（视觉、触觉）功能、信息传输系统(神经系统)、信息处理器官(大脑)功能6、传感、通信和计算机第二章习题：一、填空题1、确定性信号可分为和两类。

2、信号的有效值又称为，它反映信号的。

3、概率密度函数是在域，相关函数是在域，功率谱密度是在域上描述随机信号。

4、周期信号在时域上可用、和参数来描述。

5、自相关函数和互相关函数图形的主要区别是。

6、因为正弦信号的自相关函数是同频率的，因此在随机噪声中含有时，则其自相关函数中也必然含有，这是利用自相关函数检测随机噪声中含有的根据。

7、周期信号的频谱具有以下三个特点：_________、________、_________。

8、描述周期信号的数学工具是__________；描述非周期信号的数学工具是________。

9、同频的正弦信号和余弦信号,其相互相关函数是的。

10、信号经典分析方法是和。

11、均值E[x(t)]表示集合平均值或数学期望，反映了信号变化的，均方值反映信号的。

12、奇函数的傅立叶级数是，偶函数的傅立叶级数是。

实验十一 FIR 滤波器的相位特性和幅度特性一、实验目的1. 了解 FIR 滤波器具有线性相位的条件。

2. 了解四种类型 FIR 滤波器的幅频特性和相频特性及用途。

3. 学会用 MA TLAB 工具分析 二、 实验原理与方法FIR 滤波器。

实验十六中已经讲过脉冲相应的对称与反对称，即满足)1()(n M h n h --=为对称满足)1()(n M h n h ---=为反对称。

当在M 为奇数偶数的下结合对称和反对称的情况，就可以得到四种类型的线性相位 FIR 滤波器。

对其中每种类型其频率响应函数都有特有的表达式和独特的形状。

可将)(ωj e H 写成：21,2;)()()(-===-M a e H e H a j r j πβωωβω式中)(ωr H 是振幅响应函数。

线性相位实系数FIR 滤波器按其M 值奇偶和)(n h 的奇偶对称性分为四种：1、Ⅰ类线性相位 FIR 滤波器：)(n h 为对称，M 为奇数。

可以证明：2/)1(2/)1(0])c o s()([)(---=∑=M j M n j e n n a e H ωωω式中)(n a 由)(n h 求得为：)21()0(-=M h a ；中间样本。

231),21(2)(-≤≤--=M n n M h n a 。

且振幅响应函数∑-==2/)1(0)cos()()(M n r n n a H ωω。

该幅值关于ππω2,,0=成偶对称。

MATLAB 中用函数Hr_Typel 来计算振幅响应。

2、Ⅱ类线性相位 FIR 滤波器：)(n h 为对称，M 为偶数.可以证明：2/)1(2/1])}21(cos{)([)(--=∑-=M j M n j e n n b e H ωωω式中2,...2,1),2(2)(M n n M h n b =-=且振幅响应函数∑=-=2/1)}21(cos{)()(M n r n n b H ωω可得0)(=πrH 。

滤波器的频率响应与幅频特性频率响应是对滤波器在不同频率下的响应能力进行描述的指标。

幅频特性则是指滤波器在不同频率下对信号幅度的影响程度。

1. 引言滤波器在电子工程中起着至关重要的作用。

它可以用来去除噪声、滤波信号以及频率选择等功能。

为了确保滤波器的设计和使用能够满足实际需求，了解滤波器的频率响应与幅频特性是非常关键的。

2. 频率响应滤波器的频率响应是指在不同频率下，滤波器对输入信号的响应情况。

通常情况下，频率响应是以频率为横坐标，增益为纵坐标进行绘制的。

不同类型的滤波器对频率的响应特性各不相同，如低通滤波器会对低频信号通过较好，而对高频信号进行衰减。

3. 幅频特性幅频特性是指在不同频率下，滤波器对信号幅度的影响程度。

它是通过绘制滤波器的增益-频率曲线来表示的。

由于滤波器对不同频率下的信号具有不同的增益，因此幅频特性是描述滤波器对信号增益的变化情况。

4. 不同类型滤波器的幅频特性4.1 低通滤波器低通滤波器的幅频特性表现为在低频范围内通过信号，并对高频信号进行衰减。

这种滤波器适用于需要去除高频噪声或只关注低频信号的应用场景。

4.2 高通滤波器高通滤波器的幅频特性表现为在高频范围内通过信号，并对低频信号进行衰减。

这种滤波器适用于需要去除低频噪声或只关注高频信号的应用场景。

4.3 带通滤波器带通滤波器的幅频特性表现为在某个频率范围内通过信号，并对其他频率的信号进行衰减。

这种滤波器适用于需要选择性地通过一定范围内的信号的应用场景。

4.4 带阻滤波器带阻滤波器的幅频特性表现为在某个频率范围内衰减信号，并对其他频率的信号进行通过。

这种滤波器适用于需要选择性地阻止一定范围内的信号的应用场景。

5. 影响滤波器频率响应与幅频特性的因素5.1 滤波器类型不同类型的滤波器由于其具体结构和设计参数的不同，其频率响应和幅频特性也会有所不同。

5.2 截止频率截止频率是影响滤波器频率响应和幅频特性的一个重要参数。

它表示滤波器在该频率下信号衰减或增益到一定程度的情况。

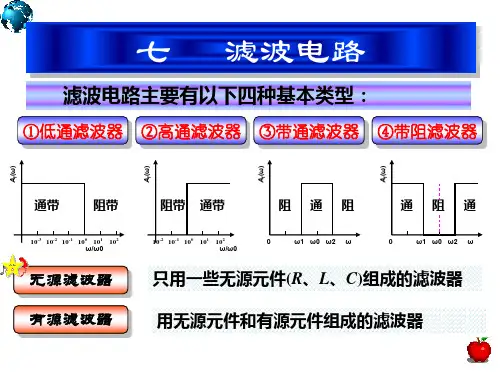
一．滤波器的基础知识1．滤波器的功能滤波器的功能就是允许某一部分频率的信号顺利的通过，而另外一部分频率的信号则受到较大的抑制，它实质上是一个选频电路。

滤波器中，把信号能够通过的频率范围，称为通频带或通带；反之，信号受到很大衰减或完全被抑制的频率范围称为阻带；通带和阻带之间的分界频率称为截止频率；理想滤波器在通带内的电压增益为常数，在阻带内的电压增益为零；实际滤波器的通带和阻带之间存在一定频率范围的过渡带。

2．滤波器的分类( 1）按所处理的信号分为模拟滤波器和数字滤波器两种。

( 2）按所通过信号的频段分为低通、高通、带通和带阻滤波器四种。

低通滤波器：它允许信号中的低频或直流分量通过，抑制高频分量或干扰和噪声。

高通滤波器：它允许信号中的高频分量通过，抑制低频或直流分量。

带通滤波器：它允许一定频段的信号通过，抑制低于或高于该频段的信号、干扰和噪声。

带阻滤波器：它抑制一定频段内的信号，允许该频段以外的信号通过。

( 3）按所采用的元器件分为无源和有源滤波器两种。

①．无源滤波器：仅由无源元件(R、L 和C)组成的滤波器，它是利用电容和电感元件的电抗随频率的变化而变化的原理构成的。

这类滤波器的优点是：电路比较简单，不需要直流电源供电，可靠性高；缺点是：通带内的信号有能量损耗，负载效应比较明显，使用电感元件时容易引起电磁感应，当电感L较大时滤波器的体积和重量都比较大，在低频域不适用。

②．有源滤波器：由无源元件(一般用R和C)和有源器件(如集成运算放大器）组成。

这类滤波器的优点是：通带内的信号不仅没有能量损耗，而且还可以放大，负载效应不明显，多级相联时相互影响很小，利用级联的简单方法很容易构成高阶滤波器，并且滤波器的体积小、重量轻、不需要磁屏蔽(由于不使用电感元件）；缺点是：通带范围受有源器件(如集成运算放大器）的带宽限制，需要直流电源供电，可靠性不如无源滤波器高，在高压、高频、大功率的场合不适用。

3. 滤波器的主要参数(1）通带增益A0：滤波器通带内的电压放大倍数。

四种滤波器的幅频特性四种滤波器的幅频特性本次实验是观察四种滤波器（低通、高通、带宽、带阻）的幅频特性，以加强对各种滤波器的功能认知。

本次实验我们选用的放大器为324型，其功能图如下所示:下面我们来逐步观察一下四种滤波器的特性。

1.低通滤波器其电路图如下所示：图中，电阻R1=R2=R=10KΩ，C1=C2=0.01uF,Ro=0.8R=8Ω，Vcc+＝+12V，Vcc-＝-12V ，低通滤波器的传递函数20022)(ωαωω++=s s K s H p ，，其中2221102121001111;1;1C R K R R C C C R R RRK K ff p -+⎪⎪⎭⎫ ⎝⎛+==+==αωω带入数据w 。

＝10000rad/s ，Kp ＝1.8，α＝1.2，()()222202225/2425/78.1)(ωωωωω+-=j H ；当w ＝0时)(ωj H ＝1.8，；w 增加且w<4800rad/s 时，)(ωj H 增加；当>4800rad/s 时, )(ωj H 减小,;w 趋近无穷时, )(ωj H 趋近于0。

此时wc=1.17rad/s 。

对于不同的α，滤波器的幅频特性也不相同对于实验中的低通，α＝1.2，与1.25的相似，我们对于实验数据的测量如下：输入为100mV 频率f （Hz ）输出V （v ） 频率f （Hz ） 输出V （v ） 10 1.965 2200 0.756 30 1.965 2300 0.698 50 1.960 2400 0.650 100 1.950 2500 0.596 2001.94526000.548500 1.945 2700 0.518 800 1.945 2800 0.484 1000 1.855 2900 0.438 1100 1.795 3000 0.414 1200 1.755 3500 0.311 1300 1.700 4000 0.238 1400 1.490 4500 0.180 1500 1.400 5000 0.148 1600 1.290 5500 0.123 1700 1.195 6000 0.105 1800 1.095 7000 0.078 1900 0.966 8000 0.057 2000 0.898 9000 0.046 2100 0.818 10000 0.036 范围10～6kHz输出不失真绘出的幅频特性图如下：2、高通滤波器其电路图如下：其中R1=R2=R=10K,C1=C2=0.01uF,Ro=0.8R=8K高通的传递函数为2022)(ωαω++=s s s K s H p ，()()222022)(ωαωωωωω+-=p K j H ，1121202121001111;1;1CR K C C R C C R R RR K K f f p -+⎪⎪⎭⎫ ⎝⎛+==+==αωω带入数值后，Kp ＝1.8，W=0时)(ωj H ＝0；w<4800rad/s 时)(ωj H 增加;w 趋近于无穷时, )(ωj H 保持不变。

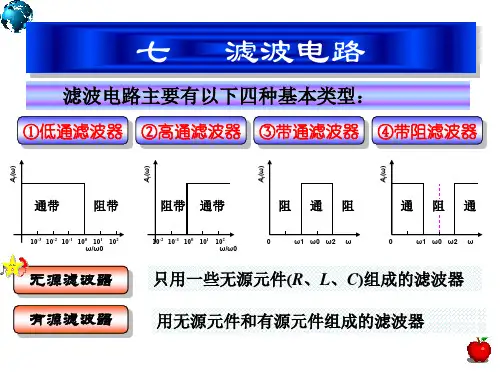
四种滤波器的幅频特性本次实验是观察四种滤波器(低通、高通、带宽、带阻)的幅频特性，以加强对各F面我们来逐步观察一下四种滤波器的特性。

1.低通滤波器其电路图如下所示：Vcc+K p o=+12V，Vcc- = -12V，低通滤波器的传递函数H (S) —s o S，其中K p K f 11 K fR1R2C1C2C1 R1R2R2C2带入数据w。

= 10000rad/s,H(j )Kp = 1.8 ,a= 1.2,1.8 o-------------------------------------------------------------------- ?2 2 2 2 227/25 0 24/25 0当w = 0 时H (j ) = 1.8, ; w 增加且w<4800rad/s 时，H(j )增加；当>4800rad/s 时, H(j )减小,;w趋近无穷时，H(j )趋近于0。

此时wc=1.17rad/s。

对于不同的a,滤波器的幅频特性也不相同对于实验中的低通，a=1.2，与1.25的相似，我们对于实验数据的测量如下: 输入为范围10〜6kHz输出不失真绘出的幅频特性图如下：2、高通滤波器其电路图如下:其中R仁R2=R=10K,C仁C2=0・01uF,Ro=0・8R=8K高通的传递函数为H (s)K p S2 £2，H(j )S 0 S 0K p K f 1 R°; 1 ;J R R2C1C2带入数值后，Kp = 1.8,1R2K p1C11 K fR1C1 W=0时H (j ) = 0；w<4800rad/s时| H(j )增加;w趋近于无穷时，H(j )保持不变。

对于不同的a,滤波器的幅频特性也不相同［频率f（Hz）输出V（v）频率f（Hz）输出V (v)100 0.018 1.3k 1.485 200 0.050 1.4k 1.615 300 0.095 1.5k 1.720 400 0.168 1.6k 1.790 500 0.260 1.8K 1.890 600 0.382 2.0K 1.920 700 0.517 2.5K 1.975 800 0.676 3.0K 1.970 900 0.846 4.0K 1.965 1K 1.008 5.0K 1.965 1.1K 1.200 10K 1.965 1.2K 1.3552 K(P(；QQ)S2，H(j ) • s( 0/Q)s 0(o/Q)s K P2；2 2 2 2 '/Q3带通滤波器其电路图如下所示:带通的传递函数为H （s）11 K f频率f ( Hz )输出V (v ) 频率f ( Hz ) 输出V (v )20 0.016 3K 0.760 50 0.035 3.5K 0.686 100 0.067 4K 0.610 200 0.139 4.5K 0.572 300 0.205 5K 0.518 400 0.268 6K 0.434 500 0.341 7K 0.368 600 0.398 8K 0.340 700 0.453 9K 0.310 800 0.516 10K 0.263 900 0.570 12K 0.223 1K 0.618 15K 0.180 1.5K 0.814 18K 0.151 1.8K 0.866 20K 0.140 2.0K 0.872 25K 0.105 2.02K 0.880(最大) 30K 0.092 2.2K 0.868 40K 0.0662.5K0.82650K0.055 （出现失真）输出范围200〜40KHZ 绘制的幅频特性图如下:K p K f 1G F31 K fR R 2 ；R R 2 ;.R&R3GG ；R|G R3C 1RC2 &GQ 为品质因数，不同的 Q 对幅频特性影响如下图:4、带阻滤波器 其电路图如下所示:数据如下: 频率f （ Hz ）输出V （v ） 频率f （ Hz ） 输出V (v )10 1.891.39K 0.069K p K fR o R ；1 CR ;2 RCK fH(j )不同的Q 产生的影响如下:。

FRM 滤波器设计组员：郑志龙 宋文波 丁毅 张丹娜 毛鑫萍 蒋维1. FRM 原理FIR 滤波器的幅频特性具体形式有以下四种：情况 1：N 为奇数，{}10)(-=N n n h 为偶对称形式。

∑-==2/)1(0),cos()()(ˆN n wn n a w H (1)其中：)2/)1(()0(-=N h a ，)2/)1((2)(n N h n a --=，2/)1,...(2,1-=N n .情况 2：N 为偶数，{}10)(-=N n n h 为偶对称形式。

∑=-=2/0),2/1(cos )()(ˆN n n w n b w H (2) 其中：)2/(2)(n N h n b -=，2/,...2,1N n =。

情况 3：N 为奇数，{}10)(-=N n n h 为奇对称形式。

∑-==2/)1(0),sin()()(ˆN n wn n c w H (3)其中：)2/)1((2)(n N h n c --=，.2/)1(...,2,1-=N n情况 4：N 为偶数，{}10)(-=N n n h 为奇对称形式． ∑=-=2/0),2/1(sin )()(ˆN n n w n d w H(4) 其中：),2/(2)(n N h n d -= .2/,...2,1N n =窄过渡带F I R 滤波器的几种设计技术：滤波器—均衡器技术，有限脉冲响应内插技术，并行结构技术，频率响应屏蔽技术。

本次实验我们采用的是FRM ，也就是频率响应屏蔽技术。

频率响应屏蔽(Frequency —Response Masking ，FRM)技术是L i m 于1986年[1]提出的。

为了说明频率屏蔽响应技术的基本原理，我们以一个低通滤波器a H 作为例子。

)(z H a )为低通滤波器的Z 变换传递函数，其频率响应为)(jw a e H ，过渡带宽度为a ∆，如图1(a)所示。

如果将滤波器的每个延时单元替换成M 个延时单元，则滤波器的传递函数变为)()(M a b z H z H =，频率响应变为)()(jMw a jw b e H e H =，过渡带宽度变为M a /∆，如图1(b)所示。

滤波器的四种基本类型的幅频是什么在信号处理和电子学领域中，滤波器是一种用于选择性地传递特定频率范围内信号的设备。

滤波器有多种类型，其中包括低通滤波器、高通滤波器、带通滤波器和带阻滤波器。

每种类型的滤波器都有其独特的幅频特性，下面我们将分别介绍这四种基本类型滤波器的幅频响应。

低通滤波器低通滤波器是一种能够传递低频信号而抑制高频信号的滤波器。

其幅频响应特点是在低频处有较高的增益，随着频率的增加，幅频响应逐渐下降，最终趋近于零。

低通滤波器常被用于消除高频噪声或选择性地保留低频信号。

高通滤波器高通滤波器与低通滤波器相反，它能够传递高频信号而抑制低频信号。

其幅频响应特点是在高频处有较高的增益，随着频率的减小，幅频响应逐渐下降至零。

高通滤波器通常用于消除低频噪声或选择性地保留高频信号。

带通滤波器带通滤波器是一种能够只传递指定频率范围内信号而阻塞其他频率信号的滤波器。

其幅频响应特点是在一个特定的频率范围内有较高的增益，而在该范围之外的频率上有较低的响应。

带通滤波器通常用于接收特定频段的信号或滤除特定频段的干扰。

带阻滤波器带阻滤波器与带通滤波器相反，它能够阻止指定频率范围内的信号而通过其他频率信号。

其幅频响应特点是在指定频率范围内有较低的响应，而在该范围之外则有较高的增益。

带阻滤波器通常用于消除特定频段的干扰或阻止特定频段的信号传输。

综合来看，四种基本类型的滤波器在频率响应特性上各有所长，根据具体的应用需求选择合适的滤波器类型能够有效地实现信号处理和控制。

通过了解不同滤波器类型的幅频特性，我们可以更好地运用它们来满足不同的工程需求。

1。