matlab-小波分解与重构-滤波
- 格式:doc
- 大小:14.00 KB
- 文档页数:3

matlab t1小波滤波算法Matlab T1小波滤波算法是一种用于信号处理的有效工具。
它可以帮助我们去除噪音、平滑信号、提取特征等。
本文将从介绍小波滤波算法的基本概念开始,然后详细说明如何在Matlab中实现T1小波滤波算法。
小波变换是一种数学变换方法,可以将信号分解为不同尺度的子信号。
通过将信号分解为多个频率段,我们可以更好地理解信号的频谱特征。
利用小波变换的特性,我们可以将信号分解为低频和高频成分。
低频成分包含信号的主要特征,而高频成分包含信号的细节信息。
T1小波滤波算法是一种基于小波变换的滤波方法。
它利用了小波分解和重构的原理,从而实现对信号的滤波处理。
该算法主要包含以下几个步骤:1. 读取信号数据:首先,我们需要在Matlab中读取待处理的信号数据。
这可以通过使用Matlab的读取文件函数来实现。
读取的数据可以是一个矩阵,每一列表示一个时刻的采样。
2. 小波分解:接下来,在Matlab中进行小波分解。
这可以通过调用Matlab 中的小波变换函数来实现。
小波变换函数中的参数包括信号数据和小波基。
小波基决定了小波分解的性质,常用的小波基包括haar小波、db小波等。
3. 提取低频成分:在小波分解后,我们可以得到具有不同尺度的低频和高频子信号。
低频子信号包含了主要特征,而高频子信号包含了信号的细节信息。
在T1小波滤波算法中,我们选择保留低频成分,并将高频成分设为零。
4. 小波重构:接下来,在Matlab中进行小波重构。
这可以通过调用Matlab 中的小波重构函数来实现。
小波重构函数中的参数包括低频成分和高频成分。
在T1小波滤波算法中,我们将高频成分设为零,只保留低频成分。
5. 过滤后的信号:最后,我们可以得到滤波后的信号。
通过比较滤波前后的信号,我们可以发现滤波算法的效果。
滤波后的信号能够减少噪音、平滑信号、提取特征等。
在使用Matlab T1小波滤波算法时,需要注意以下几个问题:1. 选择合适的小波基:不同的小波基具有不同的频谱特性。

matlab小波分解重构
在MATLAB中,小波分解和重构的实现主要依赖于几个关键的函数,包括dwt2,idwt2和wavedec2。
首先,使用dwt2函数进行二维离散小波变换。
基本语法是:[CA,CH,CV,CD] = dwt2(X,'wname')。
其中,X是输入图像,'wname'是你选择的小波名字,例如'haar','db2'等。
输出CA,CH,CV和CD分别代表近似系数、水平细节系数、垂直细节系数和对角线细节系数。
然后,你可以使用idwt2函数进行小波重构。
基本语法是:X = idwt2(CA,CH,CV,CD,'wname')。
这将使用相同的小波名字和分解系数来重构原始图像。
另一种更复杂的多层小波分解与重构可以通过wavedec2函数实现。
基本语法是:[C,S] = wavedec2(X,N,'wname')。
其中,X是输入图像,N 是你想要的分解层数,'wname'是你选择的小波名字。
输出C是一个包含所有分解信息的向量,S则包含了分解后各个频段图像的尺寸大小。

matlab小波分解与重构-回复什么是小波分解与重构?小波分解与重构是一种在信号处理领域广泛应用的技术。
它是基于小波函数的变换方法,能够将信号分解成多个频率和时域上局部化的子信号,以及通过这些子信号重构原始信号。
小波分解与重构广泛应用于图像处理、语音识别、数据压缩等领域。
小波分解过程中,信号被分解为多个低频和高频子带信号。
低频子带信号描述了信号的缓慢变化,而高频子带信号描述了信号的快速变化。
分解后的子带信号包含了原始信号的不同频率成分和时域局部特征。
小波重构是将这些子带信号进行逆变换来重构原始信号。
小波分解与重构的步骤如下:1. 选择适当的小波函数:小波函数是用来描述信号的形状和特征的数学函数。
常用的小波函数有Haar小波、Daubechies小波、Symlet小波等。
选择适当的小波函数能够更好地适应信号的特征。
2. 进行分解:使用选择的小波函数进行信号分解。
分解过程中,信号被分解为多个尺度和频率上的子带信号。
通常使用多级分解来获取信号的不同细节和近似信息。
3. 选择分解层数:确定分解的层数是一个重要的步骤。
分解层数的选择取决于信号的特征和应用的要求。
通常,随着分解层数的增加,信号的细节和频率成分会更加详细。
4. 单位归一化:对分解得到的子带信号进行单位归一化处理。
这是为了避免各个子带信号幅值的差异影响分析和重构。
5. 进行重构:使用逆小波变换将分解得到的子带信号重构成原始信号。
逆小波变换使用的是与分解所用小波函数相对应的小波函数。
需要注意的是,小波分解与重构是一种无损的信号处理方法,可以保留原始信号的细节信息。
相比傅里叶变换,小波分解在时域和频域上都具有局部特征,因此能够更好地描述信号的局部特性和时变性。
在MATLAB中,可以使用Wavelet Toolbox进行小波分解与重构。
该工具箱包含了多种小波函数和相关的分析和重构函数,可以方便地进行信号处理和分析。
使用MATLAB进行小波分解与重构的一般步骤如下:1. 导入信号数据:使用MATLAB的数据导入函数将原始信号导入到工作空间。

MATLAB小波变换指令及其功能介绍(超级有用)MATLAB小波变换指令及其功能介绍1 一维小波变换的 Matlab 实现(1) dwt函数功能:一维离散小波变换格式:[cA,cD]=dwt(X,'wname')[cA,cD]=dwt(X,Lo_D,Hi_D)别可以实现一维、二维和 N 维DFT 说明:[cA,cD]=dwt(X,'wname') 使用指定的小波基函数'wname'对信号X 进行分解,cA、cD 分别为近似分量和细节分量;[cA,cD]=dwt(X,Lo_D,Hi_D) 使用指定的滤波器组 Lo_D、Hi_D 对信号进行分解。
(2) idwt 函数功能:一维离散小波反变换格式:X=idwt(cA,cD,'wname')X=idwt(cA,cD,Lo_R,Hi_R)X=idwt(cA,cD,'wname',L)函数 fft、fft2 和 fftn 分X=idwt(cA,cD,Lo_R,Hi_R,L)说明:X=idwt(cA,cD,'wname') 由近似分量 cA 和细节分量 cD 经小波反变换重构原始信号 X 。
'wname' 为所选的小波函数X=idwt(cA,cD,Lo_R,Hi_R) 用指定的重构滤波器 Lo_R 和Hi_R 经小波反变换重构原始信号 X 。
X=idwt(cA,cD,'wname',L) 和X=idwt(cA,cD,Lo_R,Hi_R,L) 指定返回信号 X 中心附近的 L 个点。
2 二维小波变换的 Matlab 实现二维小波变换的函数别可以实现一维、二维和 N 维 DFT函数名函数功能---------------------------------------------------dwt2 二维离散小波变换wavedec2 二维信号的多层小波分解idwt2 二维离散小波反变换waverec2 二维信号的多层小波重构wrcoef2 由多层小波分解重构某一层的分解信号upcoef2 由多层小波分解重构近似分量或细节分量detcoef2 提取二维信号小波分解的细节分量appcoef2 提取二维信号小波分解的近似分量upwlev2 二维小波分解的单层重构dwtpet2 二维周期小波变换idwtper2 二维周期小波反变换----------------------------------------------------------- (1) wcodemat 函数功能:对数据矩阵进行伪彩色编码函数 fft、fft2 和 fftn 分格式:Y=wcodemat(X,NB,OPT,ABSOL)Y=wcodemat(X,NB,OPT)Y=wcodemat(X,NB)Y=wcodemat(X)说明:Y=wcodemat(X,NB,OPT,ABSOL) 返回数据矩阵 X 的编码矩阵Y ;NB 伪编码的最大值,即编码范围为 0~NB,缺省值 NB=16;OPT 指定了编码的方式(缺省值为 'mat'),即:别可以实现一维、二维和 N 维 DFTOPT='row' ,按行编码OPT='col' ,按列编码OPT='mat' ,按整个矩阵编码函数 fft、fft2 和 fftn 分ABSOL 是函数的控制参数(缺省值为 '1'),即:ABSOL=0 时,返回编码矩阵ABSOL=1 时,返回数据矩阵的绝对值 ABS(X)1. 离散傅立叶变换的 Matlab实现(2) dwt2 函数功能:二维离散小波变换格式:[cA,cH,cV,cD]=dwt2(X,'wname')[cA,cH,cV,cD]=dwt2(X,Lo_D,Hi_D)说明:[cA,cH,cV,cD]=dwt2(X,'wname')使用指定的小波基函数'wname' 对二维信号 X 进行二维离散小波变幻;cA,cH,cV,cD 分别为近似分量、水平细节分量、垂直细节分量和对角细节分量;[cA,cH,cV,cD]=dwt2(X,Lo_D,Hi_D) 使用指定的分解低通和高通滤波器 Lo_D 和 Hi_D 分解信号 X 。

Matlab小波函数一、Matlab小波去噪基本原理1、带噪声的信号一般是由含有噪声的高频信号和原始信号所在的低频信号。
利用多层小波,将高频噪声信号从混合信号中分解出来。
2、选择合适的阈值对图像的高频信号进行量化处理3、重构小波图像:依据图像小波分解的低频信号与处理之后的高频信号来重构图像的信息。
二、第二代小波变换1、构造方法特点:(1)继承了第一代小波的多分辨率的特性。
(2)不依赖fourior变换,直接在时域完成小波变换。
(3)变换之后的系数可以是整数。
(4)图像恢复质量与变换是边界采用何种延拓方式无关。
2、优点:算法简单,速度快,适合并行处理。
对存需求量小,便于DSP芯片实现、可用于本位操作运算。
3、提升原理:构造紧支集双正交小波(1)步骤:分裂—预测—更新(2)分解与重构三、matlab小波函数库1、matlab小波通用函数:(1)wavemngr函数【小波管理器(用于小波管理,添加、删除、储存、读取小波)】wavemngr(‘add’,FN,FSN,WT,NUMS,FILE)wavemngr(‘add’,FN,FSN,WT,NUMS,FILE,B)% 添加小波函数,FN为family name,FSN为family short name WT为小波类型:WT=1表示正交小波,=2表示非正交小波,=3表示带尺度函数的小波,=4表示无尺度函数的小波,=5表示无尺度函数的复小波。
小波族只有一个小波,则NUMS=“,否则NUMS表示小波参数的字符串FILE表示文件名B=[lb ub]指定小波有效支撑的上下界wavemngr(‘del’,N) %删除小波wavemngr(‘restore’)/ wavemngr(‘restore’,IN2) %保存原始小波OUT1= wavemngr(‘read’) %返回小波族的名称OUT1= wavemngr(‘read’,IN2) %返回所有小波的名称OUT1= wavemngr(‘read_asc’)%读取wavelets.asc文件并返回小波信息(2)scal2frq函数【尺度转换频率】F=scal2frq(A,’wname’,DELTA)%返回由尺度A,小波函数“wname”和采样周期DELTA决定的准频率。

matlab小波分解与重构-回复Matlab小波分解与重构小波分解与重构是一种在信号处理领域广泛应用的技术,通过对信号进行小波分解可以提取信号中的不同频率成分,并对这些成分进行重构,从而实现信号的压缩、降噪、特征提取等一系列应用。
在Matlab中,小波分解与重构可以通过Wavelet Toolbox实现。
本文将详细介绍Matlab中的小波分解与重构的步骤和应用。
一、准备工作在进行小波分解与重构之前,首先需要导入Wavelet Toolbox。
在MATLAB命令窗口中输入"wavelet"命令,或者直接点击MATLAB工具栏的"Apps"选项卡,然后在"Wavelet Toolbox"中选择Wavelet Analyzer 来打开Wavelet Toolbox工具箱。
二、小波分解1. 导入信号在开始之前,需要先导入需要进行小波分解与重构的信号。
可以通过MATLAB的文件读取函数来读取信号数据。
例如,可以使用`audioread`函数来导入音频信号:matlab[x, fs] = audioread('your_audio_file.wav');其中,`x`为读取到的音频信号,`fs`为采样率。
2. 选择小波函数和参数在进行小波分解之前,需要选择合适的小波函数和分解层数。
在Wavelet Analyzer工具箱中,可以通过"Wavelet"选项卡来选择小波函数。
常用的小波函数有haar、db、sym等。
选择小波函数后,需要指定小波的分解层数。
3. 进行小波分解在选择好小波函数和参数后,可以使用`wavedec`函数进行小波分解。
语法如下:matlab[c, l] = wavedec(x, n, wavelet)其中,`x`为输入信号,`n`为小波的分解层数,`wavelet`为选择的小波函数。
`c`为分解系数向量,`l`为各个分解层级的长度向量。

function [cA,cD] = mydwt(x,lpd,hpd,dim);% 函数[cA,cD]=MYDWT(X,LPD,HPD,DIM) 对输入序列x进行一维离散小波分解,输出分解序列[cA,cD]% 输入参数:x——输入序列;% lpd——低通滤波器;% hpd——高通滤波器;% dim——小波分解级数。
% 输出参数:cA——平均部分的小波分解系数;% cD——细节部分的小波分解系数。
cA=x; % 初始化cA,cDcD=[];for i=1:dimcvl=conv(cA,lpd); % 低通滤波,为了提高运行速度,调用MATLAB提供的卷积函数conv()dnl=downspl(cvl); % 通过下抽样求出平均部分的分解系数cvh=conv(cA,hpd); % 高通滤波dnh=downspl(cvh); % 通过下抽样求出本层分解后的细节部分系数cA=dnl; % 下抽样后的平均部分系数进入下一层分解cD=[cD,dnh]; % 将本层分解所得的细节部分系数存入序列cDendfunction y=downspl(x);% 函数Y=DOWMSPL(X) 对输入序列进行下抽样,输出序列Y。
% 下抽样是对输入序列取其偶数位,舍弃奇数位。
例如x=[x1,x2,x3,x4,x5],则y=[x2,x4].N=length(x); % 读取输入序列长度M=floor(N/2); % 输出序列的长度是输入序列长度的一半(带小数时取整数部分)i=1:M;y(i)=x(2*i); function y = myidwt(cA,cD,lpr,hpr);% 函数MYIDWT() 对输入的小波分解系数进行逆离散小波变换,重构出信号序列y% 输入参数:cA ——平均部分的小波分解系数;% cD ——细节部分的小波分解系数;% lpr、hpr ——重构所用的低通、高通滤波器。
lca=length(cA); % 求出平均、细节部分分解系数的长度lcd=length(cD);while (lcd)>=(lca) % 每一层重构中,cA 和cD 的长度要相等,故每层重构后,% 若lcd小于lca,则重构停止,这时的cA 即为重构信号序列y 。

matlab小波滤波器代码-回复在MATLAB中实现小波滤波器的代码,可以通过以下步骤来完成:第一步:导入信号数据在MATLAB中,首先需要导入待处理的信号数据。
可以使用`wavread`函数读取声音文件,或者使用`load`函数导入其他格式的数据。
matlab[data, fs] = wavread('sound.wav');这里`data`是读取到的信号数据,`fs`是采样率。
第二步:选择小波基函数小波滤波器通过对信号进行小波变换来实现滤波效果。
在MATLAB 中,可以选择不同的小波基函数进行变换。
常用的小波基函数包括`haar`、`dbN`(N是小波基的阶数)、`coifN`、`symN`等。
这里以`haar`小波基为例。
matlabwaveletName = 'haar';第三步:进行小波变换使用`wavedec`函数进行小波变换,将信号分解为多个尺度的小波系数。
matlab[level1, level2, level3, level4] = wavedec(data, 4, waveletName);这里将信号分解为4个尺度的小波系数,分别存储在`level1`、`level2`、`level3`和`level4`变量中。
第四步:滤波在小波变换后,可以对小波系数进行滤波操作。
可以通过设定一个阈值,将小波系数中小于该阈值的部分设为0,从而达到去噪的效果。
matlabthreshold = 0.5;level1(filteredLevel1 < threshold) = 0;level2(filteredLevel2 < threshold) = 0;level3(filteredLevel3 < threshold) = 0;level4(filteredLevel4 < threshold) = 0;这里使用了一个阈值为0.5的例子,小于该阈值的小波系数将被设为0。

matlab程序的高斯谐波小波滤波的实现-概述说明以及解释1.引言1.1 概述概述:在数字图像处理领域,滤波是一种常用的图像增强技术,旨在消除图像中的噪声,并凸显图像中的细节和特征。
高斯谐波小波滤波是一种有效的滤波方法,通过结合高斯滤波、谐波滤波和小波变换技术,能够在保持图像细节的同时有效地去除噪声。
本文将介绍如何利用Matlab编程实现高斯谐波小波滤波,包括原理、实现步骤以及实现效果评估等内容。
通过本文的学习,读者将能够了解该滤波方法的优势和应用前景,为进一步的图像处理工作提供参考和指导。
1.2 文章结构本文主要分为引言、正文和结论三个部分。
在引言部分中,我们将介绍本文的概述,包括高斯谐波小波滤波的背景和意义,引出文章的主要内容。
同时,我们还会说明文章的结构,分析每个部分的主要内容和目标。
在正文部分中,我们将首先介绍Matlab程序的基本信息,包括程序的功能和特点。
然后,我们将详细解释高斯谐波小波滤波的原理,包括其工作原理和优势。
最后,我们将详细阐述实现这一滤波方法的步骤,以便读者能够清楚地了解如何在Matlab中实现高斯谐波小波滤波。
在结论部分,我们将对实现效果进行评估,分析该滤波方法的优点和不足。
同时,我们还将展望该方法在未来的应用前景,总结全文的主要内容,为读者提供一个全面的结论。
1.3 目的本文的目的是介绍利用Matlab程序实现高斯谐波小波滤波的方法。
通过详细介绍高斯谐波小波滤波的原理和实现步骤,读者可以了解这种滤波方法的具体操作步骤和实现过程。
同时,通过对实现效果的评估和应用前景的展望,希望读者能够深入了解高斯谐波小波滤波在信号处理中的作用和价值,以及它在实际应用中的潜力和优势。
最终,通过总结本文的内容,读者能够对高斯谐波小波滤波有一个全面的认识,并能够运用Matlab 程序进行相关领域的研究和应用。
2.正文2.1 Matlab程序介绍Matlab是一种强大的数学软件,广泛应用于科学计算、数据分析和图形绘制等领域。

《现代信号处理》大作业基于Matlab的小波分解、去噪与重构目录一作业内容及要求 (3)1.1 作业内容 (3)1.2 作业要求 (3)二系统原理 (3)2.1 小波变换原理 (3)2.2 阈值去噪原理 (3)三系统分析及设计 (5)3.1 图像分解 (5)3.2 高频去噪 (5)3.3 图像重构 (6)四程序编写 (7)4.1 main函数 (7)4.2 分解函数 (9)4.2.1 二维分解函数 (9)4.2.2 一维分解函数 (10)4.3 卷积函数 (10)4.4 采样函数 (11)4.4.1 下采样函数 (11)4.4.2 上采样函数 (11)4.5 重构函数 (12)4.5.1 二维重构函数 (12)4.5.2 一维重构函数 (13)五结果分析及检验 (14)5.1 结果分析 (14)5.2 结果检验 (16)六心得体会 (18)参考文献 (19)一作业内容及要求1.1 作业内容用小波对图像进行滤波分解、去噪,然后重构。
1.2 作业要求用小波对图像进行滤波分解、去噪,然后重构。
具体要求:(1) 被处理图像可选择:woman, wbarb, wgatlin, detfingr, tire.;(2) 可以选择db等正交小波、或双正交小波(或用几种小波);(3) 用选用小波的分解滤波器通过定义的卷积函数conv_my( )对图像二维数组进行小波分解,并进行下采样,获取CA、CV、CD、CH等分解子图;(4) 对高频信号子图进行去噪处理,可以采用软阈值、硬阈值等方法;(5) 用选用小波的综合滤波器对去噪的子图进行图像重构。
二系统原理2.1 小波变换原理小波变换的一级分解过程是,先将信号与低通滤波器卷积再下采样可以得到低频部分的小波分解系数再将信号与高通滤波器卷积后下采样得到高频部分的小波分解系数;而多级分解则是对上一级分解得到的低频系数再进行小波分解,是一个递归过程。
二维小波分解重构可以用一系列的一维小波分解重构来实现。
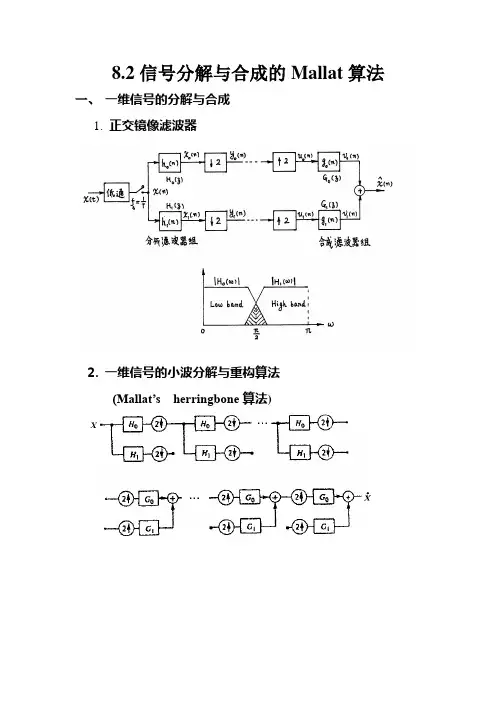
8.2信号分解与合成的Mallat算法一、一维信号的分解与合成1. 正交镜像滤波器2. 一维信号的小波分解与重构算法(Mallat’s herringbone算法)二、二维信号的分解与重构三、用Matlab实现图像的分解与合成1.dwt2与idwt2dwt2为一层二维离散小波分解函数,调用格式:[cA,cH,cV,cD]=dwt2(X,’wname’)% 用指定小波基对图像X进行一层二维离散小波变换分解。
’wname’为小波基的名称,cA为近似(低频)图像矩阵,cH, cV, cD分别为小波分解的水平方向细节系数,垂直方向细节系数,对角线方向细节系数。
[cA,cH,cV,cD]=dwt2(X,Lo_D,Hi_D) % 用指定的低通分解滤波器Lo_D和高通分解滤波器Hi_D对图像X进行二维离散小波分解。
Lo_D与Hi_D的长度必须一致。
idwt2为一层二维离散小波重构函数,调用格式为:X=idwt2(cA,cH,cV,cD,’wname’)% 用指定小波重构图像X,wname为小波基的名称。
X=idwt2(cA,cH,cV,cD,Lo_R,Hi_R)% 用指定低通重构滤波器Lo_R和高通重构滤波器Hi_R重构图像X,Lo_R与Hi_R的长度必须一致。
2.wavedec2与vaverec2wavedec2为多层二维离散小波分解函数,其调用格式为:[C,S]=wavedec2(X,N,’wname’)% 用指定小波基对图像X进行N层二维离散小波分解。
N为正整数,C为小波分解矢量,S为相应的标记矩阵。
C = [ A(N) | H(N) | V(N) | D(N) | ...H(N-1) | V(N-1) | D(N-1) | ... | H(1) | V(1) | D(1) ].A = approximation coefficientsH = horizontal detail coefficientsV = vertical detail coefficientsD = diagonal detail coefficients矩阵S形如S(1,:) = size of approximation coefficients(N)S(i,:) = size of detail coefficients(N-i+2) for i = 2, ...N+1 S(N+2,:) = size(X).wavwrec2为多层二维离散小波重构函数,其调用格式为:X=waverec2(C,S,’wname’) %利用指定小波基由矢量C和标记矩阵S重构图像X。
Matlab中的小波包重构是一种基于小波分析的信号处理方法,可以用于信号的去噪、压缩和重构等方面。
下面简单介绍一下Matlab中的小波包重构方法。
1. 小波包分解
首先,需要对待处理的信号进行小波包分解。
在Matlab中,可以使用wavedec函数进行小波包分解。
该函数的输入参数为待处理的信号和小波包参数,输出参数为小波包系数。
2. 小波包重构
小波包重构是指根据小波包系数重构原始信号的过程。
在Matlab中,可以使用waverec函数进行小波包重构。
该函数的输入参数为待重构的信号和小波包系数,输出参数为重构后的信号。
除了waverec函数,Matlab中还提供了其他一些小波重构相关的函数,如wfilters函数用于获取小波函数,wrcoef函数用于获取小波系数等。
需要注意的是,小波包重构的结果受到小波函数的选择、分解层数和重构参数等因素的影响。
因此,在进行小波包重构时需要根据实际情况进行参数调整和优化,以获得更好的重构效果。
matlab小波变换滤波小波变换滤波是一种常用的信号处理方法,该方法可以将信号分解成不同的频率成分,并可以根据需要选择性地去除或增强特定频率成分。
在Matlab中,我们可以使用小波变换函数进行滤波处理。
我们需要了解什么是小波变换。
小波变换是一种时频分析方法,它可以在时间和频率上同时描述信号的特征。
与傅里叶变换不同,小波变换可以提供更加精细的频率分辨率,因此在信号处理中有着广泛的应用。
在Matlab中,我们可以使用`wavelet`工具箱中的函数来实现小波变换滤波。
首先,我们需要选择一个合适的小波函数作为基函数。
常用的小波函数有Haar小波、Daubechies小波、Symlet小波等等。
选择不同的小波函数会对信号的分解和重构产生不同的效果。
对于一个给定的信号,我们可以使用`wavedec`函数进行小波分解,得到信号在不同尺度上的小波系数。
小波系数表示了信号在不同频率上的能量分布情况。
然后,我们可以根据需要选择性地去除或增强特定频率成分。
去除高频成分可以实现信号的平滑处理,而去除低频成分可以实现信号的细节增强。
在滤波之后,我们可以使用`waverec`函数进行小波重构,得到滤波后的信号。
重构后的信号可以保留原始信号的主要特征,同时去除或增强特定频率成分。
通过调整滤波器的参数,我们可以实现不同程度的滤波效果。
除了滤波之外,小波变换还可以用于信号的压缩和去噪。
通过选择合适的小波基函数和调整滤波器的参数,我们可以将信号的冗余信息去除,从而实现信号的压缩。
同时,小波变换还可以有效地去除信号中的噪声,提高信号的质量。
在实际应用中,小波变换滤波经常用于图像处理、音频处理、语音识别等领域。
例如,在图像处理中,我们可以利用小波变换滤波对图像进行边缘检测、纹理分析等操作;在音频处理中,我们可以利用小波变换滤波对音频信号进行降噪、音调分析等操作;在语音识别中,我们可以利用小波变换滤波对语音信号进行特征提取、语音识别等操作。
m=load('A.txt');N=length(m);for i=1:N-1 ;q(i,1)=m(i,1);end;d=q';s1=d;change=1000;[c,l] = wavedec(d,3,'db4');%提取小波分解后的低频系数ca3=appcoef(c,l,'db4',3);%提取各层小波分解后的高频系数cd3=detcoef(c,l,3);cd2=detcoef(c,l,2);cd1=detcoef(c,l,1);%对信号强制消噪cdd3=zeros(1,length(cd3));%第三层高频系数cd3全置0 cdd2=zeros(1,length(cd2));%第二层高频系数cd2全置0 cdd1=zeros(1,length(cd1));%第一层高频系数cd1全置0c1=[ca3,cdd3,cdd2,cdd1];%构建新的系数矩阵s2=waverec(c1,l,'db4')%分解新的结构%[thr,sorh,keepapp]=ddencmp('den','wv',d);%s2=wdencmp('gbl',c,l,'db4',4,thr,sorh,keepapp);%subplot(413)%plot(1:change,s2(1:change));%title('默认软阈值消噪后信号')figure(1)subplot(9,2,1)plot(1:change,s1(1:change))title('原始信号')ylabel('S1')subplot(9,2,2)plot(1:change,s2(1:change))title('强制消噪后信号')ylabel('S2')wpt=wpdec(s1,3,'db1','shannon');%plot(wpt);%重构第三层8个节点小波系数s130=wprcoef(wpt,[3,0]);s131=wprcoef(wpt,[3,1]);s132=wprcoef(wpt,[3,2]);s133=wprcoef(wpt,[3,3]);s134=wprcoef(wpt,[3,4]);s135=wprcoef(wpt,[3,5]);s136=wprcoef(wpt,[3,6]);s137=wprcoef(wpt,[3,7]);%计算第三层8个节点小波能量s10=norm(s130);s11=norm(s131);s12=norm(s132);s13=norm(s133);s14=norm(s134);s15=norm(s135);s16=norm(s136);s17=norm(s137);%计算方差st10=std(s130);st11=std(s131);st12=std(s132);st13=std(s133);st14=std(s134);st15=std(s135);st16=std(s136);st17=std(s137);disp('正常信号的特征向量');snorm1=[s10,s11,s12,s13,s14,s15,s16,s17];std1=[st10,st11,st12,st13,st14,st15,st16,st17];%显示三层个节点小波系数subplot(9,2,3);plot(1:change,s130(1:change));ylabel('S130'); subplot(9,2,5);plot(1:change,s131(1:change));ylabel('S131'); subplot(9,2,7);plot(1:change,s132(1:change));ylabel('S132'); subplot(9,2,9);plot(1:change,s133(1:change));ylabel('S133'); subplot(9,2,11);plot(1:change,s134(1:change));ylabel('S134');subplot(9,2,13);plot(1:change,s135(1:change));ylabel('S135'); subplot(9,2,15);plot(1:change,s136(1:change));ylabel('S136'); subplot(9,2,17);plot(1:change,s137(1:change));ylabel('S137');。
去年11月发布了一系列有关小波变换和图像处理的文章,把学习小波过程中的心得体会和编写的程序放在网上和大家共享交流。
半年来,感谢大家的关注和帮助,在相互的讨论交流中,我不断地从大家提出的问题中拓展自己的知识面,对小波的理论及其应用有了更深入的了解和掌握。
根据和大家讨论交流中发现的问题,对博客中的程序进行修正。
有关小波图像分解和重构的两篇文章中分享的程序,存在下列问题:(1)程序所用的小波函数只有非标准的Haar小波,其滤波器组为Lo_D=[1/2 1/2], Hi_D=[-1/2 1/2],是固化在mydwt2.m 的程序中的,不能选择其他的小波函数;(2)非标准的Haar小波,其分解出来的系数矩阵中,高频系数的细节内容(轮廓、边缘等特征)不明显;(3)函数mydwt2 中列变换的矩阵对象为输入矩阵,这是错误的,其矩阵对象应该是行变换后的缓存矩阵;(4)函数mydwt2 的输出用[LL,HL,LH,HH]表示,不是很规范,应改为[cA,cV,cH,cD]来表示,即一级小波变换输出的系数矩阵有4个部分:平均部分、垂直细节部分、水平细节部分和对角线细节部分。
(5)函数mywavedec2 的输出y 是与输入矩阵x 相同大小的矩阵,并且已将N级分解后所有的平均、细节系数组合成一体的。
实际上,这种定义只对Haar小波有效。
(6)原程序中要调用modmat 函数对图像矩阵进行修剪,使之能被2 的N 次方整除,主要是为了生成塔式结构图像而设的,对上述问题修正后,这个modmat 函数已不需使用了。
针对上述问题,我对程序作了修正,发布在今天的3篇文章里,请大家点击查看。
新修正的程序更为简洁易懂,功能也有所增强,可以用任意的小波函数进行小波分解,可根据小波分解系数矩阵重构出指定分解级的低频系数和原始图像.Matlab小波分析工具箱丰富的函数和强大的仿真功能为我们学习小波、用好小波提供了方便、快捷的途径,但是,如果我们要深入掌握小波分析的原理,真正学好、用好小波,就应该尽量用自己编写的程序去实现小波变换和信号分析,尽量在自己的程序中少调用Matlab提供的函数,多用自己的理解去编写相关的小波函数,这样的过程是一个探索、求知的过程,更能让我们体会到小波的强大和学习的乐趣。
matlab t1小波滤波算法-回复Matlab T1小波滤波算法中括号内的内容是:matlab t1小波滤波算法。
在本文中,将详细介绍这一算法,并一步一步回答相关问题。
T1小波滤波算法是一种在Matlab 环境下进行信号处理的方法,它通过小波变换将信号分解成不同尺度的频率成分,并通过滤波将噪声去除,从而得到更清晰的信号。
1. 什么是小波滤波算法?小波滤波算法是一种通过小波分析进行滤波的方法。
小波分析是一种将信号分解成不同频率分量的技术,与傅里叶变换类似,但具有更好的时频局部化特性。
小波滤波算法利用小波的这种特性,能够更精确地定位和去除信号中的噪声。
2. 如何进行T1小波变换?T1小波变换是一种多尺度的小波变换方法,通过将信号进行多次迭代的小波分解,得到不同尺度的逼近系数和细节系数。
在Matlab中,可以使用内置的函数`wavedec`来实现T1小波变换。
使用方法如下:matlabwavelet = 'db4'; 选择小波基函数level = 5; 分解的层数[x, fs] = audioread('signal.wav'); 读取信号[c, l] = wavedec(x, level, wavelet); 进行T1小波变换这里选择了db4小波作为小波基函数,分解的层数为5。
函数`wavedec`的返回值`c`是小波系数的向量,`l`是每个尺度的系数长度。
3. 如何进行小波阈值滤波?小波阈值滤波是通过对小波系数进行阈值处理来去除噪声。
常用的小波阈值处理方法有软阈值和硬阈值。
软阈值将小于阈值的系数设置为0,并对大于阈值的系数进行缩放。
硬阈值直接将小于阈值的系数设置为0。
在Matlab中,可以使用内置的函数`wthresh`来实现小波阈值滤波。
使用方法如下:matlabthreshold = 0.1; 阈值s = wthresh(c, 's', threshold); 软阈值滤波h = wthresh(c, 'h', threshold); 硬阈值滤波这里选择了阈值为0.1,对小波系数进行软阈值和硬阈值滤波,分别得到了滤波后的系数`s`和`h`。
m=load('A.txt');
N=length(m);
for i=1:N-1 ;
q(i,1)=m(i,1);
end;
d=q';
s1=d;
change=1000;
[c,l] = wavedec(d,3,'db4');
%提取小波分解后的低频系数
ca3=appcoef(c,l,'db4',3);
%提取各层小波分解后的高频系数
cd3=detcoef(c,l,3);
cd2=detcoef(c,l,2);
cd1=detcoef(c,l,1);
%对信号强制消噪
cdd3=zeros(1,length(cd3));%第三层高频系数cd3全置0 cdd2=zeros(1,length(cd2));%第二层高频系数cd2全置0 cdd1=zeros(1,length(cd1));%第一层高频系数cd1全置0
c1=[ca3,cdd3,cdd2,cdd1];%构建新的系数矩阵
s2=waverec(c1,l,'db4')%分解新的结构
%[thr,sorh,keepapp]=ddencmp('den','wv',d);
%s2=wdencmp('gbl',c,l,'db4',4,thr,sorh,keepapp);
%subplot(413)
%plot(1:change,s2(1:change));
%title('默认软阈值消噪后信号')
figure(1)
subplot(9,2,1)
plot(1:change,s1(1:change))
title('原始信号')
ylabel('S1')
subplot(9,2,2)
plot(1:change,s2(1:change))
title('强制消噪后信号')
ylabel('S2')
wpt=wpdec(s1,3,'db1','shannon');
%plot(wpt);
%重构第三层8个节点小波系数
s130=wprcoef(wpt,[3,0]);
s131=wprcoef(wpt,[3,1]);
s132=wprcoef(wpt,[3,2]);
s133=wprcoef(wpt,[3,3]);
s134=wprcoef(wpt,[3,4]);
s135=wprcoef(wpt,[3,5]);
s136=wprcoef(wpt,[3,6]);
s137=wprcoef(wpt,[3,7]);
%计算第三层8个节点小波能量
s10=norm(s130);
s11=norm(s131);
s12=norm(s132);
s13=norm(s133);
s14=norm(s134);
s15=norm(s135);
s16=norm(s136);
s17=norm(s137);
%计算方差
st10=std(s130);
st11=std(s131);
st12=std(s132);
st13=std(s133);
st14=std(s134);
st15=std(s135);
st16=std(s136);
st17=std(s137);
disp('正常信号的特征向量');
snorm1=[s10,s11,s12,s13,s14,s15,s16,s17];
std1=[st10,st11,st12,st13,st14,st15,st16,st17];
%显示三层个节点小波系数
subplot(9,2,3);plot(1:change,s130(1:change));ylabel('S130'); subplot(9,2,5);plot(1:change,s131(1:change));ylabel('S131'); subplot(9,2,7);plot(1:change,s132(1:change));ylabel('S132'); subplot(9,2,9);plot(1:change,s133(1:change));ylabel('S133'); subplot(9,2,11);plot(1:change,s134(1:change));ylabel('S134');
subplot(9,2,13);plot(1:change,s135(1:change));ylabel('S135'); subplot(9,2,15);plot(1:change,s136(1:change));ylabel('S136'); subplot(9,2,17);plot(1:change,s137(1:change));ylabel('S137');。