2018-2019年石家庄一模：河北省石家庄市2018届高三第一次模拟考试数学(理)试题-附答案精品

2018届河北省石家庄市高三第一次模拟考试卷数学（文）注意事项：1．答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2．选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。

3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

4．考试结束后，请将本试题卷和答题卡一并上交。

第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合，，则（ ） A ． B ．C ．D ．2．复数（ ） A ． B ． C ．D ．3．已知四个命题：①如果向量与共线，则或；②是的必要不充分条件；③命题：，的否定：，；④“指数函数是增函数，而是指数函数，所以是增函数”此三段论大前提错误，但推理形式是正确的． 以上命题正确的个数为（ ） A ．0B ．1C ．2D ．34．若数列满足，，则的值为（ ） A ．2 B ．-3 C ． D ．5．函数，其值域为，在区间上随机取一个数，则的概率是（ ） A ．B ．C ．D ．6．程序框图如图所示，该程序运行的结果为，则判断框中可填写的关于的条件是（ ）A ．B ．C ．D ．{}1,2,3,4,5,6,7U ={}3,A x x x =≥∈N U A =ð{}1,2{}3,4,5,6,7{}1,3,4,7{}1,4,712i1i-=+i i -13i2--33i2-a b =a b =-a b 3x ≤3x ≤p 0(0,2)x ∃∈200230x x --<p ⌝(0,2)x ∀∈2230x x --≥x y a =12x y ⎛⎫= ⎪⎝⎭12xy ⎛⎫= ⎪⎝⎭{}n a 12a =111nn na a a ++=-2018a 12-13()()20x f x x =<D ()1,2-x x D ∈1213142325s =i i 4?≤i 4?≥i 5?≤i 5?≥此卷只装订不密封 班 姓名 准考证号 考场号 座位号7．南宋数学家秦九韶早在《数书九章》中就独立创造了已知三角形三边求其面积的公式：“以小斜幂并大斜幂，减中斜幂，余半之，自乘于上，以小斜幂乘大斜幂减之，以四约之，为实，一为从隅，开方得积．”（即：，），并举例“问沙田一段，有三斜（边），其小斜一十三里，中斜一十四里，大斜一十五里，欲知为田几何？”则该三角形田面积为（ ） A ．84平方里B ．108平方里C ．126平方里D ．254平方里8．如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的体积为（ ）A ．B ．C ．D ．9．已知是定义在上的偶函数，且在上为增函数，则的解集为（ ） A ． B ．C ．D ．10．抛物线：的焦点为，其准线与轴交于点，点在抛物线上，当的面积为（ ）A ．1B ．2C ．D ．411．在中，，，则的最大值为（ ） AB ．C ．D ．12．已知，分别为双曲线的左焦点和右焦点，过的直线与双曲线的右支交于，两点，的内切圆半径为，的内切圆半径为，若，则直线的斜率为（ ） A ．1BC ．2D．第Ⅱ卷二、填空题：本大题共4小题，每小题5分．13．设向量，，若，则 ．14．，满足约束条件：，则的最大值为 ．15．甲、乙、丙三位同学，其中一位是班长，一位是体育委员，一位是学习委员，已知丙的年龄比学委的大，甲与体委的年龄不同，体委比乙年龄小．据此推断班长是 ．16．一个直角三角形的三个顶点分别在底面棱长为2的正三棱柱的侧棱上，则该直角三角形斜边的最小值为 ．三、解答题：解答应写出文字说明、证明过程或演算步骤．17．（12分）已知是公差不为零的等差数列，满足，且、、成等比数列．S =a b c >>23π43π2π83π()f x []2,3b b -+[]2,0b -()()13f x f -≥[]3,3-[]2,4-[]1,5-[]0,6C 214y x =F l y A M C MA MF=AMF △ABC △2AB =6C π=AC 1F 2F ()222210,0x y a b a b-=>>2F l A B 12AF F ∆1r 12BF F △2r 122r r =l ()1,2m =a ()1,1m =+b ⊥a b m =x y 11y x x y y ≤⎧⎪-≤⎨⎪≥-⎩2z x y =+{}n a 37a =2a 4a 9a（1）求数列的通项公式；（2）设数列满足，求数列的前项和．18．（12分）四棱锥的底面为直角梯形，，，，为正三角形．（1）点为棱上一点，若平面，，求实数的值； （2）若，求点到平面的距离．19．（12分）小明在石家庄市某物流派送公司找到了一份派送员的工作，该公司给出了两种日薪薪酬方案．甲方案：底薪100元，每派送一单奖励1元；乙方案：底薪140元，每日前55单没有奖励，超过55单的部分每单奖励12元．（1）请分别求出甲、乙两种薪酬方案中日薪（单位：元）与送货单数的函数关系式；（2）根据该公司所有派送员100天的派送记录，发现派送员的日平均派送单数满足以下表格：①根据以上数据，设每名派送员的日薪为（单位：元），这100天中甲、乙两种方案的日薪平均数及方差；②结合①中的数据，根据统计学的思想，帮助小明分析，他选择哪种薪酬方案比较合适，并说明你的理由．{}n a {}n b 1n n n b a a +=⋅1n b ⎧⎫⎨⎬⎩⎭n n S S ABCD -ABCD AB CD ∥AB BC ⊥222AB BC CD ===SAD △M AB BC ∥SDM AM AB λ=λBC SD ⊥B SAD y n X X（参考数据：，，，，，，，，）20．（12分）已知椭圆：的左、右焦点分别为，，且离心率为，为椭圆上任意一点，当时，的面积为1． （1）求椭圆的方程；（2）已知点是椭圆上异于椭圆顶点的一点，延长直线，分别与椭圆交于点，，设直线的斜率为，直线的斜率为，求证：为定值．20.60.36=21.4 1.96=22.6 6.76=23.411.56=23.612.96=24.621.16=215.6243.36=220.4416.16=244.41971.36=C 22221(0)x y a b a b +=>>1F 2F 2M 1290F MF ∠=︒12F MF △C A C 1AF 2AF B D BD 1k OA 2k 12k k ⋅21．（12分）已知函数，，在处的切线方程为． （1）求，；（2）若，证明：．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分． 22．（10分）【选修4-4：坐标系与参数方程】在平面直角坐标系中，曲线的参数方程为（，为参数），以坐标原点为极点，轴正半轴为极轴建立极坐标系，直线的极坐标方程为，若直线与曲线相切；（1）求曲线的极坐标方程；（2）在曲线上取两点，与原点构成，且满足，求面积的最大值．()()()e x f x x b a =+-()0b >()()1,1f --()e 1e e 10x y -++-=a b 0m ≤()2f x mx x ≥+xOyC cos 1sin x r y r ϕϕ⎧=⎪⎨=+⎪⎩0r >ϕO x l sin 13ρθπ⎛⎫-= ⎪⎝⎭l C C C M N O MON △6MON π∠=MON △23．（10分）【选修4-5：不等式选讲】已知函数； （1）求实数的取值范围；（2）设实数为的最大值，若实数，，满足，求的最小值．()f x =R m t m a b c 2222a b c t ++=222111123a b c +++++2018届河北省石家庄市高三第一次模拟考试卷数学（文） 答 案一、选择题． 1-5：ACDBB 6-10：CABBB 11、12：DD二、填空题．13． 14．3 15．乙 16．三、解答题．17．【答案】（1）；（2）． 【解析】（1）设数列的公差为，且由题意得，即，解得， ∴数列的通项公式． （2）由（1）得，13-32n a n =-31n nS n =+{}n a d 0d ≠242937a a a a ⎧=⎪⎨=⎪⎩()()()21777627d d d a d ⎧+=-+⎪⎨+=⎪⎩13,1d a =={}n a 32n a n =-()()13231n n n b a a n n +=⋅=-+111133231n b n n ⎛⎫∴=- ⎪-+⎝⎭12111111111134473231n n S b b b n n ⎛⎫=+++=-+-++- ⎪-+⎝⎭． 18．【答案】（1）；（2【解析】（1）∵平面SDM ，平面ABCD ， 平面平面，∴，∵，∴四边形BCDM 为平行四边形， 又，∴M 为AB 的中点． ∵，．（2）∵， ， ∴平面， 又∵平面，∴平面平面，平面平面，在平面内过点作直线于点，则平面， 在和中，11133131nn n ⎛⎫=-= ⎪++⎝⎭12BC ∥BC ⊂SDMABCD DM =BC DM ∥DC AB //CD AB 2=AB AM λ=12λ∴=BC ⊥SD BC ⊥CD BC ⊥SCD BC ⊂ABCD SCD ⊥ABCD SCDABCD CD =SCD S SE ⊥CD E SE ⊥ABCD Rt SEA Rt SED∵，∴， 又由题知，∴， 由已知求得，∴，连接BD ，则，又求得∴由点B 到平面的距离为． 19．【答案】（1）见解析；（2）①见解析；②见解析．【解析】（1）甲方案中派送员日薪（单位：元）与送单数的函数关系式为：，乙方案中派送员日薪（单位：元）与送单数的函数关系式为：， （2）①、由表格可知，甲方案中，日薪为152元的有20天，日薪为154元的有30天，日薪为156元的有20天，日薪为158元的有20天，日薪为160元的有10天，则， SA SD =AE DE =45EDA ∠=AE ED ⊥AD 1AE ED SE ===111133S ABD V -=⨯⨯=三棱锥SAD B ASD S ABD V V --=三棱锥三棱锥SAD y n 100,y n n =+∈N y n ()()140,55,12520,55,n n y n n n ≤∈⎧⎪=⎨->∈⎪⎩N N ()1=15220+15430+15620+15820+16010=155.4100x ⨯⨯⨯⨯⨯甲，乙方案中，日薪为140元的有50天，日薪为152元的有20天，日薪为176元的有20天，日薪为200元的有10天，则， ， ②、答案一：由以上的计算可知，虽然，但两者相差不大，且远小于，即甲方案日薪收入波动相对较小，∴小明应选择甲方案． 答案二：由以上的计算结果可以看出，，即甲方案日薪平均数小于乙方案日薪平均数，∴小明应选择乙方案．20．【答案】（1）；（2）见解析．【解析】（1）设，，由题得， 解得，则，()()()()222221=20152155.4+30154155.4+20156155.4+20158155.4100S ⎡⨯-⨯-⨯-⨯-⎣甲()210160155.4 6.44⎤+⨯-=⎦()1=14050+15220+17620+20010155.6100x ⨯⨯⨯⨯乙=()()()()222221=50140155.6+20152155.6+20176155.6+10200155.6100S ⎡⎤⨯-⨯-⨯-⨯-⎣⎦乙404.64=x x <乙甲2S 甲2S 乙x x <乙甲2212x y +=11MF r =22MF r =12222121224112c e a r r ar r c r r ⎧==⎪⎪+=⎪⎨+=⎪⎪⋅=⎪⎩a =1c =21b =椭圆的方程为．（2）设，，，当直线的斜率不存在时，设，则，直线的方程为代入，可得，直线的斜率为，直线的斜率为， 当直线的斜率不存在时，同理可得．当直线、的斜率存在时，设直线的方程为，则由消去可得：，又，则，代入上述方程可得 ∴C 2212x y +=()()0000,0A x y x y ⋅≠()11,B x y ()22,C x y 1AF 1,2A ⎛- ⎝⎭1,2B ⎛-- ⎝⎭2AF )1y x =-2212x y +=25270x x --=275x ∴=2y =7,510D ⎛- ⎝⎭∴BD ()1715k ⎛- ⎝⎭==--OA 2k =121626k k ⎛∴⋅=-=- ⎝⎭2AF 1216k k ⋅=-1AF 2AF 10±≠x 1AF ()0011y y x x =++()00221112y y x x x y ⎧=+⎪+⎪⎨⎪+=⎪⎩x ()()222222000001242210x y x y x y x ⎡⎤++++-+=⎣⎦220012x y +=220022y x =-，，则 ，设直线的方程为，同理可得， 直线的斜率为， 直线的斜率为， ． ∴直线与的斜率之积为定值，即．21．【答案】（1），；（2）见解析．【解析】（1）由题意，∴，又，∴， 若，则，与矛盾，故，．()()22200003222340x x x x x x ++---=2000101003434,3232x x x x x x x x ----∴⋅=∴=++000100034113232y x y y x x x ⎛⎫--=+=-⎪+++⎝⎭000034,2323x y B x x ⎛⎫+∴-- ⎪++⎝⎭2AF ()0011y y x x =--000034,2323x y D x x ⎛⎫- ⎪--⎝⎭∴BD 00000001220000002323434341224362323y y x x x y x y k x x x x x x +-+===-+--+-+OA 020y k x =∴20200001222200001123636366x x y y y k k x x x x -⋅=⋅===----BD OA 16-1216k k ⋅=-1a =1b =()10f -=()()1110e f b a ⎛⎫-=-+-= ⎪⎝⎭()()1e x f x x b a '=++-()111e eb f a '-=-=-+1ea =2e 0b =-<0b >1a =1b =（2）由（1）可知，， 由，可得，令， ， 当时，， 当时，设， ， 故函数在上单调递增，又，∴当时，，当时，， ∴函数在区间上单调递减，在区间上单调递增， 故 故．22．【答案】（1）；（2）【解析】（1）由题意可知直线的直角坐标方程为，曲线是圆心为，半径为的圆，直线与曲线相切，可得；可知曲线C 的方程为，∴曲线C 的极坐标方程为，()()()1e 1x f x x=+-()()00,10f f =-=0m ≤2x mx x ≥+()()()1e 1x g xx x =+--()()2e 2x g x x '=+-2x ≤-()()2e 220x g x x '=+-<-<2x >-()()()2e 2x h x g x x '==+-()()3e 0x h x x '=+>()g x '()2,-+∞()00g '=(),0x ∈-∞()0g x '<()0,x ∈+∞()0g x '>()g x (),0-∞()0,+∞()()()()2001e 1x g x g x x mx x ≥=⇒+-≥≥+()2f x mx x ≥+4sin 3ρθπ⎛⎫=+ ⎪⎝⎭2+l 2y =+C )r l C 2r ==(()2214x y +-=2cos 2sin 0ρθρθ--=即．（2）由（1）不妨设，，当时，∴面积的最大值为23．【答案】（1）；（2）．【解析】（1）由题意可知恒成立，令，去绝对值可得，画图可知的最小值为，∴实数的取值范围为； （2）由（1）可知，∴，4sin 3ρθπ⎛⎫=+ ⎪⎝⎭()1,M ρθ2,6N ρθπ⎛⎫+ ⎪⎝⎭()120,0ρρ>>121sin 4sin sin 231462MON S OM ON ρρθθπππ⎛⎫⎛⎫=⋅=+⋅+ ⎪ ⎪⎝⎭⎝⎭△22sin cos sin 2θθθθθ=+=sin 32θπ⎛⎫++ ⎪⎝⎭=12θπ=2MON S ≤△MON △23m ≤-3532x x m --≥()32x g x x -=-()()()()36,3263,036,0x x x g x x x x x x --≥⎧⎪=-=-<<⎨⎪-≤⎩()g x 3-m 3m ≤-2229a b c ++=22212315a b c +++++=()22222222211112311112312315a b c a b c a b c ⎛⎫++⋅+++++ ⎪+++⎝⎭++=+++， 当且仅当，即等号成立， ∴的最小值为．22222222222221313239312132315155b a c a c b a b a c b c ++++++++++++++++++=≥=2221235a b c +=+=+=2224,3,2a b c ===222111123a b c +++++35。

2018届石家庄市高中毕业班第一次模拟考试试卷文科综合能力测试第I卷（选择题共140分）本卷共35个小题，每小题4分，共140分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

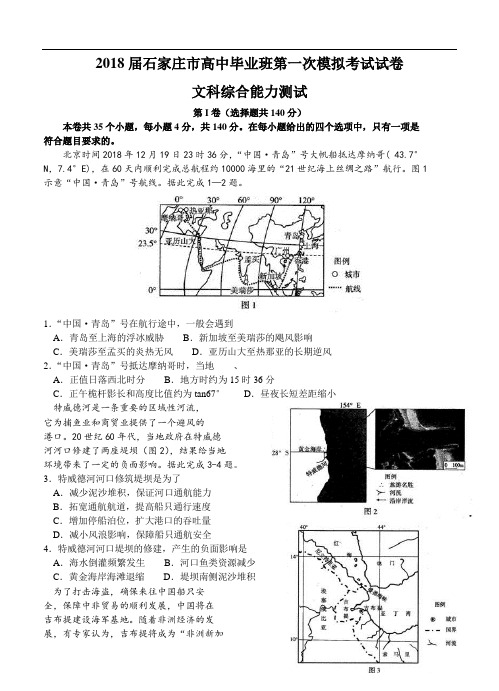
北京时间2018年12月19日23时36分，“中国·青岛”号大帆船抵达摩纳哥( 43.7°N，7.4°E)，在60天内顺利完成总航程约10000海里的“21世纪海上丝绸之路”航行。

图1 示意“中国·青岛”号航线。

据此完成1—2题。

1．“中国·青岛”号在航行途中，一般会遇到A．青岛至上海的浮冰威胁B．新加坡至美瑞莎的飓风影响C．美瑞莎至孟买的炎热无风D．亚历山大至热那亚的长期逆风2．“中国·青岛”号抵达摩纳哥时，当地、A．正值日落西北时分B．地方时约为15时36分C．正午桅杆影长和高度比值约为tan67°D．昼夜长短差距缩小特威德河是一条重要的区域性河流，它为捕鱼业和商贸业提供了一个避风的港口。

20世纪60年代，当地政府在特威德河河口修建了两座堤坝（图2），结果给当地环境带来了一定的负面影响。

据此完成3-4题。

3．特威德河河口修筑堤坝是为了A．减少泥沙堆积，保证河口通航能力B．拓宽通航航道，提高船只通行速度C．增加停船泊位，扩大港口的吞吐量D．减小风浪影响，保障船只通航安全4．特威德河河口堤坝的修建，产生的负面影响是A．海水倒灌频繁发生B．河口鱼类资源减少C．黄金海岸海滩退缩D．堤坝南侧泥沙堆积为了打击海盗，确保来往中国船只安全，保障中非贸易的顺利发展，中国将在吉布提建设海军基地。

随着非洲经济的发展，有专家认为，吉布提将成为“非洲新加坡”。

图3示意吉布提位置。

据此完成5-6题。

5．中国海军基地的建设，对当地社会经济的主要有利影响是A．促进基础设施的建设和完善B．加快产业结构的优化与升级C．带动旅游业等第三产业发展D．提高劳动力的科学文化素质6．吉布提将成为“非洲新加坡”的区位条件是A．海岸线曲折，多优良港湾B．非洲物产的重要出海门户C．沟通亚非国家的“十字路口”D．扼守曼德海峡，位于海上要冲罗讷河发源于阿尔卑斯山，每年注入地中海的水量占注入地中海河水总量的1/6以上，但是全流域性的大洪水并不多见。

2018年石家庄市高中毕业班第一次模拟考试高三数学(理科答案) 一、 选择题（A 卷）1-5 CBACD 6-10 BADCB 11-12BA 一、选择题（B 卷）1-5 DBADC 6-10 BACDB 11-12BA 二、 填空题14 815 []1,2- 16 2a π三、 解答题（阅卷时发现的正确解答，请教师参阅此评分标准酌情给分） 17解：（1）解法1∵11(),n n a S n N λ*+=+∈ ∴11n n a S λ-=+(2)n ≥∴1n n n a a a λ+-=，即1(1)n n a a λ+=+(2),10n λ≥+≠， 又1211,11,a a S λλ==+=+∴数列{}n a 为以1为首项，公比为1λ+的等比数列，…………………………………2分 ∴23(1)a λ=+， ∴24(1)1(1)3λλ+=+++，整理得2210λλ-+=，得1λ= (4)分∴12n n a -=，13(1)32n b n n =+-=- (6)分解法2：∵111,1(),n n a a S n N λ*+==+∈∴2111,a S λλ=+=+2321(11)121,a S λλλλλ=+=+++=++ ∴24(1)1213λλλ+=++++，整理得2210λλ-+=，得1λ= (2)分∴11(),n n a S n N *+=+∈ ∴11n n a S -=+(2)n ≥∴1n n n a a a +-=，即12n n a a +=(2)n ≥， 又121,2a a ==∴数列{}n a 为以1为首项，公比为2的等比数列，………………………………………4分 ∴12n n a -=，13(1)32n b n n =+-=-………………………………………………………………………6分 （2）1(32)2n n n a b n -=-g ∴121114272(32)2n n T n -=⋅+⋅+⋅++-⋅L L L ………………………① ∴12312124272(35)2(32)2n nn T n n -=⋅+⋅+⋅++-⋅+-⋅L ………②…………8分 ① —②得12111323232(32)2n n n T n --=⋅+⋅+⋅++⋅--⋅L12(12)13(32)212n nn -⋅-=+⋅--⋅-…………………………………10分整理得：(35)25n n T n =-⋅+…………………………………………………………12分18解：（Ⅰ）三个电子元件能正常工作分别记为事件,,A B C ，则112(),(),()223p A p B p C ===.依题意，集成电路E 需要维修有两种情形： ①3个元件都不能正常工作，概率为11111()()()()22312p p ABC p A p B p C ===⨯⨯=； …………2分②3个元件中的2个不能正常工作，概率为2()()()()p p ABC ABC ABC p ABC p ABC p ABC =++=++11111111241223223223123=⨯⨯+⨯⨯+⨯⨯== ……………5分所以,集成电路E 需要维修的概率为1211512312p p +=+=． ……………6分（Ⅱ）设ξ为维修集成电路的个数，则5(2,)12B ξ:，而100X ξ=，2257(100)()()(),0,1,2.1212k k kP X k P k C k ξ-=====…………9分X 的分布列为：………………10分4935252500100200144721443EX ∴=⨯+⨯+⨯=或52501001002123EX E ξ==⨯⨯=. …………12分 19解：(1)证明一连接AC BD ，交于点F ,在平面PCA 中做EF ∥PC 交PA 于E ,因为PC ⊄平面BDE ，EF ⊂平面BDE PC ∥平面BDE ，---------------2AD 因为∥,BC 1,3AF AD FCBC ==所以因为EF ∥PC ,1=.3AE AF EP FC =所以-------------4证明二在棱PA 上取点E ，使得13AE EP=,------------2连接AC BD ，交于点F ,AD 因为∥,BCC1,2,AF AD FC BC AE AF EP FC ===所以所以 所以，EF ∥PC因为PC ⊄平面BDE ，EF ⊂平面BDE所以PC ∥平面BDE -------------4(2)取BC 上一点G使得BG =连结DG ,则ABGD 为正方形.过P 作PO ⊥平面ABCD ,垂足为O . 连结,,,OA OB OD OG .0,60AP AD AB PAB PAD ==∠=∠=，所以PAB ∆和PAD ∆都是等边三角形，因此PA PB PD ==, 所以OA OB OD ==,即点O 为正方形ABGD 对角线的交点,---------------7（或取BC 的中点G ,连结DG ,则ABGD 为正方形. 连接,AG BD 交于点O ，连接PO ，0,60AP AD AB PAB PAD ==∠=∠=，00,,,90,90.PAB PAD PA PB PD OD OB POB POD POB POD POA POB POA PO ABCD ∆∆===∆≅∆∠=∠=∆≅∆∠=⊥所以和都是等边三角形，因此又因为所以得到，同理得，所以平面-----------7）,,OG OB OP 因为两两垂直，以O 坐标原点，分别以,,OG OB OP u u u u r u u u r u u u r的方向为x 轴，y 轴,z 轴的正方向建立如图所示的空间直角坐标系O xyz -.000001100010010100O P A B D G --则（，，），（，，），（，，），（，，），（，，）（，，）设棱BC 的长为t ，则 ,1,0)C ,(1,0,1),(0,1,1),(,1,1),(0,1,1)22PA PB PC PD =--=-=--=--u u u r u u u r u u u r u u u r --------------9,111(,,),00,001,(1,1,1)PAB x y z PA x z y z PB x PAB =⎧=--=⎧⎪⎨⎨-==⎩⎪⎩=-=-u u u r g u u u r g 设平面的法向量则即不妨令可得为平面的一个法向量.m m m m-----------10222(,,),0(1)0,001,(1,1,1)PCD x y z PC y z PD y z y PCD t =⎧=+-=⎪⎨=⎪⎪⎩--=⎩==--u u u r g u u u r g 设平面的法向量则即不妨令可得为平面的一个法向量.n n n n-----------110,=g m n 解得t=BC 即棱的长为20解：（1）由题意可知圆心到1(,0)2的距离等于到直线12x =-的距离，由抛物线的定义可知，圆心的轨迹方程：22y x = (4)分（2）设00(,)P x y ，(0,),(0,)B b C c ， 直线PB 的方程为：000()0y b x x y x b --+=， 又圆心（1，0）到PB 的距离为1，1=，整理得：2000(2)20x b y b x -+-=， (6)分同理可得：2000(2)20x c y c x -+-=，所以，可知,b c是方程2000(2)20x x y x x -+-=的两根，所以：00002,,22y x b c bc x x --+==--……………………8分依题意0bc <，即02x >，则22200020448()(2)x y x b c x +--=-，因为2002y x =，所以：0022x b c x -=-，………………10分所以00014(2)482(2)S b c x x x =-=-++≥-， 当04x =时上式取得等号，所以PBC∆面积最小值为8.………………………12分 解二：（2）设00(,)P x y ，直线PB ：00()y y k x x -=-与圆D 相切，则1=，整理得：22200000(2)2(1)10x x k x y k y -+-+-=，……………………6分20001212220002(1)1,22x y y k k k k x x x x--+=-=--,………………………8分依题意02x > 那么010020120()()B C y y y k x y k x k k x -=---=-，由韦达定理得：12022k k x -=-，则022B Cx y y x -=-，…………………10分所以00014()(2)482(2)B C S y y x x x =-=-++≥-当04x =时上式取得等号，所以PBC∆面积最小值为8.…………………12分 21. 解：（1）由()22ln f x x a x x=++，得()'222af x x x x =-+．因为()f x 在区间[]2,3上单调递增，则()'2220af x x x x=-+≥在[]2,3上恒成立，………………2分即222a x x≥-在[]2,3上恒成立，设22()2g x x x =-，则22()40g x x x '=--<，所以()g x 在[]2,3上单调递减，故max ()(2)7g x g ==-，所以7a ≥-． (4)分（2） 解法一：12121212()()11()()f x f x k f x f x x x x x ''-''>⇔>⇔->--而()()12f x f x ''-＝122211222222a a x x x x x x⎛⎫⎛⎫-+--+ ⎪ ⎪⎝⎭⎝⎭＝()121222121222x x ax x x x x x +-⋅+-故欲证()()''1212f x f x x x ->- ，只需证()12221212221x x ax x x x ++->…………………6分即证()1212122x x a x x x x +<+成立∵()121212122x x x x x x x x ++>…………………8分设t =，()()240u t t t t=+>，则()242u t t t'=- 令()0u t '=得t =，列表如下：()4u t a ≥=>≥ (10)分 ∴()1212122x x x x a x x ++> ∴()()''1212f x f x x x ->-， 即1212()()1f x f x x x ''->-∴当4a ≤时，1k >…………………12分解法二：对于任意两个不相等的正数1x 、2x 有()1212122x x x x x x ++>12x x＝12x x3≥＝3 4.5a >> …………………8分∴ ()12221212221x x a x x x x ++-> 而()'222a f x x x x =-+∴()()12f x f x ''-＝122211222222a a x x x x x x⎛⎫⎛⎫-+--+ ⎪ ⎪⎝⎭⎝⎭＝()121222121222x x ax x x x x x +-⋅+-12x x >-…………………10分故：()()''1212f x f x x x ->- ， 即1212()()1f x f x x x ''->- ∴当4a ≤时，1k >………12分22. 证明：（1）连结AB ，AC ， ∵AD 为M e 的直径，∴090ABD ∠=，∴AC为Oe 的直径,∴0=90CEF AGD ∠=∠,∵DFG CFE ∠=∠，∴ECF GDF ∠=∠, ∵G 为弧BD 中点，∴DAG GDF ∠=∠， ∴DAG ECF ∠=∠,ADG CFE ∠=∠ ∴CEF ∆∽AGD ∆，……………3分 ∴CE AG EFGD=，∴GD CE EF AG ⋅=⋅。

河北省石家庄市2018届高三年级第一次模拟考试理科数学试卷一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. （）A. B.C. D.2. 设集合，，则（）A. B. C. D.3. 已知，且，则（）A. B. C. D.4. 两个单位向量，的夹角为，则（）A. B. C. D.5. 用两个，一个，一个，可组成不同四位数的个数是（）A. B. C. D.6. 已知，，，则（）A. B. C. D.7. 如图是根据南宋数学家杨辉的“垛积术”设计的程序框图，该程序所能实现的功能是（）A. 求B. 求C. 求D. 求8. 为了得到函数的图象，可以将函数的图象（）A. 向左平移个单位长度B. 向右平移个单位长度C. 向右平移个单位长度D. 向左平移个单位长度9. 某几何体的三视图如图所示，则该几何体的表面积是（）A. B. C. D.10. 已知为双曲线：的右焦点，过点向的一条渐近线引垂线，垂足为，交另一条渐近线于点.若，则的离心率是（）A. B. C. D.11. 已知函数，则下列关于的表述正确的是（）A. 的图象关于轴对称B. ，的最小值为C. 有个零点D. 有无数个极值点12. 已知，，，是半径为的球面上的点，，，点在上的射影为，则三棱锥体积的最大值是（）A. B.C. D.二、填空题：本题共4小题，每小题5分，共20分.13. 设，满足约束条件，则的最小值是__________．14. 的展开式中，二项式系数最大的项的系数是__________．（用数字作答）15. 已知为抛物线上异于原点的点，轴，垂足为，过的中点作轴的平行线交抛物线于点，直线交轴于点，则__________．16. 在中，角，，的对边分别为，，，边上的高为，若，则的取值范围是__________．三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17～21题为必考题，每个试题考生都必须作答.第（22）、（23）题为选考题，考生根据要求作答. （一）必考题：共60分.17. 已知数列为单调递增数列，为其前项和，.（1）求的通项公式；（2）若，为数列的前项和，证明：.18. 某水产品经销商销售某种鲜鱼，售价为每公斤元，成本为每公斤元.销售宗旨是当天进货当天销售.如果当天卖不出去，未售出的全部降价处理完，平均每公斤损失元.根据以往的销售情况，按，，，，进行分组，得到如图所示的频率分布直方图.（1）求未来连续三天内，该经销商有连续两天该种鲜鱼的日销售量不低于公斤，而另一天日销售量低于公斤的概率；（2）在频率分布直方图的需求量分组中，以各组区间的中点值代表该组的各个值.（i）求日需求量的分布列；（ii）该经销商计划每日进货公斤或公斤，以每日利润的数学期望值为决策依据，他应该选择每日进货公斤还是公斤？19. 如图，在三棱柱中，平面平面，.（1）证明：；（2）若是正三角形，，求二面角的大小.20. 已知椭圆：的左焦点为，上顶点为，长轴长为，为直线：上的动点，，.当时，与重合.（1）若椭圆的方程；（2）若直线交椭圆于，两点，若，求的值.21. 已知函数，.（1）设，求的最小值；（2）证明：当时，总存在两条直线与曲线与都相切.（二）选考题：共10分.请考生在（22）、（23）题中任选一题作答，如果多做，则按所做的第一题记分.22. 选修4-4：坐标系与参数方程在直角坐标系中，圆：，圆：.以坐标原点为极点，轴的正半轴为极轴建立极坐标系.（1）求，的极坐标方程；（2）设曲线：（为参数且），与圆，分别交于，，求的最大值.23. 选修4-5：不等式选讲设函数的最大值为.（1）求的值；（2）若正实数，满足，求的最小值.。

河北省石家庄市2018届高考一模考试数学理科试题（A ）含答案石家庄市2018届高中毕业班模拟考试（一）理科数学（A 卷）一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合{1,2,3,4,5,6,7}U =，{|3,}A x x x N =≥∈，则U C A =（ ） A ．{1,2} B ．{3,4,5,6,7} C ．{1,3,4,7} D ．{1,4,7}2.已知i 为虚数单位，(1)2i x yi +=+，其中,x y R ∈，则x yi +=（ ）A ．B C ．2 D ．43.函数()2(0)xf x x =<，其值域为D ，在区间(1,2)-上随机取一个数x ，则x D ∈的概率是（ ） A ．12 B ．13 C ．14 D ．234.点B 是以线段AC 为直径的圆上的一点，其中2AB =，则AC AB ⋅=（ ） A ．1 B ．2 C ．3 D ．45. x ，y 满足约束条件：11y xx y y ≤⎧⎪+≤⎨⎪≥-⎩，则2z x y =+的最大值为（ ）A ．-3B ．32C ．3D ．4 6.程序框图如图所示，该程序运行的结果为25s =，则判断框中可填写的关于i 的条件是（ ）A ．4?i ≤B ．4?i ≥C ．5?i ≤ D．5?i ≥7.南宋数学家秦九韶早在《数书九章》中就独立创造了已知三角形三边求其面积的公式：“以小斜幂并大斜幂，减中斜幂，余半之，自乘于上，以小斜幂乘大斜幂减之，以四约之，为实，一为从隅，开方得积.”（即：S =a b c >>），并举例“问沙田一段，有三斜（边），其小斜一十三里，中斜一十四里，大斜一十五里，欲知为田几何？”则该三角形田面积为（ ）A ．82平方里B ．83平方里C ．84平方里D ．85平方里8.如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的表面积为（ ）A ．83π+B ．84π+C ．85π+D ．86π+9.已知()f x 是定义在[2,1]b b -+上的偶函数，且在[2,0]b -上为增函数，则(1)(2)f x f x -≤的解集为（ ） A ．2[1,]3- B ．1[1,]3- C ．[1,1]- D ．1[,1]310.在ABC ∆中，2AB =，6C π=，则3AC BC +的最大值为（ ）A B ．．．11.过抛物线214y x =焦点F 的直线交抛物线于A ，B 两点，点C 在直线1y =-上，若ABC ∆为正三角形，则其边长为（ ）A ．11B ．12C ．13D ．1412.设xOy ，''x Oy 为两个平面直角坐标系，它们具有相同的原点，Ox 正方向到'Ox 正方向的角度为θ，那么对于任意的点M ，在xOy 下的坐标为(,)x y ，那么它在''x Oy 坐标系下的坐标(',')x y 可以表示为：'cos sin x x y θθ=+，'cos sin y y x θθ=-.根据以上知识求得椭圆223'''5'10x y y -+-=的离心率为（ ）A ．3．4．3 D ．4二、填空题：本大题共4小题，每题5分，共20分.13.命题p ：01x ∃≥，200230x x --<的否定为 ．14.甲、乙、丙三位同学，其中一位是班长，一位是体育委员，一位是学习委员，已知丙的年龄比学委的大，甲与体委的年龄不同，体委比乙年龄小.据此推断班长是 ．15.一个直角三角形的三个顶点分别在底面棱长为2的正三棱柱的侧棱上，则该直角三角形斜边的最小值为 ．16.已知函数31()1x x f x x -+=-，ln ()xg x x =，若函数(())y f g x a =+有三个不同的零点1x ，2x ，3x （其中123x x x <<），则1232()()()g x g x g x ++的取值范围为 ．三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17～21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答. （一）必考题：共60分17.已知等比数列{}n a 的前n 项和为n S ，且满足122()n n S m m R +=+∈.（Ⅰ）求数列{}n a 的通项公式； （Ⅱ）若数列{}n b 满足211(21)log ()n n n b n a a +=+⋅，求数列{}n b 的前n 项和n T .18.四棱锥S ABCD -的底面ABCD 为直角梯形，//AB CD ，AB BC ⊥，222AB BC CD ===，SAD ∆为正三角形.（Ⅰ）点M 为棱AB 上一点，若//BC 平面SDM ，AM AB λ=，求实数λ的值； （Ⅱ）若BC SD ⊥，求二面角A SB C --的余弦值.19.小明在石家庄市某物流派送公司找到了一份派送员的工作，该公司给出了两种日薪薪酬方案.甲方案：底薪100元，每派送一单奖励1元；乙方案：底薪140元，每日前55单没有奖励，超过55单的部分每单奖励12元. （Ⅰ）请分别求出甲、乙两种薪酬方案中日薪y （单位：元）与送货单数n 的函数关系式；（Ⅱ）根据该公司所有派送员100天的派送记录，发现派送员的日平均派送单数满足以下条件：在这100天中的派送量指标满足如图所示的直方图，其中当某天的派送量指标在2(1)2(,]1010n n-(1,2,3,4,5)n =时，日平均派送量为502n +单.若将频率视为概率，回答下列问题：①根据以上数据，设每名派送员的日薪为X （单位：元），试分别求出甲、乙两种方案的日薪X 的分布列，数学期望及方差；②结合①中的数据，根据统计学的思想，帮助小明分析，他选择哪种薪酬方案比较合适，并说明你的理由. （参考数据：20.60.36=，21.4 1.96=，22.6 6.76=，23.411.56=，23.612.96=，24.621.16=，215.6243.36=，220.4416.16=，244.41971.36=）20.已知椭圆C ：22221(0)x y a b a b+=>>的左、右焦点分别为1F ，2F ，M 为椭圆上任意一点，当1290F MF ∠=时，12F MF ∆的面积为1. （Ⅰ）求椭圆C 的方程；（Ⅱ）已知点A 是椭圆C 上异于椭圆顶点的一点，延长直线1AF ，2AF 分别与椭圆交于点B ，D ，设直线BD 的斜率为1k ，直线OA 的斜率为2k ，求证：12k k ⋅为定值.21.已知函数()()()xf x x b e a =+-，(0)b >，在(1,(1))f --处的切线方程为(1)10e x ey e -++-=. （Ⅰ）求a ，b ；（Ⅱ）若方程()f x m =有两个实数根1x ，2x ，且12x x <，证明：21(12)11m e x x e--≤+-.（二）选考题：共10分，请考生在22、23题中任选一题作答，并用2B 铅笔将答题卡上所选题目对应的题号右侧方框涂黑，按所涂题号进行评分；多涂、多答，按所涂的首题进行评分；不涂，按本选考题的首题进行评分. 22.[选修4-4：坐标系与参数方程]在平面直角坐标系xOy 中，曲线C 的参数方程为cos 1sin x r y r ϕϕ⎧=⎪⎨=+⎪⎩（0r >，ϕ为参数），以坐标原点O 为极点，x 轴正半轴为极轴建立极坐标系，直线l 的极坐标方程为sin()13πρθ-=，若直线l 与曲线C 相切；（Ⅰ）求曲线C 的极坐标方程；（Ⅱ）在曲线C 上取两点M ，N 与原点O 构成MON ∆，且满足6MON π∠=，求面积MON ∆的最大值.23.[选修4-5：不等式选讲]已知函数()f x =R ；（Ⅰ）求实数m 的取值范围；（Ⅱ）设实数t 为m 的最大值，若实数a ，b ，c 满足2222a b c t ++=，求222111123a b c +++++的最小值.石家庄市2017-2018学年高中毕业班第一次模拟考试试题理科数学答案一、选择题1-5: AABDC 6-10: CCDBD 11、12：BA 二、填空题13. 2:1,230p x x x ⌝∀≥--≥ 14. 乙 15. 22,0e e ⎛⎫-⎪-⎝⎭三、解答题 17解：(1) 法一：由122()n n S m m R +=+∈得122()nn S m m R -=+∈，当当2n ≥时，12222n n n n a S S -=-=，即12(2)n n a n -=≥， 又1122ma S ==+，当2m =-时符合上式，所以通项公式为12n n a -=. 法二：由122()n n S m m R +=+∈得1232;4;8()S m S m S m m R =+⎧⎪=+⎨⎪=+∈⎩，从而有2213322,4a S S a S S =-==-=， 所以等比数列公比322a q a ==，首项11a =，因此通项公式为12n n a -=. （2）由（1）可得1212log ()log (22)21n n n n a a n -+⋅=⋅=-，1111()(21)(21)22121n b n n n n ∴==-+--+，12111111(1)2335212121n n nT b b b n n n ∴=+++=-+-++-=-++. 18.（1）因为//BC 平面SDM ，BC ⊂平面ABCD ，平面SDM 平面ABCD=DM ， 所以DM BC //，因为DC AB //,所以四边形BCDM 为平行四边形， 又CD AB 2=,所以M 为AB 的中点. 因为λ=，12λ∴=.（2）因为BC ⊥SD ， BC ⊥CD ，所以BC ⊥平面SCD ， 又因为BC ⊂平面ABCD ， 所以平面SCD ⊥平面ABCD ， 平面SCD平面ABCD CD =，在平面SCD 内过点S 作SE ⊥直线CD 于点E ， 则SE ⊥平面ABCD ， 在Rt SEA 和Rt SED 中， 因为SA SD =，所以AE DE ===，又由题知45EDA ∠=， 所以AE ED ⊥所以1AE ED SE ===， 以下建系求解.以点E 为坐标原点，EA 方向为X 轴，EC 方向为Y 轴，ES 方向为Z 轴建立如图所示空间坐标系，则(0,0,0)E ，(0,0,1)S ，(1,0,0)A ，(1,2,0)B ，(0,2,0)C ，(1,0,1)SA =-，(0,2,0)AB =，(0,2,1)SC =-，(1,0,0)CB =，设平面SAB 的法向量1(,,)n x y z =，则110n SA n AB ⎧⋅=⎪⎨⋅=⎪⎩，所以020x z y -=⎧⎨=⎩，令1x =得1(1,0,1)n =为平面SAB 的一个法向量，同理得2(0,1,2)n =为平面SBC 的一个法向量，12121210cos ,5||||n n n n n n ⋅<>==⋅，因为二面角A SB C --为钝角， 所以二面角A SB C --余弦值为5-.19.解：（1）甲方案中派送员日薪y （单位：元）与送单数n 的函数关系式为： N ,100∈+=n n y ， 乙方案中派送员日薪y （单位：元）与送单数n 的函数关系式为：⎩⎨⎧∈>-∈≤=N),55(,52012N),55(,140n n n n n y ， （2）①由已知，在这100天中，该公司派送员日平均派送单数满足如下表格：所以X 甲的分布列为：所以()=1520.21540.31560.21580.21600.1155.4E X ⨯+⨯+⨯+⨯+⨯=甲，()()()()()222222=0.2152155.4+0.3154155.4+0.2156155.4+0.2158155.4+0.1160155.4=6.44S ⨯-⨯-⨯-⨯-⨯-甲，所以X 乙的分布列为：所以()=1400.51520.21760.22000.1=155.6E X ⨯+⨯+⨯+⨯乙，()()()()22222=0.5140155.6+0.2152155.6+0.2176155.6+0.1200155.6=404.64S ⨯-⨯-⨯-⨯-乙，②答案一：由以上的计算可知，虽然()()E X E X <乙甲，但两者相差不大，且2S 甲远小于2S 乙，即甲方案日工资收入波动相对较小，所以小明应选择甲方案.答案二：由以上的计算结果可以看出，()()E X E X <乙甲，即甲方案日工资期望小于乙方案日工资期望，所以小明应选择乙方案. 20解：（1）设,,2211r MF r MF ==由题122221212224112c e a r r ar r c r r ⎧==⎪⎪+=⎪⎨+=⎪⎪⋅=⎪⎩，解得1a c ==，则21b =，∴椭圆C 的方程为2212x y +=.（2）设0000(,)(0)A x y x y ⋅≠，1122(,),(,)B x y C x y ， 当直线1AF 的斜率不存在时，设2(1,)2A -，则2(1,)2B --， 直线2AF的方程为(1)4y x =--代入2212x y +=，可得25270x x --= 275x ∴=，210y =-，则7(,510D -∴直线BD的斜率为1(10276(1)5k -==--，直线OA的斜率为22k =-121(626k k ∴⋅=-=-， 当直线2AF 的斜率不存在时，同理可得1216k k ⋅=-. 当直线1AF 、2AF 的斜率存在时，10±≠x设直线1AF 的方程为00(1)1y y x x =++，则由0022(1)112y y x x x y ⎧=+⎪+⎪⎨⎪+=⎪⎩消去x 可得：22222200000[(1)2]422(1)0x y x y x y x ++++-+=， 又220012x y +=，则220022y x =-，代入上述方程可得2220000(32)2(2)340x x x x x x ++---=，2000101003434,3232x x x x x x x x ----∴⋅=∴=++，则000100034(1)13232y x y y x x x --=+=-+++ 000034(,)2323x y B x x +∴--++，设直线2AF 的方程为00(1)1y y x x =--，同理可得000034(,)2323x y D x x ---， ∴直线BD 的斜率为000000001220000002323434341224362323y y x x x y x y k x x x x x x +-+===-+--+-+， 直线OA 的斜率为020y k x =， ∴20200001222200001123636366x x y y y k k x x x x -⋅=⋅===----. 所以，直线BD 与OA 的斜率之积为定值16-，即1216k k ⋅=-. 21．解：（Ⅰ）由题意()10f -=，所以()1(1)10f b a e ⎛⎫-=-+-=⎪⎝⎭， 又()()1x f x x b e a '=++-，所以1(1)1b f a e e'-=-=-+， 若1a e=，则20b e =-<，与0b >矛盾，故1a =，1b =.（Ⅱ）由（Ⅰ）可知()()()11x f x x e =+-， (0)0,(1)0f f =-=， 设)(x f 在(-1，0)处的切线方程为)(x h ， 易得，()1()11h x x e ⎛⎫=-+ ⎪⎝⎭，令()()()F x f x h x =- 即()()()1()1111x F x x e x e ⎛⎫=+---+ ⎪⎝⎭，()1()2x F x x e e '=+-， 当2x ≤-时，()11()20x F x x e e e '=+-<-< 当2x >-时，设()1()()2x G x F x x e e'==+-， ()()30x G x x e '=+>， 故函数()F x '在()2,-+∞上单调递增，又(1)0F '-=，所以当(),1x ∈-∞-时，()0F x '<，当()1,x ∈-+∞时，()0F x '>， 所以函数()F x 在区间(),1-∞-上单调递减，在区间()1,-+∞上单调递增， 故0)1()(=-≥F x F ，11()()f x h x ≥，设()h x m =的根为1x '，则111me x e'=-+-， 又函数()h x 单调递减，故111()()()h x f x h x '=≥，故11x x '≤，设()y f x =在(0,0)处的切线方程为()y t x =，易得()t x x =，令()()()()()11x T x f x t x x e x =-=+--，()()22x T x x e '=+-， 当2x ≤-时，()()2220x T x x e '=+-<-<，当2x >-时，故函数()T x '在()2,-+∞上单调递增，又(0)0T '=，所以当(),0x ∈-∞时，()0T x '<，当()0,x ∈+∞时，()0T x '>，所以函数()T x 在区间(),0-∞上单调递减，在区间()0,+∞上单调递增， 0)0()(=≥T x T ，22()()f x t x ≥ ，设()t x m =的根为2x '，则2x m '=，又函数()t x 单调递增，故222()()()t x f x t x '=≥，故22x x '≥， 又11x x '≤，2121(12)1111me m e x x x x m e e -⎛⎫''-≤-=--+=+ ⎪--⎝⎭. 选作题22（1）由题意可知直线l 的直角坐标方程为2y =+，曲线C 是圆心为，半径为r 的圆，直线l 与曲线C 相切，可得：2r ==；可知曲线C 的方程为22((1)4x y +-=，所以曲线C 的极坐标方程为2cos 2sin 0ρθρθ--=， 即4sin()3ρθπ=+. (2)由（1）不妨设M （1,ρθ），)6,(2πθρ+N ，（120,0ρρ>>）6πS MON =∆. 当12πθ=时, 32+≤∆MON S ，所以△MON 面积的最大值为2.23. 【解析】（1）由题意可知32x x m --≥恒成立，令3()2x g x x -=-， 去绝对值可得：36,(3)()263,(03)6,(0)x x x g x x x x x x --≥⎧⎪=-=-<<⎨⎪-≤⎩，画图可知()g x 的最小值为-3，所以实数m 的取值范围为3m ≤-；（2）由（1）可知2229a b c ++=，所以22212315a b c +++++=，222222222111()(123)11112312315a b c a b c a b c ++⋅++++++++++=+++ 22222222222221313239312132315155b a c a c b a b a c b c ++++++++++++++++++=≥=， 当且仅当2221235a b c +=+=+=，即2224,3,2a b c ===等号成立， 所以222111123a b c +++++的最小值为35.。

2018届石家庄市高中毕业班第一次模拟考试试卷第Ⅰ卷（共60分）一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知全集U=R，集合M={x|x2﹣2x﹣3≤0}，N={y|y=3x2+1}，则M∩（∁U N）=（）A．{x|﹣1≤x＜1}B．{x|﹣1≤x≤1}C．{x|1≤x≤3}D．{x|1＜x≤3}2．若复数z满足（3﹣4i）z=|4+3i|，则z的虚部为（）A．﹣4 B．﹣C．D．43．设实数x，y满足不等式组，若z=x+2y，则z的最大值为（）A．﹣1 B．4 C．D．4．若tanθ+=4，则sin2θ=（）A．B．C．D．5．若m∈R，则“log6m=﹣1”是“直线l1：x+2my﹣1=0与l2：（3m﹣1）x﹣my﹣1=0平行”的（）A．充分不必要条件 B．必要不充分条件C．充要条件D．既不充分也不必要条件6．已知双曲线=1（a＞0，b＞0）的左、右焦点分别为F1、F2，以F1F2为直径的圆与双曲线渐近线的一个交点为（3，4），则此双曲线的方程为（）A．B．C．D．7．设f（x）=lg（+a）是奇函数，则使f（x）＜0的x的取值范围是（）A．（﹣1，0）B．（0，1） C．（﹣∞，0）D．（﹣∞，0）∪（1，+∞）8．已知四棱锥，它的底面是边长为2的正方形，其俯视图如图所示，侧视图为直角三角形，则该四棱锥的侧面中直角三角形的个数为（）A．1 B．2 C．3 D．49．执行如图所示的程序框图，则输出结果S的值为（）A．B．0 C．﹣D．﹣110．甲、乙、丙三人站到共有7级的台阶上，若每级台阶最多站2人，同一级台阶上的人不区分站的位置，则不同的站法种数是（）A．258 B．306 C．336 D．29611．在Rt△ABC中，CA=CB=3，M，N是斜边AB上的两个动点，且，则的取值范围为（）A．B．[2，4]C．[3，6]D．[4，6]12．设△A n B n C n的三边长分别为a n，b n，c n，n=1，2，3，…，若b1＞c1，b1+c1=2a1，=a n，，，则∠A n的最大值为（）a n+1A．B．C．D．第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13.已知命题p ：n N ∀∈，22n n <，则p ⌝为 ．14.程序框图如图所示，若输入1S =，1k =，则输出的S 为 ．15.已知1F 、2F 分别为双曲线22221x y a b-=（0a >，0b >）的左、右焦点，点P 为双曲线右支上一点，M 为12PF F ∆的内心，满足1212MPF MPF MF F S S S λ∆∆∆=+，若该双曲线的离心率为3，则λ= （注：1MPF S ∆、2MPF S ∆、12MF F S ∆分别为1MPF ∆、2MPF ∆、12MF F ∆的面积）．16.已知等比数列{}n b 满足1132n n n a a -++=⋅，*n N ∈.设数列{}n a 的前n 项和为n S ，若不等式2n n S ka >-对一切*n N ∈恒成立，则实数k 的取值范围为 ．三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） 17.在ABC ∆中，内角A ，B ，C 的对边分别是a ，b ，c ，且sin sin sin C a bA B a c+=--.（Ⅰ）求角B 的大小；（Ⅱ）点D 满足2BD BC =，且线段3AD =，求2a c +的最大值.18.在四棱锥S ABCD -中，底面ABCD 为平行四边形，60DBA ∠=︒，30SAD ∠=︒，AD SD ==，4BA BS ==.（Ⅰ）证明：BD ⊥平面SAD ； （Ⅱ）求点C 到平面SAB 的距离．19.某港口有一个泊位，现统计了某月100艘轮船在该泊位停靠的时间（单位：小时），如果停靠时间不足半小时按半小时计时，超过半小时不足1小时按1小时计时，以此类推，统计结果如表：停靠时间 2.5 3 3.5 4 4.5 5 5.5 6 轮船数量12121720151383（Ⅰ）设该月100艘轮船在该泊位的平均停靠时间为a 小时，求a 的值；（Ⅱ）假定某天只有甲、乙两艘轮船需要在该泊位停靠a 小时，且在一昼夜的时间段中随机到达，求这两艘轮船中至少有一艘在停靠该泊位时必须等待的概率．20.已知椭圆C ：2212x y +=的左顶点为A ，右焦点为F ，O 为原点，M ，N 是y 轴上的两个动点，且MF NF ⊥，直线AM 和AN 分别与椭圆C 交于E ，D 两点．（Ⅰ）求MFN ∆的面积的最小值； （Ⅱ）证明：E ，O ，D 三点共线. 21.已知函数21()ln 2f x x x a x =-+，a R ∈.（Ⅰ）若函数()f x 为定义域上的单调函数，求实数a 的取值范围； （Ⅱ）当209a <<时，函数()f x 的两个极值点为1x ，2x ，且12x x <.证明：12()51ln 3123f x x >--. 请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分. 22.选修4-4：坐标系与参数方程在平面直角坐标系，将曲线1C 上的每一个点的横坐标保持不变，纵坐标缩短为原来的12，得到曲线2C ，以坐标原点O 为极点，x 轴的正半轴为极轴，建立极坐标系，1C 的极坐标方程为2ρ=．（Ⅰ）求曲线2C 的参数方程；（Ⅱ）过原点O 且关于y 轴对称的两条直线1l 与2l 分别交曲线2C 于A 、C 和B 、D ，且点A 在第一象限，当四边形ABCD 的周长最大时，求直线1l 的普通方程． 23.选修4-5：不等式选讲已知函数()|24|||f x x x a =++-．（Ⅰ）当2a <-时，()f x 的最小值为1，求实数a 的值； （Ⅱ）当()|4|f x x a =++时，求x 的取值范围．2018届石家庄市高中毕业班第一次模拟考试试卷数学(文科)一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知全集U=R，集合M={x|x2﹣2x﹣3≤0}，N={y|y=3x2+1}，则M∩（∁U N）=（）A．{x|﹣1≤x＜1}B．{x|﹣1≤x≤1}C．{x|1≤x≤3}D．{x|1＜x≤3}【考点】交、并、补集的混合运算．【分析】解一元二次不等式求得M，求函数的值域得到N，根据补集的定义求得∁U N，再根据两个集合的交集的定义求得M∩（∁U N）．【解答】解：∵集合M={x|x2﹣2x﹣3≤0}={x|﹣1≤x≤3}，N={y|y=3x2+1}={y|y ≥1}，∴∁U N={y|y＜1}，∴M∩（∁U N）={x|﹣1≤x＜1}，故选：A．2．若复数z满足（3﹣4i）z=|4+3i|，则z的虚部为（）A．﹣4 B．﹣C．D．4【考点】复数求模；复数的基本概念．【分析】根据复数的有关概念进行运算即可．【解答】解：由（3﹣4i）z=|4+3i|，得（3﹣4i）z=5，即z===+i，故z的虚部为，故选：C3．设实数x，y满足不等式组，若z=x+2y，则z的最大值为（）A．﹣1 B．4 C．D．【考点】简单线性规划．【分析】作出不等式对应的平面区域，利用线性规划的知识，通过平移即可求z的最大值．【解答】解：作出不等式对应的平面区域，由z=x+2y，得y=﹣，平移直线y=﹣，由图象可知当直线y=﹣经过点A时，直线y=﹣的截距最大，此时z最大．由，得，即A（，），此时z的最大值为z=+2×=，故选：C4．若tanθ+=4，则sin2θ=（）A．B．C．D．【考点】二倍角的正弦；同角三角函数间的基本关系．【分析】先利用正弦的二倍角公式变形，然后除以1，将1用同角三角函数关系代换，利用齐次式的方法化简，可求出所求．【解答】解：sin2θ=2sinθcosθ=====故选D．5．若m∈R，则“log6m=﹣1”是“直线l1：x+2my﹣1=0与l2：（3m﹣1）x﹣my﹣1=0平行”的（）A．充分不必要条件 B．必要不充分条件C．充要条件D．既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断．【分析】根据直线平行的等价条件求出m，利用充分条件和必要条件的定义进行判断即可．【解答】解：由log6m=﹣1得m=，若l1：x+2my﹣1=0与l2：（3m﹣1）x﹣my﹣1=0平行，则直线斜率相等或斜率不存在，解得m=0或m=，则“log6m=﹣1”是“直线l1：x+2my﹣1=0与l2：（3m﹣1）x﹣my﹣1=0平行”的充分不必要条件，故选：A6．已知双曲线=1（a＞0，b＞0）的左、右焦点分别为F1、F2，以F1F2为直径的圆与双曲线渐近线的一个交点为（3，4），则此双曲线的方程为（）A．B．C．D．【考点】双曲线的简单性质．【分析】根据题意，点（3，4）到原点的距离等于半焦距，可得a2+b2=25．由点（3，4）在双曲线的渐近线上，得到=，两式联解得出a=3且b=4，即可得到所求双曲线的方程．【解答】解：∵点（3，4）在以|F1F2|为直径的圆上，∴c=5，可得a2+b2=25…①又∵点（3，4）在双曲线的渐近线y=x上，∴=…②，①②联解，得a=3且b=4，可得双曲线的方程﹣=1．故选：C．7．设f（x）=lg（+a）是奇函数，则使f（x）＜0的x的取值范围是（）A．（﹣1，0）B．（0，1） C．（﹣∞，0）D．（﹣∞，0）∪（1，+∞）【考点】奇函数；对数函数的单调性与特殊点．【分析】首先由奇函数定义，得到f（x）的解析式的关系式（本题可利用特殊值f（0）=0），求出a，然后由对数函数的单调性解之．【解答】解：由f（﹣x）=﹣f（x），，，即=，1﹣x2=（2+a）2﹣a2x2此式恒成立，可得a2=1且（a+2）2=1，所以a=﹣1则即解得﹣1＜x＜0故选A8．已知四棱锥，它的底面是边长为2的正方形，其俯视图如图所示，侧视图为直角三角形，则该四棱锥的侧面中直角三角形的个数为（）A．1 B．2 C．3 D．4【考点】简单空间图形的三视图．【分析】由俯视图判断出PO⊥平面ABCD，由线面垂直的定义、判定定理判断出侧面中直角三角形的个数．【解答】解：由俯视图可得，PO⊥平面ABCD，∴PO⊥AB，∵AB⊥BC，且PO∩BC=O，∴AB⊥PB，同理可证，CD⊥PC，则△PAB、△PDC是直角三角形，∵侧视图为直角三角形，∴△PBC是直角三角形，且PC⊥PB，∴四棱锥的侧面中直角三角形的个数是3，如图所示．故选：C．9．执行如图所示的程序框图，则输出结果S的值为（）A．B．0 C．﹣D．﹣1【考点】程序框图．【分析】算法的功能是求S=的值，根据条件确定跳出循环的n值，利用余弦函数的周期性求输出S的值．【解答】解：由程序框图知：算法的功能是求S=的值，∵跳出循环的n值为2014，∴=故选C．10．甲、乙、丙三人站到共有7级的台阶上，若每级台阶最多站2人，同一级台阶上的人不区分站的位置，则不同的站法种数是（）A．258 B．306 C．336 D．296【考点】排列、组合及简单计数问题．【分析】由题意知本题需要分类解决，共有两种情况，对于7个台阶上每一个只站一人，若有一个台阶有2人另一个是1人，根据分类计数原理得到结果．【解答】解：由题意知本题需要分类解决，∵对于7个台阶上每一个只站一人有A73种；若有一个台阶有2人另一个是1人共有C31A72种，∴根据分类计数原理知共有不同的站法种数是A73+C31A72=336种．故选C．11．在Rt△ABC中，CA=CB=3，M，N是斜边AB上的两个动点，且，则的取值范围为（）A．B．[2，4]C．[3，6]D．[4，6]【考点】平面向量数量积的运算．【分析】通过建立直角坐标系求出AB所在直线的方程，设出M，N的坐标，将=2（b﹣1）2，0≤b≤1，求出范围．【解答】解：以C为坐标原点，CA为x轴建立平面坐标系，则A（3，0），B（0，3），∴AB所在直线的方程为：y=3﹣x，设M（a，3﹣a），N（b，3﹣b），且0≤a≤3，0≤b≤3不妨设a＞b，∵MN=，∴（a﹣b）2+（b﹣a）2=2，∴a﹣b=1，∴a=b+1，∴0≤b≤2，∴=（a，3﹣a）•（b，3﹣b）=2ab﹣3（a+b）+9=2（b2﹣2b+3），0≤b≤2，∴b=1时有最小值4；当b=0，或b=2时有最大值6，∴的取值范围为[4，6]故选：D12．设△A n B n C n的三边长分别为a n，b n，c n，n=1，2，3，…，若b1＞c1，b1+c1=2a1，a n+1=a n，，，则∠A n的最大值为（）A．B．C．D．【考点】数列递推式．【分析】根据数列的递推关系得到b n+c n=2a1为常数，然后利用余弦定理以及基本不等式即可得到结论．【解答】解：∵a n+1=a n，∴a n=a1，∵，，∴b n+1+c n+1=a n+=a1+，∴b n+1+c n+1﹣2a1=（b n+c n﹣2a1），又b1+c1=2a1，∴当n=1时，b2+c2﹣2a1=（b1+c1+﹣2a1）=0，当n=2时，b3+c3﹣2a1=（b2+c2+﹣2a1）=0，…∴b n+c n﹣2a1=0，即b n+c n=2a1为常数，∵b n﹣c n=（﹣）n﹣1（b1﹣c1），∴当n→+∞时，b n﹣c n→0，即b n→c n，则由基本不等式可得b n+c n=2a1≥2，∴b n c n ≤（a1）2，由余弦定理可得=﹣2b n c n cosA n =（b n +c n ）2﹣2b n c n ﹣2b n c n cosA n ， 即（a 1）2=（2a 1）2﹣2b n c n （1+cosA n ），即2b n c n （1+cosA n ）=3（a 1）2≤2（a 1）2（1+cosA n ），即3≤2（1+cosA n ），解得cosA n ≥，∴0＜A n ≤，即∠A n 的最大值是， 故答案为：．二、填空题 13.0n N ∃∈，0202n n ≥ 14.57 15.13 16.(,2]-∞ 三、解答题17.解：（Ⅰ）∵sin sin sin C a b A B a c +=--，由正弦定理得c a b a b a c+=--， ∴()()()c a c a b a b -=+-，即222a c b ac +-=，又∵2222cos a c b ac B +-=， ∴1cos 2B =， ∵(0,)B π∈，∴3B π=．（Ⅱ）在ABC ∆中由余弦定理知：222(2)22cos603c a a c +-⋅⋅⋅︒=，∴2(2)932a c ac +-=⋅， ∵ 222()2a c ac +≤， ∴223(2)9(2)4a c a c +-≤+，即2(2)36a c +≤，当且仅当2a c =，即32a =，3c =时取等号，所以2a c +的最大值为6．18.（Ⅰ）证明：在ABD ∆中，sin sin AB AD ADB DBA=∠∠，由已知60DBA ∠=︒，AD =4BA =，解得sin 1ADB ∠=，所以90ADB ∠=︒，即AD BD ⊥，可求得2BD =．在SBD ∆中，∵SD =4BS =,2BD =,∴222DB SD BS +=,∴SD BD ⊥,∵BD ⊄平面SAD ,SD AD D =,∴BD ⊥平面SAD ．（Ⅱ）由题意可知，//CD 平面SAB ，则C 到面SAB 的距离等于D 到面SAB 的距离， 在SAD ∆中，易求6SA =，1sin1202SAD S ∆=⨯︒=且162SAB S ∆=⨯=BD ⊥面SAD ，则B SAD D SAB V V --=，即11233h ⨯=⨯，则h =，即点C 到平面ABF 的距离为7h =．19.解：（Ⅰ） 2.512312 3.517420 4.515513 5.58634100a ⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯==． （Ⅱ）设甲船到达的时间为x ，乙船到达的时间为y ，则024,024,x y <<⎧⎨<<⎩若这两艘轮船在停靠该泊位时至少有一艘船需要等待，则||4y x -<，所以必须等待的概率为22201112436P =-=． 答：这两艘轮船中至少有一艘在停靠该泊位时必须等待的概率为1136．20.解：（Ⅰ）设(0,)M m ，(0,)N n ，∵MF NF ⊥，可得1mn =-，11||||||22AMFN S AF MN MN ==， ∵222||||||2||||MN MF NF MF NF =+≥⋅，当且仅当||||MF NF =时等号成立． ∴min ||2MN =， ∴min 1()||12MFN S MN ==， ∴四边形AMFN 的面积的最小值为1．（Ⅱ）∵(A ，(0,)M m ，∴直线AM的方程为y x m =+，由22,22,y x m x y ⎧=+⎪⎨⎪+=⎩得2222(1)2(1)0m x x m +++-=，由222(1)1E m x m -=+，得221)1E m x m -=+，①同理可得221)1D n x n -=+， ∵1m n ⋅=-，∵221()11()1D m x m⎤-⎥⎣⎦=+22),1m m -=+②故由①②可知：E D x x =-，代入椭圆方程可得22E D y y =∵MF NF ⊥，故M ，N 分别在x 轴两侧，E D y y =-， ∴E D E Dy y x x =，∴E ，O ，D 三点共线．21.解：（Ⅰ）函数()f x 的定义域为(0,)+∞． 由题意'()1a f x x x =-+2x x a x-+=，0x >，14a ∆=-. ①若140a ∆=-≤，即14a ≥，则20x x a -+≥恒成立，则()f x 在(0,)+∞上为单调减函数；②若140a ∆=->，即14a <，方程20x x a -+=的两个根为112x =，2x =，当21(,)2x x ∈时，'()0f x <，所以函数()f x 单调递减，当2(,)x x ∈+∞时，'()0f x >，所以函数()f x 单调递增，不符合题意．综上，若函数()f x 为定义域上的单调函数，则实数a 的取值范围为14a ≥. （Ⅱ）因为函数()f x 有两个极值点，所以'()0f x =在0x >上有两个不等的实根，即20x x a -+=有两个不等的实根1x ，2x ， 可得14a <，且12121,x x x x a+=⎧⎨⋅=⎩，因为2(0,)9a ∈，则1120(1)9x x <-<，可得11(0,)3x ∈. 2211111121122211ln ln ()22x x a x x x x x x f x x x x -+-+==21111112ln 1x x x x x -=+-， 11(0,)3x ∈. 令212()ln 1x x g x x x x -=+-，212()1x x h x x-=-，()ln m x x x =， ∵211'()02(1)2h x x =--<-， 又'()1ln m x x =+，1(0,)x e ∈时，'()0m x <， 而113e <，故'()0m x <在1(0,)3x ∈上恒成立， 所以'()()()0g x h x m x =+<在1(0,)3x ∈上恒成立， 即212()ln 1x x g x x x x-=+-在1(0,)3x ∈上单调递减， 所以151()()ln 33123g x g >=--，得证． 22.解：（Ⅰ）2214x y +=，2cos sin x y θθ=⎧⎨=⎩（θ为参数）． （Ⅱ）设四边形ABCD 的周长为l ，设点(2cos ,sin )A q q ，8cos 4sin l θθ=+))θθθϕ=+=+，且cos ϕ=，sin ϕ= 所以，当22k πθϕπ+=+（k Z ∈）时，l 取最大值， 此时22k πθπϕ=+-，所以，2cos 2sin θϕ==，sin cos θϕ==此时，A ，1l 的普通方程为14y x =． 23.解：（Ⅰ）当2a <-时，函数34,,()|24|||4,2,34, 2.x a x a f x x x a x a a x x a x -+-<⎧⎪=++-=---≤≤-⎨⎪-+>-⎩可知，当2x =-时，()f x 的最小值为(2)21f a -=--=，解得3a =-． （Ⅱ）因为()|24||||(24)()||4|f x x x a x x a x a =++-≥+--=++， 当且仅当(24)()0x x a +-≤时，()|4|f x x a =++成立，所以，当2a <-时，x 的取值范围是{}|2x a x ≤≤-；当2a =-时，x 的取值范围是{}2-；当2a >-时，x 的取值范围是{}|2x x a -≤≤．。

石家庄市第一中学2018-2019学年上学期高三期中数学模拟题班级__________ 座号_____ 姓名__________ 分数__________一、选择题（本大题共12小题，每小题5分，共60分.每小题给出的四个选项中，只有一项是符合题目要求的.）1．若集合,则= ( )ABCDx ，则输出的所有x的值的和为（）2．执行如图所示的程序，若输入的3A．243B．363C．729D．1092【命题意图】本题考查程序框图的识别和运算，意在考查识图能力、简单的计算能力．3． 若当R x ∈时，函数||)(x a x f =（0>a 且1≠a ）始终满足1)(≥x f ，则函数3||log xx y a =的图象大致是 （ ）【命题意图】本题考查了利用函数的基本性质来判断图象，对识图能力及逻辑推理能力有较高要求，难度中等． 4． 已知在数轴上0和3之间任取一实数，则使“2log 1x <”的概率为（ ） A ．14 B ．18 C ．23 D ．1125． 如图所示，网格纸表示边长为1的正方形，粗实线画出的是某几何体的三视图，则该几何体的表面积为（ ）A．15 B． C．15 D．15【命题意图】本题考查三视图和几何体体积等基础知识，意在考查空间想象能力和基本运算能力． 6． 已知复数z 满足（3+4i ）z=25，则=（ ） A ．3﹣4iB ．3+4iC ．﹣3﹣4iD ．﹣3+4i7． 已知直线l的参数方程为1cos sin x t y t αα=+⎧⎪⎨=⎪⎩（t 为参数，α为直线l 的倾斜角），以原点O 为极点，x 轴正半轴为极轴建立极坐标系，圆C 的极坐标方程为4sin()3πρθ=+，直线l 与圆C 的两个交点为,A B ，当||AB 最小时，α的值为（ ）A ．4πα=B ．3πα=C ．34πα=D ．23πα=8． 已知()(2)(0)x b g x ax a e a x =-->，若存在0(1,)x ∈+∞，使得00()'()0g x g x +=，则b a的 取值范围是（ ）A ．(1,)-+∞B ．(1,0)- C. (2,)-+∞ D ．(2,0)-9． 圆222(2)x y r -+=（0r >）与双曲线2213y x -=的渐近线相切，则r 的值为（ ）A B ．2 C D ．【命题意图】本题考查圆的一般方程、直线和圆的位置关系、双曲线的标准方程和简单几何性质等基础知识，意在考查基本运算能力．10．已知集合2{|20}A x R x x =∈+-<，2{|0}1x B x R x -=∈≤+，则A B =（ ） A ．[1,1]- B ．(1,1)- C ．[1,1)- D ．(1,1]-11．已知函数()x e f x x=，关于x 的方程2()2()10f x af x a -+-=（a R Î）有3个相异的实数根，则a 的取值范围是（ ）A ．21(,)21e e -+?-B ．21(,)21e e --?-C ．21(0,)21e e --D ．2121e e 禳-镲睚-镲铪【命题意图】本题考查函数和方程、导数的应用等基础知识，意在考查数形结合思想、综合分析问题解决问题的能力．12．某几何体的三视图如图所示，则该几何体的体积为（ ） A ．16163π-B ．32163π-C ．1683π-D ．3283π-【命题意图】本题考查三视图、圆柱与棱锥的体积计算，意在考查识图能力、转化能力、空间想象能力．二、填空题（本大题共4小题，每小题5分，共20分.把答案填写在横线上）13．函数)(x f （R x ∈）满足2)1(=f ，且)(x f 在R 上的导函数)('x f 满足3)('>x f ，则不等式123)2(-⋅<x x f 的解集为 .【命题意图】本题考查利用函数的单调性解抽象不等式问题，本题对运算能力、化归能力及构造能力都有较高要求，难度大.14．已知x ，y 为实数，代数式2222)3(9)2(1y x x y ++-++-+的最小值是 .【命题意图】本题考查两点之间距离公式的运用基础知识，意在考查构造的数学思想与运算求解能力.15．在ABC ∆中，角A B C 、、的对边分别为a b c 、、，若1cos 2c B a b ⋅=+，ABC ∆的面积12S c =， 则边c 的最小值为_______．【命题意图】本题考查正弦定理、余弦定理、三角形面积公式、基本不等式等基础知识，意在考查基本运算能力．16．函数2()cos sin ((,))6f x x x x ππ=+∈的值域是__________.三、解答题（本大共6小题，共70分。

2021届石家庄市高中毕业班第一次模拟考试试卷数学〔理科〕A 卷第一卷〔选择题，共 60分〕一、选择题：本大题共12个小题,每题5分,共60分.在每题给出的四个选项中，只 有一项是符合题目要求的.. 假设复数z 2i〔i 是虚数单位〕，那么z)iA ．1iB ．1iC ．1iD ．1i2. 集合 A{x|x 25x 6 0}，B {x|3 x3}，那么AB()A ．( 3,3)B ．( 3,6)C ．( 1,3) D ．( 3,1)x 1 03. 设变量,y 满足约束条件 x 2y 2 0，那么目标函数z3x4y 的最小值为()2x y 2 0A ．1B．3C．26D． 195f(11)的值为() 4. 函数f(x)Asin( x)(A 0,0)的局部图像如右图所示，那么24A ．6 B．3C．2 D．12225.程序框图如图，当输入x 为2021时，输出的 y 的值为( )A．1B．1C．2D．4 86.为比拟甲乙两地某月11时的气温情况，随机选取该月中的5天中11时的气温数据〔单位：℃〕制成如下图的茎叶图，考虑以下结论：甲乙982689210311①甲地该月11时的平均气温低于乙地该月11时的平均气温②甲地该月11时的平均气温高于乙地该月11时的平均气温③甲地该月11时的气温的标准差小于乙地该月11时的气温的标准差④甲地该月11时的气温的标准差大于乙地该月11时的气温的标准差其中根据茎叶图能得到的正确结论的编号为()A．①③B．①④C．②③D．②④7.过点A(0,1)作直线，与双曲线x2y21有且只有一个公共点，那么符合条件的直线的条数为9()A．0B．2C．4D．无数8.如下图的数阵中，用A(m,n)表示第m行的第n个数，那么依此规律A(15,2)为()A．29B．7C．17D．73 4210241029.函数yf(x2)的图象关于直线x2对称，且当x(0,)时，f () |log 2 | ，假设x xaf(3)，bf(1 ，那么a,b,c 的大小关系是( ))，cf(2)4A ．abcB ．bacC ．cabD ．acb10.某几何体的三视图如下图，图中网格小正方形边长为 1，那么该几何体的体积是()A ．4B ．16C ．20D ．123 311.A,B,C〔R,是圆O 上不同的三点，线段CO 与线段R 〕，那么的取值范围是 ( )AB交于D ，假设OCOAOBA ．(0,1)B ．(1,)C ．(1,2]D ．(1,0)12.如下图，一个圆柱形乒乓球筒，高为20厘米，底面半径为2厘米.球筒的上底和下底分别粘有一个乒乓球，乒乓球与球筒底面及侧面均相切〔球筒和乒乓球厚度忽略不计〕 .一个平面与两乒乓球均相切，且此平面截球筒边缘所得的图形为一个椭圆，那么该椭圆的离心率为( )A ． 15B ．1C ．26D ．14 5 54第二卷〔非选择题，共 90分〕二、填空题〔每题 5分，总分值20分，将答案填在答题纸上〕13. (x1)6的展开式中常数项为.4xsin x, 1x 01，那么x 的值为.14. 函数f(x)2，且f(x)log 2(x 1),0 x 1215.ABC 中，AC4,BC27,BAC60,ADBC 于D ，那么BD的值为.CD16. 假设函数f x ) x 3ax 2 bxabRA(m,0)(m0)，且 f(x)的极大((, )的图象与x 轴相切于一点值为1，那么m 的值为.2三、解答题〔本大题共6小题，共70分.解容许写出文字说明、证明过程或演算步骤 .〕〔本小题总分值12分〕〔本小题总分值12分〕在平面四边形ACBD 〔图①〕中， ABC 与ABD 均为直角三角形且有公共斜边AB ，设AB2，BAD30，BAC45，将ABC 沿AB 折起，构成如图②所示的三棱锥 C'ABC ，且使C'D2.〔Ⅰ〕求证：平面〔Ⅱ〕求二面角C'ABAC'D 平面DABB的余弦值；.C'CA B A B①D②D〔本小题总分值12分〕某篮球队对篮球运发动的篮球技能进行统计研究，针对篮球运发动在投篮命中时，运发动在篮筐中心的水平距离这项指标，对某运发动进行了假设干场次的统计，依据统计结果绘制如下频率分布直方图：〔Ⅰ〕依据频率分布直方图估算该运发动投篮命中时，他到篮筐中心的水平距离的中位数；〔Ⅱ〕在某场比赛中，考察他前4次投篮命中到篮筐中心的水平距离的情况，并且规定：运发动投篮命中时，他到篮筐中心的水平距离不少于4米的记1分，否那么扣掉 1分.用随机变量X表示第4次投篮后的总分，将频率视为概率，求X的分布列和数学期望.〔本小题总分值12分〕抛物线C：22pxp0)过点M(m,2)|MF|2，其焦点为F，且.(〔Ⅰ〕求抛物线C的方程；〔Ⅱ〕设E为y轴上异于原点的任意一点，过点E作不经过原点的两条直线分别与抛物线C和圆F：(x1)2y21相切，切点分别为A,B，求证：直线AB过定点.〔本小题总分值12分〕f(x)e x ax22x b〔e为自然对数的底数，a,bR〕.〔Ⅰ〕设f'(x)为f(x)的导函数，证明：当a0时，f'(x)的最小值小于0；〔Ⅱ〕假设a0,f(x)0恒成立，求符合条件的最小整数b.请考生在22、23、24三题中任选一题作答，如果多做，那么按所做的第一题记分.〔本小题总分值10分〕选修4-1：几何证明选讲如下图，过点P分别做圆O的切线PA、PB和割线PCD，弦BE交CD于F，满足P、B、F、A四点共圆.〔Ⅰ〕证明：AE//CD；〔Ⅱ〕假设圆O的半径为5，且PC CF FD 3，求四边形PBFA的外接圆的半径.〔本小题总分值10分〕选修4-4：坐标系与参数方程在极坐标系中，曲线C1：2cos和曲线C2：cos3，以极点O为坐标原点，极轴为x轴非负半轴建立平面直角坐标系.〔Ⅰ〕求曲线C1和曲线C2的直角坐标方程；〔Ⅱ〕假设点P是曲线C1上一动点，过点P作线段OP的垂线交曲线C2于点Q，求线段PQ长度的最小值.〔本小题总分值10分〕选修4-5：不等式选讲函数f(x) |x| |x1|.〔Ⅰ〕假设f(x)|m1|恒成立，求实数m的最大值M；〔Ⅱ〕在〔Ⅰ〕成立的条件下，正实数a,b满足a2b2M，证明：ab2ab.2021届高三数学一模理科答案一．选择题：A卷答案：1-5BCBDA6-10CCCBB11-12BAB卷答案：1-5ACADB6-10CCCAA11-12AB二．填空题：13..514.1 16315.616.3 2三、解答题：2a2a3a5=4a1+8d=2017.解：〔I〕由得109，-------------------------------2分10a1+2d=10a1+45d=100解得a11-------------------------------4分d，2所以{a n}的通项公式为a n52(n3)2n1，--------------------------------5分〔II〕由〔I〕可知a n b n(2n1)22n1，所以S n121323525(2n3)22n3(2n1)22n1，①4S n123325527(2n3)22n1(2n1)22n1，②---------------------7分①-②得：3S n22(232522n1)(2n1)22n1S n 22(232522n1)(2n1)22n13⋯⋯⋯⋯⋯⋯9分22(8(14n1))(2n1)22n1143628(14n1)(6n3)22n1分9---------------------1110 (6n 5)22n1--------------------------12分9解：〔1〕取AB的中点O，CO,DO，在RTACB,RT ADB，AB2，CO DO1，又CD2，CO2DO2CD2，即COOD，⋯⋯⋯⋯2分又CO AB，ABODO，AB,OD平面ABDCO平面ABD，⋯⋯⋯⋯⋯⋯⋯4分又CO平面ABC平面CAB平面DAB5分〔2〕以O原点，AB，OC所在的直分y,z，建立如空直角坐系，A(0,1,0),B(0,1,0),C(0,0,1),D(3,1,0)，2 2AC(0,1,1),BC(0, 1,1),CD( 3,1, 1)⋯⋯⋯⋯6分2 2平面ACD 的法向量n 1n 1ACn 1 AC(x 1,y 1,z 1)，，即n 1，n 1CDCDy 1 z 1 03x 11 ，令z 11，y 11，x 13，2 y 1z 12n 1( 3,1,1)⋯⋯⋯⋯8分平面BCD 的法向量n 2n 2BCn 2 BC 0(x 2,y 2,z 2)，，即n 2 CD，n 2CDy 2 z 2 03，3 1 ，令z 21，y 21，x 22 x 22 y 2z 23n(3,1,1)⋯⋯⋯⋯⋯⋯10分233 3 ( 1)111cosn 1,n 23 1105，173531 115133二面角ACDB105 分的余弦-.⋯⋯⋯⋯⋯123519.解：〔I 〕运到筐的水平距离的中位数 x ，∵2，且0.20) 1，∴x[4,5]⋯⋯⋯⋯⋯⋯⋯ 2分随机量的所有可能取 -4，-2,0,2,4；⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯8分4PX4216，P(X2)C 43(2)1(3)321656255 5625P(X2)C 41(2)3(3)965 5 625P(X0) C 42(2)2(3)2216 ；5 5 625P(X2) C 43(2)1(3)32165 5625481PX435625X-4-20 2 4P16 96216 216 81625625625625625⋯⋯⋯⋯⋯⋯⋯ 10分EX4 16 ( 2) 96 0 2162 216 4 814625 625 625625 625 5 ⋯⋯⋯⋯⋯⋯⋯12分20.解：〔1〕抛物C 的准方程：xp ，p2p|MF|m2，又 4 2pm ，即42p(2 )--------------------2分22p 24p 4 0, p 2抛物C 的方程y 24x .-------------------4 分〔2〕点E(0,t)(t 0)，由切不 y ，EA:y kx ty kx t(2kt 4)x t 2联立y24x ，消去y ，可得k 2x 2直线EA 与抛物线C 相切，(2kt4)2 4k 2t 20，即kt1代入12x 22xt 20， xt 2，即A(t 2,2t)-------------------------------------- 6分t设切点B(x 0,y 0)，那么由几何性质可以判断点O,B 关于直线EF:ytx t 对称，那么y 0 t 01x 02t222t 222t)-------------------------------x 0 0 1t 2 1，即B(，解得： t , 8分y 0 t x 0 ty 02t 1t 12 2t21思路1：直线AB 的斜率为k AB2t (t 1)t 21直线AB 的方程为y2t (x t 2) 2t ，--------------------------------------10分2tt 2 1整理yt 1(x1)2直线AB 过定点恒过定点 F(1,0)--------------------------------------11分当t1时，A(1, 2),B(1,1)，此时直线AB 为x1 ，过点F(1,0).综上，直线AB 过定点恒过定点F(1,0)--------------------------------------12 分思路2：直线AF 的斜率为k AF2t2(t1) ，t 12t 0 2t直线BF 的斜率为k BFt 2 1 (t1) ，2t 2 t 21t 211kAFk BF ，即A,B,F 三点共线--------------------------------------10 分当t1时，A(1,2),B(1, 1) ，此时 A,B,F 共线.--------------------------------------11分直线AB 过定点F .--------------------------------------12分21.解：〔Ⅰ〕证明：令 g(x) f(x)e x 2ax2,那么g(x)e x 2a因为a 0 ，令g(x 0)0，x 0ln2a所以当x ( ,ln2a)时，g(x)0，g(x)单调递减；当x (ln2a,)时，g(x)0，g(x)单调递增-------------------- 2分那么f(x)ming(x)min g(ln2a)e ln2a2aln2a2=2a2aln2a 2 --------------------3分令G(x) x xlnx2，(x0)G(x)1 (lnx1)lnx当x (0,1)时，G(x) 0，G(x)单调递增当x(1,)时，G(x)0，G(x)单调递减所以G(x)maxG(1) 1 0，所以f(x)min0成立.-------------------- 5 分〔Ⅱ〕证明： f(x)0恒成立，等价于 f(x)min 0恒成立令g(x)f(x) e x2ax 2，那么g(x) e x 2a因为a0 ，所以g(x)0，所以g(x)单调递增，又g(0) 1 0， g(1) e2a2 0 ，所以存在x 0(0,1)，使得g(x 0)0---------------------6分那么x(,x)时，g(x) f (x)0, f(x)单调递减；x(x 0,)时，g(x) f(x)0, f(x)单调递增；所以f(x)minf(x 0)e x 0ax 022x 0 b 0 恒成立 (1)且ex2ax 0 20 (2)由〔1〕〔2〕,bexax 2 2xexx(ex 01)2x(x0 1)e x 0x 即可-----------------8 分22又由〔2〕aex20 ，所以x 0 (0,ln 2)---------------------9 分2x 0令m(x)(x1)e x x,x (0,ln2)2 1(x1)e xn(x)m(x)112n(x)xe x 0 ，2所以n(x)n(0) 1 0 所以m(x)单调递增，2，m(x)m(0)(1)e 01，m(x)m(ln2)(ln21)e ln2ln22ln22---------------------11 分2所以b1，所以符合条件的b=0---------------------12分法2：令x 0,f(0) 1 b 0,b1 ，故符合条件的最小整数 b 0.-------------------6分现证明b 0 时，f(x)求f(x)e x ax 22x 的最小值即可令g(x) f (x) e x 2ax 2，那么g(x)e x 2a因为a 0 ，所以g(x)0，所以g(x)单调递增，又g(0) 1 0，g(1) e 2a 2 0，所以存在x 0(0,1)，使得g(x 0)0那么x (,x 0)时，g(x)f(x)0,f(x)单调递减；x(x 0,)时，g(x)f (x) 0,f(x)单调递增；所以f(x)minf(x 0)e x 0ax 02 2x 0.(1)且e x 0 2ax 0 2 0 (2)f(x)minf(x 0)exx 0(e x2) 2x 0 (1x 0)e x 0x 0---------------8分22又由〔2〕aex2 0 ，所以x 0 (0,ln2)---------------9分2x 0现在求函数p(x)(1x)e x x,x(0,ln2)的范围2q(x0)p(x)1(1x)e x1，q(x0)1xe x0，212所以q(x)q(0)0，所以p(x)单调递减，2p(x)p(0)(1)e01p(x)p(ln2)(1ln2)e ln2ln22ln20-------------11分2所以b=0是符合条件的.-------------12分选做题：22.解：〔I〕连接AB,P、B、F、A四点共圆，PAB PFB．．．．．．．．．．．．．．．．．．2分又PA与圆O切于点A,PAB AEB,．．．．．．．．．．．．．4分PFB AEBAE//CD.．．．．．．．．．．．．．5分〔II〕因为PA、PB是圆O的切线，所以P、B、O、A四点共圆，由PAB外接圆的唯一性可得P、B、F、A、O共圆，四边形PBFA的外接圆就是四边形PBOA的外接圆，OP是该外接圆的直径.．．．．．．．．．．．．．7分由切割线定理可得PA2PC PD3927．．．．．．．．．．．．．9分OP PA2OA22725213.四边形PBFA的外接圆的半径为13.．．．．．．．．．．．．10分23解：〔I〕C1的直角坐标方程为x 12y21，．．．．．．．．．．．．2分C2的直角坐标方程为x3；．．．．．．．．．．．．4分〔II〕设曲线C1与x轴异于原点的交点为A, PQOP,PQ过点A(2,0),设直线PQ的参数方程为x2tcost为参数，y tsin代入C1可得t22tcos0,解得t10或t22cos，可知|AP||t2||2cos|．．．．．．．．．．．．6分代入C2可得2tcos3,解得t/1，1cos可知|AQ||t/|||．．．．．．．．．．．．8分cos11所以PQ=|AP||AQ||2cos||22,当且仅当|2cos||||时取等号，cos cos所以线段PQ长度的最小值为22.．．．．．．．．．．．．10分12x,x024.解：〔I〕由可得f(x)1,0x1，2x1,x1所以f min(x)1，．．．．．．．．．．．．3分所以只需|m 1| 1，解得 1 m 1 1，0 m2，所以实数m的最大值M2.．．．．．．．．．．．．5分〔II〕法一：综合法a2b22abab1ab1，当且仅当a b时取等号，①．．．．．．．．．．．．7分又ab a b 2ab1a b2ab ab，当且仅当ab时取等号，②．．．．．．．．．．．．9分a b2由①②得，ab 1，所以ab2ab.．．．．．．．．．．．．10分a b2法二：分析法因为 a 0,b0,所以要证a b2ab，只需证(a b)24a2b2，即证a2b22ab4a2b2，a2b2M，所以只要证22ab4a2b2，．．．．．．．．．．．．7分即证2(ab)2ab10，即证(2ab1)(ab1)0，因为2ab10，所以只需证，ab1下证ab1，因为2a2b22ab，所以ab 成立，1所以a b2ab．．．．．．．．．．．．10分精品文档强烈推荐精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有。