教育统计学公式汇总

统计学常用公式统计学是一门研究数据收集、分析、解释和表达的科学。

在统计学中，有许多常用的公式被广泛应用于数据处理和推断分析。

本文将介绍一些统计学常用公式，并对其进行说明和用途解释。

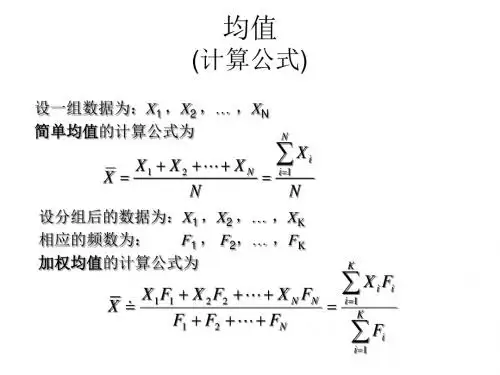
一、描述统计学公式1. 平均值（Mean）平均值是一组数据的总和除以数据的个数，即：$\bar{X} = \frac{X_1 + X_2 + \cdots + X_n}{n}$其中，$\bar{X}$表示平均值，$X_i$表示第i个数据，n表示数据的个数。

2. 中位数（Median）中位数是将一组数据按照大小排列后，处于中间位置的数值。

当数据个数为奇数时，中位数即为排列后正中间的数；当数据个数为偶数时，中位数为排列后中间两个数的平均值。

3. 众数（Mode）众数是一组数据中出现频率最高的数值。

4. 标准差（Standard Deviation）标准差衡量数据的离散程度，其计算公式为：$SD = \sqrt{\frac{(X_1 -\bar{X})^2 + (X_2 -\bar{X})^2 + \cdots + (X_n -\bar{X})^2}{n-1}}$5. 方差（Variance）方差是标准差的平方，即：$Var = SD^2$6. 百分位数（Percentile）百分位数是指一组数据中某个特定百分比处的数值。

比如，第25百分位数是将一组数据从小到大排列后，处于前25%位置的数值。

二、概率与统计公式1. 随机变量期望（Expectation）随机变量期望是描述随机变量平均值的指标，也称为均值。

对于离散型随机变量X，其期望计算公式为：$E(X) = \sum_{i=1}^{n} X_i \cdot P(X_i)$对于连续型随机变量X，其期望计算公式为：$E(X) = \int_{-\infty}^{\infty} x \cdot f(x)dx$其中，$X_i$表示随机变量X的取值，$P(X_i)$表示对应取值的概率，$f(x)$表示X的概率密度函数。

教育統計學計算公式列表 01.算數平均數NX x i∑=02.加權平均數 N1∑∑∑===Ki ii iii Xf x X x 或ωω03.幾何平均數)][log(exp{)][log()log(121X GM X GM XX X X GM NNi iNn 平均數平均數===⋅=∏=04.調和平均數)]}([{)]([)HM (1)111(11121X HM X X N X X X N HM Ni iN倒數平均數倒數倒數平均數倒數===+++=∑=05.探索性資料分析4/)2(2/)(2/)(3131min Q Md Q Q Q X X MAX ++=+=-=三重平均數中間四分距中間全距06.全距 min X X MAX -=ω 07.平均差NNx X AD ∑∑=-=χ08.標準差定義式NNX X S NNX X Sx X SS x x∑∑∑∑∑∑=-==-==-=2222222)()()(χχχ均方根差變異數離均差平方和09.樣本變異數代替母群體變異數1)(1)(2222--==--=∑∑∑N x X S vN X X S x x χ10.標準差計算式NNX XNX X S NNX XNX X SN X X x X SS x x∑∑∑∑∑∑∑∑∑-=-=-=-=-=-=2222222222)()()()()()(11.變異係數 100⨯=xS CV x15.四分差 213Q Q Q -=16.四分位數變異係數 3113Q Q Q Q CQV +-=17.中位數絕對差NMdX MAD i∑-=18.分散係數 ))((Md N MdX CD i∑-=19.變異比 Nf VR Mo -=1 20.分歧性指標∑=-=----=ki i kP P P P ID 12222211121.質的變異指標 kk P P P IQV k /)1(122221-----=22.百分等級 NR PR )50100(100--= 23.百分位數 h f F N PRl P pp )100(-+= 24.z 分數 xx S S x X z χ=-=25.各種標準分數 5001002051002010015100165010+=+=+=+=+=+=z SAT z ACT z AGCT z WISC z BSS z T26.積差相關 yx xy yxxyS S S Nz z r ==∑27.共變數 Nxy N y Y x X S xy∑∑=--))((28.以和、平方和、交叉乘積和計算積差相關NY YNX XNY X XY r xy ∑∑∑∑∑∑∑---=2222)()(29.原始分數回歸方程式x b y aS S NX X N Y X XY b a bX Y xxy ˆˆ)(ˆmin)(2222-==--==--∑∑∑∑∑∑30.標準分數回歸方程式 xy Z Z β=ˆ xy yx xy x r S S bS S S b ===2β31.離均差平方和nX XnY X XY NY Y SS NX XN YX XY SS NY Y SS y Y y Y y Y SS SS SS res reg t resreg t 2222222222222)(][])([)(][)()ˆ()ˆ()(∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑----=--=-=-+-=-+=32.決定係數])(][)([][222222NY Y NX X NY X XY SS SS r treg ∑∑∑∑∑∑∑---==33.期望值 ∑==i i X P X E μ)( 34.期望值變異數222222)()(μμμσ-=-=-=∑i i X P X E X E35.期望值共變數y x xy XY E Y E x E XY E S μμ-=-=)()()()(36.母群體變異數2σ的不偏估計值算法2222221)()()(σμσ=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--+=∑∑∑N N X X E N X E 37.ｚ分配 N x x z x/σμσμ-=-=38.Ｘ2分配 ∑∑=-==212)(i ni i z X σμχ39.Ｆ分配 122221df df F χχ=40.ｔ分配 dfzt 2χ=41.積差相關係數t 考驗公式 2212-=---=N df N r r t ρ。

《统计学原理》常用公式汇总组距＝上限－下限组中值＝（上限+下限）÷2 缺下限开口组组中值＝上限－1/2邻组组距缺上限开口组组中值＝下限+1/2邻组组距111平均指标 1.简单算术平均数：2.加权算术平均数或iii.变异指标1.全距＝最大标志值－最小标志值2.标准差: 简单σ=；加权σ= 3.标准差系数:第五章抽样估计1.平均误差：重复抽样：不重复抽样：2.抽样极限误差3.重复抽样条件下：平均数抽样时必要的样本数目成数抽样时必要的样本数目4.不重复抽样条件下：平均数抽样时必要的样本数目第七章相关分析 1.相关系数2.配合回归方程ｙ＝ａ＋ｂｘ3.估计标准误：第八章指数分数一、综合指数的计算与分析(1)数量指标指数此公式的计算结果说明复杂现象总体数量指标综合变动的方向和程度。

(-)此差额说明由于数量指标的变动对价值量指标影响的绝对额。

(2)质量指标指数此公式的计算结果说明复杂现象总体质量指标综合变动的方向和程度。

（-）此差额说明由于质量指标的变动对价值量指标影响的绝对额。

加权算术平均数指数=加权调和平均数指数=(3)复杂现象总体总量指标变动的因素分析相对数变动分析：=×绝对值变动分析：-= (-)×（-）第九章动态数列分析一、平均发展水平的计算方法：(1)由总量指标动态数列计算序时平均数①由时期数列计算②由时点数列计算在间断时点数列的条件下计算：a.若间断的间隔相等，则采用“首末折半法”计算。

公式为：b.若间断的间隔不等，则应以间隔数为权数进行加权平均计算。

公式为：(2)由相对指标或平均指标动态数列计算序时平均数基本公式为：式中：代表相对指标或平均指标动态数列的序时平均数；代表分子数列的序时平均数；代表分母数列的序时平均数；逐期增长量之和累积增长量二. 平均增长量＝─────────＝─────────逐期增长量的个数逐期增长量的个数(1)计算平均发展速度的公式为：(2)平均增长速度的计算平均增长速度＝平均发展速度-１（100%）。

统计学常用公式统计学是一门研究数据收集、整理、分析和解释的学科。

在统计学中，公式是非常重要的工具，用于计算和推导各种统计指标和结果。

下面是一些统计学中常用的公式，它们可以帮助我们理解和应用统计学的基本概念和方法。

1. 数据的中心趋势度量在统计分析中，我们经常需要了解数据的中心趋势，即数据的集中程度或平均水平。

以下是几个常用的中心趋势度量公式：- 平均值（Mean）：一组数据中所有观测值的总和除以观测值的个数。

- 中位数（Median）：将一组数据按照大小排序，位于中间位置的观测值。

- 众数（Mode）：出现次数最多的观测值。

- 加权平均值（Weighted Mean）：将每个观测值乘以相应的权重，然后求和并除以总的权重和。

2. 数据的离散程度度量除了了解数据集中在哪里，我们还需要了解数据的离散程度，即数据分散的程度。

以下是几个常用的离散程度度量公式：- 方差（Variance）：一组数据与其平均值之差的平方的平均值。

- 标准差（Standard Deviation）：方差的算术平方根。

- 平均绝对偏差（Mean Absolute Deviation）：一组数据与其平均值之差的绝对值的平均值。

3. 数据的相关性度量在统计分析中，我们常常需要了解两个或多个变量之间的相关性。

以下是几个常用的相关性度量公式：- 协方差（Covariance）：一组数据中两个变量之间的协方差。

协方差的正负表示两个变量是正相关还是负相关。

- 相关系数（Correlation Coefficient）：协方差除以两个变量各自的标准差的乘积。

相关系数的取值范围为-1到1，越接近-1或1表示相关性越强。

4. 抽样误差估计在统计学中，我们通常只能对样本数据进行分析，从而推断总体的特征。

以下是几个常用的抽样误差估计公式：- 样本标准差（Sample Standard Deviation）：类似于总体标准差，但在计算时使用样本数据。

- 样本均值（Sample Mean）：类似于总体均值，但在计算时使用样本数据。

平均数基本公式: 一、总体单位总量总体标志总量算术平均数=（调和平均数）简单算术平均： nx x ∑=加权算术平均： ∑∑=fxf x 或 ∑∑=ffxx二、调和平均数： 简单调和平均： ∑=xn H 1 加权调和平均： ∑∑=xm m H三、几何平均数： 简单：nx G ∏= 加权： ∑∏=ff x G四、众数：下限： d L M O 211∆+∆∆+= 上限：d U M O 212∆+∆∆-=五、中位数:下限： d f S fL M mm e 12--+=∑ 上限：d f S fU M mm e 12+--=∑中位数的位次: M e 2∑=f标志变异指标：标准差： 简单: nx x ∑-=2)(σ 加权：∑∑-=ffx x 2)(σ方差： 简单： nx x ∑-=22)(σ加权： ∑∑-=ffx x 22)(σ成数： N N p 1=NN q 0= 1=+p q交替标志： 平均数：p x = 标准差： )1(p p p -=σ方差)1(2P P P -=σ标准差系数: %100⨯=xV σσ分析计算题:1、星河公司2009年四个季度的销售利润率分别是12％、11％、13%和10％，同期的销售额分别是1000万元、1200万元、1250万元和1000万元.友谊公司同期的销售利润率分别是13％、11％、10%和12％，利润额分别是130万元、132万元、120万元和144万元，试通过计算比较两家公司2009年全年销售利润率的高低。

2、课本 P 93 17题动态分析指标：一、平均发展水平： 总量指标时间数列：1、时期数列：na a ∑=2、时点数列: 连续型： 等间隔:na a ∑=不等间隔：∑∑=ffa a不连续型： 等间隔: na a a a a n n 22110++⋅⋅⋅++=-不等间隔： 12111232121222---+⋅⋅⋅++++⋅⋅⋅++++=n n n n f f f f a a f a a f a a a相对指标时间数列： ba c =平均指标时间数列： 同上二、增长量： 逐期增长量： 01a a -12a a - 23a a -… 1--n n a a 累计增长量： 01a a -02a a -03a a -…0a a n -平均增长量1)1()()()(011201-+-=-+⋅⋅⋅+-+-=-n a a n a a a a a a n n n三、发展速度： 环比发展速度：1a a12a a23a a …1-n n a a 定基发展速度:1a a2a a3a a …a a n两者之间关系： 1、112010-⨯⨯⨯=n n n a a a a a a a a 2、110--=n n n na a a a a a平均发展速度： n x x ∏=nn a a x 0= n R x =长期趋势测定方法：(时间数列变动分析）方程法：根据时间数列的数据特征，建立一个合适的趋势方程来描述时间数列的趋势变动,推算或预测个时期的趋势值。

公式一1. 众数【MODE 】（1） 未分组数据或单变量值分组数据众数的计算未分组数据或单变量值分组数据的众数就是出现次数最多的变量值。

（2） 组距分组数据众数的计算对于组距分组数据，先找出出现次数最多的变量值所在组，即为众数所在组，再根据下面的公式计算计算众数的近似值。

下限公式： 1012M =L++i ∆⨯∆∆ 式中：0M 表示众数；L 表示众数的下线；1∆表示众数组次数与上一组次数之差；2∆表示众数组次数与下一组次数之差；i 表示众数组的组距。

上限公式：2012M =U-+i ∆⨯∆∆ 式中：U 表示众数组的上限。

2．中位数【MEDIAN 】（1）未分组数据中中位数的计算根据未分组数据计算中位数时，要先对数据进行排序，然后确定中位数的位置。

设一组数据按从小到大排序后为12N X X X ，，…，，中位数e M ，为则有：e N+M =X1（）2当N 为奇数e N N +1221M =X +X 2⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭⎧⎫⎪⎪⎨⎬⎪⎪⎩⎭ 当N 为偶数（2）分组数据中位数的计算分组数据中位数的计算时，要先根据公式N / 2 确定中位数的位置，并确定中位数所在的组，然后采用下面的公式计算中位数的近似值：N=1m-1e m-S 2M =L+ii fd f ⨯∑式中：e M 表示中位数；L 表示中位数所在组的下限；m-1S 表示中位数所在组以下各组的累计次数；m f 表示中位数所在组的次数；d 表示中位数所在组的组距。

3．均值的计算【A VERAGE 】（1）未经分组均值的计算未经分组数据均值的计算公式为： 112n ++==nii x x x x x n n=∑…（2）分组数据均值计算分组数据均值的计算公式为： 11221121+++==+ki ik k i k kii x f x f x f x f x f f f f==+∑∑+4．几何平均数【GEOMEAN 】几何平均数是N 个变量值乘积的N 次方根，计算公式为：式中：G 表示几何平均数；∏表示连乘符号。

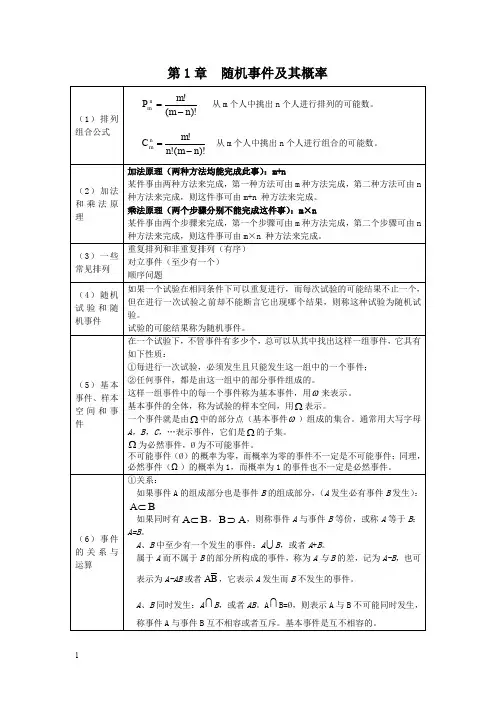
华东师大心理统计学大纲教材：《教育统计学》第一章绪论第一节什么是统计学和心理统计学一、什么是统计学统计学是研究统计原理和方法的科学。

具体地说，它是研究如何搜集、整理、分析反映事物总体信息的数字资料，并以此为依据，对总体特征进行推断的原理和方法。

统计学分为两大类。

一类是数理统计学。

它主要是以概率论为基础，对统计数据数量关系的模式加以解释，对统计原理和方法给予数学的证明。

它是数学的一个分支。

另一类是应用统计学。

它是数理统计原理和方法在各个领域中的应用，如数理统计的原理和方法应用到工业领域，称为工业统计学；应用到医学领域，称为医学统计学；应用到心理学领域，称为心理统计学，等等。

应用统计学是与研究对象密切结合的各科专门统计学。

二、统计学和心理统计学的内容统计学和心理统计学的研究内容，从不同角度来分，可以分为不同的类型。

从具体应用的角度来分，可以分成描述统计，推断统计和实验设计三部分。

1．描述统计对已获得的数据进行整理、概括，显示其分布特征的统计方法，称为描述统计。

2．推断统计根据样本所提供的信息，运用概率的理论进行分析、论证，在一定可靠程度上，对总体分布特征进行估计、推测，这种统计方法称为推断统计。

推断统计的内容包括总体参数估计和假设检验两部分。

3．实验设计实验者为了揭示试验中自变量和因变量的关系，在实验之前所制定的实验计划，称为实验设计。

其中包括选择怎样的抽样方式；如何计算样本容量；确定怎样的实验对照形式；如何实现实验组和对照组的等组化；如何安排实验因素和如何控制无关因素；用什么统计方法处理及分析实验结果，等等。

以上三部分内容，不是截然分开，而是相互联系的。

第二节统计学中的几个基本概念一、随机变量具有以下三个特性的现象，成为随机变量。

第一，一次试验有多中可能结果，其所有可能结果是已知的；第二，试验之前不能预料哪一种结果会出现；第三，在相同的条件下可以重复试验。

随机现象的每一种结果叫做一个随机事件。

我们把能表示随机现象各种结果的变量称为随机变量。

概念及公式汇总1、统计学是以现象的数量特征为研究对象，利用自身特有方法，发现现象应有规律的一门方法论科学。

2、总体是指具有相同性质的一组个体组成的集合，样本是从其中获得的一个群或组。

3、指标是用来说明统计总体或样本数量特征的名称和数值的综合。

4、普查是一种专门组织的、一次性的全面调查。

5、重点调查是对总体中的重点单位进行的专门调查。

重点单位是指此类单位的变量值（调查所要了解的变量）在总体变量值中有较大比重。

6、典型调查时对总体中的有代表性的单位进行的专门调查，是为了了解总体的特殊情况。

7、抽样调查是指按随机原则对总体抽取样本，以样本资料来推断总体的有关特征的一种专门调查。

8、统计误差是指在统计工作中由于种种原因产生的与研究对象本来状态有差异的结果。

9、统计分布数列有两个基本要素，一是分组标准，二是次数。

10、统计分组是根据研究目的，选择一个或几个分组标准，对总体各单位进行分类的一项工作过程。

11、按品质标志分组所形成的分布数列称为属性分布数列；按数量标志分组所形成的分布数列称为变量数列。

12、按品质标志分组所形成的分布数列称为属性分布数列；按数量标志分组所形成的分布数列称为变量数列。

13、以一个变量值代表一个组，按一定的顺序排列所形成的变量数列称为单项数列。

14、由表示一定变动范围的两个变量值代表一个组，按一定的顺序排列所形成的变量数列称为组距数列。

15、在异距数列中，反映次数在各组分布密集程度的指标是次数密度，它是本组的次数与本组组距之比。

16、向上累计是将各组次数和比率，由变量值低的组向变量值高的逐组累计，表明各组上限以下一共所包含的总体次数和比率有多少。

17、向下累计是将各组次数和比率，由变量值高的组向变量值低的逐组累计，表明各组下限以上一共所包含的总体次数和比率有多少。

18、集中趋势是指一组数据向分布的中心集中的现象。

19、调和平均数是各个变量值倒数的算术平均数的倒数，又称倒数平均数。

20、把总体各变量值按大小顺序排列，处于中点位置的变量值就是中位数。

教育统计学王孝玲第一章绪论教育统计学是运用数理统计的原理和方法研究教育问题的一门应用科学。

它的主要任务是研究如何搜集、整理、分析由教育调查和教育实验等途径所获得的数字资料，并以此为依据,进行科学推断,从而揭示蕴含在教育现象中的客观规律.统计学和教育统计学的内容：从具体应用角度来分,可以分成：描述统计、推断和实验设计三部分。

描述统计：对已获得的数据进行整理、概括，显现其分布特征的统计方法。

通过教育调查和教育实验获得了大量的数据，用归组、编表、绘图等统计方法对这进行归纳、整理，以直观形象的形式反映其分布特征;通过计算各种特征量，来反映它们分布上的数字特征.推断统计：根据样本所提供的信息，运用概率的理论进行分析、论证，在一定可靠程度上对总体分布特征进行估计、推测。

描述统计是推断统计的基础，推断统计是通过样本信息估计、推测总体，从已知情况估计、推测未知情况。

学习统计学和教育统计的学的意义：一、统计学为科学研究提供了一种科学方法,统计推理的方法是归纳法。

二、教育统计学是教育科研定量分析的重要工具。

三、广大教育工作者学习教育统计学的具体意义：1、可以顺利地阅读运用统计方法进行定量分析的科研报告.2、可以提高教育工作的科学性和效率。

3、为学习教育测量及教育评价打下基础。

随机现象：1、一次试验有多种可能结果,其所有可能结果是已知的；2、试验之前不能预料哪一种可能结果会出现;3、在相同的条件下可以重复试验。

随机现象的每一种结果叫做一个随机事件。

总体：研究的具有某种共同特性的个体的总和。

总体中的每个单位称为个体。

样本是从总体中抽取的作为观察对象的一部分个体。

样本上的数字特征是统计量.总体上的各种数字特征是参数。

在进行统计推断时，就是根据样本统计量来推断总体相应的参数。

第二章数据的初步整理教育统计资料的来源：经常性资料、专题性资料（教育调查、教育实验）数据的种类:按来源分:点计数据和度量数据，按随机变量取值情况分:间断型（取值个数有限的数据，一般为整数）和连续型随机变量（取值个数无限的不可数的数据可用小数表示）。

统计学计算公式范文统计学是一门研究数据收集、数据整理、数据分析和数据解释的科学。

它涵盖了许多数学和概率的知识，应用于各个领域，包括经济学、社会学、心理学等等。

在统计学中，有许多常用的计算公式，本文将会介绍一些常见的统计学计算公式。

一、描述统计学计算公式1.平均数平均数（Mean）是一组数据的算术平均值，计算公式为：Mean = (X1 + X2 + X3 + ... + Xn) / n2.中位数中位数（Median）是将数据按升序排列后，位于中间位置的值（如果数据个数为奇数），或位于中间两个位置的值的平均值（如果数据个数为偶数）。

计算公式为：Median = (X[(n+1)/2] + X[(n+1)/2+1]) / 2 （数据个数为偶数）Median = X[(n+1)/2] （数据个数为奇数）3.众数众数（Mode）是一组数据中出现次数最多的值。

计算公式为：找到出现次数最多的值即可。

4.方差方差（Variance）度量了一组数据的离散程度。

计算公式为：Variance = Σ((Xi - Mean)²) / (n-1)5.标准差标准差（Standard Deviation）是方差的平方根，用于衡量一组数据的离散程度。

计算公式为：Standard Deviation = √Variance二、概率论计算公式1.随机变量的期望随机变量的期望是衡量随机变量的平均值，计算公式为：E(X)=Σ(X*P(X))2.随机变量的方差随机变量的方差是衡量随机变量的离散程度，计算公式为：Var(X) = Σ(X² * P(X)) - [E(X)]²3.协方差协方差（Covariance）刻画了两个变量间的线性关系程度，计算公式为：Cov(X, Y) = Σ((Xi - Mean(X)) * (Yi - Mean(Y))) / (n-1)4.相关系数相关系数（Correlation Coefficient）度量了两个变量之间的线性关系强度和方向，计算公式为：Corr(X, Y) = Cov(X, Y) / (Standard Deviation(X) * Standard Deviation(Y))三、假设检验计算公式1.标准误差标准误差（Standard Error）衡量样本统计量与总体参数之间的差异。

统计公式及说明范文统计公式是一种数学表达方法，用于表示和求解统计学问题。

统计公式广泛应用于各个领域，包括经济学、社会学、管理学和自然科学等。

本文将介绍一些常见的统计公式及其说明。

一、描述统计公式1. 平均值（Mean）：平均值是一组数据的总和除以数据个数。

平均值可以表示数据集的集中趋势。

平均值的公式如下：mean = (x1 + x2 + ... + xn) / n2. 中位数（Median）：中位数是有序数据集中的中间值。

对于有奇数个数据，中位数是中间那个数；对于有偶数个数据，中位数是中间两个数的平均值。

中位数的公式如下：median = (n + 1) / 23. 众数（Mode）：众数是数据集中出现次数最多的数值。

一个数据集可以有一个众数或多个众数。

众数的公式没有统一的数学表示，通常使用频数表或直方图来表示。

4. 标准差（Standard Deviation）：标准差是数据集的离散度度量，表示数据集中各个数据与平均值之间的偏离程度。

标准差的公式如下：standard deviation = sqrt((x1-mean)^2 + (x2-mean)^2 + ... + (xn-mean)^2) / n5. 方差（Variance）：方差是标准差的平方，也是数据集的离散度度量。

方差的公式如下：variance = ((x1-mean)^2 + (x2-mean)^2 + ... + (xn-mean)^2) / n二、概率统计公式1. 概率密度函数（Probability Density Function，PDF）：概率密度函数描述了连续随机变量的概率分布。

它表示了随机变量取一些值的概率密度。

概率密度函数的公式如下：f(x) = dF(x) / dx2. 累积分布函数（Cumulative Distribution Function，CDF）：累积分布函数描述了随机变量小于等于一些值的概率。

累积分布函数的公式如下：F(x)=P(X<=x)3. 期望值（Expectation）：期望值是随机变量的平均值，表示对随机变量取值的长期平均结果。

公式一1. 众数【MODE 】（1） 未分组数据或单变量值分组数据众数的计算未分组数据或单变量值分组数据的众数就是出现次数最多的变量值。

（2） 组距分组数据众数的计算对于组距分组数据，先找出出现次数最多的变量值所在组，即为众数所在组，再根据下面的公式计算计算众数的近似值。

下限公式： 1012M =L++i ∆⨯∆∆ 式中：0M 表示众数；L 表示众数的下线；1∆表示众数组次数与上一组次数之差；2∆表示众数组次数与下一组次数之差；i 表示众数组的组距。

上限公式：2012M =U-+i ∆⨯∆∆ 式中：U 表示众数组的上限。

2．中位数【MEDIAN 】（1）未分组数据中中位数的计算根据未分组数据计算中位数时，要先对数据进行排序，然后确定中位数的位置。

设一组数据按从小到大排序后为12N X X X ，，…，，中位数e M ，为则有：e N+M =X1（）2当N 为奇数e N N +1221M =X +X 2⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭⎧⎫⎪⎪⎨⎬⎪⎪⎩⎭ 当N 为偶数（2）分组数据中位数的计算分组数据中位数的计算时，要先根据公式N / 2 确定中位数的位置，并确定中位数所在的组，然后采用下面的公式计算中位数的近似值：N=1m-1e m-S 2M =L+ii fd f ⨯∑式中：e M 表示中位数；L 表示中位数所在组的下限；m-1S 表示中位数所在组以下各组的累计次数；m f 表示中位数所在组的次数；d 表示中位数所在组的组距。

3．均值的计算【A VERAGE 】（1）未经分组均值的计算未经分组数据均值的计算公式为： 112n ++==nii x x x x x n n=∑…（2）分组数据均值计算分组数据均值的计算公式为： 11221121+++==+ki ik k i k kii x f x f x f x f x f f f f==+∑∑+4．几何平均数【GEOMEAN 】几何平均数是N 个变量值乘积的N 次方根，计算公式为：式中：G 表示几何平均数；∏表示连乘符号。

教育统计学公式汇总1、 众数：2、 中数：3、 加权平均数：4、 众数、中数和算术平均数之间的关系：5、 几何平均数：6、 调和平均数：7、 平均差：8、 样本标准差：9、 标准差的合成： 10、差异系数：11、百分位数： 0ab a bf M L if f =+•+2bd b n F M L i f-=+•2a d a n F M L i f -=-•1112212k j j j k kw k t n X n X n X n X X n n n n =++⋯+==++⋯+∑0M 3Mdn 2X =－g X =11lg lg nii g xX n-=⎛⎫⎪ ⎪=⎪⎪⎝⎭∑12111111111()H niinM n x x x n x x===++⋯+∑∑11'nni ii i x X x AD nn==-==∑∑S ==w σ=100%SCV X =⨯100b m mN F P L i f•-=+•(1)100ammN F P U i f--=-•12、百分等级分数：13、协方差：14、积差相关系数：15、斯皮尔曼等级相关：16、肯德尔和谐系数：17、点双列相关：18、双列相关：19、多系列相关：20、φ（fai ）相关：21、列联相关：22、 的分布（标准分）：()100b x L f F i PR N-⎡⎤+⎢⎥⎣⎦=⨯1()()(,)niii x X yY COV X Y n=--=∑1()()i iiiXY x y x y r -=∑∑∑2261(1)R D r n n =--∑43(1)1(1)X YR R R r n n n n ⎡⎤=•-+⎢⎥-+⎣⎦∑231()12iR SS W k n n =-p qpb XX X r S -=p qb X X X pq r S Y-=•()2()L H i s L H t iY Y X r Y Y S p ⎡⎤-•⎣⎦=-∑∑r ϕ=C =X X XX X Z μμσσ--==23、总体平均数的置信区间：24、样本容量的估计：25、平均数之差的标准误：两组相关样本的情况：26、检验统计量：27、已知两组样本相关系数r 时的检验统计量：两组独立样本的情况： 28、两个总体方差都已知时的检验统计量：29、两个总体方差都未知时的检验统计量：（1） 两总体方差相等： （2） 两总体方差不等：1） 阿斯平—威尔士检验：2) 柯克兰—柯克斯检验： 222121)1(2222)1(2121221··n Sn S t n St n S t n n ++='--ααα22/X Z X Z αασσ⎡-•+•⎢⎣()22()df t Sn dα•=12X X σ-=d t=X X t =X X Z =X X t =22S F S =大小211221212S n k S S n n =+22121(1)df k k n n =-+30、样本比率抽样分布的标准误：31、总体比率的置信区间：32、样本比率显著性检验的检验统计量：33、相关样本比率差异的显著性检验： Z34、独立样本比率差异的显著性检验：（1） 独立样本之差（p 1-p 2）的抽样分布：（2） 独立样本之差（p 1-p 2）在抽样分布中的标准误：（3） 独立样本比率差异显著性检验的检验统计量：其中，35、t 分布的检验统计量：其中，相关系数区间估计的置信区间为：p σ=/2/2p Z P p Zαα-•≤≤+•Z =12p p σ-==12p p σ-==121212()()p p p p P P ZS ----==112212'n p n p p n n +=+rr t ρσ-==r σ=(2)(2)22rrn n r tr t αασρσ---⋅≤≤+⋅36、两总体相关系数的差异性检验：37、检验统计量的一般表达式：38、独立性检验：（1）在“R变量与C变量相互独立，彼此无关”的假设成立的条件下，第r行第c列的那个类别的理论期待次数：自由度：（2）对2×2表的资料进行独立性检验，计算检验统计量：39、非参数检验连续性校正校正公式：40、符号秩次检验：（1）大样本的情况：T的总体平均数为μT=n(n+1)4T的总体标准差为σT=√n(n+1)(2n+1)24Z=2χ220()keef ffχ-=∑221()2ecef ffχ--=∑()c r cren n nnf N P NN N N•=•=••=(1)(1)df r c=-•-22()()()()()N ad bca b a c b d c dχ•-=++++0.5Z±=n（r）-其检验统计量为 24)12)(1(4/)1(+++-=-=Z n n n n n T T TTσμ其中，n= n ++n − T=min(T +，T −）41、秩和检验 （1）T 的总体平均数为：2)1(211++=n n n T μ（2）T 的总体标准差为：12)1(2121++=n n n n T σ（3）其检验统计量为： 12)1(2/)1(2121211++++-=-=Z n n n n n n n T T TTσμ42、中数检验两个样本中数差异的显著性检验：md f i f N L )2(∑-+=M。

统计学重要公式()()D 22221. X X2. N3. Q4. 1 (2) S 1U L iiXnIQR Q Q XNX n μμσμ====--=-=-∑∑∑∑样本平均数：总体平均数：四分位差：方差：（）总体方差：样本方差：225. 1 2 S S6.100%100%100%CV S CV X σσσμ==⎛⎫⎛⎫=⨯=⨯ ⎪ ⎪⎝⎭⎝⎭⎛⎫=⨯ ⎪⎝⎭标准差：（）总体标准差：（）样本标准差：变异系数标准差总体：平均数样本：()()()()()22121111117.() ,8. (,)19. ,,,i i i i iiXY XYXYXY X YXX YYn i nni XX i ii i n n i i nni i XY iii i i i YY i X X X Z Z Z S XXYYCov X Y S n S L r S S L L X L X XXnX Y L XXYYX Y nL Y μσ=======--==--==-==⎛⎫ ⎪⎝⎭=-=-⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭=--=-=-∑∑∑∑∑∑∑∑标准分数分数或样本协方差皮尔逊相关系数()22121111,,n i nni ii i nniii i Y YYnX YX Y n n=====⎛⎫ ⎪⎝⎭=-==∑∑∑∑∑()()()()()2210. X 11. X 12. S 113.!121,!!12,!,!!!iiiiiiiim nm mn nm n mn nW X WF X FF XXn n P n n n n m m n n P n Cm m n m C C -==-=-==--⋅⋅⋅-+=⨯⨯⋅⋅⋅⨯==-=∑∑∑∑∑加权平均数分组数据样本平均数分组数据样本方差排列组合公式ni i 114. ()1()15. P(A B)P(A)P(B)-P(A B)P(A B)P(A B)16. P(A|B), P(B|A)()()17. P(A B)()P(A|B)()P(B|A)18. P(A B)()()19. P(B)()P(B|A )20.i P A P A P B P A P B P A P A P B P A ==-⋃=+⋂⋂⋂==⋂=⋅=⋅⋂==⋅∑事件补的概率加法公式条件概率乘法公式独立事件全概率公式贝叶i i i njj 1()P(B|A )()P(B|A )P(A |B)P(B)()P(B|A )i i jP A P A P A =⋅⋅==⋅∑斯公式()22221.()()22.()()23.(),0,1,2,...,,124.(),()(1)25.()!!27.()x x n x n x x x n xr N rE X xp x Var X x p x p x C p q x n q p E X np Var X np p e e p x x x C C p x C μλμσμμσμλ-----====-===-====-==⋅=∑∑离散型随机变量的数学期望离散型随机变量的方差二项分布的概率函数二项分布的数学期望和方差泊松分布超几何分布()222,0128.()229.nN x x r f x e x Z μσπσμσ--≤≤=-=正态概率密度函数标准正态分布变换30. X :(), 131.:(),(1)1(1)X X PPE X N n N n nP E p p N n p p N n p p nμσσσσσσ=-⎛⎫= ⎪-⎝⎭==⎛⎫--= ⎪ ⎪-⎝⎭-=的数学期望和标准差有限总体时无限总体时比例的数学期望和标准差有限总体时无限总体时2222222232.:33.(1):,(2):,(3),,,(4),,34.:X X Z n S X Z nX Z n S X t nZ n αααααμμσσσμ-±±±±=∆估计时的抽样误差总体均值的区间估计大样本且方差已知大样本且方差未知总体正态小样本方差已知总体正态小样本方差未知估计时所需的样本容量222200(1)35.(1)36.37.::,/:/38.:,1/39.:(1)p p P p Z nZ p p p n X Z n X Z S nX t df n S np p Z p p nααμσμμ-±⋅-=∆-=-=-==--=-总体比率的区间估计的区间估计时所需的样本容量大样本总体均值的检验统计量方差已知方差未知小样本总体均值的检验统计量总体比率检验统计量()()()122222011212121222121240.:,41.,::(),XX Z Z n Z Z X X X X E X X n n αβαασμμμμσσσ--=----=-=+总体均值的单侧检验中所需样本容量用代替即为双侧检验的公式独立样本时两个总体均值之差的点估计量的期望值与标准差()()()()()()()()()()12121212121212121222212121212222222121212121212242.:(1)(,30),,:(2),, 11,()(3),X X X X X X X XX X X Xn n XX Z S S S n n X X Z S X X n n n n XX t S ααασσσσσσσσσσσσ------≥-±=+-±=-=+=+-±两个总体均值之差的区间估计大样本已知的点估计量为大样本未知时的标准差小样本正态()()()()()12121222121212122121212121211221112143.X (1) Z ,X (2),11(3)44.:(1)(1)(1)p dd p p X n n X t S n n d t S np p p p E p p p p p p p p p p p n n n μμσσμμμσ----=+---=⎛⎫+ ⎪⎝⎭-=---=----=+=+两个总体均值之差的假设检验统计量大样本小样本相关样本两个比率之差的点估计量的期望值与标准差1212222112212(1)(1)(1):p p p p p n p p p p S n n σ-----=+的点估计量 ()()()()()()12121212111122221221212112212121245.:,(1),,(1)5,46.::11:(1)p p pppp p p n p n p n p n p p p Z S p p p p Z n p n p p n n p p S p p n n ασσ------≥-±---=+=+⎛⎫==-+ ⎪⎝⎭两个总体比率之差的区间估计大样本时两个总体比率之差的检验统计量总体比率合并估计时的点估计量()()()()()22222/2(1/2)2222122221221147.:148.:49.:50.:,151.::ki ii ii j ij ij ijjijn S n S n S S F S f e df k e RT CT i j e n f e e αασχχχσχχ-=--≤≤-==-==-⨯⨯==-=∑一个总体方差的区间估计一个总体方差的检验统计量两个总体方差的检验统计量拟合优度检验统计量独立假设条件下列联表的期望频数第行之和第列之和样本容量独立性检验统计量()(),11idf R C =--∑∑()()1221111212152.:,:,1:,1:,1:():,:1jjjn iji jjn ij ji jj n kijkj i t t jj t kjjt j t kjjj K XXn XXSn XX n nn SSTRMSTR k SSTR nXX SSEMSE n kSSE nS k ========-=-==-=-=-=-=-∑∑∑∑∑∑∑检验个均值的相等性第ｊ个处理的样本均值第ｊ个处理的样本方差总样本均值处理均方处理平方和误差均方误差平方和个均值相等检()211i ::::X LSD :t 11jn kij tj i ji j MSTRF MSESST X X SST SSTR SSE XFisher MSE n n ====-=+-=⎛⎫+⎪ ⎪⎝⎭∑∑验统计量总平方和平方和分解多重比较方法的检验统计量()()()()()()2112.12.12254.::,1,:,1,:,1,:,11::,1,:k at ij tt t j i k b j t b j ar i tr i e t b r e ij t ijt i b SS X X df n SS a X X df k SS k X X df a SS SS SS SS df k a X SS Xdf ak akX SS =====-=-=-=-=-=-=--=--=-=-=∑∑∑∑∑∑∑∑随机化区组设计总平方和处理平方和区组平方和误差平方和求平方和的另一种方法总平方和处理平方和()()()()()()2222,1,:,1,:,11j ij b ijijr r e t b r e X df k aakX X SS df a k akSS SS SS SS df k a -=-=-=-=--=--∑∑∑∑∑∑∑∑区组平方和误差平方和()()()()()()21112.12.12..1155.::,1:,1,:,1,:,11:,abrijk ttt i j k ai tAi bj tB j abij i j tABi j e SST X X dfn A SSA br X X df a B SSB ar X X df b SSAB r X X X X dfa b SSE SST SSA SSB SSAB df a ========-=-=-=-=-=-=--+=--=---=∑∑∑∑∑∑∑析因试验总平方和因子平方和因子平方和交互作用平方和误差平方和(1)br ab ab r -=-()()()()01010121220157.::::min :,i i iii i i y x E y xy b b xy y x y x y nb x xnb y b xββεββ=++=+=+--=-=-∑∑∑∑∑∑简单线性回归模型简单线性回归方程估计的简单线性回归方程最小二乘法估计的回归方程的斜率和截距()()()()()()()()()222222222222221122::::()::():i i iiiii i i i i i iixy SST SSR SSESSE y y y SST yyynX SSR y yb X nX Y X Y n X XnSSRR r SSTr b b r S M σ=+=-=-=-⎡⎤⎢⎥=-=-⎢⎥⎣⎦⎡⎤-⎢⎥⎢⎥⎣⎦=-=====∑∑∑∑∑∑∑∑∑∑∑∑平方和分解误差平方和总平方和回归平方和判定系数决定系数样本相关系数的符号判定系数的符号均方误差的估计量2:2SSE SE n SSE S MSE n =-==-估计量的标准误差()()()()()1110012212212002200/20::::1:1:():1:1b iib i ib y i i y y y b X XnSb S X Xnb t t S SSR SSRMSR SSRMSRF F MSE X Xy S S n X X n E y y t S X XS S n ασσ-=-=-=====-=+⎡⎤⎢⎥-⎢⎥⎣⎦±⋅-=++∑∑∑∑∑∑的标准差的估计的标准差统计量回归均方自变量的个数检验统计量的估计的标准差的置信区间估计一个个别值估计的标准差()0022200/2:i i yy X X n y y t S α-⎡⎤⎢⎥-⎢⎥⎣⎦±⋅∑∑的预测区间估计()()()0112201122222258.::::min ,,::1:111::1p p p pi i a y x x x E y x x x y y SST SSR SSE SST SSR SSESSRR SSTn R R n p SSRMSR p SSEMSE n p F ββββεββββ=+++⋅⋅⋅++=+++⋅⋅⋅+-=+=-=--⋅--==--∑ 多元线性回归模型多元回归方程估计的多元回归方程最小二乘法之间的关系多元决定系数修正的多元决定系数回归均方误差均方检::iib MSRF MSE bt t S ==验统计量检验统计量。

教育统计学是运用数理统计的原理和方法研究教育问题的一门应用科学。

它的主要任务是研究如何搜集、整理、分析由教育调查和教育实验等途径所获得的数字资料，并以此为依据，进行科学推断，从而揭示蕴含在教育现象中的客观规律。

统计学和教育统计学的内容：从具体应用角度来分，可以分成：描述统计、推断和实验设计三部分。

描述统计：对已获得的数据进行整理、概括，显现其分布特征的统计方法。

通过教育调查和教育实验获得了大量的数据，用归组、编表、绘图等统计方法对这进行归纳、整理，以直观形象的形式反映其分布特征；通过计算各种特征量，来反映它们分布上的数字特征。

推断统计：根据样本所提供的信息，运用概率的理论进行分析、论证，在一定可靠程度上对总体分布特征进行估计、推测。

描述统计是推断统计的基础，推断统计是通过样本信息估计、推测总体，从已知情况估计、推测未知情况。

学习统计学和教育统计的学的意义：一、统计学为科学研究提供了一种科学方法，统计推理的方法是归纳法。

二、教育统计学是教育科研定量分析的重要工具。

三、广大教育工作者学习教育统计学的具体意义：1、可以顺利地阅读运用统计方法进行定量分析的科研报告。

2、可以提高教育工作的科学性和效率。

3、为学习教育测量及教育评价打下基础。

随机现象：1、一次试验有多种可能结果，其所有可能结果是已知的；2、试验之前不能预料哪一种可能结果会出现；3、在相同的条件下可以重复试验。

随机现象的每一种结果叫做一个随机事件。

总体：研究的具有某种共同特性的个体的总和。

总体中的每个单位称为个体。

样本是从总体中抽取的作为观察对象的一部分个体。

样本上的数字特征是统计量。

总体上的各种数字特征是参数。

在进行统计推断时，就是根据样本统计量来推断总体相应的参数。

第二章数据的初步整理教育统计资料的来源：经常性资料、专题性资料（教育调查、教育实验）数据的种类：按来源分：点计数据和度量数据，按随机变量取值情况分：间断型（取值个数有限的数据，一般为整数）和连续型随机变量（取值个数无限的不可数的数据可用小数表示）。