正丁醇表面张力的测定-最终版
- 格式：xls
- 大小：22.00 KB
- 文档页数：1
下载文档原格式
合集下载
正丁醇表面张力的测定实验报告
正丁醇表面张力的测定实验报告实验目的：- 了解正丁醇表面张力测定的方法和原理；- 掌握测定表面张力的基本操作和步骤；- 探究温度对正丁醇表面张力的影响。
实验原理：表面张力(T)是指单位长度的表面所能承受的最小力，单位是N/m。
通过测量液体的表面张力，可以了解液体的表面性质，如渗透性、流速、黏度等等。
测量表面张力的方法有很多种，常见的有均匀膜法和压降法。
在本次实验中，我们采用均匀膜法来测量正丁醇的表面张力。
均匀膜法是指加入一定量液体在测量池内，慢慢地添加被测液体，形成一个平衡膜，然后测量膜的长度和被测液体的体积，从而计算出表面张力。
在均匀膜法中，有一个重要的参量叫做膜厚度(h)，它是指平衡膜的厚度，单位是米(m)。
膜厚度的大小对表面张力的测定影响很大，所以需要在实验中注意精确控制。
实验步骤：1.准备工作（1）将测量池清洗干净，用纯水冲洗，然后用酒精擦拭干净；（2）准备一小瓶正丁醇；（3）打开表面张力仪，检查各项指标是否正常。
2.测定过程（1）将测量池放在表面张力仪上，调节好仪器的温度；（2）向测量池中加入一定量的纯水，记录体积和温度；（3）将一滴正丁醇滴在纯水表面，使其均匀分布；（4）逐渐加入正丁醇，直到形成均匀膜，注意控制滴加速度和控制膜厚度；（5）测量膜的长度L和膜厚度h，在计算表面张力之前，还需要进行一些修正，比如摩擦修正和悬滴修正等，这些均可以在仪器中自动进行。
3.数据处理通过实验测量数据和仪器处理数据，可以计算出正丁醇的表面张力，通常情况下，正丁醇的表面张力在20-30 mN/m之间。
4.影响因素分析在实验过程中，我们还发现了一个有趣的现象，那就是温度对正丁醇的表面张力有很大的影响。
随着温度的升高，正丁醇的表面张力逐渐降低。
这是因为温度的升高会使分子运动更加剧烈，分子间的相互作用力也会减弱，从而导致表面张力降低。
结论：通过本次实验，我们对正丁醇的表面张力测定方法和原理有了更深入的了解，同时还探究了温度对表面张力的影响。
表面张力的测定实验数据
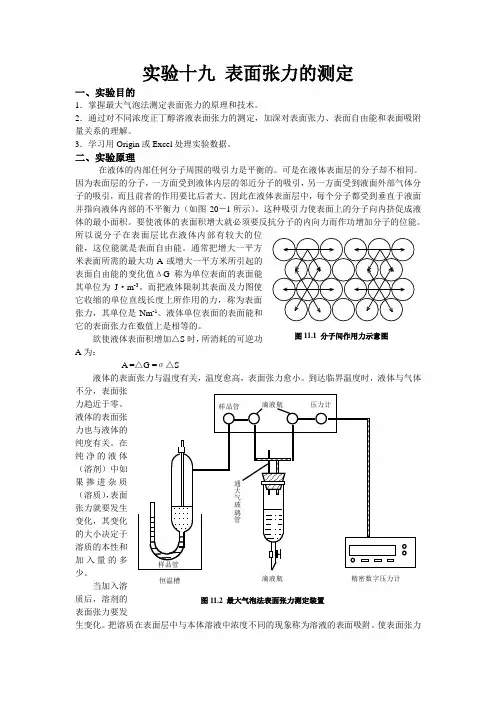
实验十九 表面张力的测定一、实验目的1．掌握最大气泡法测定表面张力的原理和技术。
2．通过对不同浓度正丁醇溶液表面张力的测定，加深对表面张力、表面自由能和表面吸附量关系的理解。
3．学习用Origin 或Excel 处理实验数据。
二、实验原理在液体的内部任何分子周围的吸引力是平衡的。
可是在液体表面层的分子却不相同。
因为表面层的分子，一方面受到液体内层的邻近分子的吸引，另一方面受到液面外部气体分子的吸引，而且前者的作用要比后者大。
因此在液体表面层中，每个分子都受到垂直于液面并指向液体内部的不平衡力（如图20－l 所示）。
这种吸引力使表面上的分子向内挤促成液体的最小面积。
要使液体的表面积增大就必须要反抗分子的内向力而作功增加分子的位能。
所以说分子在表面层比在液体内部有较大的位能，这位能就是表面自由能。
通常把增大一平方米表面所需的最大功A 或增大一平方米所引起的表面自由能的变化值ΔG 称为单位表面的表面能其单位为J ·m -3。
而把液体限制其表面及力图使它收缩的单位直线长度上所作用的力，称为表面张力，其单位是Nm -1。
液体单位表面的表面能和它的表面张力在数值上是相等的。
欲使液体表面积增加△S 时，所消耗的可逆功A 为：-A =△G =σ△S液体的表面张力与温度有关，温度愈高，表面张力愈小。
到达临界温度时，液体与气体不分，表面张力趋近于零。
液体的表面张力也与液体的纯度有关。
在纯净的液体（溶剂）中如果掺进杂质（溶质），表面张力就要发生变化，其变化的大小决定于溶质的本性和加入量的多少。
当加入溶质后，溶剂的表面张力要发生变化。
把溶质在表面层中与本体溶液中浓度不同的现象称为溶液的表面吸附。
使表面张力图11.1 分子间作用力示意图样品管滴液瓶压力计样品管恒温槽滴液瓶通大气玻璃管精密数字压力计图11.2 最大气泡法表面张力测定装置降低的物质称为表面活性物质。
用吉布斯公式(Gibbs)表示：Tc d RT dc σ⎛⎫Γ=⎪⎝⎭ （11-1） 式中：Γ为表面吸附量(mol ·m -2)，σ为表面张力（J ·m -2）。
正丁醇表面张力
正丁醇表面张力正丁醇是一种常用的有机溶剂，具有重要的应用价值。
而它的表面张力在其应用中也是一个比较重要的参数。
正丁醇表面张力的研究，对于了解其物理性质，优化应用性能具有重要意义。
一、表面张力概述表面张力，指液体表面上分子间的相互作用力。
当液体中分子间的相互作用力与表面上分子间的相互作用力不同时，便会形成表面张力。
表面张力越大，液面越难展开，越小，则液面越容易展平。
二、正丁醇表面张力的实验研究实验方法：威尔逊法测定表面张力实验步骤：1. 准备一个表面张力计，调零。
2. 准备两种液体，分别是正丁醇和甲醇。
3. 抽取少量液体分别滴于两只试管中。
4. 然后将试管接在表面张力计上，直到液面平衡。
5. 根据威尔逊公式计算出求数值。
实验结果：正丁醇表面张力为23.6 mN/m。
三、正丁醇表面张力的影响因素1. 温度：正丁醇表面张力随着温度升高而降低。
这是因为温度升高，分子热运动加剧，使表面分子受到局部拉扯力降低，表面张力也随之降低。
2. 杂质：正丁醇中含有杂质可以影响表面张力的大小和稳定性。
杂质能够破坏正丁醇表面的分子排列，使分子分布不均匀，从而影响表面张力。
3. 溶质：溶质的存在也会影响正丁醇表面张力。
当溶质分子尺寸小于正丁醇分子时，会占据液体表面的空位，导致正丁醇表面的张力变小。
四、正丁醇表面张力的应用正丁醇的表面张力在其应用中具有重要的作用。
在工业中，正丁醇被广泛应用于涂料、树脂、荧光增白剂、合成材料等领域。
在这些应用中，正丁醇的表面张力直接影响产品的抗水性、附着力和混合性。
五、总结正丁醇表面张力的研究，对于了解其物理性质和优化应用性能具有重要的意义。
通过实验可以发现，正丁醇的表面张力大小受到温度、杂质、溶质等多个因素的影响。
在工业中，正丁醇表面张力的大小也是影响产品性能的一个关键因素。
表面张力1
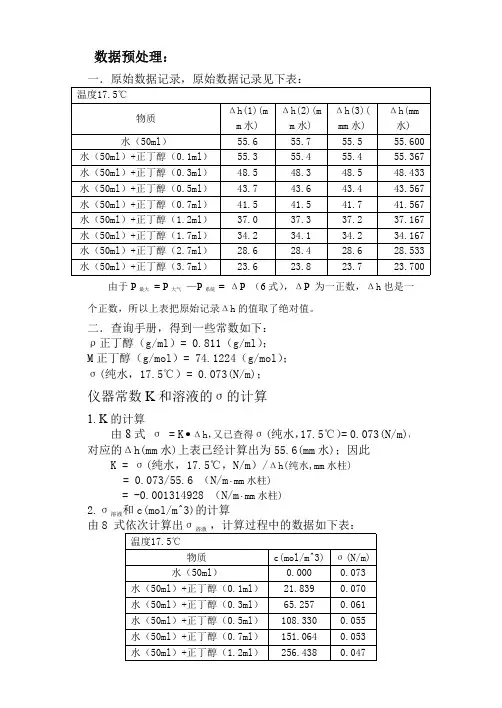
数据预处理：一．原始数据记录，原始数据记录见下表：温度17.5℃物质Δh(1)(mm水)Δh(2)(mm水)Δh(3)(mm水)Δh(mm水)水（50ml）55.655.755.555.600水（50ml）+正丁醇（0.1ml）55.355.455.455.367水（50ml）+正丁醇（0.3ml）48.548.348.548.433水（50ml）+正丁醇（0.5ml）43.743.643.443.567水（50ml）+正丁醇（0.7ml）41.541.541.741.567水（50ml）+正丁醇（1.2ml）37.037.337.237.167水（50ml）+正丁醇（1.7ml）34.234.134.234.167水（50ml）+正丁醇（2.7ml）28.628.428.628.533水（50ml）+正丁醇（3.7ml）23.623.823.723.700由于P最大=P大气—P系统=ΔP（6式），ΔP为一正数，Δh也是一个正数，所以上表把原始记录Δh的值取了绝对值。
二．查询手册，得到一些常数如下：ρ正丁醇（g/ml）=0.811（g/ml）；M正丁醇（g/mol）=74.1224（g/mol）；σ(纯水，17.5℃）=0.073(N/m)；仪器常数K和溶液的σ的计算1.K的计算由8式σ=K•Δh，又已查得σ(纯水，17.5℃）=0.073(N/m)，对应的Δh(mm水)上表已经计算出为55.6(mm水)；因此K=σ(纯水，17.5℃，N/m）/Δh(纯水,mm水柱)=0.073/55.6（N/m⋅mm水柱)=-0.001314928（N/m⋅mm水柱)2.σ溶液和c(mol/m^3)的计算由8式依次计算出σ溶液，计算过程中的数据如下表：温度17.5℃物质c(mol/m^3)σ(N/m)水（50ml）0.0000.073水（50ml）+正丁醇（0.1ml）21.8390.070水（50ml）+正丁醇（0.3ml）65.2570.061水（50ml）+正丁醇（0.5ml）108.3300.055水（50ml）+正丁醇（0.7ml）151.0640.053水（50ml）+正丁醇（1.2ml）256.4380.0470.030.040.050.060.070.08s (N /m )c(mol/m^3)水（50ml）+正丁醇（1.7ml）359.7740.043水（50ml）+正丁醇（2.7ml）560.5630.036水（50ml）+正丁醇（3.7ml）753.8740.030计算机处理过程一．σ-c 数据处理及散点图表1σ-c 数据处理表格温度17.5（℃）物质σ(N/m)c(mol/m^3)水（50ml）0.0731********0.000000000水（50ml）+正丁醇（0.1ml）0.07280318345321.83904562水（50ml）+正丁醇（0.3ml）0.06368634892165.25663135水（50ml）+正丁醇（0.5ml）0.057287032374108.3303154水（50ml）+正丁醇（0.7ml）0.054657176259151.0641676水（50ml）+正丁醇（1.2ml）0.048871492806256.4381685水（50ml）+正丁醇（1.7ml）0.044926708633359.7739875水（50ml）+正丁醇（2.7ml）0.037519280576560.5631311水（50ml）+正丁醇（3.7ml）0.0311********753.8740943用上表中的数据画σ-c 散点图，并拟合如下拟合曲线类型Log3P1：图1σ-c 散点图-100100200300400500600700800-0.00020-0.00018-0.00016-0.00014-0.00012-0.00010-0.00008-0.00006-0.00004-0.000020.00000d s /d c (N *m o l ^-1*m ^4)c(mol/m^3)Origin 7.5在拟合过程中计算出的部分参数如下：Model:Log3P1Equation:y =a -b*ln(x+c)Weighting:y No weighting Chi^2/DoF R^2----------------------------------------4.5064E-70.99838----------------------------------------Parameter Value Error ----------------------------------------a 0.157110.00681b 0.018650.00103c 89.986812.41971----------------------------------------二．求dσ/dc用origin 7.5对图1的拟合曲线求出它的斜率曲线如下图：图2dσ/dc 曲线求算出dσ/dc 的部分数据如下表2：表2dσ/dc 的部分数据c(mol/m^3)dσ/dc(N*mol^-1*m^4)c(mol/m^3)dσ/dc(N*mol^-1*m^4)0.00000-2.93368E-04383.32581-3.50175E-0512.77753-2.63933E-04396.10334-3.40025E-0525.55505-2.14925E-04408.88086-3.30448E-0538.33258-1.81389E-04421.65839-3.21395E-0551.11011-1.56959E-04434.43592-3.12825E-0563.88764-1.38355E-04447.21345-3.04700E-0576.66516-1.23709E-04459.99097-2.96987E-0589.44269-1.11876E-04472.76850-2.89655E-05102.22022-1.02113E-04485.54603-2.82676E-05114.99774-9.39214E-05498.32355-2.76026E-05三．由dcd σ•−=R c Γ求得部分Γ如下表3Γ的部分数据c(mol/m^3)Γ(mol*m^-2)c(mol/m^3)Γ(mol*m^-2)0.000000.00000E+00383.32581 5.59916E-0612.77753 1.40673E-06396.10334 5.61810E-0625.55505 2.29105E-06408.88086 5.63599E-0638.33258 2.90034E-06421.65839 5.65288E-0651.11011 3.34629E-06434.43592 5.66888E-0663.88764 3.68707E-06447.21345 5.68404E-0676.66516 3.95612E-06459.99097 5.69845E-0689.44269 4.17399E-06472.76850 5.71215E-06102.220224.35399E-06485.546035.72518E-06四．由表3的Γ求出C/Γ与C 的部分关系如下表4：表4C/Γ与C 的部分关系c(mol/m^3)C/Γc(mol/m^3)C/Γc(mol/m^3)C/Γ12.777534349439.853370.5482887394634.523587.76624138659017.97425.555055488380.616383.3258190410404.005689.98646162780250.94038.332588698864.235396.1033493426386.767702.76399165796334.96551.1101111803658.101600.54377141674531.909715.54151168810855.39963.8876414870867.918613.32130144689597.028728.31904171825885.64376.6651617920033.854626.09882147704528.022741.09657174841754.18889.4426920959282.653638.87635150720410.956753.87409176361119.525102.2202223992240.753651.65388153735311.867408.8808696442042.788114.9977427021196.830664.43141156750618.534421.6583999457842.2520.00E+0002.00E+0074.00E+0076.00E+0078.00E+0071.00E+0081.20E+0081.40E+0081.60E+0081.80E+0082.00E+008CC/G127.7752730047267.826600.54377141674531.909434.43592102473888.430140.5528033071242.628613.32130144689597.028447.21345105489399.423153.3303236093706.738626.09882147704528.022459.99097108505000.355166.1078539115010.037677.20893159765407.983472.76850111520320.124178.8853842135308.641357.7707684378634.915485.54603114536105.023191.6629145154954.153408.8808696442042.788498.32355117551473.522204.4404348173906.620421.6583999457842.252511.10108120566817.527217.2179651192433.532434.43592102473888.430523.87861123582099.885229.9954954210528.533447.21345105489399.423536.65613126597873.409242.7730157228250.364459.99097108505000.355549.43366129613210.797255.5505460245687.638472.76850111520320.124562.21119132628076.360268.3280763262912.413485.54603114536105.023574.98872135643437.554293.8831269296701.397511.10108120566817.527600.54377141674531.909306.6606572313352.159523.87861123582099.885613.32130144689597.028319.4381875329796.115536.65613126597873.409626.09882147704528.022332.2157078346183.172549.43366129613210.797638.87635150720410.956344.9932381362505.490562.21119132628076.360651.65388153735311.867五．拟合C/Γ与C 的直线：用表4的数据作C/Γ与C 的直线并拟合该曲线得到一条直线如下图3，在拟合过程中计算出的部分参数也已经给出，在图3下面。
表面张力的测定——最大气泡法
溶液表面张力的测定测定姓名：夏胜军 学号：2015011944 班级：材52 同组：韦尧洁 实验日期：2016年11月17日 提交报告日期：2016年11月22日助教：段炼1 引言1.1 实验目的1.1.1 测定不同浓度正丁醇溶液的表面张力。
1.1.2 根据吉布斯公式计算正丁醇溶液的表面吸附量。
1.1.3 掌握用最大气泡法测定表面张力的原理和技术。
1.2 实验原理在液体内部，任何分子受周围分子的吸引力是平衡的。
可是表面层的分子受内层分子的吸引与受表面层外介质的吸引并不相同，所以，表面层的分子处于力不平衡状态，表面层的分子比液体内部分子具有较大势能，如欲使液体产生新的表面，就需要对其做功。
在温度、压力和组成恒定时，可逆地使表面积增加dA 所需做的功为γdA =δW - （1）比例系数γ表示在等温等压下形成单位表面所需的可逆功，其数值等于作用在界面上每单位长度边缘的力，称为表面张力。
纯物质表面层的组成与内部的组成相同，因此纯液体降低表面自由能的唯一途径是尽可能缩小其表面积。
对于溶液，由于溶质使溶剂表面张力发生变化，因此可以调节溶质在表面层的浓度来降低表面自由能。
根据能量最低原则，溶质能降低溶剂的表面张力时，表面层溶质的浓度比溶液内部大；反之，溶质使溶剂的表面张力升高时，表面层溶质的浓度比内部的浓度低。
这种表面浓度与溶液内部浓度不同的现象叫做溶液的表面吸附。
显然，在指定的温度和压力下，溶质的吸附量与溶液的浓度及溶液的表面张力随浓度的变化率有关，从热力学方法可知它们之间的关系遵守吉布斯公式：p T dc d RT c ,⎪⎭⎫ ⎝⎛-=Γγ (2) 式中：Γ为表面吸附量（mol •m -2）；γ为表面张力（N •m -1）；c 为溶质的浓度（-3m mol ⋅）；T 为热力学温度（K ）；R 为摩尔气体常数（8.314-1K mol J ⋅⋅）。
Γ值可正可负，正值为正吸附，负值为负吸附。
显然，Γ不仅能表明吸附的性质，而且其值还能说明表面吸附的程度：Γ＝0表明无吸附现象；其值越远离0，表明吸附程度越大。
测定不同浓度正丁醇溶液表面张力
实验七
溶液表面张力的测定
2、调节恒温槽温度为25C。 3、仪器常数的测定：将干燥的毛细管垂直地插到使毛 细管的端点刚好与水面相切，打开滴液漏斗，控制滴 液速度，使毛细管逸出的气泡，速度约为5s10s 1个。 当气泡刚脱离管端的一瞬间，压力计中液面差达到最 大值，记录压力计读数，连续读取三次，取其平均值。 可以通过手册查出实验温度时水的表面张力，利用公 式 K=水/ Δp最大，求出仪器常数K。
实验八
粘度法测定高聚物的分子量
注意事项
实验过程中恒温槽的温度要恒定，溶液每次 稀释恒温后才能测量。
黏度计要垂直放置，实验过程中不要振动黏 度计，否则影响结果的准确性。
实验八
数据处理
粘度法测定高聚物的分子量
1.将所测的实验数据及计算结果填入下表中：
原始溶液浓度c0
C/ g· cm-3 t1 / s
[ ] K M
式中，M为黏均摩尔质量；K为比例常数； α 是与分子形 状有关的经验参数。 K 和 α 值与温度、聚合物、溶剂性质 有关，也和分子量大小有关。K值受温度的影响较明显， 而α 值主要取决于高分子线团在某温度下，某溶剂中舒展 的程度，其数值介于0.5～1之间。
实验八
粘度法测定高聚物的分子量
实验八
粘度法测定高聚物的分子量
实验步骤
3. 溶液流出时间的测定 用移液管分别吸取已知 浓 度 的 聚 丙 烯 胺 溶 液 10mL 和 NaNO3 溶 液 (3mol· dm-3)5mL ，由 A 管注入黏度计中，在 C 管处用洗耳球打气，使溶液混合均匀，浓度 记为C1，恒温15min，进行测定。
压差测量仪上读出。其关系式为
p最大= p大气 – p系统 Δp
实验七
实验最大泡压法测定正丁醇水溶液的表面张力
▪ 对于同一套表面张力仪，毛细管半径r，测 压液体密度、重力加速度都为定值，因此 为了数据处理方便，将上述因子放在一起， 用仪器常数K来表示，上式简化为：
Kh最大
▪ 式中的仪器常数K可用已知表面张力的标准 物质测得，通常用纯水来标定。
5. 溶液中的表面吸附-吸附现象的发生
▪ 在定温下纯液体的表面张力为定值，只能依靠缩小表面 积来降低自身的能量。而对于溶液，既可以改变其表面 张力，也可以减小其面积来降低溶液表面的能量。通常 以降低溶液表面张力的方法来降低溶液表面的能量。
1.将实验数据记录于表中。
2. 数据处理
1）计算仪器常数K和不同浓度正丁醇溶液的 表面张力σ，绘制σ - C等温线。 ▪ 2）根据吉布斯吸附等温式，求出Г，C/Г。 ▪ 3）绘制Г-C，C/Г-C等温线，求饱和吸附量 Г∞，并计算正丁醇分子截面积So和吸附单分 子层厚度δ。
六、思考题
▪ 1）系统检漏过程中，U型管测压计两端液面出现高度 差，测量溶液的表面张力时也是在存在此高度差的前 提下（即气密性好）测量的。请问，该高度差的大小 是否影响测量结果？
▪ 在指定的温度和压力下，溶质的吸附 量与溶液的表面张力及溶液的浓度之 间的关系遵守吉布斯(Gibbs)吸附方程：
Γ C d
RT dC T
式中，Г为溶质在表层的吸附量；σ为表面张力； C为吸附达到平衡时溶质在溶液中的浓度。
（1）
(
d
dc
)T
<0，Г>0，溶质能增加溶剂的表面张力， 溶液表面层的浓度大于内部的浓度，称为
▪2）仪器常数的测量 ▪ 打开抽气瓶活塞，调节抽气速度，使气泡由毛细管尖端 成单泡逸出，且每个气泡形成的时间约为5 ～ 10 s。当气 泡刚脱离管端的一瞬间，压差计显示最大压差时，记录最 大压力差，连续读取三次，取其平均值。再由手册中，查 出实验温度时，水的表面张力σ，则仪器常数
中国科大物化实验9 溶液中的吸附作用和表面张力的测定报告
50
2、实验试剂： 名称 蒸馏水 正丁醇
参数 分析纯
三、实验步骤
1、毛细管常数的测定 按实验装置图装好仪器，打开恒温水浴，使其温度稳定于 25℃。取一支浸 泡在洗液中的毛细管依次次用自来水、蒸馏水反复清洗若干次，同样把玻璃套管 也清洗干净，加上蒸馏水，插上毛细管，用套管下端的开关调节液面恰好与毛细 管端面相切，使样品在其中恒温 10 分钟。在分液漏斗中加入适量的自来水，注 意切勿使体系漏气。然后调节分液漏斗下的活塞使水慢慢滴下，这时体系压力逐 渐减小，直至气泡由毛细管口冒出，细心调节出泡速度，使之在 5－10 秒钟内出 一个。 注意气泡爆破前数字式微压差测量仪的读数，并用电脑采集数据得到最大 的压差值，求平均值而得 hH 2 O 。根据手册查出 25℃时水的表面张力为＝71.97 ×10-3N·m-1，以/h=K 求出所使用的毛细管常数，此值控制在 8cm 左右为宜， 否则毛细管太粗误差较大，毛细管太细，易堵塞，气泡很难逸出。 2、不同浓度的正丁醇溶液表面张力的测定 用 2mL 移液管分别移取 0.40ml、0.80ml、1.20ml、1.60ml、2.00ml、2.40ml、 2.80ml 正丁醇到 100ml 容量瓶中，然后稀释到刻度。重复上述实验步骤，按照 由稀至浓的顺序依次进行测量。求得一系列浓度的正丁醇溶液的h。 本实验的关键在于溶液浓度的准确性和所用毛细管、恒温套管的清洁程度。 因此除事先用热的洗液清洗它们以外， 每改变一次测量溶液必须用待测的溶液反 复洗涤它们， 以保证所测量的溶液表面张力与实际溶液的浓度相一致。并控制好 出泡速度、平稳地重复出现压力差。而不允许气泡一连串地出。洗涤毛细管时切 勿碰破其尖端，影响测量。 温度对该实验的测量影响也比较大，实验中请注意观察恒温水浴的温度， 溶 液加入测量管后恒温 10min 后再进行读数测量。
2、实验试剂： 名称 蒸馏水 正丁醇
参数 分析纯
三、实验步骤
1、毛细管常数的测定 按实验装置图装好仪器，打开恒温水浴，使其温度稳定于 25℃。取一支浸 泡在洗液中的毛细管依次次用自来水、蒸馏水反复清洗若干次，同样把玻璃套管 也清洗干净，加上蒸馏水，插上毛细管，用套管下端的开关调节液面恰好与毛细 管端面相切，使样品在其中恒温 10 分钟。在分液漏斗中加入适量的自来水，注 意切勿使体系漏气。然后调节分液漏斗下的活塞使水慢慢滴下，这时体系压力逐 渐减小，直至气泡由毛细管口冒出，细心调节出泡速度，使之在 5－10 秒钟内出 一个。 注意气泡爆破前数字式微压差测量仪的读数，并用电脑采集数据得到最大 的压差值，求平均值而得 hH 2 O 。根据手册查出 25℃时水的表面张力为＝71.97 ×10-3N·m-1，以/h=K 求出所使用的毛细管常数，此值控制在 8cm 左右为宜， 否则毛细管太粗误差较大，毛细管太细，易堵塞，气泡很难逸出。 2、不同浓度的正丁醇溶液表面张力的测定 用 2mL 移液管分别移取 0.40ml、0.80ml、1.20ml、1.60ml、2.00ml、2.40ml、 2.80ml 正丁醇到 100ml 容量瓶中，然后稀释到刻度。重复上述实验步骤，按照 由稀至浓的顺序依次进行测量。求得一系列浓度的正丁醇溶液的h。 本实验的关键在于溶液浓度的准确性和所用毛细管、恒温套管的清洁程度。 因此除事先用热的洗液清洗它们以外， 每改变一次测量溶液必须用待测的溶液反 复洗涤它们， 以保证所测量的溶液表面张力与实际溶液的浓度相一致。并控制好 出泡速度、平稳地重复出现压力差。而不允许气泡一连串地出。洗涤毛细管时切 勿碰破其尖端，影响测量。 温度对该实验的测量影响也比较大，实验中请注意观察恒温水浴的温度， 溶 液加入测量管后恒温 10min 后再进行读数测量。
表面张力测定的数据处理
正丁醇溶液表面张力测定的数据处理表1 原始数据记录及数据处理c/(mol·dm -3)Δp/（kPa ）表面张力/(N·m -1)σ吸附量×106/Γ（mol·m -2）710-⨯Γc0.7440.072140.0000/0.020.6990.067781.56971.27420.050.6430.062353.02991.65020.10.5790.056144.39172.27700.150.5390.052265.16562.90380.200.4950.048005.66473.53060.250.4490.043546.01334.15740.300.4330.041986.27064.78420.350.4040.039176.4683 5.4110 自定义c ~σ函数拟合根据经验公式进行自定义函数拟)21ln(100P cP +⨯⨯-=σσσ合；拟合结果：P2=81.63965; P1=0.27398吸附量Γ表面吸附量由Gibbs 吸附等温式将上述公式求导后整理并进Γ行计算得到T dc d RT c ⎪⎭⎫ ⎝⎛-=Γσ210P c c RT P +⨯=σ曲线线c c~Γ性拟合计算饱和吸附量∞Γ线性拟合直线的斜率为125360.0；取倒数得到饱和吸附量Γ∞为7.97706E-06 mol·m -2被测分子的横截面积S 0L S ⋅Γ=∞10;S 0=2.01219E-19m 2（1）由原始实验数据根据式①求出各浓度下正丁醇溶液表面张力：σ①00σσp p ∆∆=式中各项的含义：为溶液的最大附加压力（取平均值），单位kPa ；p ∆为纯溶剂（水）的最大附加压力（取平均值），单位kPa ；0p ∆为实验温度下纯溶剂（水）的表面张力，可查表得到。
例如 T=298K 时水的0σ表面张力为0.07214 N·m -1为实验温度下溶液的表面张力，单位为N·m -1σ（2）由数据通过origin 绘制散点图如图1所示，并进行自定义函数拟合c ~σ出参数P1和P2的数值表面张力和浓度之间符合下列公式②)21ln(100P cP +⨯⨯-=σσσ式中各项的含义：- 溶液的表面张力，单位为N·m -1σ -纯溶剂的表面张力。
表面张力的测定
演
示
注意事项
思考题
实验演示
实验目的 实验原理 仪器试剂 实验步骤
演
示
注意事项
思考题
数据处理
1.以纯水测量结果按式（4）计算 值。纯水的表 以纯水测量结果按式（ ）计算K值 以纯水测量结果按式 面张力见附录。 面张力见附录。 2.计算各溶液的表面张力值。 计算各溶液的表面张力值。 计算各溶液的表面张力值 3.作表面张力－浓度图，曲线要求光滑。用镜象 作表面张力－浓度图，曲线要求光滑。 作表面张力 法在曲线的整个范围内取10个点左右作切线 个点左右作切线， 法在曲线的整个范围内取 个点左右作切线， 示得相应的Z值 示得相应的 值。 4.计算出值后，作出吸附等温线，即Γ-c图。 计算出值后，作出吸附等温线， 计算出值后 图
r 将 ρg 合并成一个常数 k ，则上式变为 2
r σ = hm ρg 2
σ =khm
（4） ）
（4）式中的仪器常数K可用已知表面张力的标准物质测得。 ）式中的仪器常数 可用已知表面张力的标准物质测得。 可用已知表面张力的标准物质测得
实验目的 实验原理 仪器试剂 实验步骤
演
示
注意事项
思考题
仪器试剂
实验目的 实验原理 仪器试剂 实验步骤
演
示
注意事项
思考题
实验原理
在指定温度和压力下， 在指定温度和压力下，溶质的吸附量与溶液的 表面张力及溶液的浓度有关， 其关系可用Gibbs Gibbs等 表面张力及溶液的浓度有关 ， 其关系可用 Gibbs 等 温吸附方程表示： 温吸附方程表示：
c dσ Γ= RT dc T
实验目的 实验原理 仪器试剂 实验步骤
演
示
注意事项