苏科版七年级数学教案

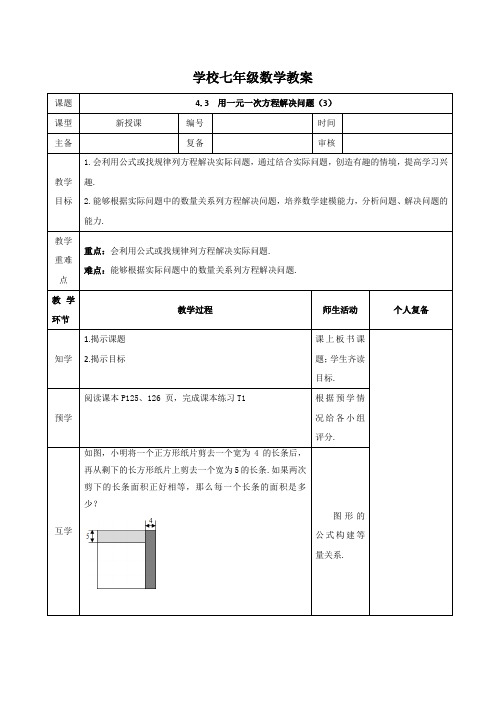
学校七年级数学教案课题4.3用一元一次方程解决问题（3）课型新授课编号时间主备复备审核教学目标1.会利用公式或找规律列方程解决实际问题，通过结合实际问题，创造有趣的情境，提高学习兴趣.2.能够根据实际问题中的数量关系列方程解决问题，培养数学建模能力，分析问题、解决问题的能力.教学重难点重点：会利用公式或找规律列方程解决实际问题.难点：能够根据实际问题中的数量关系列方程解决问题.教学环节教学过程师生活动个人复备知学1.揭示课题2.揭示目标课上板书课题；学生齐读目标.预学阅读课本P125、126 页，完成课本练习T1根据预学情况给各小组评分.互学如图，小明将一个正方形纸片剪去一个宽为4的长条后，再从剩下的长方形纸片上剪去一个宽为5的长条.如果两次剪下的长条面积正好相等，那么每一个长条的面积是多少？图形的公式构建等量关系.导学例1：已知三角形三个角的度数之比为2:3:5，判断这个三角形的形状.例2：用黑白两色棋子按如图所示的方式摆图形，依次规律，图形中黑色棋子的个数有可能是50吗？例3：制作一张桌子要用1个桌面和4条桌腿，1m3木材可制作20个桌面或制作400条桌腿，现有12m3木材，应怎样计划用料才能制作尽可能多的桌子？利用三角形内角和定理得到等量关系.引导学生从“数”和“形”两个方面找规律，注意理解为什么不可能.小组交流.检学1．宋代数学家杨辉称幻方为纵横图，传说最早出现的幻方是夏禹时代的“洛书”，杨辉在他的著作《续占摘奇算法》中总结了“洛书”的构造，在如图所示的三阶幻方中，每行，每列、每条对角线上的三个数之和都相等，则m+n的值是（）A．7 B．1 C．2（1）（2）2．如图，涂色部分是正方形，图中最大的长方形的周长是厘米．独立完成，课堂交流．总结谈谈你这一节课有哪些收获．各抒己见.课后作业板书设计教后记。

学校七年级数学教案课题 4.3 用一元一次方程解决问题（2）课型新授课编号时间主备复备审核教学目标1.能用画线形示意图作为建模策略，分析实际问题中的等量关系，列方程解决问题.2.经历用方程解决问题的过程，进一步体会建立方程模型的作用，培养抽象、概括、分析问题、解决问题的能力和克服困难的意志.教学重难点重点：线形示意图的构建和分析.难点：如何画线形示意图来反映问题中的数量关系.教学环节教学过程师生活动个人复备知学1.揭示课题：2.揭示目标课上板书课题；学生齐读目标.预学阅读课本P 123、124页，完成课本练习T1 根据预学情况给各小组评分.互学1.生活中，我们经常可以在各种售货平台看见一些商品优惠信息，要想知道商家有没有少赚，我们需要知道什么？上述的基本量之间有什么样的关系呢？2.如图，可列方程为：让学生从常见实际生活情境中感受数学.回顾进价、标价、售价、利润等关系.导学活动：用线形示意图分析问题例1：一件羽绒服的标价为进价的1.5倍，在促销活动中以8折出售，获利96元，这件羽绒服的进价是多少元?例2：小明、小亮相约从学校去博物馆，小明以5km/h的速度步行0.5h后，小亮骑自行车以15km/h的速度沿相同路线出发，并在途中追上了小明，小亮出发多久后可以追上小明?例3：运动场环形跑道周长400m，小红跑步的速度是爷爷的53倍，他们从同一起点沿跑道的同一方向同时出发，5min后小红第一次与爷爷相遇．小红和爷爷跑步的速度各是多少？分层教学，一部分学生直接列式，一部分学生借助线形示意图分析.明确等量关系，注意草稿检验和答.追及问题，关键是理解“追上”.感受利用线形示意图分析等量关系的优越性，并引导学生观察线形示意图以及如何画线形示意图．检学1．沿河县为进一步提升旅游业质量和档次，满足游客消费需求，开通了沿河——洪渡古镇的乌江水上旅游航线，已知游艇在乌江河中来往航行于沿河、洪渡古镇两码头之间，顺流航行全程需2小时，逆流航行全程需3小时，已知水流速度为每小时3km，求沿河、洪渡古镇两码头间的距离，若设沿河、洪渡古镇两码头间距离为x km，则所列方程为（）A．B．独立完成，课堂交流．C．D．2．A，B两站间的距离为335km，一列慢车从A站开往B 站，每小时行驶55km，慢车行驶1h后，另有一列快车从B站开往A站，每小时行驶85km，设快车行驶了x h后与慢车相遇，可列方程为（）A．55x +85x ＝335 B．55（x﹣1）+85x ＝335C．55x +85（x﹣1）＝335 D．55（x+1）+85x ＝335总结谈谈你这一节课有哪些收获．课后作业板书设计教后记。

苏科版初中数学七年级上册全册教案《生活数学》教案教学目标1.通过生活中常见的数字、图形的观察，思考感受生活中处处有数学.2.乐于接触社会环境中的数字、图形信息，了解数学是我们表达和交流的工具.教学过程：引入：(1)结合课本P6—P7图片，感受我们生活在在丰富多彩的数学世界中；(2)同学们谈谈小学研究数学的体会，并举例说说数学和生活的联系.例题分析：例1数字与生活(1)展示车票，分析车票中的数字及其作用(2)身份证号码提供给我们很多信息，如(3)商品的条形码你还能举出这样的例子吗？例2、图形与生活(1)自行车车轮(2)奥林匹克五环旗，2008北京申奥标志，2008北京奥运会会徽(3)上海世博会会标你还能举出这样的例子吗？3小结：教室操演：1.猜猜看：数字虽小却在百万之上(打一数字)2，4，6，8，10(打一成语)从严判刑(打一数学名词)2.2012年9月1日是礼拜六，那么2013年除夕是礼拜．3.某粮店出售的三种品牌的面粉袋上，分别标有质量为(25.1)kg、(25.2)kg、(25.3)kg的字样，从中任意拿出两袋，它们的质量最多相差kg．4.XXX每天起床后要做的事情有穿衣(4分钟)、整理床(3分钟)、洗脸梳头(5分钟)、上厕所(5分钟)、烧饭(20分钟)、吃早饭(12分钟)，完成这些工作共需49分钟，你认为最合理安排应是多少分钟？5.XXX初一有6个班，采用淘汰制进行篮球比赛，问共需进行多少场比赛？若采用单循环制呢？若采用主客场制单循环赛制呢？1《活动思考》教案研究目标经历观察、实验、操作、猜想和归纳等数学活动，引发思考，并尝试从不同角度寻找解决问题的方法，进而有效地解决问题，通过收集、选择、处理数据信息，做出合理的推断或大胆的猜测.研究重点在活动中感受“做”数学的乐趣，提高研究数学的好奇心和求知欲.研究难点合理地表述自己的观点.研究过程活动一：把一张长方形纸片按下图折叠、裁剪、展开.问题1：你得到的是什么图形？说说你的理由.问题2：你得到的正方形是最大的吗？你有其它举措剪成正方形吗？分组动手试一试.问题3：就这一张纸片，你还能剪出其它的图形吗？活动二：按图示的方式，用火柴棒搭成三角形. 搭1个三角形需要火柴棒根搭2个三角形需要火柴棒根搭3个三角形需要火柴棒根搭10个三角形需求洋火棒根搭100个三角形需要火柴棒根活动三：观察月历：2日一二6718三29 16 2330四310 17 2431 五411 1825六512 19 26(1)图中的415112框内，对角线上两个数的和相等，你是否还能找出满足这一条件的方框？能找多少个？(2)图中的781191645222312方框内有9个数，你知道它们之间有什么关系吗？把你的发现告诉同学们.(3)XXX一家外出旅游5天，这5天的日期之和是20，XXX几号回家？活动四：中学与小学的不同，不仅体现在环境的变化，学科设计也与小学不同.1.同学们，你比较喜欢哪些学科？你知道班上其他同学比较喜欢哪些学科吗？你怎样去了解？2.你会设计调查表吗？分组试一试.3.怎样调查呢？4.由调查的数据，你能获得什么信息？XXX《正数和负数》教案教学目标1、在熟的生活情形中，能用正数和负数表示生活中具有相反意义的量、晓得负数的写法和读法，会用负数表示一些一样平常生活中的量.2、使学生履历数学化，符号化的进程，体味负数发生的必要性.3、感受正、负数和生活的密切接洽，享用创造性研究的乐趣，并联合史料对学生举行爱国主义思想教诲.3教学重点体会负数的意义，学会用正、负数表示日常生活中具有相反意义的量.教学难点体会负数的意义，通过描述性定义认识正数、负数和“”.教学进程感受相反方向的数量，经历负数产生的过程.课前谈话：“上下”是表示什么的词？再如“胜负”，你能举出哪些意思相反的一组词呢？词汇真丰富，说明你们的语文学得好.今天，是数学课，离不开“数”.1、出示信息在下列横线上填上适当的词，使前后构成意义相反的量：(1)妈妈在银行存入1300元，1300元；(2)电梯30米，降落30米；(3)XXX向北走30米，向走30米；2、指名读信息，你发现了什么？3、师：刚才同学们用了不同的方法去记录，大家说得也都有道理.可是如果每个人都按照自己的想法去表示，结果会怎么样呢？那你觉得应该怎么办？要想让大家都明白，数学家们制定出了一个统一的标准.那你认为数学家们会怎样表达呢？4、总结正负数(1)这些数很特别，都带上了符号，它们是一种“新数”.-1300、-80等都叫负数；+1300、+80等都叫正数.你会读吗？请你读给大家听.注意“-”叫负号，“+”叫正号.(2)读给你的同伴听.(3)把你新认识的负数再写两个读一读.下面让我们走进正数和负数的世界，进一步了解它们.(板书课题)借助实际生活情境的直观，丰富对正负数的认识.1、用正数或负数表示下列数量.(1)赢利元，用+元表示；那么亏损元用( )元表示.(2)假如向东走10.5米，用+10.5米表示；那么向西走10.5米用( )米表示.(3)球队胜利4场，用+4场表示；那么失利3场用( )场表示.(4)零上15度用+15度表示；那么零下15度用( )度表示.2、像这样的例子有很多，你能说出一组这样的情况来吗？谁愿意和老师合作？上车15人和下车8人.公元前221年和公元后2006年.4地面以上6层和地面以下2层.种了100棵树，死了5棵树.我在银行存入了500元(取出了500元).知识竞赛中，四(1)班得了20分(扣了20分).10月份，学校小卖部赚了500元.(亏了500元).零上10摄氏度(零下10摄氏度).树上飞来了5只鸟.3、同桌同学一人说信息，一人说正负数.4、出示北京地区天气情况，你发现负数了吗？有正数吗？它怎么没有“+”呢？那么，负数可以把“-”去掉吗？科学家把水结冰的温度定为℃.读作：摄氏度.观察温度计上的刻度是怎样布列的？你觉得它像哪种测量工具？温度计零上有刻度10，零下也有刻度10，这两个刻度一样吗？为什么？比℃低的温度用带“-”号的数表示，如：-10℃；比℃高的温度用带“+”号的数表示，如：+1℃(“+”号可以省略不写).的新意义理解.(利用数轴，了解负数、和正数的大小关系.)《有理数与在理数》教案教学目标1．理解有理数的意义和会对有理数进行分类；2．了解在理数的意义.教学重、难点重点：1．有理数的意义和分类；2．在理数的意义．难点：有理数的分类，区分有理数和无理数.教学过程1.有理数我们学过整数(正整数、负整数、零)和分数(正分数、负分数)．实际上，所有整数都可以写成分母为1的分数的形式．如5=,4=514,0=.11我们把能写成分数形式想一想：m(m、n是整数，n≠)的数叫做有理数．XXX小学里学过的有限小数和无穷循环小数是有理数吗？5根据有理数的定义，有理数可以进行如下的分类：正整数正整数正有理数整数零正分数负整数有理数有理数，或零负整数正分数分数负有理数负分数负分数引入有理数的界说，并依照界说申明整数、分数是有理数．通过将有限小数和无穷循环小数转化为分数，申明有限小数和无穷循环小数也是有理数，为有理数的分类做好铺垫．2.在理数议一议：是不是所有的数都是有理数呢？将两个边长为1的小正方形，沿图中红线剪开，从头拼成一个大正方形，它的面积为2．假如大正方形的边长为a，那么a2＝2．a是有理数吗？事实上，a不能写成分数形式1.…．m(m、n是整数，n≠)，a是无穷不循环小数，它的值是XXX无限不循环小数叫做无理数．小学学过的圆周率π是无穷不循环小数，它的值是3.…，π是在理数．此外，像.…、－.…这样的无限不循环小数也是无理数．例题、练.例1:将下列各数分别填入相应的集合中：－5，7.3，－9，+22，28，，－.5，，－30%，25，10033自然数集合：{……}；正整数集合：{……}；负整数集合：{……}；正分数调集：{……}；负分数集合：{……}69.3，例1：将下列各数填入相应括号内：6，1，42，，-0.33，0.3336，1.414 213 56，－2π，3.303 003 000 3正数调集：{…}；负数调集：{…}；正有理数集合：{…}；负有理数集合：{…}．，-3.141 592 6．例2:对下列语句的描述，错误的有①是自然数.②是整数.③是偶数④海拔米就是没有海拔.⑤是非负数.⑥一个数，不是正数就必定是负数.教室操演：1.下列说法正确的是( )A．正整数和负整数构成整数；B.零是整数，但不是正数，也不是负数；C.分数包括正分数、负分数和零；D.有理数不是正数就是负数.2.把下列各数填入表示它所在的数集的圈里：5，，，，－15，.618，－3.14，－.002，34%…………整数集分数集233438……负数集四、小结……有理数集初学有理数分类，多数学生会发生殽杂，此后要加强锻炼，使其逐渐提高对数的判断能力.《数轴》教案教学目标掌握数抽三要素，能正确画出数轴.理解和会找出有理数与数轴上点的对应干系.教学重点数轴的画法和用数轴上的点表示有理数.7教学难点有理数与数轴上点的对应关系.思想与方法理解数形结合的数学方法.教学进程一．复：1．有理数包括哪些数？有何意义？是怎样分类的？2．小学时是如何利用直线上的点来表示自然数的？二．新授课:适才我们回顾了小学时用直线上的点来表示自然数，上节课我们又研究了负数，大家明白负数与正数的接洽，那么可否用直线上的点来表示有理数呢？首先，我们先来研究一下生活中最常接触的应用正、负数的例子——温度.在零以上的数字表示零上几何度，零以下表示零下几何度，用一条直线表示即为(如右图)：15105-5-10-15不仅在温度上，在其它很多方面都要用到有理数，这样简单地在一条直线上标上零、正数、负数为我们带来了很多方便.惯上，我们将此直线画成水平位置，并规定向右为正方向，具体做法如下；画一条直线(平日画成水平位置)，在这条直线上任取一点我们称之为原点，用它表示，划定直线上从原点向右为正偏向，画上箭头，而相反偏向为负偏向，再拔取适当的长度作为单位长度，从原点向右，每隔一个单位长度取一点，依次标上1、2、3……，从原点向左，每隔一个单位长度取一点，依次标上-1、-2、-3……，如下图：-7-6-5-4-3-2-像这样，规定了原点，正方向和单位长度的直线叫做数轴.问题：在一条东西向的马路上，有一个汽车站牌，汽车站牌东3m和7.5m处分别有一棵柳树和一棵杨树，汽车站牌西3m和4.8m处分别有一棵槐树和一根电线杆，情境图表示如下：8画一条直线表示马路，从左到右表示从东到西的偏向，在直线上取任一点O表示汽车站牌的位置，划定1个单位长度(线段OA的长)代表1米长.于是，在点O 的右边，与点O距离3个和7.5个单位长度的点B和点C，分别表示柳树和杨树的位置；点O左边，与点O 距离3个和4.8个单位长度的点D和点E，分别表示槐树和电线杆的位置.如下图：申明：1、数轴有三要素——原点，正偏向和单位长度.三者缺一不可；2、三要素是规定的，可灵活选取原点位置与单位长度，一般正方向的指向是自左向右；3、对同一数轴的单位长度不能变.例：画出数轴，并在数轴上画出表示下列各数的点.6，-4，-2，-4.5，1.5，-7，解：如图所示：-7-6-5-4-3-2《绝对值与相反数》教案-教学目标绝对值知识是解决有理数比较大小、距离等知识的重要依据，同时它也是我们后面研究有理数运算的基础.借助数轴引出对绝对值的观点，并通过计较、观察、交流、发现绝对值的性子特征，利用绝对值来比较两个负数的大小.借助数轴，使学生了解相反数的观点.会求一个有理数的相反数.教学重点与难点重点：理解绝对值的概念；理解相反数的意义.9难点：求一个数的绝对值；比较两个负数的大小；理解相反数的意义.教学设想绝对值：一.情境引入.问题：两辆汽车从统一处O出发，西偏向行驶10km.抵达A、B两处如图，它们的行驶门路相同吗？它们形式的路程的远近(线段OA、OB的长度)相同吗？学生讨论回答.教师总结：两辆车的行驶门路相反，它们行驶的路程相称都是10km.我们把上面这个进程看成一个数轴，那么就有数轴上表示-10喝10的两个点到原点的距离都是10.数轴上，一个点到原点的距离，是“形”的描述，那么关于“数”是表示一个数的绝对值.下面我们一起来研究本日的新知识—绝对值.XXX新授.问题1如图数轴上有A、B、C、D四个点.点A表示的数是( )，点A到原点的距离是( )个长度单位.点B表示的数是( )，点B到原点的距离是( )个长度单位.点C表示的数是( )，点C到原点的距离是( )个长度单位.点D表示的数是( )，点D到原点的距离是( )个长度单位.学生活动：小组合作探究.教师总结：点A-22；点B22；点C-.5.5；点D.5.5；10数学上定义：一般地，数轴上表示数a的点与原点的距离叫做a的绝对值.如上面的-2的绝对值是2；2的绝对值也是2.还有-.5喝.5的绝对值都是.5.用绝对值符号表示为：|-2|=2，|2|=2，|-.5|=.5，|.5|=.5.显然||=.问题2a的绝对值等于什么？学生活动：总结任意正、附属a的绝对值怎么表示.师生合作探究：a在这里可能是整数、、负数，那么我们应该分类来讨论a的绝对值，结果去掉绝对值符号并用含a的狮子来表示.我们可以利用绝对值定义写成下面的式子：(1)当a是正数时，|a|=；(2)当a是负数时，|a|=；(3)当a是时，|a|=；教师总结：一个正数的绝对值等于它本身；一个负数的绝对值等于它的相反数；的绝对值是.(1)当a是正数时，|a|=a；(2)当a是负数时，|a|=-a；(3)当a是时，|a|=；完成题：1.比较下列每组数的大小：(1)-1和-5(2)5和-2.762.一个数的绝对值是它本身，那么这个数一定是.3.绝对值小于3的整数有个，分别是.4.假如一个数的绝对值等于4，那么这个数等于.5.用“>”、“<”和“=”号填空.│-5││+3││+8││-8││-5││-8│相反数：提问:111.数轴的三要素是什么？2.填空：数轴上与原点的距离是2的点有个，这些点表示的数是；与原点的距离是5的点有个，这些点表示的数是.相反数的概念：只有符号不同的两个数，我们称它们互为相反数，零的相反数是零.概念的理解：(1)互为相反数的两个数分别在原点的两旁，且到原点的距离相称.(2)一般地，数a的相反数是a，a不一定是负数.(3)在一个数的前面添上“-”号，就表示这个数的相反数，如：-3是3的相反数，-a是a的相反数，因此，当a是负数时，-a是一个正数.-(-3)是(-3)的相反数，所以-(-3)=3，于是互为相反数的两个数之和是.即假如x与y互为相反数，那么x+y=；反之，若x+y=，则x与y互为相反数.(4)相反数是指两个数之间的一种特殊的关系，而不是指一个种类.如：“-3是一个相反数”这句话是不对的.例1.求下列各数的相反数：(1)-5(2)1(3)2(4)a(5)-2b(6)a-b3(7)a+2例2.判断：(1)-2是相反数.(2)-3和+3都是相反数.(3)-3是3的相反数.(4)-3与+3互为相反数.(5)+3是-3的相反数.(6)一个数的相反数不多是它本身.例3.化简下列各数中的符号：(1)(2)(2)-(+5)(3)(7)(4)例4.填空：13(3)12(1)a-4的相反数是，3-x的相反数是.(2)2x是的相反数.3(3)如果-a=-9，那么-a的相反数是.例5.填空：(1)若-(a-5)是负数，则a-5.(2)若(x y)是负数，则x+y.例6.已知a、b在数轴上的位置如图所示.(1)在数轴上作出它们的相反数；(2)用“<”按从小到大的顺序将这四个数连接起来.例7.如果a-5与a互为相反数，求a.《有理数的加法与减法》教案教学目标比较，归纳等得出有理数加法法则.能运用有理数加法法则解决实际问题.使学生理解有理数的加减法法可以互相转化，并了解代数的概念.使学生闇练地举行有理数的加减夹杂运算.学会用计较器举行比较庞大的数的计较.教学重点会用有理数的加法法则进行运算．会用有理数的减法法则进行运算.教学难点异号两数相加的法例．减法直接转化为加法运算的准确性.教学过程有理数的加法：【活动一】教师提出问题，让学生思考：有理数如何举行加法运算，有理数加法有几种情况？问题：足球循环赛中，平日把进球数记为正数，失球数记为负数，他们饿得和叫做净胜13球数，假设某次比赛中红队进4球，失2球；蓝队进1球失1球，于是红队的净进球数为4+(-2)XXX净进球数为1+(-1)这里用到的是正数与负数的加法.教师总结：有理数加法的情况归结为同号两数相加，异号两数相加，一个数与相加三种情况.【活动二】教师请同学依照自己的指令表演，并联合数轴申明两正数的加法.问题：1.一个物体做左右方向的运动，我们规定向左方向为负，向右运动5m记作5m，向左运动5m记作-5m.假如物体先向右运动5m再向右运动3m，那么两次运动后的总结果是什么？学生：两次运动后物体从起点向右运动了8m，写成算式就是：5+3=8教师继续请同学参与表演，并类比两正数的加法说明两负数的加法.问题：2.假如物体先向左运动5m，再向左运动3m，那么两次运动后的总结果是什么？两次运动从起点向左运动了8m，写成算式就是：(-5)+(-3)=-8这个算式也能够用数轴表示，其中假定原点为运动起点.【活动三】1.如果物体先向左运动3m再向右运动5m，那么两次运动后物体从起点向右运动了2m，写成算式是：5+(-3)=22.探究：利用数轴，求以下情况时物体两次运动的结果：先向右运动3m再向左运动5m.先向左运动5m再向右运动5m.教师总结：有理数加法法则：1.同号两数相加，取相同的符号，并把绝对值相加.2.绝对值不相等的异号两数相加，取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值.互为相反数的两个数相加等于.3、一个数同相加仍得这个数.【活动四】探究：计算30+(-20) (-20)+30.师生探讨发现两式和相称.14总结：两个数相加，交换加数的位置，和不变.即：加法交换律:a+b=b+a.计算[8+(-5)]+(-4)，8+[(-5)+(-4)].结果仍相同.总结：三个数相加，先把前两个数相加，或者先把后两个数相加，和不变.即：加法结合律：(a+b)+c=a+(b+c).1.例1计算：(-3)+(-9)=-(3+9)=-122.计较：16+(-25)+24+(-35)=16+24+[(-25)+(-35)]=40+(-60)=-20【活动五】应用举例，变式练.1.答下列算式的结果(1)(+4)+(+3)(2)(-4)+(-3)(3)(+4)+(-3)(4)(+3)+(-4)(5)(+4)+(-4)(6)(-3)+2.教师在算出XXX的净胜球数后，学生自己算黄队和蓝队的净胜球数(1)(-.9)+(+1.5)(2)(+2.7)+(-3)(3)(-1.1)+(-2.9)有理数的减法：一.创设情形，引入新课.问题1：(出示本书引言中的图片)这是北京某一天的天气情况：白天的最高气温是3℃，夜晚的最低温度是－3℃．请问这一天的温差怎么计算呢？这就是我们今天要研究的问题——有理数的减法．二.主体探讨，归纳法例.为了解决上述问题我们可以首先考虑式子3－(－3)的结果，即要求一个数x，使得x与－153的和为3，因为6与－3相加为3于是(改为从数轴上容易看出，表示3的点在表示－3的点的右边，两点相距6个单位长度，于是)3－(－3)＝6，另一方面，3＋3＝6，这表明3－(－3)＝6，按照这个思路计算下列各题．问题2：计算下列各题，你能发现什么？(1)(-3)－(－5)；(2)―7.学生活动设计.学生依照上述思绪举行思考，逐一计较结果，然后观察结果发现，减去－5相当于加上5，即加上它的相反数，是不是普遍成立呢？学生能够再举出一些例子举行验证，末了归纳出减法法例．普通地，假如a－b＝c，那么c＋b＝a，所以c＝a ＋(－b)，即a－b＝a＋(－b)．有理数的减法法例：减去一个数等于加上这个数的相反数，用数学式子表示为：a－b＝a+(－b)．阐发法例不难发现，减法法例其实是一个转化法例，转化成了加法法例，然后利用加法法例举行计较，从而体味转化的数学思想．三.应用迁移、巩固提高，培养学生的理解能力、计算能力．问题3：办理下列问题．1．计较下列各题，你能发现什么？(1)7.24.8；(2)35121；45634(3)1.51.43.64.3；(4)3.451．学生活动设计.学生黑板板演，其余学生独立思考，板演结束后，等到其余学生计算完成后，请同学进行分析，若有问题，请同学分析问题所在，进一步巩固新的知识，使同学在相互交流中逐步完善自己的想法．对于(1)7.24.8＝7.2＋4.8＝12；(2)3 5121113＝3(5)8；2444(3)1.5 1.4 3.64.3( 1.5)( 1.4)( 3.6)( 4.3)＝ 1.5 1.4 3.6 4.3.8；(4)3.451( 3.4)(5)(1)3 .4 5比较。

苏科版（2024）七年级上册数学第3章代数式3.3 整式的加减教案【教材分析和学情分析】教材分析：整式的加减是苏科版七年级上册代数式这一章的重要内容，主要介绍了如何对含有相同字母的多项式进行合并同类项，以及如何在实际问题中应用整式的加减法则。

这一部分的知识点是代数运算的基础，为后续的代数学习，如解一元一次方程、二次方程等奠定了基础。

教材通过丰富的实例和练习，引导学生理解并掌握整式加减的规则，同时培养他们的抽象思维能力和逻辑推理能力。

此外，通过解决实际问题，也锻炼了学生应用数学知识解决实际问题的能力。

学情分析：七年级的学生已经学习了基本的代数知识，如变量、常量、单项式、多项式等，对数学符号和运算规则有一定的理解和应用能力。

然而，对于抽象的整式加减，尤其是如何识别和合并同类项，可能会感到一定的困难。

部分学生可能还停留在具体的数的运算上，对于字母表示的数的运算可能会感到陌生和困惑。

此外，这个阶段的学生好奇心强，喜欢探索，但注意力集中时间可能较短，需要教师通过生动有趣的教学方式，激发他们的学习兴趣，保持他们的学习动力。

【教学目标】1. 知识与技能：学生应能理解整式的加减运算法则，掌握同类项的概念，能正确地进行整式的加减运算。

2. 过程与方法：通过实例，让学生经历整式加减的抽象过程，培养他们的观察、比较、抽象和概括能力，提高他们的运算能力。

3. 情感态度与价值观：培养学生严谨的数学思维习惯，体验数学的简洁美，提高学习数学的兴趣。

【教学重难点】1. 整式的加减运算法则及其应用。

2. 同类项的识别和整式加减的简化过程。

【教学过程】一、情境导入1. 展示几个生活中的实际问题，如：苹果和香蕉的总数，两本书的总价格等，引出含有加减运算的数学表达式。

二、新知探究1. 整式和同类项的概念：通过实例，引导学生总结出整式的定义，即字母和数字的乘积，且字母可以是任意次幂。

引导学生发现同类项的特征，即字母相同，字母的指数也相同的项。

苏教版七年级数学教案【篇一：苏教版初一数学一元一次方程教案】苏教版初一数学一元一次方程教案教师:xxx 学生:xxx日期: 2011年 12月24日星期: 六12345【篇二：苏科版七年级数学上册教学案全册集体备课】 1.1生活数学主要内容：1. 通过生活中常见的数字、图形的观察，思考感受生活中处处有数学。

2. 乐于接触社会环境中的数字、图形信息，了解数学是我们表达和交流的工具。

教学过程：1．引入（1）结合课本p4—p6图片，感受我们生活在在丰富多彩的数学世界中；（2）同学们谈谈小学学习数学的体会，并举例说说数学和生活的联系。

2．例题分析：例1、数字与生活（1）展示车票，分析车票中的数字及其作用（2）身份证号码提供给我们很多信息，如320106************ （3）商品的条形码你还能举出这样的例子吗？例2、图形与生活（1）自行车车轮（2）奥林匹克五环旗，2008北京申奥标志，2008北京奥运会会徽（3）上海世博会会标你还能举出这样的例子吗？课本p7试一试3小结：课堂练习：1.猜猜看：数字虽小却在百万之上（打一数字）2，4，6，8，10（打一成语）从严判刑（打一数学名词）2.2008年9月1日是星期一，那么2009年元旦是星期．3.某粮店出售的三种品牌的面粉袋上，分别标有质量为（25?0.1)kg、(25?0.2)kg、(25?0.3)kg的字样，从中任意拿出两袋，它们的质量最多相差．4.小华每天起床后要做的事情有穿衣（4分钟）、整理床（3分钟）、洗脸梳头（5分钟）、上厕所（5分钟）、烧饭（20分钟）、吃早饭（12分钟），完成这些工作共需 49分钟，你认为最合理安排应是多少分钟？5.光明中学初一有6个班，采用淘汰制进行篮球比赛，问共需进行多少场比赛？若采用单循环制呢？若采用主客场制单循环赛制呢？1.2活动思考主要内容：1.经历观察、实验、操作、猜想和归纳等数学活动，引发学生的思考2.能收集、选择、处理数字信息，作出合理的推断或大胆的猜想教学过程：1、创设情境，开展活动：活动一：用一张长方形纸片按Ｐ８的方法折叠、裁剪、展开，你会得到什么图形？试说明理由．活动二：按下图方式，用火柴棒搭三角形??搭1个三角形需要火柴棒根；搭2个三角形需要火柴棒根；搭3个三角形需要火柴棒根；搭10个三角形需要火柴棒根；搭100个三角形需要火柴棒根；活动三：观察月历(1)月历中右上角2?2方框中的四个数之间有什么关系？任意一个这样的方框都存在这样的规律吗？(2)月历中中间3?3方框中的9个数之间有什么关系？(3)小明一家外出旅游5天，这5天的日期之和是20．你能说出小明几号回家？2、例题分析：例1．观察下列已有式子的特点，在内填入恰当的数：?1+2+3+?+2006+2007+2008+2007+2006+?+3+2+1=例2、将一些数排列成下表：试探索：（1）第10行第2列的数是多少？（2）81所在的行和列分别是多少？（3）100所在的行和列分别是多少？3、小结课堂练习：1、在上填上适当的数：（1）2，4，6，，10，?（2）1，12，123，1234，，123456，? （3）1，3，6，，15，21，? （4）1，1，2，3，5，，13，21，?2、将一张长方形的纸对折，如图，可得到一条折痕（图中虚线），连续对折，对折时每次折痕与上次折痕保持平行，连续对折三次后，可以得到7条折痕；那么连续对折四次后，可以得到条折痕；连续对折五次后，可以得到条折痕．第1次对折第2次对折第3次对折第2题图第3题图 3、把一个长为9、宽为4的长方形分成两块，然后拼成一个正方形.4、按下图方式摆放餐桌和椅子：???（1）1张餐桌可坐6人，2张餐桌可坐人；（22.1 比0小的数（1）主要内容：正负数的概念，区分正负数，用正负数表示具有相反意义的量. 教学过程： 1．引入：①我们知道珠穆朗玛峰海拔8844米，那么吐鲁番盆地的最低处海拔高度比海平面低155米该如何表示呢？②结合课本p12四幅图片，说出图中所给数字所代表的含义. 2．新授:正负数概念：____________________________________________________，正负数表示方法：________________________________________________；0既不是__________________________，也不是________________________.3.生活中常会遇到一些具有相反意义的量:如增加与收入与对于这些具有相反意义的量，若规定其中一个量为正，则另一个就为负.4．例题讲解：例1：指出下列各数中，哪些是正数？哪些是负数？ ?7,?9,1,3?4.5,998,?9,10练一练：请把下列各数填入相应的集合中： ?9,?6,2,58.7,2002,1?,3?4.2正数集合负数集合例2：填空（1）如果向北行走8km记作+8km，那么向南行走5km记作；（2）如果运进粮食3t记作+3t，则－4t表示；（3）如果节约了－20千瓦，实际上是；（4）如果负一场得－1分，实际上是.【篇三：苏教版初中数学七年级上册教案全集】1.1生活数学一、教学目标及教材重难点分析（一）教学目标1．通过对生活中常见的图形、数字的观察和思考，感受生活中处处有数学。

学校七年级数学教案
定义：像2r=3v，S=xy，12a+3b=58这样，_____________________________叫等式.
例1.根据下列情境中的等量关系列出一个等式：
（1）某高铁列车以vm/h的平均速度行驶0.5h，行驶的路程为150km：等量关系：___________________，用等式表示为
___________________
（2）如图4-1.一个正方形纸片被分割成四部分：
等量关系：___________________，用等式表示为
___________________
（3）按盐和水的质量之比为1：10的配比，把g盐配成550g的盐水.等量关系：___________________，用等式表示为___________________
活动一：如图4-2（1），天平平衡.对天平两边进行如图4-2（2）所示的操作，可以在保持天平平衡的状态下称出一个小球的质量，请写出每一步操作对应的等式，并解释对应等式的实际意义，你能否说出等式是如何变形的？你能说明变形的合理性吗？
活动二：如图4-3.仿照上述过程设计天平操作过程.求出小球的质量y，写出每一步操作对应的等式，并解释等式的变形过程.
根据上面的活动、我们发现：
等式的基本性质
1：等式两边都加上（或减去）同一个数或整式，所得结果仍是等式2：等式两边都乘（或除以）同一个数（除数不能为0），所得结果仍是等式.
例2.利用等式的基本性质，将下面的等式变形为x=c (c为常数)的形式：
(1) x+ 5 = 2；(2) -2x = 4；(3) 6x =x + 5.
练习利用等式的性质解下列方程:
（1）x-5=6; （2）3x=4x; （3）2-1
4
x=3 (需检验).。