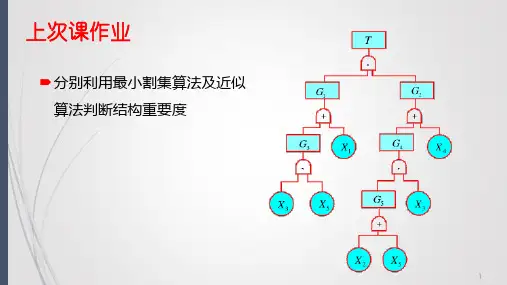
最小割集间存在重复事件事故树定性定量分析修改概况共18页

第一节事故树分析概述一、事故树分析的基本概念事故树分析 (Fault Tree Analysis,简称FTA) 是安全系统工程中常用的一种分析方法。

1961年,美国贝尔电话研究所的维森 (H.A.Watson)首创了FTA 并应用于研究民兵式导弹发射控制系统的安全性评价中,用它来预测导弹发射的随机故障概率。

接着,美国波音飞机公司的哈斯尔 (Hassle) 等人对这个方法又作了重大改进,并采用电子计算机进行辅助分析和计算。

1974 年,美国原子能委员会应用FTA对商用核电站进行了风险评价,发表了拉斯姆逊报告 (Rasmussen Report),引起世界各国的关注。

目前事故树分析法已从宇航、核工业进入一般电子、电力、化工、机械、交通等领域,它可以进行故障诊断、分析系统的薄弱环节,指导系统的安全运行和维修,实现系统的优化设计。

事故树分析 (FTA) 是一种演绎推理法,这种方法把系统可能发生的某种事故与导致事故发生的各种原因之间的逻辑关系用一种称为事故树的树形图表示,通过对事故树的定性与定量分析,找出事故发生的主要原因,为确定安全对策提供可靠依据,以达到预测与预防事故发生的目的。

FTA法具有以下特点:(1) 事故树分析是一种图形演绎方法,是事故事件在一定条件下的逻辑推理方法。

它可以围绕某特定的事故作层层深入的分析,因而在清晰的事故树图形下,表达系统内各事件间的内在联系,并指出单元故障与系统事故之间的逻辑关系,便于找出系统的薄弱环节。

(2) FTA具有很大的灵活性,不仅可以分析某些单元故障对系统的影响,还可以对导致系统事故的特殊原因如人为因素、环境影响进行分析。

(3) 进行FTA的过程,是一个对系统更深入认识的过程,它要求分析人员把握系统内各要素间的内在联系,弄清各种潜在因素对事故发生影响的途径和程度,因而许多问题在分析的过程中就被发现和解决了,从而提高了系统的安全性(4) 利用事故树模型可以定量计算复杂系统发生事故的概率,为改善和评价系统安全性提供了定量依据。

（一）事故树分析法FTA事故树-最小割集-结构重要度-事故结论--叙述事故树基本事件的防措施1：对液化石油气储罐销爆处理过程中可能发生的火灾或爆炸事故进行安全评价，预先分析和判断设备和工人操作中可能发生的危险及可能导致燃烧爆炸灾害的条件，并制定安全预防对策措施事故树中各代码的含义：T，火灾或爆炸事故；X4，射频电（如手机等）；A，点火源；X5，惰性气体置换；B，LPG(液化石油气)泄漏；X6，水置换；C，静电；X7，水冲洗；D，LPG储罐静电放电；X8，水蒸气冲洗；a，LPG达到极限；X9，人体静电放电；X1，明火；X10，水冲洗过程水流太快；X2，撞击火花；X11，静电积累；X3，电火花；X12，接地不良。

答：第一步：分析逻辑关系T，火灾或爆炸事故；A，点火源；B，LPG(液化石油气)泄漏；C，静电D，LPG储罐静电放电；a，LPG达到极限X1，明火X2，撞击火花X3，电火花；X4，射频电（如手机等；X5，惰性气体置换；X6，水置换；X7，水冲洗；X8，水蒸气冲洗；X9，人体静电放电；X10，水冲洗过程水流太快；X11，静电积累；X12，接地不良。

第二步：选取“火灾或爆炸事故”作为顶上事件，绘制火灾或爆炸事故树2.事故树分析，结构函数式：T=ABa=ax1x5+ax1x6+ax1x7+ax1x8+ax2x5+ax2x6+ax2x7+ax2x8+ax3x5+ax3x6+ax3x7+ax3x8+ax4x5+ax4x6+ax4x7+ax4x8+ax9x5+ax9x6+ax9x7+ax9x8+ax10x11x12x5+ax10x11x12x6+ax10x11x12x7+ax10x11x12x83.通过事故树分析，得到24个最小割集｛a,x1,x5｝……………｛a，x10，x11，x12，x8｝4.根据事故树最小割集结果，选择结构重要度近似判别式则有如下结果：I(a)=1-（1-1/2^（3-1））^20×（1-1/2^（5-1））^4※20个割集中包含a事件，这20个割集中，每个包含3个基本事件※4个割集中包含a事件，这4个割集中，每个包含5个基本事件5.评价结论由计算结果可以看出，LPG达到爆炸极限是销爆过程中发生火灾或爆炸的主要因素，条件事件a结构重要度最大，是燃爆事故发生的最重要条件，因此，在销爆过程中必须采取必要的预防措施，避免LPG达到爆炸极限。

事故树分析(FTA)-定性分析事故树定性分析就是对事故树中各事件不考虑发生概率多少,只考虑发生和不发生两种情况｡通过定性分析可以知道哪一个或哪几个基本事件发生,顶上事件就一定发生,哪一个事件发生对顶上事件影响大,哪一个影响少,从而可以采取经济有效的措施,防止事故发生｡事故树定性一分析包括求最小割集和最小径集,计算各基本事件的结构重要度,在此基础上确定安全防灾对策｡(1)最小割集和最小径集在事故树中,如果所有的基本事件都发生则顶上事件必然发生｡但是在很多情况下并非如此,往往是只要某个或几个事件发生顶上事件就能发生｡凡是能导致顶上事件发生的基本事件的集合就叫割集｡割集也就是系统发生故障的模式｡在一棵事故树中,割集数目可能有很多,而在内容上可能有相互包含和重复的情况,甚至有多余的事件出现,必须把它们除去,除去这些事件的割集叫最小割集｡也就是说凡能导致顶上事件发生的最低限度的基本事件的集合称为最小割集｡在最小割集里,任意去掉一个基本事件就不成其为割集｡在事故树中,有一个最小割集,顶上事件发生的可能性就有一种｡事故树中最小割集越多,顶上事件发生的可能性就越多,系统就越危险｡相反地,在事故树中,有一组基本事件不发生,顶上事件就不发生,这一组基本事件的集合叫径集｡径集是表示系统不发生故障而正常运行的模式｡同样在径集中也存在相互包含和重复事件的情况,去掉这些事件的径集叫最小径集｡也就是说,凡是不能导致顶上事件发生的最低限度的基本事件的集合叫最小径集｡在最小径集中,任意去掉一个事件也不成其径集｡事故树有一个最小径集,顶上事件不发生的可能性就有一种｡最小径集越多,顶上事件不发生的途径就越多,系统也就越安全｡上述所谓的集合,就是满足某种条件或具有某种属性的事物的全体｡集合的每一个成员称为这个集合的元素｡例如一个班级全体学生构成了一个集合,一个车队的全部汽车也构成一个集合｡同样一个割集所包含的几个基本事件就组成一个集合,这个集合中的每个基本事件就是它的元素｡集合一般用大写字母表示,而用其他字母或数字表示集合的元素｡如:若a是集合A的一个元素,则记为aA(读作a属于A)｡对一个集合的所有元素要用大括号括起来,例如,其集合含有1､2､3三个元素,这个集合就写成{1,2,3}或{2,1,3}或{3,1,2}等记号｡一个最小割集如含有X1,X2两个基本事件,则记为{X1,X2}｡由于在事故树分析中,最小割集和最小径集非常有用,因此需要求出最小割集和最小径集｡(2)最小割集和最小径集的求法最小割集和最小径集求法有许多种,现只介绍布尔代数化简法和行列法｡①最小割集求法｡a.布尔代数化简法｡对比较简单的事故树可用此法求取,它主要利用布尔代数的几个运算定律,例如:a)结合律:(a+b)+c=a+(b+c)(a·b)·c=a·(b·c)b)交换律:a+b=b+aa·b=b·ac)分配律:a·(b+c)=(a·b)+(a·c)a+(b·c)=(a+b)·(a+c)d)等幂律:a+a=aa·a=ae)吸收律:a+a·b=aa·(a+b)=af)互补律:a+a′=1a·a′=0g)对合律:(a′)′=ah)德·莫根律:(a+b)′=a′·b′(a·b)′=a′+b′注:1——表示全集,所谓全集是指一个集合中所有子集合的全体元素构成的集合｡0——表示空集,没有任何元素的集合,空集是每个集合的子集｡a′——补集,全集1中不属于集合A的元素的全体构成的集合称为A的补集｡子集——如果集合A的元素都是集合B的元素,则称A是B的子集,并记为(读作A被B包含或B包含A)在一个系统中,不安全事件就是安全事件的补事件,不安全事故发生概率用P(S)表示,安全事件发生概率用P(S′)表示,P(S)+P(S′)=1布尔代数法求最小割集的步骤是:首先列出事故树的布尔表达式,即从事故树的第一层输入事件开始,"或门"的输入事件用逻辑加表示,"与门"的输入事件用逻辑积表示｡再用第二层输入事件代替第一层,第三层输入事件代替第二层,直至事故树全体基本事件都代完为止｡布尔表达式整理后得到若干个交集的并集,每个交集就是一个割集,然后再利用布尔代数运算定律化简,就可以求出最小割集｡所谓并集就是把两个集合A和B的元素合并在一起｡如果合并后的元素构成的集合叫S,则S是A与B的并集,记为S=AB或S=A+B｡事故树中,或门的输出事件就是所有输入事件的并集｡若两个集合A和B有公共元素,则公共元素构成的集合P称为A与B的交集,记为P=AB或P=A·B｡事故树中,与门的输出事件就是其输入事件的交集｡下面以图2事故树为例,求最小割集｡图2事故树图T=AB=(X1+C)(X3+X4)=(X1+X2X3)(X3+X4=X1X3+X2X3X3+X1X4+X2X3X4=X1X3+X2X3+X1X4+X2X3X4=X1X3+X2X3+X1X4事故树经化简得到三个交集的并集,也就是说该事故树有三个最小割集:K1={X1,X3},K2={X2,X3},K3={X1,X4}化简后的事故树,其结构如图3所示,它是图2的等效树｡图3图2事故树的等效图由图可见,用最小割集表示的事故树,共有两层逻辑门,第一层为或门,第二层为与门｡由事故树等效树可清楚看出事故发生的各种模式｡再以图4为例,求事故树的最小割集｡图4事故树图T=AB=(X1+C)(X2+D)a=a(X1+X2X3)(X2+X4X5)=a(X1X2+X2X3X2+X1X4X5+X2X3X4X5)=aX1X2+aX2X3+aX1X4X5+aX2X3X4X5=aX1X2+aX2X3+aX1X4X5该事故树含有三个最小割集:K1={a,X1,X2}K2={a,X2,X3}K3={a,X1,X4,X5}b.行列法｡行列法是1972年由富赛尔(Fussel)提出的,所以又称富赛尔法｡这种方法的原理是:从顶上事件开始,按逻辑门顺序用下面的输入事件代替上面的输出事件,逐层代替,直到所有基本事件都代完为止｡在代替过程中,"或门"连接的输入事件纵向列出,"与门"连接的输入事件横向列出｡这样会得到若干行基本事件的交集,再用布尔代数化简,就得到最小割集｡从顶上事件T开始,第一层逻辑门为与门,与门连接的两个事件横向排列代表T;A下面的逻辑门为或门,连接X1,C两个事件,应纵向排列,变成X1B和CB两行;C 下面的与门连接X2,X3两个事件;因此X2,X3写在同一行上代替C,此时得到二个交集X1B,X2X3B｡同理将事件B用下面的输入事件代入,得到四个交集,经化简得到三个最小割集｡这三个最小割集是:K1={X1,X3},K2={X1,X4},K3={X2,X3}｡此法求得的结果与布尔代数法相同,但用手工计算,布尔代数法较为简单,这种方法适合于计算机编程求最小割集｡目前国内外已经开发出许多用计算机求得最小割集的程序,在此不一一叙述｡②最小径集求法｡最小径集的求法是利和最小径集与最小割集的对偶性,首先画事故树的对偶树,即成功树｡求成功树的最小割集,就是原事故树的最小径集｡成功树的画法是将事故树的"与门"全部换成"或门","或门"全部换成"与门",并把全部事件的发生变成不发生,就是在所有事件上都加"/",使之变成原事件补的形式｡经过这样变换后得到的树形就是原事故树的成功树｡这种做法的原理是根据布尔代数的德·摩根定律｡例如图5所示的事故树,其布尔表达式为T=X1+X21此式表示事件X1,X2任一个发生,顶上事件T就会发生｡要顶上事件不发生,X1,X2两个事件必须都不发生｡那么,在式1两端取补,得到下式T′=(X1+X2)′=X1′·X2′2式2用图形表示就是图5,b是a的成功树｡由图可见,图中所有事件都变化,逻辑门也由"或门"转换成"与门"｡图5事故树变成功树示例同理可知,画成功树时事故树的"与门"要变成"或门",事件也都要变为原事件初的形式｡如图6所示｡图6事故树变成功树示例条件与门､条件或门､限制门的变换方式同上,变换时把条件作为基本事件处理｡下面仍以图2事故树为例求最小径集｡首先画出事故树的对偶树——成功树,如图7所示,求成功树的最小割集｡图7图2事故树的成功树T′=A′+B′=X1′C′=X3′X4′=X1′(X2′+X3′)+X3′X4′=X1′X2′+X1′X3′+X3′X4′成功树有三个最小割集,就是事故树的三个最小径集:P1={X1,X2},P2={X1,X3},P3={X3,X4}｡用最小径集表示的事故树结构式为:T=(X1+X2)(X1+X3)(X3+X4)同样,用最小径集也可画事故树的等效树｡用最小径集画图2事故树的等效树,结果如图8所示｡图8图2事故树的等效树用最小径集表示的等效树也有两层逻辑门,与用最小割集表示的等效树比较,所不同的是两层逻辑门符号正好相反｡(3)基本事件的结构重要度分析结构重要度分析,就是不考虑基本事件发生的概率是多少,仅从事故树结构上分析各基本事件的发生对顶上事件发生的影响程度｡事故树是由众多基本事件构成的,这些基本事件对顶上事件均产生影响,但影响程度是不同的,在制定安全防范措施时必须有个先后次序,轻重缓急,以便使系统达到经济､有效､安全的目的｡结构重要度分析虽然是一种定性分析方法,但在目前缺乏定量分析数据的情况下,这种分析显得很为重要｡结构重要度分析方法归纳起来有两种,一种是计算出各基本事件的结构重要度系数,按系数由大到小排列各基本事件的重要顺序;第二种是用最小割集和最小径集近似判断各基本事件的结构重要度的大小,并排列次序｡下面介绍结构重要度系数的求取方法｡假设某事故树有几个基本事件,每个基本事件的状态都有两种:1表示基本事件状态发生X=0表示基本事件状态不发生已知顶上事件是基本事件的状态函数,顶上事件的状态用表示,(X)=(X1,X2,X3,……Xn),则(X)也有两种状态:1表示顶上事件发生X=0表示顶上事件不发生(X)叫做事故树的结构函数｡在其他基本事件状态都不变的情况下,基本事件Xi的状态从0变到1,顶上事件的状态变化有以下三种情况:①(0i,X)=0(1i,X)=0则(1i,X)-(0i,X)=0不管基本事件是否发生,顶上事件都不发生;②(0i,X)=0(1i,X)=1则(1i,X)-(0i,X)=1顶上事件状态随基本事件状态的变化而变化;③(0i,X)=0(1i,X)=1则(1i,X)-(0i,X)=0不管基本事件是否发生,顶上事件都发生｡上述三种情况,只有第二种情况是基本事件Xi不发生,顶上事件就不发生,基本事件Xi发生,顶上事件也发生｡这说明Xi基本事件对事故发生起着重要作用,这种情况越多,Xi的重要性就越大｡对有n个基本事件构成的事故树,n个基本事件两种状态的组合数为2n个｡把其中一个事件Xi作为变化对象(从0变到1),其他基本事件的状态保持不变的对照组共有2n-1个｡在这些对照组中属于第二种情况((1i,X)-(0i,X)=1)所占的比例即是Xi基本事件的结构重要度系数,用I(i),可以用下式计算:3下面以图9所示的事故树为例,说明各基本事件结构重要度系数的求法｡图9事故树图此事故树有五个基本事件,按照二进制列出所有基本事件两种状态的组合数,共有25=32个,这些组合列于表2｡为便于对照,将32组分成左右两部分各占16组,然后根据事故树图或最小割集确定(0i,X)和(1i,X)的值,以0和1两种状态表示｡X1X2X3X4X5(0i,X)X1X2X3X5 (1i,X) 0111110 0 1 0 0 1 0 0 0 0 0 1 1 0 1 0 0 1 1 1 0 0 1 0 0 0 1 0 10 1 0 0 1 0 1 0 1 0 1 0 1 1 0 0 1 1 0 1 1 0 1 1 0 1 0 0 11 1 1 0 1 1 1 1 0 1 0 0 0 0 1 1 0 0 0 0 0 1 0 0 1 0 1 1 01 1 0 1 0 1 0 0 1 1 0 1 0 0 0 1 0 1 1 1 1 1 0 1 1 1 0 1 10 0 1 1 1 0 0 1 0 1 1 0 1 0 1 1 1 0 1 1 0 1 1 1 0 1 1 1 1111111111111表2基本事件状态值与顶上事件状态值由表可见,1在左半部的状态值都为0,右半部都为1,右半部和左半部对应找出(1i,X)-(0i,X)=1的组合,共有7个｡因此,基本事件X1的结构重要度系数｡基本事件X2在表中左右两侧,其状态值都分成上下两部分,每部分8组,在同一侧上部分对照找出(01i,X)-(0i,X)=1的组合,只有1个,故｡同理可得出,,｡按各基本事件I(i)值的大小排列起来,其结果为:I(1)=I(3)>I(4)=I(5)>I(2)用计算基本事件结构重要度系数的方法进行结构重要度分析,其结果较为精确,但很繁锁｡特别当事故树比较庞大,基本事件个数比较多时,要排列2n个组合是很困难的,有时即使用计算机也难以进行｡结构重要度分析的另一种方法是用最小割集或最小径集近拟判断各基本事件的结构重要度大小｡这种方法虽然精确度比求结构重要度系数法差一些,但操作简便,因此目前应用较多｡用最小割集或最小径集近似判断结构重要度大小的方法也有几种,这里只介绍其中的一种,就是用四条原则来判断,这四条原则是:①单事件最小割(径)集中基本事件结构重要度最大｡例如,某事故树有三个最小径集:P1={X1},P2={X2,X3},P3={X4,X5,X6}｡第一个最小径集只含一个基本事件X1,按此原则X1的结构重要系数最大｡I(1)>I(i)i=2,3,4,5,6｡②仅出现在同一个最小割(径)集中的所有基本事件结构重要度相等｡例如:上述事故树X2,X3只出现在第二个最小径集,在其他最小径集中都未出现,所以I(2)=I(3);同理,I(4)=I(5)=I(6)｡③仅出现在基本事件个数相等的若干个最小割(径)集中的各基本事件结构重要度依出现次数而定,出现次数少,其结构重要度小;出现次数多,其结构重要度大;出现次数相等,其结构重要度相等｡例如:某事故树有三个最小割集:K1={X1,X2,X3}K2={X1,X3,X4}K3={X1,X4,X5}此事故树有五个基本事件,都出现在含有三个基本事件的最小割集中｡X1出现三次,X3､X4出现2次,X2､X5只出现1次,按此原则I(1)>I(3)=I(4)>I(2)=I(5)｡④两个基本事件出现在基本事件个数不等的若干个最小割(径)集中,其结构重要系数依下列情况而定:·若它们在各最小割(径)集中重复出现的次数相等,则在少事件最小割(径)集中出现的基本事件结构重要度大;例如:某事故树有四个最小割集: K1={X1,X3}K2={X1,X4}K3={X2,X4,X5}K4={X2,X5,X6}X1､X2两个基本事件都出现两次,但X1所在的两个最小割集都含有2个基本事件,而X2所在的两个最小割集都含有3个基本事件,所以I(1)>I(2)｡·若它们在少事件最小割(径)集中出现次数少,在多事件最小割(径)集中出现次数多,以及其他更为复杂的情况,可用下列近似判别式计算:4式中I(i)——基本事件Xi结构重要度系数的近似判别值,I(i)大则也大;——基本事件Xi属于Kj最小割(径)集;ni——基本事件Xi所在最小割(径)集中包含基本事件的个数｡假设某事故树共有五个最小径集:P1={X1,X3}P2={X1,X4}P3={X2,X4,X5}P4={X2,X5,X6}P5={X2,X6,X7}基本事件X1与X2比较,X1出现二次,但所在的两个最小径集都含有2个基本事件;X2出现三次,所在的三个最小径集都含有三个基本事件,根据这个原则判断由此可知,I(1)>I(2)｡利用上述四条原则判断基本事件结构重要度大小时,必须从第一至第四条按顺序进行,不能单纯使用近似判别式,否则会得到错误的结果｡用最小割集或最小径集判断基本事件结构重要度顺序其结果应该是一样的｡选用哪一种要视具体情况而定｡一般来说,最小割集和最小径集哪一种数量少就选那一种,这样对包含的基本事件容易比较｡例如:图9事故树含四个最小割集,K1={X1,X3},K2={X1,X5},K3={X3,X4},K4={X2,X4,X5};三个最小径集,P1={X1,X4},P2={X1,X2,X3},P3={X3,X5}｡显然,用最小径集比较各基本事件的结构重要度顺序比用最小割集方便｡根据以上四条原则判断:X1,X3都各出现2次,且2次所在的最小径集中基本事件个数相等,所以I(1)=I(3),X2,X4,X5,都各出现1次,但X2所在的最小径集中基本事件个数比X4､X5所在最小径集的基本事件个数多,故I(4)=I(5)>I(2),由此得各基本事件的结构重要度顺序为:I(1)=I(3)>I(4)=I(5)>I(2)在这个例子中,近似判断法与精确计算各基本事件结构重要度系数方法的结果是相同的｡分析结果说明:仅从事故树结构来看,基本事件X1和X3对顶上事件发生影响最大,其次是X4和X5,X2对顶上事件影响最小｡据此,在制定系统防灾对策时,首先要控制住X1和X2二个危险因素,其次是X4和X5,X2要根据情况而定｡基本事件的结构重要度顺序排出后,也可以作为制定安全检查表､找出日常管理和控制要点的依据｡(4)最小割集和最小径集在事故树分析中的作用最小割集和最小径集在事故树分析中有非常重要的作用,归纳起来主要有以下几方面:①最小割集表示系统的危险性｡定义可知,事故树中有一个最小割集顶上事件发生的可能性就有一种,有几个最小割集顶上事件发生的可能性就有几种｡事故树中最小割集越多,系统发生事故的途径越多,因而就越危险｡②最小径集表示系统的安全性｡由最小径集定义可知,事故树中有一个最小径集,则顶上事件不发生的可能性就有一种,事故树中最小径集越多,说明控制顶上事件不发生的方案就越多,系统的安全性就越高｡③最小割集可直观比较各种故障模式的危险性｡事故树中有一个最小割集,说明系统就有一种故障模式｡在这些故障模式中,有的只含有1个基本事件,有的含有2个基本事件,还有的含有3个､4个甚至更多个基本事件｡含有1个基本事件的最小割集,只要1个基本事件发生,顶上事件就会发生;含有2个基本事件的,必须2个基本事件同时发生,顶上事件才会发生｡很显然,1个事件发生的概率要比2个事件同时发生的概率大得多,3个事件同时发生的概率就更少了｡因此,最小割集含有的基本事件越小,这种故障模式越危险｡只含1个基本事件的割集最危险｡④从最小径集可选择控制事故的最佳方案｡事故树中有一个最小径集,控制顶上事件不发生的方案就有一种｡事故树有几个最小径集,使顶上事件不发生的方案就有几种｡在这些方案中,选择哪一种最好,一般来说,控制少事件最小径集中的基本事件比控制多个基本事件省工､省时､经济､有效｡当然也有例外,有时小事件径集中的基本事件由于经济或技术上的原因,难以控制,这种情况下应选择其他方案｡⑤利用最小割集和最小径集,可进行结构重要度分析｡⑥利用最小割集和最小径集可对系统进行定量分析和评价｡。

视窗×loading...第一阶段在线作业单选题(共20道题)收起1.（2.5分）安全是A、没有危险的状态B、没有事故的状态C、达到可接受的伤亡和损失的状态D、舒适的状态我的答案：C 此题得分：2.5分2.（2.5分）安全系统的认识论产生于（）A、20世纪初B、20世纪50年代后C、20世纪末D、21世纪初我的答案：B 此题得分：2.5分3.（2.5分）生产事故的特性不包括那一项A、因果性B、随机性C、潜伏性D、可预防性E、严重性我的答案：E 此题得分：2.5分4.（2.5分）海因里希的因果连锁论所建立的多米诺骨牌模型中最后一块骨牌所代表的是A、人的不安全行为B、物的不安全状态C、伤害D、事故我的答案：C 此题得分：2.5分5.（2.5分）在系统安全分析中，FMECA指的是A、事故树法B、故障类型及影响分析法C、原因—后果分析法D、故障类型、影响及致命度分析法我的答案：D 此题得分：2.5分6.（2.5分）海因里希对5000多起伤害事故案例进行了详细调查研究后得出海因里希法则，事故后果为严重伤害、轻微伤害和无伤害的事故件数之比为A、1:29:300B、1:10:300C、1:10:100D、1:100:500我的答案：A 此题得分：2.5分7.（2.5分）安全系统工程的研究对象A、人子系统B、机器子系统C、环境子系统D、人—机—环我的答案：D 此题得分：2.5分8.（2.5分）下列属于安全系统工程研究内容的是（）A、地质灾害B、社会治安C、安全评价D、疾病防治我的答案：C 此题得分：2.5分9.（2.5分）()是系统安全的主要观点A、安全是绝对的B、安全只是系统运行阶段的要考虑的工作C、在系统的各个阶段都要进行危险源辨识、评价和控制D、事故是系统的危险源我的答案：C 此题得分：2.5分10.（2.5分）事故和隐患是A、完全相同的B、后者是前者的可能性C、后者是前者的必然条件D、前者是后者的必然条件我的答案：B 此题得分：2.5分11.（2.5分）安全检查表方法不可以用于A、方案设计B、开发研制C、生产样机D、日常运行我的答案：B 此题得分：2.5分12.（2.5分）危险性与可操作研究可用于A、方案设计B、开发研制C、事故调查D、日常运行我的答案：B 此题得分：2.5分13.（2.5分）故障类型和影响分析（FMEA）与故障类型和影响、危险度分析（FMECA）的区别是A、前者是后者的基础B、后者仅进行危险度分析C、前者是定量分析，后者是定性分析D、后者是以前者为基础的定性分析我的答案：B 此题得分：2.5分14.（2.5分）进行危险性分级，即把预计到的潜在事故划分为危险等级，划分的目的是为了分清轻重缓急，即等级高的作为重点控制的对象。

事故树的定性定量分析一、计算题1、某事故树的最小割集为K1={X1，X2，X5}；K2={X1，X3，X5}；K3={X1，X4，X5}，各基本事件的发生概率为q1=q3=q4=0.01，q2=0.1，q5=0.95，求顶上事件发生概率。

2、某事故树的最小割集为K1={X1，X2}；K2={X3，X4}；K3={X5，X6}，各基本事件的发生概率为q1=q2 =0.01，q3=q4=0.02，q5=q6=0.05，求顶上事件发生概率3、某事故树有三个最小径集：P 1=｛ X1｝，P 2=｛ X2，X3｝，P 3=｛ X4， X5 ，X6｝。

求基本事件的结构重要度。

二、选择题1、某事故树的最小径集为：Pl＝{Xl，X2，X4}，P2＝{Xl，X2，X5}，P3＝{Xl，X3，X6}，P4＝{Xl，X3，X7}，则结构重要程度为（）A、I(1)＞I(2)＝I(3)＞I(4)＝I(5)B、I(1)＞I(2)＜I(3)＞I(4)＝I(5)C、I(1)＞I(2)＞I(3)＜I(4)＝I(5)D、I(3)＞I(2)＜I(1)＞I(4)＝I(5)三、填空题1、基本事件的概率重要度是指顶上事件发生概率对该基本事件发生概率的（）。

2、临界重要度也称（），它是基本事件发生概率的变化率与顶上事件发生概率的变化率的比来确定基本事件的重要程度。

答案：一、1、，本题中最小割集有重复因子，因此需将公式展开后消去重复因子才能带入数据进行计算。

P(T)=q1q2q5+q1q3q5+q1q4q5-(q1q2q3q5+q1q2q4q5+q1q3q4q5)+ q1q2q3q4q5=1.12020 x10-32、本题中最小割集没有重复因子，因此公式不需要展开，直接带数据进行计算。

=1-（1-qK1）·（1-qK2）·（1-qK3）=1-(1-q1q2)(1-q3q4)(1-q5q6)=1.4996x10-3 3、I（1）＞I（i） i=2，3 ）＞ I（i）i= 4，5，6二、1、A三、1、变化率；2、危险重要度火力发电厂应当建在哪里我国某大型产煤矿区要建设坑口火力发电厂（p），已知有n 处产煤矿口，并且修建至电厂的运煤轨道的费用与产煤量及距离成正比（W*L ），运用MPA学科中定量分析的方式方法，为坑口火力发电厂选址，要求目标是费用最小。

事故树分析法事故树分析法（FTA）事故树分析法是一种既能定性又能定量的逻辑演绎评价方法，是从结果到原因描绘事故发生的有向逻辑树，在逻辑树中相关原因事件之间用逻辑门连接，构成逻辑树图，为判明事故发生的途径及损害间关系提供一种最形象、最简洁的表达方式。

事故树法又称为故障树分析法，是一种逻辑演绎的系统评价方法，是安全系统工程中重要的分析方法之一。

它能对各种系统的危险性进行识别评估，既适用于定性分析，又能进行定量分析。

具有简明、形象的特点。

其分析方法是从要分析的特定事故或故障顶上事件开始，层层分析其发生原因（中间事件），一直分析到不能再分解或没有必要分析时为止，即分析至基本原因事件为止，用逻辑门符号将各层中间事件和基本原因事件连接起来，得到形象、简洁地表达其因果关系的逻辑树图形即故障树。

通过对其简化计算得到分析评价目的的方法。

故障树分析法的主要功能1、对导致事故的各种因素及其逻辑关系作出全面的描述2、便于发觉和查明系统内固有的大概潜在的风险因素，为安全设计、制定技术措施及采取管理对策提供按照3、使作业人员全面了解和掌握各项防灾要点4、对已发生的事故进行原因分析妨碍树的分析步骤1、确定所分析的系统2、熟悉所分析的系统3、调查系统发生的事故4、确定事故的顶上事件5、调查与顶上变乱有关的所有原因变乱6、故障树作图7、妨碍树的定性分析8、故障树的定量分析9、安全性评价熟悉系统确定顶上变乱调查事故收集系统材料建造事故树调查原因变乱修改简化事故树定性分析定量分析制定安全措施事故树的主要符号变乱符号顶上事件、中间事件符号，需要进一步的分析基本变乱符号，不克不及进一步往下分析正常事件，正常情况下存在的事件省略变乱，不克不及大概不需要分析逻辑符号XXX·XXX·a事故树的建造方法顶上变乱中央变乱基本变乱直接原因事件可以从以下几个方面考虑：1、电气设备妨碍2、人的差错（操作、管理、指挥）3、环境不良事故树的数学描述事故树的结构函数XiXi=1表示单元i是发生的Xi=0表示单元i是没有发生的y=1表示顶上变乱是发生的y=0表示顶上变乱是没有发生的y=Φ(X)或y=Φ(x1,x2,…,xn)系统的结构函数事故树的定性分析利用布尔代数简化事故树割集+或门，任意一变乱发生，顶上变乱发生与门，两个变乱同时发生，顶上变乱发生+a条件或门，任意事件发生，并且满足a，顶上事件才发生a条件与门，两变乱同时发生，并满足a，顶上变乱才发生限制门，变乱发生，并满足a，顶上变乱才发生y割集：事故树种某些基本事件的组合，当这些基本事件都发生时，顶上事件必然发生。