第02章 常见图形的截面面积、形心坐标、惯性矩和惯性积
- 格式:pdf
- 大小:116.50 KB
- 文档页数:2

惯性矩是一个物理量,通常被用作描述一个物体抵抗扭动,扭转的能力。
惯性矩的国际单位为(m^4)。
工程构件典型截面几何性质的计算2.1面积矩1.面积矩的定义图2-2.1任意截面的几何图形如图2-31所示为一任意截面的几何图形(以下简称图形)。
定义:积分和分别定义为该图形对z轴和y轴的面积矩或静矩,用符号S z和S y,来表示,如式(2—2.1)(2—2.1)面积矩的数值可正、可负,也可为零。
面积矩的量纲是长度的三次方,其常用单位为m3或mm3。
2.面积矩与形心平面图形的形心坐标公式如式(2—2.2)(2—2.2)或改写成,如式(2—2.3)(2—2.3)面积矩的几何意义:图形的形心相对于指定的坐标轴之间距离的远近程度。
图形形心相对于某一坐标距离愈远,对该轴的面积矩绝对值愈大。
图形对通过其形心的轴的面积矩等于零;反之,图形对某一轴的面积矩等于零,该轴一定通过图形形心。
3.组合截面面积矩和形心的计算组合截面对某一轴的面积矩等于其各简单图形对该轴面积矩的代数和。
如式(2—2.4)(2—2.4)式中,A和y i、z i分别代表各简单图形的面积和形心坐标。
组合平面图形的形心位置由式(2—2.5)确定。
(2—2.5)2.2极惯性矩、惯性矩和惯性积1.极惯性矩任意平面图形如图2-31所示,其面积为A。
定义:积分称为图形对O点的极惯性矩,用符号I P,表示,如式(2—2.6)(2—2.6)极惯性矩是相对于指定的点而言的,即同一图形对不同的点的极惯性矩一般是不同的。
极惯性矩恒为正,其量纲是长度的4次方,常用单位为m4或mm4。
(1)圆截面对其圆心的极惯性矩,如式(2—7)(2—2.7)(2)对于外径为D、内径为d的空心圆截面对圆心的极惯性矩,如式(2—2.8)(2—2.8)式中,d/D为空心圆截面内、外径的比值。
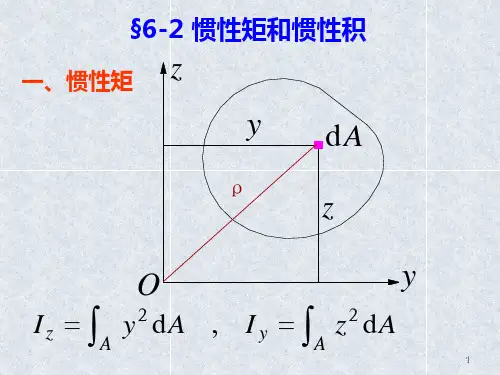
2.惯性矩在如图6-1所示中,定义积分,如式(2—2.9)(2—2.9)称为图形对z轴和y轴的惯性矩。
惯性矩是对一定的轴而言的,同一图形对不同的轴的惯性矩一般不同。

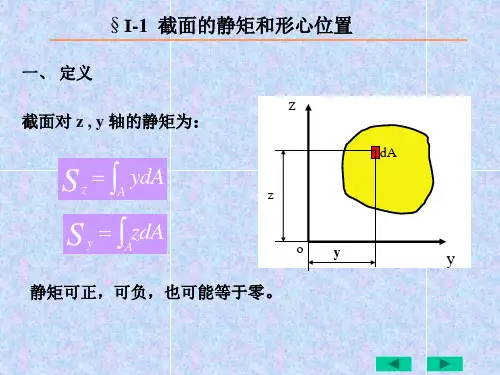
资料范本本资料为word版本,可以直接编辑和打印,感谢您的下载惯性矩、静矩,形心坐标公式地点:__________________时间:__________________说明:本资料适用于约定双方经过谈判,协商而共同承认,共同遵守的责任与义务,仅供参考,文档可直接下载或修改,不需要的部分可直接删除,使用时请详细阅读内容§I−1 截面的静矩和形心位置dACZzyyyCZcO图I−1Z如图I−1所示平面图形代表一任意截面,以下两积分(I−1)分别定义为该截面对于z轴和y轴的静矩。
静矩可用来确定截面的形心位置。
由静力学中确定物体重心的公式可得利用公式(I−1),上式可写成(I−2)或(I−3)(I−4)如果一个平面图形是由若干个简单图形组成的组合图形,则由静矩的定义可知,整个图形对某一坐标轴的静矩应该等于各简单图形对同一坐标轴的静矩的代数和。
即:(I−5)式中Ai、yci和zci分别表示某一组成部分的面积和其形心坐标,n为简单图形的个数。
将式(I−5)代入式(I−4),得到组合图形形心坐标的计算公式为(I−6)yC0.12m0.4myⅡyⅠⅠ0.6m0.2mOyzⅠⅡCⅠⅠCⅡC例题I−1图例题I−1 图a所示为对称T型截面,求该截面的形心位置。
解:建立直角坐标系zOy,其中y为截面的对称轴。
因图形相对于y轴对称,其形心一定在该对称轴上,因此zC=0,只需计算yC值。
将截面分成Ⅰ、Ⅱ两个矩形,则AⅠ=0.072m2,AⅡ=0.08m2yⅠ=0.46m,yⅡ=0.2m§I−2 惯性矩、惯性积和极惯性矩dAρyyO图I−2zz如图I−2所示平面图形代表一任意截面,在图形平面内建立直角坐标系zOy。
现在图形内取微面积dA,dA的形心在坐标系zOy中的坐标为y和z,到坐标原点的距离为ρ。
现定义y2dA和z2dA为微面积dA对z轴和y轴的惯性矩,ρ2dA为微面积dA对坐标原点的极惯性矩,而以下三个积分(I−7)分别定义为该截面对于z轴和y轴的惯性矩以及对坐标原点的极惯性矩。

常用截面几何性质计算公式JX1.矩形截面:矩形截面是一种常见的结构截面形式。
假设矩形截面宽度为b,高度为h,则其面积可以通过以下公式计算:A=b*h质心位置可以通过以下公式计算:x=b/2y=h/2惯性矩可以通过以下公式计算:Ix=(b*h^3)/12Iy=(h*b^3)/12截面模数可以通过以下公式计算:Wx=(b*h^2)/6Wy=(h*b^2)/62.圆形截面:圆形截面是另一种常见的结构截面形式。
假设圆形截面的半径为r,则其面积可以通过以下公式计算:A=π*r^2质心位置在圆心上,即x=0,y=0。
惯性矩可以通过以下公式计算:Ix=(π*r^4)/4Iy=(π*r^4)/4截面模数可以通过以下公式计算:Wx=(π*r^3)/4Wy=(π*r^3)/43.等边三角形截面:等边三角形截面是一个等边三角形形状的结构截面。
假设等边三角形截面的边长为a,则其面积可以通过以下公式计算:A = (sqrt(3) * a^2) / 4质心位置可以通过以下公式计算:x=a/2y = (sqrt(3) * a) / 6惯性矩可以通过以下公式计算:Ix = (a^4 * sqrt(3)) / 48Iy=(a^4)/48截面模数可以通过以下公式计算:Wx = (a^3 * sqrt(3)) / 12Wy=(a^3)/12以上是常见的几种截面几何性质的计算公式,通过这些公式可以方便地计算结构截面的重要性质,为结构设计和分析提供参考。
在实际应用中,还需要根据具体的截面形状和尺寸选择相应的公式进行计算。


惯性矩的计算方法及常用截面惯性矩计算公式截面图形的几何性质重点及难点:(一)•截面静矩和形心1・静矩的定义式如图1所示任意有限平面图形,取其单元如面积定义它对任意轴的一次矩为它对该轴的静矩,即dS、=xdA dSx=ydA整个图形对y、z轴的静矩分别为Sv = M Sx(1-1)= £ ydA2.形心与静矩关系设平面图形形心C的坐标为则Oc S y =一x = —(1-2)A A推论1如果y轴通过形心(即x = 0),则静矩S v=0;同理,如果x轴通过形心(即y二o),则静矩5x = 0;反之也成立。
推论2如果x、y轴均为图形的对称轴,则其交点即为图形形心;如果y轴为图形对称轴,则图形形心必在此轴上。
3.组合图形的静矩和形心设截面图形由儿个面积分别为A P A2,A S……A”的简单图形组成,且一直各族图形的形心坐标分别为召,刃;W2;无3,%....,则图形对y轴和X轴的静矩分别为S)・二£刀: : (1-3)Sx二工S ” 二22 A Vri-1 r-1截面图形的形心坐标为耳EAV/元二一, 2 —(1-4)EA ZA/-I 1-14.静矩的特征(1)界面图形的静矩是对某一坐标轴所定义的,故静矩与坐标轴有关。
(2)静矩有的单位为〃Fo(3)静矩的数值可正可负,也可为零。
图形对任意形心轴的静矩必定为零,反之,若图形对某一轴的静矩为零,则该轴必通过图形的形心。
(4)若已知图形的形心坐标。
则可由式(1・1)求图形对坐标轴的静矩。
若已知图形对坐标轴的静矩,则可由式(1-2)求图形的形心坐标。
组合图形的形心位置,通常是先由式(1-3)求出图形对某一坐标系的静矩,然后由式(1・4)求出其形心坐标。
(二)•惯性矩惯性积惯性半径1・惯性矩定义设任意形状的截面图形的面积为A (图1・3),则图形对0点的极惯性矩定义为厶二八p2dA(I〜5)图形对y轴和x轴的光性矩分别定义为I、= A xVA , I x= £y2dA(1-6)惯性矩的特征(1)界面图形的极惯性矩是对某一极点定义的;轴惯性矩是对某一坐标轴定义的。

惯性矩是一个物理量,通常被用作描述一个物体抵抗扭动,扭转的能力。
惯性矩的国际单位为(m^4)。
工程构件典型截面几何性质的计算2.1面积矩1.面积矩的定义图2-2.1任意截面的几何图形如图2-31所示为一任意截面的几何图形(以下简称图形)。
定义:积分和分别定义为该图形对z轴和y轴的面积矩或静矩,用符号S z和S y,来表示,如式(2—2.1)(2—2.1)面积矩的数值可正、可负,也可为零。
面积矩的量纲是长度的三次方,其常用单位为m3或mm3。
2.面积矩与形心平面图形的形心坐标公式如式(2—2.2)(2—2.2)或改写成,如式(2—2.3)(2—2.3)面积矩的几何意义:图形的形心相对于指定的坐标轴之间距离的远近程度。
图形形心相对于某一坐标距离愈远,对该轴的面积矩绝对值愈大。
图形对通过其形心的轴的面积矩等于零;反之,图形对某一轴的面积矩等于零,该轴一定通过图形形心。
3.组合截面面积矩和形心的计算组合截面对某一轴的面积矩等于其各简单图形对该轴面积矩的代数和。
如式(2—2.4)(2—2.4)式中,A和y i、z i分别代表各简单图形的面积和形心坐标。
组合平面图形的形心位置由式(2—2.5)确定。
(2—2.5)2.2极惯性矩、惯性矩和惯性积1.极惯性矩任意平面图形如图2-31所示,其面积为A。
定义:积分称为图形对O点的极惯性矩,用符号I P,表示,如式(2—2.6)(2—2.6)极惯性矩是相对于指定的点而言的,即同一图形对不同的点的极惯性矩一般是不同的。
极惯性矩恒为正,其量纲是长度的4次方,常用单位为m4或mm4。
(1)圆截面对其圆心的极惯性矩,如式(2—7)(2—2.7)(2)对于外径为D、内径为d的空心圆截面对圆心的极惯性矩,如式(2—2.8)(2—2.8)式中,d/D为空心圆截面内、外径的比值。
2.惯性矩在如图6-1所示中,定义积分,如式(2—2.9)(2—2.9)称为图形对z轴和y轴的惯性矩。
惯性矩是对一定的轴而言的,同一图形对不同的轴的惯性矩一般不同。

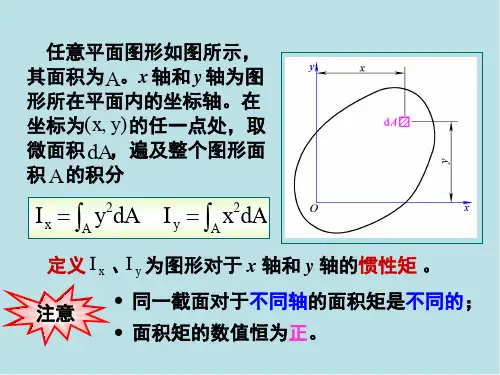
工程构件典型截面几何性质的计算2.1面积矩如图2-31所示为一任意截面的几何图形(以下简称图形)。
定义:积分上t 和A分别定义为该图形对z 轴和y 轴的面积矩或静矩,用符号S z 和S y ,来表示,如式(2 — 2.1)面积矩的数值可正、可负,也可为零。
面积矩的 量纲是长度的三次方,其常用单位为m 3或mm2 •面积矩与形心平面图形的形心坐标公式如式(2 — 2.2)(2 — 2.2)或改写成,如式(2 — 2.3):二 X 乙 (2面积矩的几何意义:图形的形心相对于指定的坐标轴之间距离的远近程度。
图形形心相对于某一坐标距 离愈远,对该轴的面积矩绝对值愈大。
—2.3)1 •面积矩的定义图2-2.1任意截 面的几何图形图形对通过其形心的轴的面积矩等于零;反之, 图形对某一轴的面积矩等于零,该轴一定通过图形形心。
3 •组合截面面积矩和形心的计算组合截面对某一轴的面积矩等于其各简单图形对该轴面积矩的代数和。
如式(2—2.4)鬲=刀殆=£4订(2 — 2.4)式中,A和y i、乙分别代表各简单图形的面积和形心坐标。
组合平面图形的形心位置由式(2 —2.5)确定迟4吗i-i(2 —2.5)2.2极惯性矩、惯性矩和惯性积1 •极惯性矩任意平面图形如图2-31所示,其面积为A。
定义:积分1 称为图形对0点的极惯性矩,用符号I P,表示,如式(2 —2.6)' (2 —2.6)极惯性矩是相对于指定的点而言的,即同一图形对不同的点的极惯性矩一般是不同的。
极惯性矩恒为正,其量纲是长度的4次方,常用单位为m4或mm(1)圆截面对其圆心的极惯性矩,如式(2 —7)(2 —2.7)⑵对于外径为D内径为d的空心圆截面对圆心的极惯性矩,如式(2 —2.8)p 32 (2—2.8)式中,.:二d/D为空心圆截面内、外径的比值。
2 •惯性矩在如图6-1所示中,定义积分,如式(2 —2.9)^2 =J "沁卜'厂(2 — 2.9)称为图形对z轴和y轴的惯性矩。