当前位置：文档之家 › 机械工程测试技术基础(第三版)段富海-第一章 信号及其描述

机械工程测试技术基础(第三版)段富海-第一章 信号及其描述

  • 格式：ppt
  • 大小：1.64 MB
  • 文档页数：88

下载文档原格式

  / 88

合集下载

机械工程测试技术基础

机械工程测试技术基础


追求至善凭技术开拓市场，凭管理增 创效益 ，凭服 务树立 形象。2020年10月25日星期 日下午1时55分 57秒13:55:5720.10.25
最大峰值与最小
4、带宽B和品质因数Q值
峰谷的中点
上下两截止频率之间的频率
范围称为滤波器带宽B。
A(f)
中心频率 f0 和带宽B之比称
A0
d
.
d
为滤波器的品质因数Q，即 Q=f0/B
A0 2
5、倍频程选择性
1~5
常用
0
fc1
fc2 f
倍频程选择性是指在上截止频率 fc2 与 2 fc2 之间，
或者在下截止频率 fc1 与 fc1 / 2 之间幅频特性的衰减
知，所描述物理现象是一种随机过程。
噪声信号(平稳)
噪声信号(非平稳 )
统计特性变异
！！！
时域分析与频域分析的关系
幅值
关于其它信号的频谱分布 情况可以参看 P21的 表1-1
信号频谱X(f)代表了 信号在不同频率分量成分 的大小，能够提供比时域 信号波形更直观，丰富的 信息。
时域分析
理论依据是傅里叶展开式 频域分析
A() H (J) S
1 ( )2
() H ( j) tg 1( )
用普通坐标表示
A( )
1 0.707
()
1
4 2
由: A() S 1 ( )2
() tg 1( )
当:
0
1
A() 1, () 0, A() 1, () 0,
1 A() 1 2, () 4 1 A() 0, () 2
传递函数的定义：x(t)、y(t)及其各阶导数的
初始值为零，系统输出信号的拉普拉斯变
机械工程测试技术基础(第三版)段富海-第一章.ppt

机械工程测试技术基础(第三版)段富海-第一章.ppt


注意： 1. e j2 f0t cos 2 f0t j sin 2 f0t
Im
2 f0t
Re
0
2. 2cos cos cos( ) cos( )
3. 三角函数系的正交
所谓三角函数系
以上等式，都可以通过计算定积分来验证。
x(t)
1
T
0
1
Tt
wR (t)
0
t
x1 (t )
1
0
t
1
x(t)
1
T
0
1
Tt
WR ( f )
0
f
X1( f )
1
2
f0
0
f0
f
X(f)
f0
0
f0
f
方法三
X ( f ) x(t)e j2 ftdt
T
cos 2
T
f0t cos 2
ft
j sin 2
ft dt
T
T cos 2 f0t cos 2 ftdt
x( f ) x(t)e j2 ftdt x(t)e j2 ftdt （单边）
0
Aeate j2 ft dt 0
A e(a j2 f )t dt 0
A
A(a j2 f )
a j2 f a2 4 2 f 2
绘图：
幅值谱Βιβλιοθήκη x( f ) Aa2 4 2 f 2
相位谱
(
f
)
arctan
方法一：
wR (t) x1(t) WR ( f ) * X1( f )
所以：
X ( f ) WR ( f ) * X1( f ) 2T sin c(2
fT ) * 1 ( f
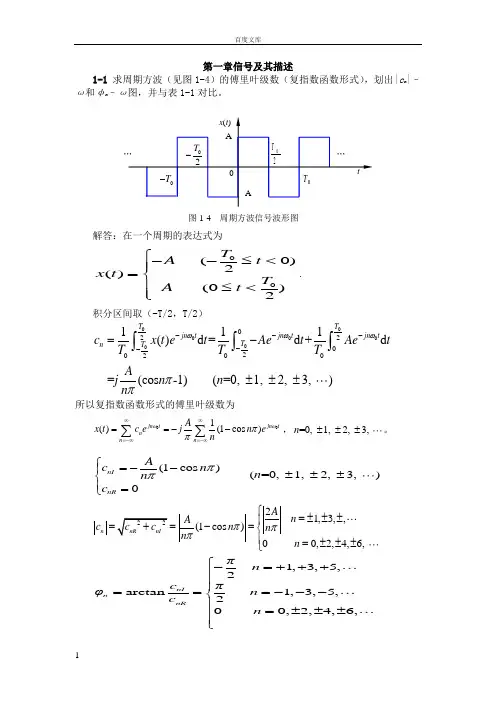
机械工程测试技术基础第三版课后习题答案汇总

机械工程测试技术基础第三版课后习题答案汇总

第五章信号处理初步
5-2假定有一个信号x(t)，它由两个频率、相角均不相等的余弦函数叠加而成，其数学表达式为
x(t)=A1cos(1t+1)+A2cos(2t+2)
求该信号的自相关函数。
解：设x1(t)=A1cos(1t+1)；x2(t)=A2cos(2t+2)，则
因为12，所以 ， 。
又因为x1(t)和x2(t)为周期信号，所以
解：
所以
根据频移特性和叠加性得：
可见调幅信号的频谱等于将调制信号的频谱一分为二，各向左右移动载频ω0，同时谱线高度减小一半。
若 将发生混叠。
2-2用一个时间常数为的一阶装置去测量周期分别为1s、2s和5s的正弦信号，问稳态响应幅值误差将是多少？
解：设一阶系统 ，
，T是输入的正弦信号的周期
稳态响应相对幅值误差 ，将已知周期代入得
解：设 ，则
， ，即
，
将fn= 800Hz，= ，f= 400Hz，代入上面的式子得到
A(400)，(400)−
如果= ，则A(400)，(400)−
2-11对一个可视为二阶系统的装置输入一单位阶跃函数后，测得其响应的第一个超调量峰值为,振荡周期为。设已知该装置的静态增益为3，求该装置的传递函数和该装置在无阻尼固有频率处的频率响应。
幅频图为
4-5已知调幅波xa(t)=(100+30cost+20cos3t)cosct，其中fc=10kHz，f=500Hz。试求：
1）xa(t)所包含的各分量的频率及幅值；
2）绘出调制信号与调幅波的频谱。
解：1）xa(t)=100cosct+15cos(c-)t+15cos(c+)t+10cos(c-3)t+10cos(c+3)t
机械工程测试技术基础ppt

机械工程测试技术基础ppt


1 1 x( t ) (sin 0t sin 30t sin 50t ) 3 5 2 0 T0
4A
式中ω0=2π/T0。ω0称为基波频率，简称基频。 上式可改写为：
x( t ) 4A

(
n0
1 sin t ) n 1 n n 1,3,5

•
例如某大型水电站在某一发电工况下，其厂 房产生强烈振动。按理论分析和经验估计，振源 可能来自水轮机或发电机的机械振动，或来自流 道某一部份（如引水管、涡壳、导叶、尾水管） 的水体振动。为查找振源及振源向厂房传递的路 径，在水轮发电机组和厂房的多处安置拾振器， 在流道多处安置压力传感器。试验时，用多台磁 带记录仪同步记录近百个测点的振动及压力波动。 试验完后，对记录的信号进行频谱分析，查找出 强振振源来自导叶与尾水管间的局部水体共振。
为什么要对信号进行频域描述：
信号的时域描述反映了信号瞬时值随时间变化的情况， 频域描述反映了信号的频率组成及其幅值、相角的大 小。 为解决不同问题，需掌握信号不同方面的特征，因而 可采用不同的描述方式。例如：评定机器振动烈度 （时域描述）和寻找振源（频域描述）。 两种描述方法能互相转换，而且包含同样的信息量。
X( f )
x (t )




x ( t ) e j 2 ft dt
(1-28) (1-29)

X ( f ) e j 2 ft df
这样就避免了傅里叶变换中出现1/2π,简化了公式，且有
X ( f ) 2X ( )
非周期函数x（t）存在傅里叶变换的充 分条件是x（t）在区间(-∞, ∞)上绝对 可积，即
则
x ( t ) C 0 C n e
机械工程测试技术基础（第三版）课后习题答案

机械工程测试技术基础（第三版）课后习题答案

机械⼯程测试技术基础（第三版）课后习题答案第⼀章信号及其描述1-1 求周期⽅波（见图1-4）的傅⾥叶级数（复指数函数形式），划出|c n |–ω和φn –ω图，并与表1-1对⽐。

解答：在⼀个周期的表达式为00 (0)2() (0)2T A t x t T A t ?--≤积分区间取（-T/2，T/2）0000000022020002111()d =d +d =(cos -1) (=0, 1, 2, 3, )T T jn t jn tjn t T T n c x t e t Ae t Ae tT T T Aj n n n ωωωππ-----=-±±±?所以复指数函数形式的傅⾥叶级数为001()(1cos )jn tjn tnn n Ax t c e=-∞==--∑∑ωωππ，=0, 1, 2, 3, n ±±±。

(1cos ) (=0, 1, 2, 3, )0nI nR A c n n n c ?=--?±±±?=ππ2221,3,,(1cos )00,2,4,6,n nR nI An A c c c n n n n ?=±±±?=+=-=??=±±±πππ1,3,5,2arctan1,3,5,200,2,4,6,nI n nRπn c πφn c n ?-=+++===---??=±±±??图1-4 周期⽅波信号波形图0 tx (t ) T 02-T 020T -没有偶次谐波。

其频谱图如下图所⽰。

1-3 求指数函数()(0,0)at x t Ae a t -=>≥的频谱。

解答：(2)22022(2)()()(2)2(2)a j f tj f tat j f te A A a jf X f x t edt Ae edt Aa j f a j f a f -+∞∞---∞-∞-=====-+++??πππππππ22()(2)k X f a f π=+Im ()2()arctanarctan Re ()X f ff X f a==-π?π/2 -π/2 ωωω0ω0 3ω05ω03ω05ω02A/π2A/3π 2A/5π幅频图相频图周期⽅波复指数函数形式频谱图2A/5π 2A/3π 2A/π -ω0-3ω0-5ω0-ω0 -3ω0-5ω0 单边指数衰减信号频谱图f|X (f )A /aφ(f )fπ/-π/2a)符号函数的频谱10()sgn()10t x t t t +>?==?-t =0处可不予定义，或规定sgn(0)=0。

机械工程测试技术基础 _第三版_第一章

机械工程测试技术基础 _第三版_第一章


30
第四节 随机信号
二、随机信号的主要特征参数
1、 均值、方差和均方值 均值表示信号的常值分量
方差描述随机信号的波动分量。
均方值描述随机信号的强度。
31
第四节 随机信号
二、随机信号的主要特征参数
2、 概率密度函数 随机信号的概率密度函数是表示信号幅值落在指定区间的概率。如图1-22所示。
图1-22
一、概述
随机信号是不能用确定的数学关系式来描述的，不能预测其未来的任何瞬时值。 任何一次观测值只代表在其变动范围中可能产生的结果之一，但其值的变动服 从统计规律。 随机过程与样本函数如图1-21所示。
图1-21
29
第四节 随机信号
二、随机信号的主要特征参数
1） 均值、方差和均方值 2） 概率密度函数 3） 自相关函数 4） 功率谱密度函数
图1-3
4
第一节 信号的分类与描述
一、信号的分类
3.能量信号和功率信号 当电压信号满足一定条件时：则认为信号的能量是有限的，并称之为能 量有限信号。简称能量信号。 若信号在区间（- ∞ ， ∞ ）的能量是无限的，但它在有限区间的平均功
率是有限的。这种信号称为功率有限信号，或功率信号。



x 2 (t )dt
通常所说的非周期信号是指瞬变非周期信号如图1-11所示。图1-11a为矩 形脉冲信号，图1-11b为指数衰减信号，图1-11c为衰减振荡，图1-11d为 单一脉冲。
图1-11
14
第三节 瞬变非周期信号与连续频谱
一、傅里叶变换
图1-11 非周期性信号
15
第三节 瞬变非周期信号与连续频谱
一、傅里叶变换
图1-7
9
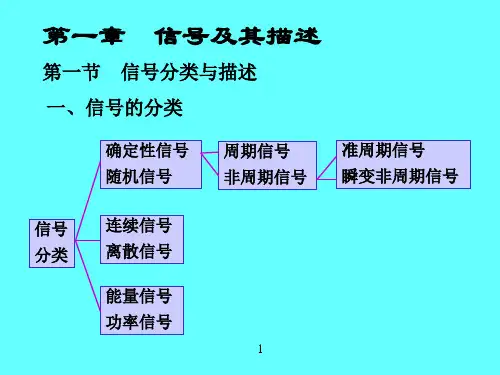
机械工程测试技术精品课件：第一章-信号及其描述

机械工程测试技术精品课件：第一章-信号及其描述


25
x(t) 1
-T/2 0 T/2 t
Re<0
Ie Re>0 Re
W(f) T
-3/T -1/T 1/T 3/T
-2/T 0 2/T
f
φ(f) π
-4/T -3/T -2/T –1/T 0 1/T;2/T;;3/T;4/T f
图1-12
26
二．傅里叶变换的主要性质
1、奇偶虚实性
一般X(f)是实变量f的复变函数，由欧拉公式可写成
cn
1 2 (an
jbn )
12 2 T0
T0 / 2
[ x(t) cosn0tdt
T0 / 2
T0 / 2
j x(t)sin n0tdt]
T0 / 2
cn
1 T0
[
T0
/
2
x(t
)
1
(e
jn0t
e jnot )dt
j
T0 / 2
x(t)
j
(e jn0t
T0 / 2
cn
2
1 T0
T0 / 2
6
二、信号的时域描述和频域描述
时域描述—直接观测或测量的信号，一般以时间为 独立变量的描述。 特点：直接反映信号幅值随时间变化的关系。
频域描述—把时域描述信号经适当方法变换，以频率 为独立变量来表示的信号。 特点：分解信号频率结构，呈现频率与幅值、频 率与相位的关系。
7
例：一个周期方波的一种时域描述形式表示为：
21
上式原括号中积分后为ω的函数，记为X(ω)
X ()
1
x(t)e jt dt
2
付里叶变换
（1-26）
x(t) X ( )e jt d 付里叶逆变换 （1-27）
机械工程测试技术基础

机械工程测试技术基础


二、连续信号和离散信号 • 分类依据：
–自变量即时间t是连续的还是离散的 –信号的幅值是连续的还是离散的；
• 连续信号：
–自变量和幅值均为连续的信号称为模拟信号； –自变量是连续、但幅值为离散的信号则称为量化信号
• 离散信号：
–信号的自变量为离散值、但其幅值为连续值时则称该 信号为被采样信号
–信号的自变量及幅值均为离散的则称为数字信号；
Cn
C n
C0
1 2
(an
1 2
(an
a0
jbn ) jbn )
n 1,2,3
则
x (t) C 0 C n e j n 0 t C n ej n 0 t n 1 ,2 ,3
n 1
n 1
或Leabharlann x(t) Cnejn0t n0,1,2,一-一
n
五
这就是傅里叶级数的复指数展开形式
n0td e tj n0t
• 小结： – 从式一－二九可知一个非（ZHOU）期函数可分解成 频率f连续变化的谐波的叠加式中Xfdf的是谐波ej二πf 的系数决定着信号的振幅和相位 – Xf或Xω为xt的连续频谱 – 由于Xf一般为实变量f的复函数故可将其写为
X(f)X(f)ej(f)
将上式中的称X非(（f )ZHOU）期信号xt的连续幅值谱 称(xft)的连续相位谱 例题一－三求矩形窗函数的频谱
二、傅里叶级数的复指数函数展开式
由欧拉公式可知：
ejt cotsjsin t(j1) cso i n tts 1 2j((e e jj tt e ejj tt))
2
代入式一－七有：
x ( 令t) a 0 n 1 1 2 (a n jn b ) e j n 0 t 1 2 (a n jn b ) e j n 0 t
机械工程测试技术基础课后答案

机械工程测试技术基础课后答案

机械工程测试技术基础习题解答第一章 信号的分类与描述1-1 求周期方波（见图1-4）的傅里叶级数（复指数函数形式），划出|c n |–ω和φn –ω图，并与表1-1对比。

解答：在一个周期的表达式为00 (0)2() (0)2T A t x t T A t ⎧--≤<⎪⎪=⎨⎪≤<⎪⎩.积分区间取（-T/2，T/2）00000002202002111()d =d +d =(cos -1) (=0, 1, 2, 3, )T T jn tjn tjn t T T n c x t et Aet Ae tT T T Ajn n n ωωωππ-----=-±±±⎰⎰⎰所以复指数函数形式的傅里叶级数为001()(1cos )jn tjn t n n n Ax t c ejn e n∞∞=-∞=-∞==--∑∑ωωππ，=0, 1, 2, 3, n ±±±。

(1cos ) (=0, 1, 2, 3, )0nInR A c n n n c ⎧=--⎪±±±⎨⎪=⎩ππ图1-4 周期方波信号波形图0 tx (t ) T 02-T 020T -……A-AT 02221,3,,(1cos )00,2,4,6,n nR nI An A c c c n n n n ⎧=±±±⎪=+=-=⎨⎪=±±±⎩πππ1,3,5,2arctan 1,3,5,200,2,4,6,nI n nR πn c πφn c n ⎧-=+++⎪⎪⎪===---⎨⎪=±±±⎪⎪⎩没有偶次谐波。

其频谱图如下图所示。

1-2 求正弦信号0()sin x t x ωt =的绝对均值x μ和均方根值rms x 。

解答：2200002211()d sin d sin d cos TTT Tx x x x x μx t t x ωt t ωt t ωt T T TT ωT ωπ====-==⎰⎰⎰222200rms000111cos 2()d sin d d 22T T Tx x ωtx x t t x ωt t t T T T-====⎰⎰⎰1-3 求指数函数()(0,0)atx t Ae a t -=>≥的频谱。

1.信号及其描述pp PPT课件

1.信号及其描述pp PPT课件


（1-10，11，12）
14
第1章 信号及其描述
第2节 傅里叶级数的展开与周期信号的离散频谱
1.2.1 傅里叶级数的三角函数展开式 因此式（1-7）可改写为：
x(t)

a0

n1
1 2
an
jbn
e j0t
1 2
an
jbn
e
j0t
cn1源自21.2.1 傅里叶级数的三角函数展开式

x(t) a0 (an cosn0t bn sin 0t) n1

a0 An sin(n0t n ) n1
（1-7，8，9）
10
第1章 信号及其描述
第2节 傅里叶级数的展开与周期信号的离散频谱
11
第1章 信号及其描述
37
第1章 信号及其描述
第3节 傅立叶变换与瞬变非周期信号的连续频谱
1.3.2傅立叶变换的主要性质
• 傅立叶变换构建了信号时域描述和频域描述的对 应关系，了解其性质有助于分析和简化复杂的工程 问题。
38
第1章 信号及其描述
第3节 傅立叶变换与瞬变非周期信号的连续频谱
表1-3 傅立叶变换的主要性质
x 2 (t)dt
能量信号 能量有限信号
功率信号 功率有限信号
1 t2 x 2 (t)dt
t2 t1 t1
3
第1章 信号及其描述
1.1.1 信号的分类
电压信号x(t)加到R=1的电阻上，其瞬时功 率对时间积分就是信号在该积分时间内的能 量。
注意：信号的功率和能量未必具有真实的量 纲。
a
n

jbn
机械工程测试技术基础(第三版)段富海-第一章

机械工程测试技术基础(第三版)段富海-第一章

数据分析和报告
分析测试结果、撰写测试报告，为产品改进提 供决策依据。
执行和监控
执行测试方案并监控测试过程，及时发现问题 并进行修正。
持续学习和改进
不断学习新的测试技术和方法，推动测试工作 的改进和创新。
测试流程
1
需求分析
分析产品需求，明确测试目标和测试要
测试计划
2
求。
制定测试计划，确定测试方法和测试资
源。
3
测试执行
按照测试计划执行测试，收集测试数据。
数据分析
4
对测试数据进行分析，评估产品性能和
可靠性。
5
测试报告
撰写测试报告，总结测试结果和问题。
改进措施
6
提出产品改进建议，优化产品设计和制 造。
数据分析和解释
通过数据分析和解释，我们可以深入了解产品的性能特点和问题所在，为产品改进提供指导和决策依据。
测试范围和限制
1 范围明确
明确测试的范围和测试对 象，确保测试结果的可靠 性。
2 资源限制
受限于测试设备、时间和 人力资源等因素，测试工 程师需要合理利用资源。
3 技术限制
某些测试方法和技术在特 定场景下可能存在一定限 制，需要综合考虑。
机械工程测试技术基础 (第三版)段富海-第一章
介绍机械工程测试的基本概念和方法，探讨测试的重要性、测试工程师的角 色、测试流程以及数据分析和解释的重要性。
本书概述
深入讲解机械工程测试的核心理论和应用技术，帮助读者全面了解测试的概念、目的和方法，为工程实践提供 可靠的测试技术支持。
技术测试的重要性
1 提高产品质量
通过测试，发现产品的问 题和缺陷，进一步改进和 提升产品质量。

[工学]机械工程测试技术基础第三版课后答案全集

机械工程测试技术基础习题解答第一章信号的分类与描述1-1 求周期方波(见图1-4)的傅里叶级数(复指数函数形式)，划出|c|–ω和φ–nnω图，并与表1-1对比。

x(t)ATT00 … … ,22t 0 T ,T00-A图1-4 周期方波信号波形图解答:在一个周期的表达式为T,0,,,,At (0),,2xt(),. ,T0, (0)At,,,,2积分区间取(-T/2，T/2)TT000111,,,jntjntjnt,,,22000cxtetAetAet,,()d=d+dTTn0,,,0,0,TTT20002A,jnn,,, =(cos-1) (=0, 1, 2, 3, )n,所以复指数函数形式的傅里叶级数为,,A1jntjnt,,00 ，。

,,,,,n=0, 1, 2,3, ,,,xtcejne()(1cos),,n,nnn,,,,,,A,(1cos),cn,,,,nI (=0, 1, 2, 3, )n,,, n,,,0c,nR,,2A n ,,,,1,3,,A,22,cccn ,，,,,(1cos) ,n,nnRnIn,,00,2,4,6, n,,,,,π,,,，，，n1,3,5,,2,cπ,nI arctan1,3,5,φ,,,,,,n,nc2nR,00,2,4,6,n,,,,,,,没有偶次谐波。

其频谱图如下图所示。

| |cnφn2A/π 2A/ππ/2ω 5ω 3ω0002A/3π 2A/3π 2A/5π 2A/5π -5ω -3ω ω -ω000-π/2 ω -5ω -3ω -ω ω 3ω 5ω 000000幅频图相频图周期方波复指数函数形式频谱图1-2 求正弦信号的绝对均值和均方根值。

xtx()sin,ωtμx0rmsx解答:TTTT2242xxxx11000022μ,,,,,,,xttx()dsindsindcosωttωttωt0x,,,0000TTTTωTωπ2TTTxx111cos2,ωt22200 xxttx,,,,()dsinddωtttrms0,,,000TTT22,at 1-3 求指数函数的频谱。

机械工程测试技术基础课后习题及答案详解

第一章 信号的分类与描述1-1 求周期方波（见图1-4）的傅里叶级数（复指数函数形式），划出|c n |–ω和φn –ω图，并与表1-1对比。

解答：在一个周期的表达式为00 (0)2() (0)2T A t x t T A t ⎧--≤<⎪⎪=⎨⎪≤<⎪⎩ 积分区间取（-T/2，T/2）000000002202002111()d =d +d =(cos -1) (=0, 1, 2, 3, )T T jn tjn tjn t T T n c x t et Aet Ae tT T T Ajn n n ωωωππ-----=-±±±⎰⎰⎰所以复指数函数形式的傅里叶级数为 001()(1cos )jn tjn t n n n Ax t c ejn e n∞∞=-∞=-∞==--∑∑ωωππ，=0, 1, 2, 3, n ±±±。

(1cos ) (=0, 1, 2, 3, )0nI nR A c n n n c ⎧=--⎪±±±⎨⎪=⎩ππ21,3,,(1cos )00,2,4,6,n An A c n n n n ⎧=±±±⎪==-=⎨⎪=±±±⎩πππ1,3,5,2arctan1,3,5,200,2,4,6,nI n nRπn c πφn c n ⎧-=+++⎪⎪⎪===---⎨⎪=±±±⎪⎪⎩没有偶次谐波。

其频谱图如下图所示。

图1-4 周期方波信号波形图1-2 求正弦信号0()sin x t x ωt =的绝对均值x μ和均方根值rms x 。

解答：00002200000224211()d sin d sin d cos TTT Tx x x x x μx t t x ωt t ωt t ωt T T TT ωT ωπ====-==⎰⎰⎰222200rms0000111cos 2()d sin d d 22T T Tx x ωtx x t t x ωt t t T T T-====⎰⎰⎰1-3 求指数函数()(0,0)at x t Ae a t -=>≥的频谱。

机械工程测试技术基础【第三版,机械工业出版社】课后习题答案

机械工程测试技术基础 第三版-------机械工业出版社信号及其描述习题1.1求周期方波（图1-4）的傅立叶级数（复指数函数形式）。

画出频谱图|C n |—ω ；φn —ω 图并与表1-1对比。

解：傅立叶级数的复指数形式表达式：⋅⋅⋅±±±==∑+∞-∞=,3,2,1,0;)(0n eC t x n tjn nω式中：所以：幅值频谱：相位频谱：傅立叶级数的复指数形式的幅值频谱图和相位频谱都是双边频谱图。

1.2求正弦信号 x (t )=x 0sin ωt 的绝对均值μ|x |和均方根值x rms解：[]()⎪⎩⎪⎨⎧⋅⋅⋅±±±=⋅⋅⋅±±±=-=--=+⨯+-=⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡--=⎥⎦⎤+⎢⎣⎡-==---------⎰⎰⎰,6,4,2;0,5,3,1;2cos 12111)(1)(1200002002002022000000000000n n n A j n n A j e e n jA n jA e jn A T e jn A T dt Ae dt e A T dt e t x T C jn jn T t jn T t jn T t jn T t jn T T t jn n πππππωωππωωωωω⋅⋅⋅±±±±=⎪⎭⎫ ⎝⎛-=∑+∞-∞=,7,5,3,1;2)(0n en A j t x t jn n ωπ⋅⋅⋅±±±==+=,5,3,1;222n n A C C C nI nR n π⎪⎩⎪⎨⎧⋅⋅⋅---=⋅⋅⋅=-=⎪⎪⎪⎪⎭⎫⎝⎛-==,5,3,1;2,5,3,1;202n n n A arctg C C arctg nR nI n πππϕωππωμ2;2sin 1)(lim 0000000====⎰⎰∞→T x tdt x T dt t x T T T x 式中：110220x T T1.3求指数函数 的频谱。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

3.能量信号和功率信号 不考虑量纲，把信号x(t)的平方及其对时间
的积分分别称为信号的功率和能量。
功率：x 2 ( t ) 能量： x 2 (t )dt
当满足： x2(t)dt 认为信号的能量是有限的，称为能量有限
信号，简称能量信号。如：矩形脉冲信号、衰 减指数函数等。
a
DATE: 2020/8/72020/8/72020/8/10
产生。即给一个时间，就可确定一个相应的函数值， 如压电晶体受力作用产生电荷输出，电容极间距变化 产生电容变化输出。又分为周期信号和非周期信号。
周期信号：按一定时间间隔周而复始地重复出现， 无始无终的信号。
有明确数学关系，有周期
a
DATE: 2020/8/72020/8/72020/8/10
PAGE: 3
第一节 信号的分类与描述
例：集中参量的单自由度系统做无阻尼自由振动
x(t) x0 sin
kt m
0
T0 2/ k m
0
a
DATE: 2020/8/72020/8/72020/8/10
PAGE: 4
第一节 信号的分类与描述
复杂
x(t)sin0t1 2sin30t1 4sin50t x(t)sin80t3sin100t5sin120t.....
PAGE: 6
第一节 信号的分类与描述
瞬变非周期信号是一些或在一定时间区间内存 在，或随着时间的增长而衰减至零的信号。
x(t)x0 e tsin 0 t (0)
弹簧振子+阻尼 衰减到零
a
DATE: 2020/8/72020/8/72020/8/10
PAGE: 7
第一节 信号的分类与描述
②非确定性信号（随机信号）
第一章 信号及其描述
第一节 信号的分类与描述 第二节 周期信号与离散频谱 第三节 瞬变非周期信号与连续频谱 第四节 随机信号
本章内容： 信号分解——傅立叶级数、傅立叶变换; 信号分解后描述——频谱图，将信号在时域
中的描述转变为频率中的描述。
a
DATE: 2020/8/72020/8/72020/8/10
x(t) x(t nT0 )
x(t
)
A
A
0 t T0 2
T0 t 0 2
时域方波信号
a
DATE: 2020/8/72020/8/72020/8/10
PAGE: 13
第一节 信号的分类与描述
x (t)4 A sin0 t 1 3 sin 30 t 1 5 sin 50 t ...
a
DATE: 2020/8/72020/8/72020/8/10
PAGE: 12
第一节 信号的分类与描述
二、信号的时域描述和频域描述
信号的时域描述反映信号幅值随时间变化的关 系，不能明显揭示信号的频率组成关系。
为研究信号的频率结构和各频率成分的幅值、 相位关系，把信号的时域描述通过适当方法变成信 号的频域描述，即以频率为独立变量来表示信号。
不能用明确的数学关系来描述，只能用概率、 数理统计的方法来描述，如干扰噪声。
③复合信号：确定性信号+随机信号
测试技术任务之一就是从噪声信号（随机信号） 的背景下，提取我们感兴趣的信号（确定性信号）。
2.连续信号和离散信号
若信号数学表示式中的独立变量取值是连续 的，则成为连续信号，否则是离散信号。
a
DATE: 2020/8/72020/8/72020/8/10
PAGE: 11
第一节 信号的分类与描述
若信号在区间（-∞，∞）的能量是无限的
x2(t)dt
但它在有限区间（t1，t2）的平均功率是有限的
1 t2 x2(t)dt
t2 t1 t1
称这种信号为功率有限信号，或功率信号 图1-1是功率有限信号，图1-2是能量有限信号。
注意：信号的功率和能量，未必有真实的相应量纲
2
3
(b ) f(t) [sin (t/6 )]2
(c )
f(t) [c o s(2t)]u (t)
u (t )
1, t
0,
t
0 0
(d ) f(t) s in0 t s in20 t
cos212sin2
a
DATE: 2020/8/72020/8/72020/8/10
PAGE: 10
第一节 信号的分类与描述
PAGE: 8
第一节 信号的分类与描述
若独立变量和幅值均取连续值的信号称为模拟 信号。
若离散信号的幅值也是离散的，则称为数字信 号。
a
DATE: 2020/8/72020/8/72020/8/10
PAGE: 9
第一节 信号的分类与描述
思考题
判断下列每个信号是否是周期的，如果是确定其最
小周期。
(a ) f(t) 2 c o s(3 t/4 )
PAGE: 1
第一节 信号的分类与描述
通过传感器及测量电路，将被测非电量转变成 电信号，如电压、电流信号，这些信号便于观察、 记录和分析。在这些信号中包含有多种信息，如机 床振动信号就包含幅值、频率和相位等信息。信号 形式是多种多样的，从不同的角度有不同的分类方 法。在动态测试中，信号可作为时间函数来讨论。
其频率比为有理数，所以是周期函数，周期的确定 是根据各频率值最大公约数的倒数来确定。
x(t)sint1sin3t1sin5t 24
2 1.128
1
f(x) 0
1 1.128
2 0 0
5 x
10 12.56
a
DATE: 2020/8/72020/8/72020/8/10
PAGE: 5
第一节 信号的分类与描述
非周期信号：有明确数学关系，无周期。非周 期信号又有准周期信号和瞬变非周期信号。
准周期信号是由两种以 上的周期信号合成的， 但其组成分量间无法找 到公共周期，因而无法 按一定时间间隔周而复 始地重复出现。
x(t)sintsin 2t
2 2
1
x(t) 0
1
1.993 2 0 0
20
40
60
t
60
a
DATE: 2020/8/72020/8/72020/8/10
一、信号分类
1.确定性信号、非确定性信号（随机信号）
按信号随时间变化的规律划分为确定性信号和 非确定性信号。
a
DATE: 2020/8/72020/8/72020/8/10
PAGE: 2
x (t) x (t n0 )T(n 1 ,2 ,3 , )
第一节 信号的分类与描述
①确定性信号： 可以用明确的数学关系来描述，在实验上可重复