当前位置：文档之家 › 机械工程测试技术基础PDF版课件1

机械工程测试技术基础PDF版课件1

  • 格式：pdf
  • 大小：489.81 KB
  • 文档页数：31

下载文档原格式

  / 31

合集下载

机械工程测试技术课件整理版

机械工程测试技术课件整理版

当ω=0 X(ω)=A/α ω→+∞ X(ω) →+0 ω→-∞ X(ω) →-0
Φ(ω)=0 Φ(ω) →- π/2 Φ(ω) → +π/2
三、几种典型信号的频谱
1、矩形窗函数的频谱
1 t 0
t t T 2 T 2
W f t e

j 2 ft
3 两个极端发展
• 两个极端就是指相对于现在测量尺寸的大尺寸和小尺寸。 通常尺寸的测量已被广为注意，也开发了多种多样的测试 方法。近年来，由于国民经济的快速发展和迫切需要，使 得很多方面的生产和工程中测试的要求超过了我们所能测 试的范围，如飞机外形的测量、大型机械关键部件测量、 高层建筑电梯导轨的准直测量、油罐车的现场校准等都要 求能进行大尺寸测量；微电子技术、生物技术的快速发展， 探索物质微观世界的需求，测量精度的不断提高，又要求 进行微米、纳米测试。纳米测量也多种多样，有光干涉测 量仪、量子干涉仪、电容测微仪、X射线干涉仪、频率跟 踪式法珀标准量具、扫描电子显微镜(SEM)、扫描隧道显 微镜(STM)、原子力显微镜(AFM)、分子测量机 M3(molecular measuring machine)等。
t 2 t1

2
t1
x (t )dt
则称为功率信号。
二 信号的时域和频域描述 • 时域描述以时间t为独立变量的，直接观测 或记录到的信号。信号时域描述直观地出 信号瞬时值随时间变化的情况。 • 频域描述信号以频率f为独立变量的，称为 信号的。频域描述则反映信号的频率组成 及其幅值、相角之大小。 • 时域描述和频域描述为从不同的角度观察、 分析信号提供了方便。运用傅里叶级数、 傅里叶变换及其反变换，可以方便地实现 信号的时、频域转换。

机械工程测试技术基础

机械工程测试技术基础

机械⼯程测试技术基础第⼀章：概述本系列实验课程是组成课程的重要环节，是理论课程的补充和完善。

能够引导学⽣在科学实验的实践中，掌握⼀些基本的实验技能与实践⽅法，在安排实验时重点突出了学⽣动⼿能⼒、分析判断问题的能⼒以及解决问题的能⼒的培养。

在实验过程中，学⽣可以通过更直观的⽅法，了解理论课程中的⼀些知识点，不但加深对理论知识的理解和认识，同时，培养了学⽣求真务实的思想作风，以及理论联系实际的科学态度，提⾼了学⽣的综合素质，为学⽣的就业，创业奠定了⼀定的基础。

本系列实验是根据理论教学的顺序⽽设⽴的，且实验的安排也是根据理论教学的顺序和要求安排的。

既注重了理论知识点的实验，⼜注重了这些知识点的联系，本系列实验所使⽤的测试仪器设备的选择⽐较典型。

通过实验让学⽣掌握了机械⼯程测试⽅法和⼿段，对学习和掌握其它专业课程知识具有积极的作⽤。

1第⼆章：实验要求及注意事项1．实验前要认真复习有关理论知识、详细阅读实验指导书。

预习有关测量⽅法；步骤以及有关测试实验设备的使⽤⽅法。

针对不同的实验列出实验的实验⼤纲，并结合理论知识分析判断实验过程中出现的问题。

2．严格按照实验室管理规定执⾏。

3．严格按照仪器设备的操作规程操作。

4．按照实验指导完成接线后经⽼师检查同意⽅可进⾏实验。

5．实验过程中遇到问题不要擅⾃处理，请指导⽼师解决。

6．实验完毕，整理实验设备、设施，搞好实验室卫⽣。

2第三章：实验项⽬实验⼀：信号的合成与分解实验⼀、实验⽬的：1．掌握利⽤傅⽒级数谐波分析的⽅法2．学习和掌握不同频率的正弦波相位差是否为零的鉴别和测试⽅法。

3．掌握带通滤波器的有关特性测试。

4．全⾯了解波形分析与合成的原理。

⼆、实验属性：本实验为验证性实验。

三、实验仪器：1．XPF-4型谐波分析实验仪。

2．晶体管毫伏表3．双踪⽰波器四、实验要求：1．实验前认真收集资料，复习有关电⼦测量的⽅法，仪器使⽤⽅法，复习锯齿波、⽅波和频谱分量。

2．实验中应精⼼操作仪器，结合实验指导书完成每⼀实验步骤，对实验中出现的问题要认真分析。

机械工程测试技术基础PDF版课件1

机械工程测试技术基础PDF版课件1

第四章、测试信号调理技术
4.2 信号放大
分类
直流放大器 交流放大器 放大器 直流电桥 交流电桥 电荷放大器 特点 低频保留,高频截止 高频保留,低频截止
4.2 信号放大电路
1 直流放大电路
1) 反相放大器 电压增益:
RF Av = − R1
反馈电阻RF值不能太大，否则会产生较大的 噪声及漂移，一般为几十千欧至几百千欧。R1的 取值应远大于信号源Ui的内阻。
4.3调制与解调
3 幅度调制
调幅是将一个高频正弦信号（或称载波）与 测试信号相乘，使载波信号幅值随测试信号的变 化而变化．
y (t ) = [ A0 * x(t )] cos(2πft + φ )
调制
放大
缓变信号
高频信号
放大高 频信号
解调
放大缓 变信号
4.3调制与解调 幅度调制与解调过程（波形分析）
z(t)
0 t
4.3调制与解调 a) 幅度凋制(AM)
y (t ) = [ A * x(t )] cos(2πft + φ )
b) 频率调制(FM)
y(t) = Acos(2π[ f0 + x(t)]*t + φ)
c) 相位调制(PM)
y (t ) = A cos(2πft + [φ0 + x(t )])
y (t ) = A cos(2π [ f 0 + x(t )] * t + φ )
4.3调制与解调
4.3调制与解调
鉴频：
T2
T4
T1 F
T3
4.3调制与解调
优点：抗干扰能力强。
因为调频信号所携带的信息包含在频率变化 之中，并非振幅之中，而干ຫໍສະໝຸດ 波的干扰作用则主 要表现在振幅之中．

机械工程测试技术基础教学PPT

机械工程测试技术基础教学PPT
测量的基础知识
#2022
*
测量的基础知识
基本量和导出量 基本量： 长度、质量、时间、温度、电流、发 光强度、物质的量 导出量：由基本量按一定函数关系来定义的
*
测量的基础知识
3、基准与标准
基准：用来保存、复现计量单位的计量器具，是最高准确度的计量器具。 国家基准、副基准和工作基准 计量标准：用于检定工作计量器具的计量器具 工作计量器具是指用于现场测量而不用检定工作的计量器具。
物质所固有，客观存在或运动状态的特征 非物质，不具有能量，传输依靠物质和能量
*
四、测试技术的内容
测试技术的内容 测量原理：实现测量所依据的物理、化 学、生物等现象及有关定律。 测量方法：分为直接或间接测量、接触 或非接触测量、破坏或非破坏测量 测量系统 数据处理
*
测试过程：首先利用酒精（敏感元件）检测出被测对象温度变化并将其转换成自身体积的变化（热胀冷缩），然后经过等截面的中空玻璃管（中间变换器）再转换成高度的变化（分析处理），最后由外面的刻度线显示出测试结果（显示、记录）并提供给观察者或输入后续的控制系统。
*
教材、参考书与课时安排 教材 机械工程测试技术基础(第3版) 熊诗波 黄长艺编著 机械工业出版社 测试技术与信号处理 郭迎福，焦锋，李曼主编 中国矿业大学出版社 课时安排 授课 ：36学时 实验 ：4学时
教材、参考书与课时安排
*
教学目的和要求 测试技术是工科院校机械类各专业本科生一门重要的技术基础课，内容包括传感器、测量电路、测试系统的特性，信号分析与数据处理 。 通过本课程的学习： 掌握传感器的原理、特点及应用，常用测试系统和测量电路以及信号分析的基本原理和分析方法。为后续课程打好基础。
领域：工业、农业、航天、军事等

机械工程测试技术基础

机械工程测试技术基础
类： 包括性能测试、 可靠性测试、安
全性测试等。
测试技术的应用： 广泛应用于汽车、 航空、航天、机 械制造等领域。
古代：手工测量经验判断 近代：仪器测量数据记录 现代：计算机辅助测试自动化测试 未来：智能化测试远程测试大数据分析
传感器：用于采集 被测对象的物理量
数据采集系统：用 于将传感器采集到 的信号转换为数字 信号
温度传感器：通过热敏电阻或热电 偶等元件测量温度变化广泛应用于 工业、医疗等领域。
流量传感器：通过电磁感应或超声 波等原理测量流体流量广泛应用于 供水、供气等领域。
添加标题
添加标题
添加标题
添加标题
压力传感器：通过压敏电阻或压电 晶体等元件测量压力变化广泛应用 于液压、气动等领域。
加速度传感器：通过压电晶体或电容 式等元件测量加速度变化广泛应用于 汽车安全、航空航天等领域。
数据处理系统：用 于对采集到的数据 进行处理和分析
显示系统：用于显 示测试结果和图表
信号及其描述
信号的定义：信号是信息的载体是物理量随时 间变化的过程
信号的分类：根据信号的性质和特点可以分为 连续信号和离散信号
连续信号：信号的取值是连续的如正弦波、三 角波等
离散信号：信号的取值是离散的如数字信号、 脉冲信号等
实时化：测试技 术将更加实时化 能够实时监测和 预警设备状态
绿色化：测试技 术将更加绿色化 减少对环境的影 响提高能源利用 效率
智能化：测试技术将更加智能化能够自动识别和诊断机械故障 集成化：测试技术与其他技术如物联网、大数据等更加紧密地集成提高测试效率和准确性 实时化：测试技术将更加实时化能够实时监测和预警机械设备的运行状态 绿色化：测试技术将更加注重环保和节能降低机械设备的能耗和污染排放

机械工程测试技术课件整理版

机械工程测试技术课件整理版
机械工程测试技术课件 整理版
,
汇报人：
目录
01 添 加 目 录 项 标 题 03 机 械 工 程 测 试 系 统
组成
05 机 械 工 程 测 试 技 术 实例分析
02 机 械 工 程 测 试 技 术 概述
04 机 械 工 程 测 试 技 术 原理
06 机 械 工 程 测 试 技 术 发展趋势与展望
压力测试原理
压力测试的定义：通过施加压力来 检测机械设备的性能和稳定性
压力测试的方法：包括静态压力测 试和动态压力测试
添加标题
添加标题
添加标题
添加标题
压力测试的目的：确保机械设备在 正常工作条件下能够承受压力避免 故障和损坏
压力域
流量测试原理
传感器是机械工程测试系统 的重要组成部分
传感器的种类繁多包括温度 传感器、压力传感器、流量
传感器等
传感器的性能直接影响测试 系统的精度和稳定性
信号处理装置
功能：对采集到的信号进行处理和分析 组成：包括信号放大器、滤波器、/D转换器等 工作原理：将模拟信号转换为数字信号并进行滤波、放大等处理 应用：广泛应用于各种机械工程测试系统中如振动测试、噪声测试等
新型传感器技术发展与应用
传感器技术发展 趋势：智能化、 微型化、集成化
新型传感器技术 应用领域：汽车 电子、医疗电子、 工业自动化等
新型传感器技术 特点：高精度、 高灵敏度、高可 靠性
新型传感器技术发 展趋势：无线传感 器网络、物联网、 大数据分析等
虚拟仪器技术在机械工程测试中的应用与展望
虚拟仪器技术：利用计算机软件和硬件模拟真实仪器的功能 应用领域：机械工程测试、控制系统设计、数据分析等 发展趋势：智能化、网络化、集成化 展望：未来将更加广泛应用于机械工程测试提高测试效率和准确性

机械工程测试技术ppt

机械工程测试技术ppt


x(t )
n
C e
n

jn0t
n 0,1,2,3,
1 1 T2 Cn an jbn x(t )e jn0t dt 2 T T 2
Cn Cn e
jn
1 2 2 Cn an bn 2
bn n arctan an
n 各阶谐波分量的初相角。
1.2 周期信号与离散频谱
1.2.2 几点说明 1）满足狄里赫利条件的任何周期信号可分解成直流 分量及许多简谐分量的叠加，且这些简谐分量的角 频率必定是基波角频率的整数倍。各次谐波频率之 比必定是有理数。 信号的频率组成： {0 ,20 ,30 ,......} 例如： xt sin 2t sin 2t 准周期信号
x(t ) a0 an cos n0t bn sin n0t bn jn0t an jn0t jn0t jn0 t a0 ( e e ) j (e e ) 2 n 1 2 an jbn jn0t an jbn jn0t a0 e e 2 2 n 1
1.2 周期信号与离散频谱 4）物理意义：
A0、A1、…… An均为常数，称为谐波系数 n为从１到∞的正整数，称为谐波阶数 n ＝１时， A1为基波分量的幅值 为基波或一次谐波分量 A1 cos0t 1 n ＝2 时， A2为二次谐波分量的幅值 为二次谐波分量 A2 cos20t 2 2 0 为基波圆频率 0 2f 0 T f 0 为基波频率 T 为周期信号的周期
An
● ● ● ● ● ●
0 ω0(f0) 2ω0
(2f0)
ω(f)
1.2 周期信号与离散频谱

机械工程测试技术基础PPT(共41页)

机械工程测试技术基础PPT(共41页)

！！！
x t a 0 n 1 1 2 a n jn b e j n 0 t 1 2 a n jn b e j n 0 t
实频谱、虚频谱 余弦函数
正弦函数
！！！
！！！
由于
0
2
T0
当 T 0 趋于无穷 时，频率间隔 成为 d，
离散谱中相邻的谱线紧靠在一起，n0 成为连续变
量，求和符号 就变为积分符号 ，则

且有
A na n 2 b n 2
tg n
an bn
*
xta0 A nco n s0tn
0
注意此二 式的区别
且有
A na n 2 b n 2
tg n
bn an
P 22-23
算例：求右图周期性三角波的傅立叶级数
解：在x(t)的一个周期中可表示为X(t)
xt
A A
2A T0 2A
t t
T0 t 0 2
xt d x t ejtdtejt
2
1 x t ejtdtejtd
2
这就是傅立叶积分
二、傅立叶变换的主要性质(P 30) 熟悉傅立叶变换的性质的重要意义 简化作用,推广于复杂复杂情况！！！
第2章 测试装置的基本特性
§2.1 概述 §2.2 测试装置的静态特性 §2.3 测试装置动态特性的数学描述 §2.4 测试装置对任意输入的响应 §2.5 实现不失真测试的条件 §2.6 测试装置动态特性的测试
0 t T0
t
T 0
2
常值分量
1 T0
a0
T0
x 2
T0
t
dt
2
2 T0
T0 2
0
A

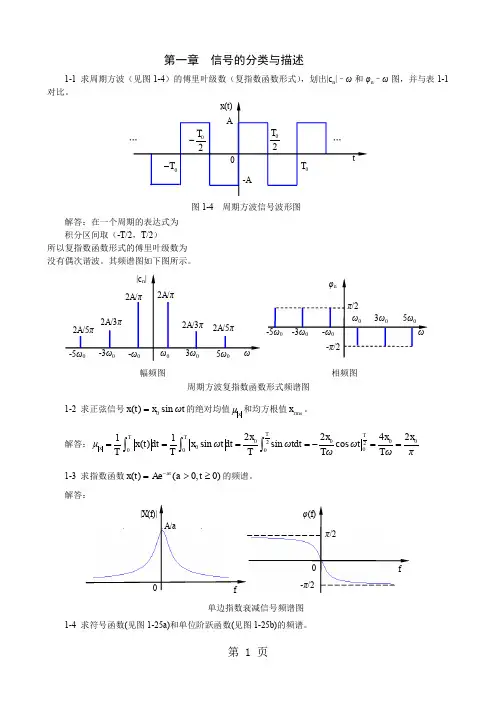
机械工程测试技术基础共19页word资料

机械工程测试技术基础共19页word资料

第一章 信号的分类与描述1-1 求周期方波（见图1-4）的傅里叶级数（复指数函数形式），划出|c n |–ω和φn –ω图，并与表1-1对比。

解答：在一个周期的表达式为 积分区间取（-T/2，T/2）所以复指数函数形式的傅里叶级数为 没有偶次谐波。

其频谱图如下图所示。

1-2 求正弦信号0()sin x t x ωt =的绝对均值x μ和均方根值rms x 。

解答：00002200000224211()d sin d sin d cos TTT Tx x x x x μx t t x ωt t ωt t ωt T T TT ωT ωπ====-==⎰⎰⎰1-3 求指数函数()(0,0)atx t Ae a t -=>≥的频谱。

解答：1-4 求符号函数(见图1-25a)和单位阶跃函数(见图1-25b)的频谱。

单边指数衰减信号频谱图A /aπ/2-π/2幅频图相频图周期方波复指数函数形式频谱图图1-4 周期方波信号波形图a)符号函数的频谱t =0处可不予定义，或规定sgn(0)=0。

该信号不满足绝对可积条件，不能直接求解，但傅里叶变换存在。

可以借助于双边指数衰减信号与符号函数相乘，这样便满足傅里叶变换的条件。

先求此乘积信号x 1(t)的频谱，然后取极限得出符号函数x (t )的频谱。

b)阶跃函数频谱在跳变点t =0处函数值未定义，或规定u (0)=1/2。

阶跃信号不满足绝对可积条件，但却存在傅里叶变换。

由于不满足绝对可积条件，不能直接求其傅里叶变换，可采用如下方法求解。

解法1：利用符号函数结果表明，单位阶跃信号u (t )的频谱在f =0处存在一个冲激分量，这是因为u (t )含有直流分量，在预料之中。

同时，由于u (t )不是纯直流信号，在t =0处有跳变，因此在频谱中还包含其它频率分量。

解法2：利用冲激函数 根据傅里叶变换的积分特性单位阶跃信号频谱f|U (f )|(1/2)1()sgn()at x t e t -=符号函数tx 1(t ) 01-1符号函数频谱图1-25 题1-4图a)符号函数b)阶跃函数1-5 求被截断的余弦函数0cos ωt (见图1-26)的傅里叶变换。

机械工程测试技术基础 _第三版_第一章

机械工程测试技术基础 _第三版_第一章

30
第四节 随机信号
二、随机信号的主要特征参数
1、 均值、方差和均方值 均值表示信号的常值分量
方差描述随机信号的波动分量。
均方值描述随机信号的强度。
31
第四节 随机信号
二、随机信号的主要特征参数
2、 概率密度函数 随机信号的概率密度函数是表示信号幅值落在指定区间的概率。如图1-22所示。
图1-22
一、概述
随机信号是不能用确定的数学关系式来描述的，不能预测其未来的任何瞬时值。 任何一次观测值只代表在其变动范围中可能产生的结果之一，但其值的变动服 从统计规律。 随机过程与样本函数如图1-21所示。
图1-21
29
第四节 随机信号
二、随机信号的主要特征参数
1） 均值、方差和均方值 2） 概率密度函数 3） 自相关函数 4） 功率谱密度函数
图1-3
4
第一节 信号的分类与描述
一、信号的分类
3.能量信号和功率信号 当电压信号满足一定条件时：则认为信号的能量是有限的，并称之为能 量有限信号。简称能量信号。 若信号在区间（- ∞ ， ∞ ）的能量是无限的，但它在有限区间的平均功
率是有限的。这种信号称为功率有限信号，或功率信号。



x 2 (t )dt
通常所说的非周期信号是指瞬变非周期信号如图1-11所示。图1-11a为矩 形脉冲信号，图1-11b为指数衰减信号，图1-11c为衰减振荡，图1-11d为 单一脉冲。
图1-11
14
第三节 瞬变非周期信号与连续频谱
一、傅里叶变换
图1-11 非周期性信号
15
第三节 瞬变非周期信号与连续频谱
一、傅里叶变换
图1-7
9

机械工程测试技术基础

机械工程测试技术基础

机械工程测试技术基础
机械工程测试技术基础是针对机械工程中的实验试验和设备检测技术的基本知识。

它主要包括测量原理、测量方法、试验技术、装置和设备等内容。

通过机械工程测试技术的基础知识学习，可以帮助人们更深刻的理解实际的机械工程测试技术，以便在后续的工作中能够更准确的判断出机械设备的参数和性能特点，有效提高设备制造和使用的质量和效率。

同时还可以为机械工程试验过程及结果的分析提供正确的理论依据，并对机械设备的安全性、稳定性和可靠性提供可靠的保证。

机械工程测试技术基础ppt

机械工程测试技术基础ppt
因而可确定其任何时刻的量值。 随机信号：具有不能被预测的特性，无法用数
学关系式来描述，只能(zhī nénɡ)通过统计 观察来加以描述的信号。
第三页，共71页。
确定性信号又分为(fēn wéi)周期信号和非周期信 号。
周期信号： 定义：满足下面关系式的信号： x(t)=x(t+nT0)
式中，T0——周期。 非周期信号： 定义：不具有周期重复性的确定性信号。 非周期信号又可分成准周期信号和瞬态信号两类。
x (t ) X ( f ) e j 2ft df
(1-29)
这样(zhèyàng)就避免了傅里叶变换中出现1/2π,简化了公 式，且有
X ( f ) 2X ( )
第三十页，共71页。
非周期函数x（t）存在傅里叶变换的充分条件 是x（t）在区间(-∞, ∞)上绝对可积，即
但上述(shàngshùx)条(t件) 并dt非必要条件。因为
An
an2 bn2
tgn
an bn
n＝1,2, …
n
An称信号频率成分的幅值， 称初相角。
第二十页，共71页。
讨论：
式中第一项a0为周期信号中的常值或直流分量 ；
从第二项依次向下分别称信号的基波或一次谐波、二次谐波、三 次谐波、……、n次谐波 ；
将信号的角频率(pínlǜ)ω0作为横坐标，可分别画出信号幅值An
• 由于X(f)一般为实变量f的复函数，故可将其写为
•
X ( f ) X ( f ) e j ( f )
• 将上式中的 X (称f 非) 周期信号x(t)的连续幅值谱，
• (称f )x(t)的连续相位谱。
• 例题(lìtí)1－3，求矩形窗函数的频谱。
第三十二页，共71页。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

y (t ) = A cos(2π [ f 0 + x(t )] * t + φ )
4.3调制与解调
4.3调制与解调
鉴频：
T2
T4
T1 F
T3
4.3调制与解调
优点：抗干扰能力强。
因为调频信号所携带的信息包含在频率变化 之中，并非振幅之中，而干扰波的干扰作用则主 要表现在振幅之中．
缺点：占频带宽度大，复杂
调频波通常要求很宽的频带，甚至为调幅 所要求带宽的20倍；调频系统较之调幅系统复 杂，因为频率调制足一种非线性调制。
4.3调制与解调
案例：旋转机械扭距测量
4.3调制与解调
案例：铁路机车调度 信号检测
调制频率8.5Hz，绿灯 调制频率23.5Hz，红灯
x(t)
乘法器 乘法器 放大器 放大器
z(t)
x m(t)
乘法器 乘法器 滤波器 滤波器
x(t)
z(t)
4.3调制与解调 幅度调制与解调过程（频谱分析）
x(t)
乘法器 乘法器 放大器 放大器
z(t)
x m(t)
乘法器 乘法器 滤波器 滤波器
x(t)
z(t)
4.3调制与解调 幅度调制与解调过程（数学分析）
4.3调制与解调 实验：同步调治与解调实验 上述调制方法，将信号x(t)
直接与载波z(t)相乘．这种 调幅波具有极性变化，解调 时必须再乘与z(t)相位相同 的z’(t) 方能复原出原信 号，故称同步解调．
4.3调制与解调
非抑制调幅
若对信号x(t)进行偏置，叠加一个直流分量 D，使偏置后的信号都具有正电压。
4.3调制与解调 b)重叠失真：调幅波是由一对每边为fm的双边带信 号组成．当载波频率fz较低时，正频端的下边带将 与负频端的下边带相重叠．要求: fz＞fm
4.3调制与解调
4 频率调制
调频是利用信号x(t)的幅值调制载波的频 率，或者说，调频波是一种随信号x(t)的电压 幅值而变化的疏密度不同的等幅波.
4.3调制与解调
3 幅度调制
调幅是将一个高频正弦信号（或称载波）与 测试信号相乘，使载波信号幅值随测试信号的变 化而变化．
y (t ) = [ A0 * x(t )] cos(2πft + φ )
调制
放大
缓变信号
高频信号
放大高 频信号
解调
放大缓 变信号
4.3调制与解调 幅度调制与解调过程（波形分析）
RF Av = 1 + R1
R1一般取几十千欧。耦合电容C1、C3可根据交流 放大器的下限频率fL来确定。
C1 = C3 = (3 ~ 10) /(2πRL f L )
4.2 信号放大电路
3 直流电桥
R1 E R2 R3
●平衡条件
R1 R 3 = R 2 R 4
R4
V
R1 R3 − R2 R4 V = E ( R1 + R2 )( R3 + R4 )
4.2 信号放大电路 令：
R1 = R
R2 = R
R3 = R
R4 = R + dR
RR − R ( R + dR ) V = E ( R + R )( R + R + dR )
E dR = − ⋅ 4 R
4.2 信号放大电路
4 交流电桥
传感器
传感器
●平衡条件 电感
Z1 Z 3 = Z 2 Z 4
第五章、测试信号调理技术 先将微弱的缓变信号加载到高频交流信号中 去，然后利用交流放大器进行放大，最后再从放大 器的输出信号中取出放大了的缓变信号。 例：交流电桥
R1 Vin R2 R3
Vo
R4
4.3调制与解调
2 种类
x(t) 调制信号
0 t
载波信号
z (t ) = A cos(2πft + φ )
x(t ) x' (t ) = D + x(t )
xm (t ) = [ D + x(t )] cos(2πft )
4.3调制与解调
调幅
4.3调制与解调
解调
二极管Байду номын сангаас波
低通滤波
4.3调制与解调
调幅波的波形失真
a）过调失真：对于非抑制调幅，要求其直流偏 置必须足够大，否则x(t)的相位将发生180。
工程测试技术基础
第四章、测试信号调理技术
本章学习要求：
1.了解模拟信号放大电路原理 2.了解信号调制解调原理 3.了解信号滤波器工作原理
第四章、测试信号调理技术
4.1 信号调理的目的
信号调理的的目的是便于信号的传输与处理。 1.传感器输出的电信号很微弱，大多数不能 直接输送到显示、记录或分析仪器中去，需 要进一步放大，有的还要进行阻抗变换。 2.有些传感器输出的是电信号中混杂有干扰噪 声，需要去掉噪声，提高信噪比。 3.某些场合，为便于信号的远距离传输，需要 对传感器测量信进行调制解调处理。
x(t)
乘法器 乘法器 放大器 放大器
z(t)
x (t )
z (t )
x m(t)
xm (t ) = x(t ) • cos(2πf z t )
z (t )
z(t)
乘法器 乘法器 滤波器 滤波器
x(t)
y m (t ) = x (t ) cos 2πf z t
2
= x(t ) + 1 x(t ) cos(2π 2 f z t ) 2
烟雾报警器
酒精传感器
二氧化碳传感器
4.2 信号放大电路 2)同相放大器 同相放大器也是最基 本的电路 ，其闭环电压 增益Av为:
RF Av = 1 + R1
同相放大器具有输入阻抗非常高，输出阻 抗很低的特点，广泛用于前置放大级。
4.2 信号放大电路
2 交流放大电路
若只需要放大交流信号，可采用图示的集成 运放交流电压同相放大器。其中电容C1、C2及C3 为隔直电容。
电容
4.2 信号放大电路 电桥的接法：
单臂
半桥
全桥
4.2 信号放大电路
4 电荷放大器
q ≈ ei (C a + C c + C i ) + (ei − e y )C f
− Kq ey = (C + C f ) + KC f
+
F
第四章、测试信号调理技术
4.3调制与解调
1 目的 解决微弱缓变信号的放大以及信号 的传输问题。
第四章、测试信号调理技术
4.2 信号放大
分类
直流放大器 交流放大器 放大器 直流电桥 交流电桥 电荷放大器 特点 低频保留,高频截止 高频保留,低频截止
4.2 信号放大电路
1 直流放大电路
1) 反相放大器 电压增益:
RF Av = − R1
反馈电阻RF值不能太大，否则会产生较大的 噪声及漂移，一般为几十千欧至几百千欧。R1的 取值应远大于信号源Ui的内阻。
z(t)
0 t
4.3调制与解调 a) 幅度凋制(AM)
y (t ) = [ A * x(t )] cos(2πft + φ )
b) 频率调制(FM)
y(t) = Acos(2π[ f0 + x(t)]*t + φ)
c) 相位调制(PM)
y (t ) = A cos(2πft + [φ0 + x(t )])