(完整版)常用数学符号大全
- 格式:doc
- 大小:200.01 KB
- 文档页数:5
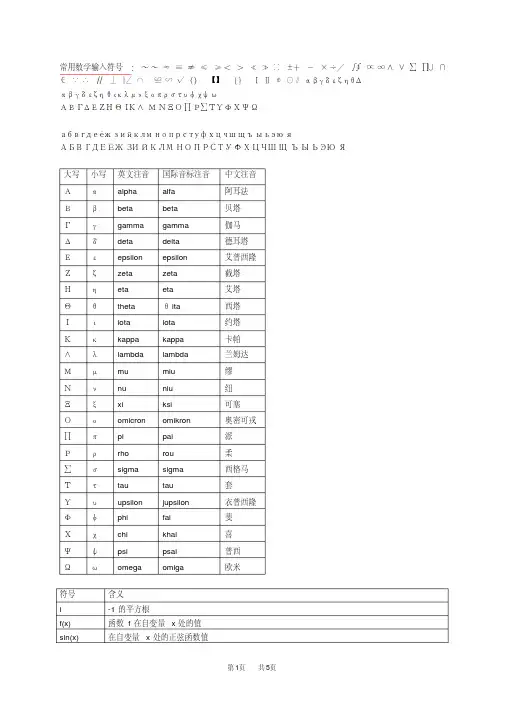
常用数学输入符号:~~≈≡≠ ∪∩ ∮∝∞ ∧∨∑∏ =≤≥ <>≮≯∷±+-×÷/∫ ∠⌒≌∽√()【】{}ⅠⅡ⊕⊙∥αβγδεζηθΔ∈∵∴//⊥‖ αβγδεζηθικλμνξοπρστυφχψωΑΒΓΔΕΖΗΘΙΚ∧ΜΝΞΟ∏Ρ∑ΤΥΦΧΨΩабвгдеёжзийклмнопрстуфхцчшщъыьэюяАБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ大写小写英文注音国际音标注音中文注音Ααalpha alfa 阿耳法Ββbeta beta 贝塔Γγgamma gamma 伽马Δδdeta delta 德耳塔Εεepsilon epsilon 艾普西隆Ζζzeta zeta 截塔Ηηeta eta 艾塔Θθtheta θita西塔Ιιiota iota 约塔Κκkappa kappa 卡帕∧λlambda lambda 兰姆达Μμmu miu 缪Ννnu niu 纽Ξξxi ksi 可塞Οοomicron omikron 奥密可戎∏πpi pai 派Ρρrho rou 柔∑σsigma sigma 西格马Ττtau tau 套Υυupsilon jupsilon 衣普西隆Φφphi fai 斐Χχchi khai 喜Ψψpsi psai 普西Ωωomega omiga 欧米符号含义i -1的平方根f(x) 函数f在自变量x处的值sin(x) 在自变量x处的正弦函数值exp(x) 在自变量x处的指数函数值,常被写作e xa^x a的x次方;有理数x由反函数定义ln x exp x 的反函数a x同a^xlog b a 以b为底a的对数;b log b a = acos x 在自变量x处余弦函数的值tan x 其值等于sin x/cos xcot x 余切函数的值或cos x/sin xsec x 正割含数的值,其值等于1/cos xcsc x 余割函数的值,其值等于1/sin xasin x y,正弦函数反函数在x处的值,即x = sin yacos x y,余弦函数反函数在x处的值,即x = cos yatan x y,正切函数反函数在x处的值,即x = tan yacot x y,余切函数反函数在x处的值,即x = cot yasec x y,正割函数反函数在x处的值,即x = sec yacsc x y,余割函数反函数在x处的值,即x = csc yθ角度的一个标准符号,不注明均指弧度,尤其用于表示atan x/y,当x、y、z用于表示空间中的点时i, j, k 分别表示x、y、z方向上的单位向量(a, b, c) 以a、b、c为元素的向量(a, b) 以a、b为元素的向量(a, b) a、b向量的点积a?b a、b向量的点积(a?b)a、b向量的点积|v| 向量v的模|x| 数x的绝对值Σ表示求和,通常是某项指数。

数学符号大全一、基础符号1. 数字:0、1、2、3、4、5、6、7、8、92. 加号:+3. 减号:-4. 乘号:×5. 除号:÷6. 等号:=7. 左括号:(8. 右括号:)9. 百分号:%二、数学运算符号1. 平方:²2. 立方:³3. 开平方根:√4. 开立方根:∛5. 阶乘:n!6. 绝对值:|x|7. 取整函数:⌊x⌋8. 取余函数:x mod y9. 英文逗号:,10. 圆周率:π11. 自然对数底数:e12. 函数符号:a. 一元函数:f(x)b. 多元函数:f(x, y, z)13. 向量符号:→14. 求和符号:∑15. 无穷大:∞16. 积分符号:∫17. 微分符号:d/dx三、代数符号1. 大于号:>2. 小于号:<3. 大于等于号:≥4. 小于等于号:≤5. 不等于号:≠6. 比例符号:∷7. 成比例符号:∝8. 幂符号:^9. 集合符号:a. 前者属于后者:∈b. 前者不属于后者:∉c. 子集:⊆d. 真子集:⊂e. 交集:∩f. 并集:∪10. 等价符号:≡11. 拉丁字母符号:a、b、c、…、x、y、z12. 希腊字母符号:a. α、β、γ、δ、ε、ζ、η、θ、ι、κ、λ、μ、ν、ξ、ο、π、ρ、σ、τ、υ、φ、χ、ψ、ωb. 大写字母:Α、Β、Γ、Δ、Ε、Ζ、Η、Θ、Ι、Κ、Λ、Μ、Ν、Ξ、Ο、Π、Ρ、Σ、Τ、Υ、Φ、Χ、Ψ、Ω13. 求导符号:f'(x) 或∂f/∂x四、几何符号1. 垂线符号:⊥2. 平行符号:∥3. 三角形:a. 各边长:a、b、cb. 各角度:α、β、γ4. 角度符号:a. 度数符号:°b. 弧度符号:rad五、统计符号1. 样本均值:x̄或 $\overline{x}$2. 总体均值:μ3. 样本方差:s²4. 总体方差:σ²5. 标准差:s6. 总体标准差:σ7. 协方差符号:cov8. 相关系数符号:r六、数学课程常用符号1. 代数符号:a. 复数:z = a + bib. 多项式:f(x) = anxn + an-1xn-1 + … + a1x + a02. 几何符号:a. 直线:ABb. 射线:OPc. 线段:PQd. 圆:Oe. 直角符号:∟3. 三角函数符号:a. 正弦:sinb. 余弦:cosc. 正切:tand. 余切:cote. 正割:secf. 余割:csc4. 对数符号:log5. 极限符号:lim6. 矩阵符号:a. 行列式符号:detb. 矩阵:A、B、C、D、E、…c. 矩阵乘法符号:× 或乘号d. 逆矩阵符号:A-17. 向量符号:a. 点积符号:·b. 叉积符号:×c. 向量长度:|v|8. 概率统计符号:a. 期望值:Eb. 方差:Varc. 标准差:SDd. 正态分布符号:N(μ,σ²)9. 微积分符号:a. 一元函数导数:f'(x) 或 dy/dxb. 一元函数微分:df/dxc. 一元函数微积分:∫f(x)dx 或∫dyd. 二元函数偏导数:i. ∂f/∂xii. ∂f/∂ye. 二元函数偏微分:i. ∂f/∂x ∂z/∂xii. ∂f/∂y ∂z/∂yiii. ∂f/∂x ∂z/∂yiv. ∂f/∂y ∂z/∂xf. 多元函数积分:∫∫f(x,y)dxdyg. 梯度符号:∇h. 散度符号:divi. 旋度符号:curl以上是数学符号的大全,不论是初学者或是专业人士都可以对这些符号进行了解,为以后的学习和工作提供便利。

常用数学符号大全1、几何符号ⅷⅶ↋ↆↄ△2、代数符号ⅴⅸⅹ~ⅼↅↇↈↃⅵↀ3、运算符号如加号(+),减号(-),乘号(³或²),除号(÷或/),两个集合的并集(ⅻ),交集(ⅺ),根号(ⅳ),对数(log,lg,ln),比(:),微分(dx),积分(ⅼ),曲线积分(ⅽ)等。
4、集合符号ⅻⅺⅰ5、特殊符号ⅲπ(圆周率)6、推理符号|a| ↂ△ⅶⅺⅻↅↆ±ↈↇⅰⅬⅭⅮⅯ↖↗↘↙ⅷⅸⅹ&; §←↑→↓↔↕↖↗ΓΔΘΛΞΟΠΣΦΧΨΩαβγδεδεζηθικλμνπξζηυθχψωⅠ Ⅱ Ⅲ Ⅳ Ⅴ Ⅵ Ⅶ Ⅷ Ⅸ Ⅹ Ⅺ Ⅻⅰ ⅱ ⅲ ⅳ ⅴ ⅵ ⅶ ⅷ ⅸ ⅹⅰⅱⅲ↚ⅳⅴⅵ↛ ⅶ↜ⅷⅸⅹⅺⅻⅼⅽⅾⅿↀↁↂↃↄ↝ↅↆↇↈ↞↟↉↊⊕↋↠℃指数0123:o1237、数量符号如:i,2+i,a,x,自然对数底e,圆周率π。
8、关系符号如“=”是等号,“Ↄ”是近似符号,“ↅ”是不等号,“>”是大于符号,“<”是小于符号,“ↈ”是大于或等于符号(也可写作“↉”),“ↇ”是小于或等于符号(也可写作“↊”),。
“Ⅾ ”表示变量变化的趋势,“ↂ”是相似符号,“ↄ”是全等号,“ⅷ”是平行符号,“”是垂直符号,“ⅴ”是成正比符号,(没有成反比符号,但可以用成正比符号配倒数当作成反比)“ⅰ”是属于符号,“??”是“包含”符号等。
9、结合符号如小括号“()”中括号“[]”,大括号“{}”横线“—”10、性质符号如正号“+”,负号“-”,绝对值符号“| |”正负号“±”11、省略符号如三角形(△),直角三角形(Rt△),正弦(sin),余弦(cos),x的函数(f(x)),极限(lim),角(ⅶ),ⅿ因为,(一个脚站着的,站不住)ⅾ所以,(两个脚站着的,能站住)总和(ⅲ),连乘(ⅱ),从n个元素中每次取出r个元素所有不同的组合数(C(r)(n) ),幂(A,Ac,Aq,x^n)等。

数学符号大全数学符号是数学语言的核心部分,它们用于表示数学概念、关系和操作。
以下是一些基本且常见的数学符号大全分类:1. 几何符号:-⊥(垂直符号)-∥(平行符号)-∠(角符号)-⌒(弧线或弧度符号)-⊙(圆的符号)-≡(恒等于或全等符号)-≌(几何图形全等符号)-△(三角形符号)-∽(相似符号)2. 代数符号:-∝(正比符号)-∧(逻辑与,集合论中的交集符号在特定上下文中)-∨(逻辑或,集合论中的并集符号在特定上下文中)- ~(同余或相关性符号,也可能表示逆元素或相似)-∫(积分符号)-≠(不等于符号)-≤(小于等于符号)-≥(大于等于符号)-≈(约等于或近似等于符号)-∞(无穷大符号)-∶(比例符号或比率)3. 集合符号:-∪(集合并运算符)-∩(集合交运算符)-∈(属于符号,表示元素属于某个集合)-∅(空集符号)4. 运算符号:- +(加号)--(减号或负号)-×或·(乘号)-÷或/(除号)-√(平方根符号)- ^ 或∙∙∙(幂运算符,例如a^2 表示a 的平方)- !(阶乘符号)-∑(求和符号,表示对一系列数进行求和)-π(圆周率)-∏(乘积符号,表示对一系列数进行连乘)5. 推理和逻辑符号:-⇒或→(蕴含符号)-⇔或↔(双箭头,表示逻辑上的等价)- ¬(逻辑非符号)-∀(全称量词,对于所有)-∃(存在量词,存在某一个)-⊢(推导出符号,表示从前提可以得出结论)-⊤和⊥(真和假命题符号,在逻辑学中使用)6. 其他符号:- lim(极限符号)-∂(偏导数符号)-Δ(增量或变化量符号)-θ、α、β、γ等希腊字母常用于数学表达式中的变量-⊂、⊃(子集和超集符号)-≡(定义或同构符号,在某些上下文中)以上列出的是许多常用的数学符号,实际数学领域中的符号远不止这些,还包括了更高级的分析、概率论、统计学、拓扑学以及其他分支学科中的特殊符号。

常用符号1、几何符号⊥:垂直于‖:平行于∠:角⌒:弧线或半圆⊙:圆≡、≌:全等于△:三角形2、代数符号∝:成正比∧、∨:逻辑与、逻辑或~:约等于∫:积分≠、≤、≥、≈:不等于、小于、大于、约等于∞:无穷大∶:比例3、运算符号×:乘号÷:除号√:平方根±:正负号4、集合符号∪:并集∩:交集∈:属于5、特殊符号∑:求和符号π:圆周率①②③…:序号符号ⅠⅡⅢ…:罗马数字αβγ…:希腊字母6、推理符号∴:所以∵:因为→:趋向于7、数学中的结合符号():小括号[]:中括号{}:大括号—:横线(用于表示范围或平均值等)8、数学中的性质符号+:正号-:负号| |:绝对值符号9、数学中省略符号△:表示三角形或表示变量增量Rt△:直角三角形sin、cos:正弦、余弦f(x):x的函数lim:极限∠:角10、货币符号$:美元¥:人民币€:欧元£:英镑¢:美分11、物理符号m:质量F:力v:速度a:加速度g:重力加速度h:高度ρ:密度λ:波长f:频率E:能量Φ:磁通量12、化学符号H₂O:水CO₂:二氧化碳HCl:氯化氢NaOH:氢氧化钠H⁺:氢离子OH⁻:氢氧根离子→:反应箭头⇌:可逆反应13、计算机符号#:井号$:美元符号%:百分号&:与符号*:星号@:在电子邮件地址中表示“at”\:反斜杠_:下划线14、逻辑与集合符号¬:逻辑非∧:逻辑与(AND)∨:逻辑或(OR)⊕:逻辑异或(XOR)∅:空集∁:补集∀:全称量词(对所有)∃:存在量词(存在)15、单位符号m:米kg:千克s:秒A:安培V:伏特W:瓦特K:开尔文mol:摩尔cd:坎德拉16、其他常用符号§:段落符号©:版权符号®:注册商标符号™:商标符号№:编号符号°:度(角度或温度)′:分(角度或时间)″:秒(角度或时间)17、音乐符号♩:全音符♬:八分音符♭:降号♯:升号♪:重复记号∩:连音记号⌒:连音线♫:音乐小节18、天文学符号☉:太阳符号♀:金星符号♁:地球符号♂:火星符号♃:木星符号♄:土星符号♅:天王星符号♆:海王星符号☽:月亮符号19、数学逻辑符号∃!:存在且唯一量词∄:不存在量词├:证明过程中“因为”的符号┴:证明过程中“所以”的符号≮:不小于≯:不大于⊂:真子集⊆:子集20、电子工程符号AC:交流电DC:直流电VCC:电源正极GND:地线或电源负极VDD:芯片工作电压VSS:芯片工作地电平RES:复位EN:使能CLK:时钟信号21、国际单位制(SI)前缀k:千(10^3)M:兆(10^6)G:吉(10^9)T:太(10^12)P:拍(10^15)E:艾(10^18)m:毫(10^-3)μ:微(10^-6)n:纳(10^-9)p:皮(10^-12)22、数学中的特殊函数符号sin:正弦函数cos:余弦函数tan:正切函数exp:指数函数log:对数函数ln:自然对数函数lg:以10为底的对数函数。

常用数学符号大全常用数学符号大全1、几何符号≱‖θδΩΩΦΦφφΨ﹟∠≲≰≡≌△° |a| ≱∸∠∟‖|2、代数符号? ∝∧∨~∫ ≤ ≥ ≈ ∞ :〔〕[ ]〈〉《》「」『』】【〖3、运算符号× ‚ √ ± ≠ ≡≮≯﹟4、集合符号∪∩ⅰΦ ? ¢5、特殊符号∑ π(圆周率)@#☆★◈●◉◇◆□■▓⊿※¥Γ Δ Θ ∧Ξ Ο ∏ ∑ Φ Χ ΨΩ∏6、推理符号ⅬⅭⅮⅯ↖↗↘↙∴∵∶∷T ? ü7、标点符号` ˉ ˇ ¨ 、· ‘’8、其他& ; §℃№ $£¥‰ ℉☈☇≳≴≵≶≷≸≹≺≻≼Γ Δ Θ ∧Ξ Ο ∏ ∑ Φ Χ Ψ Ωα β γ δ εδ ε ζ η θ ι κλ μ ν π ξ ζ η υ θ χ ψ ωⅠⅡⅢⅣⅤⅥⅦⅧⅨⅩⅪⅫⅰⅱⅲⅳⅴⅵⅶⅷⅸⅹⅰ∏ ∑ ∕ √ ∝∞ ∟∠∣‖∧∨∩∪∫ ∮∴∵∶∷∸≈ ≌≈ ≠ ≡≤ ≥ ≤ ≥ ≮≯⊕≰≱⊿≲指数0123:o123 〃? ? ?符号意义∞ 无穷大PI 圆周率|x| 函数的绝对值∪集合并∩集合交≥ 大于等于≤ 小于等于≡恒等于或同余ln(x) 以e为底的对数lg(x) 以10为底的对数floor(x) 上取整函数ceil(x) 下取整函数x mod y 求余数{x} 小数部分x - floor(x)∫f(x)δx 不定积分∫[a:b]f(x)δx a到b的定积分∑[1≤k≤n]f(k) 对n进行求和,可以拓广至很多情况,如:∑[n is prime][n < 10]f(n)∑∑[1≤i≤j≤n]n^2lim f(x) (x->?) 求极限C(n:m) 组合数,n中取mP(n:m) 排列数m|n m整除n(m,n)=1 m与n互质a ⅰA a属于集合ACard(A) 集合A中的元素个数|a| ≱∸△∠∩∪≠ ∵∴≡± ≥ ≤ ⅰⅬⅭⅮⅯ↖↗↘↙‖∧∨¼ ½ ¾§≳≴≵≶≷≸≹≺≻≼α β γ δ ε δ ε ζ η θ ι κ λ μ ν π ξ ζ η υ θ χ ψ ωⅰⅱⅲⅳⅴⅵⅶⅷⅸⅹⅰ∏∑∕√∝∞∟∠∣‖∧∨∩∪∫∮∴∵∶∷∸≈≌≈≠≡≤≥≤≥≮≯⊕≰≱⊿≲为了方便,也做些约定!x的平方,可以打成x^2 (其它的以此类推)x+1的开方,可以打成√(x+1),记住加括号;x分之一,可以输入1/x;如果是x+1分之一,请输入1/(x+1),分子、分母请加括号<> 或>< 表示不等于例:a<>b 即a不等于b;<= 表示小于等于(不大于)例:a<=b 即a不大于b;>= 表示大于等于(不小于)例:a>=b 即a不小于b;^ 表示乘方例:a^b 即a的b次方, 也可用于开根号,例:a^(1/2) 表示a的平方根* 表示乘……/ 表示浮点除例:3/2=1.5\ 表示整除例:3\2=1……1()广义括号,允许多重嵌套,无大、中、小之分,优先级最高。

常用数学符号大全、关系代数符号1、几何符号⊥∥∠⌒⊙≡≌△2、代数符号∝∧∨~∫≠≤≥≈∞∶3、运算符号如加号(+),减号(-),乘号(×或·),除号(÷或/),两个集合的并集(∪),交集(∩),根号(√),对数(log,lg,ln),比(:),微分(dx),积分(∫),曲线积分(∮)等。
4、集合符号∪∩∈5、特殊符号∑π(圆周率)6、推理符号|a| ⊥∽△∠∩∪≠≡±≥≤∈←↑→↓↖↗↘↙∥∧∨&; §①②③④⑤⑥⑦⑧⑨⑩ΓΔΘΛΞΟΠΣΦΧΨΩαβγδεζηθικλμνξοπρστυφχψωⅠⅡⅢⅣⅤⅥⅦⅧⅨⅩⅪⅫⅰⅱⅲⅳⅴⅵⅶⅷⅸⅹ∈∏∑∕√∝∞∟∠∣∥∧∨∩∪∫∮∴∵∶∷∽≈≌≒≠≡≤≥≦≧≮≯⊕⊙⊥⊿⌒℃指数0123:o1237、数量符号如:i,2+i,a,x,自然对数底e,圆周率π。
8、关系符号如“=”是等号,“≈”是近似符号,“≠”是不等号,“>”是大于符号,“<”是小于符号,“≥”是大于或等于符号(也可写作“≮”),“≤”是小于或等于符号(也可写作“≯”),。
“→”表示变量变化的趋势,“∽”是相似符号,“≌”是全等号,“∥”是平行符号,“⊥”是垂直符号,“∝”是成正比符号,(没有成反比符号,但可以用成正比符号配倒数当作成反比)“∈”是属于符号,“??”是“包含”符号等。
9、结合符号如小括号“()”中括号“[]”,大括号“{}”横线“—”10、性质符号如正号“+”,负号“-”,绝对值符号“| |”正负号“±”11、省略符号如三角形(△),直角三角形(Rt△),正弦(sin),余弦(cos),x的函数(f(x)),极限(lim),角(∠),∵因为,(一个脚站着的,站不住)∴所以,(两个脚站着的,能站住)总和(∑),连乘(∏),从n个元素中每次取出r个元素所有不同的组合数(C(r)(n) ),幂(A,Ac,Aq,x^n)等。
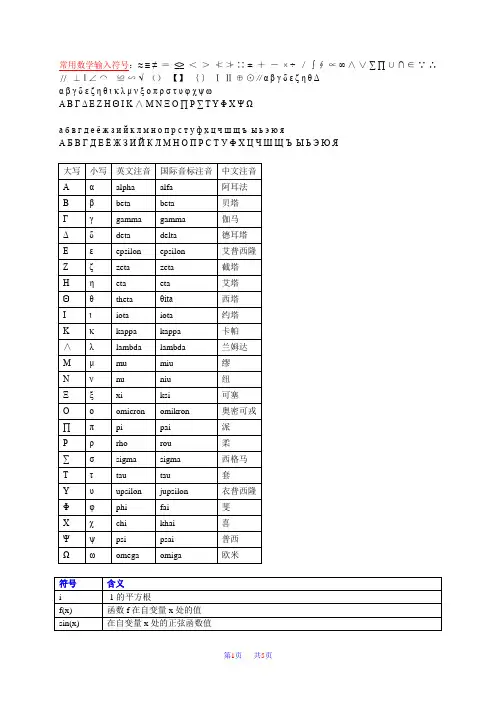
常用数学输入符号:≈ ≡ ≠ =≤≥ <>≮≯∷ ±+-× ÷/∫ ∮∝∞ ∧∨∑ ∏ ∪∩ ∈∵∴//⊥‖ ∠⌒≌∽√()【】{}ⅠⅡ⊕⊙∥αβγδεζηθΔαβγδεζηθικλμνξοπρστυφχψωΑΒΓΔΕΖΗΘΙΚ∧ΜΝΞΟ∏Ρ∑ΤΥΦΧΨΩабвгдеёжзийклмнопрстуфхцчшщъыьэюяАБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯexp(x) 在自变量x处的指数函数值,常被写作e xa^x a的x次方;有理数x由反函数定义ln x exp x 的反函数a x同a^xlog b a 以b为底a的对数;b log b a = acos x 在自变量x处余弦函数的值tan x 其值等于sin x/cos xcot x 余切函数的值或cos x/sin xsec x 正割含数的值,其值等于1/cos xcsc x 余割函数的值,其值等于1/sin xasin x y,正弦函数反函数在x处的值,即x = sin yacos x y,余弦函数反函数在x处的值,即x = cos yatan x y,正切函数反函数在x处的值,即x = tan yacot x y,余切函数反函数在x处的值,即x = cot yasec x y,正割函数反函数在x处的值,即x = sec yacsc x y,余割函数反函数在x处的值,即x = csc yθ角度的一个标准符号,不注明均指弧度,尤其用于表示atan x/y,当x、y、z用于表示空间中的点时i, j, k 分别表示x、y、z方向上的单位向量(a, b, c) 以a、b、c为元素的向量(a, b) 以a、b为元素的向量(a, b) a、b向量的点积a•b a、b向量的点积(a•b)a、b向量的点积|v| 向量v的模|x| 数x的绝对值Σ表示求和,通常是某项指数。
下边界值写在其下部,上边界值写在其上部。

常用单位数学符号集合大全1. 算术运算符加号(+):表示两个数相加减号():表示两个数相减乘号(× 或):表示两个数相乘除号(÷ 或 /):表示两个数相除等于号(=):表示两个数相等2. 比较运算符大于号(>):表示一个数大于另一个数小于号(<):表示一个数小于另一个数大于等于号(≥):表示一个数大于或等于另一个数小于等于号(≤):表示一个数小于或等于另一个数不等于号(≠):表示两个数不相等3. 分数与根号分数(/):表示两个数相除,如 3/4根号(√):表示求一个数的平方根,如√4 = 24. 指数与对数指数(^ 或):表示一个数的乘方,如 2^3 = 8对数(log):表示求一个数的对数,如 log10(100) = 2 5. 函数符号正弦函数(sin):表示求一个角的正弦值余弦函数(cos):表示求一个角的余弦值正切函数(tan):表示求一个角的正切值反正弦函数(arcsin 或 asin):表示求一个数的反正弦值反余弦函数(arccos 或 acos):表示求一个数的反余弦值反正切函数(arctan 或 atan):表示求一个数的反正切值6. 微积分符号导数('):表示求一个函数的导数,如 f'(x)积分(∫):表示求一个函数的不定积分,如∫f(x)dx极限(lim):表示求一个函数的极限,如lim(x→0)f(x)7. 集合符号属于(∈):表示一个元素属于某个集合,如x ∈ A不属于(∉):表示一个元素不属于某个集合,如 x ∉ A空集(∅):表示一个不包含任何元素的集合并集(∪):表示两个集合的并集,如 A ∪ B交集(∩):表示两个集合的交集,如 A ∩ B8. 其他符号无穷大(∞):表示一个无限大的数虚数单位(i):表示虚数单位,如√1求和(Σ):表示求一个序列的和,如Σn = 1^∞ an求积(Π):表示求一个序列的积,如Πn = 1^∞ an9. 矩阵和向量符号矩阵([a_{ij}]):表示一个由数字组成的矩形阵列,如[a_{11} a_{12}; a_{21} a_{22}]向量(<a_1, a_2, , a_n>):表示一个由数字组成的有序序列,如 <1, 2, 3>转置(^T):表示一个矩阵的转置,如 A^T矩阵乘法(A B):表示两个矩阵的乘积,如 A B = C矩阵加法(A + B):表示两个矩阵的加法,如 A + B = C矩阵减法(A B):表示两个矩阵的减法,如 A B = C矩阵的行列式(det(A)):表示一个矩阵的行列式,如 det(A)矩阵的逆(A^{1}):表示一个矩阵的逆,如 A^{1}10. 几何符号平行(∥):表示两条线段或直线平行,如AB ∥ CD垂直(⊥):表示两条线段或直线垂直,如AB ⊥ CD相似(~):表示两个几何图形相似,如△ABC ~ △DEF全等(≅):表示两个几何图形全等,如△ABC ≅ △DEF圆(O):表示一个圆,如 O弧(⌒):表示圆的一部分,如AB⌒角(∠):表示一个角,如∠ABC11. 概率与统计符号概率(P):表示某个事件发生的概率,如 P(A)期望值(E):表示随机变量的期望值,如 E(X)方差(Var):表示随机变量的方差,如 Var(X)标准差(σ):表示随机变量的标准差,如σ(X)累积分布函数(CDF):表示随机变量的累积分布函数,如 F(x)概率密度函数(PDF):表示随机变量的概率密度函数,如 f(x) 12. 逻辑符号与(∧):表示两个条件同时成立,如 A ∧ B或(∨):表示两个条件中至少有一个成立,如 A ∨ B非(¬):表示对一个条件取反,如¬A包含(⊆):表示一个集合是另一个集合的子集,如 A ⊆ B等价(≡):表示两个表达式等价,如 A ≡ B13. 其他常用符号平方(^2):表示一个数的平方,如 2^2 = 4立方(^3):表示一个数的立方,如 2^3 = 8平方根(√):表示求一个数的平方根,如√4 = 2立方根(∛):表示求一个数的立方根,如∛8 = 2求和(Σ):表示求一个序列的和,如Σn = 1^∞ an求积(Π):表示求一个序列的积,如Πn = 1^∞ an14. 复数符号复数(a + bi):表示一个由实部和虚部组成的复数,如 3 + 4i共轭复数(a bi):表示一个复数的共轭复数,如 3 4i模长(|a + bi|):表示一个复数的模长,如 |3 + 4i| = 5辐角(arg(a + bi)):表示一个复数的辐角,如 arg(3 + 4i) ≈ 0.92715. 三角函数符号正弦函数(sin):表示求一个角的正弦值,如sin(θ)余弦函数(cos):表示求一个角的余弦值,如cos(θ)正切函数(tan):表示求一个角的正切值,如tan(θ)余切函数(cot):表示求一个角的余切值,如cot(θ)正割函数(sec):表示求一个角的正割值,如sec(θ)余割函数(csc):表示求一个角的余割值,如csc(θ)16. 不等式符号大于号(>):表示一个数大于另一个数,如 a > b小于号(<):表示一个数小于另一个数,如 a < b大于等于号(≥):表示一个数大于或等于另一个数,如 a ≥ b小于等于号(≤):表示一个数小于或等于另一个数,如 a ≤ b不等于号(≠):表示两个数不相等,如a ≠ b17. 几何符号平行(∥):表示两条线段或直线平行,如AB ∥ CD垂直(⊥):表示两条线段或直线垂直,如AB ⊥ CD相似(~):表示两个几何图形相似,如△ABC ~ △DEF全等(≅):表示两个几何图形全等,如△ABC ≅ △DEF圆(O):表示一个圆,如 O弧(⌒):表示圆的一部分,如AB⌒角(∠):表示一个角,如∠ABC18. 概率与统计符号概率(P):表示某个事件发生的概率,如 P(A)期望值(E):表示随机变量的期望值,如 E(X)方差(Var):表示随机变量的方差,如 Var(X)标准差(σ):表示随机变量的标准差,如σ(X)累积分布函数(CDF):表示随机变量的累积分布函数,如 F(x)概率密度函数(PDF):表示随机变量的概率密度函数,如 f(x)19. 逻辑符号与(∧):表示两个条件同时成立,如 A ∧ B或(∨):表示两个条件中至少有一个成立,如 A ∨ B非(¬):表示对一个条件取反,如¬A包含(⊆):表示一个集合是另一个集合的子集,如 A ⊆ B 等价(≡):表示两个表达式等价,如 A ≡ B20. 其他常用符号平方(^2):表示一个数的平方,如 2^2 = 4立方(^3):表示一个数的立方,如 2^3 = 8平方根(√):表示求一个数的平方根,如√4 = 2立方根(∛):表示求一个数的立方根,如∛8 = 2求和(Σ):表示求一个序列的和,如Σn = 1^∞ an求积(Π):表示求一个序列的积,如Πn = 1^∞ an。

符号大全2010-07-22 12:29数学物理里面的公式符号读法:Αα:阿尔法 AlphaΒβ:贝塔 BetaΓγ:伽玛 GammaΔδ:德尔塔 DelteΕε:艾普西龙 EpsilonΖζ:捷塔 ZetaΕη:依塔 EtaΘθ:西塔 ThetaΙι:艾欧塔 IotaΚκ:喀帕 Kappa∧λ:拉姆达 LambdaΜμ:缪 MuΝν:拗 NuΞξ:克西 XiΟο:欧麦克轮 Omicron∏π:派 PiΡρ:柔 Rho∑σ:西格玛 SigmaΤτ:套 TauΥυ:宇普西龙 UpsilonΦφ:fai PhiΧχ:器 ChiΨψ:普赛 PsiΩω:欧米伽 Omega符号大全:(1)数量符号:如 :i,2+ i,a,x,自然对数底e,圆周率∏。
(2)运算符号:如加号(+),减号(-),乘号(×或·),除号(÷或/),两个集合的并集(∪),交集(∩),根号(),对数(log,lg,ln),比(∶),微分(d),积分(∫)等。
(3)关系符号:如“=”是等号,“≈”或“”是近似符号,“≠”是不等号,“>”是大于符号,“<”是小于符号,“”表示变量变化的趋势,“∽”是相似符号,“≌”是全等号,“‖”是平行符号,“⊥”是垂直符号,“∝”是正比例符号,“∈”是属于符号等。
(4)结合符号:如圆括号“()”方括号“[]”,花括号“{}”括线“—”(5)性质符号:如正号“+”,负号“-”,绝对值符号“‖”(6)省略符号:如三角形(△),正弦(sin),X的函数(f(x)),极限(lim),因为(∵),所以(∴),总和(∑),连乘(∏),从N个元素中每次取出R个元素所有不同的组合数(C ),幂(aM),阶乘(!)等。
符号意义∞无穷大PI 圆周率|x| 函数的绝对值∪集合并∩集合交≥大于等于≤小于等于≡恒等于或同余ln(x) 以e为底的对数lg(x) 以10为底的对数floor(x) 上取整函数ceil(x) 下取整函数x mod y 求余数小数部分 x - floor(x)∫f(x)δx 不定积分∫[a:b]f(x)δx a到b的定积分P为真等于1否则等于0∑[1≤k≤n]f(k) 对n进行求和,可以拓广至很多情况如:∑[n is prime][n < 10]f(n)∑∑[1≤i≤j≤n]n^2lim f(x) (x->?) 求极限f(z) f关于z的m阶导函数C(n:m) 组合数,n中取mP(n:m) 排列数m|n m整除nm⊥n m与n互质a ∈ A a属于集合A#A 集合A中的元素个数初中物理公式:物理量(单位)公式备注公式的变形速度V(m/S) v= S:路程/t:时间重力G (N) G=mg m:质量 g:9.8N/kg或者10N/kg 密度ρ(kg/m3)ρ=m/V m:质量 V:体积合力F合(N)方向相同:F合=F1+F2方向相反:F合=F1—F2 方向相反时,F1>F2浮力F浮(N) F浮=G物—G视 G视:物体在液体的重力浮力F浮(N) F浮=G物此公式只适用物体漂浮或悬浮浮力F浮(N) F浮=G排=m排g=ρ液gV排 G排:排开液体的重力m排:排开液体的质量ρ液:液体的密度V排:排开液体的体积(即浸入液体中的体积)杠杆的平衡条件 F1L1= F2L2 F1:动力 L1:动力臂F2:阻力 L2:阻力臂定滑轮 F=G物S=h F:绳子自由端受到的拉力G物:物体的重力S:绳子自由端移动的距离h:物体升高的距离动滑轮 F= (G物+G轮)S=2 h G物:物体的重力G轮:动滑轮的重力滑轮组 F= (G物+G轮)S=n h n:通过动滑轮绳子的段数机械功W(J) W=Fs F:力s:在力的方向上移动的距离有用功W有总功W总 W有=G物hW总=Fs 适用滑轮组竖直放置时机械效率η= ×100%功率P(w) P=W:功t:时间压强p(Pa) P=F:压力S:受力面积液体压强p(Pa) P=ρgh ρ:液体的密度h:深度(从液面到所求点的竖直距离)热量Q(J) Q=cm△t c:物质的比热容 m:质量△t:温度的变化值燃料燃烧放出的热量Q(J) Q=mq m:质量q:热值常用的物理公式与重要知识点一.物理公式单位)公式备注公式的变形串联电路电流I(A) I=I1=I2=……电流处处相等串联电路电压U(V) U=U1+U2+……串联电路起分压作用串联电路电阻R(Ω) R=R1+R2+……并联电路电流I(A) I=I1+I2+……干路电流等于各支路电流之和(分流)并联电路电压U(V) U=U1=U2=……并联电路电阻R(Ω) = + +……欧姆定律 I=电路中的电流与电压成正比,与电阻成反比电流定义式 I=Q:电荷量(库仑)t:时间(S)电功W(J) W=UIt=Pt U:电压 I:电流t:时间 P:电功率电功率 P=UI=I2R=U2/R U:电压 I:电流R:电阻电磁波波速与波长、频率的关系 C=λν C:物理量单位公式名称符号名称符号质量 m 千克 kg m=pv温度 t 摄氏度°C速度 v 米/秒 m/s v=s/t密度 p 千克/米3 kg/m3 p=m/v力(重力) F 牛顿(牛) N G=mg压强 P 帕斯卡(帕) Pa P=F/S功 W 焦耳(焦) J W=Fs功率 P 瓦特(瓦) w P=W/t电流 I 安培(安) A I=U/R电压 U 伏特(伏) V U=IR电阻 R 欧姆(欧) R=U/I电功 W 焦耳(焦) J W=UIt电功率 P 瓦特(瓦) w P=W/t=UI 热量 Q 焦耳(焦) J Q=cm(t-t°) 比热 c 焦/(千克°C) J/(kg°C) 真空中光速 3×108米/秒g 9.8牛顿/千克15°C空气中声速 340米/秒初中物理公式汇编【力学部分】1、速度:V=S/t2、重力:G=mg3、密度:ρ=m/V4、压强:p=F/S5、液体压强:p=ρgh6、浮力:(1)、F浮=F’-F (压力差)(2)、F浮=G-F (视重力)(3)、F浮=G (漂浮、悬浮)(4)、阿基米德原理:F浮=G排=ρ液gV排7、杠杆平衡条件:F1 L1=F2 L28、理想斜面:F/G=h/L9、理想滑轮:F=G/n10、实际滑轮:F=(G+G动)/ n (竖直方向)11、功:W=FS=Gh (把物体举高)12、功率:P=W/t=FV13、功的原理:W手=W机14、实际机械:W总=W有+W额外15、机械效率:η=W有/W总16、滑轮组效率:(1)、η=G/ nF(竖直方向)(2)、η=G/(G+G动) (竖直方向不计摩擦) (3)、η=f / nF (水平方向)【热学部分】1、吸热:Q吸=Cm(t-t0)=CmΔt2、放热:Q放=Cm(t0-t)=CmΔt3、热值:q=Q/m4、炉子和热机的效率:η=Q有效利用/Q燃料5、热平衡方程:Q放=Q吸6、热力学温度:T=t+273K【电学部分】1、电流强度:I=Q电量/t2、电阻:R=ρL/S3、欧姆定律:I=U/R4、焦耳定律:(1)、Q=I2Rt普适公式)(2)、Q=UIt=Pt=UQ电量=U2t/R (纯电阻公式) 5、串联电路:(1)、I=I1=I2(2)、U=U1+U2(3)、R=R1+R2(4)、U1/U2=R1/R2 (分压公式)(5)、P1/P2=R1/R26、并联电路:(1)、I=I1+I2(2)、U=U1=U2(3)、1/R=1/R1+1/R2 [ R=R1R2/(R1+R2)] (4)、I1/I2=R2/R1(分流公式)(5)、P1/P2=R2/R17定值电阻:(1)、I1/I2=U1/U2(2)、P1/P2=I12/I22(3)、P1/P2=U12/U228电功:(1)、W=UIt=Pt=UQ (普适公式) (2)、W=I2Rt=U2t/R (纯电阻公式) 9电功率:(1)、P=W/t=UI (普适公式) (2)、P=I2R=U2/R (纯电阻公式) 【常用物理量】1、光速:C=3×108m/s (真空中)2、声速:V=340m/s (15℃)3、人耳区分回声:≥0.1s4、重力加速度:g=9.8N/kg≈10N/kg5、标准大气压值:760毫米水银柱高=1.01×105Pa6、水的密度:ρ=1.0×103kg/m37、水的凝固点:0℃8、水的沸点:100℃9、水的比热容:C=4.2×103J/(kg?℃)10、元电荷:e=1.6×10-19C11、一节干电池电压:1.5V12、一节铅蓄电池电压:2V13、对于人体的安全电压:≤36V(不高于36V)14、动力电路的电压:380V15、家庭电路电压:220V16、单位换算:(1)、1m/s=3.6km/h(2)、1g/cm3 =103kg/m3(3)、1kw?h=3.6×106J初中物理公式汇编【力学部分】1、速度:V=S/t2、重力:G=mg3、密度:ρ=m/V4、压强:p=F/S5、液体压强:p=ρgh6、浮力:(1)、F浮=F’-F (压力差)(2)、F浮=G-F (视重力)(3)、F浮=G (漂浮、悬浮)(4)、阿基米德原理:F浮=G排=ρ液gV排7、杠杆平衡条件:F1 L1=F2 L28、理想斜面:F/G=h/L9、理想滑轮:F=G/n10、实际滑轮:F=(G+G动)/ n (竖直方向)11、功:W=FS=Gh (把物体举高)12、功率:P=W/t=FV13、功的原理:W手=W机14、实际机械:W总=W有+W额外15、机械效率:η=W有/W总16、滑轮组效率:(1)、η=G/ nF(竖直方向)(2)、η=G/(G+G动) (竖直方向不计摩擦) (3)、η=f / nF (水平方向)【热学部分】1、吸热:Q吸=Cm(t-t0)=CmΔt2、放热:Q放=Cm(t0-t)=CmΔt3、热值:q=Q/m4、炉子和热机的效率:η=Q有效利用/Q燃料5、热平衡方程:Q放=Q吸6、热力学温度:T=t+273K【电学部分】1、电流强度:I=Q电量/t2、电阻:R=ρL/S3、欧姆定律:I=U/R4、焦耳定律:(1)、Q=I2Rt普适公式)(2)、Q=UIt=Pt=UQ电量=U2t/R (纯电阻公式) 5、串联电路:(1)、I=I1=I2(2)、U=U1+U2(3)、R=R1+R2(4)、U1/U2=R1/R2 (分压公式)(5)、P1/P2=R1/R26、并联电路:(1)、I=I1+I2(2)、U=U1=U2(3)、1/R=1/R1+1/R2 [ R=R1R2/(R1+R2)] (4)、I1/I2=R2/R1(分流公式)(5)、P1/P2=R2/R17定值电阻:(1)、I1/I2=U1/U2(2)、P1/P2=I12/I22(3)、P1/P2=U12/U228电功:(1)、W=UIt=Pt=UQ (普适公式)(2)、W=I2Rt=U2t/R (纯电阻公式)9电功率:(1)、P=W/t=UI (普适公式)(2)、P=I2R=U2/R (纯电阻公式)【常用物理量】1、光速:C=3×108m/s (真空中)2、声速:V=340m/s (15℃)3、人耳区分回声:≥0.1s4、重力加速度:g=9.8N/kg≈10N/kg5、标准大气压值:760毫米水银柱高=1.01×105Pa6、水的密度:ρ=1.0×103kg/m37、水的凝固点:0℃8、水的沸点:100℃9、水的比热容:C=4.2×103J/(kg?℃)10、元电荷:e=1.6×10-19C11、一节干电池电压:1.5V12、一节铅蓄电池电压:2V13、对于人体的安全电压:≤36V(不高于36V)14、动力电路的电压:380V15、家庭电路电压:220V16、单位换算:(1)、1m/s=3.6km/h(2)、1g/cm3 =103k数学符号大全:(1)数量符号:如:i,2+i,a,x,自然对数底e,圆周率π。

数学符号及读法大全常用数学输入符号:≈≡≠=≤≥<>≮≯∷ ± +-× ÷ /∫∮∝∞∧∨∑∏∪∩∈∵∴⊥‖∠⌒≌∽√()【】{}ⅠⅡ⊕⊙∥αβγδεζηθΔ大写小写英文注音国际音标注音中文注音Ααalpha alfa阿耳法Ββbeta beta贝塔Γγgamma gamma伽马Δδdeta delta德耳塔Εεepsilon epsilon艾普西隆Ζζzeta zeta截塔Ηηeta eta艾塔Θθthetaθita西塔Ιιiota iota约塔Κκkappa kappa卡帕∧λlambda lambda兰姆达Μμmu miu缪Ννnu niu纽Ξξxi ksi可塞Οοomicron omikron奥密可戎∏πpi pai派Ρρrho rou柔∑σsigma sigma西格马Ττtau tau套Υυupsilon jupsilon衣普西隆Φφphi fai斐Χχchi khai喜Ψψpsi psai普西Ωωomega omiga欧米符号含义i-1的平方根f(x)函数f在自变量x处的值sin(x)在自变量x处的正弦函数值exp(x)在自变量x处的指数函数值,常被写作exa^x a的x次方;有理数x由反函数定义ln x exp x 的反函数ax同a^xlogba以b为底a的对数;blogba = acos x在自变量x处余弦函数的值tan x其值等于sin x/cos xcot x余切函数的值或cos x/sin xsec x正割含数的值,其值等于1/cos xcsc x余割函数的值,其值等于1/sin xasin x y,正弦函数反函数在x处的值,即x = sin yacos x y,余弦函数反函数在x处的值,即x = cos yatan x y,正切函数反函数在x处的值,即x = tan yacot x y,余切函数反函数在x处的值,即x = cot yasec x y,正割函数反函数在x处的值,即x = sec y acsc x y,余割函数反函数在x处的值,即x = csc yθ角度的一个标准符号,不注明均指弧度,尤其用于表示atan x/y,当x、y、z用于表示空间中的点时i, j, k分别表示x、y、z方向上的单位向量(a, b, c)以a、b、c为元素的向量(a, b)以a、b为元素的向量(a, b)a、b向量的点积a•b a、b向量的点积(a•b)a、b向量的点积|v|向量v的模|x|数x的绝对值Σ表示求和,通常是某项指数。
数学符号及读法大全第一部分:基本数学符号1. 加号 (+)读作:加2. 减号 ()读作:减3. 乘号(×)读作:乘4. 除号(÷)读作:除5. 等号 (=)读作:等于6. 不等号(≠)读作:不等于7. 大于号 (>)读作:大于8. 小于号 (<)读作:小于9. 大于等于号(≥)读作:大于等于10. 小于等于号(≤)读作:小于等于467. 静谧之海468. 翱翔天际469. 晨曦微光470. 暮色温柔471. 琴瑟和鸣472. 碧波荡漾473. 风轻云淡474. 星河滚烫475. 雨后初晴476. 月下独酌477. 寂静之声478. 花前月下479. 时光荏苒480. 笑忘书481. 梦开始的地方482. 时光旅行者483. 漫步星河484. 风起云涌485. 雨落花飞4. 月影斑驳487. 晨光熹微488. 暮色苍茫489. 静谧之夜490. 翱翔天际491. 晨曦微光492. 暮色温柔493. 琴瑟和鸣494. 碧波荡漾495. 风轻云淡496. 星河滚烫497. 雨后初晴498. 月下独酌499. 寂静之声500. 花前月下501. 时光荏苒502. 笑忘书503. 梦开始的地方504. 时光旅行者505. 漫步星河506. 风起云涌507. 雨落花飞508. 月影斑驳509. 晨光熹微510. 暮色苍茫511. 静谧之夜512. 翱翔天际513. 晨曦微光514. 暮色温柔515. 琴瑟和鸣516. 碧波荡漾517. 风轻云淡518. 星河滚烫519. 雨后初晴520. 月下独酌521. 寂静之声522. 花前月下523. 时光荏苒524. 笑忘书525. 梦开始的地方526. 时光旅行者527. 漫步星河528. 风起云涌529. 雨落花飞530. 月影斑驳531. 晨光熹微532. 暮色苍茫533. 静谧之夜534. 翱翔天际535. 晨曦微光536. 暮色温柔537. 琴瑟和鸣538. 碧波荡漾539. 风轻云淡540. 星河滚烫541. 雨后初晴542. 月下独酌543. 寂静之声544. 花前月下545. 时光荏苒546. 笑忘书547. 梦开始的地方548. 时光旅行者549. 漫步星河550. 风起云涌551. 雨落花飞552. 月影斑驳553. 晨光熹微554. 暮色苍茫555. 静谧之夜556. 翱翔天际557. 晨曦微光558. 暮色温柔559. 琴瑟和鸣560. 碧波荡漾561. 风轻云淡562. 星河滚烫563. 雨后初晴565. 寂静之声566. 花前月下567. 时光荏苒568. 笑忘书569. 梦开始的地方570. 时光旅行者571. 漫步星河572. 风起云涌573. 雨落花飞574. 月影斑驳575. 晨光熹微576. 暮色苍茫577. 静谧之夜578. 翱翔天际579. 晨曦微光580. 暮色温柔581. 琴瑟和鸣582. 碧波荡漾583. 风轻云淡584. 星河滚烫585. 雨后初晴5. 月下独酌587. 寂静之声589. 时光荏苒590. 笑忘书591. 梦开始的地方592. 时光旅行者593. 漫步星河594. 风起云涌595. 雨落花飞596. 月影斑驳597. 晨光熹微598. 暮色苍茫599. 静谧之夜600. 翱翔天际601. 晨曦微光602. 暮色温柔603. 琴瑟和鸣604. 碧波荡漾605. 风轻云淡606. 星河滚烫607. 雨后初晴608. 月下独酌609. 寂静之声610. 花前月下611. 时光荏苒612. 笑忘书613. 梦开始的地方614. 时光旅行者615. 漫步星河616. 风起云涌617. 雨落花飞618. 月影斑驳619. 晨光熹微620. 暮色苍茫621. 静谧之夜622. 翱翔天际623. 晨曦微光624. 暮色温柔625. 琴瑟和鸣626. 碧波荡漾627. 风轻云淡628. 星河滚烫629. 雨后初晴630. 月下独酌631. 寂静之声632. 花前月下633. 时光荏苒634. 笑忘书635. 梦开始的地方636. 时光旅行者637. 漫步星河638. 风起云涌639. 雨落花飞640. 月影斑驳641. 晨光熹微642. 暮色苍茫643. 静谧之夜644. 翱翔天际645. 晨曦微光646. 暮色温柔647. 琴瑟和鸣648. 碧波荡漾649. 风轻云淡650. 星河滚烫651. 雨后初晴652. 月下独酌653. 寂静之声654. 花前月下655. 时光荏苒656. 笑忘书657. 梦开始的地方658. 时光旅行者659. 漫步星河660. 风起云涌661. 雨落花飞662. 月影斑驳663. 晨光熹微664. 暮色苍茫665. 静谧之夜666. 翱翔天际667. 晨曦微光668. 暮色温柔669. 琴瑟和鸣670. 碧波荡漾671. 风轻云淡672. 星河滚烫673. 雨后初晴674. 月下独酌675. 寂静之声676. 花前月下677. 时光荏苒678. 笑忘书679. 梦开始的地方680. 时光旅行者681. 漫步星河682. 风起云涌683. 雨落花飞684. 月影斑驳685. 晨光熹微6. 暮色苍茫687. 静谧之夜688. 翱翔天际689. 晨曦微光690. 暮色温柔691. 琴瑟和鸣692. 碧波荡漾693. 风轻云淡694. 星河滚烫695. 雨后初晴696. 月下独酌697. 寂静之声698. 花前月下699. 时光荏苒700. 笑忘书701. 梦开始的地方702. 时光旅行者703. 漫步星河704. 风起云涌705. 雨落花飞706. 月影斑驳707. 晨光熹微708. 暮色苍茫709. 静谧之夜710. 翱翔天际711. 晨曦微光712. 暮色温柔713. 琴瑟和鸣714. 碧波荡漾715. 风轻云淡716. 星河滚烫717. 雨后初晴718. 月下独酌719. 寂静之声720. 花前月下721. 时光荏苒722. 笑忘书723. 梦开始的地方724. 时光旅行者725. 漫步星河726. 风起云涌727. 雨落花飞728. 月影斑驳729. 晨光熹微730. 暮色苍茫731. 静谧之夜732. 翱翔天际733. 晨曦微光734. 暮色温柔735. 琴瑟和鸣736. 碧波荡漾737. 风轻云淡738. 星河滚烫739. 雨后初晴740. 月下独酌741. 寂静之声742. 花前月下743. 时光荏苒744. 笑忘书745. 梦开始的地方746. 时光旅行者747. 漫步星河748. 风起云涌749. 雨落花飞750. 月影斑驳751. 晨光熹微752. 暮色苍茫753. 静谧之夜754. 翱翔天际755. 晨曦微光756. 暮色温柔757. 琴瑟和鸣758. 碧波荡漾759. 风轻云淡760. 星河滚烫761. 雨后初晴762. 月下独酌763. 寂静之声764. 花前月下765. 时光荏苒766. 笑忘书767. 梦开始的地方768. 时光旅行者769. 漫步星河770. 风起云涌771. 雨落花飞772. 月影斑驳773. 晨光熹微774. 暮色苍茫775. 静谧之夜776. 翱翔天际777. 晨曦微光778. 暮色温柔779. 琴瑟和鸣780. 碧波荡漾781. 风轻云淡782. 星河滚烫783. 雨后初晴784. 月下独酌785. 寂静之声7. 花前月下787. 时光荏苒788. 笑忘书789. 梦开始的地方790. 时光旅行者791. 漫步星河792. 风起云涌793. 雨落花飞794. 月影斑驳795. 晨光熹微796. 暮色苍茫797. 静谧之夜798. 翱翔天际799. 晨曦微光800. 暮色温柔801. 琴瑟和鸣802. 碧波荡漾803. 风轻云淡804. 星河滚烫805. 雨后初晴806. 月下独酌807. 寂静之声808. 花前月下809. 时光荏苒810. 笑忘书811. 梦开始的地方812. 时光旅行者813. 漫步星河814. 风起云涌815. 雨落花飞816. 月影斑驳817. 晨光熹微818. 暮色苍茫819. 静谧之夜820. 翱翔天际821. 晨曦微光822. 暮色温柔823. 琴瑟和鸣824. 碧波荡漾825. 风轻云淡826. 星河滚烫827. 雨后初晴829. 寂静之声830. 花前月下831. 时光荏苒832. 笑忘书833. 梦开始的地方834. 时光旅行者835. 漫步星河836. 风起云涌837. 雨落花飞838. 月影斑驳839. 晨光熹微840. 暮色苍茫841. 静谧之夜842. 翱翔天际843. 晨曦微光844. 暮色温柔845. 琴瑟和鸣846. 碧波荡漾847. 风轻云淡848. 星河滚烫849. 雨后初晴850. 月下独酌851. 寂静之声853. 时光荏苒854. 笑忘书855. 梦开始的地方856. 时光旅行者857. 漫步星河858. 风起云涌859. 雨落花飞0. 月影斑驳1. 晨光熹微2. 暮色苍茫3. 静谧之夜4. 翱翔天际5. 晨曦微光6. 暮色温柔7. 琴瑟和鸣8. 碧波荡漾9. 风轻云淡870. 星河滚烫871. 雨后初晴872. 月下独酌873. 寂静之声874. 花前月下875. 时光荏苒876. 笑忘书877. 梦开始的地方878. 时光旅行者879. 漫步星河880. 风起云涌881. 雨落花飞882. 月影斑驳883. 晨光熹微884. 暮色苍茫885. 静谧之夜8. 翱翔天际887. 晨曦微光888. 暮色温柔889. 琴瑟和鸣890. 碧波荡漾891. 风轻云淡892. 星河滚烫893. 雨后初晴894. 月下独酌895. 寂静之声896. 花前月下897. 时光荏苒898. 笑忘书899. 梦开始的地方900. 时光旅行者901. 漫步星河902. 风起云涌903. 雨落花飞904. 月影斑驳905. 晨光熹微906. 暮色苍茫907. 静谧之夜908. 翱翔天际909. 晨曦微光910. 暮色温柔911. 琴瑟和鸣912913. 紫藤花下914. 雪域之鹰915. 翠竹清风916. 风华正茂917. 水墨青花918. 晨曦暮雪919. 琴韵墨香920. 梦里江南921. 花影轻舞922. 时光流转923. 笑忘江湖924. 梦开始的地方925. 时光旅行者926. 漫步星河927. 风起云涌928. 雨落花飞929. 月影斑驳930. 晨光熹微931. 暮色苍茫932. 静谧之夜933. 翱翔天际934. 晨曦微光935. 暮色温柔936. 琴瑟和鸣937. 碧波荡漾938. 风轻云淡939. 星河滚烫940. 雨后初晴941. 月下独酌942. 寂静之声943. 花前月下944. 时光荏苒945. 笑忘书946. 梦开始的地方947. 时光旅行者948. 漫步星河949. 风起云涌950. 雨落花飞951. 月影斑驳952. 晨光熹微953. 暮色苍茫954. 静谧之夜955. 翱翔天际956. 晨曦微光957. 暮色温柔958. 琴瑟和鸣959. 碧波荡漾960. 风轻云淡961. 星河滚烫962. 雨后初晴963. 月下独酌964. 寂静之声965. 花前月下966. 时光荏苒967. 笑忘书968. 梦开始的地方969. 时光旅行者970. 漫步星河971. 风起云涌972. 雨落花飞973. 月影斑驳974. 晨光熹微975. 暮色苍茫976. 静谧之夜977. 翱翔天际978. 晨曦微光979. 暮色温柔980. 琴瑟和鸣981. 碧波荡漾982. 风轻云淡983. 星河滚烫984. 雨后初晴985. 月下独酌9. 寂静之声987. 花前月下988. 时光荏苒989. 笑忘书990. 梦开始的地方991. 时光旅行者992. 漫步星河993. 风起云涌994. 雨落花飞995. 月影斑驳996. 晨光熹微997. 暮色苍茫998. 静谧之夜999. 翱翔天际1000. 晨曦微光。
数学符号及读法大全常用数学输入符号:≈≡≠=≤≥<>≮≯∷±+-× ÷/∫∮∝∞∧∨∑∏∪∩∈∵∴//⊥‖∠⌒≌∽√()【】{}ⅠⅡ⊕⊙∥αβγδεζηθΔ大写小写英文注音国际音标注音中文注音Ααalpha alfa 阿耳法Ββbeta beta 贝塔Γγgamma gamma 伽马Δδdeta delta 德耳塔Εεepsilon epsilon 艾普西隆Ζζzeta zeta 截塔Ηηeta eta 艾塔Θθtheta θita 西塔Ιιiota iota 约塔Κκkappa kappa 卡帕∧λlambda lambda 兰姆达Μμmu miu 缪Ννnu niu 纽Ξξxi ksi 可塞Οοomicron omikron 奥密可戎∏πpi pai 派Ρρrho rou 柔∑σsigma sigma 西格马Ττtau tau 套Υυupsilon jupsilon 衣普西隆Φφphi fai 斐Χχchi khai 喜Ψψpsi psai 普西Ωωomega omiga 欧米i -1的平方根f(x) 函数f在自变量x处的值sin(x) 在自变量x处的正弦函数值exp(x) 在自变量x处的指数函数值,常被写作e x a^x a的x次方;有理数x由反函数定义ln x exp x 的反函数a x同 a^xlogb a 以b为底a的对数; b logba = acos x 在自变量x处余弦函数的值tan x 其值等于 sin x/cos xcot x 余切函数的值或 cos x/sin xsec x 正割含数的值,其值等于 1/cos xcsc x 余割函数的值,其值等于 1/sin xasin x y,正弦函数反函数在x处的值,即 x = sin y acos x y,余弦函数反函数在x处的值,即 x = cos y atan x y,正切函数反函数在x处的值,即 x = tan y acot x y,余切函数反函数在x处的值,即 x = cot y asec x y,正割函数反函数在x处的值,即 x = sec y acsc x y,余割函数反函数在x处的值,即 x = csc yθ角度的一个标准符号,不注明均指弧度,尤其用于表示atan x/y,当x、y、z用于表示空间中的点时i, j, k 分别表示x、y、z方向上的单位向量(a, b, c) 以a、b、c为元素的向量(a, b) 以a、b为元素的向量(a, b) a、b向量的点积a•b a、b向量的点积(a•b) a、b向量的点积|v| 向量v的模|x| 数x的绝对值Σ表示求和,通常是某项指数。
数学符号大全,你都认识吗?1、几何符号⊥ ∥ ∠ ⌒ ⊙ ≡ ≌ △2、代数符号∝ ∧ ∨ ~∫ ≠ ≤ ≥ ≈ ∞ ∶3、运算符号如加号(+),减号(-),乘号(×或·),除号(÷或/),两个集合的并集(∪),交集(∩),根号(√),对数(log,lg,ln),比(:),微分(dx),积分(∫),曲线积分(∮)等。
4、集合符号∪ ∩ ∈5、特殊符号∑ π(圆周率)6、推理符号|a| ⊥ ∽ △ ∠ ∩ ∪ ≠ ≡± ≥ ≤ ∈←↑ → ↓ ↖ ↗ ↘ ↙∥ ∧ ∨&; §① ② ③ ④ ⑤ ⑥ ⑦ ⑧ ⑨ ⑩Γ Δ Θ Λ Ξ Ο Π Σ Φ ΧΨ Ωα β γ δ ε ζ η θ ι κ λμ νξ ο π ρ σ τ υ φ χ ψ ωⅠ Ⅱ Ⅲ Ⅳ Ⅴ Ⅵ Ⅶ Ⅷ Ⅸ Ⅹ Ⅺ Ⅻⅰ ⅱ ⅲ ⅳ ⅴ ⅵ ⅶ ⅷ ⅸ ⅹ∈ ∏ ∑ ∕ √ ∝ ∞ ∟ ∠ ∣∥ ∧ ∨ ∩ ∪ ∫ ∮∴ ∵ ∶ ∷ ∽ ≈ ≌ ≒ ≠≡ ≤ ≥ ≦ ≧ ≮ ≯ ⊕⊙ ⊥⊿ ⌒ ℃指数0123:o1237、数量符号如:i,2+i,a,x,自然对数底e,圆周率π。
8、关系符号如“=”是等号,“≈”是近似符号,“≠”是不等号,“>”是大于符号,“<”是小于符号,“≥”或“≮”是大于或等于符号,“≤”或“≯”)是小于或等于符号。
“→ ”表示变量变化的趋势,“∽”是相似符号,“≌”是全等号,“∥”是平行符号,“⊥”是垂直符号,“∝”是成正比符号,(没有成反比符号)“∈”是属于符号,“??”是“包含”符号等。
9、结合符号如小括号“()”中括号“[]”,大括号“{}”横线“—”10、性质符号如正号“+”,负号“-”,正负号“±”绝对值符号“| |”11、省略符号如三角形(△),直角三角形(Rt△),正弦(sin),余弦(cos),x的函数(f(x)),极限(lim),角(∠),∵因为,(一个脚站着的,站不住)∴所以,(两个脚站着的,能站住)总和(∑),连乘(∏),从n个元素中每次取出r个元素所有不同的组合数(C(r)(n) ),幂(A,Ac,Aq,x^n)等。
(完整版)常用数学符号大全1. 加号(+):表示两个数相加,例如 2 + 3 = 5。
2. 减号():表示两个数相减,例如 5 3 = 2。
3. 乘号(×):表示两个数相乘,例如2 × 3 = 6。
4. 除号(÷):表示两个数相除,例如6 ÷ 2 = 3。
5. 等号(=):表示两个数或表达式相等,例如 2 + 3 = 5。
6. 不等号(≠):表示两个数或表达式不相等,例如2 + 3 ≠ 4。
7. 大于号(>):表示一个数大于另一个数,例如 5 > 3。
8. 小于号(<):表示一个数小于另一个数,例如 3 < 5。
9. 大于等于号(≥):表示一个数大于或等于另一个数,例如 5 ≥ 3。
10. 小于等于号(≤):表示一个数小于或等于另一个数,例如3 ≤ 5。
11. 分数线(/):用于表示分数,例如 1/2 表示一半。
12. 开方号(√):用于表示求一个数的平方根,例如√9 = 3。
13. 乘方号(^):用于表示求一个数的幂,例如 2^3 = 8。
14. 求和号(∑):用于表示求和,例如∑(i=1 to n) i 表示求从 1 到 n 的和。
15. 积分号(∫):用于表示求定积分,例如∫(f(x)dx) 表示求函数 f(x) 在某个区间上的定积分。
16. 对数号(log):用于表示求对数,例如 log10(100) = 2。
17. 三角函数符号(sin、cos、tan):用于表示求三角函数的值,例如sin(30°) = 0.5。
18. 倒数符号(1/x):用于表示求一个数的倒数,例如 1/2 =0.5。
19. 无穷大符号(∞):表示无穷大,例如lim(x→∞) f(x) 表示求函数 f(x) 当 x 趋向于无穷大时的极限。
(完整版)常用数学符号大全1. 矩阵符号([ ]):用于表示矩阵,例如 [1 2; 3 4] 表示一个 2x2 的矩阵。
数学符号及读法大全常用数学输入符号:≈≡≠=≤≥<>≮≯∷±+-×÷/∫∮∝∞∧∨∑∏∪∩∈∵∴//≱‖符号含义i -1的平方根f(x) 函数f在自变量x处的值sin(x) 在自变量x处的正弦函数值exp(x) 在自变量x处的指数函数值,常被写作e xa^x a的x次方;有理数x由反函数定义ln x exp x 的反函数a x同 a^xlogb a 以b为底a的对数; b logba = acos x 在自变量x处余弦函数的值tan x 其值等于 sin x/cos xcot x 余切函数的值或 cos x/sin xsec x 正割含数的值,其值等于 1/cos xcsc x 余割函数的值,其值等于 1/sin xasin x y,正弦函数反函数在x处的值,即 x = sin y acos x y,余弦函数反函数在x处的值,即 x = cos y atan x y,正切函数反函数在x处的值,即 x = tan y acot x y,余切函数反函数在x处的值,即 x = cot y asec x y,正割函数反函数在x处的值,即 x = sec y acsc x y,余割函数反函数在x处的值,即 x = csc yζ角度的一个标准符号,不注明均指弧度,尤其用于表示atan x/y,当x、y、z用于表示空间中的点时i, j, k 分别表示x、y、z方向上的单位向量(a, b, c) 以a、b、c为元素的向量(a, b) 以a、b为元素的向量(a, b) a、b向量的点积a•b a、b向量的点积(a•b) a、b向量的点积|v| 向量v的模|x| 数x的绝对值Σ表示求和,通常是某项指数。
下边界值写在其下部,上边界值写在其上部。
如j从1到100 的和可以表示成:。
这表示 1 + 2 + … + nM 表示一个矩阵或数列或其它|v> 列向量,即元素被写成列或可被看成k×1阶矩阵的向量<v| 被写成行或可被看成从1×k阶矩阵的向量dx 变量x的一个无穷小变化,dy, dz, dr等类似ds 长度的微小变化ξ变量 (x2 + y2 + z2)1/2或球面坐标系中到原点的距离r 变量 (x2 + y2)1/2或三维空间或极坐标中到z轴的距离|M| 矩阵M的行列式,其值是矩阵的行和列决定的平行区域的面积或体积||M|| 矩阵M的行列式的值,为一个面积、体积或超体积det M M的行列式M-1矩阵M的逆矩阵v×w向量v和w的向量积或叉积ζvw向量v和w之间的夹角A•B×C标量三重积,以A、B、C为列的矩阵的行列式uw在向量w方向上的单位向量,即 w/|w|df 函数f的微小变化,足够小以至适合于所有相关函数的线性近似df/dx f关于x的导数,同时也是f的线性近似斜率f ' 函数f关于相应自变量的导数,自变量通常为x∂f/∂x y、z固定时f关于x的偏导数。
常用数学输入符号:~~≈ ≡ ≠ =≤≥ <>≮≯∷ ±+-× ÷/∫ ∮∝∞ ∧∨∑ ∏ ∪∩ ∈∵∴//⊥‖ ∠⌒≌∽√()【】{}ⅠⅡ⊕⊙∥αβγδεζηθΔ
αβγδεζηθικλμνξοπρστυφχψω
ΑΒΓΔΕΖΗΘΙΚ∧ΜΝΞΟ∏Ρ∑ΤΥΦΧΨΩ
абвгдеёжзийклмнопрстуфхцчшщъыьэюя
АБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ
exp(x) 在自变量x处的指数函数值,常被写作e x
a^x a的x次方;有理数x由反函数定义
ln x exp x 的反函数
a x同a^x
log b a 以b为底a的对数;b log b a = a
cos x 在自变量x处余弦函数的值
tan x 其值等于sin x/cos x
cot x 余切函数的值或cos x/sin x
sec x 正割含数的值,其值等于1/cos x
csc x 余割函数的值,其值等于1/sin x
asin x y,正弦函数反函数在x处的值,即x = sin y
acos x y,余弦函数反函数在x处的值,即x = cos y
atan x y,正切函数反函数在x处的值,即x = tan y
acot x y,余切函数反函数在x处的值,即x = cot y
asec x y,正割函数反函数在x处的值,即x = sec y
acsc x y,余割函数反函数在x处的值,即x = csc y
θ角度的一个标准符号,不注明均指弧度,尤其用于表示atan x/y,当x、y、z用于表示空间中的点时
i, j, k 分别表示x、y、z方向上的单位向量
(a, b, c) 以a、b、c为元素的向量
(a, b) 以a、b为元素的向量
(a, b) a、b向量的点积
a•b a、b向量的点积
(a•b)a、b向量的点积
|v| 向量v的模
|x| 数x的绝对值
Σ表示求和,通常是某项指数。
下边界值写在其下部,上边界值写在其上部。
如j从1到
100 的和可以表示成:。
这表示1 + 2 + … + n
M 表示一个矩阵或数列或其它
|v> 列向量,即元素被写成列或可被看成k×1阶矩阵的向量
<v| 被写成行或可被看成从1×k阶矩阵的向量
dx 变量x的一个无穷小变化,dy, dz, dr等类似
ds 长度的微小变化
ρ变量(x2 + y2 + z2)1/2或球面坐标系中到原点的距离
r 变量(x2 + y2)1/2或三维空间或极坐标中到z轴的距离
|M| 矩阵M的行列式,其值是矩阵的行和列决定的平行区域的面积或体积
||M|| 矩阵M的行列式的值,为一个面积、体积或超体积
det M M的行列式
M-1矩阵M的逆矩阵
v×w 向量v和w的向量积或叉积
θvw向量v和w之间的夹角
A•B×C标量三重积,以A、B、C为列的矩阵的行列式
u w在向量w方向上的单位向量,即w/|w|
df 函数f的微小变化,足够小以至适合于所有相关函数的线性近似
df/dx f关于x的导数,同时也是f的线性近似斜率
f ' 函数f关于相应自变量的导数,自变量通常为x
∂f/∂x y、z固定时f关于x的偏导数。
通常f关于某变量q的偏导数为当其它几个变量固定时df 与dq的比值。
任何可能导致变量混淆的地方都应明确地表述
(∂f/∂x)|r,z保持r和z不变时,f关于x的偏导数
grad f 元素分别为f关于x、y、z偏导数[(∂f/∂x), (∂f/∂y), (∂f/∂z)] 或(∂f/∂x)i + (∂f/∂y)j + (∂f/∂z)k;
的向量场,称为f的梯度
∇向量算子(∂/∂x)i + (∂/∂x)j + (∂/∂x)k, 读作"del"
∇f f的梯度;它和u w的点积为f在w方向上的方向导数
∇•w向量场w的散度,为向量算子∇同向量w的点积, 或(∂w x/∂x) + (∂w y/∂y) + (∂w z/∂z) curl w 向量算子∇同向量w 的叉积
∇×w w的旋度,其元素为[(∂f z/∂y) - (∂f y/∂z), (∂f x/∂z) - (∂f z/∂x), (∂f y/∂x) - (∂f x/∂y)]
∇•∇拉普拉斯微分算子:(∂2/∂x2) + (∂/∂y2) + (∂/∂z2)
f "(x) f关于x的二阶导数,f '(x)的导数
d2f/dx2f关于x的二阶导数
f(2)(x) 同样也是f关于x的二阶导数
f(k)(x) f关于x的第k阶导数,f(k-1) (x)的导数
T 曲线切线方向上的单位向量,如果曲线可以描述成r(t), 则T = (dr/dt)/|dr/dt|
ds 沿曲线方向距离的导数
κ曲线的曲率,单位切线向量相对曲线距离的导数的值:|dT/ds|
N dT/ds投影方向单位向量,垂直于T
B 平面T和N的单位法向量,即曲率的平面
τ曲线的扭率:|dB/ds|
g 重力常数
F 力学中力的标准符号
k 弹簧的弹簧常数
p i第i个物体的动量
H 物理系统的哈密尔敦函数,即位置和动量表示的能量
{Q, H} Q, H的泊松括号
以一个关于x的函数的形式表达的f(x)的积分
函数f 从a到b的定积分。
当f是正的且 a < b 时表示由x轴和直线y = a, y = b 及在这
些直线之间的函数曲线所围起来图形的面积
L(d) 相等子区间大小为d,每个子区间左端点的值为f的黎曼和
R(d) 相等子区间大小为d,每个子区间右端点的值为f的黎曼和
M(d) 相等子区间大小为d,每个子区间上的最大值为f的黎曼和
m(d) 相等子区间大小为d,每个子区间上的最小值为f的黎曼和
公式输入符号
≈≡≠=≤≥<>≮≯∷±+-× ÷/∫∮∝∞∧∨∑∏∪∩∈∵∴//⊥‖∠⌒⊙≌∽√
引理→Lemma
是辅助定理(auxiliary theorem),是为了叙述主要的定理而事先叙述的基本概念(concept)、基本原理(principle)、基本规则(rule)、基本特性(property).
推理→Deduce,Deduction
是证明的过程(proving),逻辑推理的过程(logic reasoning),也就是前提推演(derive,deduce)出一个定理(theorem)的过程(process,procedure).
公理(Axiom)是不需要证明的立论、陈述(statement),例如:过一点可画无数条直线;过两点只可画一条直线。
定理(theorem)是理论(theory)的核心,在科学上,定律(Law)是不可以证明的,是无法证明的。
从定律出发,得出一系列的定理,通常我们又将定理称为公式(formula),它们是物理量跟物理量(physical quantity)之间的关系,是一种恒等式关系(identity),不同于普通的方程(equation),普通的方程是有条件的成立(conditional equation),如x+2=5,只有x=3才能满足。
如电磁学上的高斯定理指的是电荷分布与电场强度分布的关系。
数学上的Law指的是运算规则,如分配律、结合律、交换律、传递律等等,theorem指的也是量与量(variable)之间的关系,如勾股定理、相交弦定理等等。
微积分中高斯定理,是将电磁场中的高斯定理进一步理论化,变成面积分与体积分之间的关系。
由定理、运算规则,加以拓展,形成理论。