高中数学归纳法课件(呕心沥血版)

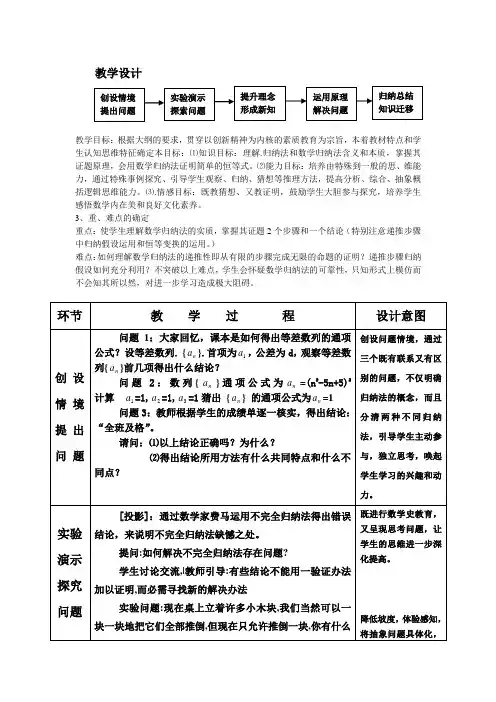
教学设计
教学目标：根据大纲的要求，贯穿以创新精神为内核的素质教育为宗旨，本着教材特点和学生认知思维特征确定本目标：⑴知识目标：理解.归纳法和数学归纳法含义和本质，掌握其证题原理，会用数学归纳法证明简单的恒等式。

⑵能力目标：培养由特殊到一般的思、维能力，通过特殊事例探究、引导学生观察、归纳、猜想等推理方法，提高分析、综合、抽象概括逻辑思维能力。

⑶.情感目标：既教猜想、又教证明，鼓励学生大胆参与探究，培养学生感悟数学内在美和良好文化素养。

3、重、难点的确定
重点：使学生理解数学归纳法的实质，掌握其证题2个步骤和一个结论（特别注意递推步骤中归纳假设运用和恒等变换的运用。

）
难点：如何理解数学归纳法的递推性即从有限的步骤完成无限的命题的证明？递推步骤归纳假设如何充分利用？不突破以上难点，学生会怀疑数学归纳法的可靠性，只知形式上模仿而不会知其所以然，对进一步学习造成极大阻碍。

附：板书设计。

数学归纳法课件高中数学课件教学内容：本节课的教学内容来自于高中数学教材必修三的第二章第三节，主要是数学归纳法。

数学归纳法是一种证明数学命题的方法，可以用来证明与自然数有关的命题。

本节课将详细介绍数学归纳法的定义、步骤和应用。

教学目标：1. 理解数学归纳法的定义和步骤，能够运用数学归纳法证明简单的数学命题。

2. 培养学生的逻辑思维能力和证明能力，提高学生解决数学问题的能力。

3. 通过数学归纳法的学习和运用，培养学生的数学兴趣和探索精神。

教学难点与重点：重点：数学归纳法的定义和步骤，以及如何运用数学归纳法证明数学命题。

难点：如何正确地选择归纳基础和归纳步骤，以及如何写出简洁明了的证明过程。

教具与学具准备：教具：多媒体课件、黑板、粉笔。

学具：笔记本、笔。

教学过程：一、情景引入（5分钟）教师通过一个简单的数学问题引导学生思考，如何用数学的方法来证明一个命题的正确性。

学生可以尝试用直观的方法来解决这个问题，为后续学习数学归纳法打下基础。

二、新课讲解（15分钟）1. 教师引导学生回顾已学的数学证明方法，提出数学归纳法的概念。

2. 教师详细讲解数学归纳法的两个步骤：归纳基础和归纳步骤。

3. 教师通过例题讲解数学归纳法的应用，引导学生理解并掌握数学归纳法的证明过程。

三、随堂练习（10分钟）学生分组讨论并完成随堂练习，教师巡回指导并解答学生的疑问。

四、课堂小结（5分钟）板书设计：板书数学归纳法板书内容：一、定义：数学归纳法是一种证明与自然数有关的命题的方法。

二、步骤：1. 归纳基础：证明当n取某个值时，命题成立。

2. 归纳步骤：假设当n取某个值时，命题成立，证明当n取这个值的下一个值时，命题也成立。

作业设计：1. 请用数学归纳法证明：对于任意的自然数n，都有n²+n+41是一个质数。

答案：当n=1时，1²+1+41=43，43是一个质数。

假设当n=k时，k²+k+41是一个质数。

当n=k+1时，(k+1)²+(k+1)+41=k²+2k+1+k+1+41=k²+k+42=(k²+k+41)+1。

数学归纳法完整版课件一、教学内容本节课将深入探讨数学归纳法，这是高中数学的一个重要部分。

教学内容基于教材第四章第四节“数学归纳法”，详细内容包括：1. 数学归纳法的定义与基本思想；2. 数学归纳法证明步骤；3. 数学归纳法在实际问题中的应用。

二、教学目标1. 理解数学归纳法的概念，掌握其基本步骤；2. 能够运用数学归纳法证明等式和不等式；3. 培养学生逻辑思维能力和解决实际问题的能力。

三、教学难点与重点重点：数学归纳法的定义、证明步骤及在实际问题中的应用。

难点：如何引导学生从具体问题中发现规律，并运用数学归纳法进行证明。

四、教具与学具准备1. 教具：PPT课件、黑板、粉笔；2. 学具：练习本、笔。

五、教学过程1. 实践情景引入（5分钟）利用PPT展示一个与数学归纳法相关的生活实例，引发学生思考，激发学习兴趣。

例：有一堆砖，第1块砖摞1厘米，以后每增加1块砖，摞的高度增加2厘米。

求第n块砖摞的高度。

2. 知识讲解（10分钟）详细讲解数学归纳法的定义、证明步骤，通过例题解释如何运用数学归纳法。

例题：证明1+2+3++n = n(n+1)/2。

3. 随堂练习（10分钟）让学生独立完成练习题，巩固所学知识。

练习题：证明2+4+6++2n = n(n+1)。

4. 互动讨论（5分钟）邀请几名学生分享解题思路，共同讨论解决方法。

六、板书设计1. 板书左侧：数学归纳法的定义与证明步骤；2. 板书右侧：例题及解题过程。

七、作业设计1. 作业题目：证明1^3+2^3+3^3++n^3 = (1+2++n)^2。

答案：数学归纳法证明如下：（1）当n=1时，等式成立；（2）假设当n=k时，等式成立，即1^3+2^3++k^3 = (1+2++k)^2；（3）当n=k+1时，等式左侧为1^3+2^3++k^3+(k+1)^3，根据归纳假设，等于(1+2++k)^2+(k+1)^3；（4）将(1+2++k)^2+(k+1)^3展开，得到(1+2++k+k+1)^2，即(1+2++n)^2，等式成立。