第2课时 立体图形的表面积和体积

立体几何的表面积公式和体积公式一、棱柱。

1. 直棱柱。

- 表面积公式：S = 2S_底+S_侧，其中S_底为底面多边形的面积，S_侧=Ch （C为底面多边形的周长，h为直棱柱的高）。

- 体积公式：V = S_底h。

2. 斜棱柱。

- 侧面积公式：S_侧=C'l（C'为直截面（垂直于侧棱的截面）的周长，l为侧棱长）。

- 体积公式：V = S_直截面l。

二、棱锥。

1. 棱锥。

- 表面积公式：S = S_底+S_侧，其中S_侧=∑_i = 1^n(1)/(2)l_ih_i（n为侧面三角形的个数，l_i为第i个侧面三角形的底边长，h_i为第i个侧面三角形的高）。

- 体积公式：V=(1)/(3)S_底h（h为棱锥的高）。

三、棱台。

1. 棱台。

- 表面积公式：S = S_上底+S_下底+S_侧，其中S_侧=∑_i =1^n(1)/(2)(l_i+l_i')h_i（n为侧面梯形的个数，l_i为棱台上底面第i条边的长，l_i'为棱台下底面第i条边的长，h_i为第i个侧面梯形的高）。

- 体积公式：V=(1)/(3)h(S_上底+S_下底+√(S_上底)S_{下底})（h为棱台的高）。

四、圆柱。

1. 圆柱。

- 表面积公式：S = 2π r^2+2π rh（r为底面半径，h为圆柱的高）。

- 体积公式：V=π r^2h。

五、圆锥。

1. 圆锥。

- 表面积公式：S=π r^2+π rl（r为底面半径，l为圆锥的母线长）。

- 体积公式：V=(1)/(3)π r^2h（h为圆锥的高，且l=√(r^2) + h^{2}）。

六、圆台。

1. 圆台。

- 表面积公式：S=π r^2+π R^2+π l(r + R)（r为上底面半径，R为下底面半径，l为圆台的母线长）。

- 体积公式：V=(1)/(3)π h(r^2+R^2+rR)（h为圆台的高）。

七、球。

1. 球。

- 表面积公式：S = 4π R^2（R为球的半径）。

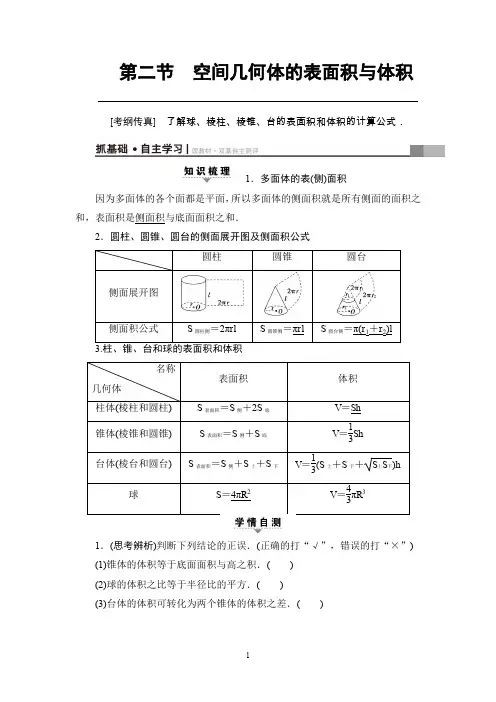
第二节空间几何体的表面积与体积————————————————————————————————[考纲传真]了解球、棱柱、棱锥、台的表面积和体积的计算公式．1．多面体的表(侧)面积因为多面体的各个面都是平面，所以多面体的侧面积就是所有侧面的面积之和，表面积是侧面积与底面面积之和．2．圆柱、圆锥、圆台的侧面展开图及侧面积公式1．(思考辨析)判断下列结论的正误．(正确的打“√”，错误的打“×”)(1)锥体的体积等于底面面积与高之积．()(2)球的体积之比等于半径比的平方．()(3)台体的体积可转化为两个锥体的体积之差．()(4)已知球O 的半径为R ，其内接正方体的边长为a ，则R ＝32a .( ) [答案] (1)× (2)× (3)√ (4)√2．(教材改编)已知圆锥的表面积等于12π cm 2，其侧面展开图是一个半圆，则底面圆的半径为( )A ．1 cmB ．2 cmC ．3 cmD.32 cmB [S 表＝πr 2＋πrl ＝πr 2＋πr ·2r ＝3πr 2＝12π，∴r 2＝4，∴r ＝2(cm)．] 3．(2015·全国卷Ⅰ)《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺．问：积及为米几何？”其意思为：“在屋内墙角处堆放米(如图7-2-1，米堆为一个圆锥的四分之一)，米堆底部的弧长为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少？”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放的米约有( )图7-2-1A ．14斛B ．22斛C ．36斛D ．66斛B [设米堆的底面半径为r 尺，则π2r ＝8，所以r ＝16π，所以米堆的体积为V ＝14×13π·r 2·5＝π12×⎝ ⎛⎭⎪⎫16π2×5≈3209(立方尺)．故堆放的米约有3209÷1.62≈22(斛)．故选B.]4．(2016·全国卷Ⅱ)体积为8的正方体的顶点都在同一球面上，则该球的表面积为( )A ．12π B.323π C ．8πD ．4πA [设正方体棱长为a ，则a 3＝8，所以a ＝2.所以正方体的体对角线长为23，所以正方体外接球的半径为3，所以球的表面积为4π·(3)2＝12π，故选A.]5．(2017·郑州质检)某几何体的三视图如图7-2-2所示(单位：cm)，则该几何体的体积是________cm 3.图7-2-2323 [由三视图可知该几何体是由棱长为 2 cm 的正方体与底面为边长为 2 cm 的正方形、高为2 cm 的四棱锥组成，V ＝V 正方体＋V 四棱锥＝8 cm 3＋83 cm 3＝323cm 3.](1)某几何体的三视图如图7-2-3所示，则该几何体的表面积等于( )图7-2-3A ．8＋22B ．11＋2 2C ．14＋2 2D ．15(2)(2016·全国卷Ⅰ)如图7-2-4，某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径．若该几何体的体积是28π3，则它的表面积是( )图7-2-4A ．17πB ．18πC ．20πD ．28π(1)B (2)A [(1)由三视图知，该几何体是一个直四棱柱，上、下底面为直角梯形，如图所示．直角梯形斜腰长为12＋12＝2，所以底面周长为4＋2，侧面积为4＋22＋2＋2＝8＋22，两底面的面积和为2×12×1×(1＋2)＝3.所以该几何体的表面积为8＋22＋3＝11＋2 2.(2)由几何体的三视图可知，该几何体是一个球体去掉上半球的14，得到的几何体如图．设球的半径为R ，则43πR 3－18×43πR 3＝283π，解得R ＝2.因此它的表面积为78×4πR 2＋34πR 2＝17π.故选A.][规律方法] 1.(1)多面体与旋转体的表面积等于侧面面积与底面面积之和．(2)简单组合体：应搞清各构成部分，并注意重合部分的处理．2．若以三视图的形式给出，解题的关键是对给出的三视图进行分析，从中发现几何体中各元素间的位置关系及数量关系，得到几何体的直观图，然后根据条件求解．[变式训练1] (2016·全国卷Ⅲ)如图7-2-5，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的表面积为( )【导学号：31222245】图7-2-5A ．18＋36 5B ．54＋18 5C ．90D ．81B [由三视图可知该几何体是底面为正方形的斜四棱柱，其中有两个侧面为矩形，另两个侧面为平行四边形，则表面积为(3×3＋3×6＋3×35)×2＝54＋18 5.故选B.](1)在梯形ABCD 中，∠ABC ＝π2，AD ∥BC ，BC ＝2AD ＝2AB ＝2.将梯形ABCD 绕AD 所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )A.2π3B.4π3C.5π3D ．2π(2)(2016·天津高考)已知一个四棱锥的底面是平行四边形，该四棱锥的三视图如图7-2-6所示(单位：m)，则该四棱锥的体积为________m 3.图7-2-6(1)C (2)2 [(1)过点C 作CE 垂直AD 所在直线于点E ，梯形ABCD 绕AD 所在直线旋转一周而形成的旋转体是由以线段AB 的长为底面圆半径，线段BC 为母线的圆柱挖去以线段CE 的长为底面圆半径，ED 为高的圆锥，如图所示．由于V 圆柱＝π·AB 2·BC ＝π×12×2＝2π， V 圆锥＝13π·CE 2·DE ＝13π·12×(2－1)＝π3，所以该几何体的体积V ＝V 圆柱－V 圆锥＝2π－π3＝5π3.(2)由三视图知，四棱锥的高为3，底面平行四边形的一边长为2，对应高为1，所以其体积V ＝13Sh ＝13×2×1×3＝2.][规律方法] 1.若所给定的几何体是柱体、锥体或台体，则可直接利用公式进行求解．2．若所给定的几何体的体积不能直接利用公式得出，则常用转换法(转换的原则是使底面面积和高易求)、分割法、补形法等方法进行求解．3．若以三视图的形式给出几何体，则应先根据三视图得到几何体的直观图，然后根据条件求解．[变式训练2] 一个几何体的三视图如图7-2-7所示(单位：m)，则该几何体的体积为________m 3.图7-2-783π [由几何体的三视图可知该几何体由两个圆锥和一个圆柱构成，其中圆锥的底面半径和高均为1，圆柱的底面半径为1且其高为2，故所求几何体的体积为V ＝13π×12×1×2＋π×12×2＝83π.]111V 的球．若AB⊥BC，AB＝6，BC＝8，AA1＝3，则V的最大值是()A．4π B.9π2C．6π D.32π3B[由AB⊥BC，AB＝6，BC＝8，得AC＝10，要使球的体积V最大，则球与直三棱柱的部分面相切，若球与三个侧面相切，设底面△ABC的内切圆的半径为r.则12×6×8＝12×(6＋8＋10)·r，则r＝2.此时2r＝4＞3，不合题意．因此球与三棱柱的上、下底面相切时，球的半径R最大．由2R＝3，即R＝3 2.故球的最大体积V＝43πR3＝92π.][迁移探究1]若本例中的条件变为“直三棱柱ABC-A1B1C1的6个顶点都在球O的球面上”，若AB＝3，AC＝4，AB⊥AC，AA1＝12，求球O的表面积．[解]将直三棱柱补形为长方体ABEC-A′B′E′C′，则球O是长方体ABEC-A′B′E′C′的外接球，∴体对角线BC′的长为球O的直径．因此2R＝32＋42＋122＝13，故S球＝4πR2＝169π.[迁移探究2]若本例中的条件变为“正四棱锥的顶点都在球O的球面上”，若该棱锥的高为4，底面边长为2，求该球的体积．[解]如图，设球心为O，半径为r，则在Rt △AOF 中，(4－r )2＋(2)2＝r 2， 解得r ＝94，则球O 的体积V 球＝43πr 3＝43π×⎝ ⎛⎭⎪⎫943＝243π16.[规律方法] 1.与球有关的组合体问题，一种是内切，一种是外接．球与旋转体的组合通常是作它们的轴截面解题，球与多面体的组合，通过多面体的一条侧棱和球心，或“切点”、“接点”作出截面图，把空间问题化归为平面问题．2．若球面上四点P ，A ，B ，C 中P A ，PB ，PC 两两垂直或三棱锥的三条侧棱两两垂直，可构造长方体或正方体确定直径解决外接问题．[变式训练3] (2015·全国卷Ⅱ)已知A ，B 是球O 的球面上两点，∠AOB ＝90°，C 为该球面上的动点．若三棱锥O -ABC 体积的最大值为36，则球O 的表面积为( )A ．36πB ．64πC ．144πD ．256πC [如图，设球的半径为R ，∵∠AOB ＝90°，∴S △AOB ＝12R 2.∵V O -ABC ＝V C -AOB ，而△AOB 面积为定值，∴当点C 到平面AOB 的距离最大时，V O -ABC 最大，∴当C 为与球的大圆面AOB 垂直的直径的端点时，体积V O -ABC 最大为13×12R2×R＝36，∴R＝6，∴球O的表面积为4πR2＝4π×62＝144π.故选C.][思想与方法]1．转化与化归思想：计算旋转体的侧面积时，一般采用转化的方法来进行，即将侧面展开化为平面图形，“化曲为直”来解决，因此要熟悉常见旋转体的侧面展开图的形状及平面图形面积的求法．2．求体积的两种方法：①割补法：求一些不规则几何体的体积时，常用割补法转化成已知体积公式的几何体进行解决．②等积法：等积法包括等面积法和等体积法．等积法的前提是几何图形(或几何体)的面积(或体积)通过已知条件可以得到，利用等积法可以用来求解几何图形的高或几何体的高．[易错与防范]1．求组合体的表面积时，要注意各几何体重叠部分的处理，防止重复计算．2．底面是梯形的四棱柱侧放时，容易和四棱台混淆，在识别时要紧扣定义，以防出错．课时分层训练(三十九)空间几何体的表面积与体积A组基础达标(建议用时：30分钟)一、选择题1．已知等腰直角三角形的直角边的长为2，将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为()A.22π3 B.42π3C．22πD．42πB[依题意知，该几何体是以2为底面半径，2为高的两个同底圆锥组成的组合体，则其体积V＝13π(2)2×22＝423π.]2．已知底面边长为1，侧棱长为2的正四棱柱的各顶点均在同一个球面上，则该球的体积为()【导学号：31222246】A.32π3B．4πC．2π D.4π3D[依题意可知正四棱柱体对角线的长度等于球的直径，可设球半径为R，则2R＝12＋12＋(2)2＝2，解得R＝1，所以V＝4π3R3＝4π3.]3．(2016·山东高考)一个由半球和四棱锥组成的几何体，其三视图如图7-2-8所示，则该几何体的体积为()图7-2-8A.13＋23πB.13＋23πC.13＋26πD ．1＋26πC [由三视图知，该四棱锥是底面边长为1，高为1的正四棱锥，结合三视图可得半球半径为22，从而该几何体的体积为13×12×1＋12×43π×⎝ ⎛⎭⎪⎫223＝13＋26π.故选C.]4．某几何体的三视图如图7-2-9所示，且该几何体的体积是3，则正视图中的x 的值是( )【导学号：31222247】图7-2-9A ．2 B.92 C.32D ．3D [由三视图知，该几何体是四棱锥，底面是直角梯形，且S底＝12×(1＋2)×2＝3，∴V＝13x·3＝3，解得x＝3.]5．(2016·江南名校联考)一个四面体的三视图如图7-2-10所示，则该四面体的表面积是()图7-2-10A．1＋ 3 B．2＋ 3C．1＋2 2 D．2 2B[四面体的直观图如图所示．侧面SAC⊥底面ABC，且△SAC与△ABC均为腰长是2的等腰直角三角形，SA＝SC＝AB＝BC＝2，AC＝2.设AC的中点为O，连接SO，BO，则SO⊥AC，∴SO⊥平面ABC，∴SO⊥BO.又OS＝OB＝1，∴SB＝2，故△SAB与△SBC均是边长为2的正三角形，故该四面体的表面积为2×1 2×2×2＋2×34×(2)2＝2＋ 3.]二、填空题6．现有橡皮泥制作的底面半径为5、高为4的圆锥和底面半径为2，高为8的圆柱各一个，若将它们重新制作成总体积与高均保持不变，但底面半径相同的新的圆锥和圆柱各一个，则新的底面半径为______．【导学号：31222248】7 [设新的底面半径为r ，由题意得13×π×52×4＋π×22×8＝13×π×r 2×4＋π×r 2×8， ∴r 2＝7，∴r ＝7.]7．一个六棱锥的体积为23，其底面是边长为2的正六边形，侧棱长都相等，则该六棱锥的侧面积为________．12 [设正六棱锥的高为h ，棱锥的斜高为h ′. 由题意，得13×6×12×2×3×h ＝23，∴h ＝1，∴斜高h ′＝12＋(3)2＝2，∴S 侧＝6×12×2×2＝12.]8．某几何体的三视图如图7-2-11所示，则该几何体的体积为________．图7-2-11136π [由三视图可知，该几何体是一个圆柱和半个圆锥组合而成的几何体，其体积为π×12×2＋12×13π×12×1＝136π.]三、解答题9．如图7-2-12，在三棱锥D -ABC 中，已知BC ⊥AD ，BC ＝2，AD ＝6，AB ＋BD ＝AC ＋CD ＝10，求三棱锥D -ABC 的体积的最大值．图7-2-12[解] 由题意知，线段AB ＋BD 与线段AC ＋CD 的长度是定值，∵棱AD 与棱BC 相互垂直，设d 为AD 到BC 的距离，4分则V D -ABC＝AD ·BC ×d ×12×13＝2d ， 当d 最大时，V D -ABC 体积最大.8分 ∵AB ＋BD ＝AC ＋CD ＝10， ∴当AB ＝BD ＝AC ＝CD ＝5时， d 有最大值42－1＝15.此时V ＝215.12分10．四面体ABCD 及其三视图如图7-2-13所示，平行于棱AD ，BC 的平面分别交四面体的棱AB ，BD ，DC ，CA 于点E ，F ，G ，H .图7-2-13(1)求四面体ABCD 的体积； (2)证明：四边形EFGH 是矩形．[解] (1)由该四面体的三视图可知，BD ⊥DC ，BD ⊥AD ，AD ⊥DC ，BD ＝DC ＝2，AD ＝1，∴AD ⊥平面BDC ，3分∴四面体ABCD 的体积V ＝13×12×2×2×1＝23.5分(2)证明：∵BC ∥平面EFGH ，平面EFGH ∩平面BDC ＝FG ，平面EFGH ∩平面ABC ＝EH ，8分∴BC ∥FG ，BC ∥EH ，∴FG ∥EH . 同理EF ∥AD ，HG ∥AD ，∴EF ∥HG ， ∴四边形EFGH 是平行四边形． 又∵AD ⊥平面BDC ，∴AD ⊥BC ，∴EF ⊥FG . ∴四边形EFGH 是矩形.12分B 组 能力提升 (建议用时：15分钟)1．(2015·全国卷Ⅰ)圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体，该几何体三视图中的正视图和俯视图如图7-2-14所示．若该几何体的表面积为16＋20π，则r ＝( )图7-2-14A ．1B ．2C ．4D ．8B [如图，该几何体是一个半球与一个半圆柱的组合体，球的半径为r ，圆柱的底面半径为r ，高为2r ，则表面积S ＝12×4πr 2＋πr 2＋4r 2＋πr ·2r ＝(5π＋4)r 2.又S ＝16＋20π，∴(5π＋4)r 2＝16＋20π，∴r 2＝4，r ＝2，故选B.]2．三棱锥P -ABC 中，D ，E 分别为PB ，PC 的中点，记三棱锥D -ABE 的体积为V 1，P -ABC 的体积为V 2，则V 1V 2＝________.14 [设点A 到平面PBC 的距离为h .∵D ，E 分别为PB ，PC 的中点，∴S △BDE ＝14S △PBC ， ∴V 1V 2＝V A -DBEV A -PBC＝13S △BDE ·h 13S △PBC ·h＝14.] 3．(2016·全国卷Ⅰ)如图7-2-15，已知正三棱锥P -ABC 的侧面是直角三角形，P A ＝6，顶点P 在平面ABC 内的正投影为点D ，D 在平面P AB 内的正投影为点E ，连接PE 并延长交AB 于点G.图7-2-15(1)证明：G 是AB 的中点；(2)在图中作出点E 在平面P AC 内的正投影F (说明作法及理由)，并求四面体PDEF 的体积．[解] (1)证明：因为P 在平面ABC 内的正投影为D ， 所以AB ⊥PD.因为D在平面P AB内的正投影为E，所以AB⊥DE.3分因为PD∩DE＝D，所以AB⊥平面PED，故AB⊥PG.又由已知可得，P A＝PB，所以G是AB的中点.5分(2)在平面P AB内，过点E作PB的平行线交P A于点F，F即为E在平面P AC内的正投影.7分理由如下：由已知可得PB⊥P A，PB⊥PC，又EF∥PB，所以EF⊥P A，EF⊥PC.又P A∩PC＝P，因此EF⊥平面P AC，即点F为E在平面P AC内的正投影．连接CG，因为P在平面ABC内的正投影为D，所以D是正三角形ABC的中心．由(1)知，G是AB的中点，所以D在CG上，故CD＝23CG.10分由题设可得PC⊥平面P AB，DE⊥平面P AB，所以DE∥PC，因此PE＝23PG，DE＝13PC.由已知，正三棱锥的侧面是直角三角形且P A＝6，可得DE＝2，PE＝2 2. 在等腰直角三角形EFP中，可得EF＝PF＝2，所以四面体PDEF的体积V＝13×12×2×2×2＝43.12分。

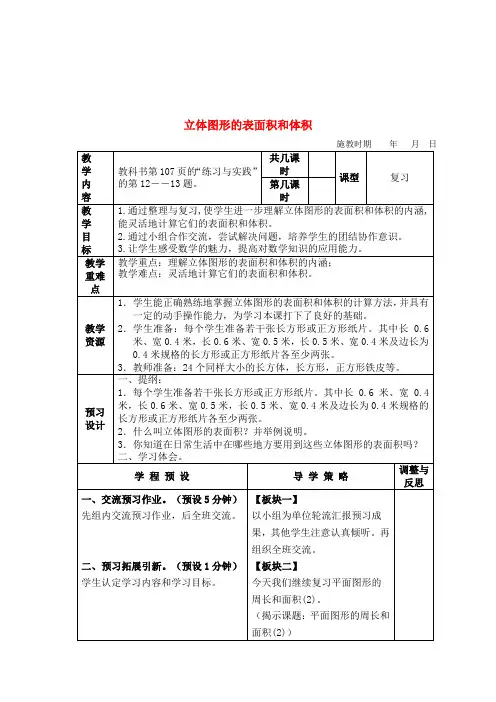
第2讲 空间几何体的表面积与体积一、知识梳理1．多面体的表(侧)面积多面体的各个面都是平面，则多面体的侧面积就是所有侧面的面积之和，表面积是侧面积与底面面积之和．2．圆柱、圆锥、圆台的侧面展开图及侧面积公式圆柱 圆锥 圆台侧面展开图侧面积公式S 圆柱侧＝2πrl S 圆锥侧＝πrlS 圆台侧＝π(r ＋r ′)l表面积 体积柱体 (棱柱和圆柱)S 表面积＝S 侧＋2S 底 V ＝S 底h锥体 (棱锥和圆锥)S 表面积＝S 侧＋S 底 V ＝13S 底h 台体 (棱台和圆台)S 表面积＝S 侧＋S 上＋S 下V ＝13(S 上＋S 下＋S 上S 下)h 球S ＝4πR 2 V ＝43πR 31．正方体与球的切、接常用结论 正方体的棱长为a ，球的半径为R ，(1)若球为正方体的外接球，则2R ＝3a ； (2)若球为正方体的内切球，则2R ＝a ；(3)若球与正方体的各棱相切，则2R＝2a .2．长方体共顶点的三条棱长分别为a ，b，c ，外接球的半径为R ，则2R ＝a 2＋b 2＋c 2. 二、习题改编1．(必修2P27练习1改编)已知圆锥的表面积等于12π cm 2，其侧面展开图是一个半圆，则底面圆的半径为 cm.解析：由题意，得S 表＝πr 2＋πrl ＝πr 2＋πr ·2r ＝3πr 2＝12π，解得r 2＝4，所以r ＝2(cm)．答案：22．(必修2P27例4改编)圆柱的底面直径与高都等于球的直径，则球的体积与圆柱的体积比V 球∶V 柱为 ．解析：设球的半径为R ，则V 球V 柱＝43πR 3πR 2×2R ＝23.答案：23一、思考辨析判断正误(正确的打“√”，错误的打“×”) (1)多面体的表面积等于各个面的面积之和．( ) (2)锥体的体积等于底面积与高之积．( ) (3)球的体积之比等于半径比的平方．( )(4)简单组合体的体积等于组成它的简单几何体体积的和或差．( ) (5)长方体既有外接球又有内切球．( ) 答案：(1)√ (2)× (3)× (4)√ (5)× 二、易错纠偏常见误区(1)锥体的高与底面不清楚致误； (2)不会分类讨论致误．1．如图，长方体ABCD ­A 1B 1C 1D 1的体积是120，E 为CC 1的中点，则三棱锥E ­BCD 的体积是 ．解析：设长方体中BC ＝a ，CD ＝b ，CC 1＝c ，则abc ＝120，所以V E ­BCD＝13×12ab ×12c ＝112abc ＝10. 答案：102．将一个相邻边长分别为4π，8π的矩形卷成一个圆柱，则这个圆柱的表面积是 ．解析：当底面周长为4π时，底面圆的半径为2，两个底面的面积之和是8π；当底面周长为8π时，底面圆的半径为4，两个底面的面积之和为32π.无论哪种方式，侧面积都是矩形的面积32π2，故所求的表面积是32π2＋8π或32π2＋32π.答案：32π2＋8π或32π2＋32π空间几何体的表面积(师生共研)(1)(2018·高考全国卷Ⅰ)已知圆柱的上、下底面的中心分别为O 1，O 2，过直线O 1O 2的平面截该圆柱所得的截面是面积为8的正方形，则该圆柱的表面积为( )A ．122πB ．12πC ．82πD ．10π(2)(2020·湖南省五市十校联考)某四棱锥的三视图如图所示，其侧视图是等腰直角三角形，俯视图的轮廓是直角梯形，则该四棱锥的各侧面面积的最大值为( )A ．8B ．4 5C ．8 2D ．12 2【解析】 (1)因为过直线O 1O 2的平面截该圆柱所得的截面是面积为8的正方形，所以圆柱的高为22，底面圆的直径为22，所以该圆柱的表面积为2×π×(2)2＋22π×22＝12π.(2)由三视图可知该几何体是一个底面为直角梯形，高为4的四棱锥，如图，其中侧棱PA ⊥平面ABCD ，PA ＝4，AB ＝4，BC ＝4，CD ＝6，所以AD ＝25，PD ＝6，PB ＝42，连接AC ，则AC ＝42，所以PC ＝43，显然在各侧面面积中△PCD 的面积最大，又PD ＝CD ＝6，所以PC 边上的高为62－⎝ ⎛⎭⎪⎫4322＝26，所以S △PCD ＝12×43×26＝122，故该四棱锥的各侧面面积的最大值为122，故选D.【答案】 (1)B (2)D空间几何体表面积的求法(1)以三视图为载体的几何体的表面积问题，关键是分析三视图确定几何体中各元素之间的位置关系及数量关系．(2)多面体的表面积是各个面的面积之和；组合体的表面积问题应注意衔接部分的处理． (3)旋转体的表面积问题应注意其侧面展开图的应用．1.(2020·江西七校第一次联考)一个半径为1的球对称削去了三部分，其俯视图如图所示，那么该立体图形的表面积为( )A ．3πB ．4πC ．5πD ．6π解析：选C.由题中俯视图可知该球被平均分成6部分，削去了3部分，剩余的3部分为该几何体，所以该立体图形的表面积为2×π×12＋3×π×12＝5π，故选C.2．(2020·辽宁丹东质量测试(一))一个圆锥的轴截面是面积为1的等腰直角三角形，则这个圆锥的侧面积为 ．解析：设圆锥的底面圆半径为r ，因为圆锥的轴截面是面积为1的等腰直角三角形，所以等腰直角三角形的斜边长为2r ，斜边上的高为r ，所以12×2r ×r ＝1，解得r ＝1，圆锥的母线长l ＝12＋12＝2，圆锥的侧面积为πrl ＝2π. 答案：2π空间几何体的体积(多维探究) 角度一 求简单几何体的体积(1)(2020·石家庄质量检测)某几何体的三视图如图所示(图中小正方形网格的边长为1)，则该几何体的体积是( )A ．8B ．6C ．4D ．2(2)将一张边长为12 cm 的正方形纸片按如图(1)所示将阴影部分的四个全等的等腰三角形裁去，余下部分沿虚线折叠并拼成一个有底的正四棱锥，如图(2)放置，如果正四棱锥的主视图是正三角形，如图(3)所示，则正四棱锥的体积是( )A.3236 cm 3B.6436 cm 3C.3232 cm 3D ．6432 cm 3【解析】 (1)由三视图可得该几何体为底面是直角梯形的直四棱柱(如图所示)，其中底面直角梯形的上、下底分别为1，2，高为2，直四棱柱的高为2，所以该几何体的体积为（1＋2）×22×2＝6，故选B.(2)设折成的四棱锥的底面边长为a cm ，高为h cm ，则h ＝32a cm ，由题设可得四棱锥侧面的高等于四棱锥的底面边长，所以12a ＋a ＝12×22⇒a ＝42，所以四棱锥的体积V ＝13×(42)2×32×42＝6463cm 3，故选B. 【答案】 (1)B (2)B简单几何体体积的求法对于规则几何体，直接利用公式计算即可．若已知三视图求体积，应注意三视图中的垂直关系在几何体中的位置，确定几何体中的线面垂直等关系，进而利用公式求解．角度二 求组合体的体积(2020·唐山市摸底考试)已知某几何体的三视图如图所示(俯视图中曲线为四分之一圆弧)，则该几何体的表面积为( )A ．1－π4B ．3＋π2C ．2＋π4D ．4【解析】 由题设知，该几何体是棱长为1的正方体被截去底面半径为1的14圆柱后得到的，如图所示，所以表面积S ＝2×(1×1－14×π×12)＋2×(1×1)＋14×2π×1×1＝4.故选D.【答案】 D(1)处理体积问题的思路(2)求体积的常用方法 直接法 对于规则的几何体，利用相关公式直接计算割补法把不规则的几何体分割成规则的几何体，然后进行体积计算；或者把不规则的几何体补成规则的几何体，不熟悉的几何体补成熟悉的几何体，便于计算 等体积法选择合适的底面来求几何体体积，常用于求三棱锥的体积，即利用三棱锥的任一个面作为三棱锥的底面进行等体积变换1．(2019·高考北京卷)某几何体是由一个正方体去掉一个四棱柱所得，其三视图如图所示．如果网格纸上小正方形的边长为1，那么该几何体的体积为 ．解析：如图，由三视图可知，该几何体为正方体ABCD ­A 1B 1C 1D 1去掉四棱柱B 1C 1GF ­A 1D 1HE 所得，其中正方体ABCD ­A 1B 1C 1D 1的体积为64，VB 1C 1GF ­A 1D 1HE ＝(4＋2)×2×12×4＝24，所以该几何体的体积为64－24＝40.答案：402．(2019·高考全国卷Ⅲ)学生到工厂劳动实践，利用3D 打印技术制作模型．如图，该模型为长方体ABCD ­A 1B 1C 1D 1挖去四棱锥O ­EFGH 后所得的几何体，其中O 为长方体的中心，E ，F ，G ，H 分别为所在棱的中点，AB ＝BC ＝6 cm ，AA 1＝4 cm.3D 打印所用原料密度为0.9 g/cm 3.不考虑打印损耗，制作该模型所需原料的质量为 g.解析：长方体ABCD ­A 1B 1C 1D 1的体积V 1＝6×6×4＝144(cm 3)，而四棱锥O ­EFGH 的底面积为矩形BB 1C 1C 的面积的一半，高为AB 长的一半，所以四棱锥O ­EFGH 的体积V 2＝13×12×4×6×3＝12(cm 3)，所以长方体ABCD ­A 1B 1C 1D 1挖去四棱锥O ­EFGH 后所得几何体的体积V ＝V 1－V 2＝132(cm 3)，所以制作该模型所需原料的质量为132×0.9＝118.8(g)．答案：118.8球与空间几何体的接、切问题(师生共研)(1)若直三棱柱ABC ­A 1B 1C 1的6个顶点都在球O 的球面上，且AB ＝3，AC ＝4，AB⊥AC ，AA 1＝12，则球O 的表面积为 ．(2)(一题多解)(2019·高考天津卷)已知四棱锥的底面是边长为2的正方形，侧棱长均为 5.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点，另一个底面的圆心为四棱锥底面的中心，则该圆柱的体积为 ．【解析】 (1)将直三棱柱补形为长方体ABEC ­A 1B 1E 1C 1，则球O 是长方体ABEC ­A 1B 1E 1C 1的外接球．所以体对角线BC 1的长为球O 的直径． 因此2R ＝32＋42＋122＝13. 故S 球＝4πR 2＝169π.(2)法一：由题意得圆柱的高为四棱锥高的一半，底面圆的直径为以四棱锥侧棱的四个中点为顶点的正方形的对角线，易求得圆柱的底面圆的直径为1，高为1，所以该圆柱的体积V ＝π×⎝ ⎛⎭⎪⎫122×1＝π4.法二：由题可得，四棱锥底面对角线的长为2，则圆柱底面的半径为12，易知四棱锥的高为5－1＝2，故圆柱的高为1，所以该圆柱的体积为π×⎝ ⎛⎭⎪⎫122×1＝π4. 【答案】 (1)169π (2)π4处理球的“切”“接”问题的求解策略解决与球有关的切、接问题，其通法是作截面，将空间几何问题转化为平面几何问题求解，其解题的思维流程是：1．正四棱锥P ­ABCD 的侧棱和底面边长都等于22，则它的外接球的表面积是( ) A ．16π B ．12π C．8πD ．4π解析：选A.设正四棱锥的外接球半径为R ，顶点P 在底面上的射影为O ，因为OA ＝12AC＝12 AB 2＋BC 2＝12（22）2＋（22）2＝2，所以PO ＝PA 2－OA 2＝（22）2－22＝2.又OA ＝OB ＝OC ＝OD ＝2，由此可知R ＝2，于是S 球＝4πR 2＝16π.2．设球O 内切于正三棱柱ABC ­A 1B 1C 1，则球O 的体积与正三棱柱ABC ­A 1B 1C 1的体积的比值为 ．解析：设球O 半径为R ，正三棱柱ABC ­A 1B 1C 1的底面边长为a ，则R ＝33×a 2＝36a ，即a ＝23R ，又正三棱柱ABC ­A 1B 1C 1的高为2R ，所以球O 的体积与正三棱柱ABC ­A 1B 1C 1的体积的比值为43πR 334a 2×2R ＝43πR 334×12R 2×2R ＝23π27.答案：23π27核心素养系列14 直观想象——数学文化与空间几何体(2020·甘肃、青海、宁夏3月联考)汉朝时，张衡得出圆周率的平方除以16等于58.如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，俯视图中的曲线为圆，利用张衡的结论可得该几何体的体积为( )A ．32B ．40 C.32103D ．40103【解析】 将三视图还原成如图所示的几何体：半个圆柱和半个圆锥的组合体，底面半径为2，高为4，则体积V ＝12π×22×4＋13×12π×22×4＝323π，因为圆周率的平方除以16等于58，即π216＝58，所以π＝10，所以V ＝32103.故选C.【答案】 C本题是数学文化与三视图结合，主要是根据几何体的三视图及三视图中的数据，求几何体的体积或侧(表)面积．此类问题难点：一是根据三视图的形状特征确定几何体的结构特征；二是将三视图中的数据转化为几何体的几何度量．考查了直观想象这一核心素养．(2020·安徽六安一中模拟(四))我国南北朝时期的数学家祖暅提出了一条原理：“幂势既同，则积不容异”．意思是：两个等高的几何体若在所有等高处的水平截面的面积相等，则这两个几何体的体积相等．椭球体是椭圆绕其轴旋转所成的旋转体．如图，将底面直径都为2b ，高皆为a 的半椭球体和已被挖去了圆锥体的圆柱放置于同一平面β上，用平行于平面β且与平面β任意距离d 处的平面截这两个几何体，可横截得到S 圆及S 环两截面．可以证明S 圆＝S 环总成立．据此，短半轴长为1，长半轴长为3的椭球体的体积是 ．解析：因为S 圆＝S 环总成立，所以半椭球体的体积为πb 2a －13πb 2a ＝23πb 2a ，所以椭球体的体积V ＝43πb 2a .因为椭球体的短半轴长为1，长半轴长为3. 所以椭球体的体积V ＝43πb 2a ＝43π×12×3＝4π.答案：4π[基础题组练]1．(2020·安徽合肥质检)已知圆锥的高为3，底面半径为4，若一球的表面积与此圆锥侧面积相等，则该球的半径为( )A ．5 B. 5 C ．9D ．3解析：选B.因为圆锥的底面半径r ＝4，高h ＝3，所以圆锥的母线l ＝5，所以圆锥的侧面积S ＝πrl ＝20π，设球的半径为R ，则4πR 2＝20π，所以R ＝5，故选B.2．(2020·蓉城名校第一次联考)已知一个几何体的正视图和侧视图如图1所示，其俯视图用斜二测画法所画出的水平放置的直观图是一个直角边长为1的等腰直角三角形(如图2所示)，则此几何体的体积为( )A ．1 B. 2 C ．2D ．2 2解析：选B.根据直观图可得该几何体的俯视图是一个直角边长分别是2和2的直角三角形(如图所示)，根据三视图可知该几何体是一个三棱锥，且三棱锥的高为3，所以体积V ＝13×⎝ ⎛⎭⎪⎫12×2×2×3＝ 2.故选B.3．(2020·武汉市武昌调研考试)中国古代数学名著《九章算术》中记载了公元前344年商鞅监制的一种标准量器——商鞅铜方升，其三视图如图所示(单位：寸)，若π取3，其体积为12.6(单位：立方寸)，则图中的x 为( )A ．1.2B ．1.6C ．1.8D ．2.4解析：选B.该几何体是一个组合体，左边是一个底面半径为12的圆柱，右边是一个长、宽、高分别为5.4－x ，3，1的长方体，所以组合体的体积V ＝V 圆柱＋V 长方体＝π·⎝ ⎛⎭⎪⎫122×x ＋(5.4－x )×3×1＝12.6(其中π＝3)，解得x ＝1.6.故选B.4．(2020·辽宁大连第一次(3月)双基测试)我国古代数学名著《九章算术》中有如下问题：“今有羡除，下广六尺，上广一丈，深三尺，末广八尺，无深，袤七尺．问积几何 ”．羡除是一个五面体，其中三个面是梯形，另两个面是三角形，已知一个羡除的三视图如图中粗线所示，其中小正方形网格的边长为1，则该羡除的表面中，三个梯形的面积之和为( )A ．40B ．43C ．46D ．47解析：选C.由三视图可知，该几何体的直观图如图所示，其中平面ABCD ⊥平面ABEF ，CD ＝2，AB ＝6，EF ＝4，等腰梯形ABEF 的高为3，等腰梯形ABCD 的高为4，等腰梯形FECD的高为9＋16＝5，三个梯形的面积之和为2＋62×4＋4＋62×3＋2＋42×5＝46，故选C.5．(2020·辽宁沈阳东北育才学校五模)将半径为3，圆心角为2π3的扇形围成一个圆锥，则该圆锥的内切球的表面积为( )A ．πB ．2πC ．3πD ．4π解析：选B.将半径为3，圆心角为2π3的扇形围成一个圆锥，设圆锥的底面圆半径为R ，则有2πR ＝3×2π3，所以R ＝1.设圆锥的内切球半径为r ，圆锥的高为h ，内切球球心必在圆锥的高线上，因为圆锥的母线长为3，所以h ＝9－1＝22，所以有rh －r ＝R 3，解得r ＝22，因此内切球的表面积S ＝4πr 2＝2π.故选B. 6．现有橡皮泥制作的底面半径为5、高为4的圆锥和底面半径为2、高为8的圆柱各一个．若将它们重新制作成总体积与高均保持不变，但底面半径相同的新的圆锥和圆柱各一个，则新的底面半径为 ．解析：设新的底面半径为r ，由题意得13πr 2·4＋πr 2·8＝13π×52×4＋π×22×8，解得r ＝7.答案：77．(2020·沈阳质量监测)某四棱锥的三视图如图所示，则该四棱锥的侧面积是 ．解析：由三视图可知该几何体是一个四棱锥，记为四棱锥P ­ABCD ，如图所示，其中PA ⊥底面ABCD ，四边形ABCD 是正方形，且PA ＝2，AB ＝2，PB ＝22，所以该四棱锥的侧面积S 是四个直角三角形的面积和，即S ＝2×⎝ ⎛⎭⎪⎫12×2×2＋12×2×22＝4＋4 2.答案：4＋4 28．(2020·长春市质量监测(一))已知一所有棱长都是2的三棱锥，则该三棱锥的体积为 ．解析：记所有棱长都是2的三棱锥为P ­ABC ，如图所示，取BC 的中点D ，连接AD ，PD ，作PO ⊥AD 于点O ，则PO ⊥平面ABC ，且OP ＝63×2＝233，故三棱锥P ­ABC 的体积V ＝13S △ABC·OP ＝13×34×(2)2×233＝13.答案：139．如图，在四边形ABCD 中，∠DAB ＝90°，∠ADC ＝135°，AB ＝5，CD ＝22，AD ＝2，求四边形ABCD 绕AD 旋转一周所成几何体的表面积及体积．解：由已知得CE ＝2，DE ＝2，CB ＝5，S 表面积＝S圆台侧＋S圆台下底＋S圆锥侧＝π(2＋5)×5＋π×25＋π×2×22＝(60＋42)π，V ＝V 圆台－V圆锥＝13(π·22＋π·52＋22·52π2)×4－13π×22×2＝1483π. 10.(应用型)现需要设计一个仓库，它由上下两部分组成，上部的形状是正四棱锥P ­A 1B 1C 1D 1，下部的形状是正四棱柱ABCD ­A 1B 1C 1D 1(如图所示)，并要求正四棱柱的高O 1O 是正四棱锥的高PO 1的4倍，若AB ＝6 m ，PO 1＝2 m ，则仓库的容积是多少？解：由PO 1＝2 m ，知O 1O ＝4PO 1＝8 m.因为A 1B 1＝AB ＝6 m ，所以正四棱锥P ­A 1B 1C 1D 1的体积V 锥＝13·A 1B 21·PO 1＝13×62×2＝24(m 3)；正四棱柱ABCD ­A 1B 1C 1D 1的体积V 柱＝AB 2·O 1O ＝62×8＝288(m 3)，所以仓库的容积V ＝V 锥＋V 柱＝24＋288＝312(m 3)． 故仓库的容积是312 m 3.[综合题组练]1．(2019·高考全国卷Ⅰ)已知三棱锥P­ABC的四个顶点在球O的球面上，PA＝PB＝PC，△ABC是边长为2的正三角形，E，F分别是PA，AB的中点，∠CEF＝90°，则球O的体积为( )A．86πB．46πC．26πD．6π解析：选D.因为点E，F分别为PA，AB的中点，所以EF∥PB，因为∠CEF＝90°，所以EF⊥CE，所以PB⊥CE.取AC的中点D，连接BD，PD，易证AC⊥平面BDP，所以PB⊥AC，又AC∩CE＝C，AC，CE⊂平面PAC，所以PB⊥平面PAC，所以PB⊥PA，PB⊥PC，因为PA＝PB＝PC，△ABC为正三角形，所以PA⊥PC，即PA，PB，PC两两垂直，将三棱锥P­ABC放在正方体中如图所示．因为AB＝2，所以该正方体的棱长为2，所以该正方体的体对角线长为6，所以三棱锥P­ABC的外接球的半径R＝62，所以球O的体积V＝43πR3＝43π⎝⎛⎭⎪⎫623＝6π，故选D.2．如图，正方体ABCD­A1B1C1D1的棱长为3，线段B1D1上有两个动点E，F且EF＝1，则当E，F移动时，下列结论不正确的是( )A．AE∥平面C1BDB．四面体ACEF的体积不为定值C．三棱锥A­BEF的体积为定值D．四面体ACDF的体积为定值解析：选B.对于A，如图1，AB1∥DC1，易证AB1∥平面C1BD，同理AD1∥平面C1BD，且AB 1∩AD 1＝A ，所以平面AB 1D 1∥平面C 1BD ，又AE ⊂平面AB 1D 1，所以AE ∥平面C 1BD ，A 正确；对于B ，如图2，S △AEF ＝12EF ·h 1＝12×1×（32）2－⎝ ⎛⎭⎪⎫3222＝364，点C 到平面AEF的距离为点C 到平面AB 1D 1的距离d 为定值，所以V A ­CEF＝V C ­AEF＝13×364×d ＝64d 为定值，所以B 错误；对于C ，如图3，S △BEF ＝12×1×3＝32，点A 到平面BEF 的距离为A 到平面BB 1D 1D 的距离d 为定值，所以V A ­BEF＝13×32×d ＝12d 为定值，C 正确；对于D ，如图4，四面体ACDF 的体积为V A ­CDF＝V F ­ACD＝13×12×3×3×3＝92为定值，D 正确．3．(2020·东北师大附中、重庆一中等校联合模拟)若侧面积为4π的圆柱有一外接球O ，当球O 的体积取得最小值时，圆柱的表面积为 ．解析：设圆柱的底面圆半径为r ，高为h ， 则球的半径R ＝r 2＋⎝ ⎛⎭⎪⎫h 22.因为球的体积V ＝4π3R 3，故V 最小当且仅当R 最小．圆柱的侧面积为2πrh ＝4π，所以rh ＝2.所以h 2＝1r，所以R ＝r 2＋1r 2≥2，当且仅当r 2＝1r2.即r ＝1时取等号，此时k 取最小值，所以r ＝1，h ＝2，圆柱的表面积为2π＋4π＝6π.答案：6π4．(2020·新疆第一次毕业诊断及模拟测试)如图，A 1B 1C 1D 1是以ABCD 为底面的长方体的一个斜截面，其中AB ＝4，BC ＝3，AA 1＝5，BB 1＝8，CC 1＝12，求该几何体的体积．解：过A 1作A 1E ⊥BB 1于点E ， 作A 1G ⊥DD 1于点G ， 过E 作EF ⊥CC 1于点F ，过D 1作D 1H ⊥CC 1于点H ，连接EH ，GF ， 因为平面ABB 1A 1∥平面DCC 1D 1， 所以A 1B 1∥D 1C 1.因为AA 1＝BE ＝5，所以EB 1＝8－5＝3，C 1H ＝EB 1＝3，GD 1＝HF ＝12－5－3＝4，则几何体被分割成一个长方体ABCD ­A 1EFG ，一个斜三棱柱A 1B 1E ­D 1C 1H 和一个直三棱柱A 1D 1G ­EHF .故该几何体的体积为V ＝3×4×5＋12×3×4×4＋12×3×4×3＝102.。