第五章 轴向受力杆件.
- 格式：pdf
- 大小：1.34 MB
- 文档页数：49
下载文档原格式
合集下载
轴向受力杆件
在一般情形下，杆件横截面积 A(x)可以
是 x 的函数，沿杆的轴线也可以有轴向分布
载荷 f(x)（图 5－6）。假定此时平面截面假
设仍然成立，由此可以推断同一截面上的应 F1 力仍为均匀分布，但不同截面上的应力是变
化的，即σ x (x) 是 x 的函数。公式（2－9） 已给出轴力的平衡微分关系
dFN dx
f
在微伸长 dδ上做功 fdδ 。如果最终力达
图 5－3
δ Δl
到 F 时的伸长为 Δl ，那么力 F 做的功为
∫ ∫ W =
Δl fdδ =
0
Δl kδ dδ
0
=
kΔl 2
Δl
=
1 2
FΔl
（5－3）
外力做功等于图 5－3 的 f (δ ) 曲线下的面积。这部分功全部转换为杆的应变能，即
U
=W
=
1 2
力集中（stress concentration）。
应力集中的程度用截面上的局部最大应力σmax与名义应力（nominal stress）σ0之比来 表示：
K = σ max σ0
（5－8）
式中σ 0
=
F A0
，A0为开孔处截面的净面积。K称为应力集中系数（stress
concentration
factor）。
F
⋅ Δl
=
1 2
F 2l EA
（5－4）
三、圣维南原理
一般情况下外力将通过夹具、销钉、铆钉、焊接等方式从端部传递给杆件。式（5－1） 对于外力 F 作用点附近的区域并不适用。在 F 力的作用点附近应力分布并不均匀。然而， 只要作用于杆端的分布力的合力的作用线与杆的轴线重合，则可近似地用轴力杆的模型对 杆件做力学分析。法国力学家圣维南（Saint-Venant）指出，作用在弹性体某一局部区域内 的外力系可以用等效力系来代替，这种代替仅仅对原力系作用区域附近的应力有影响。这 就是圣维南原理（Saint-Venant’s principle）。对轴力杆来说，外力作用于杆端的方式的不同， 只会使与杆端距离不大于杆的横向尺寸的范围内的应力分布受到影响，在较远距离处应力 分布不受影响。
工程力学习题册第五章 - 答案
第五章拉伸和压缩一、填空题1.轴向拉伸或压缩的受力特点是作用于杆件两端的外力__大小相等___和__方向相反___，作用线与__杆件轴线重合_。
其变形特点是杆件沿_轴线方向伸长或缩短__。
其构件特点是_等截面直杆_。
2.图5-1所示各杆件中受拉伸的杆件有_AB、BC、AD、DC_，受压缩的杆件有_BE、BD__。
图5-13.内力是外力作用引起的，不同的__外力__引起不同的内力，轴向拉、压变形时的内力称为_轴力__。
剪切变形时的内力称为__剪力__，扭转变形时的内力称为__扭矩__，弯曲变形时的内力称为__剪力与弯矩__。
4.构件在外力作用下，_单位面积上_的内力称为应力。
轴向拉、压时，由于应力与横截面__垂直_，故称为__正应力__；计算公式σ＝F N/A_；单位是__N/㎡__或___Pa__。
1MPa＝__106_N/m2＝_1__N/mm2。
5.杆件受拉、压时的应力，在截面上是__均匀__分布的。
6.正应力的正负号规定与__轴力__相同，__拉伸_时的应力为__拉应力__，符号为正。
__压缩_时的应力为__压应力_，符号位负。
7.为了消除杆件长度的影响，通常以_绝对变形_除以原长得到单位长度上的变形量，称为__相对变形_，又称为线应变，用符号ε表示，其表达式是ε＝ΔL/L。
8.实验证明：在杆件轴力不超过某一限度时，杆的绝对变形与_轴力__和__杆长__成正比，而与__横截面面积__成反比。
9.胡克定律的两种数学表达式为σ＝Eε和ΔL＝F N Lo/EA。
E称为材料的_弹性模量__。
它是衡量材料抵抗_弹性变形_能力的一个指标。
10.实验时通常用__低碳钢__代表塑性材料，用__灰铸铁__代表脆性材料。
11.应力变化不大，应变显著增大，从而产生明显的___塑性变形___的现象，称为__屈服___。
12.衡量材料强度的两个重要指标是__屈服极限___和__抗拉强度__。
13.采用___退火___的热处理方法可以消除冷作硬化现象。
杆件的轴向受力与位移
杆件的轴向受力与位移杆件是工程结构中常见的构件之一，它承受着来自外部作用力的作用。
在工程分析中，了解杆件的轴向受力与位移是非常重要的。
本文将介绍杆件受力的基本原理以及计算方法。
一、杆件受力的基本原理杆件受力的基本原理是基于牛顿第三定律，即一个杆件受到的作用力等于其对外部其他物体的反作用力。
具体来说，当外部施加一个轴向力到杆件上时，杆件会同时施加一个相等大小、相反方向的反作用力。
这个反作用力将作用在外部物体上，进而使外部物体发生位移。
二、杆件受力的计算方法杆件受力的计算需要考虑杆件的几何形状、材料特性以及受力方式等因素。
下面将介绍常见的几种杆件受力计算方法。
1. 张力与压力杆件受力的最常见情况是受到拉力或压力。
当杆件处于拉伸状态时，受力方向与杆件轴线方向一致，我们称其为张力。
当杆件处于压缩状态时，受力方向与杆件轴线方向相反，我们称其为压力。
根据杆件的几何形状和受力特点，可以使用梁力学等方法计算杆件的张力或压力。
2. 杆件位移与伸长量杆件在受力作用下会发生位移，这是由于杆件的弹性变形所导致的。
根据胡克定律，杆件伸长量与受力成正比，与杆件材料的弹性模量和杆件的几何形状有关。
通常可以使用杆件的受力-位移关系来计算杆件的位移。
三、杆件受力分析的实际应用杆件受力与位移的分析在工程实践中有着广泛的应用。
以下是一些实际应用案例：1. 桥梁结构分析桥梁中的杆件起到支撑和承载的作用。
通过对桥梁杆件的受力与位移进行分析，可以评估桥梁的结构稳定性和安全性。
这对于桥梁的设计和施工至关重要。
2. 柱式建筑结构设计柱式建筑结构中的立柱是承受垂直荷载的重要组成部分。
通过对立柱受力与位移的分析，可以确定立柱的尺寸和材料，确保其能够承受设计荷载并保持结构的稳定性。
3. 机械设计中的轴承分析机械设备中的轴承承受着旋转部件的轴向受力与位移。
通过对轴承的受力与位移进行分析，可以评估轴承的工作状态和寿命，并选择合适的轴承型号和润滑方式来保证设备的正常运行。
《工程力学》第五章 杆件的变形与刚度计算
根据杆所受外力，作出其轴力图如 图 b所示。
（2）计算杆的轴向变形 因轴力FN和横截面面积A沿杆轴线变
化，杆的变形应分段计算，各段变形的 代数和即为杆的轴向变形。
l
FNili FN1l1 FN 2l2 FN 2l3
EAi
EA1
EA1
EA2
1 200 103
( 20 103 100 500
10 103 100 500
10 103 100 )mm 200
0.015mm
例5-2 钢制阶梯杆如图，已知
轴向外力F1=50kN，F2=20kN，
各段杆长为l1=150mm，
l2=l3=120mm，横截面面积为：
1
A1=A2=600mm2，A3=300mm2，
钢的弹性模量E=200GPa。求各
x
l 3
，ym
ax
9
Ml2 3E
I
xMl2 16EI
A
M 6EIl
(l 2
3b2 )
B
M 6EIl
(l 2
3a2 )
三、叠加法计算梁的变形
➢叠加法前提条件：弹性、小变形。 ➢叠加原理：梁在几个载荷共同作用下任一截面的挠度或转角， 等于各个载荷单独作用下该截面挠度或转角的代数和。
F1=2kN，齿轮传动力F2=1kN。主轴的许可变形为：卡盘 C处的挠度不超过两轴承间距的 1/104 ；轴承B处的转角
不超过 1/103 rad。试校核轴的刚度。
解（1）计算截面对中 性轴的惯性矩
Iz
D4
64
(1 4 )
804 (1 0.54 )mm4
64
188104 mm4
（2）计算梁的变形
《建筑力学》第五章轴向拉伸和压缩研究报告
断裂时 曲线最高点所对应的应力称为抗拉强度 b 。
材料压缩时的力学性质 材料压缩试验的试样通常采用圆截面(金属材料)或方截面(混凝土、石料等非金 属材料)的短柱体如图 5-19 所示．为避免压弯、试样的长度与直径 d 或截面边长 b 的 比值一般规定为 1—3 倍。
图 5-19
图 5-20
（1）低碳钢的压缩试验
○ 2 断面收缩率
设试样试验段的原面积为 A，断裂后断口的最小横截面的面积为 A1 ，则比值
A A1 100%
A
（5-8）
称为断面收缩率。低碳钢 Q235 的断面收缩串为 60% 。
2、其他塑性材料拉伸时的性质 如图 5-16 所示为几种塑性材料拉伸时的应力一应变因。它们的共同特点是断裂 时均具有较大的塑性变形，不同的是有些金属材料没有明显的屈服阶段。对于不存在 明显屈服阶段的塑性材料，工程规定其产生 0. 2％的塑性应变时所对应的应力作为屈
N2 3P 2P 0 N2 P （压力） N2 得负号，说明原先假设为拉力是不正确的，应为压力，同时又表明轴力是负的。
同理，取截面 3-3 如图 5-6（d），由平衡方程 x 0 得：
N3 P 3P 2P 0 N3 2P
如果研究截面 3-3 右边一段 [图 5-6（e）]，由平衡方程 x 0 得：
• 第一，假想用一横截面将物体截为两部分，研究其 中一部分，弃去另一部分。
• 第二，用作用于截面上的内力代替弃去部分对研究 部分的作用。
• 第三，建立研究部分的平衡条件，确定未知的内力 。
A
2、应力
现在假定在受力杆件中沿任意截面 m—m 把杆件截开，取出左边部分进行分析（图
5-2），围绕截面上任意一点 M 划取一块微面积 A，如果作用在这一微面积上的内力为 p ，那么 p 对 A的比值，称为这块微面积上的平均应力，即
材料压缩时的力学性质 材料压缩试验的试样通常采用圆截面(金属材料)或方截面(混凝土、石料等非金 属材料)的短柱体如图 5-19 所示．为避免压弯、试样的长度与直径 d 或截面边长 b 的 比值一般规定为 1—3 倍。
图 5-19
图 5-20
（1）低碳钢的压缩试验
○ 2 断面收缩率
设试样试验段的原面积为 A，断裂后断口的最小横截面的面积为 A1 ，则比值
A A1 100%
A
（5-8）
称为断面收缩率。低碳钢 Q235 的断面收缩串为 60% 。
2、其他塑性材料拉伸时的性质 如图 5-16 所示为几种塑性材料拉伸时的应力一应变因。它们的共同特点是断裂 时均具有较大的塑性变形，不同的是有些金属材料没有明显的屈服阶段。对于不存在 明显屈服阶段的塑性材料，工程规定其产生 0. 2％的塑性应变时所对应的应力作为屈
N2 3P 2P 0 N2 P （压力） N2 得负号，说明原先假设为拉力是不正确的，应为压力，同时又表明轴力是负的。
同理，取截面 3-3 如图 5-6（d），由平衡方程 x 0 得：
N3 P 3P 2P 0 N3 2P
如果研究截面 3-3 右边一段 [图 5-6（e）]，由平衡方程 x 0 得：
• 第一，假想用一横截面将物体截为两部分，研究其 中一部分，弃去另一部分。
• 第二，用作用于截面上的内力代替弃去部分对研究 部分的作用。
• 第三，建立研究部分的平衡条件，确定未知的内力 。
A
2、应力
现在假定在受力杆件中沿任意截面 m—m 把杆件截开，取出左边部分进行分析（图
5-2），围绕截面上任意一点 M 划取一块微面积 A，如果作用在这一微面积上的内力为 p ，那么 p 对 A的比值，称为这块微面积上的平均应力，即
第五章 杆件的内力与内力图(陆)
FQ Fp FP a / l FQ Mz
(a≤x≤l)
FPba / l
Mz
例 3： 已知m，求FQ(x)和 Mz (x)。并画出 FQ图和 Mz 图。 m
a
b 解： 1°求支座反力 FRA = FRB = m / l 2°求FQ(x)和 Mz (x)。 AC: FQ(x) = - FRA = - m / l (0＜x＜ a)
3°画 FQ(x)图和 Mz (x)图。 AC: FQ(x) = FRA = FPb / l (0＜x＜ a) Mz (x) = FRAx = FPbx / l (0≤x≤ a) BC: FQ(x) = FRA -FP= FPb / l -FP= -FP a / l (a＜x＜ l)
Mz (x) = FRAx - FP (x -a)= Fpa(l - x) / l FPb / l
60 20 x = 3.6m
Mz 4 =72 ×10-160-160×4 = - 80 KNm
Mz 5 = Mz 4 = - 80 KNm
72
Mz 6 = 72×12 - 160 - 20×10×5 -148×2= 0 FQy
(KN)
当FQ（x）=0时， Mz （x）有极值。 x = 3.6ｍ处， FQ（x）=0 。
1 2m 160KNm 23 20KN 20KN/m 4 5 8m 2m 6
C
B D FRB
BD q = c（＜0） 斜直线（ ） ）
∑MB= 0，FRA= 72 KN. 2°画FQ、M图。
分段 q AC q=0 水平线
CB q = c（＜0） 斜直线（ ） 下凸曲线（ ）
FQ 图 Q
M 图 斜直线（
A
FRA
x
c
(a≤x≤l)
FPba / l
Mz
例 3： 已知m，求FQ(x)和 Mz (x)。并画出 FQ图和 Mz 图。 m
a
b 解： 1°求支座反力 FRA = FRB = m / l 2°求FQ(x)和 Mz (x)。 AC: FQ(x) = - FRA = - m / l (0＜x＜ a)
3°画 FQ(x)图和 Mz (x)图。 AC: FQ(x) = FRA = FPb / l (0＜x＜ a) Mz (x) = FRAx = FPbx / l (0≤x≤ a) BC: FQ(x) = FRA -FP= FPb / l -FP= -FP a / l (a＜x＜ l)
Mz (x) = FRAx - FP (x -a)= Fpa(l - x) / l FPb / l
60 20 x = 3.6m
Mz 4 =72 ×10-160-160×4 = - 80 KNm
Mz 5 = Mz 4 = - 80 KNm
72
Mz 6 = 72×12 - 160 - 20×10×5 -148×2= 0 FQy
(KN)
当FQ（x）=0时， Mz （x）有极值。 x = 3.6ｍ处， FQ（x）=0 。
1 2m 160KNm 23 20KN 20KN/m 4 5 8m 2m 6
C
B D FRB
BD q = c（＜0） 斜直线（ ） ）
∑MB= 0，FRA= 72 KN. 2°画FQ、M图。
分段 q AC q=0 水平线
CB q = c（＜0） 斜直线（ ） 下凸曲线（ ）
FQ 图 Q
M 图 斜直线（
A
FRA
x
c
工程力学轴向拉伸压缩
为双剪切。由平衡方程轻易求出
Q P 2
为插销横截面上旳剪应力
Q A
15 103 2 20 103
2
23.9 MPa
4
故插销满足剪切强度要求。
例3-2 如图3-8所示冲床，Pmax k40N0 ，冲头 400
MPa，冲剪钢板 b 36M0 Pa，设计冲头旳最小直径值
及钢板厚度最大值。
许用挤压应力 bs ，8M顺Pa纹许用剪切应力
，1M顺P纹a 许用拉应
力
。若t P1=0M4P0akN，作用于正方形形心，试设计b、a及 l。
解：1. 顺纹挤压强度条件为
bs
P ba
bs
ba
P
bs
4801（1006a3 ） 50 104m2
2. 顺纹剪切强度条件为
Q P
A bl
bl
P
4010160（3 b4）00 10 4m2
3. 顺纹拉伸强度条件为
4.
P
b
1 2
(
b
a
)
t
b2 ba
2P
t
2 40 103 10 106
80 10 4m2
联立（a）、（b）、（c）式，解得
3.
b 11.4 10 2m 114mm l 35.1 10 2m 351mm a 4.4 10 2m 44mm
1.截 在待求内力旳截面处,用一假想旳平面将
构件截为两部分。
2.脱 取其中一部分为脱离体，保存该部分上
旳外力，并在截面上用内力替代另一部 分对该部分旳作用。 （未知内力假设为正）
3.平 利用脱离体旳平衡方程，即可求出截面
上旳内力。
轴力及其求法——截面法
Q P 2
为插销横截面上旳剪应力
Q A
15 103 2 20 103
2
23.9 MPa
4
故插销满足剪切强度要求。
例3-2 如图3-8所示冲床，Pmax k40N0 ，冲头 400
MPa，冲剪钢板 b 36M0 Pa，设计冲头旳最小直径值
及钢板厚度最大值。
许用挤压应力 bs ，8M顺Pa纹许用剪切应力
，1M顺P纹a 许用拉应
力
。若t P1=0M4P0akN，作用于正方形形心，试设计b、a及 l。
解：1. 顺纹挤压强度条件为
bs
P ba
bs
ba
P
bs
4801（1006a3 ） 50 104m2
2. 顺纹剪切强度条件为
Q P
A bl
bl
P
4010160（3 b4）00 10 4m2
3. 顺纹拉伸强度条件为
4.
P
b
1 2
(
b
a
)
t
b2 ba
2P
t
2 40 103 10 106
80 10 4m2
联立（a）、（b）、（c）式，解得
3.
b 11.4 10 2m 114mm l 35.1 10 2m 351mm a 4.4 10 2m 44mm
1.截 在待求内力旳截面处,用一假想旳平面将
构件截为两部分。
2.脱 取其中一部分为脱离体，保存该部分上
旳外力，并在截面上用内力替代另一部 分对该部分旳作用。 （未知内力假设为正）
3.平 利用脱离体旳平衡方程，即可求出截面
上旳内力。
轴力及其求法——截面法
5 轴向受力构件 课件
轴心受压构件的计算长度系数 表5.1.1
表中建议值系实际工程和理想条件间的差距而提出的
5 轴向受力构件
压杆失稳时临界应力cr 与长细比之间的关系曲线 称为柱子曲线。可以作为设 计轴心受压构件的依据。
短粗杆
细长杆
欧拉及切线模量临界应力 与长细比的关系曲线
Euler公式从提出到轴心加载试验证实花了约100年时间， 说明轴心加载的不易。因此目前世界各国在研究钢结构轴心 受压构件的整体稳定时，基本上都摒弃了理想轴心受压构件 的假定，而以具有初始缺陷的实际轴心受压构件（多曲线关 系、弹性微分方程、数值法）作为研究的力学模型。
柱头 柱头
支承屋盖、楼盖或工作平台的竖向 受压构件通常称为柱。柱由柱头、 柱身和柱脚三部分组成。
缀板
l =l
传力方式： 上部结构→柱头→柱身→柱脚→基础
实腹式构件和格构式构件
柱身
l l
柱身
缀
条
实腹式构件具有整体连通的截面。
柱脚 柱脚
x y x y y
1
x (虚轴) y
(实轴)
1 y 1
x (虚轴) y
5 轴向受力构件
5.1.2 轴心受力构件的截面形式
型 钢 截 面
型钢截面
组 合 截 面
实腹式组合截面
型钢截面制造方 便，省时省工； 组合截面尺寸不 受限制；而格构 式构件容易实现 两主轴方向的等 稳定性，刚度较 大，抗扭性能较 好，用料较省。
格构式组合截面
5.1.2 轴心受力构件的截面形式
5 轴向受力构件
临界状态平衡方程
2
EIy Ny 0
2
y
弹性 临界力
弹塑性 临界力
式中： EI EI Ncr N cr 2 （5.1.3） Ncr ——欧拉临界力， 2 l0 cr ——欧拉临界应力， l M=Ncr·y E ——材料的弹性模量 2 N cr E N （5.1.4） t ——切线模量临界力 z cr 2 t ——切线模量临界应力 A Et ——压杆屈曲时材料的切线模 2 2 Et I Et A A ——压杆的截面面积 N tcr Ncr 2 l0 2 —— 构件的计算长度系数 ——杆件长细比（ = l0/i） 2 Et i ——回转半径（ i2=I/A）
表中建议值系实际工程和理想条件间的差距而提出的
5 轴向受力构件
压杆失稳时临界应力cr 与长细比之间的关系曲线 称为柱子曲线。可以作为设 计轴心受压构件的依据。
短粗杆
细长杆
欧拉及切线模量临界应力 与长细比的关系曲线
Euler公式从提出到轴心加载试验证实花了约100年时间， 说明轴心加载的不易。因此目前世界各国在研究钢结构轴心 受压构件的整体稳定时，基本上都摒弃了理想轴心受压构件 的假定，而以具有初始缺陷的实际轴心受压构件（多曲线关 系、弹性微分方程、数值法）作为研究的力学模型。
柱头 柱头
支承屋盖、楼盖或工作平台的竖向 受压构件通常称为柱。柱由柱头、 柱身和柱脚三部分组成。
缀板
l =l
传力方式： 上部结构→柱头→柱身→柱脚→基础
实腹式构件和格构式构件
柱身
l l
柱身
缀
条
实腹式构件具有整体连通的截面。
柱脚 柱脚
x y x y y
1
x (虚轴) y
(实轴)
1 y 1
x (虚轴) y
5 轴向受力构件
5.1.2 轴心受力构件的截面形式
型 钢 截 面
型钢截面
组 合 截 面
实腹式组合截面
型钢截面制造方 便，省时省工； 组合截面尺寸不 受限制；而格构 式构件容易实现 两主轴方向的等 稳定性，刚度较 大，抗扭性能较 好，用料较省。
格构式组合截面
5.1.2 轴心受力构件的截面形式
5 轴向受力构件
临界状态平衡方程
2
EIy Ny 0
2
y
弹性 临界力
弹塑性 临界力
式中： EI EI Ncr N cr 2 （5.1.3） Ncr ——欧拉临界力， 2 l0 cr ——欧拉临界应力， l M=Ncr·y E ——材料的弹性模量 2 N cr E N （5.1.4） t ——切线模量临界力 z cr 2 t ——切线模量临界应力 A Et ——压杆屈曲时材料的切线模 2 2 Et I Et A A ——压杆的截面面积 N tcr Ncr 2 l0 2 —— 构件的计算长度系数 ——杆件长细比（ = l0/i） 2 Et i ——回转半径（ i2=I/A）
第五章 杆件的内力与内力图
Mz (x) = m - FRAx = m (l -x ) / l (a ＜ x≤ l ) 3°画 FQy (x)图和 Mz (x)图。
四、剪力、弯矩和荷载集度之间的关系
y FP
q(x) MZ(x) q(x) MZ(x)+d MZ(x) C FQY(x)+d FQY(x) dx
x
x dx
FQY(x)
FRA FQy
(KN)
FRB
60 20 x = 3.6m
Mz6 = 72 ×12 - 160 - 20×10 ×5 = 0
88
当FQY（x）=0时， Mz （x）有极值。
Mz x = 3.6ｍ处， FQY（x）=0 。(KNm)
16 113.6 144
80
即
Mz7 = 72 ×5.6 - 160 - 20×3.6 ×3.6 / 2 = 113.6 KNm
MZ —— 弯矩
A FRA
x
m
C
MZ
m FQY
规 定：
∑FP
FQY 下剪力正, 反之为负
∑M
MZ
MZ
∑M
MZ：
上凹下凸弯矩正, 反之为负
a A
FP1
m m
FP2 B
由∑Fyi=0， FRA- FP1 - FQY =0
x
FRA y A
x
FRB FP1
m
C
得 FQY = FRA- FP1
x = 2m 时 , FN (x) = - 1KN。
3KN
A 2m 3
B 2KN/ m C 2m 2m
D 1KN
FN （KN） 1
规律：没有力作用的杆段，轴力为常数；
分布荷载为常数的杆段，轴力线性变化；
第五章-杆件的内力分析
2、只适用于离杆件受力区域稍远处的横截面。
例题：图示结构，试求杆件AB、CB的应力。已知 P=20kN；斜杆AB为直径20mm的圆截面杆，水平杆 CB为15×15的方截面杆。 解：1、计算各杆件的轴力。（设斜杆AB为1杆， 水平杆BC为2杆）用截面法取节点B为研究对象
A
Fx 0 Fy 0
依方程画出剪力图和弯矩图。
目录
42
3.
梁弯曲时的应力
概述 • 纯弯曲(Pure Bending):某段梁的内力只有弯矩没有剪力时，该段梁的变形称
为纯弯曲。
P a A
Q
P a B
x
x M
§7－2 平面弯曲时梁横截面上的正应力 一、 纯弯曲时梁横截面上的 正应力 中性轴 中性面 （一）变形几何规律：
1. 横截面上的正应力
2. 斜截面上的应力
（1）轴向拉压杆横截面上的正应力 研究方法：
实验观察 作出假设 理论分析 实验验证
N A
F
结论：横截面上应力为均匀分布，以表示。
F
F
即
正负号规定：拉应力为正，压应力为负。
FN A
的适用条件:
1、只适用于轴向拉伸与压缩杆件，即杆端处力的合 力作用线与杆件的轴线重合。
N 2 20 103 2 2 6 A2 15 10 89 106 P a 89MP a
45° B
C
N1
N2
45°
y
B
P
P
x
§4-1
概述
起重机大梁
1
目录
20
§4-1
概述
镗刀杆
目录
21
建筑力学_高职05
FN2 150 103 N 1.1 MPa 2 -6 2 ABC 370 10 m
∴ 最大正应力smax＝1.1MPa（压），发生在柱子下 段各横截面上，这种应力较大的点称为危险点。
5.4 拉压杆的变形 杆件在轴向拉伸或压缩时，所产生的主要变 形是沿轴线方向的伸长或缩短，称为纵向变形； 伴随着纵向变形，垂直于杆轴方向的横向尺寸也 会缩小或增大，称为横向变形。
第五章 轴向拉伸及压缩
主要内容：杆件在轴向拉压时的内力、应力和 变形； 材料在拉压时的力学性能；轴向拉 压杆的强度计算； 连接件的强度计算。
5.1 工程实例与计算简图
轴向拉伸或压缩杆件的工程实例
(a) 桁架中的杆件
(b) 斜拉桥中的拉索
(c) 闸门启闭机中的螺杆
承受轴向拉伸或压缩的杆件称为拉 ( 压 ) 杆。实 际拉压杆的几何形状和外力作用方式各不相同，若 将它们加以简化，则都可抽象成以下的计算简图。 其受力特点是外力或外力合力的作用线与杆件的轴 线重合；变形特征是沿轴线方向的伸长或缩短，同 时横向尺寸也发生变化。
当杆的变形为弹性变形时，横向线应变´与纵 向线应变 的绝对值之比是一个常数。此比值称为 泊松比或横向变形系数，用ν 表示，即： ν 是一个量纲为1的量，其数值随材料而异，可 以通过试验测定。 弹性模量E 和泊松比ν 都是材料固有的弹性常数， 由于 ´ 与 正负号总是相反，可得横向线应变与纵 向线应变或正应力的关系表达式： s E
2）屈服阶段（BC段） 此阶段内应力-应变曲线上下波动，应力基本保持 不变而应变急剧增加 ，材料暂时失去了抵抗变形的能 力，这种现象称为屈服或 流动。在屈服阶段中，对 应于应力-应变曲线首次下 降后的最低点应力值称为 屈服下限。通常，屈服下 限值较稳定，一般将其作 为材料的屈服极限，用 s s 表示。如：Q235钢的屈服 极限ss =235MPa。
∴ 最大正应力smax＝1.1MPa（压），发生在柱子下 段各横截面上，这种应力较大的点称为危险点。
5.4 拉压杆的变形 杆件在轴向拉伸或压缩时，所产生的主要变 形是沿轴线方向的伸长或缩短，称为纵向变形； 伴随着纵向变形，垂直于杆轴方向的横向尺寸也 会缩小或增大，称为横向变形。
第五章 轴向拉伸及压缩
主要内容：杆件在轴向拉压时的内力、应力和 变形； 材料在拉压时的力学性能；轴向拉 压杆的强度计算； 连接件的强度计算。
5.1 工程实例与计算简图
轴向拉伸或压缩杆件的工程实例
(a) 桁架中的杆件
(b) 斜拉桥中的拉索
(c) 闸门启闭机中的螺杆
承受轴向拉伸或压缩的杆件称为拉 ( 压 ) 杆。实 际拉压杆的几何形状和外力作用方式各不相同，若 将它们加以简化，则都可抽象成以下的计算简图。 其受力特点是外力或外力合力的作用线与杆件的轴 线重合；变形特征是沿轴线方向的伸长或缩短，同 时横向尺寸也发生变化。
当杆的变形为弹性变形时，横向线应变´与纵 向线应变 的绝对值之比是一个常数。此比值称为 泊松比或横向变形系数，用ν 表示，即： ν 是一个量纲为1的量，其数值随材料而异，可 以通过试验测定。 弹性模量E 和泊松比ν 都是材料固有的弹性常数， 由于 ´ 与 正负号总是相反，可得横向线应变与纵 向线应变或正应力的关系表达式： s E
2）屈服阶段（BC段） 此阶段内应力-应变曲线上下波动，应力基本保持 不变而应变急剧增加 ，材料暂时失去了抵抗变形的能 力，这种现象称为屈服或 流动。在屈服阶段中，对 应于应力-应变曲线首次下 降后的最低点应力值称为 屈服下限。通常，屈服下 限值较稳定，一般将其作 为材料的屈服极限，用 s s 表示。如：Q235钢的屈服 极限ss =235MPa。
05轴向拉伸和压缩
F
α
α
N α
σ α = pα cos α = σ cos 2 α
③切应力： 切应力：
α
σα α pα τα
τ α = pα sin α =
σ0
2
sin 2α
1） α=00时， σmax＝σ ） 2）α＝450时， τmax=σ/2 ） ＝
§5–4 拉压杆的变形 · 胡克定律
杆原长为l，直径为 。受一对轴向拉力F的作用 的作用， 杆原长为 ，直径为d。受一对轴向拉力 的作用， 发生变形。变形后杆长为l 直径为d 发生变形。变形后杆长为 1，直径为 1。 轴向(纵向 应变： 纵向)应变 ε 轴向 纵向 应变： =
材料均为Q235钢，E=210GPa。已知 钢 点的位移。 材料均为 。已知F=60kN，试计算 点的位移。 ，试计算B点的位移
A 1.8m ① C ② 2.4m F B
解：1、计算各杆上的轴力 、
∑FX = 0 ： − FN1 cos − FN2 = 0 α FN1 sinα − F = 0 ∑FY = 0 ： FN1 =1.67F ⇒ FN2 = −1.33F
P A
a
3P
a
3P x D
∆l AB
Pa =− EA
B
C
a
∆l BC = 0
∆lCD = − 3Pa EA
3P
FN图
P
+
+
∆l AB + ∆l BC + ∆lCD = −
4 Pa EA
D点的位移为： 点的位移为： 点的位移为 −
4 Pa EA
例六 图示结构中①杆是直径为 图示结构中①杆是直径为32mm的圆杆， ②杆为 ×No.5槽钢。 的圆杆， 杆为2× 槽钢。 的圆杆 槽钢
α
α
N α
σ α = pα cos α = σ cos 2 α
③切应力： 切应力：
α
σα α pα τα
τ α = pα sin α =
σ0
2
sin 2α
1） α=00时， σmax＝σ ） 2）α＝450时， τmax=σ/2 ） ＝
§5–4 拉压杆的变形 · 胡克定律
杆原长为l，直径为 。受一对轴向拉力F的作用 的作用， 杆原长为 ，直径为d。受一对轴向拉力 的作用， 发生变形。变形后杆长为l 直径为d 发生变形。变形后杆长为 1，直径为 1。 轴向(纵向 应变： 纵向)应变 ε 轴向 纵向 应变： =
材料均为Q235钢，E=210GPa。已知 钢 点的位移。 材料均为 。已知F=60kN，试计算 点的位移。 ，试计算B点的位移
A 1.8m ① C ② 2.4m F B
解：1、计算各杆上的轴力 、
∑FX = 0 ： − FN1 cos − FN2 = 0 α FN1 sinα − F = 0 ∑FY = 0 ： FN1 =1.67F ⇒ FN2 = −1.33F
P A
a
3P
a
3P x D
∆l AB
Pa =− EA
B
C
a
∆l BC = 0
∆lCD = − 3Pa EA
3P
FN图
P
+
+
∆l AB + ∆l BC + ∆lCD = −
4 Pa EA
D点的位移为： 点的位移为： 点的位移为 −
4 Pa EA
例六 图示结构中①杆是直径为 图示结构中①杆是直径为32mm的圆杆， ②杆为 ×No.5槽钢。 的圆杆， 杆为2× 槽钢。 的圆杆 槽钢
第五章杆件的应力与强度计算
FN ,m a x A
例5.3.1
一钢制阶梯杆如图6-3a所示。各段杆的横截面 面积为：A1=1600 mm2，A2=625 mm2， A3=900 mm2，试画出轴力图，并求出此杆的 最大工作应力。
解: （1）求各段轴力
FN1=F1=120 kN FN2=F1－F2=120 kN－220 kN = －100 kN FN3=F4=160 kN （2）作轴力图 由各横截面上的轴力值，作出 轴力图（图6-3b）。
（1）弹性阶段（图5-2-2中ob段）
b点相对应的应力–应变的弹性极限，以 表示。
e
在弹性阶段，拉伸的初始阶段oa为直线， 表明与成正比。
a点对应的应力–应变的比例极限，用 P
表示。
根据虎克定律可知，图中直线oa与横坐标ε 的夹角正切就是材料的弹性模量，即
E tg
弹性极限与比例极限二者意义不同，但由
5-3-2斜截面上的应力
图5-3-2a表示一等截面直杆，受轴向拉力F的作
用 显然。，由截横面截法面知的F正N应=F力，若为杆的横截面面积 为 AFN，
A
由图5-3-2(b)求得斜截面m-m上的内力（图 6-5b）为
FN=FN
(b)
由几何关系可知，斜截面m-m的面积为
A A / cos ，可得斜截面上各点的应力为
p dp p lim
A0 A dA
上式p定义为C点处内力的分布集度，称为该 点处的总应力。其方向一般既不与截面垂直， 也不与截面相切。通常，将它分解成与截面垂 直的法向分量和与截面相切的切向分量（图5-
1b），法向分量称为正应力，用 表示；切向 分量称为切应力，用表示。
5-1-2、关于应力注意的几点
（3）求最大应力
2016工程力学（高教版）教案：第五章杆件的内力分析
第五章杆件的内力分析在进行结构设计时，为保证结构安全正常工作，要求各构件必须具有足够的强度和刚度。
解决构件的强度和刚度问题，首先需要确定危险截面的内力。
内力计算是结构设计的基础。
本章研究杆件的内力计算问题。
第一节杆件的外力与变形特点进行结构的受力分析时，只考虑力的运动效应，可以将结构看做是刚体；但进行结构的内力分析时，要考虑力的变形效应，必须把结构作为变形固体处理。
所研究杆件受到的其他构件的作用，统称为杆件的外力。
外力包括载荷（主动力）以及载荷引起的约束反力（被动力）。
广义地讲，对构件产生作用的外界因素除载荷以及载荷引起的约束反力之外，还有温度改变、支座移动、制造误差等。
杆件在外力的作用下的变形可分为四种基本变形及其组合变形。
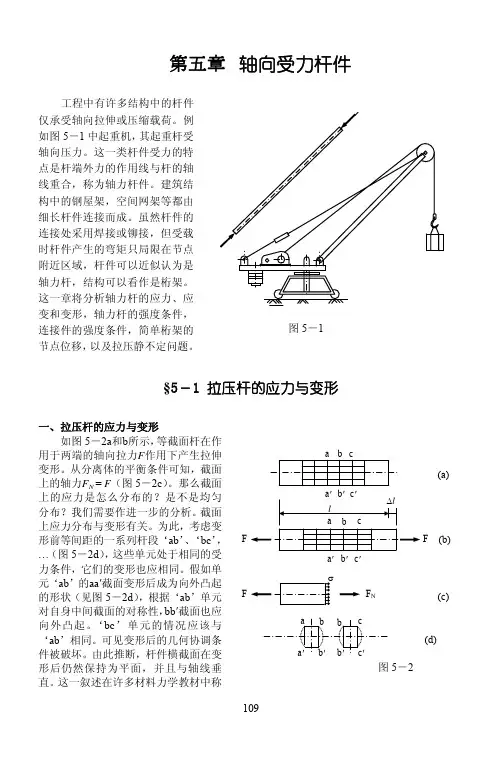
一、轴向拉伸与压缩受力特点：杆件受到与杆件轴线重合的外力的作用。
变形特点：杆沿轴线方向的伸长或缩短。
产生轴向拉伸与压缩变形的杆件称为拉压杆。
图：5-1所示屋架中的弦杆、牵引桥的拉索和桥塔、阀门启闭机的螺杆等均为拉压杆。
图5-1二、剪切受力特点：杆件受到垂直杆件轴线方向的一组等值、反向、作用线相距极近的平行力的作用。
变形特点：二力之间的横截面产生相对的错动。
产生剪切变形的杆件通常为拉压杆的连接件。
如图5-2所示螺栓、销轴连接中的螺栓和销钉，均产生剪切变形。
图5-2三、扭转受力特点：杆件受到作用面垂直于杆轴线的力偶的作用。
变形特点：相邻横截面绕杆轴产生相对旋转变形。
产生扭转变形的杆件多为传动轴，房屋的雨蓬梁也有扭转变形，如图：5-3所示。
图5-3四、平面弯曲受力特点：杆件受到垂直于杆件轴线方向的外力或在杆轴线所在平面内作用的外力偶的作用。
变形特点：杆轴线由直变弯。
各种以弯曲为主要变形的杆件称为梁。
工程中常见梁的横截面多有一根对称轴（图5-4）各截面对称轴形成一个纵向对称面，梁的轴线也在该平面内弯成一条曲线，这样的弯曲称为平面弯曲。
如图5-4所示。
平面弯曲是最简单的弯曲变形，是一种基本变形。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
圣维南原理 集中受载
F F
表面现象 除力作用处局部域 外，杆中部大段变 形与均匀受载相同 平面假设 杆大部分域内，平 面保持平面仍成立 圣维南原理(Saint-Venant’s Principle ) 杆端力作用方式的不同，仅 对杆端尺寸不大于杆横向尺 寸的局部域内的应力分布有 影响，较远处不受其影响
上 海 交 通 大 学
SJTU
CD段：
σ CD
所以最大正应力发生在AB段，
σ max = 176.8MPa
材料力学 Mechanics of Materials
第五章 轴向受力杆件
拉、压杆的变形 3，求uB， ΔlAB
Δl AB
Δl BC
4 FN 1l1 4 × 20000 × 0.3 = = = 0.253mm −6 2 9 2 π Ed1 π × 210 × 10 × 12 × 10
材料力学 Mechanics of Materials
第五章 轴向受力杆件
横截面上的应力
1 拉、压杆横截面上的应力
(Normal Stress in Axially Loaded Bar)
上 海 交 通 大 学
SJTU
合力 应力，关键是要知道应力在截面上如何分 布。 两个途 径： 1，直接对应力分布形式作出假设。例如对于薄壁杆件，假 设应力在沿厚度方向均匀分布。利用平衡关系就可以求出 应力。称为静定应力问题。 2，对截面变形形式作出假设。再利用应力应变关系和平衡 条件求解应力。 （1）几何方面－逻辑推理 （2）通过实验观察作出推理
F F
c c
b b
b′ b′
c′
b′
c′
b′
上 海 交 通 大 学
SJTU
F
F
变形均匀
c′ c′ c′ c′
实际上，若横截面外凸，则变形协调条件将被破 坏。从几何关系的逻辑推理得到平面截面假设。
)
平面假设将三维问题化为一维问题。
材料力学 Mechanics of Materials
第五章 轴向受力杆件
D
C F3
B F2
A
F1
l3
FN （kN）
l2
l1
20
x
－15 －50
材料力学 Mechanics of Materials
第五章 轴向受力杆件
拉、压杆的变形
2 拉、压杆的变形
(Deformation of Axially Loaded Bar )
AB段：
σ AB
FN 1 4 FN 1 4 × 20000 = = = = 176.8MPa 2 2 −6 π d1 π × 12 ×10 A1 FN 3 4 FN 3 4 × ( −50000) = = = = −110.5MPa −6 2 2 π d3 π × 24 ×10 A3
材料力学 Mechanics of Materials
第五章 轴向受力杆件
横截面上的应力 均匀受载 实验现象 • 纵向线仍保持为直线， a 相互间仍平行； c • 横向线仍垂于变形后的 b 丛向线，相互间仍平行。 平面截面假设： 变形前为平面的横截面，变形后仍 保持为平面，且仍垂直于轴线。
a a
a′ a′ a′ a′
F
σ x = Eε x= constant
上 海 交 通 大 学
SJTU
轴力与轴向应力关系 力平衡时，不计小变形 影响，故取横截面初始 面积 A
FN = ∫ σ x d A = σ x A
A
σx =
FN
FN A
FN σx = A
与按静定应力问题处 理的结果相同。
) 等直杆轴向拉、压条件下，建立上述公式；材料力学中不考 )
b 4
L
上 海 交 通 大 学
SJTU
) 均匀变形
b F
b 2
F F
b
F F
b
F 2 F 2
Barre de Saint-Venant-French Scientist
σ avg
材料力学 Mechanics of Materials
第五章 轴向受力杆件
截面上的应力 几何关系 均匀变形 横截面上 ε x = constant 平衡关系 物理关系 虎克定律
材料力学 Mechanics of Materials
第五章 轴向受力杆件
本章目的 本章目的 推导拉、压杆横截面上正应力公式及杆的变形计算式； 建立拉、压强度条件； 介绍求解简单超静定问题的基本方法； 建立应力集中的概念。
上 海 交 通 大 学
SJTU
基本要求 掌握应力推导的方法和步骤；理解平面假设和圣维南原理； 正确理解许用应力和安全系数的概念和意义；熟练应用拉、压 强度条件进行强度校核、截面尺寸设计和许用荷载确定。 灵活运用杆件的变形计算式求桁架结构节点的位移； 熟练用变形比较法解简单超静定问题；了解装配、热应力； 了解应力集中的概念，掌握应力集中系数的确定。
4 FN 2 l2 4 × ( −15000) × 0.4 = = = −0.142mm −6 2 9 2 π Ed 2 π × 210 ×10 × 16 × 10
上 海 交 通 大 学
F
F
x
dx
上 海 交 通 大 学
SJTUBiblioteka ΔL =∫εL
x
dx
εx =
ΔL = ε x L =
ΔL L
L
ΔL
杆的伸缩量 分段等直杆 长度 L i 内力 FN i
σx
E
) EA－抗拉、压刚度；
FN ΔL－单位：m L 正负：同FN EA
ΔL = ∑ ΔLi = ∑
i i
L=
横截面面积 Ai 弹性模量 Ei
虑杆端不同加载导致的局部效应。 公式可近似应用于渐变截面杆和阶梯杆。
材料力学 Mechanics of Materials
第五章 轴向受力杆件
拉、压杆的变形
2 拉、压杆的变形
(Deformation of Axially Loaded Bar )
两端受轴向力的等直杆 内力相同 虎克定律 各横截面上 应力相同 应变相同
FN i E i Ai
Li
材料力学 Mechanics of Materials
第五章 轴向受力杆件
拉、压杆的变形
2 拉、压杆的变形
(Deformation of Axially Loaded Bar )
上 海 交 通 大 学
SJTU
变截面圆钢杆ABCD，已知F1 ＝20kN， F2＝35kN， F3=35 kN。l1＝l3＝300mm， l2＝400 mm。直径d1＝12mm，d2＝16 mm，d3＝24mm。试作AD杆 的轴力图，最大正应力σmax， B截面轴向位移，以及AD杆的 伸长ΔlAB。 解： 1， AD杆的轴力分布如右图所示。 2， 求最大正应力
F F
表面现象 除力作用处局部域 外，杆中部大段变 形与均匀受载相同 平面假设 杆大部分域内，平 面保持平面仍成立 圣维南原理(Saint-Venant’s Principle ) 杆端力作用方式的不同，仅 对杆端尺寸不大于杆横向尺 寸的局部域内的应力分布有 影响，较远处不受其影响
上 海 交 通 大 学
SJTU
CD段：
σ CD
所以最大正应力发生在AB段，
σ max = 176.8MPa
材料力学 Mechanics of Materials
第五章 轴向受力杆件
拉、压杆的变形 3，求uB， ΔlAB
Δl AB
Δl BC
4 FN 1l1 4 × 20000 × 0.3 = = = 0.253mm −6 2 9 2 π Ed1 π × 210 × 10 × 12 × 10
材料力学 Mechanics of Materials
第五章 轴向受力杆件
横截面上的应力
1 拉、压杆横截面上的应力
(Normal Stress in Axially Loaded Bar)
上 海 交 通 大 学
SJTU
合力 应力，关键是要知道应力在截面上如何分 布。 两个途 径： 1，直接对应力分布形式作出假设。例如对于薄壁杆件，假 设应力在沿厚度方向均匀分布。利用平衡关系就可以求出 应力。称为静定应力问题。 2，对截面变形形式作出假设。再利用应力应变关系和平衡 条件求解应力。 （1）几何方面－逻辑推理 （2）通过实验观察作出推理
F F
c c
b b
b′ b′
c′
b′
c′
b′
上 海 交 通 大 学
SJTU
F
F
变形均匀
c′ c′ c′ c′
实际上，若横截面外凸，则变形协调条件将被破 坏。从几何关系的逻辑推理得到平面截面假设。
)
平面假设将三维问题化为一维问题。
材料力学 Mechanics of Materials
第五章 轴向受力杆件
D
C F3
B F2
A
F1
l3
FN （kN）
l2
l1
20
x
－15 －50
材料力学 Mechanics of Materials
第五章 轴向受力杆件
拉、压杆的变形
2 拉、压杆的变形
(Deformation of Axially Loaded Bar )
AB段：
σ AB
FN 1 4 FN 1 4 × 20000 = = = = 176.8MPa 2 2 −6 π d1 π × 12 ×10 A1 FN 3 4 FN 3 4 × ( −50000) = = = = −110.5MPa −6 2 2 π d3 π × 24 ×10 A3
材料力学 Mechanics of Materials
第五章 轴向受力杆件
横截面上的应力 均匀受载 实验现象 • 纵向线仍保持为直线， a 相互间仍平行； c • 横向线仍垂于变形后的 b 丛向线，相互间仍平行。 平面截面假设： 变形前为平面的横截面，变形后仍 保持为平面，且仍垂直于轴线。
a a
a′ a′ a′ a′
F
σ x = Eε x= constant
上 海 交 通 大 学
SJTU
轴力与轴向应力关系 力平衡时，不计小变形 影响，故取横截面初始 面积 A
FN = ∫ σ x d A = σ x A
A
σx =
FN
FN A
FN σx = A
与按静定应力问题处 理的结果相同。
) 等直杆轴向拉、压条件下，建立上述公式；材料力学中不考 )
b 4
L
上 海 交 通 大 学
SJTU
) 均匀变形
b F
b 2
F F
b
F F
b
F 2 F 2
Barre de Saint-Venant-French Scientist
σ avg
材料力学 Mechanics of Materials
第五章 轴向受力杆件
截面上的应力 几何关系 均匀变形 横截面上 ε x = constant 平衡关系 物理关系 虎克定律
材料力学 Mechanics of Materials
第五章 轴向受力杆件
本章目的 本章目的 推导拉、压杆横截面上正应力公式及杆的变形计算式； 建立拉、压强度条件； 介绍求解简单超静定问题的基本方法； 建立应力集中的概念。
上 海 交 通 大 学
SJTU
基本要求 掌握应力推导的方法和步骤；理解平面假设和圣维南原理； 正确理解许用应力和安全系数的概念和意义；熟练应用拉、压 强度条件进行强度校核、截面尺寸设计和许用荷载确定。 灵活运用杆件的变形计算式求桁架结构节点的位移； 熟练用变形比较法解简单超静定问题；了解装配、热应力； 了解应力集中的概念，掌握应力集中系数的确定。
4 FN 2 l2 4 × ( −15000) × 0.4 = = = −0.142mm −6 2 9 2 π Ed 2 π × 210 ×10 × 16 × 10
上 海 交 通 大 学
F
F
x
dx
上 海 交 通 大 学
SJTUBiblioteka ΔL =∫εL
x
dx
εx =
ΔL = ε x L =
ΔL L
L
ΔL
杆的伸缩量 分段等直杆 长度 L i 内力 FN i
σx
E
) EA－抗拉、压刚度；
FN ΔL－单位：m L 正负：同FN EA
ΔL = ∑ ΔLi = ∑
i i
L=
横截面面积 Ai 弹性模量 Ei
虑杆端不同加载导致的局部效应。 公式可近似应用于渐变截面杆和阶梯杆。
材料力学 Mechanics of Materials
第五章 轴向受力杆件
拉、压杆的变形
2 拉、压杆的变形
(Deformation of Axially Loaded Bar )
两端受轴向力的等直杆 内力相同 虎克定律 各横截面上 应力相同 应变相同
FN i E i Ai
Li
材料力学 Mechanics of Materials
第五章 轴向受力杆件
拉、压杆的变形
2 拉、压杆的变形
(Deformation of Axially Loaded Bar )
上 海 交 通 大 学
SJTU
变截面圆钢杆ABCD，已知F1 ＝20kN， F2＝35kN， F3=35 kN。l1＝l3＝300mm， l2＝400 mm。直径d1＝12mm，d2＝16 mm，d3＝24mm。试作AD杆 的轴力图，最大正应力σmax， B截面轴向位移，以及AD杆的 伸长ΔlAB。 解： 1， AD杆的轴力分布如右图所示。 2， 求最大正应力