程佩青《数字信号处理教程(第三版)》课后习题答案

9
c) 设 x(n) = δ (n) + δ (n − 1)
i)向n > 0 处递推
y3 (1) = ay3 (0) + x3 (1) = 1 y3 (2) = ay3 (1) + x3 (2) = a y3 (3) = ay3 (2) + x3 (3) = a2
┇ y3 (n) = ay3 (n − 1) + x3 (n) = a n−1 ∴ y3 (n) = a n−1 , n ≥ 1 ii)向 n < 0 处递推
解：(1 )
n
y(n) = ∑ x(m ) m = −∞
n
y1 (n ) = T [x1 (n )] = ∑ x1 (m ) m = −∞
y2 (n ) = T [x2 (n )] =
n
∑ x2 (m )
m = −∞
n
ay1(n)+ by2 (n) = ∑[ax1(m) + bx2 (n)] m = −∞
10
T [ax1(n)+ bx2 (n)] =
n
∑
[ax1
(n
)
+
bx2
(n
)]
m = −∞
T[ax1(n) + bx2(n)] = ay1(n) + by2(n)
∴ 系统是线性系统
解：(2) y(n) =
[x(n )] 2
y1(n)
= T [x1(n)] = [x1(n)] 2
y2 (n) = T [x2 (n)] = [x2 (n)] 2
试判断系统是否是线性的?是否是移不变的?
分析：已知边界条件，如果没有限定序列类型（例如因果序列、反因果序列等）， 则递推求解必须向两个方向进行（n ≥ 0 及 n < 0）。

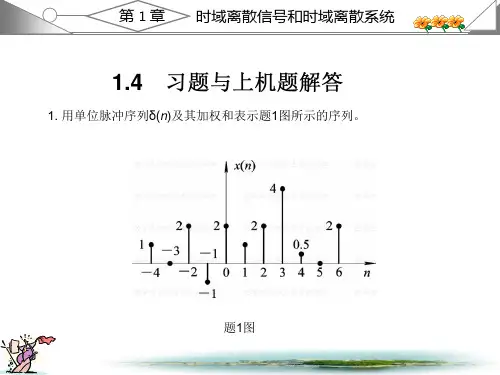
数字信号处理课后答案1.2 教材第一章习题解答1. 用单位脉冲序列()n δ及其加权和表示题1图所示的序列。

解：()(4)2(2)(1)2()(1)2(2)4(3) 0.5(4)2(6)x n n n n n n n n n n δδδδδδδδδ=+++-+++-+-+-+-+-2. 给定信号：25,41()6,040,n n x n n +-≤≤-⎧⎪=≤≤⎨⎪⎩其它（1）画出()x n 序列的波形，标上各序列的值；（2）试用延迟单位脉冲序列及其加权和表示()x n 序列； （3）令1()2(2)x n x n =-，试画出1()x n 波形； （4）令2()2(2)x n x n =+，试画出2()x n 波形； （5）令3()2(2)x n x n =-，试画出3()x n 波形。

解：（1）x(n)的波形如题2解图（一）所示。

（2）()3(4)(3)(2)3(1)6() 6(1)6(2)6(3)6(4)x n n n n n n n n n n δδδδδδδδδ=-+-+++++++-+-+-+-（3）1()x n 的波形是x(n)的波形右移2位，在乘以2，画出图形如题2解图（二）所示。

（4）2()x n 的波形是x(n)的波形左移2位，在乘以2，画出图形如题2解图（三）所示。

（5）画3()x n 时，先画x(-n)的波形，然后再右移2位，3()x n 波形如题2解图（四）所示。

3. 判断下面的序列是否是周期的，若是周期的，确定其周期。

（1）3()cos()78x n A n ππ=-，A 是常数；（2）1()8()j n x n e π-=。

解：（1）3214,73w w ππ==，这是有理数，因此是周期序列，周期是T=14； （2）12,168w wππ==，这是无理数，因此是非周期序列。

5. 设系统分别用下面的差分方程描述，()x n 与()y n 分别表示系统输入和输出，判断系统是否是线性非时变的。

数字信号处理(程佩青)课后习题解答(1)1. 什么是数字信号处理？数字信号处理（Digital Signal Processing，DSP）是指对数字信号进行滤波、采样、压缩、编码和解码等操作的一种信号处理技术。

数字信号处理通过离散采样将连续时间信号转换为离散时间信号，并利用数学算法对离散时间信号进行处理和分析。

数字信号处理广泛应用于音频处理、图像处理、视频处理、通信系统等领域。

2. 采样定理的原理是什么？采样定理又称为奈奎斯特-香农采样定理（Nyquist-Shannon Sampling Theorem），是指在进行模拟信号的离散化处理时，采样频率必须大于模拟信号中最高频率的两倍。

采样定理的原理是根据信号的频谱特性，将模拟信号转换为离散时间信号时，需要保证采样频率足够高，以避免采样后的信号出现混叠现象，即频域上的重叠造成的信息损失。

根据奈奎斯特-香农采样定理，采样频率必须大于模拟信号中最高频率的2倍，才能完全还原原始信号。

3. 什么是混叠现象？如何避免混叠现象？混叠现象是指在进行模拟信号的采样时，由于采样频率低于模拟信号中的最高频率，导致频域上的重叠，从而造成采样信号中出现与原始信号不一致的频谱。

混叠现象会使得原始信号的高频部分被错误地表示成低频部分，从而损失了原始信号的信息。

为了避免混叠现象，可以采取以下措施：- 提高采样频率：采样频率必须大于模拟信号中最高频率的两倍，以保证信号的频谱不发生重叠。

- 使用低通滤波器：在采样前，先通过低通滤波器将模拟信号中的高频成分滤除，以避免混叠现象。

滤波器的截止频率应该设置为采样频率的一半。

4. 离散时间信号和连续时间信号有哪些区别？离散时间信号和连续时间信号是两种不同的信号表示形式。

离散时间信号是在时间上离散的，通常由序列表示，每个时间点上有对应的取样值。

离散时间信号可以通过采样连续时间信号得到，采样时将连续时间信号在一定时间间隔内进行取样。

连续时间信号是在时间上连续的，可以用数学函数、图像或者波形图来表示，不存在取样点。

=2x(n)+x(n－1)+ x(n－2)
将x(n)的表示式代入上式， 得到 1 y(n)=－2δ(n+2)－δ(n+1)－0.5δ(2n)+2δ(n－1)+δ(n－2)
+4.5δ(n－3)+2δ(n－4)+δ(n－5)
第 1 章 时域离散信号和时域离散系统
8. 设线性时不变系统的单位脉冲响应h(n)和输入x(n)分别有以下三种情况，
第 1 章 时域离散信号和时域离散系统
(3) 这是一个延时器， 延时器是线性非时变系统， 下面证明。 令输入为
输出为
x(n－n1)
y′(n)=x(n－n1－n0) y(n－n1)=x(n－n1－n0)=y′(n) 故延时器是非时变系统。 由于
T［ax1(n)+bx2(n)］=ax1(n－n0)+bx2(n－n0) =aT［x1(n)］+bT［x2(n)］
（5）y(n)=x2(n)
（6）y(n)=x(n2)
（7）y(n)=
n
（8）y(n)=x(n)sin(ωxn(m) )
m0
解： （1） 令输入为
输出为
x(n－n0)
y′(n)=x(n－n0)+2x(n－n0－1)+3x(n－n0－2) y(n－n0)=x(n－n0)+2x(n—n0—1)+3(n－n0－2)
x(m)h(n－m)
m
第 1 章 时域离散信号和时域离散系统
题7图
第 1 章 时域离散信号和时域离散系统
y(n)={－2,－1,－0.5, 2, 1, 4.5, 2, 1; n=－2, －1, 0, 1, 2, 3, 4, 5}

《数字信号处理》第三版课后习题答案数字信号处理课后答案1.2 教材第一章习题解答1. 用单位脉冲序列()n δ及其加权和表示题1图所示的序列。

解：()(4)2(2)(1)2()(1)2(2)4(3)0.5(4)2(6)x n n n n n n n n n n δδδδδδδδδ=+++-+++-+-+-+-+-2. 给定信号：25,41()6,040,n n x n n +-≤≤-??=≤≤其它（1）画出()x n 序列的波形，标上各序列的值；（2）试用延迟单位脉冲序列及其加权和表示()x n 序列；（3）令1()2(2)x n x n =-，试画出1()x n 波形；（4）令2()2(2)x n x n =+，试画出2()x n 波形；（5）令3()2(2)x n x n =-，试画出3()x n 波形。

解：（1）x(n)的波形如题2解图（一）所示。

（2）()3(4)(3)(2)3(1)6()6(1)6(2)6(3)6(4)x n n n n n n n n n n δδδδδδδδδ=-+-+++++++-+-+-+-（3）1()x n 的波形是x(n)的波形右移2位，在乘以2，画出图形如题2解图（二）所示。

（4）2()x n 的波形是x(n)的波形左移2位，在乘以2，画出图形如题2解图（三）所示。

（5）画3()x n 时，先画x(-n)的波形，然后再右移2位，3()x n 波形如题2解图（四）所示。

3. 判断下面的序列是否是周期的，若是周期的，确定其周期。

（1）3()cos()78x n A n ππ=-，A 是常数；（2）1()8()j n x n e π-=。

解：（1）3214,73w w ππ==，这是有理数，因此是周期序列，周期是T=14；（2）12,168w wππ==，这是无理数，因此是非周期序列。

5. 设系统分别用下面的差分方程描述，()x n 与()y n 分别表示系统输入和输出，判断系统是否是线性非时变的。

数字信号处理（程佩青）课后习题解答（4）第四章快速傅立叶变换运算需要多少时间。

计算需要多少时间，用，问直拉点的，用它来计算每次复加速度为平均每次复乘需如果一台通用计算机的FFT DFT[x (n)]512s 5 s 50.1μμ 解: 解: ⑴ 直接计算: 复乘所需时间:复加所需时间: ⑵用FFT 计算:复乘所需时间: 复加所需时间:运算一次完成。

点试用一个为了提高运算效率值求今需要从值的点实序列是两个已知IFFT N n y n x k Y k X DFT n y n x N k Y k X ,,)(),()(),(,)(),()(),(.2s N T N 01152.0 512log 105 log 105 2251262261==??=--s T T T sN N T 013824.0 002304.0 512log 512105.0 log 105.0 2126262=+=∴===--sT T T sN N T 441536.1 130816.0 )1512(512105.0 )1(105.0 21662=+=∴=-=-=--s N T 31072.1 512105 105 262 61=??=??=--值的过程。

）（），（完成计算点）可用一次（）（）（综上所述，构造序列）（）（）（）（可得：）（）（）（再根据都是实序列，）（），（由原题可知：）（）（）（）（（）（）（性质：又根据可得序列点作对取序列依据题意解 ]Im[ ]Re[ ][][ ][ ).()( )()()( )()();()( ::n y n x IFFT N k jY k X k Z n z n y n z n x n jy n x n z n y n x n jy n x k Y jIDFT k X IDFT k jY k X IDFT DFT n z IFFT N k Z k jY k Xk Z k Y n y k X n x +===+=+=+=++=??。

4
第一章 离散时间信号与系统
1 .直接计算下面两个序列的卷积和 y( n ) = x( n )* h( n )
h (n )
=
⎧an ⎨
⎩0
, 0 ≤ n ≤ N −1 , 其他n
x (n )
=
⎧⎪ β ⎨
n−n 0
⎪⎩ 0
,n0 ≤ n , n < n0
请用公式表示。
分析：
①注意卷积和公式中求和式中是哑变量 m （ n 看作参量），
y (n ) ={1，2，3，3，2，1} ;
②δ (n)* x(n) = x(n) , δ (n − m)* x(n) = x(n − m) ;
③卷积和求解时， n 的分段处理。
6
解：(1) y(n) = x(n) * h(n) = R5(n) (2) y(n) = x(n) * h(n) = {1,2,3,3,2,1}
β α
n +1
β α β =
n +1− N −n0
N−
N
α −β
y(n) = Nα n−n0 ,
(α = β )
, (α ≠ β )
如此题所示，因而要分段求解。
2 .已知线性移不变系统的输入为 x( n ) ,系统的单位抽样响应
为 h( n ) ,试求系统的输出 y( n ) ,并画图。
(1)x(n) = δ (n)
∑ ∑( ) n α m−n0 n−m = β α = β m=n0
nn β
n0
α
n β −n0
− β n0
α
β n +1 α
1
−
β α
α β =
− n +1− n0

数字信号处理课后答案1.2 教材第一章习题解答1. 用单位脉冲序列()n δ及其加权和表示题1图所示的序列。

解：()(4)2(2)(1)2()(1)2(2)4(3) 0.5(4)2(6)x n n n n n n n n n n δδδδδδδδδ=+++-+++-+-+-+-+-2. 给定信号：25,41()6,040,n n x n n +-≤≤-⎧⎪=≤≤⎨⎪⎩其它（1）画出()x n 序列的波形，标上各序列的值；（2）试用延迟单位脉冲序列及其加权和表示()x n 序列； （3）令1()2(2)x n x n =-，试画出1()x n 波形； （4）令2()2(2)x n x n =+，试画出2()x n 波形； （5）令3()2(2)x n x n =-，试画出3()x n 波形。

解：（1）x(n)的波形如题2解图（一）所示。

（2）()3(4)(3)(2)3(1)6() 6(1)6(2)6(3)6(4)x n n n n n n n n n n δδδδδδδδδ=-+-+++++++-+-+-+-（3）1()x n 的波形是x(n)的波形右移2位，在乘以2，画出图形如题2解图（二）所示。

（4）2()x n 的波形是x(n)的波形左移2位，在乘以2，画出图形如题2解图（三）所示。

（5）画3()x n 时，先画x(-n)的波形，然后再右移2位，3()x n 波形如题2解图（四）所示。

3. 判断下面的序列是否是周期的，若是周期的，确定其周期。

（1）3()cos()78x n A n ππ=-，A 是常数；（2）1()8()j n x n e π-=。

解：（1）3214,73w w ππ==，这是有理数，因此是周期序列，周期是T=14； （2）12,168w wππ==，这是无理数，因此是非周期序列。

5. 设系统分别用下面的差分方程描述，()x n 与()y n 分别表示系统输入和输出，判断系统是否是线性非时变的。

数字信号处理课后答案1.2 教材第一章习题解答1. 用单位脉冲序列()n 及其加权和表示题1图所示的序列。

解：()(4)2(2)(1)2()(1)2(2)4(3)0.5(4)2(6)x n nn n n n nnn n 2. 给定信号：25,41()6,040,nnx n n其它（1）画出()x n 序列的波形，标上各序列的值；（2）试用延迟单位脉冲序列及其加权和表示()x n 序列；（3）令1()2(2)x n x n ，试画出1()x n 波形；（4）令2()2(2)x n x n ，试画出2()x n 波形；（5）令3()2(2)x n x n ，试画出3()x n 波形。

解：（1）x(n)的波形如题2解图（一）所示。

（2）()3(4)(3)(2)3(1)6()6(1)6(2)6(3)6(4)x n nnnn n n n n n （3）1()x n 的波形是x(n)的波形右移2位，在乘以2，画出图形如题2解图（二）所示。

（4）2()x n 的波形是x(n)的波形左移2位，在乘以2，画出图形如题2解图（三）所示。

（5）画3()x n 时，先画x(-n)的波形，然后再右移2位，3()x n 波形如题2解图（四）所示。

3. 判断下面的序列是否是周期的，若是周期的，确定其周期。

（1）3()cos()78x n A n，A 是常数；（2）1()8()j n x n e 。

解：（1）3214,73w w ，这是有理数，因此是周期序列，周期是T=14；（2）12,168ww，这是无理数，因此是非周期序列。

5. 设系统分别用下面的差分方程描述，()x n 与()y n 分别表示系统输入和输出，判断系统是否是线性非时变的。

（1）()()2(1)3(2)y n x n x n x n；（3）0()()y n x n n ，0n 为整常数；（5）2()()y n x n ；（7）0()()n m y n x m 。

（5）y(n)=x2(n)
（6）y(n)=x(n2)
（7）y(n)=
n
（8）y(n)=x(n)sin(ωxn(m) )
m0
解： （1） 令输入为
输出为
x(n－n0)
y′(n)=x(n－n0)+2x(n－n0－1)+3x(n－n0－2) y(n－n0)=x(n－n0)+2x(n—n0—1)+3(n－n0－2)
x(n)=－δ(n+2)+δ(n－1)+2δ(n－3)
h(n)=2δ(n)+δ(n－1)+ δ(n－2)
由于
x(n)*δ(n)=x(n)
1
x(n)*Aδ(n－k)=Ax(n－k)
2
故
第 1 章 时域离散信号和时域离散系统
y(n)=x(n)*h(n)
=x(n)*［2δ(n)+δ(n－1)+ δ(n－2) 1 2
(4) 令x1(n)=xe(n)+xo(n), 将x1(n)与x(n)进行比较， 你能得
第 1 章 时域离散信号和时域离散系统
解：（1） x(－n)的波形如题4 (2) 将x(n)与x(－n)的波形对应相加， 再除以2， 得到xe(n)。 毫无疑问， 这是 一个偶对称序列。 xe(n)的波形如题4解图（二）所示。 (3) 画出xo(n)的波形如题4解图（三）所示。
分别求出输出y(n)。
（1） h(n)=R4(n), x(n)=R5(n) （2） h(n)=2R4(n), x(n)=δ(n)－δ(n－2) （3） h(n)=0.5nu(n), xn=R5(n)
解： （1） y(n)=x(n)*h(n)=
R4(m)R5(n－m)

第一章 离散时间信号与系统2.任意序列x(n)与δ(n)线性卷积都等于序列本身x(n)，与δ(n-n 0)卷积x(n- n 0),所以（1）结果为h(n) (3)结果h(n-2) （2（4）3 .已知 10,)1()(<<--=-a n u a n h n，通过直接计算卷积和的办法，试确定单位抽样响应为 )(n h 的线性移不变系统的阶跃响应。

4. 判断下列每个序列是否是周期性的,若是周期性的,试确定其周期：)6()( )( )n 313si n()( )()873cos()( )(ππππ-==-=n j e n x c A n x b n A n x a分析：序列为)cos()(0ψω+=n A n x 或)sin()(0ψω+=n A n x 时，不一定是周期序列，nmm m n n y n - - -∞ = - ⋅ = = ≥ ∑ 2 31 2 5 . 0 ) ( 01当 3 4n m nm m n n y n 2 2 5 . 0 ) ( 1⋅ = = - ≤ ∑ -∞ = - 当 aa a n y n a a an y n n h n x n y a n u a n h n u n x m m nnm mn -==->-==-≤=<<--==∑∑--∞=---∞=--1)(11)(1)(*)()(10,)1()()()(:1时当时当解①当=0/2ωπ整数，则周期为0/2ωπ；②；为为互素的整数）则周期、（有理数当 , 2 0Q Q P QP =ωπ ③当=0/2ωπ无理数 ，则)(n x 不是周期序列。

解：（1）0142/3πω=，周期为14 （2）062/13πω=，周期为6 （2）02/12πωπ=，不是周期的 7.（1）[][]12121212()()()()()()[()()]()()()()[()][()]T x n g n x n T ax n bx n g n ax n bx n g n ax n g n bx n aT x n bT x n =+=+=⨯+⨯=+所以是线性的T[x(n-m)]=g(n)x(n-m) y(n-m)=g(n-m)x(n-m) 两者不相等，所以是移变的y(n)=g(n)x(n) y 和x 括号内相等，所以是因果的。

第一章 离散时间信号与系统2.任意序列x(n)与δ(n)线性卷积都等于序列本身x(n)，与δ(n-n 0)卷积x(n- n 0),所以（1）结果为h(n) (3)结果h(n-2) （2x(m)()h n m -n1 1 1 0 0 0 0 y(n) 0 11 1 1 12 2 1 1 13 3 1 1 1 1 34 0 1 1 1 1 2 511111（4）3 .已知 10,)1()(<<--=-a n u a n h n，通过直接计算卷积和的办法，试确定单位抽样响应为 )(n h 的线性移不变系统的阶跃响应。

4. 判断下列每个序列是否是周期性的,若是周期性的,试确定其周期：)6()( )( )n 313si n()( )()873cos()( )(ππππ-==-=n j e n x c A n x b n A n x a分析：序列为)cos()(0ψω+=n A n x 或)sin()(0ψω+=n A n x 时，不一定是周期序列， nmm m n n y n - - -∞ = - ⋅ = = ≥ ∑ 2 31 2 5 . 0 ) ( 01当 3 4n m nm m n n y n 2 2 5 . 0 ) ( 1⋅ = = - ≤ ∑ -∞ = - 当 aa a n y n a a an y n n h n x n y a n u a n h n u n x m m nnm mn -==->-==-≤=<<--==∑∑--∞=---∞=--1)(11)(1)(*)()(10,)1()()()(:1时当时当解①当=0/2ωπ整数，则周期为0/2ωπ；②；为为互素的整数）则周期、（有理数当 , 2 0Q Q P QP =ωπ ③当=0/2ωπ无理数 ，则)(n x 不是周期序列。

解：（1）0142/3πω=，周期为14 （2）062/13πω=，周期为6 （2）02/12πωπ=，不是周期的 7.（1）[][]12121212()()()()()()[()()]()()()()[()][()]T x n g n x n T ax n bx n g n ax n bx n g n ax n g n bx n aT x n bT x n =+=+=⨯+⨯=+所以是线性的T[x(n-m)]=g(n)x(n-m) y(n-m)=g(n-m)x(n-m) 两者不相等，所以是移变的y(n)=g(n)x(n) y 和x 括号内相等，所以是因果的。

第三章 离散傅立叶变换1.如下图，序列x(n)是周期为6的周期性序列，试求其傅立叶级数的系数。

∑∑=-===56265)(~)(~)(X ~:n nkj nkn e n x W n x k π解kj k j k j kj kj e e e e e 562462362262621068101214πππππ-----+++++=计算求得:。

339)5(~; 33)4(~ ; 0)3(~; 33)2(~;339)1(~;60)0(~j X j X X j X j X X +=-==+=-==。

并作图表示试求设)(~),(~)(~ .))(()(~),()(.264k X n x k X n x n x n R n x == ∑∑=-===56265)(~)(~)(~:n nk jnk n en x W n x k X π解k j kj k j e e e πππ---+++=3231。

计算求得： 3)5(~; 1)4(~ ; 0)3(~ ;1)2(~; 3)1(~ ; 4)0(~j X X X X j X X ====-==。

的周期卷积并作图与试求令其它，设 )(~)(~,))(()(~,))(()(~,)2()(,040,1)(.3464n h n x n h n h n x n x n R n h nn n n x ==-=⎩⎨⎧≤≤+=解：在一个周期内的计算值)(~)(~*)(~)(~m n h n h n x n y -==)(~)(~*)(~)(~m n h n h n x n y -==等各序列。

试画出所示如图已知)())((),())3((,))(()())((),())((,))((,13)(.47755633665n R n x n R n x n x n R n x n R n x n x P n x ----)()()5()(x(n)(4)N n 0 ),n -(n )()3()()()2()()(cos )()1()(52000n R n n x n nR n x n R a n x n R n a n x DFT N N N N n N ==<<===δω闭合形式表达式点试求以下有限长序列的])21sin()2sin()21sin()2sin([21])()()()([21)(]1111[)(][)(])([)()(cos )()()(cos )(:0)2(21020)2(2102)2(21)2(21)2(21222)2(21)2(21)2(21222)()(211)(10)(2110211000000000000000000002002002022002ϖπϖϖπϖωωϖπϖϖπϖϖπϖπϖπϖϖϖϖπϖπϖπϖϖϖωωωωωωωωππππππ-++⋅=--+--=--+--=+=+===---+---------+-++-----+---=---=+--=---=-∑∑∑∑k N e N e k N e N e a e ee e e e eeeee e a k R ee ee a k R eea k R e e e a k R en a k X n R n a n x k N j N j k Nj Njk Nj k Nj k Nj NjNjN jk Nj k N j k Nj NjNjNjN k j N j k j N j N N n nj N n nk j N N n nkj n j n j N n N nkj N N N N N N N 解)(111121)(21)()(21)()(cos )( )()(cos )( ) 1 (:)2()2(10)2(10)2(1020010200000k R e ee e a k R e e a k R e e e a k Re n a k X n R n a n x N k N j N j k Nj Nj N N n nN j N n nk N j N N n nk N j n j n j N n N nk N j N ⎥⎥⎦⎤⎢⎢⎣⎡--+--=⎥⎦⎤⎢⎣⎡+=⎥⎦⎤⎢⎣⎡+===--+---=---=+--=---=-∑∑∑∑ωπωωπωωπωππωωπωω解⎥⎥⎥⎦⎤---⎢⎢⎢⎣⎡--=------+-++---)()()()(21)2(21)2(21)2(21222)2(21)2(21)2(212220000000ωπωπωπωωωωπωπωπωωωk Nj k N j k N j N jN jNjk N j k N j k N j Nj N j N j e e e eeee e e e e e a⎥⎥⎥⎥⎦⎤--⎢⎢⎢⎢⎣⎡+⋅=--+--)21sin()2sin()21sin()2sin(210)2(21020)2(21020000ωπωωπωωπωωπωk N e Nek N e Ne a k Nj Njk N j N jk Nj N N n nk NjnN n aea eak X n R a n x ππ210211)()()((2)--=---===∑)( )()( )()()( 0,)()( (3)02102010200k Re k Re n n k Re n x k X N n n n n x Nk n N j NN n nk N j N n NnkN j πππδδ--=--=-=-==<<-=∑∑)(1)( 11)1()())1(()(])1)2( 2[)1( 32()1)(()()()()( )()(411)1(32)1(321)1(110)1(1k R W Nk X N W W N k R W N k R N W N W W W N W W W nW nWW k X k R nW k X W k R nW k X n nR n x N kNkNkN N N n nk N N k N N k N k N k N N kN k N k N N n kn N N n nk Nk NN n N k n N k NN n N nkN N --=∴-=--+--=+--=-+-+++--++++=-=-==∴=∑∑∑∑∑-=---=+-=-=+-=∙∙∙∙∙∙）（kNN N n nkNN W Nk X n nR n x W n k X n R n n x --===∴=∑-=1)()()()4()( )()(5111022，则小题的结论根据第）（221111122)1(232)1(23210)1(2121)1(2)1()2()(12)2()(2)2(2)2()12()1(]1()2(4[)1(94)1)(()(k N kN kNN n nk NN n nkNk N N kN k N k N N k N k N k N N n kn NN n nk NkNN n kn N k NW N W N N k X W NN N k X N N nWN N W n N N W N W W W N W W W W n W nW k X W n k X W ---=∴----=+--=+--=-+--=-+-+++--++++=-=-=∑∑∑∑∑-=-=---=+-=-=+∙∙∙∙∙∙）∙∙∙±±±===∑-=,6,4,2,0)(~)3(?])0([)()2(?)()1(:;)(~1)(~).(~.61)/2(k k x X k X k X ek X Nn x n x N k nkN j 哪些序列列能做到成虚数外除时间原点使所有的哪些序列能够通过选择成为实数时间原点使所有的哪些序列能够通过选择问傅里叶级数这些序列可以表示成列如图画出了几个周期序π条件。