压杆稳定实验讲义
- 格式:doc
- 大小:18.00 KB
- 文档页数:6

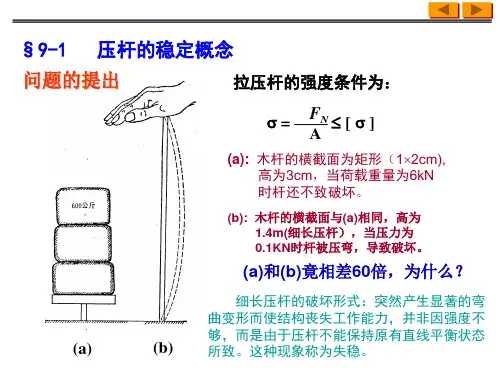








3-9 压杆稳定性实验工程实际中,失稳破坏往往是突然发生的,危害性很大,因此充分认识压杆的失稳现象,测定压杆的临界载荷,具有十分重要的工程意义。
一、试验目的1.测定两端铰支细长压杆的临界载荷F cr ,并与理论值进行比较,验证欧拉公式。
2.观察两端铰支细长压杆的失稳现象。
二、设备和仪器1.力学实验台;2.百分表(或电阻应变仪); 3.游标卡尺、钢板尺。
三、试样弹簧钢(60Si 2Mn )制成的矩形截面细长杆,经过热处理。
两端制成刀刃,以便安装在试验台的V 形支座内。
四、实验原理对于轴向受压的理想细长直杆,按小变形理论其临界载荷可由欧拉公式求得:2cr 2()EIF L πμ= (3-32)式中:E 为材料的弹性模量,I 为压杆横截面的最小惯性矩,l 为压杆的长度;μ为长度系数,对于二端铰支情况,μ=1。
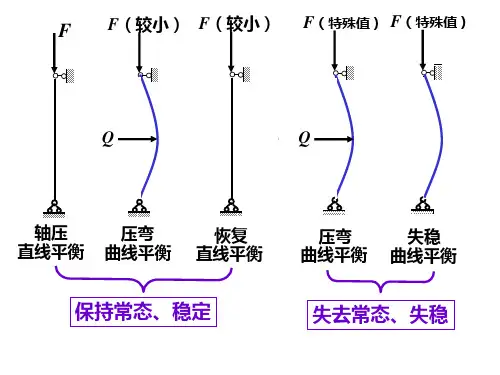
当载荷小于F cr 时,压杆保持直线形状的平衡,即使有横向干扰力使压杆微小弯曲,在撤除干扰力以后压杆仍能回复直线形状,是稳定平衡。
当载荷等于F cr 时,压杆处于临界状态,可在微弯情况下保持平衡。
如以压力F 为纵坐标,压杆中点挠度w 为横坐标。
按小变形理论绘出的F -w 图形可由二段折线OA 和AB 来描述,如图3-32所示。
而实际压杆由于不可避免地存在初始曲率,或载荷可能有微小偏心以及材料不均匀等原因,在加载初始就出现微小挠度,开始时其挠度w 增加较慢,但随着载荷增加,挠度也不断增加,当载荷接近临界载荷时,挠度急速增加,其F -w曲线如图3-32中OCD 所示。
实际曲线OCD 与理论曲线之间的偏离,表征初始曲率、偏心以及材料不均匀等因素的影响,这种影响愈大,偏离也愈大。
显然,实际曲线的水平渐进线即代表压杆的临界载荷F cr 。
工程上的压杆都在小挠度下工作,过大的挠度会产生塑性变形或断裂。
仅有部分材料制成的细长杆能承受较大的挠度使载荷稍高于cr F (图3-32中虚线DE 所示)。
实验测定临界载荷,可用百分表测杆中点处挠度w ,如图3-33a 所示。
压杆稳定实验讲义
3-9 压杆稳定性实验
工程实际中,失稳破坏往往是突然发生的,危害性很大,因此充分认识压杆的失稳现象,测定压杆的临界载荷,具有十分重要的工程意义。
一、试验目的
1(测定两端铰支细长压杆的临界载荷F,并与理论值进行比较,验证欧拉公式。
cr
2(观察两端铰支细长压杆的失稳现象。
二、设备和仪器
1(力学实验台;
2(百分表(或电阻应变仪);
3(游标卡尺、钢板尺。
三、试样
弹簧钢(60SiMn)制成的矩形截面细长杆,经过热处理。
两端制成刀刃,以便安装在2
试验台的V形支座内。
四、实验原理
对于轴向受压的理想细长直杆,按小变形理论其临界载荷可由欧拉公式求得: 2,EI (3-32) ,Fcr2()L,
式中:E为材料的弹性模量,I为压杆横截面的最小惯性矩,l为压杆的长度;为长度系,数,对于二端铰支情况,=1。
,
当载荷小于F时,压杆保持直线形状的平衡,即使有横向干扰力使压杆微小弯曲,cr
在撤除干扰力以后压杆仍能回复直线形状,是稳定平衡。
当载荷等于F时,压杆处于临界状态,可在微弯情况下crF保持平衡。
如以压力F为纵坐标,压杆中点挠度为横坐标。
按小wBEA变形理论绘出的F-w 图形可由二段折线和来描述,ABOADC如图3-32所示。
而实际压杆由于不可避免地存在初始曲率,或载荷可能
有微小偏心以及材料不均匀等原因,在加载初始就出现微小0W挠度,开始时其挠度w增加较慢,但随着载荷增加,挠度也不断增加,当载荷接近临界载荷时,挠度急速增加,其F-w5.15 F-w 曲线图3-32 F-W 曲线曲线如图3-32中OCD 所示。
实际曲线OCD与理论曲线之
间的偏离,表征初始曲率、偏心以及材料不均匀等因素的影
响,这种影响愈大,偏离也愈大。
显然,实际曲线的水平渐进线即代表压杆的临界载荷F。
cr
工程上的压杆都在小挠度下工作,过大的挠度会产生塑性变形或断裂。
仅有部分材料制成的细长杆能承受较大的挠度使载荷稍高于(图3-32中虚线DE所示)。
Fcr
实验测定临界载荷,可用百分表测杆中点处挠度w,如图3-33a所示。
绘制F-w曲线,作F-w曲线的水平渐近线就得到临界载荷F。
cr
当采用百分表测量杆中点挠度时,由于压杆的弯曲方向不能预知,应预压一定量程,以给杆向左、右弯曲留有测量余地。
由于弯曲变形的大小也反映在试件中点的应变
上,所以,也可在杆中点处两侧各粘贴一枚应变片,
F见图3-33b,将它们接成半桥,记录应变仪读数,,duF
绘制F-曲线,作F-曲线的水平渐近线,就得,,dudu
到临界载荷F。
cr
若用电测法测量杆中点应变时,被测量应变ε应t包含二个部分,即轴力引起的应变和附加弯矩引起的b应变:
,,,,,FMlRR12若将二个应变片作为工作片组成半桥,注意到二
侧弯曲应变符号相异,则有:
,,,2duM
可见此时已消除了由轴向压力产生的应变,其读w数就是测点处由弯矩M产生的真实应变的两倍。
因
此由弯矩产生的测点处的正应力为
FttMFw(b)(a),du22 (3-33) ,,,,EE,,电测法百分表法 II2
即
EI图3-33压杆稳定实验装置简图 (3-34) ,, wduFt
由上式可见,在一定的荷载F作用下,应变仪读数的大小反映了压杆挠度w的大小,,du因此可用电测法来确定临界载荷F。
cr
五、实验步骤
1(测量试样尺寸
用钢板尺测量试样长度L,用游标卡尺测量试样上、中、下三处的宽度b和厚度t,取
其平均值。
用来计算横截面的最小惯性矩。
Imin
2(拟定加载方案,并估算最大容许变形
如采用百分表或电阻应变仪测量杆件中点变形,在初载荷F到0.8F间的范围内,曲0cr线比较陡直,宜采用分级加载(4~5级),进行载荷控制;载荷每增加一级,即测定一,F个相应的变形量(挠度w或应变仪读数)。
当接近失稳时,变形量快速增加,此时应改,du
为位移控制;挠度w每增加一定数值(如0.10mm),或应变仪读数每增加一定读数(如,du
)时,即读取一个相应的载荷数。
20,,Fi
,,200MPa取许用应力,计算临界载荷理论值: ,,
2,EIF, cr2L,,,
按下列公式估算容许最大挠度或容许最大应变仪读数: wmax
FFwcrcrmax,,, (3-35) (百分表测变形时) ,,btW
FE,crdumax,,[] (3-36) (应变仪测变形时) ,bt2
3(安装试样,准备测变形仪器,加初载荷,记录初读数。
试样两端应尽量放置在上、下V形座正中央。
根据实验室设备条件确定实验方案。
若用百分表测挠度:加初载荷(如200N),安装百分表,使表测杆在试样正中位置,预压约5mm,调整表盘,使小指针指整数时,大指针在“0”附近,记录百分表读数。
若用应变仪测变形:将试样两侧的应变片组成半桥,设置应变仪测应变通道参数(桥路、灵敏系数、应变片电阻值),加载前调试所选应变通道电桥。
加初载荷(如200N)后,记录应变仪读数。
4. 力传感器接线、设置参数。
力传感器接线,设置参数(校正系数、载荷限值)。
5(按实验方案加载,记录数据。
按实验方案每级加载后,读取载荷值和百分表读数A(或应变仪读数)。
当载荷增,idui量很小(但变形不超过或)时,即可停止试验。
实验数据以表格形式记录。
w,maxdumax
6(卸去载荷,实验台回复原状。
六、实验结果处理
1(据测量数据计算试件宽度和厚度平均值,从而计算最小惯性矩I。
原始数据以表min格形式示出,可参考表3-11。
表3-11 测定压杆临界载荷数据列表
宽度b /mm 厚度t /mm 最小惯性矩长度l /mm 试样4/mm 上中下平均上中下平均尺寸性能参数:弹性模量E= Gpa; 许用应力[,]= MPa 测量次数i 0 1 2 3
载荷F /N 0 i
读数A/mm / i百分表
wAA,,/mm 测量挠度 / 0 ,,i1
应变仪读数,/με0 dui测量变形
2(据实验数据在方格纸上画出F-w(或F-)曲线,作它的水平渐近线,确定临界,du
载荷F实验值。
cr
thF3. 用欧拉公式计算临界载荷理论值,计算临界载荷实验值的相对误差。
cr
thRFF,crcr,,100%% (3-37) thFcr
七、实验报告要求
实验报告应包括实验目的,原理,加载方案,实验数据记录和处理,以及误差分析等。
八、思考题
1. 如以和分别表示左右二侧的应变,显然随着F的增加,二者差异也愈大。
如以,,12
F,,F,,压力F为纵坐标,压应变ε为横坐标,可绘出和两种曲线。
两种曲线F,,12的水平渐近线是否一致,
2. 本试验装置与理想情况有什么不同,对实验结果会产生哪些影响,
3. 对同一压杆,如支承条件不同,对其临界力的影响大吗,为什么, 九、预习要求
1. 预习压杆稳定相关内容,了解压杆临界载荷测量的原理和方法。
2. 对于给定压杆试件。
若已知材质和相应弹性模量以及压杆的名义尺寸(如b,t,l4mm×20mm×300mm)。
估算临界载荷,拟定加载方案。
3. 参考数据处理列表,按实验要求,绘制好本实验记录表。