化学计算,平均值法

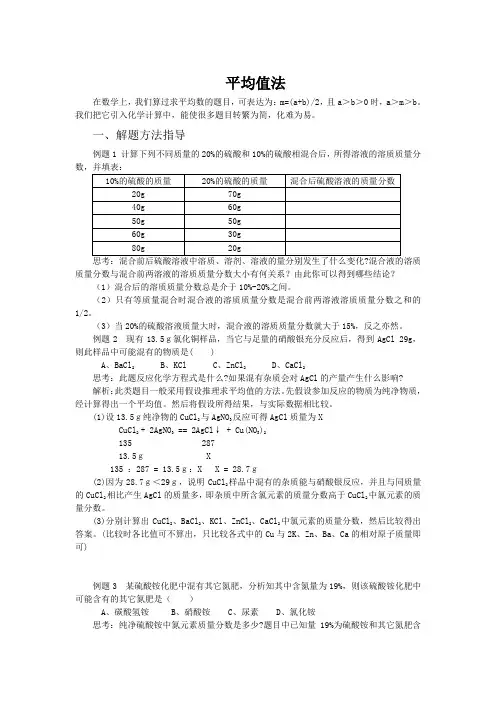
平均值法在数学上，我们算过求平均数的题目，可表达为：m=(a+b)/2，且a＞b＞0时，a＞m＞b。

我们把它引入化学计算中，能使很多题目转繁为简，化难为易。

一、解题方法指导例题1 计算下列不同质量的20%的硫酸和10%的硫酸相混合后，所得溶液的溶质质量分数，并填表：质量分数与混合前两溶液的溶质质量分数大小有何关系？由此你可以得到哪些结论？（1）混合后的溶质质量分数总是介于10%-20%之间。

（2）只有等质量混合时混合液的溶质质量分数是混合前两溶液溶质质量分数之和的1/2。

（3）当20%的硫酸溶液质量大时，混合液的溶质质量分数就大于15%，反之亦然。

例题2 现有13.5ｇ氯化铜样品，当它与足量的硝酸银充分反应后，得到AgCl 29g，则此样品中可能混有的物质是( )A、BaCl2 B、KCl C、ZnCl2D、CaCl2思考：此题反应化学方程式是什么?如果混有杂质会对AgCl的产量产生什么影响?解析：此类题目一般采用假设推理求平均值的方法。

先假设参加反应的物质为纯净物质，经计算得出一个平均值。

然后将假设所得结果，与实际数据相比较。

(1)设13.5ｇ纯净物的CuCl2与AgNO3反应可得AgCl质量为XCuCl2 + 2AgNO3== 2AgCl↓ + Cu(NO3)2135 28713.5ｇ X135 ：287 = 13.5ｇ：X X = 28.7ｇ(2)因为28.7ｇ＜29ｇ，说明CuCl2样品中混有的杂质能与硝酸银反应，并且与同质量的CuCl2相比产生AgCl的质量多，即杂质中所含氯元素的质量分数高于CuCl2中氯元素的质量分数。

(3)分别计算出CuCl2、BaCl2、KCl、ZnCl2、CaCl2中氯元素的质量分数，然后比较得出答案。

(比较时各比值可不算出，只比较各式中的Cu与2K、Zn、Ba、Ca的相对原子质量即可)例题3 某硫酸铵化肥中混有其它氮肥，分析知其中含氮量为19%，则该硫酸铵化肥中可能含有的其它氮肥是（）A、碳酸氢铵B、硝酸铵C、尿素D、氯化铵思考：纯净硫酸铵中氮元素质量分数是多少?题目中已知量19%为硫酸铵和其它氮肥含氮量的平均值，所以此平均值介于硫酸铵与另一氮肥含氮量之间。

化学计算之极值法与平均值法极值法就是将复杂的问题假设为处于某一个或某两个极端状态，并站在极端的角度分析问题，求出一个极值，推出未知量的值，或求出两个极值，确定未知量的范围，从而使复杂的问题简单化。

其主要应用于：（1）用极值法确定混合气体的平均相对分子质量；（2）用极值法确定物质的质量；（3）用极值法确定物质的成分；（4）用极值法确定反应中反应物、生成物的取值范围；（5）用极值法确定杂质的成分。

解题一般思路：（1）根据题目给定的条件和化学反应原理，确定不确定条件的范围；（2）计算相应条件下的最大值或最小值；（3）综合分析得出正确答案例1. 铝、锌组成的混合物和足量盐酸反应，产生氢气0.25g，则混合物的质量可能为（）A．2g B．4g C．8.5g D．10g练习：将一定质量的Mg、Zn、Al混合物与足量稀H2SO4反应，生成H2质量为0.25g，原混合物的质量可能是（）A.2 gB.4 gC.8 gD.10 g例2.在密闭容器中，7.2g碳与一定量氧气恰好完全反应，生成气体的质量可能是（）A.．8.4g B．17.8g C．26.4g D．44.0g练习：镁在空气中燃烧时，发生如下两个反应：3Mg+N2=Mg3N2，2Mg+O2=2MgO则24 g镁在空气中燃烧可得产物的质量为（) A．等于33.3 g B．等于40 g C．33.3 g～40 g D．小于33.3 g或大于40 g例3.某混合物含有KCl、NaCl和Na2CO3，经分析含钠31.5％，含氯27.08％（以上均为质量分数），则混合物中Na2CO3的质量分数为（）A 25％B 50％C 80％D 无法确定练习：在一定温度下，某气体中可能含有SO3、SO2、O2中的两种或三种。

则该混合气体中硫元素的质量分数不可能是（）（A）50％（B）40％（C）25％（D）70％平均值法：混合物的平均式量、元素的质量分数、生成的某指定物质的量总是介于组分的相应量的最大值M2与最小值M1之间，表达式为M1 < M < M2，已知其中两个量，可以确定另一个量的方法，称为平均值法。

化学计算题平均值计算公式在化学实验和计算中，经常需要计算一组数据的平均值。

平均值是一组数据的总和除以数据的个数，是衡量数据集中趋势的一个重要指标。

在化学领域，平均值的计算常常用于实验数据的处理和分析，以及对化学反应速率、浓度等参数的计算。

本文将介绍平均值的计算公式及其在化学计算中的应用。

平均值的计算公式如下：\[。

\bar{x} = \frac{\sum_{i=1}^{n} x_i}{n}。

\]其中，\(\bar{x}\)表示平均值，\(x_i\)表示每个数据点，\(n\)表示数据的个数。

在化学实验中，我们经常需要对一组数据进行平均值的计算。

比如，在测量某种化合物的密度时，我们可能会进行多次测量，得到一组数据，然后需要计算这组数据的平均值作为最终结果。

又如，在测量反应速率时，我们也需要对多次实验数据进行平均值的计算，以得到更加准确的结果。

除了平均值的计算，我们还经常需要计算数据的标准偏差。

标准偏差是一组数据与其平均值之间的偏差的平方的平均值的平方根。

标准偏差的计算公式如下：\[。

s = \sqrt{\frac{\sum_{i=1}^{n} (x_i \bar{x})^2}{n-1}}。

\]其中，\(s\)表示标准偏差，\(\bar{x}\)表示平均值，\(x_i\)表示每个数据点，\(n\)表示数据的个数。

标准偏差可以衡量一组数据的离散程度，即数据点与平均值之间的差异程度。

在化学实验中，标准偏差常常用于评估实验数据的稳定性和可靠性，以及对实验结果的误差进行估计。

除了平均值和标准偏差的计算，我们还经常需要进行数据的统计分析。

统计分析是通过对一组数据进行描述、总结和推断，以得出对数据总体的认识和结论。

在化学领域，统计分析常常用于对化学反应、化合物性质等进行定量分析和推断。

在进行统计分析时，我们通常会使用一些统计学的方法和工具，比如假设检验、方差分析、回归分析等。

这些方法和工具可以帮助我们对数据进行更加深入和全面的分析，从而得出更加准确和可靠的结论。

方法总论平均值法高三化学组混合物的平均式量、元素的质量分数、生成的某指定物质的量总是介于组分的相应量的最大值M2与最小值M1之间，表达式为M1 < M < M2,已知其中两个量，可以确定另一个量的方法，称为平均值法。

一•平均相对分子质量1 •在标准状况下，气体A的密度为1.25 g/L，气体B的密度为1.875 g/L , A 和B混合气体在相同状况下对H2的相对密度为16.8，则混合气体中A和B的体积比为A. 1:2B. 2:1C. 2:3D. 3:2二•平均摩尔电子质量转移1 mol电子时所对应的物质的质量就是摩尔电子质量。

如Al为27/3，Mg为24/2.2 .由两种金属组成的合金50 g与CI2完全反应，消耗CI2 71 g，则合金可能的组成是A. Cu 和Zn B . Ca 和Zn C. Fe 和Al D. Na和Al三.利用平均值的公式进行计算相对分子质量为M1 M2的物质按物质的量之比为a:b混合后，M= M1a/nt + M2b/nt。

3•有A、B、C三种一元碱，它们的相对分子质量之比为3:5:7，如果把7mol A、5 mol B 、3 mol C 混合均匀，取混合碱5.36 g ，恰好中和含0.15 mol HCI的盐酸，则A B、C三种一元碱的相对分子质量分别是_______ 、 _____ 、____ 。

24 ，40，56。

四．平均双键数法基本思想：烷烃双键数为0，单烯烃双键数为1，炔烃双键数为2。

混合烃双键数根据具体情况确定，可利用双键数的平均值求解有关问题。

4．标准状况下的22.4 L 某气体与乙烯的混合物，可与含溴8%的溴的CCI4溶液800 g 恰好加成，则该气体可能是A.乙烷 B .丙烯 C .乙炔 D . 1,3 丁二烯五．巧练5. 已知Na2S0卸Na2S0组成的混合物中，硫的质量分数为24.6%,则混合物中Na2S0听Na2SO4勺物质的量之比为A．1:3 B．3:1 C．4:1 D．1:46．现有铷和另一种碱金属形成的合金50 g ，当它与足量水反应时，放出标准状况下的氢气22.4 L ，这种碱金属可能是A．Li B．Na C．K D．Cs摩尔电子质量法根据在氧化还原反应中，得失电子相等的原则，立意是提供、得到或偏移 1 mol 电子所需要和涉及的物质的质量，利用这种物质的质量来解决的方法称为摩尔电子质量法。

一、差量法例1、用氢气还原10克CuO，加热片刻后，冷却称得剩余固体物质量为8.4克，则参加反应CuO的质量是多少克？(8克)例2、将CO和CO2的混合气体2.4克，通过足量的灼热的CuO后，得到CO2的质量为3.2克，求原混合气体中CO和CO2的质量比？(7:5)例3、将30克铁片放入CuSO4溶液中片刻后，取出称量铁片质量为31.6克，求参加反应的铁的质量(11.2克)二、平均值法例题：1、一块质量为4克的合金，与足量的盐酸反应，产生0.2克氢气。

则该合金的组成可能为（A.B ）A Fe MgB Fe AlC Fe ZnD Mg Al2、测知CO和M的混合体气体中，氧的质量分数为50% 。

则M气体可能是（B ）A CO2 B N2O C SO2D SO33、某硝酸铵（NH4NO3）样品，测知含氮量为37%，则该样品中含有的杂质可能是（ B）A （NH4）2SO4B CO（NH2）2C NH4HCO3D NH4Cl三、离子守恒法例1、某不纯的烧碱样品中含有Na2CO33.8%、Na2O 5.8% 、NaOH 90.4%。

取M克样品，溶于质量分数为18.75%的盐酸溶液100克中，并用30%的NaOH%溶液来中和剩余的盐酸至中性。

把反应后的溶液蒸干后可得到固体质量多少克（29.25克）例2、向一定量的Fe（OH）2溶液中加入200克4.9%的硫酸充分反应后，向溶液中加入一定量的铁正好完全反应，蒸发冷却可得到晶体（不含结晶水）多少克（15.2克）例3 、现有不纯的金属M（含有不溶于水也不溶于酸的杂质），取该金属样品4.0克，投入19．45 克20%的稀盐酸中，恰好完全反应，测得该金属与盐酸生成的氯化物中含氯50%，则该金属样品中金属M的质量分数为多少？（ 97.25%）四、假设极限法A 4∶1B 1∶1C 9∶1D 2∶3例3、将10克KClO3、MnO2的混合物装入大试管中，加热使之分解，冷却向试管中加入4克水，振荡后仍有4．24克未溶解。

2
• 【例 1】两种金属混合物共 15 g ，投入足 量的盐酸中，充分反应得11.2 L H2(标准状况 )，则原混合物组成中肯定不能为下列的 BD ( ) • A．Mg、Ag B．Zn、Cu • C．Al、Zn D．Mg、Al 解析 此题可用平均摩尔电子质量 ( 提 供1mole-所需的质量)法求解。15 g金属混合物 可提供1mole-，其平均摩尔电子质量为15。选 项中金属Mg、Al、Zn的摩尔电子质量分别为 12 、 9 、 32 5 。若有不能和盐酸反应的金属， 则其摩尔电子质量可视为无限大。故本题答 3 案为B、D。
• 1.差量法是根据题中的相关量或对应量的差 量求解的方法。 • 2.差量法是把化学变化过程中引起的一些物 理量的增量或减量放在化学方程式的右端，作 为已知量或未知量，利用各对应量成正比求解。 • 3.差量可以是物质的量的差，对固体、液体 而言，差量可以是质量差、粒子个数差；对气 体，差量还可以是同温、同压下的体积差。
26
解析 图中三条线的前半部分——斜 • 线的斜率大小反映了金属与酸反应的快慢(A 最快，B最慢)。后半部分——水平线的高低 反应了当等质量金属反应完全时，产生H2的 多少。当三种金属化合价相同时，相对原子 质量越小，产生H2越多，所以活动顺序为： B＜C＜A；相对原子质量顺序为：C＞B＞A， 即为氯化物摩尔质量顺序。
解析 2H2+O2 = 2H2O；H2+Cl2 = 2HCl 三种气体恰好完全反应，即n(H2)= 2n(O2) +n(Cl2) 观察选项，只有C符合。
20
点燃
点燃
• 六、讨论法 • 1．讨论法的主要特点是：物质的变化因 条件的不同有多种可能性，或变化的结果有 多种可能性，或条件和结果均不确定，必须 在一定范围内加以确定，为此要通过全面分 析，一一加以研究。 • 2．主要讨论的题型有：①讨论反应发生 的过程；②讨论反应物是否过量；③讨论反 应物和生成物的组成和取值范围。

平均值法平均值法就是根据两组分物质的某种平均值，来推断两物质某种量的范围的一种方法。

化学解题中的平均值法，就是根据X a<X(平均)<X b ，求得的X，来判断X a 、X b 的取值，从而实现巧解速解，可见平均值法适用于两元混合物的计算。

一、平均摩尔质量例1：两种金属的混合物23g与足量盐酸反应，放出标准状况下H222.4L，这两种金属可能是（）A. Zn FeB. Al ZnC. M g CuD. Al Fe解法提示：生成1molH2，需要金属23g，生成1mol H2需Zn 65g，Fe 56g，Al 18g，Mg 24g，Cu 不反应，由平均值可知，一种金属的质量须大于23克，另一种须小于23克，故选（B）(D)例2：把含有某一种氯化物杂质的MgCl2粉末95克溶于水后，与足量AgNO3溶液反应，测得生成的AgCl 300克，则该MgCl2中的杂质可能是（）A. NaClB. AlCl3C. KClD. CaCl2解法提示：提供1mol Cl—所需各物质的质量（即“平均摩尔Cl—质量”）分别为：而平均值= 95 × 143.5/300 = 45.4，小于45.4只有AlCl3，故选B.二、平均化学式法（有机物部分介绍）三、微粒数平均值例5：溴有两种同位素，在自然界中，这两种同位素大约各占一半，已知溴的原子序数为35，相对原子质量为80，则溴的这两种同位素的中子数分别为：A. 79 81B. 45 46C. 44 45D. 44 46解法提示：溴的平均中子数为80-35 = 45，则溴的同位素所含中子数一种必大于45，另一种必小于45，只有D符合。

四、百分数平均值法例6 一包氯化铵样品中混入了下列氮肥中的一种，经测定这包氯化铵中含氮质量分数为25.7%，则混入的氮肥可能是（）A. 尿素B. 碳铵C. 磷酸铵D. 硝铵解法提示：氯化铵的含铵质量分数为14/53.5 = 26.2%，大于25.7%据平均值规则可知氯化铵中混入的氮肥必为含氮质量分数小于25.7%。

化学计算专题三平均值法、极值法2-3 平均值法平均值的原理：两个数M 1和M 2（M 1＞M 2）的平均值M 一定介于M 1和M 2之间，即M 1＞M ＞M 2[例]硫铵(NH 4)2SO 4样品经测定含N 元素20.16%。

该样品中混有下列物质中的A ．(NH 4)2CO 3B ．NH 4HCO 3C ．NH 4ClD ．NH 4NO 3解析：硫铵中，氮元素的质量分数为ω)(N ＝424)(2SO NH N ×100%＝416322)4114(142⨯++⨯⨯+⨯×100%＝13228×100%＝21.2% 现样品中含氮量为20.16%，低于硫铵中的含氮量21.2%。

这里的20.16%就相当于是一个平均数值，组成这个平均值的两个数值与平均值之间的关系必然是： 最小值＜平均值＜最大值。

而硫铵中的含氮量21.2%大于平均值20.16%，因此另一物质含氮量必小于20.16%。

(NH 4)2CO 3含氮29.2% ，NH 4HCO 3含氮17.7%，NH 4Cl 含氮26.2%，NH 4NO 3含氮35%。

可见应含NH 4HCO 3[练习]（1）10g Na 2CO 3与某种碳酸盐组成的混合物与足量盐酸反应时，放出CO 2的质量和相同质量的CaCO 3与足量盐酸反应放出的CO 2质量相等。

这种碳酸盐是A ．BaCO 3B ．MgCO 3C ．K 2CO 3D ．ZnCO 3（2）11.1g 含某种杂质的CaCl 2与足量AgNO 3溶液反应生成AgCl 沉淀29.00g ，则杂质可能是A ．BaCl 2B ．ZnCl 2C ．FeCl 2D ．MgCl 2（3）某铁的氧化物样品中铁与氧质量之比为21∶8。

该样品可以是下列中的A ．Fe 2O 3和Fe 3O 4B ．FeO 和Fe 3O 4C ．Fe 2O 3D ．FeO 、Fe 2O 3和Fe 3O 4（4）体积为1L 的干燥容器中充入HCl 气体后，测得容器中气体对氧气的相对密度为1.082，将此气体倒扣在水中，进入容器中液体的体积是（ ）A ．0.25LB ．0.5LC ．0.75LD ．1L平均值常用方法2-3-1十字交叉法原理：甲气体（摩尔质量M 1）与乙气体（摩尔质量M 2）混合所得混合气体平均摩尔质量为M ，由于M ＝212211··n n M n M n ++ 得21n n ＝M M M M --12，或21V V ＝M M M M --12 十字交叉：21n n ＝21V VM M M M --12代表哪种物理量之比，需要判断M 1、M 2的单位的分母是何种物理量，即表示该分母物理量之比。

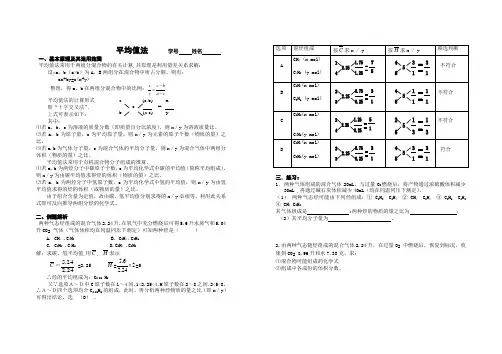
平均值法 学号 姓名一、基本原理及其运用范围平均值法常用于两组分混合物的有关计算,其原理是利用量差关系求解：设:a ，b （a>b ）为A ，B 两组分在混合物中所占分额。

则有： ax+by=c(x+y)整理，得a ，b 在两组分混合物中的比例：ca b c y x --=平均值法的计算形式即“十字交叉法”，上式可表示如下：其中：⑴若a ，b ，c 为溶液的质量分数（即质量百分比浓度），则x ／y 为溶液质量比。

⑵若a ，b 为原子量，c 为平均原子量，则x ／y 为元素的原子个数（物质的量）之比。

⑶若a.b 为气体分子量，c 为混合气体的平均分子量，则x ／y 为混合气体中两组分体积（物质的量）之比。

平均值法常用于有机混合物分子组成的推算。

⑴若a ，b 为两烃分子中碳原子个数，c 为平均化学式中碳的平均值（简称平均组成），则x ／y 为由碳平均值求得烃的体积（物质的量）之比。

⑵若a ，b 为两烃分子中氢原子数，c 为平均化学式中氢的平均值，则x ／y 为由氢平均值求得的烃的体积（或物质的量）之比。

由于组合含量为定值，故由碳、氢平均值分别求得的x ／y 必相等。

利用此关系式即可反向推导两组分烃的化学式。

二、例题解析两种气态烃组成的混合气体2.24升，在氧气中充分燃烧后可得5.6升水蒸气和5.04升CO 2 气体（气体体积均在同温同压下测定）可知两种烃是（ ） A. CH 4 .C 4H 8 B. C 2H 4 .C 3H 6 C. C 2H 2 .C 4H 6 D.C 2H 4 .C 2H 8 解：求碳、氢平均值,用C , H 表示 C ＝24.224.5 =2.25 H =224.26.5⨯=5 ∴烃的平均组成为：C 2.25 H 5又∵选项Ａ～Ｄ中C 原子数在1～4间，1<2.25<4，H 原子数在2～8之间，2<5<8，∴Ａ～Ｄ四个选项均合C 2.25H 5 的组成，此时，再分析两种烃物质的量之比（即x ／y ）可得出结论。

化学计算的基本方法化学计算是化学基础知识的重要组成部分，它贯穿于化学知识之中，通过学习化学计算，可以加深对化学基础知识的理解，检验化学基础知识是否扎实，知识运用是否灵活，提高学生的综合素质。

本专题对化学计算的基本方法中常用守恒法、差量法、十字交叉法、平均值法、估算法、极端法和关系式法进行了原理、类型和应用的剖析，以期利用这些方法技巧提高解题效率，培养敏锐的思维能力、判断、分析、归纳、推理能力。

一、守恒法化学反应是原子之间的重新组合，反应前后组成物质的原子个数、物质的质量始终保持不变，保持守恒。

正如法国化学家拉瓦锡所评价的“无论是人工的或自然的作用都没有创造出什么东西。

物质在每一化学反应前的数量等于反应后的数量，这可算是一个公理”。

守恒定律是自然界最重要的基本定律，构成了化学科学的基础。

在化学计算中，守恒法运用十分广泛，特别是有关混合物或反应关系复杂的化学试题。

运用守恒法求解，无需考虑反应体系各组成成分间相互作用过程，也无需考察变化所经历的具体途径，只需考察反应体系某些组分相互作用前后某种物理量或化学量的始态和终态，使解题过程简化，避免在纷繁复杂的解题背景中寻找关系式，提高解题效率。

守恒法主要包括以下几种类型。

1、质量守恒法：指化学反应前后各物质的质量总和不变。

它是化学反应定量化的基础。

正确、灵活得运用质量守恒可使复杂的化学问题简化，或使化学计算化繁为简。

例1、0.1mol某烃与1mol过量氧气混合，充分燃烧后，通过足量的过氧化钠固体，固体增重15g，从过氧化钠中逸出的全部气体在标准状况下为16.8L，求该烃的分子式。

解析：此题若用通常解法很麻烦，因为最后逸出的气体不仅包括剩余的氧气，也包括烃燃烧产物CO2、H2O与Na2O2反应放出的O2。

若利用质量守恒，则能达到巧解的目的。

本题中，烃的质量与1molO2质量之和等于Na2O2增重量与逸出气体质量之和。

设0.1mol某烃质量为x,由质量守恒定律得：x + 1mol×32g/mol = 15g + (16.8/22.4)mol×32g/mol 解得：x = 7(g)0.1mol烃质量为7g,该烃分子量为70g，则容易求得烃的分子式为C5H10。

常见的化学计算方法介绍4、平均值法原理：若混和物由 A、B、C…等多种成分组成，它们的特征量为M1，M2，M3…，它们在混合物中所占分数分别为n1，n2，n3…，它们的特征量的平均值为M，则若混合物只有A、B两种成分，且已知M1>M2，则必有M1>M>M2，若已知M，则M1和M2必有一个比M大，另一个比M小。

也就是说我们只要知道M就可推知M1、M2的取值范围，而不要进行复杂的计算就可以迅速得出正确的答案。

①体积平均值例1：丙烯和某气态烃组成的混和气体完全燃烧时，所需氧气的体积是混合烃体积的5倍(相同状况)，则气态烃是：析：由烃燃烧规律可推知：1体积的丙烯(C3H8)完全燃烧需要体积氧气(3C→3CO2，需3O2，6H→3H2O，需 )小于5体积，根据题意及平均值的概念得另一气态烃1体积完全燃烧时需氧量必大于5体积，经比较只有A符合要求。

②摩尔质量(或相对原子、分子质量)平均值例2:下列各组气体，不论以何种比例混和，其密度(同温同压下)不等于氮气的密度的是：和H2和CO 和Cl2和C2H2析：依题意，混和气体的平均相对分子质量不会等于28，即各组分气体的相对分子质量必须都大于28或都小于28，因此C和 D符合题意。

③百分含量平均值例3：某不纯的氯化铵，已测知其氮元素的质量分数为40% ，且只含一种杂质，则这种杂质可能是：(NH2)2析：氯化铵的含氮量为14÷×100%=%＜40%，则杂质中必含氮，且含氮量大于40%，进一步计算(估算)可得答案为D。

④中子数或其它微粒数的平均值例4：溴有两种同位素，在自然界中这两种同位素大约各占一半，已知溴的原子序数为35，相对原子质量为80，则溴的这两种同位素的中子数分别等于：、81 、45 、46 、36析：由溴的相对原子质量及原子序数知溴元素的中子数的平均值为80-36=45，则其中一种同位素的中子数必大于45，另一同位素中子数小于45，显然答案是C。

化学计算的常用方法一、平均值法例1：由两种金属组成的合金5g与足量的氯气完全反应后增重7．1g，则该合金可能是（）（A）Cu、Zn（B）Na、Al（C）Fe、Mg（D）Fe、Cu解析：用平均值法解题比较简便。

首先把5g合金看成一种金属，根据与氯气反应的质量求出其相对原子质量，为计算的方便，可以把金属定为二价金属，则有如下关系：只有一种相对原子质量大于50的金属和一种相对原子质量小于50的金属按照一定比例组合成合金，其平均相对原子质量才能为50。

由Cu、Zn组成的合金就不合题意。

上述的计算是以二价金属为标准进行的。

若不是二价金属可以按反应中消耗氯的量进行转换。

以金属铝为例，71g氯气消耗金属铝18g，所以若把金属铝作为二价金属对待，则相对原子质量可取为18。

同理，钠作为二价金属对待，相对原子质量可取为46。

铁与氯气反应时为三价，若作为二价，相对原子质量可取为37．3。

在转换后，才能根据组成平均相对原子质量为50的合金时，对各成分金属相对原子质量要求进行比较，只有D选项合理。

二、守恒法例2：取钠、钙各一小块，投入适量水中，反应完毕时共收集氢气1．568L（标准状况）。

再取碳酸钠和碳酸氢钠的混合粉末3．8g，溶于适量水中。

将以上所得的两种溶液合并，恰好使溶液中、、等离子均进入沉淀。

反应完毕后，将溶液蒸干得到8．8g 白色固体，再将该白色固体洗涤干燥，得到白色不溶物4g。

试求钠、钙各多少克？混合物中碳酸钠、碳酸氢钠的质量各多少克？解析：依题意，得到的8．8g白色固体为碳酸钙和氢氧化钠混合物，4g固体只为碳酸钙，其物质的量为：，所以钙元素的质量＝0．04×40＝1．6g 由钙产生的氢气为：0．04×22．4＝0．896L，由钠产生的氢气为：1．568－0．896＝0．672L。

所以钠的质量为：设碳酸钠的物质的量为x，碳酸氢钠的物质的量为y依据钠元素守恒，金属钠、碳酸钠与碳酸氢钠中钠原子的总物质的量等于8．8g固体中氢氧化钠的物质的量，可以列方程组：所以碳酸钠的质量：0．02×106＝2．12g，碳酸氢钠的质量：0．02×84＝1．68g 三、十字交叉法例3：将金属钠在空气中燃烧，生成与的混合物。

化学计算之平均值法的应用化学计算中的平均值法是一种重要的计算方法，广泛应用于实验数据的处理及结果的分析中。

下面将详细介绍平均值法的应用。

平均值法是指通过对多个独立测量值进行求平均运算，得到一个平均值，用来代表被测物性质的一种方法。

其应用是在实验数据处理过程中，通过统计多次实验测得的测量值，计算它们的平均值，并根据平均值来判断被测物质的性质。

首先，平均值法可以用来提高测量数据的准确性。

在实验过程中，由于各种因素的影响，不同的测量结果可能存在一定的偏差。

通过进行多次独立测量，可以减小个别测量值的影响，得到更为准确的平均值。

例如，在化学分析实验中，为了提高测定物质含量的精确度，常常需要进行多次测定，并求出平均值作为测定结果。

其次，平均值法可以用于估计测量结果的可靠性。

在进行多次测量后，可以统计计算相对平均值的标准偏差，从而评估测量结果的可靠程度。

标准偏差较大，说明测量结果的分散程度较大，可能存在系统误差或者个别误差。

相反，标准偏差较小，说明测量结果的分散程度较小，测量的可靠性较高。

平均值法也可以用于比较不同实验条件对实验结果的影响。

例如，化学反应速率实验中，可以通过在不同温度下进行反应，并测定相应的反应速率，求出平均值。

通过比较不同条件下的平均反应速率，可以判断温度对反应速率的影响。

此外，平均值法还可以应用于化学数据的分析和处理中。

在研究领域中，经常需要对一系列实验数据进行处理并求平均值。

例如，在材料科学研究中，可能需要测试材料的多个性质参数，如硬度、强度等，然后通过求平均值来描述材料的整体性能。

在化学教学中，平均值法也是一个重要的应用工具。

通过让学生进行多次实验，并计算测量平均值，可以帮助他们理解和掌握科学实验的重复性、可靠性和准确性。

总之，平均值法在化学计算中具有重要的应用价值。

它可以提高测量数据的准确性，评估测量结果的可靠性，比较不同实验条件对结果的影响，并用于数据分析和处理。

在化学教学和科学研究中，平均值法的应用能够帮助我们更好地了解和揭示化学现象的规律性。

化学实验中的数据处理方法化学实验是化学学习中不可或缺的一部分，而数据处理则是实验结果的重要环节。

通过合理的数据处理方法，我们能够准确地得出实验结果，进而对实验现象进行解释和推断。

本文将介绍几种常用的化学实验中的数据处理方法。

一、平均值计算法在实验中，重复测量同一指标能够减少误差，提高数据的可靠性。

平均值计算法是最简单的数据处理方法之一，适用于多次测量结果。

具体步骤如下：1. 记录各次测量的数值。

2. 将各次测量的数值相加。

3. 将相加的结果除以测量次数，即得到平均值。

例如，在测量某种溶液的酸度时，我们可以进行3次测量，分别得到结果为2.1、2.0、2.2。

通过平均值计算法，计算出平均值为2.1+2.0+2.2 ÷ 3 = 2.1。

二、误差分析法实验中存在着各种误差，如人为误差、仪器误差等。

误差的存在会对实验结果产生一定的影响。

因此，进行误差分析是必不可少的一环。

常见的误差分析方法有如下几种：1. 绝对误差：是指实际测量值与真实值之间的差距，一般用公式 |实际测量值 - 真实值| 来计算。

2. 相对误差：是指绝对误差与真实值之比，用公式 |实际测量值 - 真实值| ÷真实值来计算。

3. 百分误差：是指相对误差乘以100%，用公式 (|实际测量值 - 真实值| ÷真实值) × 100% 来计算。

通过误差分析，我们能够了解到实验结果的可靠程度，并对实验中的误差来源进行识别和改进。

三、标准差计算法标准差是一种统计数据离散程度的度量方式。

在化学实验中，标准差可以帮助我们评估测量结果的离散程度，进而判断实验数据的可靠性。

标准差的计算步骤如下：1. 计算平均值。

2. 将每次测量值与平均值的差的平方相加。

3. 将相加的结果除以测量次数。

4. 对结果开方，即得到标准差。

标准差越大，表示数据间的离散程度越大，实验结果的可靠性越低。

通过标准差的计算，我们能够更加全面地评估实验数据的精确性。

化学计算之平均值法的应用化学计算是化学研究与实践中不可缺少的部分，其中平均值法是化学计算中常常应用的一种方法。

平均值法是一种用来估算数据集中心趋势的方法，通过取数据集中数值的平均值来表示整体的趋势。

本文将从平均值法的原理、应用领域和具体案例三个方面进行介绍。

平均值法的原理：平均值法是基于大数定律的原理，即当样本数量足够大时，样本均值会逐渐接近总体均值。

因此使用样本均值来估算整体的平均值是一种常用的方法。

计算平均值的公式如下：平均值=总和/样本数量平均值法的应用领域：平均值法在化学研究与应用中有很广泛的应用领域，以下是一些常见的应用领域：1.实验数据处理：在实验室中，科学家通常会进行多次测量，得到一系列数据。

为了准确估算实验结果，常将多次测量的结果取平均值。

通过平均值法可以排除个别测量结果的误差，得到更准确的实验结果。

2.化学分析：化学分析中经常需要对样品进行多次测试，得到一系列结果。

通过平均值法可以计算出样品的平均含量，以便对样品进行定性和定量分析。

3.质量控制：在化工生产过程中，常常需要对产品进行质量控制和质量评估。

平均值法可以用来计算产品的平均质量，帮助确定生产过程中的优化策略。

具体案例：以化学分析为例，假设有一份包含样品A的含量数据的数据集，数据如下：样品A的含量：1.2,1.4,1.6,1.3,1.5使用平均值法可以计算出样品A的平均含量总和=1.2+1.4+1.6+1.3+1.5=7样本数量=5平均值=总和/样本数量=7/5=1.4因此，样品A的平均含量为1.4、通过计算平均值，我们可以得到样品A整体的含量趋势，并用于进一步的分析与判断。

总结起来，平均值法是化学计算中常用的一种方法，通过取数据集中数值的平均值来表示整体的趋势。

它在实验数据处理、化学分析和质量控制等领域有广泛的应用。

通过平均值法，可以估算出样品的平均含量，帮助科学家和工程师更好地进行化学研究和应用。

方法总论平均值法混合物的平均式量、元素的质量分数、生成的某指定物质的量总是介于组分的相应量的最大值M2与最小值M1之间，表达式为M1 < M < M2，已知其中两个量，可以确定另一个量的方法，称为平均值法。

一．平均相对分子质量1．在标准状况下，气体A的密度为 1.25 g/L，气体B的密度为 1.875 g/L，A和B 混合气体在相同状况下对H2的相对密度为16.8，则混合气体中A和B的体积比为A．1:2 B．2:1 C．2:3 D．3:2二．平均摩尔电子质量转移 1 mol电子时所对应的物质的质量就是摩尔电子质量。

如Al为27/3，Mg为24/2.2．由两种金属组成的合金50 g与Cl2完全反应，消耗Cl2 71 g，则合金可能的组成是A．Cu和Zn B．Ca和Zn C．Fe和Al D．Na和Al三．利用平均值的公式进行计算相对分子质量为M1、M2的物质按物质的量之比为a:b混合后，M＝M1a/n t＋M2b/n t。

3．有A、B、C三种一元碱，它们的相对分子质量之比为3:5:7，如果把7 mol A、5 mol B、3 mol C混合均匀，取混合碱 5.36 g，恰好中和含0.15 mol HCl的盐酸，则A、B、C三种一元碱的相对分子质量分别是_____、_____、_____。

24，40，56。

四．平均双键数法基本思想：烷烃双键数为0，单烯烃双键数为1，炔烃双键数为2。

混合烃双键数根据具体情况确定，可利用双键数的平均值求解有关问题。

4．标准状况下的22.4 L某气体与乙烯的混合物，可与含溴8%的溴的CCl4溶液800 g恰好加成，则该气体可能是A．乙烷 B．丙烯 C．乙炔 D．1,3丁二烯五．巧练5．已知Na2SO3和Na2SO4组成的混合物中，硫的质量分数为24.6%，则混合物中Na2SO3与Na2SO4的物质的量之比为A．1:3 B．3:1 C．4:1 D．1:46．现有铷和另一种碱金属形成的合金50 g，当它与足量水反应时，放出标准状况下的氢气22.4 L，这种碱金属可能是A．Li B．Na C．K D．Cs摩尔电子质量法根据在氧化还原反应中，得失电子相等的原则，立意是提供、得到或偏移 1 mol电子所需要和涉及的物质的质量，利用这种物质的质量来解决的方法称为摩尔电子质量法。

平均值法和极值法在化学计算中的应用贵州王昭华邮编：562400 通讯地址：贵州省兴义市名仕苑8单元402平均值法和极值法在化学计算中的应用十分广泛，并且能使问题简单化，从而实现巧解和速解。

一、使用特征⑴只有两个组分或者适合两个组分的组合形式。

⑵出现平均值或者隐含平均值或者要求计算平均值。

二、具体作用⑴根据平均值确定两个极值的取值范围或者根据两个极值确定平均值的取值范围。

即：a > w> b（令a > b）⑵利用十字交叉法计算两个组分的比值（本质上属于两个组分的物质的量之比）。

注意：①比值一般为物质的量之比或者粒子数之比；②若为气体，比值为物质的量之比或者分子数之比或者气体体积比；③若为同一溶液相混合，比值为混合前两溶液的质量之比。

三、适用范围平均相对原子质量、平均相对分子质量、平均气体密度、平均溶液质量分数、平均化合价、平均电子转移量、平均消耗量、平均变化量、平均分子式等。

四、应用举例1、根据平均值确定两个极值的取值范围或者根据两个极值确定平均值的取值范围。

例题1：将两种金属单质混合物13 g ，加到足量的稀硫酸中，充分反应后共收集到标准状况下的气体为11.2 L ，则这两种金属可能是：A. Zn和FeB. Al和ZnC. Al和MgD. Mg和Cu解析：求出平均电子摩尔质量，即平均每转移1mol 电子所消耗物质的质量。

因产生的气体为氢气（H 2 ~ 2e - ），则该混合金属的平均电子摩尔质量为：--⋅=⨯e mol g e molL L g /132/4.222.1113 选项中各金属的电子摩尔质量为：Zn ：--⋅=⋅e mol g e mol g /5.32265 Fe ： --⋅=⋅e mol g emol g /28256 Al ： --⋅=⋅e mol g e mol g /9327 Mg ： --⋅=⋅e mol g emol g /12224 Cu ： =⋅-e mol g 064 ∝ -⋅e mol g /（即为无穷大） 根据平均值观点可判断，符合题意的选项为B 和D 。