初二数学最经典例题(张义)

北师大版八年级数学下册第1章三角形的证明经典好题专题训练（附答案）1．如图，在△ABC中，DE为线段AB的垂直平分线．若△ABC的周长为18，线段AE的长度为4，则△BCD的周长为（ ）A．10B．11C．12D．142．在等腰三角形中，有一个角是50°，它的一条腰上的高与底边的夹角是（ ）A．25°B．25°或40°C．25°或35°D．40°3．如图，在△ABC中，AI平分∠BAC，BI平分∠ABC，点O是AC、BC的垂直平分线的交点，连接AO、BO，若∠AIB＝α，则∠AOB的大小为（ ）A．αB．4α﹣360°C．α+90°D．180°﹣α4．设等腰△的一边长为5，另一边长为10，则其周长为（ ）A．15B．20C．25D．20或255．如图，在△ABC中，∠C＝90°，点D是线段AB的垂直平分线与BC的交点，连接AD．若CD＝2，BD＝4，则AC的长为（ ）A．4B．3C．2D．6．如图，A，B两点在正方形网格的格点上，每个方格都是边长为1的正方形，点C也在格点上，且△ABC为等腰三角形，在图中所有符合条件的点C应该有（ ）个．A．7B．8C．9D．107．如图，在平面直角坐标系中，△ABC三个顶点的坐标分别是点A（﹣3，0）、点B（﹣1，2）、点C（3，2），则到△ABC三个顶点距离相等的点的坐标是（ ）A．（0，﹣1）B．（0，0）C．（1，﹣1）D．（1，﹣2）8．如图，已知OA＝OB＝OC，BC∥AO，若∠A＝36°，则∠B等于（ ）A．54°B．60°C．72°D．76°9．如图，△ABC的∠ABC的外角的平分线BD与∠ACB的外角平分线CE相交于点P，下列结论正确的是（ ）A．AP平分BC B．AP平分∠CAB C．AP平分∠CPB D．AP⊥BC10．如图，在△ABC中，∠ABC和∠ACB的平分线相交于点F，过点F作DE∥BC，交AB、AC于点D、E．若AB＝5，AC＝4，则△ADE的周长是（ ）A．9B．10C．12D．1411．如图所示，在△ABC中，DE，MN是边AB、AC的垂直平分线，其垂足分别为D、M，分别交BC于E、N，若AB＝8，AC＝9，设△AEN周长为m，则m的取值范围为 ．12．如图，在△ABC中，∠B＝90°，AC的垂直平分线交BC于点E、交AC于点D，若BE ＝DE，DC＝3，则AE的长为 ．13．如图，在△ABC中，AF平分∠BAC，AC的垂直平分线交BC于E点，∠B＝50°，∠FAE ＝20°，则∠C＝ 度．14．如图，在△ABC中，边AB、AC的垂直平分线交于点O，若∠BOC＝80°，则∠A ＝ ．15．已知C，D两点在线段AB的垂直平分线上，且∠ACB＝50°，∠ADB＝86°，则∠CAD 的度数是 ．16．如图，在△ABC中，∠BAC＝124°，分别作AC，AB两边的垂直平分线PM，PN，垂足分别是点M，N．以下说法正确的是 （填序号）．①∠P＝56°；②∠EAF＝68°；③PE＝PF；④点P到点B和点C的距离相等．17．如图，已知点D为△ABC内一点，AD平分∠CAB，BD⊥AD，∠C＝∠CBD．若AC＝10，AB＝6，则AD的长为 ．18．如图，AB∥CD，BP和CP分别平分∠ABC和∠DCB，AD过点P，且与AB垂直．若AD ＝10，则点P到BC的距离是 ．19．如图，AD⊥BC，BD＝DC，点C在AE的垂直平分线上．若AB＝5cm，BC＝6cm，则AC＝ ，DE＝ ．20．如图所示，在△ABC中，DE、MN是边AB、AC的垂直平分线，其垂足分别为D、M，分别交BC于E、N，且DE和MN交于点F．（1）若∠B＝20°，则∠BAE＝ ；（2）若∠EAN＝40°，则∠F＝ ；（3）若AB＝8，AC＝9，设△AEN周长为m，则m的取值范围为 ．21．如图，在Rt△ABC中，∠B＝90°，ED是AC的垂直平分线，交AC于点D，交BC于点E．已知∠C＝35°，则∠BAE的度数为 °．22．如图，在等边三角形ABC中，D是AB上的一点，E是CB延长线上一点，连接CD、DE，已知∠EDB＝∠ACD．（1）求证：△DEC是等腰三角形．（2）当∠BDC＝5∠EDB，EC＝8时，求△EDC的面积．23．如图，△ABC中，∠BAC＝80°，若MP和NQ分别垂直平分AB和AC．（1）求∠PAQ的度数．（2）若△APQ周长为12，BC长为8，求PQ的长．24．如图，△ABC中，点D在BC边上，∠BAD＝100°，∠ABC的平分线交AC于点E，过点E作EF⊥AB，垂足为F，且∠AEF＝50°，连接DE．（1）求∠CAD的度数；（2）求证：DE平分∠ADC；（3）若AB＝7，AD＝4，CD＝8，且S△ACD＝15，求△ABE的面积．25．如图，在平面直角坐标系中，已知等边△ABO的顶点A（2，0），经过点A的直线垂直于OB，交OB点C，交y轴于点E．（1）求线段OC的长度；（2）求点E的坐标；（3）确定直线AE的解析式．26．如图1，在Rt△ABC中，∠BAC＝90°，AD⊥BC于点D，BG平分∠ABC，交AD于点E，交AC于点G（1）求证：AE＝AG；（2）如图2，过点E作EF∥BC，交AC于点F，若∠C＝30°，求证：AG＝GF＝FC．27．如图，在△ABC中，AB＝AC，AD为角平分线．（1）如图1，已知AB＝13，BC＝10．求△ABC的面积；（2）在（1）的条件下，AC垂直平分线与AD交于点E，画图并求AE的长．（3）如图2，若△ABC为等边三角形，M，N分别为边AB，AC上的动点，且满足∠MDN ＝90°．设BM＝a，CN＝b，MN＝c，请用等式表示a，b，c之间的数量关系，并说明理由．参考答案1．解：∵△ABC的周长为18，∴AC+BC+AB＝18，∵DE为线段AB的垂直平分线，AE＝4，∴AB＝2AE＝8，DA＝DB，∴AC+BC＝10，∴△BCD的周长＝BD+CD+BC＝AD+CD+BC＝AC+BC＝10，故选：A．2．解：当50°为底角时，∵∠B＝∠ACB＝50°，∴∠BCD＝90°﹣50°＝40°；当50°为顶角时，∵∠A＝50°，∴∠B＝∠ACB＝65°，∴∠BCD＝90°﹣65°＝25°．故选：B．3．解：连接CO并延长至D，∵∠AIB＝α，∴∠IAB+∠IBA＝180°﹣α，∵AI平分∠BAC，BI平分∠ABC，∴∠IAB＝∠CAB，∠IBA＝∠CBA，∴∠CAB+∠CBA＝2（∠IAB+∠IBA）＝360°﹣2α，∴∠ACB＝180°﹣（∠CAB+∠CBA）＝2α﹣180°，∵点O是AC、BC的垂直平分线的交点，∴OA＝OC，OB＝OC，∴∠OCA＝∠OAC，∠OCB＝∠OBC，∵∠AOD是△AOC的一个外角，∴∠AOD＝∠OCA+∠OAC＝2∠OCA，同理，∠BOD＝2∠OCB，∴∠AOB＝∠AOD+∠BOD＝2∠OCA+2∠OCB＝4α﹣360°，故选：B．4．解：分两种情况：当腰为5时，5+5＝10，所以不能构成三角形；当腰为10时，5+10＞10，所以能构成三角形，周长是：10+10+5＝25．故选：C．5．解：∵点D是线段AB的垂直平分线与BC的交点，BD＝4，∴AD＝BD＝4，在Rt△ACD中，CD＝2，AD＝4，∴AC＝＝＝2，故选：C．6．解：如图所示：①AB为等腰三角形的底边，符合条件的点C的有5个；②AB为等腰三角形的一条腰，符合条件的点C的有3个．所以符合条件的点C共有8个．故选：B．7．解：∵点P到△ABC三个顶点距离相等，∴点P是线段BC、AB的垂直平分线的交点，由图可知，点P的坐标为（1，﹣2），故选：D．8．解：∵OA＝OC，∴∠ACO＝∠A＝36°，∵BC∥AO，∴∠BCA＝∠A＝36°，∴∠BCO＝72°，∵OB＝OC，∴∠B＝72°．故选：C．9．解：过点P作PF⊥AC交AC的延长线于点F，PG⊥BC于点G，PH⊥AB交AB的延长线于点H，∵CP平分∠BCF，PF⊥AC，PG⊥BC，∴PF＝PG，∵CP平分∠ABC，PG⊥BC，PH⊥AB，∴PH＝PG，∴PF＝PH，∴AP平分∠CAB，故选：B．10．解：∵∠ABC和∠ACB的平分线相交于点F，∴∠DBF＝∠CBF，∠ECF＝∠BCF，∵DE∥BC，∴∠DFB＝∠CBF，∠BCF＝∠EFC，∴∠DBF＝∠DFB，∠ECF＝∠EFC，∴DB＝DF，EF＝EC，∴△ADE的周长＝AD+DE+AE＝AD+DF+EF+AE＝AD+BD+EC+AE＝AB+AC＝5+4＝9．故选：A．11．解：∵DE，MN是边AB、AC的垂直平分线，∴EA＝EB，NC＝NA，∴△AEN周长为m＝EA+EN+NA＝EB+EN+NC＝BC，在△ABC中，9﹣8＜BC＜9+8，∴1＜m＜17，故答案为：1＜m＜17．12．解：∵DE是线段AC的垂直平分线，∴EA＝EC，∴∠EAC＝∠C，∵BE＝DE，∠B＝90°，ED⊥AC，∴∠EAC＝∠BAE，∴∠EAC＝∠C＝∠BAE＝30°，在Rt△CED中，EC＝＝2，∴AE＝2，故答案为：2．13．解：∵DE是线段AC的垂直平分线，∴EA＝EC，∴∠EAC＝∠C，∵AF平分∠BAC，∴∠BAF＝∠CAF＝∠FAE+∠CAE＝20°+∠C，由三角形内角和定理得，∠B+∠BAC+∠C＝180°，即50°+20°+∠C+20°+∠C+∠C＝180°，解得，∠C＝30°，故答案为：30．14．解：连接OA，∵∠BOC＝80°，∴∠OBC+∠OCB＝100°，∴∠OAB+∠OBA+∠OAC+∠OCA＝80°，∵AB、AC的垂直平分线交于点O，∴AO＝BO，AO＝CO，∴∠OAB＝∠OBA，∠OAC＝∠OCA，∴∠A＝∠OAB+∠OAC＝40°，故答案为：40°．15．解：∵C、D两点在线段AB的中垂线上，∴CA＝CB，DA＝DB，∵CD⊥AB，∴∠ACD＝∠ACB＝×50°＝25°，∠ADC＝∠ADB＝×86°＝43°，当点C与点D在线段AB两侧时，∠CAD＝180°﹣∠ACD﹣∠ADC＝180°﹣25°﹣43°＝112°，当点C与点D′在线段AB同侧时，∠CAD′＝∠AD′C﹣∠ACD′＝43°﹣25°＝18°，故答案为：18°或112°．16．解：∵PM垂直平分AC，PN垂直平分AB，∴∠PMA＝∠PNA＝90°，∴∠P＝360°﹣90°﹣90°﹣124°＝56°，①说法正确；∵∠BAC＝124°，∴∠B+∠C＝180°﹣124°＝56°，∵PM垂直平分AC，PN垂直平分AB，∴EC＝EA，FB＝FA，∴∠EAC＝∠C，∠FAB＝∠B，∴∠EAF＝∠BAC﹣∠EAC﹣∠FAB＝∠BAC﹣（∠B+∠C）＝124°﹣56°＝68°，②说法正确；△ABC不一定是等腰三角形，∴PE与PF的大小无法确定，③说法错误；连接PC、PA、PB，∵PM垂直平分AC，PN垂直平分AB，∴PC＝PA，PB＝PA，∴PB＝PC，即点P到点B和点C的距离相等，④说法正确，故答案为：①②④．17．解：如图，延长BD交AC于E，∵BD⊥AD，∴∠ADE＝∠ADB＝90°，∵AD平分∠CAB，∴∠EAD＝∠BAD，∴∠AED＝∠ABD，∴AE＝AB＝6，∴DE＝BD，∵AC＝10，∴CE＝10﹣6＝4，∵∠C＝∠CBD，∴BE＝CE＝4，∴BD＝BE＝2，由勾股定理得：AD＝＝＝4．故答案为：4．18．解：过点P作PE⊥BC于E，∵AB∥CD，AD⊥AB，∴AD⊥CD，∵BP和CP分别平分∠ABC和∠DCB，AD⊥AB，AD⊥CD，PE⊥BC，∴PA＝PE＝PD，∵AD＝10，∴PE＝5，即点P到BC的距离是5，故答案为：5．19．解：∵BC＝6cm，∴BD＝DC＝3（cm），∵AD⊥BC，BD＝DC，AB＝5cm，∴AC＝AB＝5（cm），∵点C在AE的垂直平分线上，∴EC＝AC＝5（cm），∴DE＝DC+EC＝8（cm），故答案为：5cm；8cm．20．解：（1）∵DE是线段AB的垂直平分线，∴EA＝EB，∴∠BAE＝∠B＝20°；（2））∵DE、MN是边AB、AC的垂直平分线，∴AE＝BE，AN＝CN，∴∠BAE＝∠B，∠CAN＝∠C，∵∠EAN＝40°，∠B+∠BAE+∠EAN+∠CAN+∠C＝180°，∴∠BAE+∠CAN＝70°，∴∠BAC＝∠BAE+∠CAN+∠EAN＝110°，∵∠ADF＝∠AMF＝90°，∴∠F＝360°﹣∠ADF﹣∠AMF﹣∠BAC＝360°﹣90°﹣90°﹣110°＝70°；（3）∵DE、MN是边AB、AC的垂直平分线，∴AE＝BE，AN＝CN，∴△AEN的周长＝AE+EN+AN＝BE+EN+CN＝BC，在△ABC中，AB＝8，AC＝9，∴9﹣8＜BC＜9+8，∴1＜m＜17．故答案为：（1）20°；（2）70°；（3）1＜m＜17．21．解：∵ED是AC的垂直平分线，∴AE＝CE，∴∠EAC＝∠C＝35°，在Rt△ABC中，∠B＝90°，∴∠BAC＝90°﹣∠C＝55°，∴∠BAE＝∠BAC﹣∠EAC＝20°．故答案为：20．22．（1）证明：∵△ABC是等边三角形，∴∠ABC＝∠ACB＝60°，∵∠E+∠EDB＝∠ABC＝60°，∠ACD+∠DCB＝60°，∠EDB＝∠ACD，∴∠E＝∠DCE，∴DE＝DC，∴△DEC是等腰三角形；（2）解：设∠EDB＝α，则∠BDC＝5α，∴∠E＝∠DCE＝60°﹣α，∴6α+60°﹣α+60°﹣α＝180°，∴α＝15°，∴∠E＝∠DCE＝45°，∴∠EDC＝90°，如图，过D作DH⊥CE于H，∵△DEC是等腰直角三角形，∴∠EDH＝∠E＝45°，∴EH＝HC＝DH＝EC＝8＝4，∴△EDC的面积＝EC•DH＝8×4＝16．23．解：（1）设∠PAQ＝x，∠CAP＝y，∠BAQ＝z，∵MP和NQ分别垂直平分AB和AC，∴AP＝PB，AQ＝CQ，∴∠B＝∠BAP＝x+z，∠C＝∠CAQ＝x+y，∵∠BAC＝80°，∴∠B+∠C＝100°，即x+y+z＝80°，x+z+x+y＝100°，∴x＝20°，∴∠PAQ＝20°；（2）∵△APQ周长为12，∴AQ+PQ+AP＝12，∵AQ＝CQ，AP＝PB，∴CQ+PQ+PB＝12，即CQ+BQ+2PQ＝12，BC+2PQ＝12，∵BC＝8，∴PQ＝2．24．（1）解：∵EF⊥AB，∠AEF＝50°，∴∠FAE＝90°﹣50°＝40°，∵∠BAD＝100°，∴∠CAD＝180°﹣100°﹣40°＝40°；（2）证明：过点E作EG⊥AD于G，EH⊥BC于H，∵∠FAE＝∠DAE＝40°，EF⊥BF，EG⊥AD，∴EF＝EG，∵BE平分∠ABC，EF⊥BF，EH⊥BC，∴EF＝EH，∴EG＝EH，∵EG⊥AD，EH⊥BC，∴DE平分∠ADC；（3）解：∵S△ACD＝15，∴×AD×EG+×CD×EH＝15，即×4×EG+×8×EG＝15，解得，EG＝EH＝，∴EF＝EH＝，∴△ABE的面积＝×AB×EF＝×7×＝．25．解：（1）∵A（2，0），∴OA＝2，∵△ABO是等边三角形，∴OB＝OA＝2，∠AOB＝60°，∴∠COE＝30°，∵AE⊥OB，∴OC＝OB＝1；（2）∵AE⊥OB，∠COE＝30°，∴CE＝OC＝，OE＝2CE＝，∴点E的坐标为（0，）；（3）设直线AE的解析式为y＝kx+b，由题意得：，解得：，∴直线AE的解析式为y＝﹣x+．26．证明：（1）∵∠BAC＝90°，∴∠AGB+∠ABG＝90°，∵AD⊥BC，∴∠BED+∠DBE＝90°，又∵BG平分∠ABC，∴∠ABG＝∠DBE，∴∠AGB＝∠BED，∵∠BED＝∠AEG，∴∠AGB＝∠AEG，∴AE＝AG；（2）∵∠BAC＝90°，∠C＝30°，∴∠ABC＝60°，∵AD⊥BC，∴∠BAD＝30°，∵BG平分∠ABC，∴∠ABG＝∠CBG＝30°，∴∠CBG＝∠C，∠BAD＝∠ABG，∠AGB＝90°﹣30°＝60°，∴BG＝CG，AE＝BE，由（1）得：AE＝AG，∴△AEG是等边三角形，∴AG＝GE＝AE＝BE，又∵EF∥BC，∴∠GEF＝∠CBG＝30°，∠GFE＝∠C＝30°，∴∠GEF＝∠GFE，∴GE＝GF，∴GE＝BE＝FC＝GF，∴AG＝GF＝FC．27．解：（1）∵AB＝AC，AD为角平分线．∴BD＝CD＝BC＝5，由勾股定理得，AD＝＝＝12，∴△ABC的面积＝×BC×AD＝×10×12＝60；（2）画图如图所示，∵AC垂直平分线与AD交于点E，∴EA＝EC，设AE＝CE＝x，则DE＝12﹣x，在Rt△CDE中，CE2＝DE2+CD2，即x2＝（12﹣x）2+52，解得，x＝，即AE＝；（3）延长MD至G，使DG＝MD，连接GN、GC，作GH⊥AN交AN的延长线于H，在△BDM和△CDG中，，∴△BDM≌△CDG（SAS），∴CG＝BM＝a，∠BCD＝∠B＝60°，∴∠GCH＝60°，∴∠CGH＝30°，∴CH＝a，由勾股定理得，GH＝＝a，∵MD＝DG，ND⊥MG，∴GN＝MN＝c，在Rt△NGH中，GN2＝GH2+NH2，即c2＝（a）2+（b+a）2，整理得，a2+ab+b2＝c2．。

初二数学一次函数经典试题含答案编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（初二数学一次函数经典试题含答案）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为初二数学一次函数经典试题含答案的全部内容。

初二数学一次函数超经典试题含答案一、相信你一定能填对!(每小题3分，共30分）1．下列函数中,自变量x 的取值范围是x ≥2的是（ ）A ．．． D ．2．下面哪个点在函数y=x+1的图象上（ )12A ．(2,1)B ．(-2，1)C ．（2，0）D ．（-2，0）3．下列函数中，y 是x 的正比例函数的是（ ）A ．y=2x-1B ．y=C ．y=2x 2D ．y=-2x+13x 4．一次函数y=-5x+3的图象经过的象限是（ ）A ．一、二、三B ．二、三、四C ．一、二、四D ．一、三、四6．若一次函数y=(3—k ）x-k 的图象经过第二、三、四象限，则k 的取值范围是（ )A ．k 〉3B ．0〈k ≤3C ．0≤k<3D ．0〈k 〈37．已知一次函数的图象与直线y=-x+1平行，且过点（8,2），那么此一次函数的解析式为（ ）A ．y=-x-2B ．y=—x—6C ．y=-x+10D ．y=-x—18．汽车开始行驶时，油箱内有油40升，如果每小时耗油5升，则油箱内余油量y （升）与行驶时间t （时)的函数关系用图象表示应为下图中的（ ）9．李老师骑自行车上班,最初以某一速度匀速行进， 中途由于自行车发生故障,停下修车耽误了几分钟，为了按时到校，李老师加快了速度，仍保持匀速行进,如果准时到校．在课堂上，李老师请学生画出他行进的路程y （千米）与行进时间t （小时）的函数图象的示意图，同学们画出的图象如图所示,你认为正确的是（）10．一次函数y=kx+b 的图象经过点（2，-1）和（0，3)， 那么这个一次函数的解析式为( ）A ．y=—2x+3B ．y=-3x+2C ．y=3x—2D ．y=x-312二、你能填得又快又对吗？（每小题3分,共30分)11．已知自变量为x 的函数y=mx+2—m 是正比例函数，则m=________， 该函数的解析式为_________．12．若点（1，3）在正比例函数y=kx 的图象上，则此函数的解析式为________．13．已知一次函数y=kx+b 的图象经过点A （1，3)和B （-1，-1），则此函数的解析式为_________．14．若解方程x+2=3x-2得x=2，则当x_________时直线y=x+ 2 上的点在直线y=3x—2上相应点的上方．15．已知一次函数y=-x+a 与y=x+b 的图象相交于点(m ，8），则a+b=_________．16．若一次函数y=kx+b 交于y 轴的负半轴, 且y 的值随x 的增大而减少， 则k____0，b______0．（填“>"、“〈”或“＝"）17．已知直线y=x—3与y=2x+2的交点为（-5，—8)，则方程组的解是________．30220x y x y --=⎧⎨-+=⎩18．已知一次函数y=-3x+1的图象经过点(a,1）和点（—2，b ），则a=________,b=______．19．如果直线y=-2x+k 与两坐标轴所围成的三角形面积是9，则k 的值为_____．20．如图，一与x轴交于点C,则此一次函数的解析式为__________，△AOCB两点，次函数y=kx+b的图象经过A、的面积为_________．三、认真解答，一定要细心哟!（共60分)21．（14分）根据下列条件,确定函数关系式:(1)y与x成正比，且当x=9时，y=16；（2）y=kx+b的图象经过点（3，2）和点(—2，1）．23．(12分）一农民带了若干千克自产的土豆进城出售，为了方便,他带了一些零钱备用，按市场价售出一些后,又降价出售．售出土豆千克数与他手中持有的钱数（含备用零钱)的关系如图所示,结合图象回答下列问题：（1）农民自带的零钱是多少？（2）降价前他每千克土豆出售的价格是多少？(3）降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱（含备用零钱)是26元，问他一共带了多少千克土豆?24．（10分）如图所示的折线ABC 表示从甲地向乙地打长途电话所需的电话费y（元）与通话时间t （分钟）之间的函数关系的图象（1)写出y 与t 之间的函数关系式．(2）通话2分钟应付通话费多少元？通话7分钟呢？25．(12分）已知雅美服装厂现有A 种布料70米，B 种布料52米， 现计划用这两种布料生产M 、N 两种型号的时装共80套．已知做一套M 型号的时装需用A 种布料1. 1米,B 种布料0。

初二数学经典难题一、解答题（共10小题，满分100分）1．（10分）已知：如图，P是正方形ABCD内点，∠PAD=∠PDA=15°．求证：△PBC是正三角形．（初二）2．（10分）已知：如图，在四边形ABCD中，AD=BC，M、N分别是AB、CD的中点，AD、BC的延长线交MN 于E、F．求证：∠DEN=∠F．3．（10分）如图，分别以△ABC的边AC、BC为一边，在△ABC外作正方形ACDE和CBFG，点P是EF的中点，求证：点P到AB的距离是AB的一半．4．（10分）设P是平行四边形ABCD内部的一点，且∠PBA=∠PDA．求证：∠PAB=∠PCB．5．（10分）P为正方形ABCD内的一点，并且PA=a，PB=2a，PC=3a，求正方形的边长．6．（10分）一个圆柱形容器的容积为V立方米，开始用一根小水管向容器内注水，水面高度达到容器高度一半后，改用一根口径为小水管2倍的大水管注水．向容器中注满水的全过程共用时间t分．求两根水管各自注水的速度．7．（10分）（2009•郴州）如图1，已知正比例函数和反比例函数的图象都经过点M（﹣2，﹣1），且P（﹣1，﹣2）为双曲线上的一点，Q为坐标平面上一动点，PA垂直于x轴，QB垂直于y轴，垂足分别是A、B．（1）写出正比例函数和反比例函数的关系式；（2）当点Q在直线MO上运动时，直线MO上是否存在这样的点Q，使得△OBQ与△OAP面积相等？如果存在，请求出点的坐标，如果不存在，请说明理由；（3）如图2，当点Q在第一象限中的双曲线上运动时，作以OP、OQ为邻边的平行四边形OPCQ，求平行四边形OPCQ周长的最小值．8．（10分）（2008•海南）如图，P是边长为1的正方形ABCD对角线AC上一动点（P与A、C不重合），点E在线段BC上，且PE=PB．（1）求证：①PE=PD；②PE⊥PD；（2）设AP=x，△PBE的面积为y．①求出y关于x的函数关系式，并写出x的取值范围；②当x取何值时，y取得最大值，并求出这个最大值．9．（10分）（2010•河南）如图，直线y=k1x+b与反比例函数（x＞0）的图象交于A（1，6），B（a，3）两点．（1）求k1、k2的值．（2）直接写出时x的取值范围；（3）如图，等腰梯形OBCD中，BC∥OD，OB=CD，OD边在x轴上，过点C作CE⊥OD于点E，CE和反比例函数的图象交于点P，当梯形OBCD的面积为12时，请判断PC和PE的大小关系，并说明理由．10．（10分）（2007•福州）如图，已知直线y=x与双曲线交于A，B两点，且点A的横坐标为4．（1）求k的值；（2）若双曲线上一点C的纵坐标为8，求△AOC的面积；（3）过原点O的另一条直线l交双曲线于P，Q两点（P点在第一象限），若由点A，B，P，Q为顶点组成的四边形面积为24，求点P的坐标．初二数学经典难题参考答案与试题解析一、解答题（共10小题，满分100分）1．（10分）已知：如图，P是正方形ABCD内点，∠PAD=∠PDA=15°．求证：△PBC是正三角形．（初二）考点：正方形的性质；全等三角形的判定与性质；等边三角形的性质；等边三角形的判定。

初二数学经典题型1．已知：如图，P是正方形ABCD内点，∠PAD＝∠PDA＝150．求证：△PBC是正三角形．2.已知：如图，在四边形ABCD中，AD＝BC，M、N分别是AB、CD的中点，AD、BC的延长线交MN于E、F．求证：∠DEN＝∠F．3、如图，分别以△ABC的AC和BC为一边，在△ABC的外侧作正方形ACDE和正方形CBFG，点P是EF的中点．求证：点P到边AB的距离等于AB的一半．4、设P是平行四边形ABCD内部的一点，且∠PBA＝∠PDA．求证：∠PAB＝∠PCB．为正方形ABCD内的一点，并且PA＝a，PB＝2a，PC=3a正方形的边长．6.如图，P是边长为1的正方形ABCD对角线AC上一动点（P与A、C不重合），点E在射线BC上，且PE=PB.（1）求证：①PE=PD；②PE⊥PD；（2）设AP=x, △PBE的面积为y.①求出y关于x的函数关系式，并写出x的取值范围；②当x取何值时，y取得最大值，并求出这个最大值.答案1、证明如下。

首先，PA=PD，∠PAD=∠PDA=（180°-150°）÷2=15°，∠PAB=90°-15°=75°。

在正方形ABCD之外以AD为底边作正三角形ADQ，连接PQ，则∠PDQ=60°+15°=75°，同样∠PAQ=75°，又AQ=DQ,，PA=PD，所以△PAQ≌△PDQ，那么∠PQA=∠PQD=60°÷2=30°，在△PQA中，∠APQ=180°-30°-75°=75°=∠PAQ=∠PAB，于是PQ=AQ=AB，显然△PAQ≌△PAB，得∠PBA=∠PQA=30°，PB=PQ=AB=BC，∠PBC=90°-30°=60°，所以△ABC是正三角形。

一、选择题1．一个大正方形和四个全等的小正方形按图①、②两种方式摆放，则图②的大正方形中未被小正方形覆盖部分的面积是（ ）（用含有a 、b 的代数式表示）．A ．a-bB ．a+bC ．abD ．2ab C解析：C【分析】 设小正方形的边长为x ，大正方形的边长为y ，列方程求解，用大正方形的面积减去4个小正方形的面积即可．【详解】解：设小正方形的边长为x ，大正方形的边长为y ，则：22x y a y x b+=⎧⎨-=⎩ ， 解得：42a b x a b y -⎧=⎪⎪⎨+⎪=⎪⎩， ∴阴影面积=（2a b +）2﹣4×（4a b -）22222224444a ab b a ab b ab ++-+=-=＝ab ． 故选C ．【点睛】本题考查了整式的混合运算，求得大正方形的边长和小正方形的边长是解题的关键． 2．从边长为 2a +的正方形纸片中剪去一个边长为1a -的正方形纸片()1a >，则剩余部分的面积是（ ）A ．41a +B ．43a +C ．63a +D ．2+1a C解析：C【分析】根据题意列出关系式，化简即可得到结果；【详解】根据题意可得： ()()()()()2221212132163a a a a a a a a +--=++-+-+=+=+；故答案选C ．【点睛】本题主要考查了完全平方公式的几何背景，准确分析计算是解题的关键．3．若2x y +=，1xy =-，则()()1212x y --的值是（ ）A ．7-B ．3-C ．1D ．9A 解析：A【分析】利用多项式乘以多项式法则计算，整理后将已知等式代入计算即可求出值．【详解】解：∵x+y=2，xy=-1，∴（1-2x ）（1-2y ）=1-2y-2x+4xy=1-2（x+y ）+4xy=1-2×2-4=-7；故选：A ．【点睛】本题考查了多项式乘多项式，熟练掌握运算法则是解本题的关键．4．代数式2346x x -+的值为3，则2463x x -+的值为（ ） A ．7B ．18C ．5D ．9C 解析：C【分析】由代数式3x 2−4x ＋6的值为3，变形得出x 2−43x ＝−1，再整体代入x 2−43x ＋6计算即可． 【详解】∵代数式3x 2−4x ＋6的值为3，∴3x 2−4x ＋6＝3，∴3x 2−4x ＝−3，∴x 2−43x ＝−1， ∴x 2−43x ＋6＝−1＋6＝5． 故选：C ．【点睛】本题考查了代数式求值，熟练掌握相关运算法则并运用整体思想是解题的关键． 5．如果x+y ＝6，x 2-y 2=24，那么y-x 的值为（ ）A ．﹣4B ．4C ．﹣6D ．6A解析：A【分析】先变形为x 2-y 2=（x+y ）（x-y ），代入数值即可求解．【详解】解：∵x 2-y 2=（x+y ）（x-y ）=24，∴6（x-y ）=24，∴x-y=4，∴y-x=-4，故选：A ．【点睛】本题考查了平方差公式的应用，掌握公式是解题关键．6．2a =1，b 是2的相反数，则a+b 的值是（ ）A ．1B ．-3C ．-1或-3D ．1或-3C 解析：C【分析】根据平方及相反数定义求出a 、b 的值，代入a+b 计算即可．【详解】∵2a =1，b 是2的相反数，∴1a =±，b=-2，当a=1时，a+b=1-2=-1，当a=-1时，a+b=-1-2=-3，故选：C ．【点睛】此题考查求代数式的值，根据平方及相反数定义求出a 、b 的值是解题的关键． 7．若关于x 的方程250x a b ++=的解是3x =-，则代数式6210a b --的值为（ ） A ．6-B ．0C ．12D ．18A 解析：A【分析】将方程的解代回方程得56a b +=，再整体代入代数式求值即可．【详解】解：把3x =-代入原方程得650a b -++=，即56a b +=，则()62106256126a b a b --=-+=-=-．故选：A ．【点睛】本题考查代数式求值和方程解的定义，解题的关键是掌握方程解的定义，以及利用整体代入的思想求值．8．计算2019202040.753⎛⎫⨯- ⎪⎝⎭的结果是（ ） A ．43 B ．43- C ．0.75 D ．-0.75D解析：D【分析】先将20200.75化为20193434⨯，再用幂的乘方的逆运算计算，再计算乘法即可得到答案． 【详解】2019202040.753⎛⎫⨯- ⎪⎝⎭ =20192019343434⎛⎫⎛⎫⨯-⨯ ⎪ ⎪⎝⎭⎝⎭=201934()3434⎡⎤⨯⎢⎥⎣⎦⨯- =(31)4-⨯=34-, 故选：D ．【点睛】此题考查有理数数的乘法运算，掌握幂的乘方的逆运算是解题的关键．9．下列运算正确的是（ ）A ．3m ·4m =12mB ．m 6÷m 2= m 3（m≠0）C ．236(3)27m m -=D ．（2m+1）（m-1）=2m 2-m-1D解析：D【分析】利用同底数幂的乘法和除法，积的乘方、幂的乘方，多项式乘多项式的运算法则计算即可判断．【详解】A 、 347·m m m =，该选项错误；B 、624m m m ÷=，该选项错误；C 、236(3)27m m -=-，该选项错误；D 、(()221)121m m m m +-=--，该选项正确； 故选：D ．【点睛】本题考查了同底数幂的乘法和除法，积的乘方、幂的乘方，多项式乘多项式，熟练掌握运算法则是解题的关键．10．若|a |=13，b|=7，且a +b>0，则a -b 的值是( )．A ．6或20B ．20 或-20C ．6或-6D ．-6或20A解析：A【分析】先求出a b ，的值，根据条件+a b >0，确定=13a ，b=7±，分类代入-a b 求值即可．【详解】|a |=13，=13a ±，|b|=7，b=7±，∵+a b >0，∴=13a ，b=7±，当=13a ，b=7时，=1376a b --=，当=13a ，7b =-时，=13+720a b -=，则6a b -=或20．故选择：A ．【点睛】本题考查条件限定求值问题，会根据限定条件求出字母的值，掌握分类思想求代数式的值是解题关键．二、填空题11．如图，大正方形与小正方形的面积之差是60，则阴影部分的面积是_____．30【分析】直接利用正方形的性质结合三角形面积求法利用平方差公式即可得出答案【详解】解：设大正方形的边长为a 小正方形的边长为b 故阴影部分的面积是：AE•BC+AE•BD ＝AE （BC+BD ）＝（AB ﹣解析：30【分析】直接利用正方形的性质结合三角形面积求法，利用平方差公式即可得出答案．【详解】解：设大正方形的边长为a ，小正方形的边长为b ， 故阴影部分的面积是：12AE •BC +12AE •BD ＝12AE （BC +BD ） ＝12（AB ﹣BE ）（BC +BD ） ＝12（a ﹣b ）（a +b ） ＝12（a 2﹣b 2） ＝12×60 ＝30．故答案为：30．【点睛】本题主要考查平方差公式与几何图形和三角形的面积公式，用代数式表示阴影部分的面积，是解题的关键．12．已知18m x =，16n x =，则2m n x +的值为________．【分析】根据同底数幂的乘法可得再根据幂的乘方可得然后再代入求值即可【详解】解：故答案为【点睛】此题主要考查了同底数幂的乘法和幂的乘方关键是掌握同底数幂的乘法法则：同底数幂相乘底数不变指数相加；幂的乘 解析：14 【分析】根据同底数幂的乘法可得22m n m n x x x +=⋅，再根据幂的乘方可得()22m m x x =，然后再代入18mx =，16n x =求值即可． 【详解】 解：()2222111684m n m n m n x x x x x +⎛⎫=⋅=⋅=⨯= ⎪⎝⎭ ， 故答案为14． 【点睛】 此题主要考查了同底数幂的乘法和幂的乘方，关键是掌握同底数幂的乘法法则：同底数幂相乘，底数不变，指数相加；幂的乘方法则：底数不变，指数相乘．13．如图所示，在这个运算程序当中，若开始输入的x 是2，则经过2021次输出的结果是________．4【分析】根据第一次输出的结果是1第二次输出的结果是6…总结出每次输出的结果的规律求出2021次输出的结果是多少即可【详解】解：把x=2代入得：2÷2=1把x=1代入得：1+5=6把x=6代入得：6解析：4【分析】根据第一次输出的结果是1，第二次输出的结果是6，…，总结出每次输出的结果的规律，求出2021次输出的结果是多少即可．【详解】解：把x=2代入得：2÷2=1，把x=1代入得：1+5=6，把x=6代入得：6÷2=3，把x=3代入得：3+5=8，把x=8代入得：8÷2=4，把x=4代入得：4÷2=2，把x=2代入得：2÷2=1，以此类推，∵2021÷6=336…5，∴经过2021次输出的结果是4．故答案为：4．【点睛】本题主要考查了代数式求值问题，要熟练掌握，求代数式的值可以直接代入、计算．如果给出的代数式可以化简，要先化简再求值．题型简单总结以下三种：①已知条件不化简，所给代数式化简；②已知条件化简，所给代数式不化简；③已知条件和所给代数式都要化简．14．一个三角形的面积为3xy －4y ，一边长是2y ，则这条边上的高为_____．3x －4【分析】利用面积公式计算即可得到答案【详解】设这条边上的高为a 由题意得：∴ay=3xy-4y ∴a=3x-4故答案为：3x-4【点睛】此题考查多项式除以单项式法则：用多项式中的每一项分别除以单解析：3x －4【分析】利用面积公式计算即可得到答案．【详解】设这条边上的高为a ， 由题意得：12342y a xy y ⋅⋅=-， ∴ay=3xy-4y ，∴a=3x-4，故答案为：3x-4．【点睛】 此题考查多项式除以单项式法则：用多项式中的每一项分别除以单项式，再把结果相加．15．若()230x -=，则x y -=______．7【分析】根据偶次方的非负性及算术平方根的非负性求出x=3y=-4代入x-y 中计算即可【详解】∵且∴x-3=0y+4=0∴x=3y=-4∴x-y=3-（-4）=7故答案为：7【点睛】此题考查已知字母 解析：7【分析】根据偶次方的非负性及算术平方根的非负性求出x=3，y=-4，代入x-y 中计算即可．【详解】∵()230x -=，且()230x -≥≥， ∴x-3=0，y+4=0，∴x=3，y=-4，∴x-y=3-（-4）=7，故答案为：7．【点睛】此题考查已知字母的值求代数式的值，掌握偶次方的非负性及算术平方根的非负性求出x=3，y=-4是解题的关键．16．若2a 与()23b +互为相反数，则2-=b a ______．-8【分析】根据题意得到+=0根据绝对值的非负性及偶次方的非负性求出a=2b=-3代入2b-a 计算即可【详解】由题意得：+=0∵00∴a-2=0b+3=0∴a=2b=-3∴2b-a=-6-2=8故答 解析：-8【分析】 根据题意得到2a +2(3)b +=0，根据绝对值的非负性及偶次方的非负性求出a=2，b=-3，代入2b-a 计算即可．【详解】 由题意得：2a +2(3)b +=0 ∵2a ≥0，2(3)b +≥0，∴a-2=0，b+3=0，∴a=2，b=-3，∴2b-a=-6-2=8，故答案为：-8．【点睛】此题考查相反数的定义，绝对值的非负性及偶次方的非负性，求代数式的值，根据绝对值的非负性及偶次方的非负性求出a 和b 的值是解题的关键．17．已知23x y -=，则432x y --=________．3【分析】把看成一个整体原式可化为2（）-3整体代入即可【详解】解：原式=2（）-3=2×3-3=3故答案为：3【点睛】本题考查了求代数式的值把看成一个整体是解题的关键解析：3【分析】把2x y -看成一个整体，原式可化为2（2x y -）-3，整体代入即可．【详解】解：原式=2（2x y -）-3=2×3-3=3，故答案为：3．【点睛】本题考查了求代数式的值，把2x y -看成一个整体是解题的关键．18．已知香蕉，苹果，梨的价格分别为a ，b ，c （单位：元/千克）、用20元正好可以买三种水果各1千克：买1千克香蕉，2千克苹果，3千克梨正好花去42元，若买b 千克香需w 元，则w =___________．（结果用含c 的代数式表示）【分析】根据题意得：通过计算得到b 和c 的关系式；再将b 和c 的关系式代入到得a 和c 的关系式经计算即可得到答案【详解】根据题意得：∴∴∴∴故答案为：【点睛】本题考查了三元一次方程组整式运算的知识；解题的解析：222644c c -+-【分析】根据题意得：20a b c ++=，2342a b c ++=，通过计算得到b 和c 的关系式；再将b 和c 的关系式代入到20a b c ++=，得a 和c 的关系式，经计算即可得到答案．【详解】根据题意得：20a b c ++=，2342a b c ++=∴204223a b c b c =--=--∴222b c =-∴20202222a b c c c c =--=-+-=-∴()()2222222644w a b c c c c =⨯=--=-+- 故答案为：222644c c -+-．【点睛】本题考查了三元一次方程组、整式运算的知识；解题的关键是熟练掌握三元一次方程组、整式乘法运算的性质，从而完成求解．19．计算：32(2)a b -＝________．【分析】积的乘方等于积中每个因式分别乘方再把所得的幂相乘根据法则计算即可【详解】=故答案为：【点睛】此题考查积的乘方：等于积中每个因式分别乘方再把所得的幂相乘解析：624a b【分析】积的乘方等于积中每个因式分别乘方，再把所得的幂相乘，根据法则计算即可．【详解】32(2)a b -=624a b ，故答案为：624a b ．【点睛】此题考查积的乘方：等于积中每个因式分别乘方，再把所得的幂相乘．20．因式分解()2228ac bc abc -+=______．【分析】先利用完全平方公式把原式写成再根据完全平方公式得出结果【详解】解：原式故答案是：【点睛】本题考查因式分解解题的关键是掌握利用乘法公式进行因式分解的方法解析：()22ac bc +【分析】先利用完全平方公式把原式写成2222244a c abc b c ++，再根据完全平方公式得出结果．【详解】解：原式222222448a c abc b c abc =-++2222244a c abc b c =++()22ac bc =+．故答案是：()22ac bc +．【点睛】本题考查因式分解，解题的关键是掌握利用乘法公式进行因式分解的方法． 三、解答题21．计算下列各题：（1（2）（）（3）（2解析：（1）0；（2）【分析】（1）根据平方根、立方根的意义进行计算即可；（2）利用平方差公式和实数的计算方法进行计算即可．【详解】解：（1＝2+（﹣5）+3＝0；（2）（）（3）（2＝32）2﹣2＝9﹣﹣2＝【点睛】本题考查了包含算术平方根、立方根、平方差公式的实数计算，熟练运用法则和公式是解决问题关键．22．某快餐店试销某种套餐，每份套餐的成本为5元，该店每天固定支出费用为500元（不含套餐成本）．试销售一段时间后发现，若每份套餐售价不超过10元，每天可销售400份；若每份套餐售价超过10元，每提高1元，每天的销售量就减少40份．（1）若每份套餐售价定为9元，则该店每天的利润为 元；若每份套餐售价定为12元，则该店每天的利润为 元；（2）设每份套餐售价定为x 元，试求出该店每天的利润（用含x 的代数式表示，只要求列式，不必化简）；（3）该店的老板要求每天的利润能达到1660元，他计划将每份套餐的售价定为：10元或11元或14元．请问应选择以上哪个套餐的售价既能保证达到利润要求又让顾客省钱？请说明理由．解析：（1）1100元，1740元；（2）当10x ≤时，利润为(5)400500x -⨯-；当10x >时，利润为[](5)400(10)40500x x ---⨯-；（3）选择11元，能保证达到利润要求又让顾客省钱．【分析】（1）根据题意，列出算式，即可求解；（2）分两种情况：当10x ≤时，当10x >时，分别列出代数式，即可；（3）把x=10，11，14分别代入第（2）小题的代数式，即可得到答案．【详解】解：（1）由题意得：（9-5）×400-500=1100（元），（12-5）×[400-（12-10）×40]-500=1740（元），故答案是：1100元，1740元；（2）当10x ≤时，利润为(5)400500x -⨯-，当10x >时，利润为[](5)400(10)40500x x ---⨯-；（3）∵当x ＝10时，(105)4005001500-⨯-=（元），当x ＝11时，[](115)400(1110)405001660---⨯-=（元），当x ＝14时，[](145)400(1410)405001660---⨯-=（元）， ∴当x ＝11或14时，利润均为1660元．∵11＜14，∴选择11元，能保证达到利润要求又让顾客省钱．【点睛】本题考查的是代数式的实际应用，解题的关键是根据题目中的数量关系列出代数式． 23．如图，某长方形广场的四个角都有一块半径为r 米的四分之一圆形的草地，中间有一个半径为r 米的圆形水池，长方形的长为a 米，宽为b 米．（1）整个长方形广场面积为 ；草地和水池的面积之和为 ；（2）若a ＝70，b ＝50，r ＝10，求广场空地的面积（π取3.142，计算结果精确到个位）．解析：（1）ab 平方米；22r π平方米，（2）2872平方米【分析】（1）根据长方形面积公式即可表示出广场面积；根据圆的面积公式即可表示草地和水池的面积；（2）长方形面积减去草地和水池的面积的和即可得到广场空地的面积，再代入求值即可．【详解】（1）整个长方形广场面积为ab 平方米；草地和水池的面积之和为214r 4π⨯⨯+2r π=22r π平方米，故答案是：ab 平方米；22r π平方米；（2）依题意得：空地的面积为 22ab r π-当a ＝70，b ＝50，r ＝10时，∴ 22270502 3.14210ab r π-=⨯-⨯⨯2871.62872=≈答：广场空地的面积约为2872平方米．【点睛】 本题考查列代数式、求代数式的值，列出正确的代数式是正确解答的关键．24．某公司招聘外卖送餐员，送餐员的月工资由底薪1000元加上外卖送单补贴（送一次外卖称为一单）构成，外卖送单补贴的具体方案如下：（2）设5月份某“外卖小哥”送餐x 单()500x >，求他这个月的工资总额（用含x ,m 的代数式表示）．解析：（1）3400元；（2）当500＜x≤m ，工资总额为8x ；当x ＞m ，工资总额为10x-2m【分析】（1）根据题意和表格中的数据可以求得若某“外卖小哥”4月份送餐400单，他这个月的工资总额；（2）根据题意和表格中的数据可以写出各段工资总额与x 的关系式；【详解】解：（1）工资总额=1000+400×6=3400元（2）当500＜x≤m ，工资总额为：1000+500×6+8（x-500）=8x当x ＞m ，工资总额为：1000+500×6+8（m-500）+10（x-m ）=10x-2m【点睛】本题考查列代数式，解答本题的关键是明确题意，找出所求问题需要的条件，分段分析解答．25．给出下列算式：2231842-==⨯；22531644-==⨯；22752446-==⨯；22973248-==⨯．······()1观察上面一系列式子，你能发现什么规律?()2用含(n n 为正整数)的式子表示出来你发现的规律，并证明这个规律﹔()3计算2220212019-=_ _，此时n =_ ．解析：（1）两个连续奇数的平方差（大奇数的平方减去小奇数的平方），等于夹在两个奇数之间的偶数的4倍；（2）()()22212142n n n +•＝-﹣；证明见解析；（3）8080,1010．【分析】（1）通过观察找出规律，可发现两个连续奇数的平方差等于夹在两个奇数之间的偶数的4倍；（2）由（1）进一步可得出第n 个等式为()()22212142n n n +-⋅＝-．（3）利用前面得到的规律即可求得答案．【详解】（1）规律：两个连续奇数的平方差（大奇数的平方减去小奇数的平方），等于夹在两个奇数之间的偶数的4倍；（2）设1n n ≥（）表示自然数，用关于n 的等式表示这个规律为： ()()22212142n n n +⋅﹣＝-；证明：左边()()2244144142n n n n n =++--+=⋅=右边 ()()22212142n n n ∴+-⋅﹣＝；（3）212021n +＝，解得：1010n ＝， 22420212019101088200-=⨯=⨯∴．【点睛】此题考查数字的变化规律，根据数字的特点，得出运算的规律，利用规律解决问题． 26．某园林公司现有A 、B 两个区，已知A 园区为长方形，长为()x y +米，宽为()x y -米；B 园区为正方形，边长为(3)x y +米．（1）请用代数式表示A 、B 两园区的面积之和并化简；（2）现根据实际需要对A 园区进行整改，长增加(11)x y -米，宽减少(2)x y -米，整改后A 区的长比宽多350米，且整改后两园区的周长之和为980米．①求x ，y 的值；②若A 园区全部种植C 种花，B 园区全部种植D 种花，且C 、D 两种花投入的费用与收益如表：-投入）解析：（1）（x+y ）（x-y ）+（x+3y ）2；2x 2+6xy+8y 2；（2）①x=30，y=10；②相等【分析】（1）根据长方形的面积等于长乘以宽，正方形的面积等于边长的平方，最后再求和， （2）①根据整改后A 区的长比宽多350米，且整改后两园区的周长之和为980米．列方程组求解即可，②计算出A 园区的净收益和B 园区的净收益，再比较大小．【详解】解：（1）（x +y ）（x -y ）+（x +3y ）2，＝x 2-y 2+x 2+6xy +9y 2，＝2x 2+6xy +8y 2；（2）①由题意得，()()()()()()()()()112350211243980x y x y x y x y x y x y x y x y x y ⎧⎡⎤⎡⎤++-----⎪⎣⎦⎣⎦⎨⎡⎤++-+---++⎪⎣⎦⎩＝＝，整理得，12350270x y x y -=⎧⎨+=⎩， 解得：x ＝30，y ＝10，答：x ＝30，y ＝10．②A 园区整改后长为12x 米，宽为y 米，A 园区的净收益（22-12）×12xy ＝36000元，B 园区的净收益为（26-16）（x +3y ）2＝36000元，∴B 园区的净收益等于A 园区的净收益．【点睛】本题考查二元一次方程组、整式的加减、多项式乘以多项式的计算方法等知识，正确的列出多项式，并化简是解决问题的关键．27．观察下列关于自然数的等式：（1）217295⨯+⨯= ①（2）2282106⨯+⨯= ②（3）2392117⨯+⨯= ③……根据上述规律解决下列问题：（1）完成第四个等式__________．（2）写出你猜想的第n 个等式（用含n 的式子表示），并验证其正确性．解析：（1）4×10+2×12=82；（2）n （n+6）+2（n+8）=（n+4）2，验证见解析·【分析】（1）由①②③三个等式得出规律，即可得出结果；（2）由规律得出答案，再验证即可．【详解】解：（1）根据题意得：第四个等式为：4×10+2×12=82；（2）猜想的第n 个等式为：n （n+6）+2（n+8）=（n+4）2，验证：左边=n （n+6）+2（n+8）=n 2+6n+2n+16=n 2+8n+42=（n+4）2=右边，∴n （n+6）+2（n+8）=（n+4）2．【点睛】本题主要考查了数字的变化规律、完全平方公式、归纳推理等知识；根据题意得出规律是解决问题的关键．28．先化简，再求值：()()()()()32333b a b a a b a b b a a ---+---÷-⎡⎤⎣⎦，其中212025a b ⎛⎫-+-= ⎪⎝⎭． 解析：4a b -，85【分析】先算乘法，再合并同类项，最后算除法，代入求出即可．【详解】解：()()()()()32333b a b a a b a b b a a ---+---÷-⎡⎤⎣⎦ ()()22223293ab b a ab b a a =--++-÷-()()23123ab a a =-÷-4a b =- ∵212025a b ⎛⎫-+-= ⎪⎝⎭ ∴1=02a -，2=05b - 解得：12a =，25b = ∴原式1284255=⨯-= 【点睛】本题考查了整式的混合运算和求值的应用，主要考查学生的化简能力和计算能力，注意运算顺序．。

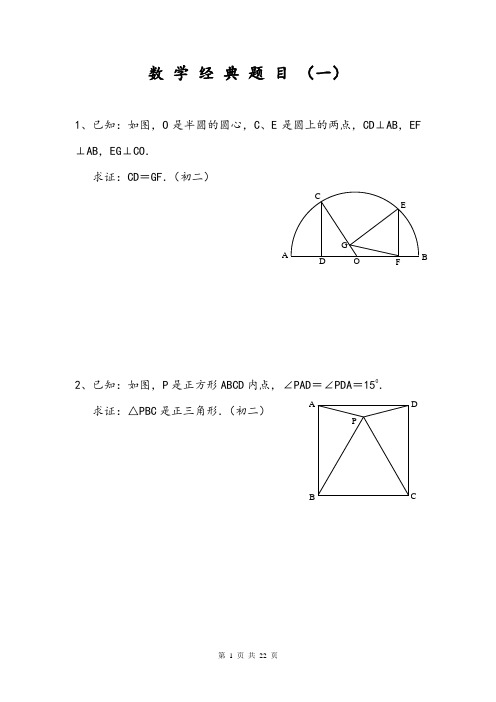
数学经典题目（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF ．（初二）2、已知：如图，P 是正方形ABCD 内点，∠PAD ＝∠PDA ＝150． 求证：△PBC 是正三角形．（初二）APCDB AFGCEBOD3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）4、已知：如图，在四边形ABCD 中，AD ＝BC ，M中点，AD 、BC 的延长线交MN 于E 、F 求证：∠DEN ＝∠F ．D 2C 2B 2 A 2D 1C 1B 1CBDAA 1B数学经典题目（二）1、已知：△ABC中，H为垂心（各边高线的交点），O为外心，且OM ⊥BC于M．（1）求证：AH＝2OM；（2）若∠BAC＝600，求证：AH＝AO．（初二）2、设MN是圆O外一直线，过O作OA⊥MN于A线，交圆于B、C及D、E，直线EB及CD 求证：AP＝AQ．（初二）F3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点AEB 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 求证：点P 到边AB 的距离等于AB数学经典题目（三）1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二）2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．3、设P是正方形ABCD一边BC上的任一点，PF⊥AP，CF平分∠DCE．4、如图，PC切圆O于C，AC与直线PO相交于B、D．求证：AB数学经典题目（四）1、已知：△ABC是正三角形，P是三角形内一点，PA＝3，PB＝4，PC ＝5．2、设P是平行四边形ABCD内部的一点，且∠PBA＝∠PDA．求证：∠PAB＝∠PCB．（初二）3、设ABCD 为圆内接凸四边形，求证：AB ·CD ＋AD ·三）4、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）数学经典题目（五）1、设P 是边长为1的正△ABC 内任一点，L ＝PA ＋PB ＋PC ，求证：≤L ＜2．2、已知：P 是边长为1的正方形ABCD 内的一点，求PA ＋PB ＋PC 的最小值．APCBACBPD3、P 为正方形ABCD 内的一点，并且PA ＝a ，PB ＝2a方形的边长．4、如图，△ABC 中，∠ABC ＝∠ACB＝800，D 、E 分别是点，∠DCA ＝300，∠EBA ＝200，求∠BED 的度数．数学经典题目（一）1.如下图做GH ⊥AB,连接EO 。

八年级数学：一次函数应用题最大利润问题20道（含答案及解析）1．如图，1l 表示某公司一种产品一天的销售收入与销售量的关系，2l 表示该公司这种产品一天的销售成本与销售量的关系．（1）1x 时，销售收入＝______万元，销售成本＝______万元，盈利（收入－成本）＝______万元； （2）一天销售______件时，销售收入等于销售成本； （3）1l 对应的函数表达式是______；（4）你能写出利润与销售量间的函数表达式吗？2．消费也扶贫，万源市某村需要销售当地的优质土特产：香米和土豆，这两种商品的相关信息如下表： （1）达州市第一中学工会第一季度采购了香米和土豆共计1000袋，为该村创造利润17000元，求达州市第一中学工会采购了香米多少袋？（2）为了加大扶贫力度，达州市第一中学工会在第二季度想为该村创造20000元以上利润的目标．该工会计划购进香米和土豆共计1200袋，且香米不低于800袋，不超过1000袋．设购进香米m 袋，香米和土豆共创造利润w 元，求出w 与m 之间的函数关系式，并通过计算说明达州市第一中学工会能否实现扶贫目标？3．某水产品商店销售1千克A 种水产品的利润为10元，销售1千克B 种水产品的利润为15元，该经销商决定一次购进A 、B 两种水产品共200千克用于销售，设购进A 种水产品x 千克，销售总利润为y 元． （1）求y 与x 之间的函数关系式；（2）若其中B 种水产品的进货量不超过A 种水产品的3倍，请你帮该经销商设计一种进货方案使销售总利润最大，并求出总利润的最大值．4．某乡镇农贸公司新开设了一家网店，销售当地农产品，其中一种当地特产在网上试销售，其成本为每千克2元．公司在试销售期间，调查发现，每天销售量y （kg ）与销售单价x （元）满足如图所示的函数关系（其中210x <≤）． （1）求y 与x 之间的函数关系式；（2）销售单价x 为多少元时，每天的销售利润最大？最大利润是多少元？5．面临毕业季，某电脑营销商瞄准时机，在五月底筹集到资金12.12万元，用于一次性购进A 、B 两种型号的电脑共30台．根据市场需求，这些电脑可以全部销售，全部销售后利润不少于1.6万元，其中电脑的进价和售价见下表：A 型电脑B 型电脑 进价(元/台) 4200 3600 售价(元/台)48004000设营销商计划购进A 型电脑x 台，电脑全部销售后获得的利润为y 万元． （1）试写出y 与x 的函数关系式；（2）该营销商有几种购进电脑的方案可供选择？（3）该营销商选择哪种购进电脑的方案获利最大？最大利润是多少？6．某运动鞋专卖店通过市场调研，准备销售A 、B 两种运动鞋，其中A 种运动鞋的进价比B 种运动鞋的进价高20元，已知鞋店用3200元购进A 种运动鞋的数量与用2560元购进B 种运动鞋的数量相同． （1）求两种运动鞋的进价．（2）设A 运动鞋的售价为250元/双，B 运动鞋的售价是180元/双，鞋店共进货两种运动鞋200双，设总利润为W 元，A 运动鞋进货m 双，且90≤m ≤105． ①写出总利润W 元关于m 的函数关系式． ②要使该专卖店获得最大利润，应如何进货7．某水果经销商需购进甲，乙两种水果进行销售．甲种水果每千克的价格为a元，如果一次购买超过40千克，超过部分的价格打八折，乙种水果的价格为25元/千克．设经销商购进甲种水果x千克，付款y元，y与x之间的函数关系如图所示．（1）求a的值，并写出当x＞40时，y与x之间的函数关系式；（2）若经销商计划一次性购进甲，乙两种水果共80千克，且甲种水果不少于30千克，但又不超过50千克．如何分配甲，乙两种水果的购进量，才能使经销商付款总金额w（元）最少？8．为落实国家精准扶贫政策，某地扶贫办决定帮助扶贫对象推销当地特色农产品，该农产品成本价为18元每千克，销售单价y（元）与每天销售量x（千克）（x为正整数）之间满足如图所示的函数关系，其中销售单价不得低于成本价．（1）求出y与x之间所满足的函数关系式，并写出自变量x的取值范围；（2）当销售量为多少时，获利最大？最大利润是多少？9．某超市经销甲、乙两种品牌的洗衣液，进货时发现，甲品牌洗衣液每瓶的进价比乙品牌高6元，用1800元购进甲品牌洗衣液的数量是用100元购进乙品牌洗衣液数量的45．销售时，甲品牌洗衣液的售价为36元/瓶，乙品牌洗衣液的售价为28元/瓶．（1）求两种品牌洗衣液的进价；（2）若超市需要购进甲、乙两种品牌的洗衣液共120瓶，且购进两种洗衣液的总成本不超过3120元，超市应购进甲、乙两种品牌洗衣液各多少瓶，才能在两种洗衣液完全售出后所获利润最大？最大利润是多少元？10．昆明斗南花卉市场是全国鲜花市场的心脏，也是亚洲最大的鲜花交易市场之一．斗南某兰花专卖店专门销售某种品牌的兰花，已知这种兰花的成本价为60元/盆．市场管理部门规定：每盆兰花的销售价格不低于成本价，又不高于成本价的2倍．经过市场调查发现，该店某天的销售数量y（盆）与销售单价x（元/盆）之间的函数关系如图所示：（1）求y与x之间的函数关系式，并写出自变量x的取值范围：（2）在销售过程中，该店每天还要支付其他费用200元，求这一天销售兰花获得的利润w（元）的最大值．11．九年级数学兴趣小组经过市场调查，整理出某种商品在第x（1≤x≤70且x为整数）天的售价与销量的相关信息如下表：已知该商品的进价为每件30元，设销售该商品的每天利润为y元．（1）求出y与x的函数关系式；（2）问销售该商品第几天时，当天销售利润最大，最大利润是多少?（3）该商品在销售过程中，共有几天每天销售利润不低于3250元?请直接写出结果．12．2021年3月20日，三星堆遗址考古新发现揭晓，出土文物500余件，三星堆考古发掘成果再次成为炙手可热的话题．某商家看准商机后，计划购进一批“考古盲盒”（三星堆文物模型盲盒）进行销售．已知该商家用1570元购进了10个甲种盲盒和15个乙种盲盒，甲种盲盒的进货单价比乙种盲盒的进货单价多2元． （1）甲种盲盒和乙种盲盒的进货单价分别是多少元；（2）由于“考古盲盒”畅销，商家决定再购进这两种盲盒共50个，其中甲种盲盒数量不多于乙种盲盒数量的2倍，且每种盲盒的进货单价保持不变．若甲种盲盒的销售单价为83元，乙种盲盒的销售单价为78元．①假设此次购进甲种盲盒的个数为a （个），售完这两批盲盒所获总利润为w （元），请写出w 与a 之间的函数关系式；①商家如何安排第二批进货方案，才能使售完这两批盲盒获得总利润最大？最大利润是多少元？13．为迎接“五一”小长假购物高潮，某品牌专卖店准备购进甲、乙两种衬衫，其中甲、乙两种衬衫的进价和售价如下表：若用3000元购进甲种衬衫的数量与用2700元购进乙种衬衫的数量相同． （1）求甲、乙两种衬衫每件的进价；（2）要使购进的甲、乙两种衬衫共300件的总利润不少于34000元，且不超过34700元，问该专卖店有几种进货方案；（3）在（2）的条件下，专卖店准备对甲种衬衫进行优惠促销活动，决定对甲种衬衫每件优惠a 元(6080)a <<出售，乙种衬衫售价不变，那么该专卖店要获得最大利润应如何进货？14．某大型水果超市销售水蜜桃，根据前段时间的销售经验，每天的售价x（元/箱）与销售量y（箱）有如下表关系：已知y与x之间的函数关系是一次函数．（1）求y与x的函数解析式；（2）水蜜桃的进价是40元/箱，若该超市每天销售水蜜桃盈利1600元，要使顾客获得实惠，每箱售价是多少元？15．迎接大运，美化深圳，园林部门决定利用现有的3490盆甲种花卉和2590盆乙种花卉搭配A、B两种园艺造型共50个摆放在迎宾大道两侧，已知搭配一个A种造型需甲种花卉80盆，乙种花卉40盆，搭配一个B种造型需甲种花卉50盆，乙种花卉90盆．（1）某校九年级（1）班课外活动小组承接了这个园艺造型搭配方案的设计，问符合题意的搭配方案有几种？请你帮助设计出来．（2）若搭配一个A种造型的成本是800元，搭配一个B种造型的成本是960元，试说明（1）中哪种方案成本最低？最低成本是多少元？16．九(4)班数学兴趣小组经过市场调查，整理出童威的某种高端商品在第x（1≤x≤90）天的售价与销量的相关信息如下表：已知该商品的进价为每件30元，设销售该商品的每天利润为y元．（1）求出y与x的函数关系式；（2）问销售该商品第几天时，当天销售利润最大，最大利润是多少？（3）该商品在前49天销售中，每销售一件商品就捐赠m元（0＜m＜10）给希望工程．若前49天销售获得的最17．玩具批发市场A、B玩具的批发价分别为每件30元和50元，张阿姨花1200元购进A、B两种玩具若干件，并分别以每件35元与60元价格出售．设购入A玩具为x件，B玩具为y件．（1）若张阿姨将玩具全部出售赚了220元，则张阿姨购进A、B型玩具各多少件？（2）若要求购进A玩具的数量不得少于B玩具的数量，问如何购进玩具A、B的数量并全部出售才能获得最大利润，此时最大利润为多少元？18．某桶装水经营部每天的房租、人员工资等固定成本为250元，每桶水的进价是5元，规定销售单价不得高于12元，也不得低于7元，调查发现日均销售量p(桶)与销售单价x(元)的函数图象如图所示．（1）求日均销售量p(桶)与销售单价x(元)的函数关系式；（2）若该经营部希望日均获利1350元，那么日均销售多少桶水？19．某商场试销一种成本为每件60元的服装，规定试销期间销售单价不低于成本单价，且获利不得高于40%．经试销发现，销售量y（件）与销售单价x（元）符合一次函数y＝kx+b，且当x＝80时，y＝40，当x＝70时，y＝50．（1）求一次函数y＝kx+b的表达式；（2）若该商场获得的利润为W元，试写出利润W与销售单价x之间的关系式；销售单价定为多少元时，商场可获得最大利润？最大利润是多少元？20．某销售商准备采购一批儿童玩具，有A，B两种品牌可供选择，其进价和售价如下：销售商购进A，B两种品牌的儿童玩具共30件.（1）若销售商购进A品牌的儿童玩具为x （件）, 求销售商售完这30件儿童玩具获得的总利润y（元）与x之间的函数关系式;（2）若想使得销售完这30件儿童玩具获得的总利润为1300元，求应购进A品牌的儿童玩具多少件?（3）若购进A品牌的儿童玩具不能少于20件，求所获总利润最多为多少元?参考答案1．（1）1，1.5，-0.5；（2）2；（3）y x =；（4）112p x =- 【分析】（1）由题意根据线段中点的求法列式计算即可求出x =1时的销售收入和销售成本，根据盈利的求法计算即可得解；（2）由题意直接根据图象找出两直线的交点的横坐标即可；（3）根据题意设l 1对应的函数表达式为y =kx （k ≠0），然后利用待定系数法求一次函数解析式即可；（4）由题意结合l 1和l 2的解析式，设利润为p 然后根据利润=销售收入-销售成本列式表示即可． 【详解】解：（1）x =1时，销售收入= 212=（万元）， 销售成本=121.52+=（万元）， 盈利（收入-成本）= 310.52-=-（万元）； 故答案为：1，1.5，-0.5；（2）由图像可知一天销售2件时，销售收入等于销售成本； 故答案为：2；（3）设l 1对应的函数表达式为：y =kx ，则2=2k ，解得：k =1， 故l 1对应的函数表达式为：y =x ， 故答案为：y =x ；（4）∵l 1的表达式为y =x ，设l 2的表达式为y =kx +b （k ≠0），代入（0①1），（2①2）可得1,12k b ==， ∴l 2的表达式为112y x =+， 设利润为p ，∴利润p =11(1)122x x x -+=-，所以利润与销售量间的函数表达式为：112p x =-. 【点睛】本题考查一次函数的应用，考查了识别函数图象的能力以及利用待定系数法求一次函数解析式，准确观察图象提供的信息是解题的关键．2．（1）达州市第一中学工会采购香米400袋．（2）w 518000m =+（800≤m ＜1000），达州市第一中学工会能实现扶贫目标． 【分析】（1）设达州市第一中学工会采购香米x 袋，利用总利润为等量关系构建方程即可； （2）根据香米每袋利润×袋数+土豆每袋利润×袋数构建一次函数，利用一次函数的性质即可解决问题； 【详解】解：（1）设达州市第一中学工会采购香米x 袋． 由题意列方程得()()()80606045100017000x x -+--=，解得400x =，答：达州市第一中学工会采购香米400袋． （2）由题意得：()20151200w m m =+-，518000m =+（800≤m ①1000），∵800m ≥，且w 随m 的增大而增大，∴800m =时，5800180002200020000w =⨯+=>， 当m =1000时，510001800023000w =⨯+=， 2200023000w ≤＜，∴达州市第一中学工会能实现扶贫目标． 【点睛】本题考查一次函数的应用、一元一次方程的应用等知识，解题的关键是理解题意，正确寻找等量关系解决问题．3．（1）y =-5x +3000；（2）购进A 水产品50kg 、B 种150kg 时，利润最大是2750元 【分析】（1）设购进A 种水产品x 千克，则购进B 种水产品（200-x ）千克，根据等量关系表示出函数解析式即可；（2）由题意得：2003x x -≤，解得：50x ≥，即50200x ≤<，根据53000y x =-+的性质得y 随x 的增大而减小，则当50x =时，销售利润最大，把50x =代入53000y x =-+即可得．【详解】解：（1）设购进A 种水产品x 千克，则购进B 种水产品（200-x ）千克，1015(200)y x x =+-10300015y x x =+-即53000y x =-+，则y 与x 之间的函数关系式为：53000y x =-+；（2）由题意得：2003x x -≤，4200x ≥解得：50x ≥，∴50200x ≤<，∵53000y x =-+，50-<，∴y 随x 的增大而减小，∴当50x =时，销售利润最大，55030002750y =-⨯+=，200-50=150（千克），故购进A 种水产品50千克，购进B 种水产品150千克，销售总利润最大，总利润的最大值为2750元．【点睛】本题考查了一次函数的应用，解题的关键是根据题意找出等量关系表示出函数解析式．4．（1）600(25)40800(510)x y x x <≤⎧=⎨-+<≤⎩；（2）当销售单价x 为10元时，每天的销售利润最大，最大利润是3200元．【分析】1）运用待定系数法计算即可；（2）列出二次函数解析式，计算最值即可．【详解】（1）当25x <≤时，600y =；当510x <≤时，设(0)y kx b k =+≠，把(5,600)，(10,400)代入得：560010400k b k b +=⎧⎨+=⎩，解得40800k b =-⎧⎨=⎩，40800y x ∴=-+，综上，y 与x 之间的函数关系式为：600(25)40800(510)x y x x <≤⎧=⎨-+<≤⎩（2）设每天的销售利润为w 元，当25x <≤时，600(2)6001200w x x =-=-，6000> w 随x 的增大而增大∴当5x =时，600512001800w =⨯-=最大（元）当510x <≤时，(40800)(2)w x x =-+-2240880160040(11)3240x x x =-+-=--+400-<抛物线开口向下对称轴为直线11x =，∴当11x <时，w 随x 的增大而增大510x <≤ ∴当10x =时，40132403200w =-⨯+=最大（元）32001800> 10x ∴=时，w 最大答：当销售单价x 为10元时，每天的销售利润最大，最大利润是3200元．【点睛】本题考查了二次函数的最值，一次函数的解析式，熟练掌握待定系数法，灵活运用二次函数的最值是解题的关键．5．（1）y =200x +12000；（2）该经销商有三种购进电脑的方案可供选择；（3）当进A 型电脑22台，B 型电脑8台时获利最大，利润为16400元【分析】（1）根据利润的计算公式，先求出A 型电脑每台的利润为：（4800-4200）元，B 型电脑每台的利润为（4000-3600)元，购进A 型电脑x 台，则购进B 型电脑为()30x -台，即可得出y 与x 的函数关系；（2）根据题意列出相应不等式组，求解，然后依据电脑台数为整数即可确定有几种方案；（3）根据（1）中一次函数性质，可得当x 取最大值22时，获利最大，代入即可求出最大利润．【详解】解（1）根据题意：购进A 型电脑x 台，则购进B 型电脑为()30x -台，A 型电脑每台的利润为：（4800-4200）元，B 型电脑每台的利润为（4000-3600)元，依据题意可得：y 与x 的函数关系式为：()()()480042004000360030?20012000y x x x =-+--=+， 即为：20012000y x =+；(2)由题意得：200120001600042003600(30)121200x x x +≥⎧⎨+-≤⎩解得2022x ≤≤，∵x 为整数 ，∴x 取20、21或22，即该经销商有三种购进电脑的方案可供选择；（3）由（1)知：20012000y x =+，∵2000>，∴y 随x 的增大而增大，即当x 取最大值22， 308x -=时，y 有最大值，y 最大=200×22+12000=16400（元）∴当进A 型电脑22台，B 型电脑8台时获利最大，利润为16400元．【点睛】题目主要考查一次函数的应用、不等式的应用，理解题意列出相应方程时解题关键． 6．（1）A 种运动鞋的进价为100元/双，B 种运动鞋的进价是80元/双；（2）①W =50m +20000；②要使该专卖店获得最大利润，此时应购进A 种运动鞋105双，购进B 种运动鞋95双【分析】（1）设B 种运动鞋的进价x 元，根据等量关系：用3200元购进A 种运动鞋的数量=用2560元购进B 种运动鞋的数量，列出分式方程并解分式方程即可；（2）①根据总利润=A 种运动鞋的利润+B 种运动鞋的利润，即可列出W 关于m 的函数关系式；②根据W 与m 的函数关系式及m 的取值范围，可确定W 的最大值．【详解】（1）设B 种运动鞋的进价x 元，则A 种运动鞋的进价(20)x +元，则3200256020x x=+ 解得：80x = 经检验80x =是原分式方程的解，且符合题意．①208020100x+=+=故A种运动鞋的进价为100元/双，B种运动鞋的进价是80元/双．（2）①W=（250-100）m+（180-80）（200-m）=50m+20000即总利润W元关于m的函数关系式为W=50m+20000②∵W=50m+20000①50＞0，W随m的增大而增大又①90≤m≤105①当m=105时，W取得最大值，200-m=95故要使该专卖店获得最大利润，此时应购进A种运动鞋105双，购进B种运动鞋95双．【点睛】本题考查了分式方程与一次函数的实际应用，对于分式方程的应用，关键是理解题意，找到相等关系并列出方程；对于一次函数的应用，关键是掌握它的性质．注意解分式方程要检验．7．（1）a=30，y=24x+240；（2）甲水果应购进30克，乙水果购进50克时，才能使经销商付款总金额w最少．【分析】（1）先根据图象求出a的值，再根据一次购买超过40千克，超过部分的价格打八折写出函数关系式；（2）先根据甲种水果不少于30千克，但又不超过50千克求出x的取值范围，在分30≤x≤40和40＜x≤50两种情况写出函数解析式，再根据函数的性质求最值．【详解】解：（1）由图象知：a=1200÷40=30（元），当x＞40时，y=30×40+（x-40）×30×80%=24x+240，∴当x＞40时，y与x之间的函数关系式为y=24x+240，a的值为30；（2）由题意，得：30≤x≤50，①当30≤x≤40时，w=30x+25（80-x）=5x+2000，∵5＞0，∴w随x的增大而增大，∴当x=30时，w最小，最小值=5×30+2000=2150（元）；②当40＜x≤50时，w=24x+240+25（80-x）=-x+2240，∵-1＜0，∴w 随x 的增大而减小，∴当x =50时，w 最小，最小值=-50+2240=2190（元），∵2150＜2190，∴x =30，∴甲水果应购进30克，乙水果购进50克时，才能使经销商付款总金额w 最少．【点睛】本题考查了一次函数的应用，关键是根据x 的取值确定函数解析式．8．（1）40(020)150(2064)2x x y x x x <≤⎧⎪=⎨-+<≤⎪⎩且为正整数且为正整数；（2）当32x ＝时，获利最大，最大利润是512元．【分析】（1）当0＜x ≤20且x 为整数时，y ＝40；当x ＞20时，设y ＝kx +b ，由待定系数法求得函数解析式；（2）设所获利润为w （元），分两种情况：①当0＜x ≤20且x 为整数时，②当20＜x ≤64且x 为整数时，分别得出w 的表达式，并分别得出w 的最大值，然后两者比较即可得出答案．【详解】解：（1）当020x <≤且x 为整数时，40y ＝；当20x >时，设y kx b +＝，代入(20,40)和(50,25)得：20405025k b k b +=⎧⎨+=⎩，解得1250k b ⎧=-⎪⎨⎪=⎩． ∴1502y x =-+． 当18y ＝时，代入1502y x =-+，得64x ＝． ∴2064x <≤且x 为整数，综上所述，y 与x 之间所满足的函数关系式为40(020)150(2064)2x x y x x x <≤⎧⎪=⎨-+<≤⎪⎩且为正整数且为正整数． （2）设所获利润为w （元），当020x <≤且x 为整数时，y ＝40，∴(4018)22w x x ==﹣．∵22＞0，∴w 随着x 的增大而增大，则当x ＝20时，w 有最大值，最大值为440；当2064x <≤且x 为整数时，1502y x =-+， ∴22111(5018)32(32)512222w x x x x x =-+-=-+=--+， ∵102-<， ∴当x ＝32时，w 最大，最大值为512元．∵512440>，∴当x ＝32时，获利最大，最大利润是512元．【点睛】本题主要考查了一次函数与二次函数实际应用问题中的销售问题，利用二次函数的性质求得最值以及数形结合思想是解题的关键．9．（1）甲品牌洗衣液进价为30元/瓶，乙品牌洗衣液进价为24元/瓶；（2）购进甲品牌洗衣液40瓶，乙品牌洗衣液80瓶时所获利润最大，最大利润是560元【分析】（1）设甲品牌洗衣液每瓶的进价是x 元，则乙品牌洗衣液每瓶的进价是（x -6）元，根据数量=总价÷单价，结合用1800元购进乙品牌洗衣液数量的45，即可得出关于x 的分式方程，解之经检验后即可得出结论；（2）设可以购买m 瓶乙品牌洗手液，则可以购买（100-m ）瓶甲品牌洗手液，根据总价=单价×数量，结合总费用不超过1645元，即可得出关于m 的一元一次不等式，解之即可得出m 的取值范围，再取其中的最大整数值即可得出结论．【详解】解：（1）设甲品牌洗衣液进价为x 元/瓶，则乙品牌洗衣液进价为()6x -元/瓶， 由题意可得，180********x x =⋅-， 解得30x =，经检验30x =是原方程的解.答：甲品牌洗衣液进价为30元/瓶，乙品牌洗衣液进价为24元/瓶.（2）设利润为y 元，购进甲品牌洗衣液m 瓶，则购进乙品牌洗衣液()120m -瓶，由题意可得，()30241203120m m +-≤，解得40m ≤，由题意可得，()()()363028*********y m m m =-+--=+，∵20k =>，∴y 随m 的增大而增大，∴当40m =时，y 取最大值，240480560y =⨯+=最大值.答：购进甲品牌洗衣液40瓶，乙品牌洗衣液80瓶时所获利润最大，最大利润是560元①【点睛】本题考查分式方程的应用，一次函数的应用，一元一次不等式的应用，解题的关键是灵活运用所学知识解决问题．10．（1）140y x =-+，自变量x 的取值范围是60120x ≤≤；（2）这一天销售兰花获得的利润的最大值为1400元．【分析】（1）根据函数图象和图象中的数据，可知该函数为一次函数，过点（80，60），（110，30），然后代入函数解析式，即可得到y 与x 之间的函数关系式，再根据每盆兰花的销售价格不低于成本价，又不高于成本价的2倍．即可得到x 的取值范围；（2）根据题意，可以得到w 与x 的函数关系式，将函数关系式化为顶点式，即可得到这一天销售兰花获得的利润w （元）的最大值．【详解】解：（1）设y 与x 之间的函数关系式为(0)y kx b k =+≠，把（80，60）和（110，30）代入，得806011030k b k b +=⎧⎨+=⎩， 解得1140k b =-⎧⎨=⎩； ∴y 与x 之间的函数关系式为140y x =-+，①每盆兰花的销售价格不低于成本价，又不高于成本价的2倍．①60≤x ≤120，由上可得，y 与x 之间的函数关系式为140y x =-+(60120)x ≤≤；（2）根据题意，得6010()(0)402w x x =--+-22008600x x =-+-21001400()x =--+；∵10-<∴当100x =时，w 有最大值，为1400．答：这一天销售兰花获得的利润的最大值为1400元．【点睛】本题考查二次函数的应用、待定系数法求一次函数解析式，解答本题的关键是明确题意，求出一次函数解析式，利用二次函数的性质求出w 的最大值．11．（1）221202250(140)1108250(4070)x x x y x x ⎧-++≤<=⎨-+≤≤⎩；（2）第30天时，当天销售利润最大，最大利润是4050元；（3）共有36天每天销售利润不低于3250元【分析】（1）根据总利润=(售价-进价)×数量，列式整理即可；（2）结合二次函数和一次函数的性质，分别求解在各自变量范围内的最值，从而对比即可得出结论；（3）分别利用两个范围内的函数解析式建立方程或不等式，并结合自变量的取值范围求解即可．【详解】解：（1）当140x ≤<时，()()45301502y x x =+--⎡⎤⎣⎦，整理得：221202250y x x =-++；当4070x ≤≤时，()()85301502y x =--，整理得：1108250y x =-+；∴221202250(140)1108250(4070)x x x y x x ⎧-++≤<=⎨-+≤≤⎩； （2）对于函数221202250y x x =-++，整理可得：()22304050y x =--+，∵20-<，∴当30x =时，y 取得最大值，最大值为4050；对于函数1108250y x =-+，∵1100-<，∴y 随x 的增大而减小，∵4070x ≤≤，∴当40x =时，y 取得最大值，最大值为3850，∵4050＞3850，∴第30天时，当天销售利润最大，最大利润是4050元；（3）当140x ≤<时，由题意，2212022503250x x -++=，解得：10x =或50x =，由（2）中，二次函数的性质可得：当1040x ≤<时，每天销售利润不低于3250元，共有30天；当4070x ≤≤时，由题意，11082503250x -+≥， 解得：54511x ≤， ∴当4045x ≤≤时，每天销售利润不低于3250元，共有6天；∴30+6=36(天)，∴共有36天每天销售利润不低于3250元．【点睛】本题考查二次函数与一次函数的综合实际应用，理解二次函数和一次函数的基本性质，准确建立不等式并分类讨论是解题关键．12．（1）甲种盲盒的进货单价为64元，则乙种盲盒的进货单价为62元；（2）①w =1230+3a ；①购进甲种盲盒33个，则购进乙种盲盒17个，最大利润是1329元．【分析】（1）设甲种盲盒的进货单价为x 元，则乙种盲盒的进货单价为（x -2）元，根据题意即可列出一元一次方程，即可求解；（2）①设购进甲种盲盒a 个，则购进乙种盲盒（50- a ）个，根据题意得到a 的取值，再列出w 关于a 的一次函数；①根据一次函数的性质即可求解．【详解】解：（1）设甲种盲盒的进货单价为x 元，则乙种盲盒的进货单价为（x -2）元，根据题意得10x +15(x -2)=1570解得x =64，∴甲种盲盒的进货单价为64元，则乙种盲盒的进货单价为62元．（2）①设购进甲种盲盒a 个，则购进乙种盲盒（50-a ）个，依题意可得()2500a a a ⎧≤-⎨≥⎩解得10003a ≤≤ ∴w =(83-64)(10+a )+（78-62）（50-a +15）=1230+3a①①w =1230+3a ，故w 随a 的增大而增大故当a =33时，50-a ＝17．w 最大=1230+3×33=1329（元）．∴第二批进货方案为：购进甲种盲盒33个，购进乙种盲盒17个．售完第二批盲盒最多获得总利润1329元．【点睛】此题主要考查一元一次方程、一次函数以及不等式组的应用，解题的关键是根据题意找到数量关系列方程或函数进行求解．13．（1）甲种衬衫每件进价100元，乙种衬衫每件进价90元；（2）共有11种进货方案；（3）当6070a <<时，应购进甲种衬衫110件，乙种衬衫190件；当70a =时，所有方案获利都一样；当7080a <<时，购进甲种衬衫100件，乙种衬衫200件．【分析】（1）依据用3000元购进甲种衬衫的数量与用2700元购进乙种衬衫的数量相同列方程解答； （2）根据题意列不等式组解答；（3）设总利润为w ，表示出w 与x 的函数解析式，再分三种情况：①当6070a <<时，②当70a =时，③当7080a <<时，分别求出利润的最大值即可得到答案．【详解】解：（1）依题意得：3000270010m m =-，整理，得：3000(10)2700m m -=，解得：100m =，经检验，100m =是原方程的根，答：甲种衬衫每件进价100元，乙种衬衫每件进价90元；（2）设购进甲种衬衫x 件，乙种衬衫(300)x -件，根据题意得：(260100)(18090)(300)34000(260100)(18090)(300)34700x x x x -+--⎧⎨-+--⎩， 解得：100110x ， x 为整数，110100111-+=，答：共有11种进货方案；（3）设总利润为w ，则(260100)(18090)(300)(70)27000(100110)w a x x a x x =--+--=-+，①当6070a <<时，700a ->，w 随x 的增大而增大，∴当110x =时，w 最大，此时应购进甲种衬衫110件，乙种衬衫190件；②当70a =时，700a -=，27000w =，（2）中所有方案获利都一样；③当7080a <<时，700a -<，w 随x 的增大而减小，∴当100x =时，w 最大，此时应购进甲种衬衫100件，乙种衬衫200件．综上：当6070a <<时，应购进甲种衬衫110件，乙种衬衫190件；当70a =时，（2）中所有方案获利都一样；当7080a <<时，购进甲种衬衫100件，乙种衬衫200件．【点睛】此题考查分式方程的实际应用，不等式组的实际应用，一次函数的性质，正确理解题意熟练应用各知识点解决问题是解题的关键．14．（1）y ＝﹣5x +380；（2）56元．【分析】（1）设y 与x 的函数解析式为y ＝kx +b （k ≠0），根据表格中的数据，利用待定系数法即可求出y 与x 的函数解析式；（2）利用该超市每天销售水蜜桃获得的利润＝每箱的利润×每天的销售量，即可得出关于。

初⼆数学第⼀章全等三⾓形证明经典例题（含答案）初⼆数学全等三⾓形证明经典例题1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD第1题图第2题图第3题图2、已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠23、已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC第4题图第5题图第6题图4、已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠C5、已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE6、已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD7、已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠C第7题图第8题图第9题图8、如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。

求证：BC=AB+DC 。

9、已知：AB=CD ，∠A=∠D ，求证：∠B=∠C第10题图第11题图第12题图10、P 是∠BAC 平分线AD 上⼀点，AC>AB ，求证：PC-PB11、已知∠ABC=3∠C ，∠1=∠2，BE ⊥AE ，求证：AC-AB=2BEF A E D C B PD A CB C D B AD B C B A C D F 2 1E ABC D E F 21 AD B CA B C D A12、已知，E 是AB 中点，AF=BD ，BD=5，AC=7，求DC第13题图第14题图第15题图第16题图13、如图，在△ABC 中，BD =DC ，∠1=∠2，求证：AD ⊥BC ．14、．如图，OM 平分∠POQ ，MA ⊥OP ,MB ⊥OQ ，A 、B 为垂⾜，AB 交OM 于点N ．求证：∠OAB =∠OBA15、如图，已知AD ∥BC ，∠PAB 的平分线与∠CBA 的平分线相交于E ，CE 的连线交AP 于D ．求证：AD +BC =AB ．16．已知：如图，DC ∥AB ，且DC =AE ，E 为AB 的中点，（1）求证：△AED ≌△EBC ．（2）在不添辅助线的情况下，除△EBC 外，请再写出两个与△AED 的⾯积相等的三⾓形．（直接写出结果，不要求证明）：17．如图，△ABC 中，∠BAC =90度，AB =AC ，BD 是∠ABC 的平分线，BD 的延长线垂直于过C 点的直线于E ，直线CE 交BA 的延长线于F ．求证：BD =2CE ．第17题图第18题图第19题图第20题图18、如图：DF=CE ，AD=BC ，∠D=∠C 。

北京喇叭沟门满族中学数学全等三角形单元测试与练习（word解析版）一、八年级数学轴对称三角形填空题（难）1．我们知道，经过三角形一顶点和此顶点所对边上的任意一点的直线，均能把三角形分割成两个三角形（1）如图，在ABC∆中，25,105A ABC∠=︒∠=︒，过B作一直线交AC于D，若BD 把ABC∆分割成两个等腰三角形，则BDA∠的度数是______．（2）已知在ABC∆中，AB AC=，过顶点和顶点对边上一点的直线，把ABC∆分割成两个等腰三角形，则A∠的最小度数为________．【答案】130︒1807︒⎛⎫⎪⎝⎭【解析】【分析】（1）由题意得：DA=DB，结合25A∠=︒，即可得到答案；（2）根据题意，分4种情况讨论，①当BD=AD，CD=AD，②当AD=BD，AC=CD，③AB=AC，当AD=BD=BC，④当AD=BD，CD=BC，分别求出A∠的度数，即可得到答案．【详解】（1）由题意得：当DA=BA，BD=BA时，不符合题意，当DA=DB时，则∠ABD=∠A=25°，∴∠BDA=180°-25°×2=130°．故答案为：130°；（2）①如图1，∵AB=AC，当BD=AD，CD=AD，∴∠B=∠C=∠BAD=∠CAD，∵∠BAC+∠B+∠C=180°，∴4∠B=180°，∴∠BAC=90°．②如图2，∵AB=AC，当AD=BD，AC=CD，∴∠B=∠C=∠BAD，∠CAD=∠CDA，∵∠CDA=∠B+∠BAD=2∠B，∴∠BAC=3∠B，∵∠BAC+∠B+∠C=180°，∴5∠B=180°，∴∠B=36°，∴∠BAC=108°．③如图3，∵AB=AC，当AD=BD=BC，∴∠ABC=∠C，∠BAC=∠ABD，∠BDC=∠C，∵∠BDC=∠A+∠ABD=2∠BAC，∴∠ABC=∠C=2∠BAC，∵∠BAC+∠ABC+∠C=180°，∴5∠BAC=180°，∴∠BAC=36°．④如图4，∵AB=AC，当AD=BD，CD=BC，∴∠ABC=∠C，∠BAC=∠ABD，∠CDB=∠CBD，∵∠BDC=∠BAC+∠ABD=2∠BAC，∴∠ABC=∠C=3∠BAC，∵∠BAC+∠ABC+∠C=180°，∴7∠BAC=180°，∴∠BAC=180 ()7︒．综上所述，∠A的最小度数为：180 ()7︒．故答案是：180 ()7︒．【点睛】本题主要考查等腰三角形的性质定理以及三角形内角和定理与外角的性质，根据等腰三角形的性质，分类讨论，是解题的关键．2．已知A、B两点的坐标分别为（0，3），（2，0），以线段AB为直角边，在第一象限内作等腰直角三角形ABC，使∠BAC＝90°，如果在第二象限内有一点P（a，12），且△ABP和△ABC的面积相等，则a＝_____．【答案】-83．【解析】【分析】先根据AB两点的坐标求出OA、OB的值，再由勾股定理求出AB的长度，根据三角形的面积公式即可得出△ABC的面积；连接OP，过点P作PE⊥x轴，由△ABP的面积与△ABC的面积相等，可知S△ABP＝S△POA+S△AOB﹣S△BOP＝132，故可得出a的值．【详解】∵A、B两点的坐标分别为（0，3），（2，0），∴OA＝3，OB＝2，∴223+213AB＝＝，∵△ABC是等腰直角三角形，∠BAC＝90°，∴1113•1313222 ABCS AB AC⨯⨯＝＝＝，作PE⊥x轴于E，连接OP，此时BE＝2﹣a，∵△ABP的面积与△ABC的面积相等，∴111•••222 ABP POA AOB BOPS S S S OA OE OB OA OB PE ++＝﹣＝﹣，111113332222222a⨯⨯+⨯⨯⨯⨯＝（﹣）﹣＝，解得a＝﹣83．故答案为﹣83．【点睛】本题考查等腰直角三角形的性质，坐标与图象性质，三角形的面积公式，解题的关键是根据S△ABP=S△POA+S△AOB-S△BOP列出关于a的方程．3．在平面直角坐标系xOy中，已知点A（2，3），在x轴上找一点P，使得△AOP是等腰三角形，则这样的点P共有_____个．【答案】4【解析】【分析】以O为圆心，OA为半径画弧交x轴于点P1、P3，以A为圆心，AO为半径画弧交x轴于点P4，作OA的垂直平分线交x轴于P2．【详解】解：如图，使△AOP是等腰三角形的点P有4个．故答案为4．【点睛】本题考查了在平面直角坐标系中寻找等腰三角形，掌握两圆一线找等腰三角形是解题的关键．4．如图，已知△ABC和△ADE都是正三角形，连接CE、BD、AF，BF=4,CF=7,求AF的长_________ .【答案】3【解析】【分析】过点A作AF⊥CE交于I，AG⊥BD交于J,证明CAE≅BAD，再证明CAI≅BAJ，求出°7830∠=∠=，然后求出12IF FJ AF==，，通过设FJ x=求出x，即可求出AF的长.【详解】解：过点A作AF⊥CE交于I，AG⊥BD交于J在CAE和BAD中AC ABCAE BADAE AD=⎧⎪∠=∠⎨⎪=⎩∴CAE≅BAD∴ICA ABJ∠=∠∴BFE CAB∠=∠（8字形）∴°120CFD∠=在CAI和BAJ中°90ICA ABJCAI BJACA BA∠=∠⎧⎪∠=∠=⎨⎪=⎩∴CAI≅BAJ,AI AJ CI BJ==∴°60CFA AFJ∠=∠=∴°30FAI FAE∠=∠=在RtAIF 和RtAJF 中°30FAI FAE ∠=∠=∴12IF FJ AF ==设FJ x = 7,4CF BF ==则47x x +=-32x ∴=2AF FJ =AF ∴=3【点睛】此题主要考查了通过做辅助线证明三角形全等，得出相关的边相等，学会合理添加辅助线求解是解决本题的重点.5．如图，在01A BA △中，20B ∠=︒，01A B A B =，在1A B 上取点C ，延长01A A 到2A ，使得121A A AC =；在2A C 上取一点D ，延长12A A 到3A ，使得232A A A D =；…，按此做法进行下去，第n 个等腰三角形的底角n A ∠的度数为__________．【答案】11()802n -︒⋅.【解析】【分析】先根据等腰三角形的性质求出∠BA 1 A 0的度数，再根据三角形外角的性质及等腰三角形的性质分别求出∠CA 2A 1，∠DA 3A 2及∠EA 4A 3的度数，找出规律即可得出第n 个等腰三角形的底角∠A n 的度数．【详解】解：∵在△A 0BA 1中，∠B=20°，A 0B=A 1B ，∴∠BA 1 A 0= 1801802022B ︒︒︒-∠-= =80°， ∵A 1A 2=A 1C ，∠BA 1 A 0是△A 1A 2C 的外角，∴∠CA 2A 1= 108022BA A ︒∠= =40°； 同理可得，∠DA 3A 2=20°，∠EA 4A 3=10°，∴第n 个等腰三角形的底角∠A n = 11()802n -︒⋅.【点睛】本题考查的是等腰三角形的性质及三角形外角的性质，根据题意得出∠CA 2A 1，∠DA 3A 2及∠EA 4A 3的度数，找出规律是解答此题的关键．6．如图，∠MON ＝30°，点A 1、A 2、A 3…在射线ON 上，点B 1、B 2，B 3…在射线OM 上，△A 1B 1A 2，△A 2B 2A 3，△A 3B 3A 4…均为等边三角形，从左起第1个等边三角形的边长记a 1，第2个等边三角形的边长记为a 2，以此类推，若OA 1＝3，则a 2=_______，a 2019=_______.【答案】6； 3×22018.【解析】【分析】根据等腰三角形的性质以及平行线的性质得出A 1B 1∥A 2B 2∥A 3B 3，以及a 2=2a 1=6，得出a 3=4a 1，a 4=8a 1，a 5=16a 1…进而得出答案．【详解】解： 如图，∵△A 1B 1A 2是等边三角形，∴A 1B 1=A 2B 1，∠3=∠4=∠12=60°，∴∠2=120°，∵∠MON=30°，∴∠1=180°-120°-30°=30°，又∵∠3=60°，∴∠5=180°-60°-30°=90°，∵∠MON=∠1=30°，∴OA 1=A 1B 1=3，∴A 2B 1=3，∵△A 2B 2A 3、△A 3B 3A 4是等边三角形，∴∠11=∠10=60°，∠13=60°，∵∠4=∠12=60°，∴A 1B 1∥A 2B 2∥A 3B 3，B 1A 2∥B 2A 3，∴∠1=∠6=∠7=30°，∠5=∠8=90°，∴a 2=2a 1=6，a 3=4a 1，a 4=8a 1，a 5=16a 1，以此类推：a 2019=22018a 1=3×22018故答案是：6；3×22018．【点睛】此题主要考查了等边三角形的性质以及等腰三角形的性质，根据已知得出a 2=2a 1=6，a 3=4a 1，a 4=8a 1，a 5=16a 1…进而发现规律是解题关键．7．如图，在ABC ∆中，ABC ∠和ACB ∠的平分线相交于点O ，过点O 作//EF BC 交AB 于E ，交AC 于F ，过点O 作OD AC ⊥于D 下列结论：①EF BE CF =+；②点O 到ABC ∆各边的距离相等；③1902BOC A ∠=+∠；④设OD m =，AE AF n +=，则AEF S mn ∆=；⑤1()2AD AB AC BC =+-.其中正确的结论是.__________．【答案】①②③⑤【解析】【分析】由在△ABC中，∠ABC和∠ACB的平分线相交于点O，根据角平分线的定义与三角形内角和定理，即可求得③∠BOC=90°+12∠A正确；由平行线的性质和角平分线的定义得出△BEO和△CFO是等腰三角形得出EF=BE+CF故①正确；由角平分线的性质得出点O到△ABC各边的距离相等，故②正确；由角平分线定理与三角形面积的求解方法，即可求得④设OD=m，AE+AF=n，则S△AEF=12mn，故④错误，根据HL证明△AMO≌△ADO得到AM=AD，同理可证BM=BN，CD=CN，变形即可得到⑤正确．【详解】∵在△ABC中，∠ABC和∠ACB的平分线相交于点O，∴∠OBC=12∠ABC，∠OCB=12∠ACB，∠A+∠ABC+∠ACB=180°，∴∠OBC+∠OCB=90°﹣12∠A，∴∠BOC=180°﹣（∠OBC+∠OCB）=90°+12∠A；故③正确；∵在△ABC中，∠ABC和∠ACB的平分线相交于点O，∴∠OBC=∠OBE，∠OCB=∠OCF．∵EF∥BC，∴∠OBC=∠EOB，∠OCB=∠FOC，∴∠EOB=∠OBE，∠FOC=∠OCF，∴BE=OE，CF=OF，∴EF=OE+OF=BE+CF，故①正确；过点O作OM⊥AB于M，作ON⊥BC于N，连接OA．∵在△ABC中，∠ABC和∠ACB的平分线相交于点O，∴ON=OD=OM=m，∴S△AEF=S△AOE+S△AOF=12AE•OM+12AF•OD=12OD•（AE+AF）=12mn；故④错误；∵在△ABC中，∠ABC和∠ACB的平分线相交于点O，∴点O到△ABC各边的距离相等，故②正确；∵AO=AO，MO=DO，∴△AMO≌△ADO（HL），∴AM=AD；同理可证：BM=BN，CD=CN．∵AM+BM=AB，AD+CD=AC，BN+CN=BC，∴AD=12（AB+AC﹣BC）故⑤正确．故答案为：①②③⑤．【点睛】本题考查了角平分线的定义与性质，等腰三角形的判定与性质．此题难度适中，解题的关键是注意数形结合思想的应用．8．如图，已知每个小方格的边长为1，A 、B 两点都在小方格的格点（顶点）上，请在图中找一个格点C ，使△ABC 是等腰三角形，这样的格点C 有________个。