最新初中数学毕业试题
- 格式:doc
- 大小:470.00 KB
- 文档页数:8

初中数学毕业试题及答案一、选择题(每题3分,共30分)1. 下列哪个数是无理数?A. 2.0B. πC. 0.33333...D. √42. 一个数的相反数是它自己,这个数是:A. 0B. 1C. -1D. 23. 一个数的倒数是它自己,这个数是:A. 0B. 1C. -1D. 24. 如果a和b是两个实数,且a > b,那么下列哪个不等式一定成立?A. a + 1 > b + 1B. a - 1 > b - 1C. 2a > 2bD. a/b > b/a5. 一个等腰三角形的两边长分别为5和8,那么这个三角形的周长是:A. 18C. 23D. 266. 一个二次方程ax^2 + bx + c = 0(a ≠ 0)的判别式Δ = b^2 - 4ac,当Δ > 0时,方程的根的情况是:A. 无实数根B. 有两个不相等的实数根C. 有两个相等的实数根D. 无法确定7. 一个圆的半径是5,那么它的面积是:A. 25πB. 50πC. 100πD. 125π8. 一个正方体的体积是8立方厘米,那么它的棱长是:A. 2厘米B. 4厘米C. 8厘米D. 16厘米9. 一个函数y = 2x + 3的图象是一条直线,这条直线的斜率是:A. 2B. 3C. -2D. -310. 一个函数y = x^2 - 4x + 4的最小值是:A. 0C. 8D. 16二、填空题(每题3分,共15分)11. 一个数的绝对值是5,这个数可以是______。
12. 一个数的平方是9,这个数可以是______。
13. 一个数的立方是-8,这个数是______。
14. 一个角的补角是120°,这个角是______。
15. 一个角的余角是30°,这个角是______。
三、解答题(每题5分,共55分)16. 计算:(3x - 2)(x + 1) = 0,求x的值。
17. 计算:(2x + 3)(2x - 3) = 0,求x的值。

初中数学毕业试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是最小的正整数?A. 0B. 1C. -1D. 22. 如果一个数的60%是120,那么这个数是多少?A. 180B. 192C. 200D. 2203. 一个长方形的长是14cm,宽是10cm,那么它的周长是多少?A. 34cmB. 42cmC. 28cmD. 56cm4. 下列哪个数是质数?A. 2B. 9C. 15D. 165. 一个数的75%加上它的25%等于这个数的多少?A. 75%B. 100%C. 125%D. 200%6. 一本书的价格是35元,如果打8折,那么折扣后的价格是多少?A. 28元B. 30元C. 42元D. 56元7. 一个数的1/3加上它的2/3等于多少?A. 1B. 2/3C. 5/3D. 1/38. 下列哪个选项表示的是负数?A. -5B. 5C. 0D. 39. 一个班级有40名学生,其中3/4是男生,那么女生有多少人?A. 10B. 12C. 15D. 2010. 一个数的2倍减去它的一半等于这个数的多少?A. 3/2倍B. 1/2倍C. 1倍D. 2倍二、填空题(每题4分,共20分)11. 圆的周长公式是__________。
12. 一个数的1/2与它的1/3的差是这个数的__________。
13. 一本书的原价是50元,如果打7折,那么折扣后的价格是__________元。
14. 一个长方体的体积公式是__________。
15. 一个数的1/4加上3/4等于__________。
三、解答题(共50分)16. (10分)小明和小红合作完成一项工作,小明单独完成需要4小时,小红单独完成需要6小时。
现在他们合作,共同完成这项工作需要多少时间?17. (15分)一个长方体的长是15cm,宽是8cm,高是10cm。
求这个长方体的表面积和体积。
18. (15分)某商店购进一批玩具,每个进价是20元,标价是30元。

初中毕业数学试题及答案一、选择题(每题3分,共30分)1. 下列哪个数是无理数?A. 0.33333…B. √2C. 4D. π答案:B2. 一个等腰三角形的底边长为6,高为4,其周长是多少?A. 16B. 14C. 18D. 20答案:C3. 函数y=2x+3的图象与x轴的交点坐标是?A. (0,3)B. (-3/2,0)C. (3/2,0)D. (0,-3)答案:B4. 一个数的相反数是-5,这个数是?A. 5C. 0D. 1答案:A5. 若a=2b,且b=3,则a的值是多少?A. 6B. 3C. 2D. 1答案:A6. 一个圆的半径是5,那么它的面积是多少?A. 25πB. 50πC. 75πD. 100π答案:B7. 一个长方体的长、宽、高分别是4、3、2,那么它的体积是多少?A. 24B. 36C. 48D. 60答案:A8. 一个数的绝对值是5,这个数可能是?B. -5C. 5或-5D. 0答案:C9. 一个数的平方根是3,这个数是?A. 9B. -9C. 3D. -3答案:A10. 一个等差数列的首项是2,公差是3,那么第5项是多少?A. 17B. 14C. 11D. 8答案:A二、填空题(每题3分,共30分)1. 一个等腰三角形的两个底角相等,如果一个底角是40°,那么顶角是____。
答案:100°2. 一个数的立方根是2,那么这个数是____。
答案:83. 一个数的平方是16,那么这个数是____。
答案:±44. 函数y=x^2-4x+4的最小值是____。
答案:05. 一个圆的直径是10,那么它的周长是____。
答案:31.46. 一个长方体的体积是60,长和宽都是3,那么高是____。
答案:6.67(保留两位小数)7. 一个等差数列的首项是1,公差是2,那么第10项是____。
答案:198. 一个数的绝对值是7,那么这个数是____。
答案:±79. 一个数的倒数是2,那么这个数是____。

江苏省苏州市初中毕业暨升学考试试卷数学一、选择题:本大题共10小题,每小题3分,共30分 1.12()2⨯-的结果是A .-4B .-1C .14-D .32【答案】B 。
【考点】有理数乘法。
【分析】利用有理数运算法则,直接得出结果数。
2.△ABC 的内角和为A .180°B .360°C .540°D .720° 【答案】A【考点】三角形的内角和定理。
【分析】利用三角形的内角和定理,直接得出.3.已知地球上海洋面积约为316 000 000km 2,316 000 000这个数用科学记数法可表示为 A .3.61×106 B .3.61×107 C .3.61×108 D .3.61×109 【答案】C 。
【考点】科学记数法。
【分析】利用科学记数法的计算方法,直接得出结果。
4.若m ·23=26,则m 等于A .2B .4C .6D .8 【答案】D .【考点】指数运算法则。
【分析】利用指数运算法则,直接得出结果,6363322228m -=÷===。
5.有一组数据:3,4,5,6,6,则下列四个结论中正确的是 A .这组数据的平均数、众数、中位数分别是4.8,6,6 B .这组数据的平均数、众数、中位数分别是5,5,5 C .这组数据的平均数、众数、中位数分别是4.8,6,5 D .这组数据的平均数、众数、中位数分别是5,6,6 【答案】C .【考点】平均数、众数、中位数。
【分析】平均数=345564.85++++=,众数6, 中位数5。
6.不等式组30,32x x -≥⎧⎪⎨<⎪⎩的所有整数解之和是A .9B .12C .13D .15【答案】B 。
【考点】不等式组。
【分析】解不等式组可得36x <≤,其间所有整数解之和是3+4+5=12。
7.已知1112a b -=,则ab a b -的值是 A .12 B .-12C .2D .-2【答案】D 。
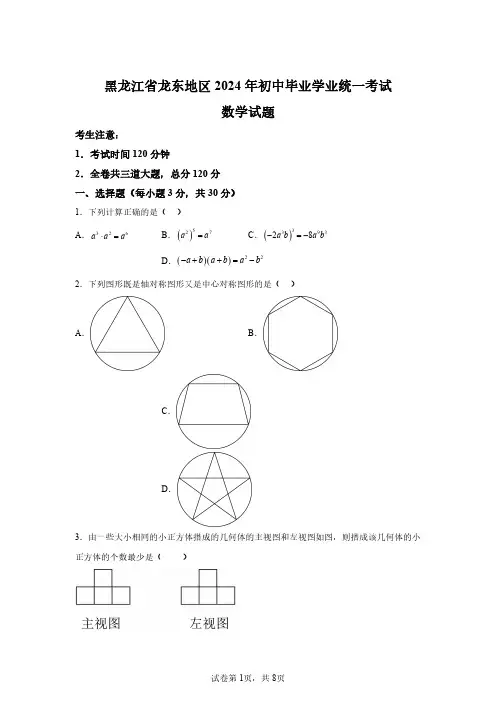
黑龙江省龙东地区2024年初中毕业学业统一考试数学试题考生注意:1.考试时间120分钟2.全卷共三道大题,总分120分一、选择题(每小题3分,共30分)1.下列计算正确的是()A .326a a a ⋅=B .()527a a =C .()339328a b a b -=-D .()()22a b a b a b-++=-2.下列图形既是轴对称图形又是中心对称图形的是()A .B .C .D .3.由一些大小相同的小正方体搭成的几何体的主视图和左视图如图,则搭成该几何体的小正方体的个数最少是()A .3B .4C .5D .64.一组数据2,3,3,4,则这组数据的方差为()A .1B .0.8C .0.6D .0.55.关于x 的一元二次方程()22420m x x -++=有两个实数根,则m 的取值范围是()A .4m ≤B .4m ≥C .4m ≥-且2m ≠D .4m ≤且2m ≠6.已知关于x 的分式方程2333x xkx -=--无解,则k 的值为()A .2k =或1k =-B .2k =-C .2k =或1k =D .1k =-7.国家“双减”政策实施后,某班开展了主题为“书香满校园”的读书活动.班级决定为在活动中表现突出的同学购买笔记本和碳素笔进行奖励(两种奖品都买),其中笔记本每本3元,碳素笔每支2元,共花费28元,则共有几种购买方案()A .5B .4C .3D .28.如图,双曲线()120y x x=>经过A 、B 两点,连接OA 、AB ,过点B 作BD y ⊥轴,垂足为D ,BD 交OA 于点E ,且E 为AO 的中点,则AEB △的面积是()A .4.5B .3.5C .3D .2.59.如图,菱形ABCD 中,点O 是BD 的中点,AM BC ⊥,垂足为M ,AM 交BD 于点N ,2OM =,8BD =,则MN 的长为()A B .5C .5D 10.如图,在正方形ABCD 中,点H 在AD 边上(不与点A 、D 重合),90BHF ∠=︒,HF 交正方形外角的平分线DF 于点F ,连接AC 交BH 于点M ,连接BF 交AC 于点G ,交CD 于点N ,连接BD .则下列结论:①45HBF ∠=︒;②点G 是BF 的中点;③若点H 是AD 的中点,则sin 10NBC ∠=;④BN =;⑤若12AH D H =,则112BND AHM S S =△△,其中正确的结论是()A .①②③④B .①③⑤C .①②④⑤D .①②③④⑤二、填空题(每小题3分,共30分)11.国家统计局公布数据显示,2023年我国粮食总产量是13908亿斤,将13908亿用科学记数法表示为.12.在函数y =中,自变量x 的取值范围是.13.已知菱形ABCD 中对角线AC BD 、相交于点O ,添加条件可使菱形ABCD成为正方形.14.七年一班要从2名男生和3名女生中选择两名学生参加朗诵比赛,恰好选择1名男生和1名女生的概率是.15.关于x 的不等式组420102x x a -≥⎧⎪⎨->⎪⎩恰有3个整数解,则a 的取值范围是.16.如图,ABC 内接于O ,AD 是直径,若25B ∠=︒,则CAD∠︒.17.若圆锥的底面半径为3,侧面积为36π,则这个圆锥侧面展开图的圆心角是︒.18.如图,在Rt ABC △中,90ACB ∠=︒,1tan 2BAC ∠=,2BC =,1AD =,线段AD 绕点A 旋转,点P 为CD 的中点,则BP 的最大值是.19.矩形ABCD 中,3AB =,4BC =,将AB 沿过点A 的一条直线折叠,折痕交直线BC 于点P (点P 不与点B 重合),点B 的对称点落在矩形对角线所在的直线上,则PC 长为.20.如图,在平面直角坐标系中,正方形OMNP 顶点M 的坐标为()3,0,OAB 是等边三角形,点B 坐标是()1,0,OAB 在正方形OMNP 内部紧靠正方形OMNP 的边(方向为O M N P O M →→→→→→ )做无滑动滚动,第一次滚动后,点A 的对应点记为1A ,1A 的坐标是()2,0;第二次滚动后,1A 的对应点记为2A ,2A 的坐标是()2,0;第三次滚动后,2A 的对应点记为3A ,3A 的坐标是1322⎛⎫-⎝⎭;如此下去,……,则2024A 的坐标是.三、解答题(满分60分)21.先化简,再求值:22222111m m m m m m ⎛⎫-+÷- ⎪-+⎝⎭,其中cos60m =︒.22.如图,在正方形网格中,每个小正方形的边长都是1个单位长度,在平面直角坐标系中,ABC 的三个顶点坐标分别为()1,1A -,()2,3B -,()5,2C -.(1)画出ABC 关于y 轴对称的111A B C △,并写出点1B 的坐标;(2)画出ABC 绕点A 逆时针旋转90︒后得到的22AB C ,并写出点2B 的坐标;(3)在(2)的条件下,求点B 旋转到点2B 的过程中所经过的路径长(结果保留π)23.如图,抛物线2y x bx c =-++与x 轴交于A 、B 两点,与y 轴交于点C ,其中()1,0B ,()0,3C .(1)求抛物线的解析式.(2)在第二象限的抛物线上是否存在一点P ,使得APC △的面积最大.若存在,请直接写出点P 坐标和APC △的面积最大值;若不存在,请说明理由.24.为贯彻落实教育部办公厅关于“保障学生每天校内、校外各一小时体育活动时间”的要求,某学校要求学生每天坚持体育锻炼.学校从全体男生中随机抽取了部分学生,调查他们的立定跳远成绩,整理如下不完整的频数分布表和统计图,结合下图解答下列问题:组别分组(cm )频数A 50100x <≤3B 100150x <≤m C150200x <≤20D 200250x <≤14E250300x <≤5(1)频数分布表中m =,扇形统计图中n =.(2)本次调查立定跳远成绩的中位数落在组别.(3)该校有600名男生,若立定跳远成绩大于200cm 为合格,请估计该校立定跳远成绩合格的男生有多少人?25.甲、乙两货车分别从相距225km 的A 、B 两地同时出发,甲货车从A 地出发途经配货站时,停下来卸货,半小时后继续驶往B 地,乙货车沿同一条公路从B 地驶往A 地,但乙货车到达配货站时接到紧急任务立即原路原速返回B 地,结果比甲货车晚半小时到达B 地.如图是甲、乙两货车距A 地的距离()km y 与行驶时间()h x 之间的函数图象,结合图象回答下列问题:(1)甲货车到达配货站之前的速度是km/h ,乙货车的速度是km/h ;(2)求甲货车在配货站卸货后驶往B 地的过程中,甲货车距A 地的距离()km y 与行驶时间()h x 之间的函数解析式;(3)直接写出甲、乙两货车在行驶的过程中,出发多长时间甲、乙两货车与配货站的距离相等.26.已知ABC 是等腰三角形,AB AC =,12MAN BAC ∠=∠,MAN ∠在BAC ∠的内部,点M 、N 在BC 上,点M 在点N 的左侧,探究线段BM NC MN 、、之间的数量关系.(1)如图①,当90BAC ∠=︒时,探究如下:由90BAC ∠=︒,AB AC =可知,将ACN △绕点A 顺时针旋转90︒,得到ABP ,则CN BP =且90PBM ∠=︒,连接PM ,易证AMP AMN △≌△,可得MP MN =,在Rt PBM △中,222BM BP MP +=,则有222BM NC MN +=.(2)当60BAC ∠=︒时,如图②:当120BAC ∠=︒时,如图③,分别写出线段BM NC MN 、、之间的数量关系,并选择图②或图③进行证明.27.为了增强学生的体质,某学校倡导学生在大课间开展踢毽子活动,需购买甲、乙两种品牌毽子.已知购买甲种品牌毽子10个和乙种品牌毽子5个共需200元;购买甲种品牌毽子15个和乙种品牌毽子10个共需325元.(1)购买一个甲种品牌毽子和一个乙种品牌毽子各需要多少元?(2)若购买甲乙两种品牌毽子共花费1000元,甲种品牌毽子数量不低于乙种品牌毽子数量的5倍且不超过乙种品牌毽子数量的16倍,则有几种购买方案?(3)若商家每售出一个甲种品牌毽子利润是5元,每售出一个乙种品牌毽子利润是4元,在(2)的条件下,学校如何购买毽子商家获得利润最大?最大利润是多少元?28.如图,在平面直角坐标系中,等边三角形OAB 的边OB 在x 轴上,点A 在第一象限,OA 的长度是一元二次方程2560x x --=的根,动点P 从点O 出发以每秒2个单位长度的速度沿折线OA AB -运动,动点Q 从点O 出发以每秒3个单位长度的速度沿折线OB BA -运动,P 、Q 两点同时出发,相遇时停止运动.设运动时间为t 秒(0 3.6t <<),OPQ △的面积为S .(1)求点A的坐标;(2)求S与t的函数关系式;(3)在(2)的条件下,当S M在y轴上,坐标平面内是否存在点N,使得以点O、P、M、N为顶点的四边形是菱形.若存在,直接写出点N的坐标;若不存在,说明理由.1.C【分析】本题主要考查同底数幂的乘法,幂的乘方与积的乘方,平方差公式,运用相关运算法则求出各选项的结果后再进行判断即可.【详解】解:A 、3256a a a a ⋅=≠,故选项A 计算错误,此选项不符合题意;B 、()52107a a a =≠,故选项B 计算错误,此选项不符合题意;C 、()339328a b a b -=-,此选项计算正确,符合题意;D 、()()()()22a b a b b a b a b a -++=-+=-,故选项D 计算错误,此选项不符合题意;故选:C .2.B【分析】本题主要考查了轴对称图形和中心对称图形,根据轴对称图形和中心对称图形的定义:如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形;中心对称图形的定义:把一个图形绕着某一个点旋转180︒,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心,进行逐一判断即可.【详解】解:A 、是轴对称图形,不是中心对称图形,故A 选项不合题意;B 、既是轴对称图形又是中心对称图形,故B 选项符合题意;C 、是轴对称图形,不是中心对称图形,故C 选项不合题意;D 、是轴对称图形,不是中心对称图形,故D 选项不合题意.故选:B .3.B【分析】根据三视图的知识,主视图是由4个小正方形组成,而左视图是由4个小正方形组成,故这个几何体的底层最少有3个小正方体,第2层最少有1个小正方体.【详解】解:根据左视图和主视图,这个几何体的底层最少有1+1+1=3个小正方体,第二层最少有1个小正方体,因此组成这个几何体的小正方体最少有3+1=4个.故选B .【点睛】本题考查了由三视图判断几何体,意在考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”就容易得到答案.4.D【分析】本题主要考查了方差的计算,解题的关键是方差的计算公式的识记.根据方差的计算公式,先算出数据的平均数,然后代入公式计算即可得到结果.【详解】平均数为:()233443+++÷=方差为:()()()()222221233333434S ⎡⎤=⨯-+-+-+-⎣⎦()110014=⨯+++0.5=故选:D .5.D【分析】本题考查了一元二次方程根的判别式.根据一元二次方程20(0)ax bx c a ++=≠的根的判别式24b ac ∆=-的意义得到20m -≠且0∆≥,即244(2)20m -⨯-⨯≥,然后解不等式组即可得到m 的取值范围.【详解】解: 关于x 的一元二次方程()22420m x x -++=有实数根,20m ∴-≠且0∆≥,即244(2)20m -⨯-⨯≥,解得:4m ≤,m ∴的取值范围是4m ≤且2m ≠.故选:D .6.A【分析】本题考查了解分式方程无解的情况,理解分式方程无解的意义是解题的关键.先将分式方程去分母,化为整式方程,再分两种情况分别求解即可.【详解】解:去分母得,2(3)3kx x --=-,整理得,(2)9k x -=-,当2k =时,方程无解,当2k ≠时,令3x =,解得1k =-,所以关于x 的分式方程2333x xkx -=--无解时,2k =或1k =-.故选:A .7.B【分析】本题考查了二元一次方程的应用,找准等量关系,正确列出二元一次方程是解题的关键.设购买x 支笔记本,y 个碳素笔,利用总价=单价⨯数量,即可得出关于x ,y 的二元一次方程,再结合x ,y 均为正整数,即可得出购买方案的个数.【详解】解:设购买x 支笔记本,y 个碳素笔,依题意得:3228x y +=,3142y x ∴=-.又x ,y 均为正整数,∴211x y =⎧⎨=⎩或48x y =⎧⎨=⎩或65x y =⎧⎨=⎩或82x y =⎧⎨=⎩,∴共有4种不同的购买方案.故选:B .8.A【分析】本题考查了反比例函数,相似三角形的判定与性质等知识,过点A 作AF BD ⊥,垂足为F ,设12,A a a ⎛⎫ ⎪⎝⎭,证明AFE ODE ∽,有AF AE EF OD OE DE ==,根据E 为AO 的中点,可得AF OD =,EF DE =,进而有1122EF DE DF a ===,162A AF OD y a===,可得6B y OD a ==,2B x a =,则有32BE BD DE a =-=,问题随之得解.【详解】如图,过点A 作AF BD ⊥,垂足为F ,设12,A a a ⎛⎫ ⎪⎝⎭,0a >,∵BD y ⊥轴,AF BD ⊥,∴AF y ∥轴,DF a =,∴AFE ODE ∽,∴AF AE EF OD OE DE==,∵E 为AO 的中点,∴AE OE =,∴1AF AE EF OD OE DE===,∴AF OD =,EF DE=∴1122EF DE DF a ===,162A AF OD y a ===,∵B OD y =,∴6B y OD a ==,∴2B x a =,∴2B BD x a ==,∴32BE BD DE a =-=,∴11639 4.52222ABE S AF BE a a =⨯⨯=⨯⨯== ,故选:A .9.C【分析】本题主要考查了解三角形,菱形的性质、直角三角形斜边中线等于斜边一半.先由菱形性质可得对角线AC 与BD 交于点O ,由直角三角形斜边中线等于斜边一半可得2OA OC OM ===,进而由菱形对角线求出边长,由sin sin 5MAC OBC ∠=∠=解三角形即可求出sin 5MC AC MAC =∠=,tan 5MN BM OBC =∠=.【详解】解:连接AC ,如图,∵菱形ABCD 中,AC 与BD 互相垂直平分,又∵点O 是BD 的中点,∴A 、O 、C 三点在同一直线上,∴OA OC =,∵2OM =,AM BC ⊥,∴2OA OC OM ===,∵8BD =,∴142OB OD BD ===,∴BC ===21tan 42OC OBC OB ===∠,∵90ACM MAC ∠+∠=︒,90ACM OBC ∠+∠=︒,∴MAC OBC∠=∠∴sin sin OC MAC OBC BC ∠=∠==∴sin MC AC MAC =∠=∴55BM BC MC =-=-=,∴1tan 525MN BM OBC =∠=⨯=故选:C .10.A【分析】连接DG,可得BD AB=AC 垂直平分BD ,先证明点B 、H 、D 、F 四点共圆,即可判断①;根据AC 垂直平分BD ,结合互余可证明DG FG =,即有DG FG BG ==,则可判断②正确;证明ABM DBN ∽,即有BN BD BM AB ==212ABM DBN S AB S BD ⎛⎫== ⎪⎝⎭ ,根据12AH D H =可得3AH AD =,再证明AHM CBM ∽,可得13AHM ABM S HM S BM == ,即可判断⑤;根据点H 是AD 的中点,设2AD =,即求出BH =,同理可证明AHM CBM ∽,可得23BM BH ==,即可得BN ==,进而可判断③.【详解】连接DG ,如图,∵四边形ABCD 是正方形,∴45BDC BAC ADB ∠=∠=∠=︒,BD AB=90BAD ADC ∠=∠=︒,AC 垂直平分BD ,∴90CDP ∠=︒,∵DF 平分CDP ∠,∴1452CDF CDP CDB ∠=∠=︒=∠,∴90BDF CDF CDB ∠=∠+∠=︒,∵90BHF BDF ∠=︒=∠,∴点B 、H 、D 、F 四点共圆,∴45HFB HDB ∠=∠=︒,DHF DBF ∠=∠,∴18045HBF HFB FHB ∠=︒-∠-∠=︒,故①正确,∵AC 垂直平分BD ,∴BG DG =,∴BDG DBG ∠=∠,∵90BDF ∠=︒,∴90BDG GDF DBG DFG ∠+∠=︒=∠+∠,∴GDF DFG ∠=∠,∴DG FG =,∴DG FG BG ==,∴点G 是BF 的中点,故②正确,∵90BHF BAH ∠=︒=∠,∴90AHB DHF AHB ABH ∠+∠=︒=∠+∠,∴DHF ABH ∠=∠,∵DHF DBF ∠=∠,∴ABH DBF ∠=∠,又∵45BAC DBC ∠=∠=︒,∴ABM DBN ∽,∴BN BD BM AB==,∴BN =,故④正确,∴212ABM DBN S AB S BD ⎛⎫== ⎪⎝⎭ ,若12AH D H =,则()1122AH HD AD AH ==-,∴3AH AD =,∴13=AH AD ,即13H H A A BC AD ==,∵AD BC ∥,∴AHM CBM ∽,∴13HM AH BM BC ==,∴13AHM ABM S HM S BM == ,∴3ABM AHM S S = ,∵12ABM DBN S S = ,∴26BND ABM AHM S S S == △,故⑤错误,如图,③若点H 是AD 的中点,设2AD =,即2AB BC AD ===,∴112AH AD ==,∴BH ==,同理可证明AHM CBM ∽,∴12HM AH BM BC ==,∴32HM BM BH BM BM+==,∴23BM BH ==,∵BN =,∴BN =,∵2BC =,∴在Rt BNC △中,23NC ==,sin NC NBC BN ∠==,故③正确,则正确的有:①②③④,故选:A .【点睛】本题是一道几何综合题,主要考查了正方形的性质,相似三角形的判定与性质,正弦,圆周角定理以及勾股定理等知识,证明点B 、H 、D 、F 四点共圆,ABM DBN ∽,是解答本题的关键.11.121.390810⨯【分析】本题考查了科学记数法,科学记数法的表示形式为10n a ⨯的形式,其中1||10a ≤<,n 为整数.确定n 的值时,要看把原来的数,变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值10≥时,n 是正数;当原数的绝对值1<时,n 是负数,确定a 与n 的值是解题的关键.【详解】1 亿81.010=⨯,13908亿48121.39081010 1.390810=⨯⨯=⨯故答案为:121.390810⨯12.3x ≥##3x≤【分析】本题主要考查函数自变量取值范围,分别根据二次根式有意义的条件和分式有意义的条件列出不等式求解即可.【详解】解:根据题意得,30x -≥,且20x +≠,解得,3x ≥,故答案为:3x ≥.13.AC BD =或AB BC⊥【分析】本题主要考查的是菱形和正方形的判定,熟练掌握菱形的判定定理是解题的关键,依据正方形的判定定理进行判断即可.【详解】解:根据对角线相等的菱形是正方形,可添加:AC BD =;根据有一个角是直角的菱形是正方形,可添加的:AB BC ⊥;故添加的条件为:AC BD =或AB BC ⊥.14.35【分析】本题考查的是用树状图法求概率.树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.画树状图,共有12种等可能的结果,其中选取的2名学生恰好是1名男生、1名女生的结果有6种,再由概率公式求解即可.【详解】解:画树状图如下:由图可知,共有20种等可能的结果,其中选取的2名学生恰好是1名男生、1名女生的结果有12种,∴选取的2名学生恰好是1名男生、1名女生的概率为:123205=,故答案为:35.15.102a -≤<【分析】本题考查解一元一次不等式(组),一元一次不等式组的整数解,解答本题的关键是明确解一元一次不等式的方法.先解出不等式组中每个不等式的解集,然后根据不等式组420102x x a -≥⎧⎪⎨->⎪⎩恰有3个整数解,即可得到关于a 的不等式组,然后求解即可.【详解】解:由420-≥x ,得:2x ≤,由102x a ->,得:2x a >, 不等式组420102x x a -≥⎧⎪⎨->⎪⎩恰有3个整数解,∴这3个整数解是0,1,2,120a ∴-≤<,解得102a -≤<,故答案为:102a -≤<.16.65【分析】本题考查了圆周角定理,直角三角形的两个锐角互余,连接CD ,根据直径所对的圆周角是直角得出=90ACD ∠︒,根据同弧所对的圆周角相等得出25D B ∠=∠=︒,进而根据直角三角形的两个锐角互余,即可求解.【详解】解:如图所示,连接CD ,∵ABC 内接于O ,AD 是直径,∴=90ACD ∠︒,∵ AC AC =,25B ∠=︒,∴25D B ∠=∠=︒∴902565CAD ∠=︒-︒=︒,故答案为:65.17.90【分析】此题主要考查了圆锥的侧面积公式以及与展开图扇形面积关系,求出圆锥的母线长是解决问题的关键.根据圆锥的侧面积公式πS rl =求出圆锥的母线长,再结合扇形面积公式即可求出圆心角的度数.【详解】根据圆锥侧面积公式:πS rl =,可得π336πl ⨯⨯=解得:12l =,2π1236π360n ⨯∴=,解得90n =,∴侧面展开图的圆心角是90︒.故答案为:90.18.12【分析】本题考查了解直角三角形,三角形中位线定理,旋转的性质,解题的关键是找出BP 取最大值时B 、P 、M 三点的位置关系.取AC 的中点M ,连接PM 、BM ,利用解三角形求出BM ==,利用三角形中位线定理推出1122PM AD ==,当AD 在AC 下方时,如果B 、P 、M 三点共线,则BP 有最大值.【详解】解:取AC 的中点M ,连接PM 、BM .∵90ACB ∠=︒,1tan 2BAC ∠=,2BC =,∴124tan 2BC AC BAC ==÷=∠,∴122AM CM AC ===,∴BM ===∵P 、M 分别是CD AC 、的中点,∴1122PM AD ==.如图,当AD 在AC 下方时,如果B 、P 、M 三点共线,则BP 有最大值,最大值为12BM MP +=+,故答案为:12.19.52或72或10【分析】本题考查了矩形与折叠问题,解直角三角形,先根据点B 的对称点落在矩形对角线所在的直线上的不同位置分三种情况,画出对应的图形,再根据矩形性质,利用解直角三角形求出PC 即可.【详解】解:①点B 的对称点落在矩形对角线BD 上,如图1,∵在矩形ABCD 中,3AB CD ==,4BC AD ==,由折叠性质可知:BB AP '⊥,∴BAP BPA BPA CBD∠+∠=∠+∠∴=BAP CBD∠∠∴3tan =tan =4CD BAP CBD BC ∠∠=,∴39tan 642BP AB BAP =∠=⨯=∴97822PC BC BP =-=-=;②点B 的对称点B '落在矩形对角线AC 上,如图2,∵在矩形ABCD 中,3AB CD ==,4BC AD ==,90B Ð=°,∴5AC ===,∴4cos 5BC ACB AC ∠==,由折叠性质可知:=90ABP AB P '∠=∠︒,3AB AB '==,∴532B C AC AB ''=-=-=∴452cos 52B C PC ACB '==÷=∠;③点B 的对称点B '落在矩形对角线CA 延长线上,如图3,∵在矩形ABCD 中,3AB CD ==,4BC AD ==,90B Ð=°,∴5AC ===,∴4cos 5BC ACB AC ∠==,由折叠性质可知:=90ABP AB P '∠=∠︒,3AB AB '==,∴538B C AC AB ''=+=+=∴4810cos 5B C PC ACB '==÷=∠;综上所述:则PC 长为52或72或10.故答案为:52或72或10.20.()1,3【分析】本题考查了点的坐标变化规律,正方形性质,等边三角形性质,根据三角形的运动方式,依次求出点A 的对应点1A ,2A , ,12A 的坐标,发现规律即可解决问题.【详解】解: 正方形OMNP 顶点M 的坐标为()3,0,3OM MN NP OP ∴====,OAB 是等边三角形,点B 坐标是()1,0,∴等边三角形高为2,由题知,1A 的坐标是()2,0;2A 的坐标是()2,0;3A 的坐标是1322⎛⎫- ⎪ ⎪⎝⎭;继续滚动有,4A 的坐标是()3,2;5A 的坐标是()3,2;6A 的坐标是5,32⎛ ⎝⎭;7A 的坐标是()1,3;8A 的坐标是()1,3;9A 的坐标是52⎫⎪⎪⎝⎭;10A 的坐标是()0,1;11A 的坐标是()0,1;12A 的坐标是12⎛ ⎝⎭;13A 的坐标是()2,0; 不断循环,循环规律为以1A ,2A , ,12A ,12个为一组, 2024121688÷= ,∴2024A 的坐标与8A 的坐标一样为()1,3,故答案为:()1,3.21.1m -+,12【分析】本题主要考查分式的化简求值及特殊三角函数值,先对分式进行化简,然后利用特殊三角函数值进行代值求解即可.【详解】解:原式()()()()21111m m m m m m-+=⋅+--1m =-+,当1cos 602m =︒=时原式12=.22.(1)作图见解析,()12,3B (2)作图见解析,()23,0B -【分析】本题考查了利用旋转变换作图,轴对称和扇形面积公式等知识,熟练掌握网格结构准确找出对应点的位置是解题的关键.(1)根据题意画出即可;关于y 轴对称点的坐标横坐标互为相反数,纵坐标不变;(2)根据网格结构找出点B 、C 以点A 为旋转中心逆时针旋转90︒后的对应点,然后顺次连接即可;(3)先求出AB 90︒,利用弧长公式即可求出.【详解】(1)解:如图,111A B C △为所求;点1B 的坐标为()2,3,(2)如图,22AB C 为所求;()23,0B -,(3)AB =,点B 旋转到点2B =.23.(1)223y x x =--+(2)存在,点P 的坐标是315,24P ⎛⎫- ⎪⎝⎭,APC △的面积最大值是278【分析】本题主要考查二次函数的图象与性质以及与几何综合:(1)将B ,C 两点坐标代入函数解析式,求出b ,c 的值即可;(2)过点P 作PE x ⊥轴于点E ,设()2,23P x x x --+,且点P 在第二象限,根据APC APE AOC PCOE S S S S =+- 梯形可得二次函数关系式,再利用二次函数的性质即可求解.【详解】(1)解:将()1,0B ,()0,3C 代入2y x bx c =-++得,103b c c -++=⎧⎨=⎩解得:23b c =-⎧⎨=⎩223y x x ∴=--+(2)解:对于223y x x =--+,令0,y =则2230,x x --+=解得,123,1x x =-=,∴()3,0A -,∴3,OA =∵()0,3C ,∴3OC =,过点P 作PE x ⊥轴于点E ,如图,设()2,23P x x x --+,且点P 在第二象限,∴,3,OE x AE x =-=+∴APC APE AOCPCOE S S S S =+- 梯形()111222AE PE OC PE OE OA OC =⨯++⨯-⨯()()()()2211132332333222x x x x x x =+--++--+--⨯⨯23327228x ⎛⎫=-++ ⎪⎝⎭∵302-<,∴S 有最大值,∴当32x =-时,S 有最大值,最大值为278,此时点P 的坐标为315,24⎛⎫- ⎪⎝⎭24.(1)8,40(2)C(3)估计该校立定跳远成绩合格的男生有228人【分析】本题主要考查了扇形统计图和频数表、中位数,用样本估计总体,(1)用A 组的频数除以所占的百分比,即可求出调查的总人数;用总人数减去其它组的人数,即可求得B 组的人数,用C 组的人数除以总人数即可求解;(2)根据中位数的求法,即可求解;(3)用总人数乘以样本中立定跳远成绩合格的男生人数所占,即可求解.【详解】(1)解:被抽取的学生数为:36%50÷=(人)故503201458m =----=(人),%205040%n =÷=,即40n =,故答案为:8,40;(2)解:把这组数据从小到大排列,第25和第26个数据的平均数为这组数据的中位数,382526+<< ,5142526+<<,∴把这组数据从小到大排列,第25和第26个数据都在C 组,故本次调查立定跳远成绩的中位数落在C 组,答案为:C ;(3)解:14560022850+⨯=(人)答:该校立定跳远成绩合格的男生有228人.25.(1)30,40(2)EF 的函数解析式是()802154 5.5y x x =-≤≤(3)经过1.5h 或45h 14或5h 甲、乙两货车与配货站的距离相等【分析】本题考查一次函数的应用,待定系数法求一次函数解析式的运用,认真分析函数图象,读懂函数图象表示的意义是解题关键.(1)由图象可知甲货车到达配货站路程为105km ,所用时间为3.5h ,乙货车到达配货站路程为120km ,到达后返回,所用时间为6h ,根据速度=距离÷时间即可得;(2)甲货车从A 地出发途经配货站时,停下来卸货,半小时后继续驶往B 地,由图象结合已知条件可知(4,105)E 和点(5.5,225)F ,再利用待定系数法求出y 与x 的关系式即可得答案;(3)分两车到达配货站之前和乙货车到达配货站时接到紧急任务立即原路原速返回B 地后、甲货车卸货,半小时后继续驶往B 地,三种情况与配货站的距离相等,分别列方程求出x 的值即可得答案.【详解】(1)解:由图象可知甲货车到达配货站路程为105km ,所用时间为3.5h ,所以甲货车到达配货站之前的速度是105 3.5=30÷(km/h )∴乙货车到达配货站路程为225105=120(km)-,到达配货站时接到紧急任务立即原路原速返回B 地,总路程为240km ,总时间是6h ,∴乙货车速度240640km /h =÷=,故答案为:30;40(2)甲货车从A 地出发途经配货站时,停下来卸货,半小时后继续驶往B 地,由图象可知(4,105)E 和点(5.5,225)F 设(4 5.5)EF y kx b x =+≤≤∴41055.5225k b k b +=⎧⎨+=⎩解得:21580b k =-⎧⎨=⎩,∴甲货车距A 地的距离()km y 与行驶时间()h x 之间的函数解析式()802154 5.5y x x =-≤≤(3)设甲货车出发h x ,甲、乙两货车与配货站的距离相等,①两车到达配货站之前:1053012040x x -=-,解得:32x =,②乙货车到达配货站时开始返回,甲货车未到达配货站:1053040120x x -=-,解得:4514x =,③甲货车在配货站卸货后驶往B 地时:0802151054012x x =---,解得:5x =,答:经过1.5h 或45h 14或5h 甲、乙两货车与配货站的距离相等.26.图②的结论是:222BM NC BM NC MN ++⋅=;图③的结论是:222BM NC BM NC MN +-⋅=;证明见解析【分析】本题主要考查等边三角形的性质,全等三角形的判定与性质,30度角所对的直角边等于斜边的一半,勾股定理等知识,选②,以点B 为顶点在ABC 外作60ABK ∠=︒,在BK 上截取BQ CN =,连接QA QM 、,过点Q 作QH BC ⊥,垂足为H ,构造全等三角形,得出AN AQ =,CAN QAB ∠=∠,再证明AQM ANM △≌△,得到MN QM =;在Rt QHM△中由勾股定理得222QH HM QM +=,即222122BQ BM BQ QM ⎫⎛⎫++=⎪ ⎪⎪⎝⎭⎝⎭,整理可得结论;选③方法同②【详解】解:图②的结论是:222BM NC BM NC MN ++⋅=证明:∵,60,AB AC BAC =∠=︒∴ABC 是等边三角形,∴60ABC ACB ∠=∠=︒,以点B 为顶点在ABC 外作60ABK ∠=︒,在BK 上截取BQ CN =,连接QA QM 、,过点Q 作QH BC ⊥,垂足为H ,AB AC = ,C ABQ ∠=∠,CN BQ=ACN ABQ∴△≌△AN AQ ∴=,CAN QAB∠=∠又30CAN BAM ∠+∠=︒30BAM QAB ∴∠+∠=︒即QAM MAN∠=∠又AM AM = ,AQM ANM ∴△≌△,MN QM ∴=;∵60,60,ABQ ABC ∠=︒∠=︒∴60QBH ∠=︒,∴30,BQH ∠=︒12B BH Q ∴=,2QH BQ =∴12HM BM BH BM BQ =+=+,在Rt QHM △中,可得:222QH HM QM +=即222122BQ BM BQ QM ⎛⎫⎛⎫++= ⎪ ⎪ ⎪⎝⎭⎝⎭整理得222BM BQ B Q M M B Q ⋅++=222NC B M N N B M M C ∴=⋅++图③的结论是:222BM NC BM NC MN +-⋅=证明:以点B 为顶点在ABC 外作30ABK ∠=︒,在BK 上截取BQ CN =,连接QA QM 、,过点Q 作QH BC ⊥,垂足为H ,AB AC = ,C ABQ ∠=∠,CN BQ=ACN ABQ∴△≌△AN AQ ∴=,CAN QAB∠=∠又60CAN BAM ∠+∠=︒60BAM QAB ∴∠+∠=︒即QAM MAN∠=∠又AM AM = ,AQM ANM ∴△≌△,MN QM∴=在Rt BQH 中,60QBH ∠=︒,30BQH ∠=︒12B BH Q ∴=,QH BQ =12HM BM BH BM BQ =-=-,在Rt QHM △中,可得:222QH HM QM +=即222122BQ BM BQ QM ⎛⎫⎛⎫+-= ⎪ ⎪ ⎪⎝⎭⎝⎭整理得222BM BQ B Q M M B Q ⋅+-=222NC B M N N B M M C ∴=⋅+-27.(1)购买一个甲种品牌毽子需15元,购买一个乙种品牌毽子需10元(2)共有3种购买方案(3)学校购买甲种品牌毽子60个,购买乙种品牌毽子10个,商家获得利润最大,最大利润是340元【分析】本题考查了二元一次方程组、一元一次不等式组以及一次函数的应用,(1)设购买一个甲种品牌毽子需a 元,购买一个乙种品牌毽子需b 元,根据题意列出二元一次方程组,问题得解;(2)设购买甲种品牌毽子x 个,购买乙种品牌毽子31002x ⎛⎫- ⎪⎝⎭个,根据题意列出一元一次不等式组,解不等式组即可求解;(3)设商家获得总利润为y 元,即有一次函数3541002y x x ⎛⎫=+- ⎪⎝⎭,根据一次函数的性质即可求解.【详解】(1)解:设购买一个甲种品牌毽子需a 元,购买一个乙种品牌毽子需b 元.由题意得:1052001510325a b a b +=⎧⎨+=⎩,解得:1510a b =⎧⎨=⎩,答:购买一个甲种品牌毽子需15元,购买一个乙种品牌毽子需10元;(2)解:设购买甲种品牌毽子x 个,购买乙种品牌毽子1000153100102x x -⎛⎫=- ⎪⎝⎭个.由题意得:3510023161002x x x x ⎧⎛⎫≥- ⎪⎪⎪⎝⎭⎨⎛⎫⎪≤- ⎪⎪⎝⎭⎩,解得:14586417x ≤≤,x 和31002x ⎛⎫-⎪⎝⎭均为正整数,60x ∴=,62,64,3100102x -=,7,4,∴共有3种购买方案.(3)设商家获得总利润为y 元,3541002y x x ⎛⎫=+- ⎪⎝⎭,400y x =-+,10k =-< ,y ∴随x 的增大而减小,∴当60x =时,340y =最大,答:学校购买甲种品牌毽子60个,购买乙种品牌毽子10个,商家获得利润最大,最大利润是340元.28.(1)点A的坐标为(A(2)()())2202233 3.6t S t t ⎧<≤⎪⎪⎪=+<≤⎨⎪⎪+<<⎪⎩(3)存在,(12,4N +,()24N,(3N -,4N ⎛ ⎝【分析】(1)运用因式分解法解方程求出OA 的长,根据等边三角形的性质得出6,60OA OB AC OAB AOB ABO ===∠=∠=∠=︒,过点A 作AC x ⊥轴,垂足为C ,求出AC 的长即可;(2)分02t <≤,23t <≤和3 3.6t <<三种情况,运用三角形面积公式求解即可;(32=2t =,得4OP =,分OP 为边和对角线两种情况可得点N 的坐标;当2+=+时不存在以点O 、P 、M 、N 为顶点的四边形是菱形【详解】(1)解:2560x x --=,解得16x =,21x =-OA 的长度是2560x x --=的根,6OA ∴=∵OAB 是等边三角形,∴6,60OA OB AC OAB AOB ABO ===∠=∠=∠=︒,过点A 作AC x ⊥轴,垂足为C ,在Rt AOC 中,60,AOC ∠=︒∴30,OAC ∠=︒116322OC OA ∴==⨯=,∴AC ===∴点A 的坐标为(A (2)解:当02t <≤时.过P 作PD x ⊥轴,垂足为点D ,∴2OP t =,3OQ t =,30OPD ∴∠=︒∴,OD t =∴PD ==,2113222S OQ PD t t ∴=⨯⨯=⨯⨯=;当23t <≤时,过Q 作QE OA ⊥,垂足为点E∵60,A ∠=︒∴30,AQE ∠=︒又123,AQ t =-∴13622AE AQ t ==-,2t QE =又2OP t =,21222S t ⎛⎫∴=⨯⨯=+ ⎪ ⎪⎝⎭当3 3.6t <<时,过O 作OF AB ⊥,垂足为F∴()1823185PQ t t t =-+=-,同理可得,132BF OB ==,∴2233OF OB BF =-=;()11533185327322S t t ∴=⨯⨯-=-+综上所述()()()223302233632321532733 3.62t t S t t t t t ⎧<≤⎪⎪⎪=-+<≤⎨⎪⎪-+<<⎪⎩(3)解:当233263t =时,解得,2,t =∴224OP =⨯=,过点P 作PG x ⊥轴于点G ,则12,2OG OP ==∴2222423,PG OP OG =--∴点P 的坐标为(2,3;当OP 为边时,将OP 沿y 轴向下平移4个单位得()2,34N ,此时()0,4M -,四边形POMN 是菱形;将OP 沿y 轴向上平移4个单位得()2,34N ,此时()0,4M ,四边形POMN 是菱形;如图,作点P 关于y 轴的对称点(2,N -,当(0,M 时,四边形PMNO 是菱形;当OP 为对角线时,设OP 的中点为T ,过点T 作TM OP ⊥,交y 轴于点M ,延长MT 到N ,使,TN TM =连接ON ,过点N 作NH x ⊥轴于点H ,则30,MOT NOT HON ∠=∠=∠=︒2,OT =∴2,ON TN =∴222ON OT TN =+,即222122ON ON ⎛⎫=+ ⎪⎝⎭,解得,ON =∴NH =2,OH =。

初中毕业考试数学试题(4)解析满分:150分 时间:120分钟一.选择题(共12个小题,每小题4分,共48分,在每题给出的四个选项中,只有一项是符合题目要求的)1.自贡恐龙博物馆是世界三大恐龙博物馆之一.今年“五一黄金周”共接待游客8.87万人次,人数88700用科学记数法表示为( )A.50.88710⨯B.38.8710⨯C.48.8710⨯D.388.710⨯2.如图是一个正方体的展开图,把展开图叠成小正方体后,有“迎”字一面的向对面上的字是( )A.百B.党C.年D.喜3.下列运算正确的是( )A.22541a a -=B.23246()a b a b -=C.933a a a ÷= D.222(2)4ab a b -=-4.下列图形中,是轴对称图形且对称轴条数最多的是( )5.如图,AC 是正五边形ABCDE 的对角线,∠ACD 的度数是( ) A.72° B.36° C.74° D.88°6.学校为了解“阳光体育”活动展开情况,随机调查了50名学生一周参加体育锻炼时间,数据如下表所示:这些学生一周参加体育锻炼时间的众数、中位数分别是( ) A.16,15 B.11,15 C.8,8.5 D.8,97.已知23120,x x --=则代数式2395x x -++的值是( ) A.31 B.-31 C.41 D.-418.如图,A (8,0),C (-2,0),以点A 为圆心,AC 长为半径画弧,交y 轴正半轴于点B ,则点B 的坐标为( )A.(0,5)B.(5,0)C.(6,0)D.(0,6)9.已知蓄电池的电压为定值,使用蓄电池时,电流I (单位:A )与电阻R (单位:Ω)是反比例函数关系,它的图象如图所示,下列说法正确的是( ) A.函数解析式为13I R=B.蓄电池的电压是18VC.当10I ≤A 时, 3.6R ≥ΩD.当6R =Ω时,4I A =时10.如图,AB 为⊙O 的直径,弦CD ⊥AB 于点F ,OE ⊥AC 于点E ,若OE=3,OB=5,则CD 的长度是( )A.9.6B. D.1011.如图,在正方形ABCD 中,AB=6,M 是AD 边上的一动点,AM :MD=1:2,将△BMA 沿BM 对折至△BMN ,连接DN ,则DN 的长是( )A.5212.如图,直线22y x =-+与坐标轴交于A 、B 两点,点P 是线段AB 上的一个动点,过点P 作y 轴的平行线交直线3y x =-+于点Q ,△OPQ 绕点O 顺时针旋转45°,边PQ 扫过区域(阴影部分)面积的最大值是( )A.23π B.12π C.1116π D.2132π二、填空题(共6个小题,每小题4分,共24分)13.请写出一个满足不等式7x >的整数解 .14.某中学规定学生的学期体育成绩满分为100,其中体育课外活动占30%,期末考试成绩占70%.小彤的这两项成绩依次是90,80.则小彤这学期的体育成绩是 .15.化简:22824a a -=-- . 16.如图,某学校“桃李餐厅”把WIFI 密码做成了数学题.小红在餐厅就餐时,思索了一会儿,输入密码,顺利地连接到了“桃李餐厅”的网络,那么她输入的密码是 .17.如图,△ABC 的顶点均在正方形网格格点上,只用不带尺度的直尺,作出△ABC 角平分线BD (不写作法,保留作图痕迹)18.当自变量13x -≤≤时,函数||y x k =-(k 为常数)的最小值为3k +,则满足条件的k 的值为 .三.解答题(共8个题,共78分)19.本题满分(80|7|(2-+.20.(本题满分8分)如图,在矩形ABCD 中,E ,F 分别是AB ,CD 的中点.求证:DE=BF21.(本题满分8分)在一次数学课外实践活动中,小明所在的学习小组从综合楼顶部B 处测得办公楼底部D 处的俯角是53°,从综合楼底部A 处测得办公楼顶部C 处的仰角恰好是30°,综合楼高24米.请你帮小明求出办公楼的高度(结果精确到0.1,参考数据tan37°≈0.75,tan53°≈1.33,,1.73)22.(本题满分8分)随着我国科技事业的不断发展,国产无人机大量进入快递行业,现有A ,B 两种型号的无人机都被用来送快递,A 型机比B 型机平均每小时多运送20件,A 型机运送700件所有时间与B 型机运送500件所用时间相等,两种无人机平均每小时分别运送多少快件? 23. (本题满分8分)为了弘扬爱国主义精神,某校组织了“共和国成就”知识竞赛,将成绩为:A (优秀)、B (优良)、C (合格)、D (不合格)四个等级.小李随机调查了部分同学的竞赛成绩,绘制成了如下统计图(1)本次抽样调查的样本容量是 ,请补全条形统计图;(2)已知调查对象中只有两位女生竞赛成绩不合格,小李准备随机回访两位竞赛成绩不合格的同学,请用树状图或列表法求出恰好回访到一男一女的概率;(3)该校共有2000名学生,请你估计该校竞赛成绩“优秀”的学生人数.24. (本题满分8分)函数图象是研究函数的重要工具.探究函数性质时,我们经历了列表、描点、连线画出函数图象,然后观察分析图象特征,概括函数性质的过程.结合自己已有的学习经验,画出函数284xy x =-+的图象,并探究其性质. 列表如下:(1)直接写出表中a ,b 的值,并在平面直角坐标系中画出该函数的图象; (2)观察函数284xy x =-+的图象,判断下列关于该函数性质的命题: ①当22x -≤≤时,函数图象关于直线y x =对称; ②2x =时,函数有最小值,最小值为-2 ③11x -<<时,函数y 的值随x 的增大而减小.其中正确的是 (请写出所有正确命题的番号) (3)结合图象,请直接写出不等式2844xx >+的解集为 .25.(本题满分12分)如图,点D 在以AB 为直径的⊙O 上,过D 作⊙O 的切线交AB 的延长线于点C ,AE ⊥CD 于点E ,交⊙O 于点F ,连接AD ,FD. (1)求证:∠DAE=∠DAC ; (2)求证:DF ·AC=AD ·DC ; (3)若sin ∠C=14,AD=,求EF 的长.26.(本题满分14分)如图,抛物线(x 1)(x a)y =+-(其中1a >)与x 轴交于A 、B 两点,交y 轴于点C.(1)直接写出∠OCA 的度数和线段AB 的长(用a 表示);(2)若点D 为△ABC 的外心,且△BCD 与△ACO 4,求此抛物线的解析式;(3)在(2)的前提下,试探究抛物线(x 1)(x a)y =+-上是否存在一点P ,使得∠CAP=∠DBA ?若存在,求出点P 的坐标;若不存在,请说明理由.参考答案与解析一.选择题1.【解析】科学记数法表示为a ×10N ,其中1≤|a|<10,故答案为C 2.【解析】根据正方体展开图可得,“迎”与“党”相对,故答案为B3.【解析】A 正确答案为a 2,B 选项正确,C 选项答案为a 6,D 选项为a 2−4ab +4b2,故答案为B4.【解析】A 选项,对称轴1条,B 选项和C 选项为中心对称图形,D 选项对称轴两条,故答案为D5.【解析】正5边形每一个内角为(n 2)180108n-︒=︒,∵AB=BC ,∴∠ACB=36°,∴∠ACD=72°,故答案为A6.【解析】众数是出现次数最多的数,故众数为8,中位数即将数据排序后,中间两个数(8和9)的平均数8.5,故答案为C7.【解析】2223=12393639531x x x x x x -⇒-+=-⇒-++=-,故答案为B8.【解析】AB=AC=10,AO=8,在Rt △AOB 中,根据勾股定理可得OB=6,故B (0,6),故答案为D 9.【解析】函数解析式为36y x=故A 选项错误,蓄电池电压是49=36⨯V ,D 选项,当6R =Ω时,6I A =,故答案为C10.【解析】在Rt △ACF 中,sin ∠BAC=CFAC,在Rt △AOE 中,sin ∠BAC=OE OA=35,故CD 的长度为245=4.8,故答案为A11.【解析】过N 作直线∥AB ,交AD 于H ,交BC 于G ,由翻折性质可知△AMB ≌△NMB ,∴∠BNM=90°,进而可得△MNH ∽△NBG ,∴MNNB =NH BG =13,设NH=y ,则BG=3y ,MH=3y-2,在Rt △MHN 中,MH 2+NH 2=MN 2,∴(3y −2)2+y 2=22,∴y =65,∴DH=CG=125,在Rt △DNH 中,DH ²+NH 2=DN 2,∴DN =6√55,故答案为D12.【解析】由旋转性质可知,该阴影部分的的面积等于以OQ 为大圆半径R ,OP 为小圆半径r 且圆心角为45°的扇形环的面积,即S 阴影=S 环=πR 28−πr 28,由题意可得,R 2=x 2+(−x +3)²r 2=x 2+(−2x +2)²,且0<x <1,∴R 2−r 2=−3(x −3)2+163,当x =13时,取得最大值163,故阴影部分面积最大值为2π3,故答案选A.二、填空题13.【解析】x >7−√2,故答案很多,最小整数为6,只需填6以上整数即可,答案不唯一 14.【解析】加权平均数计算方法为90×30%+80×70%=83,故答案为83 15.【解析】2(a+2)a 2−4−8a 2−4=2(a−2)(a+2)(a−2)=2a+2,故答案为2a+216.【解析】根据观察a ∗b 6=ac ,bc ,c (a+b )运算的结果进行的顺序排列,故密码为244872. 17.【解析】以B 为圆心,任意长为半径画圆弧交∠B 两边于两点,再分别以这两点为圆心,大于这两点间距离为半径画圆弧产生的交点与点B 所连线段即为所求,18.【解析】当k ≥3时,x=3时函数取得最小值,∴k-3=k+3,不成立,当k ≤-1时,x=-1取得最小值,此时-k-1=k+3,∴k=-2满足题意,当-1<k <3时,x=k 时取得最小值,∴k+3=0,k=-3不满足题意,综上所述,k=-2 三.解答题19.【解析】5-7+1=-120.【解析】证明:∵四边形ABCD 为矩形,∴DC ∥AB 且DC=AB ,∵E 、F 分别为AB 、CD 的中点,∴BE=12AB ,DF=12CD ,∴DF ∥BE 且DF=BE ,∴四边形EBFD 为平行四边形,∴DE=BF.21.【解析】∵在B 处测得D 处的俯角为53°,∴∠BDA=53°,在Rt △BAD 中,tan ∠BDA=BAAD ,∴AD =24tan53°,在Rt △CAD 中,tan ∠CAD=CDAD ,且∠CAD=30°,CD =√3∴CD =√3tan53°≈8.0米22.【解析】设B 型机每小时运送x 件,则A 型机每小时运送x+20件 根据题意可得700x+20=500x,解之可得x =50,经检验x =50是方程的根,也符合实际意义,∴A 型机每小时运送70件,B 型机每小时运送50件 23.【解析】(1)100,补全图形如下:(2)作出树状图如下所示:随机回访两位竞赛成绩合格的同学共20种情况,其中一男一女共12种情况,所以恰好回访到一男一女的概率为1220=35(3)2000×0.35=700人,估计该校竞赛成绩“优秀”人数为700人 24.【解析】(1)作出函数图象如图所示(2)②③ (3)将不等式284x x x >+两边同时乘以-1可得284xx x -<-+可得不等式的解集为 2x <-或02x <<25.【解析】(1)连接OD ,∵DC 为⊙O 的切线,∴OD ⊥CD ,即∠ODC=90° ∵AE ⊥CD ,∴∠AED=90°,∴∠AED=∠ODC=90°,∴AE ∥OD ,∴∠ODA=∠DAE又∵OD=OA=r,∴∠ODA=∠DAC,∴∠DAE=∠DAC(2)证明:连接BD,设∠DAE=α,又(1)可知∠CAD=∠DAE=α,∵AB为⊙O的直径,∴∠ADB=90°,在Rt△ADB中,∠BAD+∠ABD=90°,∴∠ABD=90°-α,又∵四边形ABDF为⊙O的内接四边形,∴∠AFD+∠ABD=180°,∴∠AFD=90°+α∵∠CDO=90°,∴∠ADC=90°+α在△AFD和△ADC中有∠AFD=∠ADC,∠FAD=∠DAC,∴△AFD∽△ADC∴DFDC =ADAC,即DF·AC=AD·DC(3)设OD=x,在Rt△COD中sin∠C=14,∴OC=4x,根据勾股定理可得CD=√15x,∵OA、OB、OD均为⊙O的半径,∴OA=x,∵OD∥AE,∴△COD∽△CAE,∴ODAE =OCCA=CDCE,∴AE=54x,CE=5√154x,故DE=√154x.由(2)可知△AFD∽△ADC,∴ADAC =AFAD,且AD=4√10,可得AF=32x在Rt△ADE中,AE2+DE2=AD2,∴2516x2+1516x2=160,∴x=8∴AF=32x =4,AE=54x=10,∴EF=AE-AF=10-4=626.【解析】(1)A(a,0),C(0,-a),可得OC=OA=a,∴△AOC为等腰直角三角形,∴∠OCA=45°,AB=√2a.(2)∵D为△ABC的外心,∴∠BAC为⊙D中弧BC所对的圆周角,∠BDC为弧BC所对圆心角,∴∠BDC=2∠BAC=90°,∴△BDC和△AOC均为等腰直角三角形,故△BCD∽△ACO∴△BCD与△ACO的周长之比等于相似比,记⊙D半径为R,∴Ra =√104,∴R=√104a∵在等腰直角△BCD中,BC=√1+a2,且BC=√2R,∴R=√1+a2√2∴√1+a 2√2=√104a ,解得a 2=4,又a >1,∴a=2,,故二次函数的解析式为y =x 2−x −2(3)当P 在AC 下方时,∠CBD=∠CAD=45°,且∠CAP=∠DBA ,∴∠PAO=∠CBO.tan ∠CBO=43,作PF ⊥x 轴于F ,∴43PF AF =,设AF=3m ,则PF=4m ,∴(23,4)P m m --代入二次函数可得59m =,∴120(,)39P -当P 在AC 上方时,作120(,)39-关于直线2y x =-对称点25(,)93M --,∴直线AM 的方程为3342y x =-,联立3342(1)(2)y x y x x ⎧=-⎪⎨⎪=+-⎩得1212,4x x ==-,∴此时P 点横坐标为14-,将14-代入抛物线可得,P 点纵坐标为2716,所以此时P 127(,)416- 综上所述,存在P 点的坐标为120(,)39-和127(,)416-。


2024年扬州市初中毕业升学考试数学一、选择题(本大题共有8小题,每小题3分,共24分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将该选项的字母代号填涂在答题卡相应位置上)1.实数2的倒数是()A.2- B.2C.12-D.122.“致中和,天地位焉,万物育焉”,对称之美随处可见.下列选项分别是扬州大学、扬州中国大运河博物馆、扬州五亭桥、扬州志愿服务的标识.其中的轴对称图形是()A. B. C. D.3.下列运算中正确的是()A.222()a b a b -=-B.523a a a -=C.()235a a = D.236326a a a ⋅=4.第8个全国近视防控宣传教育月的主题是“有效减少近视发生,共同守护光明未来”.某校积极响应,开展视力检查.某班45名同学视力检查数据如下表:视力 4.34.44.54.64.74.84.95.0人数7447111053这45名同学视力检查数据的众数是()A.4.6B.4.7C.4.8D.4.95.在平面直角坐标系中,点()1,2P 关于原点的对称点P'的坐标是()A.()1,2 B.()1,2- C.()1,2- D.()1,2--6.如图是某几何体的表面展开后得到的平面图形,则该几何体是()A.三棱锥B.圆锥C.三棱柱D.长方体7.在平面直角坐标系中,函数42=+y x 的图像与坐标轴的交点个数是()A.0B.1C.2D.48.1202年数学家斐波那契在《计算之书》中记载了一列数:1,1,2,3,5,……,这一列数满足:从第三个数开始,每一个数都等于它的前两个数之和.则在这一列数的前2024个数中,奇数的个数为()A.676B.674C.1348D.1350二、填空题(本大题共有10小题,每小题3分,共30分.不需写出解答过程,请把答案直接填写在答题卡相应位置上)9.近年来扬州经济稳步发展:2024年4月26日,扬州市统计局、国家统计局扬州调查队联合发布一季度全市实现地区生产总值约18700000万元,把18700000这个数用科学记数法表示为____.10.分解因式:2242a a -+=_____.11.某学习小组做抛掷一枚瓶盖的实验,整理的实验数据如表:累计抛掷次数501002003005001000200030005000盖面朝上次数2854106158264527105615872650盖面朝上频率0.56000.54000.53000.52670.52800.52700.52800.52900.530随着实验次数的增大,“盖面朝上”的概率接近于__________(精确到0.01).12.有意义,则x 的取值范围是___.13.若用半径为10cm 的半圆形纸片围成一个圆锥的侧面,则这个圆锥底面圆的半径为____cm .14.如图,已知一次函数(0)y kx b k =+≠的图象分别与x ,y 轴交于A,B 两点,若2OA =,1OB =,则关于x 的方程0kx b +=的解为_____.15.《九章算术》是中国古代的数学专著,是《算经十书》中最重要的一部,书中第八章内容“方程”里记载了一个有趣的追及问题,可理解为:速度快的人每分钟走100米,速度慢的人每分钟走60米,现在速度慢的人先走100米,速度快的人去追他.问速度快的人追上他需要____分钟.16.物理课上学过小孔成像的原理,它是一种利用光的直线传播特性实现图像投影的方法.如图,燃烧的蜡烛(竖直放置)AB 经小孔O 在屏幕(竖直放置)上成像A B ''.设36cm AB =,24cm A B ''=.小孔O 到AB 的距离为30cm ,则小孔O 到A B ''的距离为_____cm .17.如图,在平面直角坐标系中,点A 的坐标为(1,0),点B 在反比例函数(0)ky x x=>的图像上,BC x ⊥轴于点C,30BAC ∠=︒,将ABC 沿AB 翻折,若点C 的对应点D 落在该反比例函数的图像上,则k 的值为_____.18.如图,已知两条平行线1l ,2l ,点A 是1l 上的定点,2AB l ⊥于点B,点C,D 分别是1l ,2l 上的动点,且满足AC BD =,连接CD 交线段AB 于点E,BH CD ⊥于点H,则当BAH ∠最大时,sin BAH ∠的值为_____.三、解答题(本大题共有10小题,共96分.请在答题卡指定区域内作答,解答时应写出必要的文字说明、证明过程或演算步骤)19.(1)计算:0|3|2sin 302)π-+︒--(2)化简:2(2)1x x x -÷-+.20.解不等式组260412x x x -≤⎧⎪⎨-<⎪⎩,并求出它的所有整数解的和.21.2024年5月28日,神舟十八号航天员密切协同,完成出舱活动,活动时长达8.5小时,刷新了中国航天员单次出舱活动时间纪录,进一步激发了青少年热爱科学的热情.某校为了普及“航空航天”知识,从该校1200名学生中随机抽取了200名学生参加“航空航天”知识测试,将成绩整理绘制成如下不完整的统计图表:成绩统计表组别成绩x (分)百分比A 组60x <5%B 组6070x ≤<15%C 组7080x ≤<aD 组8090x ≤<35%E 组90100x ≤≤25%成绩条形统计图根据所给信息,解答下列问题:(1)本次调查的成绩统计表中=a ________%,并补全条形统计图(2)这200名学生成绩的中位数会落在________组(填A,B,C,D 或E )(3)试估计该校1200名学生中成绩在90分以上(包括90分)的人数.22.2024年“五一”假期,扬州各旅游景区持续火热.小明和小亮准备到东关街、瘦西湖、运河三湾风景区、个园、何园(分别记作A,B,C,D,E )参加公益讲解活动.(1)若小明在这5个景区中随机选择1个景区,则选中东关街的概率是______(2)小明和小亮在C,D,E 三个景区中,各自随机选择1个景区,请用画树状图或列表的方法,求小明和小亮选到相同景区的概率.23.为了提高垃圾处理效率,某垃圾处理厂购进A,B 两种机器,A 型机器比B 型机器每天多处理40吨垃圾,A 型机器处理500吨垃圾所用天数与B 型机器处理300吨垃圾所用天数相等.B 型机器每天处理多少吨垃圾?24.如图1,将两个宽度相等的矩形纸条叠放在一起,得到四边形ABCD .(1)试判断四边形ABCD 的形状,并说明理由(2)已知矩形纸条宽度为2cm ,将矩形纸条旋转至如图2位置时,四边形ABCD 的面积为28cm ,求此时直线AD CD 、所夹锐角1 的度数.25.如图,已知二次函数2y x bx c =-++的图像与x 轴交于(2,0)A -,(1,0)B 两点.(1)求b c 、的值(2)若点P 在该二次函数的图像上,且PAB 的面积为6,求点P 的坐标.26.如图,已知PAQ ∠及AP 边上一点C .(1)用无刻度直尺和圆规在射线AQ 上求作点O ,使得2COQ CAQ ∠=∠.(保留作图痕迹,不写作法)(2)在(1)的条件下,以点O 为圆心,以OA 为半径的圆交射线AQ 于点B ,用无刻度直尺和圆规在射线CP 上求作点M ,使点M 到点C 的距离与点M 到射线AQ 的距离相等.(保留作图痕迹,不写作法)(3)在(1),(2)的条件下,若3sin 5A =,12CM =,求BM 的长.27.如图,点A B M E F 、、、、依次在直线l 上,点A B 、固定不动,且2AB =,分别以AB EF 、为边在直线l 同侧作正方形ABCD ,正方形EFGH ,90PMN ∠=︒,直角边MP 恒过点C ,直角边MN 恒过点H .(1)如图1,若10BE =,12EF =,求点M 与点B 之间的距离(2)如图1,若10BE =,当点M 在点B E 、之间运动时,求HE 的最大值(3)如图2,若22BF =,当点E 在点B F 、之间运动时,点M 随之运动,连接CH ,点O 是CH 的中点,连接HB MO 、,则2OM HB +的最小值为_______.28.在综合实践活动中,“特殊到一般”是一种常用方法,我们可以先研究特殊情况,猜想结论,然后再研究一般情况,证明结论.如图,已知ABC ,CA CB =,O 是ABC 的外接圆,点D 在 O 上(AD BD >),连接AD ,BD ,CD .【特殊化感知】(1)如图1,若60ACB ∠=︒,点D 在AO 延长线上,则AD BD -与CD 的数量关系为________【一般化探究】(2)如图2,若60ACB ∠=︒,点C ,D 在AB 同侧,判断AD BD -与CD 的数量关系并说明理由【拓展性延伸】(3)若ACB α∠=,直接写出AD ,BD ,CD 满足的数量关系.(用含α的式子表示)2024年扬州市初中毕业升学考试数学解析一、选择题.题号12345678答案DCBBDCBD8.【解析】这一列数为:1,1,2,3,5,8,13,21,34,…可以发现每3个数为一组,每一组前2个数为奇数,第3个数为偶数.由于202436742÷= 即前2024个数共有674组,且余2个数∴奇数有674221350⨯+=个.故选:D二、填空题.9.【答案】71.8710⨯10.【答案】()221a -11.【答案】0.5312.【答案】2x ≥13.【答案】514.【答案】2x =-15.【答案】2.516.【答案】2017.【答案】18.【答案】13【解析】解:∵两条平行线1l ,2l ,点A 是1l 上的定点,2AB l ⊥于点B ∴点B 为定点,AB 的长度为定值∵12l l ∥∴ACE BDE ∠=∠,CAE DBE=∠∠∵AC BD=∴()ASA ACE BDE ≌∴12BE AE AB ==∵BH CD ⊥∴90BHE ∠=︒∴点H 在以BE 为直径的圆上运动如图,取线段BE 的中点O,以点O 为圆心,OB 为半径画圆则点H 在O 上运动∴当AH 与O 相切时BAH ∠最大∴OH AH ⊥∵2AE OB OE ==∴3AO AE OE OE =+=∵OH OE =∴3sin 13OH OE AO O BAH E ==∠=故答案为:13.三、解答题.19.【答案】(1)3π-.(2)11x +20.【答案】132x <≤,整数和为621.【答案】(1)20,条形统计图见详解(2)D(3)300人【小问1详解】5153522105%%%%%a -=---=C 组人数为:20020%40⨯=补全条形统计图如图所示:故答案为:20【小问2详解】055124005%%%%%+=<+51532075505%%%%++=>+∴200名学生成绩的中位数会落在D 组.【小问3详解】120025%300⨯=(人)估计该校1200名学生中成绩在90分以上(包括90分)的人数为300人.22.【答案】(1)15(2)13【小问1详解】解:由题意得从这些景区随机选择1个景区,选中东关街的有1种可能∴选中东关街的概率是15故案䅁为:15【小问2详解】共有9种等可能结果,其中小明和小亮选到相同景区的结果有3种结果∴小明和小亮选到相同景区的概率:3193P ==答:小明和小亮选到相同景区的概率13.23.【答案】B 型机器每天处理60吨【解析】解:设B 型机器每天处理x 吨垃圾,则A 型机器每天处理(40)x +吨垃圾根据题意,得50030040x x=+解得60x =.经检验,60x =是所列方程的解.答:B 型机器每天处理60吨.24.【答案】(1)四边形ABCD 是菱形,理由见详解(2)130∠=︒【小问1详解】解:四边形ABCD 是菱形,理由如下如图所示,过点A 作AT NP ⊥于点T ,过点C 作CU EH ⊥于点U 根据题意,四边形EFGH ,四边形MNPQ 是矩形∴////EH FG MQ NP,∴////AB DC AD BC,∴四边形ABCD 是平行四边形∵宽度相等,即AT CU =,且90ATB CUB ABT CBU ∠=∠=︒∠=∠,∴()ATB CUB AAS ≌∴AB CB=∴平行四边形ABCD 是菱形【小问2详解】解:如图所示,过点A 作AR CD ⊥于点R根据题意,2AR cm=∵·8ABCD S CD AR ==四边形∴4CD =由(1)可得四边形ABCD 是菱形∴4AD =在Rt ATD 中,12AR AD =∴130∠=︒.25.【答案】(1)12b c =-=,(2)122434()()P P ---,,,【小问1详解】解:二次函数2y x bx c =-++的图像与x 轴交于(2,0)A -,(1,0)B 两点∴42010b c b c --+=⎧⎨-++=⎩解得,12b c =-⎧⎨=⎩∴12b c =-=,【小问2详解】解:由(1)可知二次函数解析式为:22y x x =--+,(2,0)A -,(1,0)B ∴1(2)3AB =--=设(),P m n ∴1·62PAB S AB n == ∴4n =∴4n =±∴当224x x --+=时,1870∆=-=-<,无解,不符合题意,舍去当224x x --+=-时,13x =-,22x =∴122434()()P P ---,,,.26.【答案】(1)作图见详解(2)作图见详解(3)BM =【小问1详解】解:如图所示∴2COQ CAQ∠=∠点O 即为所求【小问2详解】解:如图所示连接BC ,以点B 为圆心,以BC 为半径画弧交AQ 于点1B ,以点1B 为圆心,以任意长为半径画弧交AQ 于点11C D ,,分别以点11C D ,为圆心,以大于1112C D 为半径画弧,交于点1F ,连接11B F 并延长交AP 于点M ∵AB 是直径∴90ACB ∠=︒,即BC AP⊥根据作图可得11111111B C B D C F D F ==,∴1MB AQ ⊥,即190MB B ∠=︒,1MB 是点M 到AQ 的距离∵1BC BB =∴()1Rt BCM Rt BB M HL ≌∴1CM B M=点M 即为所求点的位置【小问3详解】解:如图所示根据作图可得,212COQ CAQ MC MW MC AQ ∠=∠==⊥,,,连接BC ∴在Rt AMW 中,3sin 5WM A AM ==∴55122033WM AM ⨯===∴20128AC AM CM =-=-=∵AB 是直径∴90ACB ∠=︒∴3sin 5BC A AB ==设3BC x =,则5AB x =∴在Rt ABC 中,()()222538x x =+解得,2x =(负值舍去)∴36BC x ==在Rt BCM 中,BM ===.【点睛】本题主要考查尺规作角等于已知角,尺规作垂线,作平行线,勾股定理,锐角三角函数的计算方法等知识的综合,掌握以上知识的综合运用是解题的关键.27.【答案】(1)4或6.(2)12.5.(3).【小问1详解】解:设BM x =,则10ME x =-∵四边形ABCD ,EFGH 是正方形∴90ABC CBM ∠=∠=︒,90HEF MEH ∠=∠=︒,2AB BC ==∴90CBM MEH ∠=∠=︒,90BCM CMB ∠+∠=︒∵90PMN ∠=︒∴90EMH CMB ∠+∠=︒∴BCM EMH∠=∠∴BCM EMH∽∴BC BM EM EH =,即21012x x =-,则210240x x -+=解得:6x =或4x =∴6BM =或4BM =【小问2详解】设BM x =,则10ME x=-∵四边形ABCD ,EFGH 是正方形∴90ABC CBM ∠=∠=︒,90HEF MEH ∠=∠=︒,2AB BC ==∴90CBM MEH ∠=∠=︒,90BCM CMB ∠+∠=︒∵90PMN ∠=︒∴90EMH CMB ∠+∠=︒∴BCM EMH∠=∠∴BCM EMH∽∴BC BM EM EH =,即210x x HE =-∴()22115512.522HE x x x =-+=--+当5BM =时,HE 有最大,最大值为12.5【小问3详解】连接FH∵四边形EFGH 是正方形∴45HFE ∠=︒即点H 在对角线FH 所在直线上运动如图,作B 关于FH 的对称点B ',连接B C ',过C 作CQ FG ⊥于点Q ∴'BF B F =,四边形BFQC 为矩形则点'B G Q 、、三点共线,2BC FQ ==,22CQ BF ==∴'22B F FB ==∴''20B Q B F FQ =-=∵90CMH ∠= ,点O 是CH 的中点∴12OM CH =∴2OM HB CH HB+=+∴当C H B '、、三点共线时,CH HB +有最小值B C '∴在Rt 'CB Q 中,由勾股定理得:2222'2220884221B C CQ B Q '=+=+==∴2OM HB +的最小值为2221故答案为:2221.28.【答案】(1)AD BD CD -=.(2)AD BD CD -=(3)当D 在 BC上时,2sin 2CD AD BD α⋅=-.当D 在 AB 上时,2sin 2CD AD BD α⋅=+【解析】解:∵CA CB =,60ACB ∠=︒∴ABC 是等边三角形,则60CAB ∠=︒∵O 是ABC 的外接圆∴AD 是BAC ∠的角平分线,则30DAB ∠=︒∴AD BC⊥∵四边形ACDB 是圆内接四边形∴120CDB ∠=︒∴30DCB DBC ∠=∠=︒设,AD BC 交于点E ,则BE CE =设1BD =,则1CD BD ==在Rt BDE △中∴33cos3022BE BD BD =︒⋅==∴3BC =∵AD 是直径,则90ABD Ð=°在Rt △ABD 中,2AD BD =2=∴211AD BD -=-=∴AD BD CD-=(2)如图所示,在AD 上截取DF BD=∵ AB AB=∴60ADB ACB ∠=∠=︒∴DBF 是等边三角形∴BF BD =,则60BFD ∠=︒∴120AFB ∠=︒∵四边形ACDB 是圆内接四边形∴120CDB ∠=︒∴AFB CDB∠=∠∵CA CB =,60ACB ∠=︒∴ABC 是等边三角形,则60CAB ∠=︒∴AB BC=又∵ BDBD =∴BCD BAF=∠∠在,AFB CDB 中AFB CDB BAF BCD AB CB ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()AAS AFB CDB ≌∴AF CD=∴AD BD AD DF AF CD -=-==即AD BD CD-=(3)解:①如图所示,当D 在 BC上时在AD 上截取DE BD=∵ AB AB=∴ACB ADB Ð=Ð又∵,CA CB DE DB==∴CAB DEB ∽,则ABC EBD ∠=∠∴AB BC EB BD =即AB EB BC BD =又∵ABC EBD ∠=∠∴ABE CBD ∠=∠∴ABE CBD V V ∽∴AE AB BE CD BC BD ==∵AE AD DE AD BD =-=-∴AD BD AB CD BC -=如图所示,作CF AB ⊥于点F在Rt BCF 中,1122BCF BAC α∠=∠=∴sin 2BC BF α⋅=∴2sin 2AB BC α=⋅∴2sin 2AD BD CD α-=,即2sin 2CD AD BD α⋅=-②当D 在 AB 上时,如图所示,延长BD 至G ,使得DG DA =,连接AG∵四边形ACDB 是圆内接四边形∴180GAD ACB ADB ∠=∠=︒-∠又∵,CA CB DG DA==∴CAB DAG ∽,则CAB DAG ∠=∠∴AC AB AD AG =即AC AD AB AG=又∵CAB DAG ∠=∠∴CAD BAG ∠=∠∴CAD BAG∽∴CD AC BG AB=∵BG BD DG BD AD=+=+同①可得2sin2AB AC α=⋅∴2sin 2CD AC AC BD AD AB AC α==+⋅∴2sin 2CD AD BD α⋅=+综上所述,当D 在 BC 上时,2sin 2CD AD BD α⋅=-.当D 在 AB 上时,2sin 2CD AD BD α⋅=+.。

2024年浙江省初中毕业生学业模拟考试(台州卷)数 学 试题卷亲爱的考生:欢迎参加考试!请你认真审题,仔细答题,发挥最佳水平. 答题时,请注意以下几点:1. 全卷共4页,满分120分,考试时间120分钟.2. 答案必须写在答题纸相应的位置上,写在试题卷、草稿纸上无效.3. 答题前,请认真阅读答题纸上的“注意事项”,按规定答题.4. 本次考试不得使用计算器.一、选择题(本题有10小题,每小题3分,共30分.请选出各题中一个符合题意的正确选项,不选、多选、错选,均不给分)1. “中国空间站”入选了2023年全球十大工程成就.空间站离地球的距离约为380 000米,数据380 000用科学计数法可表示为( ▲ ).A. 38×104B.3.8×106C.3.8×105D.0.38×106 2.下列四个2024年巴黎奥运会项目图标中,既是轴对称图形又是中心对称图形的是( ▲ ).A. B. C. D.3. 下列计算正确的是( ▲ ).A .32x x xB .523)(x xC .33)x x (D .326x x x4. 如图,直线AB ∥CD ,BC 平分∠ABD ,若∠1=55°,则∠2=( ▲ ).A .70°B .65°C .60°D .55°5. 对于平面图形上的任意两点P ,Q ,如果经过某种变换得到新图形上的对应点P ′,Q ′,保持PQ =P ′Q ′,我们把这种变换称为“保距变换”,下列变换中不一定是“保距变换”的是( ▲ ). A . 平移 B. 旋转 C. 轴对称 D. 位似 6. 小明的期中与期末测试成绩如下表:A.小明期末与期中总分相同B.小明英语期末名次一定在中等以上C.小明数学期末成绩比期中有进步D.小明语文期末成绩比期中有退步(第4题) (第7题) (第10题)DC B AG FE D C B A 2 1 D C B A7. 如图,Rt △ABC 中,∠ABC =90°,AB =3,BC =2,以点C 为圆心,BC 长为半径作圆弧交AC 于点D ,则AD 长在( ▲ ).A. 0与1之间 B . 1与2之间 C. 2与3之间 D. 3与4之间8. 有如下数列:a 1,a 2,a 3,a 4,a 5,a 6,...,a n-2,a n-1,a n ,...,满足a n -2·a n =2a n -1,已知a 1=1,a 3=4, 则a 2024=(▲).A.8B.6C.4D.29. 学校要制作一块广告牌,请来两名工人,已知甲单独完成需4天,乙单独完成需6天,若先由乙做1天,再两人合作,完成任务后共得到报酬900元,若按各人的工作量计算报酬,则分配方案为( ▲ ). A .甲360元,乙540元B .甲450元,乙450元C .甲300元,乙600元D .甲540元,乙360元10. 如图,在Rt △ABC 中,∠ACB =90°,以AB 为边向三角形外作正方形ABDE ,作EF ⊥BC 于点F ,交对角线AD 于点G ,连接BG. 要求△BFG 的周长,只需要知道( ▲ ). A.线段BF 的长度 B.线段AC 的长度 C.线段FG 的长度 D.线段BC 的长度 二、填空题(本题有6小题,每小题4分,共24分) 11. 分解因式:x 2 xy = ▲ .12. 一个不透明的口袋中有3个质地相同的小球,其中2个红色,1个蓝色. 随机摸取一个小球是红色小球的概率是 ▲ .13. 小明用刻度尺(单位:cm )测量某三角形部件的尺寸.如图所示,已知∠ACB=90°,D 是AB 的中点,点A ,B 对应的刻度分别是1,8,则CD = ▲ cm .14. 某绿化队原来用漫灌方式浇绿地,a 天用水m 吨,现改用喷灌方式,可使这些水所用的天数为2a 天,现在比原来每天节约用水 ▲ 吨.(用含a ,m 的代数式表示)15. 在平行四边形ABCD 中,点E ,F 在BC 边上,把△ABE 沿直线AE 折叠,△CDF 沿直线DF 折叠,使点B ,C 落在对角线AC 上的点G 处,若∠AGD =110°,则∠B 的度数为 ▲ .(第13题) (第15题)16. 已知抛物线k x a y +=2)2(-上有A (-2,y 1),B (1,y 2),C (4,y 3),D (5,y 4)四个点,某数学兴趣小组研究后得到三个命题:①若y 1+y 3 > y 2+y 4,则a > 0;②若y 2-y 3 > 0,则y 1-y 4 > 0; ③若y 2 y 3 = 0,则y 1 y 4 > 0. 属于真命题是 ▲ .(填写序号)三、解答题(本题有8小题,第17~19题每题6分,第20,21题每小题8分,第22,23题每题10分,第24题12分,共66分) 17.π0(2)2 .18. 解不等式组:14,23.x x xEGFDCBAA BC D19. 图1是太阳能路灯的实物图,图2是其示意图,AB 垂直于地面l ,AB =800 cm ,BC =105 cm ,∠ABC=108°,求点C 离地面的高度. (结果精确到1cm ,参考数据:sin18°≈0.31,cos18°≈0.95 ,tan18°≈0.31 )20. 如图,一次函数b kx y 与反比例函数xcy的图象相交于A ,B 两点,A ,B 的坐标分别为(2,n ),(-4,-2).(1)分别求出一次函数和反比例函数的解析式;(2)已知点M (m ,c ),B (m ,d ),分别在一次函数和反比例函数上,当c >d 时,直接写出m 的取值范围.(第20题) (第21题)21. 如图,在△ABC 中,∠ABC 的平分线BD 交AC 边于点D ,已知∠ADB =2∠ABD .(1)求证:AB ²=AD AC ;(2)若DC =2AD =2,求∠A 的度数.22. 某中学开展专家讲座,帮助学生合理规划周末使用手机的时间,并在讲座前后对本校学生周末手机使用时间情况进行随机抽样调查,制成如下统计图表(数据分组包含左端值不包含右端值).(1)在讲座开展前抽取的学生中周末使用时长在哪个区间的人数最多?占抽取人数的百分之几? (2)该校共有学生1500人,请估计讲座开展后全校周末使用手机8小时以上的学生人数;(3)小军认为,活动开展后的样本中周末使用手机6小时以上的人数与讲座前相比变化不大,所以讲座并没有起到效果.请结合统计图表,对小军分析数据的方法及讲座宣传活动的效果谈谈你的看法.DCBAlD BCA图1 图223. 图1是某校园的紫藤花架,图2是其示意图,它是以直线AB 为对称轴的轴对称图形,其中曲线AC ,AD ,BE ,BF 均是抛物线的一部分.图1 图2 图3素材1:某综合实践小组测量得到点A ,B 到地面距离分别为5米和4米.曲线AD 的最低点到地面的距离是4米,与点A 的水平距离是3米;曲线BF 的最低点到地面的距离是289米,与点B 的水平距离是4米.素材2:按图3的方式布置装饰灯带GH ,GI ,KL ,MN ,HJ ,布置好后成轴对称分布,其中GI ,KL ,MN ,HJ 垂直于地面, GI 与HJ 之间的距离比KL 与MN 之间的距离多2米.任务一:(1)在图2中建立适当的平面直角坐标系,求曲线AD 的函数解析式; 任务二:(2)若灯带GH 长度为d 米,求 MN 的长度.(用含d的代数式表示); 任务三:(3)求灯带总长度的最小值.24. 如图,半圆O 的直径AB =6.点C 在半圆O 上,连结AC ,BC ,过点O 作OD ∥AC 分别交BC , AB于点E ,D ,连结AD 交BC 于点F . (1)求证:点D 是 BC的中点; (2)将点O 绕点F 顺时针旋转90 °到点G .①当点G 在线段AD 上,求AC 的长;②当点G 在线段AC 上,求sin ∠ABC 的值.(第24题)FBOA E CDBO备用图A数学答案第1页共5页2024年浙江省初中毕业生学业模拟考试(台州卷)数学参考答案和评分细则一、选择题(本题有10小题,每小题3分,共30分)题号12345678910答案CACADBBDBD二、填空题(本题有6小题,每小题4分,共24分)11.x (x -y )12.2313.3.514.2m a15.75°16.①③三、解答题(本题有8小题,第17~19题每题6分,第20,21题每小题8分,第22,23题每题10分,第24题12分,共66分)17.(6分)解:原式=3+1-4…3分=0…6分18.(6分)解:由①得:5x <-…2分由②得:1x <…4分∴不等式组的解集为:5x <-.…6分19.(6分)解:过点C 作CE ⊥AD ,垂足为E∵CE ⊥AD ,∴∠CEB =90°∴∠C =∠ABC -∠AEC =18°…2分∵BE =BC sin ∠C ,∴BE =105×0.31=32.55≈33(cm )…4分AE =AB +BE =833cm…6分答:点C 距离地面的高度是833cm20.(8分)解:(1)将B (-4,-2)代入xcy =42-=-c 得解得c=8…2分∴反比例函数的解析式:xy 8=令x=2代入得y=4∴A(2,4)将点A (2,4),点B (-4,-2)代入y =kx +b 得⎩⎨⎧+-=-+=bk b k 4224…4分数学答案第2页共5页解得⎩⎨⎧==21b k ∴一次函数的解析式为y =x +2…6分(2)-4<m <0或m >2(写对一个一分共2分)21.(8分)解证明:(1)∵BD 平分∠ABC ∴∠ABC =2∠ABD =2∠DBC∵∠ADB =2∠ABD ∴∠ABC =2∠ADB ……………1分∵∠ADB =∠DBC +∠C ∴∠ABD =∠C………………2分∴△ABD ∽△ACB ………………3分∴ACABAB AD =即AB ²=AD ⋅AC ………………4分(2)由(1)得∠DBC =∠C ∴BD =CD =2……………1分∵2AD =2∴AD =1∴AC =3∵AB ²=AD ⋅AC ∴AB=3……………2分∴AB ²+AD ²=BD ²……………3分∴∠A =90°……………4分22.(10分)(1)在开展前周末手机使用时长为4~6小时的同学最多.……2分5+8+15+12+10=50(人)15÷50×100%=30%……4分(2)16+24+40+16+4=100(人)4÷100×100%=4%1500×4%=60(人)……2分由样本估计总体,全校讲座开展后周末使用手机8小时以上大约有60人……3分(3)因为忽略了两次样本容量的差异,所以小军分析的方法不合理……1分样本中周末使用手机时长6小时以上的人数由44%下降为20%,所以此次讲座宣传活动是有效果的.……2分(未运用统计量说明的给1分)23.(10分)(1)如图,以地面所在直线为x 轴,AB 所在直线为y 轴,建立如图所示的直角坐标系.设()234y a x =-+,代入()05A ,得:()25034a =-+,解得:19a =,()21349y x =-+ (3)分数学答案第3页共5页(2)2H d x =,12M d x =-,2113492M d y ⎛⎫=--+ ⎪⎝⎭214523699d d =-+214523699MN d d =-+…4分(3)设曲线BF 的函数解析式为:()22849y a x =-+,代入()04B ,得:()2284049a =-+解得:118a =,()21284189y x =-+设灯带总长度为w ,GH d =,22w MN HJ GH=++22145212822436991829d d d d⎡⎤⎛⎫⎛⎫=-++-++⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦2111761239d d =-+,当2x =时,1739w =最小值.…3分24.(12分)解:(1)解法一:∵AB 是半圆O 直径∴∠C =90°……………………2分∵OD ∥AC∴∠OEB =∠C =90°,即OD ⊥BC……………………3分∴ BD= CD ,即点D 是 BC 的中点……………………4分解法二:∵OD ∥AC ∴∠D =∠CAD ……………………1分∵OA =OD ∴∠D =∠OAD …………………2分∴∠OAD =∠CAD……………………3分∴ BD= CD ,即点D 是 BC 的中点……………………4分解法三:连结CO ∵AB 是半圆O 直径∴∠ACB =90°……………………2分∵OD ∥AC ∴∠OEB =∠ACB =90°,即OD ⊥BC……………………3分∵OB =OC ,OE =OE ∴Rt △BOE ≌Rt △COE (HL )∴∠BOD =∠COD ∴ BD = CD ,即点D 是 BC的中点……………………4分(说明:各种方法合理均可.)(2)①解法一:连结OF ,作FG =OF∵点O 绕点F 顺时针旋转90°到点G ∴∠OFG =90°∴AF =DF……………………1分FBOAE CDF OAEC D G数学答案第4页共5页又∵OD ∥AC∴∠D =∠CAD ,∠C =∠DEC ∴△ACF ≌△DEF (AAS )……………………2分(由平行线直接得△ACF ∽△DEF 也给分.)∴AC =DE ∵O 是AB 中点,OD ∥AC ∴AC =2OE ……………………3分∵直径AB =6∴OE +DE =OD =3∴AC =2……………………4分解法二:连结OF ,BD ,作FG =OF ∵点O 绕点F 顺时针旋转90°到点G ∴∠OFG =90°∴AF =DF……………………1分又∵AB 是半圆O 直径∴∠ADB =90°∴OF ∥BD∴△OEF ∽△DEB ,OF :BD =1:2……………………2分∴DE =2OE ∵直径AB =6∴OE =1……………………3分∵O 是AB 中点,OD ∥AC ∴AC =2OE =2……………………4分(2)②解法一:如图,构造对应图形易证△CFG ≌△EOF………………1分∴OE =CF 由①得,AC =2OE ,△ACF ∽△DEF .设OE =CF =x ,则AC =2x ,DE =3-x ∴CF :AC =EF :DE =1:2∴EF =……………………2分∴CE =BE =CF +EF =∴在Rt △BOE 中,解得:x =1.8……………………3分∴sin ∠ABC ==0.6……………………4分(说明:各种方法合理均可.如:连结BD,通过比例和勾股定理求BD 的长等也可解决问题)解法二:如图,构造对应图形,作FH ⊥AB 于点H 易证△CFG ≌△EOF……………………1分∴OE =CF ,EF =CG ,∠OFE =∠CGF 易证△CFG ≌△HFO ,△CFA ≌△HFA ∴AC =AH =3,∠OFE =∠CGF =∠BOF ∴AG =AO =BO =BF =3……………………2分F B OAEC DGFBO AECD GF B O AE C DGH由①得,AC=2OE.设OE=CF=x,EF=CG=y,则AC=2x ∴2x-y=AG=3,x+y+y=BF=3(BC=2CE=2x+2y,再由AC2+BC2=AB2也可)解得:x=1.8……………………3分∴sin∠ABC==0.6……………………4分数学答案第5页共5页19.(本题满分6分)(第19题)21.(本题满分8分)(1)(4分)(第21题)(2)(4分)考号[0][1][2][3][4][5][6][7][8][9][0][1][2][3][4][5][6][7][8][9][0][1][2][3][4][5][6][7][8][9][0][1][2][3][4][5][6][7][8][9][0][1][2][3][4][5][6][7][8][9][0][1][2][3][4][5][6][7][8][9][0][1][2][3][4][5][6][7][8][9][0][1][2][3][4][5][6][7][8][9]20.(本题满分8分)(1)(6分)(2)(2分).(第20题)一、选择题(本题有10小题,每小题3分,共30分,请选出各题中一个符合题意的正确选项,不选、多选、错选,均不给分)18.(本题满分6分)解不等式组:1423.x x x ⎧⎨⎩+<-,<+2024年中考模拟考试(一)数学答题卷学校班级姓名说明1、准考证号和选择题请用2B 铅笔填涂;2、除选择题外请用0.5mm 黑色中性笔答题;3、保持答题卷整洁,请勿折叠.缺考标记:[](考生不得填涂)二、填空题(本题有6小题,每小题4分,共24分)11..12..13..14..15..16...17.(本题满分6分)计算:9+(π-2)0+|-2|.三、解答题(本题有8小题,第17~19题每题6分,第20,21题每小题8分,第22,23题每题10分,第24题12分,共66分)◤□■◤◥24.(本题满分12分)(1)(4分)(第24题)(2)①(4分)②(4分)22.(本题满分10分)(1)(4分)(2)(3分)(3)(3分)23.(本题满分10分)(1)(3分)(图2)(2)(4分)(图3)(3)(3分)模拟(一)数学答题卷第3页共4页模拟(一)数学答题卷第4页共4页。

扬州市2022年初中毕业、升学统一考试数学试题一、选择题:本题共8小题,每小题3分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. -2的相反数是()A. 2B. -2C. ±2D. -12【答案】A【解析】【分析】根据相反数的定义直接解答即可.【详解】解:-2的相反数是2.故选:A.【点睛】本题考查相反数,相反数的定义是:如果两个数只有符号不同,我们称其中一个数为另一个数的相反数,特别地,0的相反数还是0.2. 在平面直角坐标系中,点P(﹣3,a2+1)所在的象限是()A. 第一象限B. 第二象限C. 第三象限D. 第四象限【答案】B【解析】【详解】∵a2⩾0,∴a2+1⩾1,∴点P(−3,a2+1)所在的象限是第二象限.故选B.3. 《孙子算经》是我国古代经典数学名著,其中有一道“鸡兔同笼”问题:“今有鸡兔同笼,上有三十五头,下有九十四足.问鸡兔各几何?”学了方程(组)后,我们可以非常顺捷地解决这个问题,如果设鸡有x只,兔有y只,那么可列方程组为()A.354494x yx y+=ìí+=îB.354294x yx y+=ìí+=îC.944435x yx y+=ìí+=îD.352494x yx y+=ìí+=î【答案】D【解析】【分析】一只鸡1个头2个足,一只兔1个头4个足,利用共35头,94足,列方程组即可【详解】一只鸡1个头2个足,一只兔1个头4个足设鸡有x只,兔有y只由35头,94足,得:352494x y x y +=ìí+=î故选:D【点睛】本题考查方程组的实际应用,注意结合实际情况,即一只鸡1个头2个足,一只兔1个头4个足,去列方程4. 下列成语所描述的事件属于不可能事件的是( )A. 水落石出B. 水涨船高C. 水滴石穿D. 水中捞月【答案】D【解析】【分析】根据不可能事件的定义:在一定条件下一定不会发生的事件是不可能事件,进行逐一判断即可【详解】解:A 、水落石出是必然事件,不符合题意;B 、水涨船高是必然事件,不符合题意;C 、水滴石穿是必然事件,不符合题意;D 、水中捞月是不可能事件,符合题意;故选D【点睛】本题主要考查了不可能事件,熟知不可能事件的定义是解题的关键.5. 如图是某一几何体的主视图、左视图、俯视图,该几何体是( )A. 四棱柱B. 四棱锥C. 三棱柱D. 三棱锥【答案】B【解析】【分析】根据各个几何体三视图的特点进行求解即可.【详解】解:∵该几何体的主视图与左视图都是三角形,俯视图是一个矩形,而且两条对角线是实线,∴该几何体是四棱锥,故选B .【点睛】本题主要考查了由三视图还原几何体,熟知常见几何体的三视图是解题的关键.6. 如图,小明家仿古家具的一块三角形形状的玻璃坏了,需要重新配一块.小明通过电话给玻璃店老板提供相关数据,为了方便表述,将该三角形记为ABC D ,提供了下列各组元素的数据,配出来的玻璃不一定符合要求的是( )A. ,,AB BC CAB. ,,AB BC B ÐC. ,,AB AC B ÐD. ,,ÐÐA B BC【答案】C【解析】【分析】根据SSS ,SAS ,ASA 逐一判定,其中SSA 不一定符合要求.【详解】A. ,,AB BC CA .根据SSS 一定符合要求;B. ,,AB BC B Ð.根据SAS 一定符合要求;C. ,,AB AC B Ð.不一定符合要求;D. ,,ÐÐA B BC .根据ASA 一定符合要求.故选:C .【点睛】本题考查了三角形全等的判定,解决问题的关键是熟练掌握判定三角形全等的SSS ,SAS ,ASA 三个判定定理.7. 如图,在ABC D 中,AB AC <,将ABC V 以点A 为中心逆时针旋转得到ADE V ,点D 在BC 边上,DE 交AC 于点F .下列结论:①AFE DFC △△;②DA 平分BDE Ð;③CDF BAD Ð=Ð,其中所有正确结论的序号是( )A. ①②B. ②③C. ①③D. ①②③【答案】D【解析】【分析】根据旋转的性质可得对应角相等,对应边相等,进而逐项分析判断即可求解.【详解】解:∵将ABC V 以点A 为中心逆时针旋转得到ADE V ,∴ADE ABC V V ≌,E C \Ð=Ð,AFE DFC Ð=ÐQ ,\AFE DFC △△,故①正确;Q ADE ABC V V ≌,AB AD \=,ABD ADB \Ð=Ð,ADE ABC Ð=ÐQ ,ADB ADE \Ð=Ð,\DA 平分BDE Ð,故②正确;Q ADE ABC V V ≌,BAC DAE \Ð=Ð,BAD CAE \Ð=Ð,Q AFE DFC △△,CAE CDF \Ð=Ð,CDF BAD Ð=Ð\,故③正确故选D【点睛】本题考查了性质的性质,等边对等角,相似三角形的性质判定与性质,全等三角形的性质,掌握以上知识是解题的关键.8. 某市举行中学生党史知识竞赛,如图用四个点分别描述甲、乙、丙、丁四所学校竞赛成绩的优秀率(该校优秀人数与该校参加竞赛人数的比值)y 与该校参加竞赛人数x 的情况,其中描述乙、丁两所学校情况的点恰好在同一个反比例函数的图像上,则这四所学校在这次党史知识竞赛中成绩优秀人数最多的是( )A. 甲B. 乙C. 丙D. 丁【答案】C【解析】【分析】根据反比例函数图像与性质求解即可得到结论.【详解】解:描述乙、丁两所学校情况的点恰好在同一个反比例函数的图像上,设反比例函数表达式为k y x=,则令甲()11,x y 、乙()22,x y 、丙()33,x y 、丁()44,x y ,过甲点作y 轴平行线交反比例函数于()11,x y ¢,过丙点作y 轴平行线交反比例函数于()33,x y ¢,如图所示:由图可知1133,y y y y ¢¢><,\()11,x y ¢、乙()22,x y 、()33,x y ¢、丁()44,x y 在反比例函数k y x=图像上,根据题意可知xy =优秀人数,则①2244x y k x y ==,即乙、丁两所学校优秀人数相同;②1111x y x y k ¢<=,即甲学校优秀人数比乙、丁两所学校优秀人数少;③3333x y x y k ¢>=,即丙学校优秀人数比乙、丁两所学校优秀人数多;综上所述:甲学校优秀人数<乙学校优秀人数=丁学校优秀人数<丙学校优秀人数,\在这次党史知识竞赛中成绩优秀人数最多的是丙学校,故选:C .【点睛】本题考查反比例函数图像与性质的实际应用题,读懂题意,并熟练掌握反比例函数的图像与性质是解决问题的关键.二、填空题(本大题共有10小题,每小题3分,共30分.不需要写解答过程,请把答案直接写在答题卡相应位置上)9. 扬州市某天的最高气温是6℃,最低气温是-2℃,那么当天的日温差是__.【答案】8℃.【解析】【详解】用最高温度减去最低温度即可得当天日温差:6-(-2)=6+2=8℃.10.在实数范围内有意义,则x 的取值范围是_______.【答案】1³x 【解析】【分析】先根据二次根式有意义的条件列出关于x 的不等式,求出x 的取值范围即可.【详解】解:在实数范围内有意义,∴x -1≥0,解得x ≥1.故答案为:x ≥1.【点睛】本题考查的是二次根式有意义的条件,即被开方数大于等于0.11. 分解因式233m -=_____.【答案】3(x-1)(x+1)【解析】【分析】注意将提取公因式与乘法公式综合应用,将整式提取公因式后再次利用公式分解.【详解】解:3m 2-3=3(m 2-1)=3(m -1)(m +1)故答案:3(m -1)(m +1).【点睛】本题考查的是提公因式法与公式法分解因式的综合运用.分解因式时,有公因式的,先提公因式,再考虑运用何种公式法来分解.12. 请填写一个常数,使得关于x 方程22+-x x ____________0=有两个不相等的实数根.【答案】0(答案不唯一)【解析】【分析】设这个常数为a ,利用一元二次方程根的判别式求出a 的取值范围即可得到答案.【详解】解:设这个常数为a ,∵要使原方程有两个不同的实数根,的为的∴()2=240a D -->,∴1a <,∴满足题意的常数可以为0,故答案为:0(答案不唯一).【点睛】本题主要考查了一元二次方程根的判别式,熟知一元二次方程根的判别式是解题的关键.13. 如图,函数()0y kx b k =+<的图像经过点P ,则关于x 的不等式3kx b +>的解集为________.【答案】1x <-【解析】【分析】观察一次函数图像,可知当y >3时,x 的取值范围是1x <-,则3kx b +>的解集亦同.【详解】由一次函数图像得,当y >3时,1x <-,则y =kx+b >3的解集是1x <-.【点睛】本题考查了一次函数与不等式结合,深入理解函数与不等式的关系是解题的关键.14. 掌握地震知识,提升防震意识.根据里氏震级的定义,地震所释放出的能量E 与震级n 的关系为1.510n E k =´(其中k 为大于0的常数),那么震级为8级的地震所释放的能量是震级为6级的地震所释放能量的________倍.【答案】1000【解析】【分析】分别求出震级为8级和震级为6级所释放的能量,然后根据同底数幂的除法即可得到答案.【详解】解:根据能量E 与震级n 的关系为 1.510n E k =´(其中k 为大于0的常数)可得到,当震级为8级的地震所释放的能量为: 1.58121010k k ´´=´,当震级为6级的地震所释放的能量为: 1.5691010k k ´´=´,12391010100010k k ´==´Q ,\震级为8级的地震所释放的能量是震级为6级的地震所释放能量的1000倍.故答案为:1000.【点睛】本题考查了利用同底数幂的除法底数不变指数相减的知识,充分理解题意并转化为所学数学知识是解题的关键.15. 某射击运动队进行了五次射击测试,甲、乙两名选手的测试成绩如图所示,甲、乙两选手成绩的方差分别记为22S S 乙甲、,则2S 甲________2S 乙.(填“>”“<”或“=”)【答案】>【解析】【分析】分别求出平均数,再利用方差的计算公式计算甲、乙的方差,进行比较即可.【详解】根据折线统计图中数据,()51093857x =++++¸=甲,()8686757x =++++¸=乙,∴()()()()()222222157107973787 6.85s éù=´-+-+-+-+-=ëû甲,()()()()()222222187678767770.85s éù=´-+-+-+-+-=ëû乙,∴22s s >乙甲,故答案为:>.【点睛】本题主要考查平均数和方差的计算,掌握方差的计算公式是解答本题的关键.16. 将一副直角三角板如图放置,已知60E Ð=°,45C Ð=°,EF BC ∥,则BND Ð=________°.【答案】105【解析】【分析】根据平行线的性质可得45FAN B Ð=Ð=°,根据三角形内角和定理以及对顶角相等即可求解.【详解】45B C аÐ==Q ,EF BC ∥,\45FAN B Ð=Ð=°,∵∠E =60°,∴∠F =30°,180105BND ANF F BAF \Ð=Ð=°-Ð-Ð=°故答案为:105【点睛】本题考查了平行线的性质,三角形内角和定理,掌握平行线的性质是解题的关键.17. “做数学”可以帮助我们积累数学活动经验.如图,已知三角形纸片ABC ,第1次折叠使点B 落在BC 边上的点B ¢处,折痕AD 交BC 于点D ;第2次折叠使点A 落在点D 处,折痕MN 交AB ¢于点P .若12BC =,则MP MN +=_____________.【答案】6【解析】【分析】根据第一次折叠的性质求得12BD DB BB ¢¢==和AD BC ^,由第二次折叠得到AM DM =,MN AD ^,进而得到MN BC P ,易得MN 是ADC V 的中位线,最后由三角形的中位线求解.【详解】解:∵已知三角形纸片ABC ,第1次折叠使点B 落在BC 边上的点B ¢处,折痕AD 交BC 于点D ,∴12BD DB BB ¢¢==,AD BC ^.∵第2次折叠使点A 落在点D 处,折痕MN 交AB ¢于点P ,∴AM DM =,AN ND =,∴MN AD ^,∴MN BC P .∵AM DM =,∴MN 是ADC V 的中位线,∴12MP DB ¢=,12MN DC =.∵12BC =,2BD DC CB BD BC +=+¢=,∴()111162222MP MN DB DC DB DB B C BC +=+=+=¢+¢¢=¢.故答案为:6.【点睛】本题主要考查了折叠的性质和三角形中位线的性质,理解折叠的性质,三角形的中位线性质是解答关键.18. 在ABC D 中,90C Ð=°,a b c 、、分别为A B C ÐÐÐ、、的对边,若2b ac =,则sin A 的值为__________.【解析】【详解】解:如图所示:在Rt ABC V 中,由勾股定理可知:222+=a b c ,2ac b =Q ,22a ac c \+=,0a >Q , 0b >,0c >,2222a ac c c c +\=,即:21a a c cæö+=ç÷èø,求出a c =或a c =,\在Rt ABC V 中:in s a c A ==,【点睛】本题考查了锐角三角函数的概念及勾股定理,熟练掌握锐角三角函数的定义是解答本题的关键.在Rt ABC V 中,sin A A Ð=的对边斜边 ,cos A A Ð=的邻边斜边,tan A A A Ð=Ð的对边的邻边.三、解答题(本大题共有10小题,共96分.解答时应写出必要的文字说明、证明过程或演算步骤)19. 计算:(1)(02cos 45p °+-(2)22221121m m m m +æö+¸ç÷--+èø【答案】(1)1(2)12m -【解析】【分析】(1)根据特殊锐角三角函数值、零指数幂、二次根式进行计算即可;(2)先合并括号里的分式,再对分子和分母分别因式分解即可化简;【小问1详解】解:原式=21+-=1-.【小问2详解】解:原式=()()21211121m m m m m --æö+×ç÷--+èø=()()211121m m m m -+×-+=12m -.【点睛】本题主要考查分式的化简、特殊锐角三角函数值、零指数幂、二次根式的计算,掌握相关运算法则是解题的关键.20. 解不等式组221213x x x x -£ìï+í-<ïî,并求出它的所有整数解的和.【答案】3【解析】【分析】先解每个不等式,求得不等式组的解集,然后找出所有整数解求和即可.【详解】解:221213x x x x -£ìïí+-<ïî①②解不等式①,得2x ³-,解不等式②,得4x <,∴不等式组的解集为24x -£<,∴不等式组的所有整数解为:2- ,1- ,0 ,1 ,2 ,3∴所有整数解的和为:()2101233-+-++++=.【点睛】本题考查了求不等式组的解集,正确地解每一个不等式是解题的关键.21. 某校初一年级有600名男生 ,为增强体质,拟在初一男生中开展引体向上达标测试活动.为制定合格标准,开展如下调查统计活动.(1)A 调查组从初一体育社团中随机抽取20名男生进行引体向上测试,B 调查组从初一所有男生中随机抽取20名男生进行引体向上测试,其中_________(填“A ”或“B ”),调查组收集的测试成绩数据能较好地反映该校初一男生引体向上的水平状况;(2)根据合理的调查方式收集到的测试成绩数据记录如下:成绩/个23457131415人数/人11185121这组测试成绩的平均数为_________个,中位数为__________个;(3)若以(2)中测试成绩的中位数作为该校初一男生引体向上的合格标准,请估计该校初一有多少名男生不能达到合格标准.【答案】(1)B (2)7;5(3)90名【解析】【分析】(1)根据随机调查要具有代表性考虑即可求解;(2)利用加权平均数公式计算,再根据中位数的概念确定这组测试成绩的中位数即可;(3)根据中位数确定样本中不合格的百分比,再乘以该校初一男生的总人数即可求解.【小问1详解】解:∵随机调查要具有代表性,∴从初一所有男生中随机抽取20名男生进行引体向上测试,能较好地反映该校初一男生引体向上的水平状况,故答案为:B;【小问2详解】解:23458751314215=720+++´+´++´+;这组数据排序后,中位数应该是第10,11两个人成绩的平均数,而第10,11两人的成绩都是5,∴这组测试成绩的中位数为55=5 2+,故答案为:7;5【小问3详解】解:以(2)中测试成绩的中位数5作为该校初一男生引体向上的合格标准,则这组测试成绩不合格的人数有3人,∴不合格率为3100%=15% 20´,∴该校初一男生不能达到合格标准的人数为60015%=90´(名).【点睛】本题考查了随机调查,中位数,众数以及利用样本估计总体,读懂题意,理解概念是解题关键.22. 某超市为回馈广大消费者,在开业周年之际举行摸球抽奖活动.摸球规则如下:在一只不透明的口袋中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后先从中任意摸出1个球(不放回),再从余下的2个球中任意摸出1个球.(1)用树状图列出所有等可能出现的结果;的(2)活动设置了一等奖和二等奖两个奖次,一等奖的获奖率低于二等奖.现规定摸出颜色不同的两球和摸出颜色相同的两球分别对应不同奖次,请写出它们分别对应的奖次,并说明理由.【答案】(1)见解析(2)见解析【解析】【分析】(1)首先根据题意画出树状图,由树状图即可求得所有等可能的结果;(2)根据树状图找出颜色不同的两球和摸出颜色相同的两球的情况,即可得解.【小问1详解】解:画树状图如下:由树状图知共有6种情况;【小问2详解】解:由(1)知抽到颜色相同的两球共有2种情况,抽到颜色不同的两球共有4种情况,所以抽到颜色相同的两球对应一等奖,抽到颜色不同的两球对应二等奖.【点睛】此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.23. 某中学为准备十四岁青春仪式,原计划由八年级(1)班的4个小组制作360面彩旗,后因1个小组另有任务,其余3个小组的每名学生要比原计划多做3面彩旗才能完成任务.如果这4个小组的人数相等,那么每个小组有学生多少名?【答案】每个小组有学生10名.【解析】【分析】设每个小组有学生x名,根据题意列出方程,求出方程的解即可得到结果.【详解】解:设每个小组有学生x名,根据题意,得3603603 34-=x x,解这个方程,得x=10,经检验,x=10是原方程的根,∴每个小组有学生10名.【点睛】此题考查了分式方程的应用,弄清题意是解本题的关键.24. 如图,在ABCD Y 中,BE 、D G 分别平分ABC ADC ÐÐ、,交AC 于点E G 、.(1)求证:,BE DG BE DG =∥;(2)过点E 作EF AB ^,垂足为F .若ABCD Y 的周长为56,6EF =,求ABC D 的面积.【答案】(1)见详解(2)84【解析】【分析】(1)由平行四边形的性质证()ABE CDG ASA D @D 即可求证;(2)作EQ BC ^,由ΔΔΔABC ABE EBC S S S =+即可求解;【小问1详解】证明:在ABCD Y 中,∵//AB CD ,∴BAE DCG Ð=Ð,∵BE 、D G 分别平分ABC ADC ÐÐ、,ABC ADC Ð=Ð,∴ABE CDG Ð=Ð,在ABE D 和CDG D 中,∵BAE DCG AB CDABE CDG Ð=Ðìï=íïÐ=Ðî∴()ABE CDG ASA D @D ,∴BE DG AEB CGD =Ð=Ð,,∴BE DG ∥.【小问2详解】如图,作EQ BC ^,∵ABCD Y 的周长为56,∴28AB BC +=,∵BE 平分ABC Ð,∴6EQ EF ==,∴()1138422ABC ABE EBC S S S EF AB EQ BC AB BC D D D =+=×+×=+=.【点睛】本题主要考查平行四边形的性质、三角形的全等、角平分线的性质,掌握相关知识并灵活应用是解题的关键.25. 如图,AB 为O e 的弦,OC OA ^交AB 于点P ,交过点B 的直线于点C ,且CB CP =.(1)试判断直线BC 与O e 的位置关系,并说明理由;(2)若sin 8A OA ==,求CB 的长.【答案】(1)相切,证明见详解(2)6【解析】【分析】(1)连接OB ,根据等腰三角形的性质得出A OBA Ð=Ð,CPB CBP Ð=Ð,从而求出90AOC OBC Ð=Ð=°,再根据切线的判定得出结论;(2)分别作OM AB ^交AB 于点M ,CN AB ^交AB 于N ,根据sin 8A OA ==求出OP ,AP 的长,利用垂径定理求出AB 的长,进而求出BP 的长,然后在等腰三角形CPB 中求解CB 即可.【小问1详解】证明:连接OB ,如图所示:CP CB OA OB ==Q ,,\A OBA Ð=Ð,CPB CBP Ð=Ð,APO CPB Ð=ÐQ ,APO CBP \Ð=Ð,OC OA ^Q ,即90AOP °=∠,90A APO OBA CBP OBC \Ð+Ð=°=Ð+Ð=Ð,OB BC \^,OB Q 为半径,经过点O ,\直线BC 与O e 的位置关系是相切.【小问2详解】分别作OM AB ^交AB 于点M ,CN AB ^交AB 于N ,如图所示:AM BM \=,CP CB AO CO =^Q ,,A APO PCN CPN \Ð+Ð=Ð+Ð,PN BN =,PCN BCNÐ=ÐA BCN\Ð==Ðsin A =Q ,8OA =,sin OM OP A OA AP \===4OM AM OP AP \====,2AB AM \==111()222PN BN PB AB AP \===-=´-=sin sin BN A BCN CB \=Ð==6CB \===.【点睛】本题考查了切线的证明,垂径定理的性质,等腰三角形,勾股定理,三角函数等知识点,熟练掌握相关知识并灵活应用是解决此题的关键,抓住直角三角形边的关系求解线段长度是解题的主线思路.26. 【问题提出】如何用圆规和无刻度的直尺作一条直线或圆弧平分已知扇形的面积?【初步尝试】如图1,已知扇形OAB ,请你用圆规和无刻度的直尺过圆心O 作一条直线,使扇形的面积被这条直线平分;【问题联想】如图2,已知线段MN ,请你用圆规和无刻度的直尺作一个以MN 为斜边的等腰直角三角形MNP ;【问题再解】如图3,已知扇形OAB ,请你用圆规和无刻度的直尺作一条以点O 为圆心的圆弧,使扇形的面积被这条圆弧平分.(友情提醒:以上作图均不写作法,但需保留作图痕迹)【答案】见解析【解析】【分析】【初步尝试】如图1,作∠AOB的角平分线所在直线即为所求;【问题联想】如图2,先作MN的线段垂直平分线交MN于点O,再以O为圆心MO为半径作圆,与垂直平分线的交点即为等腰直角三角形的顶点;【问题再解】如图3先作OB的线段垂直平分线交OB于点N,再以N为圆心NO为半径作圆, 与垂直平分线的交点为M,然后以O为圆心,OM为半径作圆与扇形OAB所交的圆弧即为所求.【详解】【初步尝试】如图所示,作∠AOB的角平分线所在直线OP即为所求;【问题联想】如图,先作MN的线段垂直平分线交MN于点O,再以O为圆心MO为半径作圆,与垂直平分线的交点即为等腰直角三角形的顶点;【问题再解】如图,先作OB的线段垂直平分线交OB于点N,再以N为圆心NO为半径作圆, 与垂直平分线的交点为M,然后以O为圆心,OM为半径作圆与扇形OAB所交的圆弧CD即为所求.【点睛】本题考查了尺规作图,角平分线的性质,线段垂直平分线的性质,扇形的面积等知识,解决此类题目的关键是熟悉基本几何图形的性质,掌握基本作图方法.27. 如图是一块铁皮余料,将其放置在平面直角坐标系中,底部边缘AB 在x 轴上,且8AB =dm ,外轮廓线是抛物线的一部分,对称轴为y 轴,高度8OC =dm .现计划将此余料进行切割:(1)若切割成正方形,要求一边在底部边缘AB 上且面积最大,求此正方形的面积;(2)若切割成矩形,要求一边在底部边缘AB 上且周长最大,求此矩形的周长;(3)若切割成圆,判断能否切得半径为3dm 圆,请说明理由.【答案】(1)(296dm - ;(2)20dm ;(3)能切得半径为3dm 的圆.【解析】【分析】(1)先把二次函数解析式求出来,设正方形的边长为2m ,表示在二次函数上点的坐标,代入即可得到关于m 的方程进行求解;(2)如详解2中图所示,设矩形落在AB 上的边DE =2n ,利用函数解析式求解F点坐标,进而表示出矩的形的周长求最大值即可;(3)设半径为3dm 的圆与AB 相切,并与抛物线小脚,设交点为N ,求出交点N 的坐标,并计算点N 是M e 与抛物线在y 轴右侧的切点即可.【小问1详解】由题目可知A (-4,0),B (4,0),C (0,8)设二次函数解析式为y=ax ²+bx+c ,∵对称轴为y 轴,∴b =0,将A 、C 代入得,a =12-,c =8则二次函数解析式为2182y x =-+,如下图所示,正方形MNPQ 即为符合题意得正方形,设其边长为2m ,则P 点坐标可以表示为(m ,2m )代入二次函数解析式得,21822m m -+=,解得122,2m m =-=-(舍去),∴2m =4-,()()222496m ==-则正方形的面积为(296dm -;【小问2详解】如下如所示矩形DEFG ,设DE =2n ,则E (n ,0)将x =n 代入二次函数解析式,得2182y n =-+,则EF =2182n -+,矩形DEFG 的周长为:2(DE +EF )=2(2n +2182n -+)=22416(2)20n n n -++=--+,当n =2时,矩形的周长最大,最大周长为20dm ;【小问3详解】若能切成圆,能切得半径为3dm 的圆,理由如下:如图,N 为M e 上一点,也是抛物线上一点,过点N 作M e 的切线交y 轴于点Q ,连接MN ,过点N 作NP ⊥y 轴于P ,设21,82N m m æö-+ç÷èø,由勾股定理得:222PM PN MN +=,∴222218332m m æö+-+-=ç÷èø解得:1m =,2m =-(舍去),∴()4N ,∴431PM =-=∵1cos 3PM MN NMP MN QM Ð===∴39QM MN ==∴()0,12Q 设QN 的解析式为:y kx b=+∴124b =ìïí+=ïî∴12k b ì=-ïí=ïî∴QN的解析式为:12y =-+与抛物线联立为:218122x -+=-+21402x -+=(214402D =--´´=所以此时N 为M e 与抛物线在y 轴右侧的唯一公共点,所以若切割成圆,能够切成半径为3dm 的圆.【点睛】本题考查了二次函数与几何结合,熟练掌握各图形的性质,能灵活运用坐标与线段长度之间的转换是解题的关键.28. 如图1,在ABC D 中,90,60BAC C Ð=°Ð=°,点D 在BC 边上由点C 向点B 运动(不与点B C 、重合),过点D 作DE AD ^,交射线AB 于点E .(1)分别探索以下两种特殊情形时线段AE 与BE 的数量关系,并说明理由;①点E 在线段AB 的延长线上且BE BD =;②点E 在线段AB 上且EB ED =.(2)若6AB =.①当DE AD =AE 的长;②直接写出运动过程中线段AE 长度的最小值.【答案】(1)①2AE BE =②2AE BE =(2)①215②4【解析】【分析】(1)①算出ABD △各个内角,发现其是等腰三角形即可推出;②算出ADE V 各内角发现其是30°的直角三角形即可推出;(2)①分别过点A ,E 作BC 的垂线,得到一线三垂直的相似,即EGD DHA ∽△△,设DE =,2AD a =,利用30°直角三角形的三边关系,分别表示出ED ,AD ,EG ,DH ,列式求解a 即可;②分别过点A ,E 作BC 的垂线,相交于点G ,H ,证明EHD DGA △△∽可得AG DG DH EH =,然后利用完全平方公式变形得出AE ≥3+E H ,求出AE 的取值范围即可.【小问1详解】①∵在ABC D 中,90BAC Ð=°,60C Ð=°∴30ABC Ð=°∵BE BD=∴1152BDE ABC Ð=Ð=°,90901575BDA BDE Ð=°-Ð=°-°=°在ABD △中,180180307575BAD ABD BDA Ð=°-Ð-Ð=°-°-°=°∴75BAD BDA Ð=Ð=°∴AB BD BE==∴2AE BE =;②如图:∵BE DE =∴30EBD EDB Ð=Ð=°,60AED Ð=°∴在Rt ADE △中,30EAD =∠°∴2AE ED=∴2AE BE =;【小问2详解】①分别过点A ,E 作BC 的垂线,相交于点H ,G ,则∠EGD =∠DHA =90°,∴∠GED +∠GDE =90°,∵∠HDA +∠GDE =90°,∴∠GED =∠HDA ,∴EGD DHA ∽△△,设DE =,2AD a =,则AE ==,6BE =,在Rt ABC V 中,30ABC Ð=°,AB =6则AC ==,2BC AC ==在Rt BEG △中,30EBG Ð=°,6BE =则32BE EG ==-在Rt AHC V 中,60C Ð=°,AC =∴3AH ==∴DH ==由EGD DHA ∽△△得ED EG AD DH =,=解得:1a=2a=-(舍)故215AE==;②分别过点A,E作BC的垂线,相交于点G,H,则∠EHD=∠AGD=90°,∵∠ADE=90°,∴∠EDH=90°-∠ADG=∠DAG,∵∠EHD=∠AGD=90°,∴EHD DGA△△∽,∴AG DGDH EH=,∴AG EH DH DG=g g,∵∠BAC=90°,∠C=60°,∴∠B=30°,∴111=36-)222AG AB BE AE==,E H=(,∴3DH DG EH=g,∴2222222AE AD DE AG DG DH EH=+=+++=2229DG DH EH+++,∵22DG DH+g≥2D GD H∴2292AE DG DH EH++g≥,∴22296AE EH EH++≥≥(3+E H),∵0,0AE DH>>,∴AE≥3+E H,∵16-)2AE=E H(,∴1(6)2AE AE-≥3+,∴4AE≥,故AE的最小值为4.【点睛】本题考查了直角三角形的性质,三角形相似的判定和性质,等腰三角形的性质,一线三垂直相似模型,垂线段最短,熟练掌握直角三角形的性质,一线三垂直模型,垂线段最短原理是解题的关键.。

2024年赤峰市初中毕业、升学统一考试试卷数学温馨提示:1.本试卷卷面分值150分,共8页,考试时间120分钟.2.答题前,考生务必将姓名、座位号、考生号填写在答题卡的相应位置上,并仔细阅读答题卡上的“注意事项”.3.答题时,请将答案填涂在答题卡上,写在本试卷上无效.4.考试结束后,将本试卷和答题卡一并交回.一、选择题(每小题给出的选项中只有一个符合题意,请将符合题意的选项序号,在答题卡的对应位置上按要求涂黑.每小题3分,共42分)1.在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是()A. B. C. D.2.央视新闻2024年5月31日报道,世界最大清洁能源走廊今年一季度累计发电超52000000000度,为我国经济社会绿色发展提供了强劲动能.将数据52000000000用科学记数法表示为()A.95.210⨯ B.110.5210⨯ C.95210⨯ D.105.210⨯3.将一副三角尺如图摆放,使有刻度的两条边互相平行,则1∠的大小为()A.100︒B.105︒C.115︒D.120︒4.下列计算正确的是()A.235a a a+= B.222()a b a b+=+ C.632a a a÷= D.()236a a=5.在数据收集、整理、描述的过程中,下列说法错误..的是()A.为了解1000只灯泡的使用寿命,从中抽取50只进行检测,此次抽样的样本容量是50B.了解某校一个班级学生的身高情况,适合全面调查C.了解商场的平均日营业额,选在周末进行调查,这种调查不具有代表性D.甲、乙二人10次测试的平均分都是96分,且方差2 2.5S=甲,2 2.3S=乙,则发挥稳定的是甲6.解不等式组()322211x x x x -<⎧⎪⎨+≥-⎪⎩①②时,不等式①和不等式②的解集在数轴上表示正确的是()A.B.C.D.7.如图,是正n 边形纸片的一部分,其中l m ,是正n 边形两条边的一部分,若l m ,所在的直线相交形成的锐角为60︒,则n 的值是()A.5B.6C.8D.108.某市为了解初中学生的视力情况,随机抽取200名初中学生进行调查,整理样本数据如下表.根据抽样调查结果,估计该市16000名初中学生中,视力不低于4.8的人数是()视力 4.7以下 4.7 4.8 4.9 4.9以上人数3941334047A.120B.200C.6960D.96009.等腰三角形的两边长分别是方程210210x x -+=的两个根,则这个三角形的周长为()A.17或13B.13或21C.17D.1310.如图,AD 是O 的直径,AB 是O 的弦,半径OC AB ⊥,连接CD ,交OB 于点E ,42BOC ∠=︒,则OED ∠的度数是()A.61︒B.63︒C.65︒D.67︒11.用1块A 型钢板可制成3块C 型钢板和4块D 型钢板;用1块B 型钢板可制成5块C 型钢板和2块D 型钢板.现在需要58块C 型钢板、40块D 型钢板,问恰好用A 型钢板、B 型钢板各多少块?如果设用A 型钢板x 块,用B 型钢板y 块,则可列方程组为()A.32404558x y x y +=⎧⎨+=⎩ B.35404258x y x y +=⎧⎨+=⎩ C.35584240x y x y +=⎧⎨+=⎩ D.34585240x y x y +=⎧⎨+=⎩12.如图,ABC 中,1AB BC ==,72C ∠=︒.将ABC 绕点A 顺时针旋转得到AB C ''△,点B'与点B 是对应点,点C '与点C 是对应点.若点C '恰好落在BC 边上,下列结论:①点B 在旋转过程中经过的路径长是15π;②B B A C '∥;③BD C D '=;④AB B B AC BD'=.其中正确的结论是()A.①②③④B.①②③C.①③④D.②④13.如图,数轴上点A ,M ,B 分别表示数a a bb +,,,若AM BM >,则下列运算结果一定是正数的是()A.a b +B.a b -C.abD.a b-14.如图,正方形ABCD 的顶点A ,C 在抛物线24y x =-+上,点D 在y 轴上.若A C ,两点的横坐标分别为m n ,(0m n >>),下列结论正确的是()A.1m n +=B.1m n -=C.1mn = D.1mn=二、填空题(请把答案填写在答题卡对应的横线上.每小题3分,共12分)15.请写出一个比小的整数_____________16.因式分解:233am a -=______.17.综合实践课上,航模小组用无人机测量古树AB 的高度.如图,点C 处与古树底部A 处在同一水平面上,且10AC =米,无人机从C 处竖直上升到达D 处,测得古树顶部B 的俯角为45︒,古树底部A 的俯角为65︒,则古树AB 的高度约为________米(结果精确到0.1米;参考数据:sin 650.906︒≈,cos650.423︒≈,tan 65 2.145︒≈).18.编号为A ,B ,C ,D ,E 的五台收割机,若同时启动其中两台收割机,收割面积相同的田地所需时间如下表:收割机编号A ,B B ,C C ,D D ,E A ,E 所需时间(小时)2319202218则收割最快的一台收割机编号是________.三、解答题(在答题卡上解答,答在本试卷上无效,解答时要写出必要的文字说明、证明过程或演算步骤.共8题,满分96分)19.(1()0π12sin 602+++︒+-;(2)已知230a a --=,求代数式2(2)(1)(3)a a a -+-+的值.20.如图,在ABC 中,D 是AB 中点.(1)求作:AC 的垂直平分线l (要求:尺规作图,不写作法,保留作图痕迹);(2)若l 交AC 于点E ,连接DE 并延长至点F ,使2EF DE =,连接BE CF ,.补全图形,并证明四边形BCFE 是平行四边形.21.某校田径队为了调动队员体育训练的积极性,计划根据成绩情况对队员进行奖励.为确定一个适当的成绩目标,进行了体育成绩测试,统计了每个队员的成绩,数据如下:收集数据777876728475918578798278767991917674758575918077757587857677整理、描述数据成绩/分72747576777879808284858791人数/人11a433b111314分析数据样本数据的平均数、众数、中位数如下表:平均数众数中位数80c78解决问题(1)表格中的=a ______;b =______;c =______;(2)分析平均数、众数、中位数这三个数据,如果想让一半左右的队员都能达到成绩目标,你认为成绩目标应定为______分,如果想确定一个较高的成绩目标,这个成绩目标应定为______分;(3)学校要从91分的A ,B ,C ,D 四名队员中,随机抽取两名队员去市里参加系统培训.请利用画树状图法或列表法,求A ,B 两名队员恰好同时被选中的概率.22.一段高速公路需要修复,现有甲、乙两个工程队参与施工,已知乙队平均每天修复公路比甲队平均每天修复公路多3千米,且甲队单独修复60千米公路所需要的时间与乙队单独修复90千米公路所需要的时间相等.(1)求甲、乙两队平均每天修复公路分别是多少千米;(2)为了保证交通安全,两队不能同时施工,要求甲队的工作时间不少于乙队工作时间的2倍,那么15天的工期,两队最多能修复公路多少千米?23.在平面直角坐标系中,对于点()11,M x y ,给出如下定义:当点()22,N x y ,满足1212x x y y +=+时,称点N 是点M 的等和点.(1)已知点()1,3M ,在()14,2N ,()23,1N -,()30,2N -中,是点M 等和点的有_____;(2)若点()3,2M -的等和点N 在直线y x b =+上,求b 的值;(3)已知,双曲线1ky x=和直线22y x =-,满足12y y <的x 取值范围是4x >或20x -<<.若点P 在双曲线1ky x=上,点P 的等和点Q 在直线22y x =-上,求点P 的坐标.24.如图,ABC 中,90ACB ∠=︒,AC BC =,O 经过B ,C 两点,与斜边AB 交于点E ,连接CO 并延长交AB 于点M ,交O 于点D ,过点E 作EF CD ∥,交AC 于点F .(1)求证:EF 是O 的切线;(2)若42BM =,1tan 2BCD ∠=,求OM 的长.25.如图,是某公园的一种水上娱乐项目.数学兴趣小组对该项目中的数学问题进行了深入研究.下面是该小组绘制的水滑道截面图,如图1,人从点A 处沿水滑道下滑至点B 处腾空飞出后落入水池.以地面所在的水平线为x 轴,过腾空点B 与x 轴垂直的直线为y 轴,O 为坐标原点,建立平面直角坐标系.他们把水滑道和人腾空飞出后经过的路径都近似看作是抛物线的一部分.根据测量和调查得到的数据和信息,设计了以下三个问题,请你解决.(1)如图1,点B 与地面的距离为2米,水滑道最低点C 与地面的距离为78米,点C 到点B 的水平距离为3米,则水滑道ACB 所在抛物线的解析式为______;(2)如图1,腾空点B 与对面水池边缘的水平距离12OE =米,人腾空后的落点D 与水池边缘的安全距离DE 不少于3米.若某人腾空后的路径形成的抛物线BD 恰好与抛物线ACB 关于点B 成中心对称.①请直接写出此人腾空后的最大高度和抛物线BD 的解析式;②此人腾空飞出后的落点D 是否在安全范围内?请说明理由(水面与地面之间的高度差忽略不计);(3)为消除安全隐患,公园计划对水滑道进行加固.如图2,水滑道已经有两条加固钢架,一条是水滑道距地面4米的点M 处竖直支撑的钢架MN ,另一条是点M 与点B 之间连接支撑的钢架BM .现在需要在水滑道下方加固一条支撑钢架,为了美观,要求这条钢架与BM 平行,且与水滑道有唯一公共点,一端固定在钢架MN 上,另一端固定在地面上.请你计算出这条钢架的长度(结果保留根号).26.数学课上,老师给出以下条件,请同学们经过小组讨论,提出探究问题.如图1,在ABC 中,AB AC =,点D 是AC 上的一个动点,过点D 作DE BC ⊥于点E ,延长ED 交BA 延长线于点F .请你解决下面各组提出的问题:(1)求证:AD AF =;(2)探究DF DE 与ADDC的关系;某小组探究发现,当13AD DC =时,23DF DE =;当45AD DC =时,85DF DE =.请你继续探究:①当76AD DC =时,直接写出DFDE 的值;②当AD m DC n =时,猜想DFDE的值(用含m ,n 的式子表示),并证明;(3)拓展应用:在图1中,过点F 作FP AC ⊥,垂足为点P ,连接CF ,得到图2,当点D 运动到使ACF ACB ∠=∠时,若AD m DC n =,直接写出APAD的值(用含m ,n 的式子表示).参考答案一、选择题(每小题给出的选项中只有一个符合题意,请将符合题意的选项序号,在答题卡的对应位置上按要求涂黑.每小题3分,共42分)1.【答案】A【解析】A .是轴对称图形,故A 选项正确;B .不是轴对称图形,故B 选项错误;C .不是轴对称图形,故C 选项错误;D .不是轴对称图形,故D 选项错误.故选:A .2.【答案】D【解析】解:1052000000000 5.210=⨯,故选:D .3.【答案】B【解析】解:如图所示:由题意得:3230∠=∠=︒∴1180345105∠=︒-∠-︒=︒故选:B .4.【答案】D【解析】解:A 、2a 与3a 不是同类项,不能合并,故此选项不符合题意;B 、()222222a b a ab b a b +=++≠+,故此选项不符合题意;C 、6332a a a a ÷=≠,故此选项不符合题意;D 、()236a a =,故此选项符合题意.故选:D .5.【答案】D【解析】解:A 、为了解1000只灯泡的使用寿命,从中抽取50只进行检测,此次抽样的样本容量是50,说法正确,本选项不符合题意;B 、了解某校一个班级学生的身高情况,适合全面调查,说法正确,本选项不符合题意;C 、了解商场的平均日营业额,选在周末进行调查,这种调查不具有代表性,说法正确,本选项不符合题意;D 、甲、乙二人10次测试的平均分都是96分,且方差22.5S =甲,22.3S =乙,则发挥稳定的是乙,故原说法错误,符合题意;故选:D .6.【答案】C【解析】解:()322211x x x x -<⎧⎪⎨+≥-⎪⎩①②解不等式①得,2x <,解不等式②得,3x ≥-,所以,不等式组的解集为:32x -≤<,在数轴上表示为:故选:C .7.【答案】B【解析】解:如图,直线l m 、相交于点A ,则60A ∠=︒,∵正多边形的每个内角相等,∴正多边形的每个外角也相等,∴1806012602︒-︒∠=∠==︒,∴360660n ︒==︒,故选:B.8.【答案】D 【解析】解:334047160009600200++⨯=,∴视力不低于4.8的人数是9600,故选:D .9.【答案】C【解析】解:由方程210210x x -+=得,13x =,27x =,∵337+<,∴等腰三角形的底边长为3,腰长为7,∴这个三角形的周长为37717++=,故选:C .10.【答案】B【解析】解:∵半径OC AB ⊥,∴ AC BC=,∴42AOC BOC ∠=∠=︒,84AOB ∠=︒,∵ AC AC=,∴1212D AOC ∠=∠=︒,∴63OED AOB D ∠=∠-∠=︒,故选:B .11.【答案】C【解析】解:设用A 型钢板x 块,用B 型钢板y 块,由题意得:35584240x y x y +=⎧⎨+=⎩,故选:C .12.【答案】A【解析】解:∵AB BC =,72C ∠=︒,∴72BAC C ∠=∠=︒,180236ABC C ∠︒=︒-∠=,由旋转的性质得36AB C ABC ︒'∠=∠=,72B AC BAC ︒''∠=∠=,72AC B C ''∠︒=∠=,72AC B ADC ︒''∠=∠=,AC AC '=,∴72AC C C '∠=∠=︒,∴36CAC '∠=︒,∴36CAC BAC ''∠=∠=︒,∴723636B AB '∠=︒-︒=︒,由旋转的性质得AB AB '=,∴()118036722ABB AB B ''∠=∠=︒-︒=︒,①点B 在旋转过程中经过的路径长是36111805ππ⋅=;①说法正确;②∵36B AB ABC '∠=∠=︒,∴B B A C '∥;②说法正确;③∵18027236DC B '∠=︒-⨯︒=︒,∴36DC B ABC '∠=∠=︒,∴BD C D '=;③说法正确;④∵36BB D ABC '∠=∠=︒,72B BD BAC '∠=∠=︒,∴B BD BAC '∽△△,∴AB B B AC BD'=.④说法正确;综上,①②③④都是正确的,故选:A .13.【答案】A【解析】解:数轴上点A ,M ,B 分别表示数a a bb +,,,∴AM a b a b =+-=、()BM b a b a =-+=-,∵AM BM >,∴原点在A ,M 之间,由它们的位置可得a<0,0b >且a b <,∴0a b +>,0a b -<,00ab a b <-<,,故运算结果一定是正数的是a b +.故选:A .14.【答案】B【解析】解:如图,连接AC 、BD 交于点E ,过点A 作MN y ⊥轴于点M ,过点B 作BN MN ⊥于点N ,四边形ABCD 是正方形,AC ∴、BD 互相平分,AB AD =,90BAD ∠=︒,90BAN DAM ∴∠+∠=︒,90DAM ADM ∠+∠=︒,BAN ADM ∴∠=∠.90BNA AMD ∠=∠=︒ ,BA AD =,(AAS)ANB DMA ∴ ≌.AM NB ∴=,DM AN =.点A 、C 的横坐标分别为m 、n ,24(,)A m m ∴+-,2()4,C n n -+.(2m n E +∴,2282m n -+-,2(0,)4M m +-,设(0,)D b ,则22(,)8B m n m n b ++---,2()4,N m n m ++-,24BN n b ∴=-+-,AM m =,AN n =,24DM m b =-+.又AM NB =,DM AN =,24n m b +--∴=,24n m b =-+.24b n m ∴=--+.2244n m n m ∴=---+.∴()()m n m n m n +-=+.点A 、C 在y 轴的同侧,且点A 在点C 的右侧,0m n ∴+≠.1m n ∴-=.故选:B .二、填空题(请把答案填写在答题卡对应的横线上.每小题3分,共12分)15.【答案】1(或2)【解析】23=<<= ,满足条件的数为小于或等于2的整数均可.16.【答案】()()311a m m +-【解析】解:()()()223331311am a a m a m m -=-=+-,故答案为:()()311a m m +-.17.【答案】11.5【解析】解:如图,过点D 作DM AB ⊥,交AB 的延长线于点M ,∴四边形ACDM 是矩形,∴10DM AC ==米,∵45BDM ∠=︒,65ADM ∠=︒,90M ∠=︒,∴BDM 是等腰直角三角形,∴10BM DM ==米,在Rt ADM △中,tan 10tan 6510 2.14521.45AM DM ADM =⋅∠=⋅︒≈⨯≈(米),∴21.451011.4511.5AB AM BM =-=-=≈(米),∴古树AB 的高度约为11.5米.故答案为:11.5.18.【答案】C【解析】解:同时启动A ,B 两台收割机,所需的时间为23小时,同时启动B ,C 两台收割机,所需的时间为19小时,得到C 比A 快;同时启动B ,C 两台收割机,所需的时间为19小时,同时启动C ,D 两台收割机,所需的时间为20小时,得到B 比D 快;同时启动A 、B 两台收割机,所需的时间为23小时,同时启动A ,E 两台收割机,所需的时间为18小时,得到E 比B 快;同时启动C ,D 两台收割机,所需的时间为20小时,同时启动D ,E 两台收割机,所需的时间为22小时,得到C 比E 快.综上,收割最快的一台收割机编号是C .故答案为:C .三、解答题(在答题卡上解答,答在本试卷上无效,解答时要写出必要的文字说明、证明过程或演算步骤.共8题,满分96分)19.【答案】(1)6;(2)7.【解析】解:(1)原式331222=++⨯+42=+-,6=;(2)∵230a a --=,∴23a a -=,∴()()()2213a a a -+-+224423a a a a =-+++-,2221a a =-+,()221a a =-+,231=⨯+,7=.20.【答案】(1)见解析(2)见解析【解析】【小问1详解】解:直线l 如图所示,;【小问2详解】证明:补全图形,如图,由(1)作图知,E 为AC 的中点,∵D ,E 分别为AB ,AC 的中点,∴DE BC ∥,12DE BC =,∵2EF DE =,即:12DE EF =,∴EF BC =,∵EF BC ∥,∴四边形BCFE 是平行四边形.21.【答案】(1)5;2;75(2)78;80(3)A ,B 两名队员恰好同时被选中的概率为16.【解析】【小问1详解】解:根据收集的数据知5a =;2b =;出现最多的是75分,有5人,众数为75分,则75c =;故答案为:5;2;75;【小问2详解】解:∵由统计图可知中位数为78分,∴如果想让一半左右的队员都能达到成绩目标,成绩目标应定为78分,如果想确定一个较高的目标,成绩目标应定为80分,因为在样本的众数,中位数和平均数中,平均数最大,可以估计,如果成绩目标定为80分,努力一下都能达到成绩目标.故答案为:78;80;【小问3详解】解:画树状图表示所有等可能结果如图所示,共有12种等可能结果,A ,B 两名队员恰好同时被选中的情况有2种,∴A ,B 两名队员恰好同时被选中的概率为21126==,答:A ,B 两名队员恰好同时被选中的概率为16.22.【答案】(1)甲队平均每天修复公路6千米,则乙队平均每天修复公路9千米;(2)15天的工期,两队最多能修复公路105千米.【解析】【小问1详解】解:设甲队平均每天修复公路x 千米,则乙队平均每天修复公路()3x +千米,由题意得60903x x =+,解得6x =,经检验,6x =是原方程的解,且符合题意,39x +=,答:甲队平均每天修复公路6千米,则乙队平均每天修复公路9千米;【小问2详解】解:设甲队的工作时间为m 天,则乙队的工作时间为()15m -天,15天的工期,两队能修复公路w 千米,由题意得()69153135w m m m =+-=-+,()215m m ≥-,解得10m ≥,∵30-<,∴w 随m 的增加而减少,∴当10m =时,w 有最大值,最大值为310135105w =-⨯+=,答:15天的工期,两队最多能修复公路105千米.23.【答案】(1)()14,2N 和()30,2N -;(2)5b =;(3)()4,2--或()2,4.【解析】【小问1详解】解:由()1,3M ,()14,2N 得,12125x x y y +=+=,∴点()14,2N 是点M 的等和点;由()1,3M ,()23,1N -得,124x x +=,122y y +=,∵1212x x y y +≠+,∴()23,1N -不是点M 的等和点;由()1,3M ,()30,2N -得,12121x x y y +=+=,∴()30,2N -是点M 的等和点;故答案为:()14,2N 和()30,2N -;【小问2详解】解:设点N 的横坐标为a ,∵点N 是点()3,2M -的等和点,∴点N 的纵坐标为()325a a +--=+,∴点N 的坐标为(),5a a +,∵点N 在直线y x b =+上,∴5a a b +=+,∴5b =;【小问3详解】解:由题意可得,0k >,双曲线分布在一、三象限内,设直线与双曲线的交点分别为点A B 、,如图,由12y y <时x 的取值范围是4x >或20x -<<,可得点A 的横坐标为4,点B 的横坐标为2-,把4x =代入2y x =-得,422y =-=,∴()4,2A ,把()4,2A 代入1k y x =得,24k =,∴8k =,∴反比例函数解析式为18y x =,设8,P m m ⎛⎫ ⎪⎝⎭,点Q 的横坐标为n ,∵点Q 是点P 的等和点,∴点Q 的纵坐标为8m n m +-,∴8,Q n m n m ⎛⎫+- ⎪⎝⎭,∵点Q 在直线22y x =-上,∴82m n n m +-=-,整理得,820m m -+=,去分母得,2280m m +-=,解得14m =-,12m =,经检验,4,2m m =-=是原方程的解,∴点P 的坐标为()4,2--或()2,4.24.【答案】(1)见解析(2)5OM =【解析】【小问1详解】证明:连接OE ,延长EO ,交O 于点P ,连接,,PD BD 如图,∵,90,AB BC ACB =∠=︒∴ABC 是等腰直角三角形,∴45,ABC ∠=︒∵CD 是O 的直径,∴90,CBD ∠=︒∴904545,DBE CBD ABC ∠=∠-∠=︒-︒=︒∴45,EPD DBE ∠=∠=︒∴224590,DOE DPE ∠=∠=⨯︒=︒∵,EF CD ∥∴90,FEO DOE ∠=∠=︒即,OE EF ⊥∵OE 是O 的半径,∴EF 是O 的切线;【小问2详解】解:∵90DBC ∠=︒,1tan 2BCD ∠=,∴12DB BC =,∵,BC AC =∴12DB AC =,∵,DMB CMA ∠=∠A DBM ∠=∠,∴DBM ACM ∽ ,∴12BM DM DB AM CM AC ===,∵BM =,∴2AM BM ==∴AB AM BM =+=+=,在等腰直角三角形ABC 中,222AC BC AB +=,∴(2222AC AC AB +==,解得,12AC =,∴12AC BC ==,∴16,2DB BC ==在t R BDC 中,CD ==∴CO DO ==又12DM CM =,∴2,CM DM =∴2DM DM CD +==∴DM =∴OM OD DM =-==25.【答案】(1)()217388y x =++(2)①此人腾空后的最大高度是258米,解析式为()2125388y x =--+;②此人腾空飞出后的落点D 在安全范围内,理由见解析(3)这条钢架的长度为米【解析】【小问1详解】解:根据题意得到水滑道ACB 所在抛物线的顶点坐标为73,8C ⎛⎫- ⎪⎝⎭,且过点()0,2B ,设水滑道ACB 所在抛物线的解析式为()2738y a x =++,将()0,2B 代入,得:()272038a =++,即998a =,18a ∴=,∴水滑道ACB 所在抛物线的解析式为()217388y x =++;【小问2详解】解:① 人腾空后的路径形成的抛物线BD 恰好与抛物线ACB 关于点B 成中心对称,则设人腾空后的路径形成的抛物线的解析式为()218y x b c =-++,∴人腾空后的路径形成的抛物线BD 的顶点坐标与抛物线ACB 的顶点坐标73,8C ⎛⎫- ⎪⎝⎭关于点()0,2B 成中心对称,()7250233,2288⨯--=⨯-=,∴人腾空后的路径形成的抛物线BD 的顶点坐标为253,8⎛⎫ ⎪⎝⎭,即253,8b c ==,∴此人腾空后的最大高度是258米,人腾空后的路径形成的抛物线BD 的解析式为:()2125388y x =--+;由①知人腾空后的路径形成的抛物线BD 的解析式为:()2125388y x =--+,令0y =,则()21253088x --+=,即()2325x -=∴8x =或2x =-(舍去,不符合题意),∴点()8,0D ,8OD ∴=,12OE =,43DE OE OD ∴=-=>,∴此人腾空飞出后的落点D 在安全范围内;【小问3详解】解:根据题意可得M 点的纵坐标为4,令()2173488y x =++=,即()2325x +=,2x ∴=(舍去,不符合题意)或8x =-,()8,4M ∴-,设BM 所在直线的解析式为y kx b '=+,将()()8,4,0,2M B -代入得:248b k b =⎧⎨=-+''⎩,解得:214b k =-'⎧⎪⎨=⎪⎩,∴BM 所在直线的解析式为124y x =-+,如图,设这条钢架为GH ,与MN 交于点G ,与地面交于H, 这条钢架与BM 平行,∴设该钢架GH 所在直线的解析式为14y x n =-+,联立()21417388y x n y x ⎧=-+⎪⎪⎨⎪=++⎪⎩,即()21173488x n x -+=++,整理得:281680x x n ++-=,该钢架GH 与水滑道有唯一公共点,()2Δ8411680n ∴=-⨯⨯-=,∴0n =即该钢架所在直线的解析式为14y x =-,∴点H 与点O 重合, ()1824GN =-⨯-=,8NO =,90GNO ∠=︒,GH ∴==∴这条钢架的长度为米.26.【答案】(1)见解析(2)①73DF DE =②2DF DE m n=,证明见解析(3)2AP n AD m =【解析】【小问1详解】证明:∵AB AC =,∴B C ∠=∠,∵DE BC ⊥,∴90BEF CED ∠=∠=︒,∴90F B ∠=︒-∠,90CDE C ∠=︒-∠,且CDE ADF ∠=∠,∴F ADF ∠=∠,∴AD AF =;【小问2详解】解:①当13AD DC =时,23DF DE =;当45AD DC =时,85DF DE =,∴总结规律得:DF DE 是AD DC 的2倍,∴当76AD DC =时,14763DF DE ==;②当AD m DC n =时,猜想2DF DE m n =,证明:作AG EF ⊥于点G ,∵DE BC ⊥,∴AG CE ∥,∴AGD CED ∽△△,∵AD m DC n =,∴GD AD m DE DC n ==,由(1)知AD AF =,又AG EF ⊥,∴DG FG =,即2DF DG =,∴22GD m DE nDF DE ==;【小问3详解】2AP n AD m=,理由如下:过点D 作DG CF ⊥,∵ACF ACB ∠=∠,DE CE ⊥,∴DG DE =,由(2)知,当AD m DC n =时,2DF DE m n=,∴2DE n DF m =,∴2DG n DF m=,∵PF AC ⊥,∴90ACF CFP ∠+∠=︒,∵FE BC ⊥,∴90B AFD ∠+∠=︒,∵AB AC =,∴ACB B =∠∠,∴B ACF ∠=∠,∴AFD CFP ∠=∠,∴AFD PFD CFP PFD ∠-∠=∠-∠,∴AFP DFG ∠=∠,∴sin sin AFP DFG ∠=∠,∴2AP DG n AF DF m==,由(1)知AD AF =,∴2AP AP n AD AF m ==.。
2024年武汉市初中毕业生学业考试数学试卷亲爱的同学:在你答题前,请认真阅读下面的注意事项:1.本试卷全卷共6页,三大题,满分120分.考试用时120分钟.2.答题前,请将你的姓名、准考证号填写在“答题卡”相应位置,并在“答题卡”背面左上角填写姓名和座位号.3.答选择题时,选出每小题答案后,用2B 铅笔将“答题卡”上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案.答在“试卷”上无效.4.答非选择题时,答案用0.5毫米黑色笔迹签字笔书写在“答题卡”上.答在“试卷”上无效.5.认真阅读答题卡上的注意事项.预祝你取得优异成绩!一、选择题(共10小题,每小题3分,共30分)下列各题中有且只有一个正确答案,请在答题卡上将正确答案的标号涂黑.1.现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性.下列汉字是轴对称图形的是()A.B.C.D.2.小美和小好同学做“石头、剪刀、布”的游戏,两人同时出相同的手势,这个事件是()A.随机事件B.不可能事件C.必然事件D.确定性事件3.如图是由两个宽度相同的长方体组成的几何体,它的主视图是()A. B. C. D.4.国家统计局2024年4月16日发布数据,今年第一季度国内生产总值接近300000亿元,同比增长5.3%,国家高质量发展取得新成效.将数据300000用科学记数法表示是()A.50.310⨯ B.60.310⨯ C.5310⨯ D.6310⨯5.下列计算正确的是()A.236a a a ⋅= B.()1432a a = C.()2236a a = D.()2211a a +=+6.如图,一个圆柱体水槽底部叠放两个底面半径不等的实心圆柱体,向水槽匀速注水.下列图象能大致反映水槽中水的深度h 与注水时间t 的函数关系的是()A. B. C. D.7.小美同学按如下步骤作四边形ABCD :①画MAN ∠;②以点A 为圆心,1个单位长为半径画弧,分别交AM ,AN 于点B ,D ;③分别以点B ,D 为圆心,1个单位长为半径画弧,两弧交于点C ;④连接BC ,CD ,BD .若44A ∠=︒,则CBD ∠的大小是()A.64︒B.66︒C.68︒D.70︒8.经过某十字路口的汽车,可能直行,也可能向左转或向右转,这三种可能性大小相同.若两辆汽车经过这个十字路口,则至少一辆车向右转的概率是()A.19B.13 C.49D.599.如图,四边形ABCD 内接于O ,60ABC ∠=︒,45BAC CAD ∠=∠=︒,2AB AD +=,则O 的半径是()A.63B.223C.2D.210.如图,小好同学用计算机软件绘制函数32331y x x x =-+-的图象,发现它关于点()1,0中心对称.若点()110.1,A y ,()220.2,A y ,()330.3,A y ,……,()19191.9,A y ,()20202,A y 都在函数图象上,这20个点的横坐标从0.1开始依次增加0.1,则1231920y y y y y +++++ 的值是()A.1-B.0.729-C.0D.1二、填空题(共6小题,每小题3分,共18分)下列各题不需要写出解答过程,请将结果直接填写在答题卡指定的位置.11.中国是世界上最早使用负数的国家.负数广泛应用到生产和生活中,例如,若零上3℃记作3+℃,则零下2℃记作_________℃.12.某反比例函数ky x=具有下列性质:当0x >时,y 随x 的增大而减小,写出一个满足条件的k 的值是__________.13.分式方程131x x x x +=--的解是______.14.黄鹤楼是武汉市著名的旅游景点,享有“天下江山第一楼”的美誉.在一次综合实践活动中,某数学小组用无人机测量黄鹤楼AB 的高度,具体过程如下:如图,将无人机垂直上升至距水平地面102m 的C 处,测得黄鹤楼顶端A 的俯角为45︒,底端B 的俯角为63︒,则测得黄鹤楼的高度是__________m .(参考数据:tan632︒≈)15.如图是我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”,它是由四个全等的直角三角形和中间的小正方形MNPQ 拼成的一个大正方形ABCD .直线MP 交正方形ABCD 的两边于点E ,F ,记正方形ABCD 的面积为1S ,正方形MNPQ 的面积为2S .若(1)BE kAE k =>,则用含k 的式子表示12S S的值是___________.16.抛物线2y ax bx c =++(a ,b ,c 是常数,0a <)经过()1,1-,(),1m 两点,且01m <<.下列四个结论:①0b >;②若01x <<,则()()2111a x b x c -+-+>;③若1a =-,则关于x 的一元二次方程22ax bx c ++=无实数解;④点()11,A x y ,()22,B x y 在抛物线上,若1212x x +>-,12x x >,总有12y y <,则102m <≤.其中正确的是__________(填写序号).三、解答题(共8小题,共72分)下列各题需要在答题卡指定的位置写出文字说明、证明过程、演算步骤或画出图形.17.求不等式组3121x x x +>⎧⎨-≤⎩①②的整数解.18.如图,在ABCD Y 中,点E ,F 分别在边BC ,AD 上,AF CE =.(1)求证:C ABE DF ≌△△;(2)连接EF .请添加一个与线段相关的条件,使四边形ABEF 是平行四边形.(不需要说明理由)19.为加强体育锻炼,增强学生体质,某校在“阳光体育一小时”活动中组织九年级学生定点投篮技能测试,每人投篮4次,投中一次计1分.随机抽取m 名学生的成绩作为样本,将收集的数据整理并绘制成如下的统计图表.测试成绩频数分布表成绩/分频数4123a2151b 06根据以上信息,解答下列问题:(1)直接写出m ,n 的值和样本的众数;(2)若该校九年级有900名学生参加测试,估计得分超过2分的学生人数.20.如图,ABC 为等腰三角形,O 是底边BC 的中点,腰AC 与半圆O 相切于点D ,底边BC 与半圆O 交于E ,F 两点.(1)求证:AB 与半圆O 相切;(2)连接OA .若4CD =,2CF =,求sin OAC ∠的值.21.如图是由小正方形组成的34⨯网格,每个小正方形的顶点叫做格点.ABC 三个顶点都是格点.仅用无刻度的直尺在给定网格中完成四个画图任务,每个任务的画线不得超过三条.(1)在图(1)中,画射线AD 交BC 于点D ,使AD 平分ABC 的面积;(2)在(1)的基础上,在射线AD 上画点E ,使ECB ACB ∠=∠;(3)在图(2)中,先画点F ,使点A 绕点F 顺时针旋转90︒到点C ,再画射线AF 交BC 于点G ;(4)在(3)的基础上,将线段AB 绕点G 旋转180︒,画对应线段MN (点A 与点M 对应,点B 与点N 对应).22.16世纪中叶,我国发明了一种新式火箭“火龙出水”,它是二级火箭的始祖.火箭第一级运行路径形如抛物线,当火箭运行一定水平距离时,自动引发火箭第二级,火箭第二级沿直线运行.某科技小组运用信息技术模拟火箭运行过程.如图,以发射点为原点,地平线为x 轴,垂直于地面的直线为y 轴,建立平面直角坐标系,分别得到抛物线2y ax x =+和直线12y x b =-+.其中,当火箭运行的水平距离为9km 时,自动引发火箭的第二级.(1)若火箭第二级的引发点的高度为3.6km .①直接写出a ,b 的值;②火箭在运行过程中,有两个位置的高度比火箭运行的最高点低1.35km ,求这两个位置之间的距离.(2)直接写出a 满足什么条件时,火箭落地点与发射点的水平距离超过15km .23.问题背景:如图(1),在矩形ABCD 中,点E ,F 分别是AB ,BC 的中点,连接BD ,EF ,求证:BCD FBE ∽△△.问题探究:如图(2),在四边形ABCD 中,AD BC ∥,90BCD ∠=︒,点E 是AB 的中点,点F 在边BC 上,2AD CF =,EF 与BD 交于点G ,求证:BG FG =.问题拓展:如图(3),在“问题探究”的条件下,连接AG ,AD CD =,AG FG =,直接写出EGGF的值.24.抛物线215222y x x =+-交x 轴于A ,B 两点(A 在B 的右边),交y 轴于点C .(1)直接写出点A ,B ,C 的坐标;(2)如图(1),连接AC ,BC ,过第三象限的抛物线上的点P 作直线PQ AC ∥,交y 轴于点Q .若BC 平分线段PQ ,求点P 的坐标;(3)如图(2),点D 与原点O 关于点C 对称,过原点的直线EF 交抛物线于E ,F 两点(点E 在x 轴下方),线段DE 交抛物线于另一点G ,连接FG .若90EGF ∠=︒,求直线DE 的解析式.参考答案一、选择题(共10小题,每小题3分,共30分)1.【答案】C【解析】解:A ,B ,D 选项中的图形不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形,C 选项中的图形能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形.故选:C .2.【答案】A【解析】解:两人同时出相同的手势,,这个事件是随机事件,故选:A .3.【答案】B【解析】解:从正面看该几何体,下面是一个大长方形,上面叠着一个小长方形,故选:B .4.【答案】C【解析】解:5300000310=⨯,故选:C .5.【答案】B【解析】解:A.235a a a ⋅=,故该选项不正确,不符合题意;B.()4312a a =,故该选项正确,符合题意;C.()2239a a =,故该选项不正确,不符合题意;D.()22121a a a +=++,故该选项不正确,不符合题意;故选:B .6.【答案】D【解析】解:下层圆柱底面半径大,水面上升块,上层圆柱底面半径稍小,水面上升稍慢,再往上则水面上升更慢,所以对应图象是第一段比较陡,第二段比第一段缓,第三段比第二段缓.故选:D .7.【答案】C【解析】解:作图可得AB AD BC DC ===∴四边形ABCD 是菱形,∴,AB BC ABD CBD ∠=∠∥∵44A ∠=︒,∴44MBC A ∠=∠=︒,∴()()11180180446822CBD MBC ∠=︒-∠=︒-︒=︒,故选:C .8.【答案】D【解析】解:列树状图如图所示,共有9种情况,至少一辆车向右转有5种,∴至少一辆车向右转的概率是59,故选:D .9.【答案】A【解析】解:延长AB 至点E ,使BE AD =,连接BD ,连接CO 并延长交O 于点F ,连接AF ,∵四边形ABCD 内接于O ,∴180ADC ABC ABC CBE ∠+∠=∠+∠=︒∴ADC CBE ∠=∠∵45BAC CAD ∠=∠=︒∴45CBD CDB ∠=∠=︒,90DAB ∠=︒∴BD 是O 的直径,∴90DCB ∠=︒∴DCB △是等腰三角形,∴DC BC =∵BE AD=∴()SAS ADC EBC ≌∴ACD ECB ∠=∠∵2AB AD +=∴2AB BE AE +==又∵90DCB ∠=︒∴90ACE ∠=︒∴ACE △是等腰直角三角形∴cos 45AC AE =︒⋅=∵60ABC ∠=︒∴60AFC ∠=︒∵90FAC ∠=︒∴26sin 603AC CF ==︒∴1623OF OC CF ===故选:A .10.【答案】D【解析】解:∵这20个点的横坐标从0.1开始依次增加0.1,∴0.11.90.2 1.80.9 1.11222+++==⋅⋅⋅=,∴123911190y y y y y y +++++= ,∴12319201020y y y y y y y +++++=+ ,而()101,0A 即100y =,∵32331y x x x =-+-,当0x =时,1y =-,即()0,1-,∵()0,1-关于点()1,0中心对称的点为()2,1,即当2x =时,201y =,∴12319201020011y y y y y y y +++++=+=+= ,故选:D .二、填空题(共6小题,每小题3分,共18分)11.【答案】2-【解析】解:零上3℃记作3+℃,则零下2℃记作2-℃.,故答案为:2-.12.【答案】1(答案不唯一)【解析】解:∵当0x >时,y 随x 的增大而减小,∴0k >故答案为:1(答案不唯一).13.【答案】3x =-【解析】解:131x x x x +=--,等号两边同时乘以()()31x x --,得()()()131x x x x -=-+,去括号,得2223x x x x -=--,移项、合并同类项,得3x =-,经检验,3x =-是该分式方程的解,所以,该分式方程的解为3x =-.故答案为:3x =-.14.【答案】51【解析】解:延长BA 交距水平地面102m 水平线的的水平线于点D ,如图,由题可知,102m BD =,设AD x =,∵45DCA ∠=︒∴DC AD x==∴102tan632BD DC x︒==≈∴51mDC AD =≈∴1025151mAB BD AD =-=-≈故答案为:51.15.【答案】221(1)k k +-【解析】解:作EG AN ⊥交AN 于点G ,不妨设MN a =,设1EG = 四边形MNPQ 是正方形45PMN ∴∠=︒45EMG PMN ∴∠=∠=︒1EG MG ∴==在AEG △和ABN 中,EAG BAN ∠=∠,90AGE ANB ∠=∠=︒AEG ABN∴ ∽AE EG AG AB BN AN∴==(1)BE kAE k => (1)AB AE BE AE k ∴=+=+111AE AG AB BN AN k ∴===+1BN k∴=+由题意可知,ABN DAM△≌△1BN AM k∴==+11AG AM GM k k∴=-=+-=111AG AG k AN AM MN k a k ∴===++++21a k ∴=-2211AN AG GM MN k k k k∴=++=++-=+∴正方形ABCD 的面积222221222(1)()(1)(1)S AB BN AN k k k k k ==+=+++=++,正方形MNPQ 的面积2222222(1)(1)(1)S MN a k k k ===-=+-222221(1)(1)(1)(1)k k k k S S +++-∴=1k > 2(1)0k ∴+≠22121(1)k S S k +-∴=16.【答案】②③④【解析】解:∵2y ax bx c =++(a ,b ,c 是常数,0a <)经过()1,1-,(),1m 两点,且01m <<.∴对称轴为直线122b m x a -+=-=,11022m -+-<<,∵02b x a=-<,a<0∴0b <,故①错误,∵01m <<∴()11m -->,即()1,1-,(),1m 两点之间的距离大于1又∵a<0∴1x m =-时,1y >∴若01x <<,则()()2111a x b x c -+-+>,故②正确;③由①可得11022m -+-<<,∴1022b -<<,即10b -<<,当1a =-时,抛物线解析式为2y x bx c=-++设顶点纵坐标为224444ac b c b t a ---==-∵抛物线2y x bx c =-++(a ,b ,c 是常数,0a <)经过()1,1-,∴11b c --+=∴2c b =+∴()222224411122144444c b b ct b c b b b --+===+=++=++-∵10b -<<,104->,对称轴为直线2b =-,∴当0b =时,t 取得最大值为2,而0b <,∴关于x 的一元二次方程22ax bx c ++=无解,故③正确;④∵a<0,抛物线开口向下,点()11,A x y ,()22,B x y 在抛物线上,1212x x +>-,12x x >,总有12y y <,又12124x xx +=>-,∴点()11,A x y 离14x =-较远,∴对称轴111224m-+-<≤-解得:102m <≤,故④正确.故答案为:②③④.三、解答题(共8小题,共72分)17.【答案】整数解为:1,0,1-【解析】解:3121x x x +>⎧⎨-≤⎩①②解不等式①得:2x >-解不等式②得:1x ≤∴不等式组的解集为:21x -<≤,∴整数解为:1,0,1-18.【答案】(1)见解析(2)添加AF BE =(答案不唯一)【解析】【小问1详解】证明:∵四边形ABCD 是平行四边形,∴AB CD =,AD BC =,B D ∠=∠,∵AF CE =,∴AD AF BC CE -=-即DF BE =,在ABE 与CDF 中,AB CD B D BE DF =⎧⎪∠=∠⎨⎪=⎩,∴()SAS ABE CDF ≌;【小问2详解】添加AF BE =(答案不唯一)如图所示,连接EF.∵四边形ABCD 是平行四边形,∴AD BC ∥,即AF BE ∥,当AF BE =时,四边形ABEF 是平行四边形.19.【答案】(1)60m =,15n =,众数为3分(2)该校九年级有900名学生参加测试,估计得分超过2分的学生人数为450人【解析】【小问1详解】解:依题意,156025%m ==(人),6030%18a =⨯=(人),6012181569b =----=(人),∴9%100%15%60n =⨯=,∴15n =,∵3分的人数为18个,出现次数最多,∴众数为3分,【小问2详解】解:181290045060+⨯=(人)答:该校九年级有900名学生参加测试,估计得分超过2分的学生人数为450人.20.【答案】(1)见解析(2)45【解析】【小问1详解】证明:连接OA 、OD ,作ON AB ⊥交AB 于N ,如图ABC 为等腰三角形,O 是底边BC 的中点AO BC ∴⊥,AO 平分BAC∠AC 与半圆O 相切于点DOD AC∴⊥由ON AB⊥ ON OD∴=AC ∴是半圆O 的切线【小问2详解】解:由(1)可知AO BC ⊥,OD AC⊥90AOC ∴∠=︒,90ODC ∠=︒18090OAC OCA AOC ∴∠+∠=︒-∠=︒,18090COD OCA ODC ∠+∠=︒-∠=︒OAC COD∴∠=∠sin sin CD OAC COD OC∴∠=∠=又 OF OD =,2CF =∴在Rt ODC △中,4CD =,2OC OF FC OD =+=+ 222OC CD OD =+,∴222(2)4OD OD +=+解得:3OD =442325CD CD sin OAC sin COD OC OD ∴∠=∠====++21.【答案】(1)作图见解析(2)作图见解析(3)作图见解析(4)作图见解析【解析】【小问1详解】解:如图所示,点D 即为所求.【小问2详解】解:如图所示,点E 即为所求.【小问3详解】解:如图所示.【小问4详解】解:如图所示.22.【答案】(1)①115a =-,8.1b =;②8.4km (2)2027a -<<【解析】【小问1详解】解:①∵火箭第二级的引发点的高度为3.6km∴抛物线2y ax x =+和直线12y x b =-+均经过点()9,3.6∴3.6819a =+,13.692b =-⨯+解得115a =-,8.1b =.②由①知,18.12y x =-+,2115y x x =-+∴22111515151524y x x x ⎛⎫=-+=--+ ⎪⎝⎭∴最大值15km 4y =当15 1.35 2.4km 4y =-=时,则21 2.415x x -+=解得112x =,23x =又∵9x =时, 3.6 2.4y =>∴当 2.4km y =时,则418. 2.12x +=-解得11.4x =()11.438.4km -=∴这两个位置之间的距离8.4km .【小问2详解】解:当水平距离超过15km 时,火箭第二级的引发点为()9,819a +,将()9,819a +,()15,0代入12y x b =-+,得181992a b +=-⨯+,10152b =-⨯+解得7.5b =,227a =-∴2027a -<<.23.【答案】问题背景:见解析;问题探究:见解析;问题拓展:【解析】问题背景:∵四边形ABCD 是矩形,∴90AB CD EBF C =∠=∠=︒,,∵E ,F 分别是AB ,BC 的中点∴12BE BF AB BC ==,即12BE BF CD BC ==,∴BCD FBE ∽△△;问题探究:如图所示,取BD 的中点H ,连接,EH HC ,∵E 是AB 的中点,H 是BD 的中点,∴12EH AD =,EH AD ∥又∵2AD CF =,∴EH CF =,∵AD BC ∥,∴EH FC∥∴四边形EHCF 是平行四边形,∴EF CH∥∴GFB HCB∠=∠又∵90BCD ∠=︒,H 是BD 的中点,∴12HC BD BH ==∴HBC HCB∠=∠∴GBF GFB ∠=∠,∴GB GF =;问题拓展:如图所示,过点F 作FM AD ⊥,则四边形MFCD 是矩形,连接AF ,∵2AD CF CD ==,∴12AM MD FC AD ===,设2AD a =,则2MF CD a ==,AM a =在Rt AMF 中,AF ==,∵AG FG =,由(2)BG FG=∴AG BG =,又∵E 是AB 的中点,∴EF 垂直平分AB∴AF BF =,90BEG ∠=︒,在,AFG BFG 中,AG BG GF GF FA FB =⎧⎪=⎨⎪=⎩∴()SSS AFG BFG ≌设GBF GFB α∠=∠=,则GAF GFA α∠=∠=∴2BGE GBF GFB α∠=∠+∠=,又∵AD BC∥∴2MAF AFB GFA GFB α∠=∠=∠+∠=∴MAF EGB∠=∠又∵90BEG AFM ∠=∠=︒∴BEG FMA ∽∴5EG EG AM GF BG AF ===.24.【答案】(1)()1,0A ,()5,0B -,50,2C ⎛⎫- ⎪⎝⎭(2)92,2P ⎛⎫--⎪⎝⎭(3)152y x =--【解析】【小问1详解】解:由215222y x x =+-,当0x =时,52y =-,则50,2C ⎛⎫- ⎪⎝⎭当0y =,2152022x x +-=解得:125,1x x =-=∵A 在B 的右边∴()1,0A ,()5,0B -,【小问2详解】解:设直线AC 的解析式为()0y kx b k =+≠将()1,0A ,50,2C ⎛⎫- ⎪⎝⎭代入得,052k b b +=⎧⎪⎨=-⎪⎩解得:5252k b ⎧=⎪⎪⎨⎪=-⎪⎩∴直线AC 的解析式为5522y x =+∵PQ AC∥设直线PQ 的解析式为152y x b =+∵P 在第三象限的抛物线上设215,222P t t t ⎛⎫+- ⎪⎝⎭,()50t -<<∴215152222t b t t +=+-∴2115222t b t =--∴2150,222t Q t ⎛⎫-- ⎪⎝⎭设PQ 的中点为M ,则22352,22t t t M ⎛⎫+- ⎪ ⎪ ⎪⎝⎭由()5,0B -,50,2C ⎛⎫-⎪⎝⎭,设直线BC 的解析式为152y k x =-,将()5,0B -代入得,15052k =--,解得:112k =-∴直线BC 的解析式为1522y x =--,∵BC 平分线段PQ ,∴M 在直线BC 上,∴22351522222t t t +--⨯-=解得:122,0t t =-=(舍去)当2t =-时,21592222t t +-=-∴92,2P ⎛⎫-- ⎪⎝⎭;【小问3详解】解:如图所示,过点G 作TS x ∥轴,过点,E F 分别作TS 的垂线,垂足分别为,T S,∴90T S EGF ∠=∠=∠=︒∴90EGT FGS GFS ∠=︒-∠=∠∴ETG GSF∽∴ET TG GS FS=即ET FS GS TG⋅=⋅∵点D 与原点O 关于点50,2C ⎛⎫- ⎪⎝⎭对称,∴()0,5D -,设直线EF 的解析式为11y k x =,直线ED 的解析式为225y k x =-联立直线EF 与抛物线解析式11215222y k x y x x =⎧⎪⎨=+-⎪⎩可得,2112222k x x x =+-,即()21152022x k x +--=联立直线ED 与抛物线解析式222515222y k x y x x =-⎧⎪⎨=+-⎪⎩可得,22125222k x x x -=+-即()22152022x k x +-+=设,E F x e x f ==,G x g =,∴5ef =-,5eg =,224e g k +=-,∴f g=-()()221515122422222ET e e g g e g e g ⎛⎫=+--+-=++- ⎪⎝⎭,()()221515122422222FS f f g g f g f g ⎛⎫=+--+-=++- ⎪⎝⎭∵ET FS GS TG ⋅=⋅∴()()()()()()114422g e f g e g e g f g f g --=++-⨯++-,将f g =-代入得:5e g +=-∴2245k -=-,∴212k =-,∴直线DE 解析式为152y x =--.。
初中毕业考试试题及答案数 学(全卷共6页,共五个大题,26个小题,满分100分,时间90分钟)题号 一 二三 四 五 总分总分人19 20 21 2223 24 25 26 得分一、 填空题:(本大题共12个小题,每小题2分,共24分)把答案直接填写在题中横线上.1、计算: -3+|-1| =________2、已知点P (-2,3),则点P 关于x 轴对称的点坐标是( )3、据有关资料显示,长江三峡工程电站的总装机容量是18200000千瓦,请你用科学记数法表示电站的总装机容量,应记为 千瓦4、如图,要给这个长、宽、高分别为x 、y 、z 的 箱子打包,其打包方式如右图所示,则打包带的长至少要____________________ (单位:mm )(用含x 、y 、z 的代数式表示)5、方程 x 2 = x 的解是______________________6、圆内接四边形ABCD 的内角∠A:∠B:∠C=2:3:4,则∠D =________°7、已知一个梯形的面积为222cm ,高为2 cm ,则该梯形的中位线的长等于________cm8、 如图,在⊙O 中,若已知∠BAC=48º,则∠BOC=_________º9、若圆的一条弦长为 6 cm ,其弦心距等于 4 cm ,则该圆的半径等 于________ cm .10、函数b ax y +=的图像如图所示,则y 随 x 的增大而 11、万州区某学校四个绿化小组,在植树节这天种下白杨树的棵数如 下:10,10,x ,8,已知这组数据的众数和平均数相等,那么这组数据的中位数是 .12、如图,AD 、AE 是正六边形的两条对角线,不添加任何辅助线,请写出两个正确的结得分 评卷人论:(1) __________________; (2) ______________。
(只写出两个你认为正确的结论即可)二、选择题:(本大题共6个小题,每小题3分,共18分)在每小题给出的四个选项中,只有一项是符合题目要求的.13、下列式子中正确的是( )A 632a a a =⋅ B 633)(x x =C 933=D bc c b 933=⋅14、如图,∠1=∠2,则下列结论一定成立的是( )A AB ∥CD B AD ∥BCC ∠B=∠DD ∠3=∠415、把a 3-ab 2分解因式的正确结果是( )A (a+ab)(a -ab)B a (a 2-b 2)C a(a+b)(a -b)D a(a -b)216、某校计划修建一座既是中心对称图形又是轴对称图形的花坛,从学生中征集到的设计方案有正三角形、正五边形、等腰梯形、菱形等四种图案,你认为符合条件的是( )A 正三角形B 正五边形C 等腰梯形D 菱形 17、在函数21-=x y 中,自变量x 的取值范围是( ) A x ≥2 B x>2 C x ≤2 D x<218、如图是某蓄水池的横断面示意图,分为深水池和浅水池,如果这个蓄水池以固定的流量注水,下面能大致表示 水的最大深度h 与时间t 之间的关系的图像是( ).得分评卷人三、(本大题共3个小题,每小题8分,共24分)下列各题解答时必须给出必要的演算过程或推理步骤.19、(本题满分8分)计算:-22+ (12-1)0 + 2sin30º20、(本题满分8分)解不等式组⎪⎩⎪⎨⎧-≥+-<-x x x 221132,并把解集在数轴上表示出来。
2023年无锡市初中毕业升学考试数学试题一、选择题(本大题共10小题,每小题3分,共30分.在每小题所给出的四个选项中,只有一项是正确的)1.【答案】A3=,故选:A .2.【答案】C【解析】由题意得x-2≠0,∴x≠2.故选C .3.【答案】D【解析】解:A 选项,当12x y =⎧⎨=⎩时,24x y +=,则12x y =⎧⎨=⎩是二元一次方程24x y +=的解,不合题意;B 选项,当20x y =⎧⎨=⎩时,24x y +=,则20x y =⎧⎨=⎩是二元一次方程24x y +=的解,不合题意;C 选项,当0.53x y =⎧⎨=⎩时,24x y +=,则0.53x y =⎧⎨=⎩是二元一次方程24x y +=的解,不合题意;D 选项,当24x y =-⎧⎨=⎩时,20x y +=,则24x y =-⎧⎨=⎩不是二元一次方程24x y +=的解,符合题意;故选:D .4.【答案】D【解析】解:A 选项,235a a a ⨯=,故该选项不正确,不符合题意;B 选项,2a 与3a 不能合并,故该选项不正确,不符合题意;C 选项,22(2)4a a -=,故该选项不正确,不符合题意;D 选项,642a a a ÷=,故该选项正确,符合题意;故选:D .5.【答案】A【解析】解:∵函数21y x =+的图像向下平移2个单位长度,∴21221y x x =+-=-,故答案为:A .6.【答案】A【解析】解:由题意得:25.76(1) 6.58x +=.故选:A .7.【答案】B【解析】解:由旋转性质可得:55BAC DAE ∠=∠=︒,AB AD =,∵40α=︒,∴15DAF ∠=︒,70B ADB ADE ∠=∠=∠=︒,∴85AFE DAF ADE ∠=∠+∠=︒,故选:B .8.【答案】C【解析】解:各边相等各角相等的多边形是正多边形,只有各边相等的多边形不一定是正多边形,如菱形,故①是假命题;正三角形和正五边形就不是中心对称图形,故②为假命题;正六边形中由外接圆半径与边长可构成等边三角形,所以外接圆半径与边长相等,故③为真命题;根据轴对称图形的定义和正多边形的特点,可知正n 边形共有n 条对称轴,故④为真命题.故选:C .9.【答案】B【解析】解:过点C 作CE AD ⊥,∵60D ∠=︒,2CD =,∴sin 60CE CD =⋅︒=过点B 作BF AD ⊥,∵AD BC ∥,∴四边形BCEF 是矩形,∴BF CE ==,需使222BM BN +最小,显然要使得BM 和BN 越小越好,∴显然点F 在线段MN 的之间,设MF x =,则1FN x =-,∴22222229232(1)334113323BM BN x x x x x ⎛⎫⎡⎤+=++-+=-+=+ ⎪-⎣⎦⎝⎭,∴当23x =时取得最小值为293.故选:B .10.【答案】A【解析】①有3种情况,如图1,BC 和OD 都是中线,点E 是重心;如图2,四边形ABDC 是平行四边形,F 是AD 中点,点E 是重心;如图3,点F 不是AD 中点,所以点E 不是重心;①正确②当60α=︒,如图4时AD 最大,4AB =,∴2AC BE ==,BC AE ==6BD ==,∴8DE =,∴AD =≠∴②错误;③如图5,若60α=︒,C ABC BD ∽△△,∴60BCD ∠=︒,90CDB ∠=︒,4AB =,2AC =,23BC =,3OE =1CE =,∴3CD =32GE DF ==,32CF =,∴52EF DG ==,32OG =,∴723OD =≠,∴③错误;④如图6,ABC BCD ∽△△,∴CD BC BC AB =,即214CD BC =,在Rt ABC △中,2216BC x =-,∴()221116444CD x x =-=-+,∴22114(2)544AC CD x x x +=-+=--+,当2x =时,AC CD +最大为5,∴④正确.故选:C .二、填空题(本大题共8小题,每小题3分,共24分.)11.【答案】()22x -##()22x -【解析】解:244x x -+=()22x -;故答案为:()22x -.12.【答案】5610⨯【解析】解:56000006100000610=⨯=⨯.故答案为:5610⨯.13.【答案】1-【解析】解:去分母得:3(1)2(2)x x -=-,去括号得:3324x x -=-,移项得:3243x x -=-+,合并同类项得:=1x -,检验:把=1x -代入最简公分母中:20,10x x -≠-≠,∴原分式方程的解为:=1x -,故答案为:1-14.【答案】36+##36+【解析】解:∵侧面展开图是边长为6的正方形,∴底面周长为6,∵底面为正三角形,∴正三角形的边长为2作CD AB ⊥,ABC 是等边三角形,2AB BC AC ===,1AD ∴=,∴在直角ADC ∆中,CD ==,122ABC S ∴=⨯=∴该直三棱柱的表面积为6636⨯+=+,故答案为:36+.15.【答案】2y x =-(答案不唯一)【解析】解:设1k =,则y x b =+,∵它的图象经过点(20),,∴代入得:20b +=,解得:2b =-,∴一次函数解析式为2y x =-,故答案为:2y x =-(答案不唯一).16.【答案】8【解析】解:设门高x 尺,依题意,竿长为()2x +尺,门的对角线长为()2x +尺,门宽为24x +-=()2x -尺,∴()()22222x x x +=+-,解得:8x =或0x =(舍去),故答案为:8.17.【答案】6【解析】当点A 在y 轴上,点B 、C 在x 轴上时,连接AO ,ABC 为等边三角形且AO BC ⊥,则30BAO ∠=︒,∴tan tan 30BAO ∠=︒=33OB OA =,如图所示,过点,A B 分别作x 轴的垂线,交x 轴分别于点,E F ,AO BO ⊥,90BFO AEO AOB ∠=∠=∠=︒,∴90BOF AOE EAO ∠=︒-∠=∠,∴BFO OEA ∽ ,∴213BFO AOE S OB S OA ⎛⎫== ⎪⎝⎭ ,∴212BFO S -== ,∴3AOE S =△,∴6k =.18.【答案】910或25或212【解析】解:由(1)(5)y a x x =--,令0x =,解得:5y a =,令0y =,解得:121,5x x ==,∴()1,0A ,()5,0B ,()0,5C a ,设直线BM 解析式为y kx b =+,∴5031k b k b +=⎧⎨+=⎩解得:1252k b ⎧=-⎪⎪⎨⎪=⎪⎩∴直线BM 解析式为1522y x =-+,当0x =时,52y =,则直线BM 与y 轴交于50,2⎛⎫ ⎪⎝⎭,∵12a >,∴552a >,∴点M 必在ABC 内部.1)、当分成两个三角形时,直线必过三角形一个顶点,平分面积,必为中线设直线AM 的解析式为y mx n=+∴031k b k b +=⎧⎨+=⎩解得:1212m n ⎧=⎪⎪⎨⎪=-⎪⎩则直线AM 的解析式为1122y x =-①如图1,直线AM 过BC 中点,,BC 中点坐标为55,22a ⎛⎫ ⎪⎝⎭,代入直线求得31102a =<,不成立;②如图2,直线BM 过AC 中点,直线BM 解析式为1522y x =-+,AC 中点坐标为15,22a ⎛⎫ ⎪⎝⎭,待入直线求得910a =;③如图3,直线CM 过AB 中点,AB 中点坐标为()3,0,∴直线MB 与y 轴平行,必不成立;2)、当分成三角形和梯形时,过点M 的直线必与ABC 一边平行,所以必有“”A 型相似,因为平分面积,所以相似比为④如图4,直线EM ∥AB ,∴CEN COA∽∴CE CN CO CA ==,∴515a a -=解得25a =;⑤如图5,直线ME ∥AC ,MN CO ∥,则EMN ACO∽∴12BE AB =,又4AB =,∴2BE =,∵53222BN =-=<,∴不成立;⑥如图6,直线ME ∥BC ,同理可得2AE AB =∴22AE =222NE =-,tan tan MEN CBO ∠∠=,55222a =-,解得212a =;综上所述,910a =或225+或212+.三、解答题(本大题共10小题,共90分.解答时应写出文字说明、证明过程或演算步骤)19.【答案】(1)8;(2)24y xy-+【解析】解:(1)2(3)25|4|--954=-+8=;(2)(2)(2)()x y x y x x y +---2224x y x xy=--+24y xy =-+.20.【答案】(1)11174x -+=,21174x --=;(2)13x -<<【解析】(1)2220x x +-=解:∵2,1,2a b c ===-,∴24142217b ac ∆=-=+⨯⨯=0>,∴411724b x a -±-±==解得:11174x -+=,21174x -=;(2)32251x x x +>-⎧⎨-<⎩①②解不等式①得:1x >-解不等式②得:3x <∴不等式组的解集为:13x -<<21.【答案】(1)见解析(2)见解析【解析】(1)证明:∵点D 、E 分别为AB AC 、的中点,∴AE CE =,DE BC ∥,∴ADE F ∠=∠,在CEF △与AED △中,ADE F AED CEF AE CE ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴()AAS CEF AED ≌;(2)证明:由(1)证得CEF AED △≌△,∴A FCE ∠=∠,∴BD CF ∥,∵DF BC ∥,∴四边形DBCF 是平行四边形.22.【答案】(1)14(2)18【解析】(1)解:∵共有4张相同的卡片且任意抽取一张卡片,记录后放回,∴每张卡片抽到的概率都是14,设小明恰好抽到景区A 门票为事件A ,则1()4P A =,故答案为:14;(2)解:根据题意,画树状图如下:∴一共有16种等可能的情况,恰好抽到景区A 和景区B 门票的情况有2种,∴他恰好抽到景区A 和景区B 门票的概率为21168=;23.【答案】(1)90;10(2)七年级的平均分最高;八年级的中位数最大;九年级的众数最大【解析】(1)解:∵抽取的总人数为217%300÷=(人),∴C 组的人数为30030%90a =⨯=(人),100%7%32%30%19%2%10%m =-----=;故答案为:90,10;(2)解:七年级的平均分最高;八年级的中位数最大;九年级的众数最大.(答案不唯一).24.【答案】(1)见解析(2)π【解析】(1)解:如图,O 为所作;;(2)解:∵PM 和PN 为O 的切线,∴OM PB ⊥,ON PN ⊥,1302MPO NPO APB ∠=∠=∠=︒,∴90OMP ONP ∠=∠=︒,∴180120MON APB ∠=︒-∠=︒,在Rt POM 中,MPO 30∠=︒,∴3tan 3033OM PM =⋅︒=⨯=,∴O 的劣弧 MN与PM PN 、所围成图形的面积PMON MONS S =-四边形扇形21201232360π⨯⨯=⨯⨯-π=.故答案为:π-.25.【答案】(1)67.5︒(2)2【解析】(1)如图,连接OD .FD 为O 的切线,∴90ODF ∠=︒.DF AB ∥,∴90AOD ∠=︒.AD AD =,∴1452ACD AOD ∠=∠=︒. CF CD =,∴1(180)67.52F ACD ∠∠=⨯-=︒.(2)如图,连接AD ,AO OD =,90AOD ∠=︒,∴45EAD ∠=︒.45ACD ∠=︒,∴A C D E A D ∠=∠,且ADE CDA ∠=∠,∴DAE DCA ∽ ,∴DE DA DA DC=,即28DA DE DC =⋅=,∴2DA =,∴222OA OD AD ===,即半径为2.26.【答案】(1)()7022302100(3045)x x y x x ⎧-+≤≤=⎨-+<≤⎩(2)销售价格为35元/kg 时,利润最大为450【解析】(1)当2230x ≤≤时,设y 关于x 的函数表达式为y kx b =+,将点()()22,48,30,40代入得,∴22483040k b k b +=⎧⎨+=⎩解得:170k b =-⎧⎨=⎩∴70y x =-+()2230x ≤≤,当3045x <≤时,设y 关于x 的函数表达式为11y k x b =+,将点()()30,40,45,10代入得,111145103040k b k b +=⎧⎨+=⎩解得:112100k b =-⎧⎨=⎩∴2100y x =-+()3045x <≤,()7022302100(3045)x x y x x ⎧-+≤≤=⎨-+<≤⎩(2)设利润为w当2230x ≤≤时,22(20)(70)901400(45)625w x x x x x =--+=-+-=--+∵在2230x ≤≤范围内,w 随着x 的增大而增大,∴当30x =时,w 取得最大值为400;当3045x <≤时,22(20)(2100)214020002(35)450w x x x x x =--+=-+-=--+∴当35x =时,w 取得最大值为450450400>,∴当销售价格为35元/kg 时,利润最大为450.27.【答案】(1)8+(2)212S x =++【解析】(1)如图,连接BD 、BQ ,四边形ABCD 为菱形,∴4CB CD ==,60A C ∠=∠=︒,∴BDC 为等边三角形.Q 为CD 中点,∴2CQ =,BQ CD ⊥,∴23BQ =,QB PB ⊥.45QPB ∠=︒,∴PBQ 为等腰直角三角形,∴3PB =,62PQ = 翻折,∴90BPB ∠='︒,PB PB '=,∴26BB '=,6PE =;.同理2CQ =,∴22CC '=2QF =∴((221112222323232438222PBB CQC BB C C PBCQ S S S S ''''=-+=⨯⨯+⨯-⨯+⨯=+ 四边形梯形;(2)如图2,连接BQ 、B Q ',延长PQ 交CC '于点F .PB x =,23BQ =,90PBQ ∠=︒,∴212PQ x =+∵1122PBQ S PQ BE PB BQ =⨯=⨯ ∴22312BQ PB BE PQ x ⨯==+,∴212QE x =+,∴222123121232121212QEB S x x x ==+++ . 90BEQ BQC QFC ∠=∠=∠=︒,则90EQB CQF FCQ ∠=︒-∠=∠,∴BEQ QFC ~ ,∴2221323QFCBEQS CQ S QB ⎛⎫=== ⎪⎝⎭ ,∴24312QFC S x =+ .∵122332BQC S =⨯⨯= ∴()222123433232233121212QEB BQC QFC x x S S S S x x x ⎛⎫=++=++=+ ⎪⎪+++⎝⎭ .28.【答案】(1)3b =-,2c =-(2)①3;②2或175【解析】(1)∵二次函数()222y x bx c =++的图像与y 轴交于点A,且经过点B和点(C -∴()()244212b c b c =++⎨=-+解得:32b c =-⎧⎨=-⎩∴3b =-,2c =-,()2322y x x =--;(2)①如图1,过点E 作y 轴平行线分别交AB 、BD 于G 、H.∵()2322y x x =--,当0x =时,y =,∴(0,A ,∴AD =4BD =,∴AB ==,∴6cos 3BD ABD AB ∠==.∵90GFE GHB ∠=∠=︒,FGE HGB ∠=∠,∴FEG ABD ∠=∠,∴cos 3FEG ∠=,∴3EF EG =,∴3EF EG =.∵(0,A B 设直线AB 的解析式为y kx d=+∴4d k d ⎧=⎪⎨+=⎪⎩解得:2k d ⎧=⎪⎨⎪=⎩∴直线AB解析式为22y x =-.设2232,22E m m m ⎛-- ⎝,∴2,2G m m ⎛⎝,∴22(2)22EG m m =-+=--+∴当2m =时,EG取得最大值为,EF ∴的最大值为33⨯=.②如图2,已知tan 2ABC ∠=,令AC =,则2BC =,在BC 上取点D ,使得AD BD =,∴2ADC ABC ∠=∠,设CD x =,则2AD BD x ==-,则222(2)(2)x x +=-,解得12x =,∴tan 2AC ADC CD∠==,即()tan 22ABC ∠=.如图3构造AMF FNE ∽ ,且MN x ∥轴,相似比为:AF EF ,又∵2tan tan tan 2MFA CBA FEN ∠∠∠===,设2AM a =,则2MF a =.分类讨论:ⅰ当2FAE ABC ∠=∠时,则tan 2EF FAE AF ∠==∴AMF 与FNE V 的相似比为1:22,∴224FN a ==,2242NE MF a ==,∴()6,232E a a -,代入抛物线求得113a =,20a =(舍).∴E 点横坐标为62a =.ⅱ当2FEA ABC ∠=∠时,则tan AF FEA EF ∠==,∴相似比为,∴12FN a ==,22NE a ==,∴5,22E a a ⎛⎫+ ⎪ ⎪⎝⎭,代入抛物线求得13425a =,20a =(舍).∴E 点横坐标为51725a =.综上所示,点E 的横坐标为2或175.。
二〇二三年绥化市初中毕业学业考试数学试题考生注意:1.考试时间120分钟2.本试题共三道大题,28个小题3.所有答案都必须写在答题卡上所对应的题号后的指定区域内一、单选题1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A B. C. D.【答案】C【解析】【分析】根据轴对称图形和中心对称图形定义:如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形;中心对称图形的定义:把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心,进行逐一判断即可.【详解】解:A 、是轴对称图形,不是中心对称图形,故A 选项不合题意;B 、是轴对称图形,不是中心对称图形,故B 选项不符合题意;C 、既是轴对称图形又是中心对称图形,故C 选项合题意;D 、不是轴对称图形,是中心对称图形,故D 选项不合题意.故选:C .【点睛】本题主要考查了轴对称图形和中心对称图形,解题的关键在于能够熟练掌握轴对称图形和中心对称图形的定义.2. 计算052-+的结果是( )A. 3- B. 7 C. 4- D. 6【答案】D【解析】【分析】根据求一个数的绝对值,零指数幂进行计算即可求解.【详解】解:052-+516=+=,故选:D ..的【点睛】本题考查了求一个数的绝对值,零指数幂,熟练掌握求一个数的绝对值,零指数幂是解题的关键.3. 如图是一个正方体,被切去一角,则其左视图是( )A. B. C. D.【答案】B【解析】【分析】根据左视图的意义判断即可.【详解】根据题意,该几何体的左视图为:,故选B .【点睛】本题考查了三视图的画法,熟练掌握三视图的空间意义是解题的关键.4. 纳米是非常小的长度单位,1nm 0.000000001m =,把0.000000001用科学记数法表示为( )A. 9110-´ B. 8110-´ C. 8110´ D. 9110´【答案】A【解析】【分析】用科学记数法表示绝对值较小的数,一般形式为10n a -´,其中110a £<,n 为整数.【详解】解:90.000000001110-=´.故选:A .【点睛】此题主要考查了用科学记数法表示绝对值较小的数,一般形式为10n a -´,其中110a £<,n 为由原数左边起第一个不为零的数字前面的0的个数所决定,确定a 与n 的值是解题的关键.5. 下列计算中,结果正确的是( )A. 333()pq p q -= B. 3228x x x x x ×+×= C. 5=± D. ()326a a =【答案】D【解析】【分析】根据积的乘方与幂的乘方运算,同底数幂的乘法、合并同类项,算术平方根,进行计算即可求解.【详解】解:A. 333()pq p q =--,故该选项不正确,不符合题意;B. 43222x x x x x ×+×=,故该选项不正确,不符合题意;C. 5=,故该选项不正确,不符合题意;D. ()326a a =,故该选项正确,符合题意;故选:D .【点睛】本题考查了积的乘方与幂的乘方运算,同底数幂的乘法、合并同类项,算术平方根,熟练掌握以上运算法则是解题的关键.6. 将一副三角板按下图所示摆放在一组平行线内,125Ð=°,230Ð=°,则3Ð的度数为( )A. 55°B. 65°C. 70°D. 75°【答案】C【解析】【分析】根据两直线平行内错角相等即可求解.【详解】解:依题意,190345Ð+°=Ð+°,∵125Ð=°,∴370Ð=°,故选:C .【点睛】本题考查了平行线的性质,熟练掌握两直线平行内错角相等是解题的关键.7. 下列命题中叙述正确的是( )A. 若方差22s s >乙甲,则甲组数据的波动较小B. 直线外一点到这条直线的垂线段,叫做点到直线的距离C. 三角形三条中线的交点叫做三角形的内心D. 角的内部到角的两边的距离相等的点在角的平分线上【答案】D【解析】【分析】根据方差的意义,点到直线的距离,三角形的重心的定义,角平分线的性质,逐项分析判断即可求解.【详解】解:A. 若方差22s s >乙甲,则乙组数据的波动较小,故该选项不正确,不符合题意;B. 直线外一点到这条直线的垂线段的长度,叫做点到直线的距离,故该选项不正确,不符合题意;C. 三角形三条中线交点叫做三角形的重心,故该选项不正确,不符合题意;D. 角的内部到角的两边的距离相等的点在角的平分线上,故该选项正确,符合题意;故选:D .【点睛】本题考查了方差的意义,点到直线的距离,三角形的重心的定义,角平分线的性质,熟练掌握以上知识是解题的关键.8. 绥化市举办了2023年半程马拉松比赛,赛后随机抽取了部分参赛者的成绩(单位:分钟),并制作了如下的参赛者成绩组别表、扇形统计图和频数分布直方图.则下列说法正确的是( )组别参赛者成绩A7080x £<B8090x £<C90100x £<D100110x £<E 110120x £<A. 该组数据的样本容量是50人的B. 该组数据的中位数落在90~100这一组C. 90~100这组数据的组中值是96D. 110~120这组数据对应的扇形统计图的圆心角度数为51°【答案】B【解析】【分析】根据C 组的人数除以占比求得样本的容量,结合统计图求得8090x £<的人数为15,进而根据中位数的定义,即可判断B 选项,根据组中值为901002+=95,即可判断C 选项,根据110~120的占比乘以360°,即可判断D 选项.【详解】解:A 、 该组数据的样本容量是1224%50¸=,故该选项不正确,不符合题意;B 、8090x £<的人数为:5041212715----=,41525+<,4151225++>,该组数据的中位数落在90~100这一组,故该选项正确,符合题意;C 、 90~100这组数据的组中值是95,故该选项不正确,不符合题意;D 、 110~120这组数据对应的扇形统计图的圆心角度数为736050.450´°=°,故该选项不正确,不符合题意;故选:B .【点睛】本题考查了样本的容量,条形统计图与扇形统计图信息关联,中位数的定义,求扇形统计图的圆心角的度数,求频数分布直方图组中值,从统计图表中获取信息是解题的关键.9. 在平面直角坐标系中,点A 在y 轴的正半轴上,AC 平行于x 轴,点B ,C 的横坐标都是3,2BC =,点D 在AC 上,且其横坐标为1,若反比例函数k y x=(0x >)的图像经过点B ,D ,则k 的值是( )A. 1B. 2C. 3D. 32【答案】C 【解析】【分析】设()3,B m ,则()()3,2,1,2C m D m ++根据反比例函数的性质,列出等式计算即可.【详解】设()3,B m ,∵点B ,C 的横坐标都是3,2BC =,AC 平行于x 轴,点D 在AC 上,且其横坐标为1,∴()()3,2,1,2C m D m ++,∴32m m =+,解得1m =,∴()3,1B ,∴313k =´=,故选C .【点睛】本题考查了反比例函数解析式的确定,熟练掌握k的意义,反比例函数的性质是解题的关键.10. 某运输公司,运送一批货物,甲车每天运送货物总量的14.在甲车运送1天货物后,公司增派乙车运送货物,两车又共同运送货物12天,运完全部货物.求乙车单独运送这批货物需多少天?设乙车单独运送这批货物需x 天,由题意列方程,正确的是( )A. 11142x += B. 11111424x æö++=ç÷èøC. 1111142x æö++=ç÷èø D.11111442x æö++=ç÷èø【答案】B【解析】【分析】设乙车单独运送这批货物需x 天,由题意列出分式方程即可求解.【详解】解:设乙车单独运送这批货物需x 天,由题意列方程11111424x æö++=ç÷èø,故选:B .【点睛】本题考查了列分式方程,根据题意找到等量关系列出方程是解题的关键.11. 如图,在菱形ABCD 中,60A Ð=°,4AB =,动点M ,N 同时从A 点出发,点M 以每秒2个单位长度沿折线A B C --向终点C 运动;点N 以每秒1个单位长度沿线段AD 向终点D 运动,当其中一点运动至终点时,另一点随之停止运动.设运动时间为x 秒,AMN V 的面积为y 个平方单位,则下列正确表示y 与x 函数关系的图象是( )A. B. C. D.【答案】A【解析】【分析】连接BD ,过点B 作BE AD ^于点E ,根据已知条件得出ABD △是等边三角形,进而证明AMN ABE V ∽得出90ANM AEB Ð=Ð=°,当04t <<时,M 在AB 上,当48t £<时,M 在BC 上,根据三角形的面积公式得到函数关系式,【详解】解:如图所示,连接BD ,过点B 作BE AD ^于点E ,当04t <<时,M 在AB 上,菱形ABCD 中,60A Ð=°,4AB =,∴AB AD =,则ABD △是等边三角形,∴122AE ED AD ===,BE ==∵2,AM x AN x ==,∴2AM AB AN AE==,又A A Ð=Ð∴AMN ABEV ∽∴90ANM AEB Ð=Ð=°∴MN ==,∴212y x x =当48t £<时,M 在BC 上,∴1122y AN BE x =´=´=,综上所述,04t <<时的函数图象是开口向上的抛物线的一部分,当48t £<时,函数图象是直线的一部分,故选:A .【点睛】本题考查了动点问题的函数图象,二次函数图象的性质,一次函数图象的性质,菱形的性质,勾股定理,等边三角形的性质与判定,相似三角形的性质与判定,熟练掌握以上知识是解题的关键.12. 如图,在正方形ABCD 中,点E 为边CD 的中点,连接AE ,过点B 作BF AE ^于点F ,连接BD 交AE 于点G ,FH 平分BFG Ð交BD 于点H .则下列结论中,正确的个数为( )①2AB BF AE =×;②:2:3BGF BAF S S =△△;③当AB a =时,22BD BD HD a -×=A. 0个B. 1个C. 2个D. 3个【答案】D【解析】【分析】①根据题意可得90ABF BAF DAE Ð=°-Ð=Ð,则cos cos ABF EAD Ð=Ð,即BF AD AB AE=,又AB AD =,即可判断①;②设正方形的边长为a ,根据勾股定理求得AF ,证明GAB GED V V ∽,根据相似三角形的性质求得GE ,进而求得FG ,即可判断②;过点H 分别作,BF AE 的垂线,垂足分别为,M N ,根据②的结论求得BH ,勾股定理求得BD ,即可判断③.【详解】∵四边形ABCD 是正方形,∴90BAD ADE Ð=Ð=°,AB AD=∵BF AE^∴90ABF BAF DAEÐ=°-Ð=Ð∴cos cos ABF EADÐ=Ð即BF AD AB AE=,又AB AD =,∴2AB BF AE =×,故①正确;设正方形的边长为a ,∵点E 为边CD 的中点,∴2a DE =,∴1tan tans 2ABF EAD Ð=Ð=,在Rt ABE △中,AB a ===,∴AF =在Rt ADE △中,AE ==∴EF AE AF =-==,∵AB DE∥∴GAB GEDV V ∽∴2AG AB GE DE==∴13GE AE ==∴FG AE AF GE =--=-=∴32AF FG ==∴:2:3BGF BAF S S =△△,故②正确;∵AB a =,∴22222BD AB AD a =+=,如图所示,过点H 分别作,BF AE 的垂线,垂足分别为,M N ,又∵BF AE ^,∴四边形FMHN 是矩形,∵FH 是BFG Ð的角平分线,∴HM HN =,∴四边形FMHN 是正方形,∴FN HM HN ==∵2,BF AF FG ===∴13MH FG BM BF ==设MH b =,则34BF BM FM BM MH b b b =+=+=+=在Rt BMH V中,BH ==,∵BF a =4b =解得:b =∴BH ==,∴2222B a D BD HD a a =-×=,故④正确.故选:D .【点睛】本题考查了解直角三角形,相似三角形的性质与判定,正方形的性质,熟练掌握相似三角形的性质与判定是解题的关键.二、填空题13. 因式分解:2x xy xz yz +--=_______.【答案】()()x y x z +-【解析】【分析】先分组,然后根据提公因式法,因式分解即可求解.【详解】解:2x xy xz yz +--=()()()()x x y z x y x y x z +-+=+-,故答案为:()()x y x z +-.【点睛】本题考查了因式分解,熟练掌握因式分解的方法是解题的关键.14. x 的取值范围是_______.【答案】5x ³-且0x ¹##0x ¹且5x ³-【解析】【分析】根据分母不为零,二次根式的被开方数是非负数,列出不等式计算即可.有意义,∴50x +³且0x ¹,∴5x ³-且0x ¹,故答案为:5x ³-且0x ¹.【点睛】本题考查了分母不为零,二次根式的被开方数是非负数,熟练掌握二次根式和分式有意义的条件是解题的关键.15. 在4张完全相同的卡片上,分别标出1,2,3,4,从中随机抽取1张后,放回再混合在一起.再随机抽取一张,那么第二次抽取卡片上的数字能够整除第一次抽取卡片上的数字的概率是_________.【答案】12##0.5【解析】【分析】根据题意列表法求概率即可求解.【详解】解:列表如下,123411 1 1=1213142221=212=232142=33 3 1=32313=344441=4 2 2=43414=共有16种等可能结果,符合题意的有8种,∴第二次抽取卡片上的数字能够整除第一次抽取卡片上的数字的概率是81162=,故答案为:12.【点睛】本题考查了列表法求概率,整除,熟练掌握列表法求概率是解题的关键.16. 已知一元二次方程256x x x +=+的两根为1x 与2x ,则1211+x x 的值为_______.【答案】23-【解析】【分析】根据一元二次方程根与系数的关系得出121246x x x x +==-,,将分式通分,代入即可求解.【详解】解:∵一元二次方程256x x x +=+,即2460x x --=,的两根为1x 与2x ,∴121246x x x x +==-,,∴1211+x x 12124263x x x x +===--,故答案为:23-.【点睛】本题考查了分式的化简求值,一元二次方程根与系数的关系,熟练掌握一元二次方程根与系数的关系是解题的关键.17. 化简:2222142442x x x x x x x x x+--æö-¸=ç÷--+-èø_______.【答案】12x -##12x-+【解析】【分析】先根据分式的加减计算括号内的,同时将除法转化为乘法,再根据分式的性质化简即可求解.【详解】解:2222142442x x x x x x x x x+--æö-¸ç÷--+-èø()()()()()2221242x x x x x x x x x +----=´--()()2222442x x x x x x x x ---+=´--12x =-;故答案为:12x -.【点睛】本题考查了分式的混合运算,熟练掌握分式的运算法则是解题的关键.18. 如图,O e 的半径为2cm ,AB 为O e 的弦,点C 为 AB 上的一点,将 AB 沿弦AB 翻折,使点C 与圆心O 重合,则阴影部分的面积为_______.(结果保留p 与根号)【答案】22πcm3æ-çè【解析】【分析】根据折叠性质得出AOC V 是等边三角形,则60AOC Ð=°,1OD CD ==,根据阴影部分面积AOC AOC S S =-V 扇形即可求解.【详解】解:如图所示,连接,OA OC ,设,AB CO 交于点D∵将 AB 沿弦AB 翻折,使点C 与圆心O 重合,∴AC AO =,OC AB ^又OA OC =∴OA OC AC ==,∴AOC V 是等边三角形,∴60AOC Ð=°,1OD CD ==,∴AD ==,∴阴影部分面积)226012π22πcm 36023AOC AOC S S =-=´-´=V 扇形故答案为:22πcm 3æ-çè.19. 如图,在平面直角坐标系中,ABC V 与AB C ¢¢△的相似比为12∶,点A 是位似中心,已知点(2,0)A ,点(,)C a b ,90C Ð=°.则点C ¢的坐标为_______.(结果用含a ,b 的式子表示)【答案】(62,2)a b --【解析】【分析】过点,C C ¢分别作x 轴的垂线,CD C D ¢¢垂足分别为,D D ¢,根据题意得出2AD AD ¢=,则的2,AD a CD b =-=,得出()224,0D a ¢-+,即可求解.【详解】解:如图所示,过点,C C ¢分别作x 轴的垂线,CD C D ¢¢垂足分别为,D D ¢,∵ABC V 与AB C ¢¢△的相似比为12∶,点A 是位似中心,(2,0)A ∴2AD AD ¢=∵(,)C a b ,∴2,AD a CD b =-=,∴24,2A D a C D b ¢¢¢=-=,∴()224,0D a ¢-+∴C ¢(62,2)a b --故答案为:(62,2)a b --.【点睛】本题考查了求位似图形的坐标,熟练掌握位似图形的性质是解题的关键.20. 如图,ABC V 是边长为6的等边三角形,点E 为高BD 上的动点.连接CE ,将CE 绕点C 顺时针旋转60°得到CF .连接AF ,EF ,DF ,则CDF V 周长的最小值是______.【答案】3+3+【解析】【分析】根据题意,证明CBE CAF V V ≌,进而得出F 点在射线AF 上运动,作点C 关于AF 的对称点C ¢,连接DC ¢,设CC ¢交AF 于点O ,则=90AOC а,则当,,D F C ¢三点共线时,FC FD +取得最小值,即FC FD F C F D CD ¢¢¢¢+=+=,进而求得C D ¢,即可求解.【详解】解:∵E 为高BD 上的动点.∴1302CBE ABC Ð=Ð=°∵将CE 绕点C 顺时针旋转60°得到CF .ABC V 是边长为6的等边三角形,∴,60,CE CF ECF BCA BC AC =Ð=Ð=°=∴CBE CAF V V ≌∴30CAF CBE Ð=Ð=°,∴F 点在射线AF 上运动,如图所示,作点C 关于AF 的对称点C ¢,连接DC ¢,设CC ¢交AF 于点O ,则=90AOC а在Rt AOC V 中,30CAO Ð=°,则132CO AC ==,则当,,D F C ¢三点共线时,FC FD +取得最小值,即FC FD F C F D CD ¢¢¢¢+=+=∵6CC AC ¢==,ACO C CD ¢Ð=Ð,CO CD =∴ACO C CD ¢V V ≌∴90C DC AOC ¢Ð=Ð=°在C DC ¢V 中,C D ¢===,∴CDF V 周长的最小值为3CD FC CD CD DC ¢++=+=+故答案为:3+【点睛】本题考查了轴对称求线段和的最值问题,等边三角形的性质与判定,全等三角形的性质与判定,勾股定理,熟练掌握等边三角形的性质与判定以及轴对称的性质是解题的关键.21. 在求123100++++ 的值时,发现:1100101+=,299101+= ,从而得到123100++++= 101505050´=.按此方法可解决下面问题.图(1)有1个三角形,记作11a =;分别连接这个三角形三边中点得到图(2),有5个三角形,记作25a =;再分别连接图(2)中间的小三角形三边中点得到图(3),有9个三角形,记作39a =;按此方法继续下去,则123n a a a a ++++= _______.(结果用含n 的代数式表示)【答案】22n n -##22n n -+【解析】【分析】根据题意得出()14143n a n n =+-=-,进而即可求解.【详解】解:依题意,()1231,5,9,14143n a a a a n n ===×××=+-=-,,∴123n a a a a ++++= ()21432122n n n n n n +-==-=-,故答案为:22n n -.【点睛】本题考查了图形类规律,找到规律是解题的关键.22. 已知等腰ABC V ,120A Ð=°,2AB =.现将ABC V 以点B 为旋转中心旋转45°,得到A BC ¢¢△,延长C A ¢¢交直线BC 于点D .则A D ¢的长度为_______.【答案】44+-【解析】【分析】根据题意,先求得BC =,当ABC V 以点B 为旋转中心逆时针旋转45°,过点B 作BE A B ¢^交A D ¢于点E ,当ABC V 以点B 为旋转中心顺时针旋转45°,过点D 作DF BC ¢^交BC ¢于点F ,分别画出图形,根据勾股定理以及旋转的性质即可求解.【详解】解:如图所示,过点A 作AM BC ^于点M ,∵等腰ABC V ,120BAC Ð=°,2AB =.∴30ABC ACB Ð=Ð=°,∴112AM AB ==,BM CM ===∴BC =,如图所示,当ABC V 以点B 为旋转中心逆时针旋转45°,过点B 作BE A B ¢^交A D ¢于点E ,∵120BAC Ð=°,∴60DA B ¢Ð=°,30A EB ¢Ð=°,在Rt A BE ¢V 中,24A E A B ¢¢==,BE ==∵等腰ABC V ,120BAC Ð=°,2AB =.∴30ABC ACB Ð=Ð=°,∵ABC V 以点B 为旋转中心逆时针旋转45°,∴45ABA ¢Ð=°,∴180********DBE Ð=°-°-°-°=°,1804530105A BD ¢Ð=°-°-°=°在A BD ¢V 中,1801806010515D DA B A BD Ð=°-Ð-Ð=°-°-°=¢¢°,∴D EBD Ð=Ð,∴EB ED ==∴4A D A E DE ¢¢=+=+如图所示,当ABC V 以点B 为旋转中心顺时针旋转45°,过点D 作DF BC ¢^交BC ¢于点F ,在BFD △中,45BDF CBC Т=Ð=°,∴DF BF=在Rt DC F ¢V 中,30C ¢Ð=°∴'DF FC =∴BC BF =+=∴3DF BF ==-∴26DC DF ¢==-∴624A D C D A C ¢¢¢¢=-=-=-,综上所述,A D ¢的长度为4-或4+,故答案为:4-或4+.【点睛】本题考查了旋转的性质,勾股定理,含30度角的直角三角形的性质,熟练掌握旋转的性质,分类讨论是解题的关键.三、解答题23. 已知:点P 是O e 外一点.(1)尺规作图:如图,过点P 作出O e 的两条切线PE ,PF ,切点分别为点E 、点F .(保留作图痕迹,不要求写作法和证明)(2)在(1)的条件下,若点D 在O e 上(点D 不与E ,F 两点重合),且30EPF Ð=°.求EDF Ð的度数.【答案】(1)见解析 (2)75EDF Ð=°或105°【解析】【分析】(1)①连接PO ,分别以点,P O 为圆心,大于12PO 的长为半径画圆,两圆交于点,M N 两点,作直线MN 交OP 于点A ,②以点A 为圆心,OA 为半径画圆,与O e 交于,E F 两点,作直线,PE PF ,(2)根据切线的性质得出90PEO PFO Ð=Ð=°,根据四边形内角和得出150EOF Ð=°,进而根据圆周角定理以及圆内接四边形对角互补即可求解.【小问1详解】解:如图所示,①连接PO ,分别以点,P O 为圆心,大于12PO 的长为半径画弧,两弧交于点,M N 两点,作直线MN 交OP 于点A ,②以点A 为圆心,OA 为半径画圆,与O e 交于,E F 两点,作直线,PE PF ,则直线,PE PF 即为所求;【小问2详解】如图所示,点D 在O e 上(点D 不与E ,F 两点重合),且30EPF Ð=°,∵,PE PF 是O e 的切线,∴90PEO PFO Ð=Ð=°,∴360909030150EOF Ð=°-°-°-°=°,当点D 在优弧 E F 上时,1752EDF EOF Ð=Ð=°,当点D 在劣弧 E F 上时,18075105EDF Ð=°-°=°,∴75EDF Ð=°或105°.【点睛】本题考查了切线的性质与判定,直径所对的圆周角是直角,圆内接四边形对角互补,圆周角定理,熟练掌握以上知识是解题的关键.24. 如图,直线MN 和EF 为河的两岸,且MN EF ∥,为了测量河两岸之间的距离,某同学在河岸FE 的B 点测得30CBE Ð=°,从B 点沿河岸FE 的方向走40米到达D 点,测得45CDE Ð=°.(1)求河两岸之间的距离是多少米?(结果保留根号)(2)若从D 点继续沿DE 的方向走12)+米到达P 点.求tan CPE Ð的值.【答案】(1)河两岸之间的距离是20米(2)5tan 2CPE Ð=【解析】【分析】(1)过点C 作CM EF ^于点M ,设CM a =米,在Rt MCB △中,MB =,在Rt MCD △中,MD MC a ==,根据40BD =,建立方程,解方程即可求解;(2)根据题意求得MP 的长,进而根据正切的定义,即可求解.【小问1详解】解:如图所示,过点C 作CM EF ^于点M ,设CM a =米,∵30CBE Ð=°∴tan tan 30CM CBM PB Ð==°=,∴MB =,在Rt MCD △中,tan tan 451CM CDM MD Ð==°=,∴MD MC a==∴40BD MB MD a =-=-=解得:20a =+答:河两岸之间的距离是20米;【小问2详解】解:如图所示,依题意,4012)52PB BD DP =+=+=+,∴((20528MP MB PB =-=++=+在Rt CMP △中,5tan 2CM CPM MP Ð===,∴5tan 2CPE Ð=.【点睛】本题考查了解直角三角形的应用,熟练掌握三角函数关系是解题的关键.25. 某校组织师生参加夏令营活动,现准备租用A 、B 两型客车(每种型号的客车至少租用一辆).A 型车每辆租金500元,B 型车每辆租金600元.若5辆A 型和2辆B 型车坐满后共载客310人;3辆A 型和4辆B 型车坐满后共载客340人.(1)每辆A 型车、B 型车坐满后各载客多少人?(2)若该校计划租用A 型和B 型两种客车共10辆,总租金不高于5500元,并将全校420人载至目的地.该校有几种租车方案?哪种租车方案最省钱?(3)在这次活动中,学校除租用A 、B 两型客车外,又派出甲、乙两辆器材运输车.已知从学校到夏令营目的地的路程为300千米,甲车从学校出发0.5小时后,乙车才从学校出发,却比甲车早0.5小时到达目的地.下图是两车离开学校的路程s (千米)与甲车行驶的时间t (小时)之间的函数图象.根据图象信息,求甲乙两车第一次相遇后,t 为何值时两车相距25千米.【答案】(1)每辆A 型车、B 型车坐满后各载客40人、55人(2)共有4种租车方案,租8辆A 型车,2辆B 型车最省钱(3)在甲乙两车第一次相遇后,当3t =小时或113小时时,两车相距25千米【解析】【分析】(1)设每辆A 型车、B 型车坐满后各载客x 人、y 人,由题意列出二元一次方程组,解方程组即可求解;(2)设租用A 型车m 辆,则租用B 型车(10)m -辆,由题意列出一元一次不等式组,解不等式组,求整数解即可得出m 的值,设总租金为w 元,根据一次函数的性质即可求解;(3)设s kt =甲,1s k t b =+乙,由题意可知,甲车的函数图像经过(4,300);乙车的函数图像经过(0.5,0),(3.5,300)两点.求出函数解析式,进而即可求解.【小问1详解】解:设每辆A 型车、B 型车坐满后各载客x 人、y 人,由题意得5231034340x y x y +=ìí+=î解得4055x y =ìí=î答:每辆A 型车、B 型车坐满后各载客40人、55人.【小问2详解】设租用A 型车m 辆,则租用B 型车(10)m -辆,由题意得()()500600105500405510420m m m m ì+-£ïí+-³ïî 解得:2583m ££ m Q 取正整数,\5m =,6,7,8\共有4种租车方案设总租金为w 元,则500600(10)1006000w m m m =+-=-+Q 1000-<w \随着m 的增大而减小\8m =时,w 最小\租8辆A 型车,2辆B 型车最省钱.【小问3详解】设s kt =甲,1s k t b =+乙.由题意可知,甲车的函数图象经过(4,300);乙车的函数图象经过(0.5,0),(3.5,300)两点.∴75s t =甲,10050s t =-乙25s s -=乙甲,即100507525t t --=解得3t =或3007525t -=解得113t =所以,在甲乙两车第一次相遇后,当3t =小时或113小时时,两车相距25千米.【点睛】本题考查了二元一次方程组的应用,一元一次不等式的应用,一次函数的应用,根据题意找到等量关系,列出方程组,不等式组,以及函数解析式是解题的关键.26. 已知:四边形ABCD 为矩形,4AB =,3AD =,点F 是BC 延长线上的一个动点(点F 不与点C 重合).连接AF 交CD 于点G .(1)如图一,当点G 为CD 的中点时,求证:ADG FCG @△△.(2)如图二,过点C 作CE AF ^,垂足为E .连接BE ,设BF x =,CE y =.求y 关于x 的函数关系式.(3)如图三,在(2)的条件下,过点B 作BM BE ^,交FA 的延长线于点M .当1CF =时,求线段BM 的长.【答案】(1)见解析 (2)y =y =)(3【解析】【分析】(1)根据矩形的性质得出AD BF ∥,则D DCF Ð=Ð,根据题意得出DG CG =,即可证明(ASA)ADG FCG △≌△;(2)在Rt ABF V中,AF ==,证明CEF ABF △∽△,根据相似三角形的性质即可求解;(3)过点E 作EN BF ^于点N ,得出ABF △,CEF △为等腰直角三角形,在Rt BNE V 中,勾股定理求得BE ,证明BAM BCE △∽△,根据相似三角形的性质即可求解.【小问1详解】证明:∵四边形ABCD 为矩形,∴AD BF ∥,∴D DCF Ð=Ð,∵G 为CD 中点,∴DG CG =,在ADG △和△FCG 中D GCF DG CGAGD FGC Ð=Ðìï=íïÐ=Ðî, ∴(ASA)ADG FCG △≌△;【小问2详解】∵四边形ABCD 为矩形,∴90ABC Ð=°,∵CE AF ^,∴90CEF ABC Ð=°=Ð,∵F F Ð=Ð,∴CEF ABF △∽△, ∴CE CF AB AF=,∵4AB =,BF x =,∴在Rt ABF V 中,AF ==, ∵CE y =,∴4y =,∴y =y =;【小问3详解】过点E 作EN BF ^于点N ,∵四边形ABCD 为矩形,且3AD =,∴3AD BC ==,∵4AB =,1CF =,∴AB BF =,∴ABF △为等腰直角三角形,∴45CFE BAF Ð=Ð=°,∵CE AF ^,∴CEF △为等腰直角三角形,∴45ECF Ð=°,∵EN CF ^,∴EN 平分CF ,∴12CN NF NE ===,在Rt BNE V 中,∵222BE ,∴BE ==,∵45ECF BAF °Ð=Ð=,∴135BAM BCE Ð=Ð=°,∵BM BE ^,∴90MBA ABE Ð+Ð=°,∵90ABE EBC Ð+Ð=°,∴MBA EBC Ð=Ð,∴BAM BCE △∽△,∴43BM BA BE BC ==,43=,∴BM =.【点睛】本题考查了矩形的性质,全等三角形的性质与判定,相似三角形的性质与判定,列函数关系式,勾股定理,熟练掌握相似三角形的性质与判定是解题的关键.27. 如图,MN 为⊙O 的直径,且15MN =,MC 与ND 为圆内的一组平行弦,弦AB 交MC 于点H .点A 在¼MC上,点B 在»NC 上,90OND AHM Ð+Ð=°.(1)求证:MH CH AH BH ×=×.(2)求证: AC BC=.(3)在⊙O 中,沿弦ND 所在的直线作劣弧 ND的轴对称图形,使其交直径MN 于点G .若3sin 5CMN Ð=,求NG 的长.【答案】(1)见解析(2)见解析 (3)215【解析】【分析】(1)证明AMH CBH V V ∽即可;(2)连接OC ,交AB 于点F ,根据平行线的性质和已知条件证明垂直平分即可;(3)利用对称的性质作辅助线,根据已知条件,转化为解直角三角形问题即可.【小问1详解】Q ABC Ð和AMC Ð是 AC 所对的圆周角,\ABC AMC Ð=Ð,Q AHM CHB Ð=Ð,∴AMH CBH V :V ,∴AH MH CH BH=,∴MH CH AH BH ×=×.【小问2详解】连接OC ,交AB 于点F ,Q MC 与ND 为一组平行弦,即:MC ND ∥,\OND OMC Ð=Ð,Q OM OC =,\OMC OCM Ð=Ð,Q 90OND AHM Ð+Ð=°,\90OCM AHM OCM CHB Ð+Ð=Ð+Ð=°,\90HFC Ð=°,\OC AB ^,\OC 是AB 的垂直平分线,\ =AC BC.【小问3详解】连接DM 、DG ,过点D 作DE MN ^,垂足为E ,设点G 的对称点G ¢,连接G D ¢、G N ¢,Q DG DG ¢=,G ND GND ¢Ð=Ð,∴ 'DMDG =n ,\DG DM ¢=,\DG DM =,\DGM V 是等腰三角形,Q DE MN ^,\GE ME =,Q DN CM ∥,\CMN DNM Ð=Ð,Q MN 为直径,\90MDN Ð=°,\90MDE EDN Ð+Ð=°,Q DE MN ^,\90DEN Ð=°,\90DNM EDN Ð+Ð=°,\3sin sin sin 5EDM DNM CMN Ð=Ð=Ð=,在Rt MND △中,15MN =,\3sin 5MD DNM MN Ð==,\3155MD =,\9MD =,在Rt MED V 中,3sin 5ME EDM MD Ð==,\395ME =\275ME =,\2721215255NG MN MG MN ME =-=-=-´=\215NG =故答案为:215.【点睛】本题考查了圆的综合问题,同弧所对圆周角相等、构建合适的辅助线是解题的关键;熟练掌握相似三角形的判定与性质、垂直平分线的性质、熟悉锐角三角函数解决直角三角形.28. 如图,抛物线21y ax bx c =++的图象经过(6,0)A -,(2,0)B -,(0,6)C 三点,且一次函数6y kx =+的图象经过点B .(1)求抛物线和一次函数的解析式.(2)点E ,F 为平面内两点,若以E 、F 、B 、C 为顶点的四边形是正方形,且点E 在点F 的左侧.这样的E ,F 两点是否存在?如果存在,请直接写出所有满足条件的点E 的坐标:如果不存在,请说明理由.(3)将抛物线21y ax bx c =++的图象向右平移8个单位长度得到抛物线2y ,此抛物线的图象与x 轴交于M ,N 两点(M 点在N 点左侧).点P 是抛物线2y 上的一个动点且在直线NC 下方.已知点P 的横坐标为m .过点P 作PD NC ^于点D .求m 为何值时,12CD PD +有最大值,最大值是多少?【答案】(1)211462y x x =++,36y x =+ (2)满足条件的E 、F 两点存在,1(8,2)E -,2(4,2)E -,3(4,4)E -(3)当133m =时,12CD PD +【解析】【分析】(1)待定系数法求解析式即可求解;(2)①当BC 为正方形的边长时,分别过B 点C 点作12E E BC ^,12F F BC ^,使12E B E B BC ==,12CF CF BC ==,连接11E F 、22E F ,证明11(AAS)BE H CBO △≌△,得出112E H BO ==,16H B OC ==,则1(8,2)E -同理可得,2(4,2)E -;②以BC 为正方形的对角线时,过BC 的中点G 作33E F BC ^,使33E F 与BC 互相平分且相等,则四边形33E BF C 为正方形,过点3E 作3E N y ^轴于点N ,过点B 作3BM E N ^于点M ,证明33(AAS)CE N E BM △≌△,得出3E B =,在3Rt E NC △中,22233E C CN E N =+,解得2CN =或4,进而即可求解;(3)得出CON V 是等腰直角三角形,HPD V是等腰直角三角形,则HD DP ==,点P 在抛物线2y 上,且横坐标为m ,得出(,6)H m m -+,进而可得22132HD DP m m ö==-+=÷ø,则12CD PD+2133m ö=-+÷ø根据二次函数的性质即可求解.【小问1详解】解:把(6,0)A -,(2,0)B -,(0,6)C 代入21y ax bx c =++得36604206a b c a b c c -+=ìï-+=íï=î解得1246a b c ì=ïï=íï=ïî∴211462y x x =++ 把(2,0)B -代入6y kx =+得3k =∴36y x =+【小问2详解】满足条件的E 、F 两点存在,1(8,2)E -,2(4,2)E -,3(4,4)E -解:①当BC 为正方形的边长时,分别过B 点C 点作12E E BC ^,12F F BC ^,使12E B E B BC ==,12CF CF BC ==,连接11E F 、22E F .过点1E 作11E H x ^轴于1H .∵1111,90BE CB BOC E H B E BC =Ð=Ð=°=Ð,又111190BE H E BH CBO Ð=°-Ð=Ð,∴11(AAS)BE H CBO △≌△,∴112E H BO ==,16H B OC ==∴1(8,2)E -同理可得,2(4,2)E -②以BC 为正方形的对角线时,过BC 的中点G 作33EF BC ^,使33E F 与BC 互相平分且相等,则四边形33E BF C 为正方形,过点3E 作3E N y ^轴于点N ,过点B 作3BM E N ^于点M∵3333,90CE BE CNE E MB =Ð=Ð=°,又33390BE M CE N E CNÐ=°-Ð=Ð∴33(AAS)CE N E BM △≌△∴3CN E M =,3BM E N=∵BC =∴3E G BG ==∴3E B =在3Rt E NC △中,22233E C CN E N=+∴222(6)CN CN =+-解得2CN =或4当4CN =时,3(2,2)E ,此时点E 在点F 右侧故舍去;当2CN =时,3(4,4)E -.综上所述:1(8,2)E -,2(4,2)E -,3(4,4)E -【小问3详解】∵211462y x x =++向右平移8个单位长度得到抛物线()()22184862y x x =-+-+当20y =,即()()21848602x x -+-+=解得:122,6x x ==∴(2,0)M ,(6,0)N ∵2y 过M ,N ,C 三点∴221462y x x =-+ 在直线NC 下方的抛物线2y 上任取一点P ,作PH x ^轴交NC 于点H ,过点H 作HG y ^轴于点.G∵(6,0)N ,(0,6)C ∴ON OC=∴CON V 是等腰直角三角形∵45CHG Ð=°,90GHP Ð=°∴45PHD Ð=°又PD CN^∴HPD V 是等腰直角三角形∴HD DP HP ==∵点P 在抛物线2y 上,且横坐标m∴CG GH m==∴CH =∵6CN y x =-+为∴(,6)H m m -+∴2211646322HP m m m m m æö=-+--+=-+ç÷èø∴22132HD DP m m ö==-+=÷ø∴211332222CD PD CH HD PD CH PD æö+=++=+=++ç÷ç÷èø2133m ö=-÷ø∴当133m =时,12CD PD +.【点睛】本题考查了二次函数综合运用,正方形的性质,二次函数的性质,分类讨论,熟练掌握二次函数的性质是解题的关键.。
初中毕业、升学统一模拟试题考试样题数 学题号一二三总 分 19 20 21 22 2324 25 得分注意事项:本试题满分150分,考试时间120分钟;一、选择题:本大题8个小题,每小题3分,共24分.在每小题给出的四个选项中只有一个是正确的,请把正确选项的标号填在题后面的括号内.1. 北京国家体育场“鸟巢”建筑面积达25.8万平方米,用科学记数法表示应为 ( ) A .24108.25m ⨯ B .25108.25m ⨯ C .251058.2m ⨯ D . 261058.2m ⨯ 2.计算23(2)a -的结果为 ( ) A .68a -B .52a -C .58a -D .66a -3.如图所示,已知直线AB CD ∥,125C ∠=°, 45A ∠=°,则E ∠的度数为 ( ) A .70° B .80° C .90° D .100°4.某百货商场的女装专柜对上周女装的销售情况进行了统计,销售情况如下表所示:颜色 黄色 绿色 白色 紫色 红色 数量(件)10018022080550百货商场经理根据上周销售情况的统计表,决定本周多进一些红色的女装,可用来解释这一现象的统计知识是 ( )A.方差 B.平均数 C.众数 D.中位数 5.已知二元一次方程组2423m n m n -=⎧⎨-=⎩,,则m n +的值是 ( )A .1B .0C .2-D .1-得分 评卷人EAB C D45°125°3题图6.如果一次函数y kx b =+的图象经过第一象限,且与y 轴负半轴相交,那么 ( ) A .0k >,0b > B .0k >,0b < C .0k <,0b > D .0k <,0b < 7.如图,一个空间几何体的主视图和左视图都是边长为1的正三角形,俯视图是一个圆,那么这个几何体的侧面积是 ( ) A .4πB .π42C .π22D .2π7题图8.如图所示是二次函数2y ax bx c =++图象的一部分,图象过A 点(3,0), 二次函数图象对称轴为1x =,给出四个结论:①24b ac >;②0bc <;③20a b +=;④0a b c ++=,其中正确结论是 ( )A .②④B .①③C .②③D .①④二、填空题:本大题共8个小题,每小题4分,共32分,请把答案填在题中横线上。
9.为了美化环境,某市加大对绿化的投资.2009年用于绿化投资20万元,2011年用于绿化投资25万元,求这两年绿化投资的年平均增长率.设这两年绿化投资的年平均增长率为x ,根据题意所列方程为10.如图,为了测量一个圆形铁环的半径,某同学采用了如下办法:将铁环平放在水平 桌面上,用一个锐角为30°的三角板和一个刻度尺,按如图所示的方法得到相关数据, 进而可求得铁环的半径,若测得PA=5cm ,则铁环的半径是 cm.得分 评卷人Oyx 1x =(30)A ,8题图11题图P A10题图11.如图所示,小区公园里有一块圆形地面被黑白石子铺成了面积相等的八部分,阴影部分是黑色石子,小华随意向其内部抛一个小球,则小球落在黑色石子区域内的概 率是 .12.如图所示,AB 为O ⊙的直径,P 点为其半圆上一点,40POA C ∠=°,为另一半 圆上任意一点(不含A B 、),则PCB ∠= 度.13.如图所示,在正方形网格中,图①经过 变换(填“平移”或“旋转”或 “轴对称”)可以得到图②;图③是由图②经过旋转变换得到的,其旋转中心是点 (填“A ”或“B ”或“C ”). 14. 若一次函数b kx y +=1与反比例函数xy 22=的图像分别交于点)2,1(A 和 )1,2(--B 两点,则使12y y >的x 的取值范围是 .15. 如图,在矩形ABCD 中,E F ,分别是边AD BC ,的中点,点G H ,在DC 边上, 且12GH DC =.若10AB =,12BC =,则图中阴影部分的面积为 .16.我们把分子为1的分数叫做理想分数,如21,31,41,… ,任何一个理想分数都可以写成两个不同理想分数的和,如613121+=; 1214131+=; 2015141+=; …根据对上述式子的观察,请你思考:如果理想分数n 1=11a b+(n 是不小于2的正整数),那么b a += .(用含n 的式子表示)。
C BA P O 40° 12题图 ① ②③13题图A B C 15题图H GFEDCBA三、解答题:本大题9个小题,共102分.解答时要写出必要的文字说明、演算步骤或推理过程.17.(本小题满分12分,每小题6分)17.(每小题6分,满分12分)(1)计算:()231123123-⎛⎫+---- ⎪⎝⎭; (2)解方程:2111x x x -=-+.18.(本小题满分10分)如图,在△ABC 中,∠ACB =2B ∠.(1) 根据要求作图:① 作ACB ∠的平分线交AB 于D ;② 过D 点作DE ⊥BC ,垂足为E . (2)在(1)的基础上写出一对全等三角形和一对相似比不为.......1.的相似三角形: △ ≌△ ;△ ∽△ .请选择其中一对加以证明.19.(本小题满分10分) 为了解贫困群众对帮扶情况的满意程度,有关部门在该市所管辖的两个区内,分别随机抽取了若干名贫困群众进行问卷调查.根据收集的信息进行了统计,并绘制了下面尚不完整的统计图.已知在甲区所调查的贫困群众中,非常满意的人数占甲区所调查的总人数的35%.根据统计图所提供的信息解答下列问题: (1)甲区参加问卷调查的贫困群众有 人; (2)请将统计图补充完整; (3)小红说:“因为甲区有30人不满意,乙区有40人不满意,所以甲区的不满意得分评卷人得分 评卷人得分评卷人ACB率比乙区低.”你认为这种说法正确吗?为什么?20.(本小题满分10分)某厂家新开发的一种摩托车如图所示,它的大灯A射出的光线AB 、AC 与地面MN 的夹角分别为8°和10°,大灯A离地面距离1 m .(1)该车大灯照亮地面的宽度BC 约是多少?(不考虑其它因素)(2)一般正常人从发现危险到做出刹车动作的反应时间是0.2 s ,从发现危险到摩托车完全停下所行驶的距离叫做最小安全距离,某人以60 km/h 的速度驾驶该车,从60 km/h 到摩托车停止的刹车距离是314m ,请判断该车大灯的设计是否能满足最小安全距离的要求,请说明理由.(参考数据:2548sin ≈ ,718tan ≈,50910sin ≈ ,28510tan ≈)AM B C N得分 评卷人非常满意 人数 800 600 400 200 满意 比较满意 不满意 满意程度 甲 乙420 700 760500250 30 4021.(本小题满分10分)已知二次函数y x x 1221=--的图像和反比例函数y kx2=的图像都经过点),1(a 。
(1)求的a 值;(2)试在下图所示的直角坐标系中,画出该二次函数及反比例函数的图像,并利用图像比较y 1与y 2的大小。
22.(本题满分12分)已知:如图,在平行四边形ABCD 中,AE 是BC 边上的高,将ABE △沿BC 方向平移,使点E 与点C 重合,得GFC △.(1)求证:BE DG =;(2)若60B ∠=°,当AB 与BC 满足什么数量关系时,四边形ABFG 是菱形?证明你的结论.得分 评卷人A GBE得分 评卷人23.(本小题满分12分)某校团委组织了“歌唱祖国”有奖征文活动,并设立了一、二、三等奖.学校计划派人根据设奖情况买50件奖品,其中二等奖件数比一等奖件数的2倍还少10件,三等奖所花钱数不超过二等奖所花钱数的1.5倍.各种奖品的单价如下表所示.如果计划一等奖买x 件,买50件奖品的总钱数是w 元.(1)求w 与x 的函数关系式及自变量x 的取值范围;(2)请你计算一下,如果购买这三种奖品所花的总钱数最少?最少是多少元?24.(本小题满分12分)如图所示,已知AB 是半圆O 的直径,弦106CD AB AB CD ==∥,,,E 是AB 延长线上一点,103BE =. (1)求ODOE; (2)证明直线DE 是半圆O 的切线.得分评卷人一等奖 二等奖 三等奖 单价(元) 12 10 5 O AB EDC得分 评卷人25.(本小题满分14分)如图所示,已知在直角梯形OABC 中,A B O CB C x ∥,⊥轴于点(11)(31)C A B ,,、,.动点P 从O 点出发,沿x 轴正方向以每秒1个单位长度的速度移动.过P 点作PQ 垂直于直线..OA ,垂足为Q .设P 点移动的时间为t 秒(04t <<),O P Q △与直角梯形OABC 重叠部分的面积为S .(1)求经过O A B 、、三点的抛物线解析式; (2)求S 与t 的函数关系式;(3)将O P Q △绕着点P 顺时针旋转90°,是否存在t ,使得OPQ △的顶点O 或Q 在抛物线上?若存在,直接写出t 的值;若不存在,请说明理由.得分 评卷人2 O AB C xy 1 13PQ。