高等数学理论逻辑复习题

㊀㊀㊀㊀㊀数学学习与研究㊀２０２１ １７浅谈高等数学知识逻辑关系浅谈高等数学知识逻辑关系Һ姚兴兴㊀（武汉工程大学数理学院，湖北㊀武汉㊀４３０２０５）㊀㊀ʌ摘要ɔ本文整理了高等数学中关于连续㊁有界㊁可导㊁可积之间的关系，以及级数部分的逻辑关系，可使学生理清结构，用辩证统一的哲学思想观察思考数学问题，提高逻辑思维能力和科学研究能力．ʌ关键词ɔ高等数学；微分；积分；级数ʌ基金项目ɔ武汉工程大学科学研究基金项目（Ｋ２０１７４２）一㊁引㊀言众所周知，数学基础知识蕴含着处理智能问题的基本思想与方法，也是人们理解复杂算法的必备要素．随着信息技术与人工智能的不断发展，数学知识的作用愈发突出，尤其是高等数学中的相关知识与理论，它在实际科技发展中起到了重要的支撑作用．在工程院校数学教学过程中，教师往往只重视知识的讲解，忽略了知识间的逻辑关系，强调计算能力的提升，而大大忽视数学理论和数学思维的培养．数学课程知识间有很强的关联，并不是孤立存在的．教师在讲授高等数学过程中，要串起各个章节间的逻辑思维导图，将数学的科学研究方法融入教学过程中，这将有助于学生全面地理解高等数学，深层次㊁透彻地掌握知识．本文主要参考相关教材梳理高等数学中关于连续㊁有界㊁可导㊁可积之间的关系，以及级数部分的逻辑关系．本文意在让学生更深刻地掌握高等数学基础知识，从整体层面㊁宽角度观察思考问题，提高逻辑思维能力和科学研究能力．二㊁微分和积分（一）对于一元函数，可导⇔可微⇒连续连续不一定可微，比如ｆ（ｘ）＝ｘ，ｘɪ［－１，１］．进一步地，可以构造在［－１，１］上任意有限个点处不可导的连续函数．大家自然会问：是否存在无穷多个点处不可导的连续函数？答案是肯定的，如由缺项级数ｆ（ｘ）＝ðɕｎ＝０２－ｎａｅｉ２ｎｘ（０＜ａɤ１）给出的和函数ｆ（ｘ）就是处处不可导的连续函数．实际上，使用泛函分析中Ｂａｉｒｅ纲定理可证明：［０，１］上处处不可导的连续函数全体是通用集．（二）多元函数的微积分关系如下１．重极限与累次极限的关系若重极限和累次极限都存在，则它们必相等．累次极限存在，但重极限不一定存在，比如ｆ（ｘ，ｙ）＝ｘ２＋ｙ２＋ｘ－ｙｘ＋ｙ在原点（０，０）处两个累次极限都存在，但重极限不存在．重极限存在，但累次极限不一定存在，比如ｆ（ｘ，ｙ）＝ｘｓｉｎ１ｙ＋ｙｓｉｎ１ｘ在原点（０，０）处重极限存在，但两个累次极限都不存在．设函数ｇ（ｘ，ｙ）＝ｘｓｉｎ１ｙ＋ｙ，则易见其重极限为零，但其中一个累次极限不存在．２．连续⇐可微⇒偏导数存在，偏导数连续⇒可微连续不一定可微，比如ｆ（ｘ，ｙ）＝㊀ｘ２＋ｙ２，ｘ，ｙɪ［－１，１］在原点（０，０）处连续，但不可微．偏导数存在不一定可微，比如ｆ（ｘ，ｙ）＝ｘｙｘ２＋ｙ２（ｘ２＋ｙ２ʂ０），０（ｘ２＋ｙ２＝０）{在原点（０，０）处偏导数存在，但不可微．二元函数可微时偏导数不一定连续．（三）积分性：连续⇒可积⇒有界可积函数不一定连续，比如Ｒｉｅｍａｎｎ函数．有界函数不一定可积，比如Ｄｉｒｉｃｈｌｅｔ函数．闭区间上的单调函数可积．若函数ｆ（ｘ）可积，则ｆ（ｘ）也可积；反之不成立，如ｆ（ｘ）＝１，ｘɪ［０，１］ɘＱ，－１，ｘɪ［０，１］∉Ｑ．{实际上，对于定积分，至多只有有限个间断点的有界函数必可积．引入可数集和零集的概念后，Ｌｅｂｅｓｇｕｅ定理指出：［ａ，ｂ］上的有界函数ｆ（ｘ）可积的充要条件是ｆ（ｘ）在［ａ，ｂ］上所有间断点全体是零集．对于二重积分，若定义在平面中有界闭域Ｄ上的有界函数ｆ（ｘ，ｙ）的不连续点都落在有限条光滑曲线上，则ｆ（ｘ，ｙ）在Ｄ上可积．对于三重积分，若定义在空间中有界闭域Ｖ上的有界函数ｆ（ｘ，ｙ，ｚ）的不连续点都落在有限个光滑曲面上，则ｆ（ｘ，ｙ，ｚ）在Ｖ上可积．进一步地，［ａ，ｂ］上间断点集合的长度为零㊁平面有界闭域Ｄ上间断点集合的面积为零或空间中有界闭域Ｖ上间断点集合的体积为零的有界函数必可积．随着积分理论的发展，区间长度㊁平面区域面积㊁空间立体体积可统一为 测度 概念，Ｒｉｅｍａｎｎ积分由此提升到Ｌｅｂｅｓｇｕｅ积分，完整揭示了 可积函数的间断点集合为零测集 这一特征．（四）重要的存在性定理举例极限理论是微积分学理论的基础，而极限是否存在与数集密切相关．从运算来说，要求数集关于极限运算是封闭的．我们注意到有理数集是不行的，比如单调递增有界的有理数列１＋１ｎ()ｎ{}的极限是无理数ｅ．事实证明，实数集关于极限运算是封闭的，即实数集是连续的．由此可得闭区间上连续函数的零点定理㊁介值性定理㊁最值定理㊁中值定理，它们分别从连续㊁微分㊁积分角度观察讨论函数的整体性质，具有深刻的几何意义和广泛的理论与应用价值．此外，将维数增加便可产生多元函数微积分理论，将实数集扩充到复数集便可得到复分析理论，教师在讲授或学习这些知识时，理解其中的区别与联系，有助于深刻理解概念，掌握脉络．（五）几个微积分公式微积分学基本定理断言：若函数ｆ（ｘ）在闭区间［ａ，ｂ］上连续，则变上限积分函数Ｆ（ｘ）＝ʏｘａｆ（ｔ）ｄｔ在［ａ，ｂ］上可导，且Ｆᶄ（ｘ）＝ｆ（ｘ）．该定理不仅指出连续函数必存在原函数，而且蕴含着微积分基本公式 牛顿 莱布尼茨公式，故定积分等于被积函数的一个原函数在积分区间上的增量．将该公式推广至二维㊁三维即得格林公式㊁高斯公式．三个公式都是将积分区域内部与边界紧密联系在一起．类似地，将平. All Rights Reserved.㊀㊀㊀㊀数学学习与研究㊀２０２１ １７面区域推广至空间中曲面即有斯托克斯公式．实际上，在引入外微分形式后，这些公式可统一到一般的斯托克斯公式．三㊁级㊀数（一）数项级数数项级数ðɕｎ＝１ｕｎ收敛即是其部分和数列Ｓ{ｎ}收敛，故可用初等数学中裂项法㊁错位相减法等求数项级数的部分和，再取极限判别级数是否收敛，或求级数和，从而有数项级数收敛的柯西准则判别法．易见，数项级数ðɕｎ＝１ｕｎ收敛的必要条件是通项ｕｎ趋于０．反之不成立，例如调和级数ðɕｎ＝１１ｎ．故需要增加其他条件来判别级数的收敛性，比如：部分和序列有界的正项级数必收敛；基于正项级数一般项本身特性的比较判别法㊁比式判别法和根式判别法；有关交错级数的Ｌｅｉｂｎｉｚ判别法；对于一般项级数的Ａｂｅｌ判别法，Ｄｉｒｉｃｈｌｅｔ判别法等．因为绝对收敛级数必收敛，所以对一般项级数可对通项取绝对值转换成正项级数进行判别．由正项级数的比较判别法可得，广义调和级数ðɕｎ＝１１ｎｐ当ｐɤ１时发散，当ｐ＞１时收敛．这表明没有收敛得 最慢 的收敛级数．因此任何判别法都只能解决一类级数的收敛问题，而不能解决所有级数的收敛问题．虽然可以继续改进并给出更加精细有效的判别法，但这个过程是无限的．（二）函数项级数根据定义，函数项级数ðɕｎ＝１ｕｎ（ｘ）在数集Ｄ上一致收敛即是部分和函数列｛Ｓｎ（ｘ）｝在数集Ｄ上一致收敛，从而函数项级数ðɕｎ＝１ｕｎ（ｘ）在数集Ｄ上一致收敛的必要条件是函数列ｕｎ（ｘ）在数集Ｄ上一致收敛于零．对于函数项级数，一致收敛能保证和函数继承函数列ｕｎ（ｘ）的连续㊁可导和可积等分析性质，但是只要求 函数列ｕｎ（ｘ）在数集Ｄ上一致收敛于零 很难保证函数项级数ðɕｎ＝１ｕｎ（ｘ）在数集Ｄ上一致收敛．使用函数列一致收敛判别法可给出余项法则：ðɕｎ＝１ｕｎ（ｘ）在数集Ｄ上一致收敛于Ｓ（ｘ）当且仅当余项Ｒｎ（ｘ）＝Ｓ（ｘ）－Ｓｎ（ｘ）满足ｌｉｍｎңɕｓｕｐｘɪＤＲｎ（ｘ）｜＝０．此法则理论上很完美，但需要对函数项级数进行求和，或对级数和进行估计，实际操作比较困难．最好直接从级数中函数列ｕｎ（ｘ）的特性进行判别，如优级数判别法，Ａｂｅｌ判别法和Ｄｉｒｉｃｈｌｅｔ判别法等．一般函数项级数的收敛性不容易判别，但是幂级数㊁Ｆｏｕｒｉｅｒ级数的收敛性已经得到很好的确定，且这两类级数在数学理论和实际问题中应用也很广泛．（三）幂级数和Ｆｏｕｒｉｅｒ级数幂级数在收敛区间内绝对一致收敛，从而其和函数无穷次可导，但无穷次可导函数不一定能展开成泰勒级数，需要求其展开式余项趋于零．例如，函数ｆ（ｘ）＝ｅ－１ｘ２（ｘʂ０），０（ｘ＝０）{在ｘ＝０处的任意阶导数都等于０，从而ｆ（ｘ）在ｘ＝０处泰勒级数的和函数是０．若Ｆｏｕｒｉｅｒ级数ａ０２＋ðɕｎ＝１ａｎｃｏｓｎｘ＋ｂｎｓｉｎｎｘ()一致收敛于函数ｆ（ｘ），则ｆ（ｘ）是以２π为周期的可积函数，系数ａｎ，ｂｎ满足ａｎ＝１πʏπ－πｆ（ｘ）ｃｏｓｎｘｄｘ，ｂｎ＝１πʏπ－πｆ（ｘ）ｃｏｓｎｘｄｘ．反之，若以２π为周期的函数ｆ（ｘ）在［－π，π］上按段光滑，则在每一点ｘ处展开的Ｆｏｕｒｉｅｒ级数收敛于函数ｆ（ｘ）在ｘ处的左㊁右极限的算术平均值．在逼近理论中，幂级数可提供多项式函数逼近一般函数，计算上比较便捷，但要求函数有任意阶导数．Ｆｏｕｒｉｅｒ级数展开仅要求周期性和按段光滑，但使用三角函数近似计算比较复杂．我们通过简单运算可知，一个周期函数可以分解为一系列固定频率的简谐波之和．显然任一个有限区间上的函数可以进行周期延拓，所以在有限区间上由任意图形定义的任何函数都可以表示为单纯的正弦与余弦函数之和．进一步地，将幂级数的自变量取复数可以给出解析函数的幂级数刻画；将Ｆｏｕｒｉｅｒ级数中的自变量取复数可以导出工程技术中常用的积分变换理论．（四）积分与级数的关系设ｆ（ｘ）定义在无界区间［ａ，＋ɕ）上，则无穷积分ʏ＋ɕａｆ（ｘ）ｄｘ收敛的充要条件是对［ａ，＋ɕ）中任一趋于＋ɕ的数列Ａｎ{}（其中Ａ１＝ａ），级数ðɕｎ＝１ｕｎ都收敛于同一个数，其中ｕｎ＝ʏＡｎ＋１Ａｎｆ（ｘ）ｄｘ，且ʏ＋ɕａｆ（ｘ）ｄｘ＝ðɕｎ＝１ｕｎ．因此无穷积分与级数的敛散概念㊁敛散判别法及其性质基本上是平行的．设ｆ（ｘ，ｙ）定义在区域Ｊˑ［ｃ，＋ɕ）上，Ｊ是任意区间，则含参量无穷积分Ｉ（ｘ）＝ʏ＋ɕｃｆ（ｘ，ｙ）ｄｙ在Ｊ上一致收敛的充要条件是对任一趋于＋ɕ的递增数列Ａｎ{}（其中Ａ１＝ｃ），函数项级数ðɕｎ＝１ｕｎ（ｘ）在Ｊ上一致收敛，其中ｕｎ（ｘ）＝ʏＡｎ＋１Ａｎｆ（ｘ，ｙ）ｄｙ，故含参量无穷积分一致收敛判别法及其性质与函数项级数类似．高等数学中还有很多其他知识间也存在着密切的逻辑关系．正如希尔伯特曾指出： 数学科学是一个不可分割的有机整体，它的生命力正是在于各个部分之间的联系，数学的有机统一是这门学科固有的特点，因为它是一切精确自然科学知识的基础． 厘清数学知识间的逻辑关系有助于我们更深刻地理解概念，用辩证统一的哲学思想学习高等数学，对数学内容融会贯通，大大提高学习效率．ʌ参考文献ɔ［１］陈纪修，於崇华，金路．数学分析（第三版）［Ｍ］．北京：高等教育出版社，２０１９．［２］华东师范大学数学系．数学分析（第四版）［Ｍ］．北京：高等教育出版社，２０１２．［３］同济大学数学系．高等数学（第七版）［Ｍ］．北京：高等教育出版社，２０１４．［４］伊莱亚斯，斯坦恩，等．泛函分析［Ｍ］．王茂发，姚兴兴，译．北京：机械工业出版社，２０１９．［５］刘玉莲，傅沛仁，等．数学分析讲义（第五版）［Ｍ］．北京：高等教育出版社，２０１８．［６］周民强．实变函数论（第三版）［Ｍ］．北京：北京大学出版社，２０１６．［７］萨夫，斯奈德．复分析基础及工程应用［Ｍ］．高宗升，译．北京：机械工业出版社，２００７．. All Rights Reserved.。

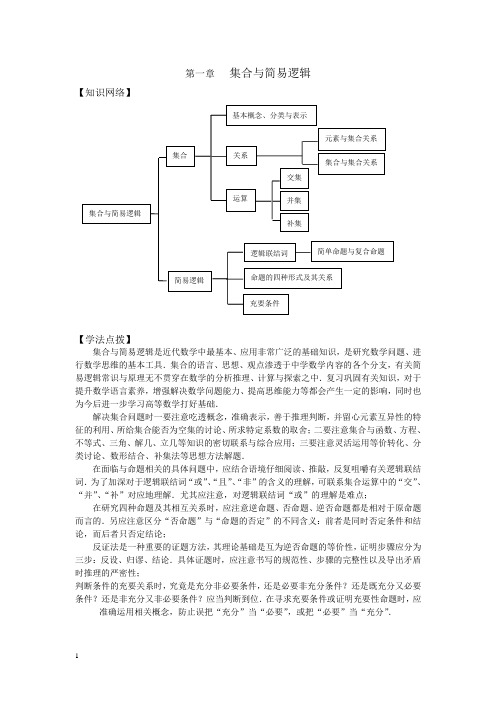
第一章集合与简易逻辑【知识网络】【学法点拨】集合与简易逻辑是近代数学中最基本、应用非常广泛的基础知识，是研究数学问题、进行数学思维的基本工具．集合的语言、思想、观点渗透于中学数学内容的各个分支，有关简易逻辑常识与原理无不贯穿在数学的分析推理、计算与探索之中．复习巩固有关知识，对于提升数学语言素养，增强解决数学问题能力、提高思维能力等都会产生一定的影响，同时也为今后进一步学习高等数学打好基础．解决集合问题时一要注意吃透概念，准确表示，善于推理判断，并留心元素互异性的特征的利用、所给集合能否为空集的讨论、所求特定系数的取舍；二要注意集合与函数、方程、不等式、三角、解几、立几等知识的密切联系与综合应用；三要注意灵活运用等价转化、分类讨论、数形结合、补集法等思想方法解题．在面临与命题相关的具体问题中，应结合语境仔细阅读、推敲，反复咀嚼有关逻辑联结词．为了加深对于逻辑联结词“或”、“且”、“非”的含义的理解，可联系集合运算中的“交”、“并”、“补”对应地理解．尤其应注意，对逻辑联结词“或”的理解是难点；在研究四种命题及其相互关系时，应注意逆命题、否命题、逆否命题都是相对于原命题而言的．另应注意区分“否命题”与“命题的否定”的不同含义：前者是同时否定条件和结论，而后者只否定结论；反证法是一种重要的证题方法，其理论基础是互为逆否命题的等价性，证明步骤应分为三步：反设、归谬、结论．具体证题时，应注意书写的规范性、步骤的完整性以及导出矛盾时推理的严密性；判断条件的充要关系时，究竟是充分非必要条件，还是必要非充分条件？还是既充分又必要条件？还是非充分又非必要条件？应当判断到位．在寻求充要条件或证明充要性命题时，应准确运用相关概念，防止误把“充分”当“必要”，或把“必要”当“充分”．第1课 集合的概念【考点指津】理解集合、子集、全集、交集、并集、补集等基本概念的内涵，了解属于、包含、相等关系的意义；正确识别与使用集合的有关术语和符号，并会用它们正确表示一些简单的集合． 【知识在线】 １．设集合A ⎭⎬⎫⎩⎨⎧∈==N m x x m ,21|，若,,21A x A x ∈∈则必有 （ ）A ．A x x ∈+21B ．A x x ∈21C ．A x x ∈-21D ．A x x ∈21２．给出6个关系式：（1）0∈∅，（2）∅∈{∅}，（3）{}0φ，（4）{}φφ≠，（5）φ{}φ，（6）{}0φ≠.其中正确的个数是 （ ）A ．6B ． 5C ． 4D ． 33．设Ｓ为全集，,B A S ⊆⊆则下列结论中不正确的是 （ ）Ａ．S S A B ⊆痧 Ｂ．A B B = Ｃ．()S A B =∅ ð Ｄ．()S A B =∅ ð 4．已知集合A=},21|{+≤≤-a x a x B=},53|{<<x x 则能使A ⊇B 成立的实数a 的取值范围是5．满足{1,2}X ⊆ {1,2,3,4,的集合X 的个数为 ．【讲练平台】例１．（2002年全国高考）设集合1,24k M x x k Z ⎧⎫==+∈⎨⎬⎩⎭，1,42k N x x k Z ⎧⎫==+∈⎨⎬⎩⎭，则 （ ） A ．M ＝N B 。

高数习题2-4的答案高数习题2-4的答案高等数学是大学数学的一门重要课程，它涉及到许多抽象的数学概念和理论。

在学习高数的过程中，习题是不可或缺的一部分。

习题可以帮助我们巩固所学的知识，培养我们的逻辑思维能力和解决问题的能力。

本文将为大家提供高数习题2-4的答案，希望能够帮助大家更好地理解和掌握高数知识。

习题2-4是一组与极限相关的题目，下面将逐一给出其答案和解析。

1. 求极限lim(x→0)(sinx/x)。

解析：这是一个非常经典的极限题目。

我们可以利用泰勒展开的方法来求解。

根据泰勒展开公式，我们有sinx = x - x^3/3! + x^5/5! - ...，因此，sinx/x = 1 -x^2/3! + x^4/5! - ...。

当x趋近于0时，x的高次项的值趋近于0，所以我们可以忽略它们，得到lim(x→0)(sinx/x) = 1。

2. 求极限lim(x→∞)(x^2 - 3x)/(2x^2 + 5)。

解析：这是一个无穷大与无穷大相除的极限题目。

我们可以利用洛必达法则来求解。

根据洛必达法则，我们对分子和分母分别求导，并求出它们的极限。

对于分子，导数为2x - 3；对于分母，导数为4x。

将导数代入极限公式，得到lim(x→∞)(2x - 3)/(4x)。

当x趋近于无穷大时，分子和分母的值都趋近于无穷大，所以我们可以继续使用洛必达法则。

对分子和分母再次求导，得到lim(x→∞)2/4 = 1/2。

3. 求极限lim(x→1)(x^3 - 1)/(x^2 - 1)。

解析：这是一个有理函数的极限题目。

我们可以尝试因式分解来求解。

分子可以写成(x - 1)(x^2 + x + 1)，分母可以写成(x - 1)(x + 1)。

将分子和分母进行约分，得到lim(x→1)(x^2 + x + 1)/(x + 1)。

当x趋近于1时，分子和分母的值都趋近于3，所以极限为3。

4. 求极限lim(x→∞)(e^x + 1)/(e^x - 1)。

《数据库原理》复习题一、填空题1．数据模型的三要素是指、和数据完整性约束。

2．数据库的模式/内模式映像能够保证数据库数据的独立性。

3．关系代数中专门的关系运算包括选择、投影、和除。

4．当局部E-R图合并成全局E-R图时可能出现冲突，这些冲突主要有三类，它们是、和结构冲突。

5．从关系规范化理论的角度讲，一个只满足1NF的关系可能存在的四个问题是数据冗余度大、修改异常、和删除异常。

6. DB并发操作通常会带来三类问题：丢失修改、和读“脏数据”。

7. 事务必须具有的四个性质是原子性、一致性、和持久性。

8．数据库的设计共分为6个阶段，它们是需求分析阶段、、数据库逻辑设计阶段、、数据库实施阶段、数据库运行和维护阶段。

9．如果一个满足1NF关系的所有属性合起来组成一个关键字，则该关系最高满足的范式是（在1NF，2NF，3NF范围内选择）。

10．数据完整性约束包括、、。

11．模式分解的准则为和12．关系模型由、、和三部分组成。

二、单选题1．DB，DBMS和DBS三者间的关系是（）。

A．DB包括DBMS和DBS B．DBMS包括DB和DBSC．DBS包括DB和DBMS D．DBS与DB和DBMS无关2．在SQL中，下列涉及空值的操作，不正确的是（）。

A．AGE IS NULL B．AGE IS NOT NULLC．AGE=NULL D．NOT(AGE IS NULL )3．视图创建完成后，数据字典中存放的是（）。

A．查询语句B．查询结果C．视图的定义D．所引用的基本表的定义4．操作系统故障属于（）。

A．人为错误B．事务故障C．介质故障D．系统故障5．下列说法中不正确的是（）。

A．数据库减少了冗余数据B．数据库中的数据可以共享C．数据库避免了一切数据的重复D．数据库具有较高的数据独立性6．关系数据模型（）。

A．只能表示实体问的1∶1联系B．只能表示实体间的1∶n联系C．只能表示实体间的m∶n联系D．可以表示实体间的上述三种联系7．自然连接是构成新关系的有效方法。

2024年全国高等数学考试真题一、选择题（共 8 小题，每小题 5 分，共 40 分）1、设函数$f(x)＝＼frac{1}｛x}＋＼ln x$，则$f(x)＄的定义域为（）A ＄（0,＋＼infty)＄B ＄（＼infty,0)＄C ＄（＼infty,0)＼cup(0,＋＼infty)＄D 以上都不对2、已知函数$f(x)＝x^3-3x^2+2$，则$f'（1)＄的值为（）A 0B －1C －2D －33、曲线$y=x^3$在点$（1,1)＄处的切线方程为（）A ＄y=3x-2$B ＄y=2x-1$C ＄y=x$D ＄y=3x-3$4、下列定积分的值为 0 的是（）A ＄＼int_{－1}＾｛1}x^2dx$B ＄＼int_{－1}＾｛1}xdx$C ＄＼int_{－1}＾｛1}＼sin xdx$ D ＄＼int_{－1}＾｛1}＼cos xdx$5、设向量$＼vec{a}＝（1,2)＄，＄＼vec{b}＝（2,－1)＄，则$＼vec{a}＼cdot\vec{b}＄的值为（）A 0B 3C 4D 56、设函数$f(x)＝＼sin x+＼cos x$，则$f(x)＄的最大值为（）A 1B ＄＼sqrt{2}＄C 2D 无法确定7、已知空间直角坐标系中，点$A(1,2,－1)＄，＄B(2,－1,3)＄，则向量$＼overrightarrow{AB}＄的模为（）A ＄＼sqrt{11}＄B ＄＼sqrt{14}＄C ＄＼sqrt{19}＄D ＄＼sqrt{26}＄8、下列级数收敛的是（）A ＄＼sum_{n=1}＾｛＼infty}＼frac{1}｛n}＄B ＄＼sum_{n=1}＾｛＼infty}＼frac{（－1)＾n}｛n}＄C ＄＼sum_{n=1}＾｛＼infty}＼frac{1}｛n^2}＄ D 以上都不对二、填空题（共 6 小题，每小题 5 分，共 30 分）9、函数$f(x)＝x^2-2x+3$的最小值为________。

触发器一、单项选择题：(1)对于D触发器，欲使Q n+1=Q n，应使输入D=。

A、0B、1C、QD、(2)对于T触发器，若原态Q n=0，欲使新态Q n+1=1，应使输入T=。

A、0B、1C、Q(4)请选择正确的RS触发器特性方程式。

A、B、C、 (约束条件为)D、(5)请选择正确的T触发器特性方程式。

A、B、C、D、(6)试写出图所示各触发器输出的次态函数(Q)。

n+1A、B、C、D、(7)下列触发器中没有约束条件的是。

A、基本RS触发器B、主从RS触发器C、同步RS触发器D、边沿D触发器二、多项选择题：(1)描述触发器的逻辑功能的方法有。

A、状态转换真值表B、特性方程C、状态转换图D、状态转换卡诺图(2)欲使JK触发器按Q n+1=Q n工作，可使JK触发器的输入端。

A、J=K=0B、J=Q,K=C、J=,K=QD、J=Q,K=0(3)欲使JK触发器按Q n+1=0工作，可使JK触发器的输入端。

A、J=K=1B、J=0,K=0C、J=1,K=0D、J=0,K=1(4)欲使JK触发器按Q n+1=1工作，可使JK触发器的输入端。

A、J=K=1B、J=1,K=0C、J=K=0D、J=0，K=1三、判断题：(1)D触发器的特性方程为Q n+1=D，与Q无关，所以它没有记忆功能。

（）n(2)同步触发器存在空翻现象，而边沿触发器和主从触发器克服了空翻。

（）(3)主从JK触发器、边沿JK触发器和同步JK触发器的逻辑功能完全相同。

（）(8)同步RS触发器在时钟CP=0时，触发器的状态不改变( )。

(9)D触发器的特性方程为Q n+1=D，与Q n无关，所以它没有记忆功能( )。

(10)对于边沿JK触发器，在CP为高电平期间，当J=K=1时，状态会翻转一次( )。

四、填空题：(1)触发器有（）个稳态，存储8位二进制信息要（）个触发器。

(2)在一个CP脉冲作用下，引起触发器两次或多次翻转的现象称为触发器的（），触发方式为（）式或（）式的触发器不会出现这种现象。

2024考研数学李林高等数学辅导讲义解析一、概述2024年考研数学高等数学一直是考研学子备战考试的焦点。

为帮助考生更好地掌握数学知识，提高解题能力，李林老师精心编写了高等数学辅导讲义。

本文将对李林老师的辅导讲义进行解析，帮助考生更好地理解和应用这些知识。

二、讲义内容概述李林老师的高等数学辅导讲义分为多个章节，涵盖了高等数学的各个知识点，包括微积分、多元函数、级数、常微分方程等内容。

讲义内容扎实，逻辑严谨，既包括基础知识的讲解，也包括典型例题的分析和解答，适合考生系统复习和巩固知识点。

三、微积分部分1.极限与连续讲义对极限与连续的概念进行了详细介绍，从基本概念到极限存在的条件，再到连续性的定义和性质，帮助考生理解和掌握这一重要知识点。

讲义中还包括了大量例题分析，帮助考生加深对极限与连续的理解，提高解题能力。

2.微分与微分中值定理针对微分的定义和微分中值定理等内容，讲义中提供了详细的公式推导和典型例题讲解，帮助考生掌握微分的概念和性质，熟练运用微分中值定理解决实际问题。

3.不定积分与定积分在不定积分与定积分部分，讲义重点讲解了换元积分法、分部积分法等解题技巧，并结合典型例题进行深入分析，帮助考生掌握积分的计算方法和技巧，提高解题效率。

四、多元函数部分1.多元函数的概念与性质讲义对多元函数的概念、多元函数的极限、连续性、偏导数等内容进行了系统介绍，并结合实际问题进行讲解，帮助考生理解多元函数的重要性及其在实际问题中的应用。

2.方向导数与梯度在方向导数与梯度的部分，讲义对方向导数的定义、计算方法和梯度的概念进行了详细讲解，并提供了大量例题进行分析，帮助考生掌握这一知识点的计算方法和应用技巧。

五、级数部分1.数项级数的收敛性与敛散性讲义对数项级数的收敛性与敛散性进行了全面介绍，包括正项级数的收敛判别法、一般项级数的审敛法等内容，帮助考生系统掌握级数收敛性的判别方法，提高解题能力。

2.幂级数与傅立叶级数在幂级数与傅立叶级数部分，讲义介绍了幂级数的收敛半径、函数展开成幂级数的方法，以及傅立叶级数的基本概念和性质，帮助考生理解级数在实际问题中的应用。

高等数学下知识点总结6篇高等数学下知识点总结6篇借鉴经验和教训，对自己的工作和生活进行反思和总结，从而不断进步。

深入学习，专攻某一领域有利于个人成长和职业发展。

下面就让小编给大家带来高等数学下知识点总结，希望大家喜欢!高等数学下知识点总结1第一，函数与导数。

主要考查集合运算、函数的有关概念定义域、值域、解析式、函数的极限、连续、导数。

第二，平面向量与三角函数、三角变换及其应用。

这一部分是高考的重点但不是难点，主要出一些基础题或中档题。

第三，数列及其应用。

这部分是高考的重点而且是难点，主要出一些综合题。

第四，不等式。

主要考查不等式的求解和证明，而且很少单独考查，主要是在解答题中比较大小。

是高考的重点和难点。

第五，概率和统计。

这部分和我们的生活联系比较大，属应用题。

第六，空间位置关系的定性与定量分析，主要是证明平行或垂直，求角和距离。

第七，解析几何。

是高考的难点，运算量大，一般含参数。

高考对数学基础知识的考查，既全面又突出重点，扎实的数学基础是成功解题的关键。

针对数学高考强调对基础知识与基本技能的考查我们一定要全面、系统地复习高中数学的基础知识，正确理解基本概念，正确掌握定理、原理、法则、公式、并形成记忆，形成技能。

以不变应万变。

对数学思想和方法的考查是对数学知识在更高层次上的抽象和概括的考查，考查时与数学知识相结合。

对数学能力的考查，强调“以能力立意”，就是以数学知识为载体，从问题入手，把握学科的整体意义，用统一的数学观点组织材料，侧重体现对知识的理解和应用，尤其是综合和灵活的应用，所有数学考试最终落在解题上。

考纲对数学思维能力、运算能力、空间想象能力以及实践能力和创新意识都提出了十分明确的考查要求，而解题训练是提高能力的必要途径，所以高考复习必须把解题训练落到实处。

训练的内容必须根据考纲的要求精心选题，始终紧扣基础知识，多进行解题的回顾、总结，概括提炼基本思想、基本方法，形成对通性通法的认识，真正做到解一题，会一类。