队列的基本操作(xinn)

队列基础动作要领
一、队列基本动作
1、校正队列格局：由教官指挥，小组队员按规定把排编成多列，排列整齐，两排之间间距约为40厘米，两端靠近立正，绳桩正对，整排按排数角度为45°倾斜状态。

2、报数：有教官指挥，或由教官指定排长，小组队员一声令下，同时亮出号码牌（右手手背正对队友），报数：“一，二，三，……”，报数完毕，收缩号码牌和抬起头，等待宣布操指令。

3、站定：有教官指挥，小组队员右手号牌横在腰部，立正，脚跟全触地，脚趾笔直立，全身挺直，腰部收紧，头抬高，双四肢垂直，以头部夹在右排队员右肩之间为划定点，确保排立正。

4、面向右：有教官指挥，小组队员在站定位置，右手持号牌按规定位置，双腿同时抬高，右腿稍长，以右脚拇指接触地面，左脚抬起，右侧抬高，脚跟全触地，其余脚趾笔直立立，转换右侧角度，以头部夹在右排队员右肩之间为划定点，确保排立正。

5、面向左：有教官指挥，小组队员在站定位置，右手持号牌按规定位置，左腿抬高，以左脚拇指接触地面，右腿抬起，左侧抬高。

数据结构-队列基本运算的实现及其应用篇一数据结构-队列基本运算的实现及其应用一、队列的基本概念队列是一种特殊的数据结构，它遵循先进先出（FIFO）的原则，即先进入队列的元素先出队列。

在队列中，新元素被添加到队列的末尾，而删除操作总是发生在队列的开头。

队列常用于解决各种问题，如处理事件、任务调度、缓冲处理等。

二、队列的基本操作队列的基本操作包括入队（enqueue）、出队（dequeue）、查看队首元素（peek）和判断队列是否为空。

入队操作：向队列的末尾添加一个新元素。

这个操作的时间复杂度通常为O(1)，可以通过在队列的末尾添加元素来实现。

出队操作：删除队列开头的元素并返回它。

这个操作的时间复杂度通常为O(1)，可以通过移除队列开头的元素来实现。

查看队首元素：返回队列开头的元素但不删除它。

这个操作的时间复杂度通常为O(1)，可以通过返回队列开头的元素来实现。

判断队列是否为空：检查队列是否包含任何元素。

这个操作的时间复杂度通常为O(1)，可以通过比较队列的长度和0来实现。

三、队列的实现队列可以通过不同的数据结构来实现，如数组、链表和循环列表等。

在这里，我们将介绍使用数组和链表来实现队列的基本操作。

使用数组实现队列使用数组实现队列时，我们需要保留一个空间来跟踪队列的开头和结尾。

通常，我们使用两个指针，一个指向队列的开头，另一个指向队列的结尾。

当我们在队列中添加一个新元素时，我们将它添加到结尾指针所指向的位置，并将结尾指针向后移动一位。

当我们要删除一个元素时，我们只需将开头指针向后移动一位并返回该位置的元素即可。

使用链表实现队列使用链表实现队列时，我们通常使用一个头指针指向队首元素，一个尾指针指向队尾元素的下一个位置。

入队操作时，我们在尾指针的位置创建一个新节点，并将尾指针移动到下一个位置。

出队操作时，我们只需删除头指针指向的节点，并将头指针移动到下一个位置。

四、队列的应用队列在计算机科学中有着广泛的应用，下面列举几个常见的例子：事件处理：在多线程编程中，队列经常用于事件驱动的系统来传递事件或消息。

顺序队列基本操作
顺序队列是一种线性数据结构，常常用于解决具有先进先出特性的问题。

下面介绍一些顺序队列的基本操作。

1. 初始化队列
在使用队列之前，需要先对其进行初始化操作。

初始化操作包括创建一个数组和两个指针。

数组用于存储队列中的元素，指针用于记录队列的头和尾。

2. 入队操作
入队操作将一个元素添加到队列的尾部。

入队操作需要更新队列尾指针的位置，并将元素存储在该位置。

3. 出队操作
出队操作将队列中的第一个元素删除并返回其值。

出队操作需要更新队列头指针的位置，并返回删除的元素。

4. 获取队头元素
获取队头元素操作返回队列中的第一个元素，并不会删除该元素。

5. 判断队列是否为空
判断队列是否为空操作用于检查队列中是否包含任何元素。

以上是顺序队列的基本操作。

顺序队列具有简单的实现和高效的性能，常常用于解决大量数据的排队和调度问题。

- 1 -。

#include<stdio.h>#include<stdlib.h>struct LQNode//链队结点的定义{int date;struct LQNode*next;};struct LQS//定义链队{struct LQNode *front,*rear;};struct LQS*ceeat();//定义队列创建函数int InitLQS(LQS*q);//初始化队列int JudgeLQS(struct LQS*q);//定义判断队列空或者列满的条件函数int IN(struct LQS*q,int x);//定义入队函数int OUT(struct LQS*q,int x);//定义出队函数void LengthLQS(LQS*q);//求长度函数void DestroyLQS(LQS*q);//销毁队列函数void printfLQS(LQS*q);//输出队列函数void main(){LQS A;InitLQS(&A);while(1){int x,e;scanf("%d",&x);switch(x){case 1:printf("请输入入队一个整型数\n");scanf("%d",&e);IN(&A,e);printfLQS(&A);break;case 2:OUT(&A,e);printfLQS(&A);break;}}}//*********************************************// int InitLQS(LQS*q)//初始化队列{q->front=(LQNode*)malloc(sizeof(LQNode));if(q->front!=NULL){q->rear=q->front;q->front->next=NULL;return(1);}else return(0);}//********************************************// void printfLQS(LQS*q)//队列输出函数{LQNode *p;p=q->front;printf("对列为");while(p->next!=NULL){p=p->next;printf("%d ",p->date);}printf("\n");}//*******************************************// int IN(struct LQS*q,int x)//定义入队函数{LQNode *p;p=(LQNode*)malloc(sizeof(LQNode));p->date=x;p->next=NULL;q->rear->next=p;q->rear=p;return 1;}//*******************************************// int OUT(struct LQS*q,int x)//定义出队函数{LQNode *p;if(q->front==q->rear){return 0;}else{p=q->front->next;q->front->next=p->next;x=p->date;free(p);}}。

数据结构队列知识点1. 队列的概念- 队列是一种线性数据结构,遵循先进先出()的原则。

- 队列中的元素只能从一端(队尾)插入,另一端(队头)删除。

2. 队列的基本操作- 入队():将新元素插入到队尾。

- 出队():从队头移除并返回元素。

- 查看队头元素(/):返回队头元素但不删除它。

- 判断队列是否为空()。

3. 队列的实现方式- 顺序队列(用数组实现)- 需要维护两个指针:(队头)和(队尾)。

- 入队时将元素插入位置,向后移动。

- 出队时移除并返回位置的元素,向后移动。

- 需要处理循环队列( == )的情况。

- 链式队列(用链表实现)- 使用单链表,头部作为队头,尾部作为队尾。

- 入队时在链表尾部插入新节点。

- 出队时删除并返回头节点。

4. 队列的应用- 计算机系统中的缓冲区、打印任务池等。

- 操作系统中的进程调度。

- 网络数据的传输和接收。

- 模拟现实世界中的排队系统。

5. 队列的变体- 双端队列():可以从两端插入和删除元素。

- 优先级队列( ):元素按照优先级排序,优先级高的先出队。

- 环形队列( ):利用数组实现,解决假溢出问题。

6. 队列的性能分析- 入队和出队操作的时间复杂度为(1)。

- 顺序队列的空间复杂度为(),链式队列的空间复杂度为(+)(为指针开销)。

以上是队列数据结构的主要知识点,包括概念、基本操作、实现方式、应用场景、变体以及性能分析。

掌握这些知识点有助于更好地理解和运用队列。

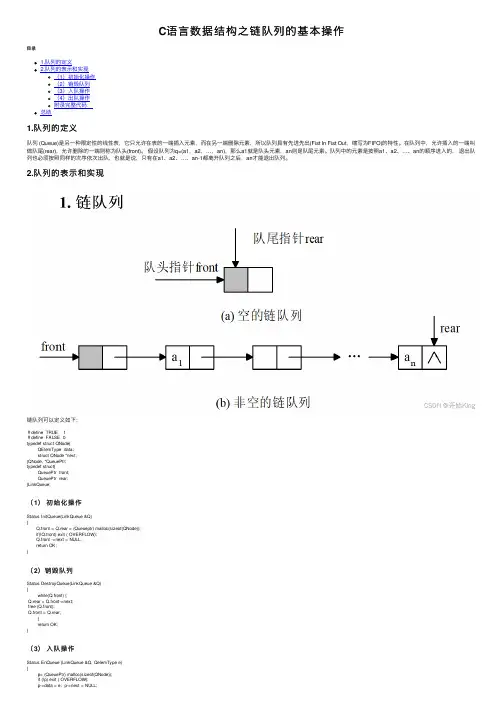
C语⾔数据结构之链队列的基本操作⽬录1.队列的定义2.队列的表⽰和实现（1）初始化操作（2）销毁队列（3）⼊队操作（4）出队操作附录完整代码：总结1.队列的定义队列 (Queue)是另⼀种限定性的线性表，它只允许在表的⼀端插⼊元素，⽽在另⼀端删除元素，所以队列具有先进先出(Fist In Fist Out，缩写为FIFO)的特性。

在队列中，允许插⼊的⼀端叫做队尾(rear)，允许删除的⼀端则称为队头(front)。

假设队列为q=(a1，a2，…，an)，那么a1就是队头元素，an则是队尾元素。

队列中的元素是按照a1、a2、…、an的顺序进⼊的，退出队列也必须按照同样的次序依次出队，也就是说，只有在a1、a2、…、an-1都离开队列之后，an才能退出队列。

2.队列的表⽰和实现链队列可以定义如下：＃define TRUE 1＃define FALSE 0typedef struct QNode{QElemType data;struct QNode *next;}QNode, *QueuePtr;typedef struct{QueuePtr front;QueuePtr rear;}LinkQueue;（1）初始化操作Status InitQueue(LinkQueue &Q){Q.front = Q.rear = (Queueptr) malloc(sizeof(QNode));if(!Q.front) exit ( OVERFLOW);Q.front ->next = NULL;return OK;}（2）销毁队列Status DestroyQueue(LinkQueue &Q){while(Q.front) {Q.rear = Q.front->next;free (Q.front);Q.front = Q.rear;}return OK;}（3）⼊队操作Status EnQueue (LinkQueue &Q, QelemType e){p= (QueuePtr) malloc(sizeof(QNode));if (!p) exit ( OVERFLOW);p->data = e; p->next = NULL;return OK;}（4）出队操作Status DeQueue (LinkQueue &Q, QelemType &e){if ( Q.front == Q.rear) return ERROR;p=Q.front->next;e=p->data;Q.front->next =p->next;if (Q.rear == p) Q.rear = Q.front;free(p);return OK;}附录完整代码：#include<iostream>using namespace std;#define OK 1#define FALSE 0typedef int QElemType;typedef int Status;typedef struct QNode{QElemType data;struct QNode *next;}QNode,*QueuePtr;typedef struct{QueuePtr font;QueuePtr near;}LinkQueue;Status InitQueue(LinkQueue &Q){Q.font=(QueuePtr)malloc(sizeof(QNode));if(!Q.font) exit(FALSE);Q.font->next=NULL;Q.near=Q.font;return OK;}Status QueueEmpty(LinkQueue Q){if(Q.font->next) return OK;return FALSE;}Status EnQueue(LinkQueue &Q,QElemType e){QueuePtr p=(QueuePtr)malloc(sizeof(QNode));p->data=e;Q.near->next = p;Q.near = Q.near->next;p->next = NULL;return OK;}Status DeQueue(LinkQueue &Q,QElemType &e){if(!Q.font->next) return FALSE;QueuePtr p;p=Q.font->next;e=p->data;Q.font->next=p->next;if(Q.near==p) Q.near=Q.font; //当是最后⼀个元素时，Q.font=NULL,Q.near=Q.font free(p);return OK;}Status ClearQueue(LinkQueue &Q){QueuePtr p;p=Q.font->next;QueuePtr q;while(p){q=p;p=p->next;Q.font->next=p;free(q);}Q.near=Q.font;return OK;}void menu(){cout<<"初始化队列:1"<<endl;cout<<"⼊队:2"<<endl;cout<<"出队:3"<<endl;cout<<"清空队列:4"<<endl;cout<<"退出:5"<<endl;}int main(){LinkQueue Q;while(true){int n;menu();scanf("%d",&n);int e=-1;switch(n){case 1:InitQueue(Q);continue;case 2:printf("请输⼊⼀个元素");scanf("%d",&e);EnQueue(Q,e);DeQueue(Q,e);printf("\n出队元素%d\n",e);continue;case 4:ClearQueue(Q);printf("清空成功\n");continue;default:break;}if(n==5)break;}}总结本篇⽂章就到这⾥了，希望能够给你带来帮助，也希望您能够多多关注的更多内容!。

《数据结构》实验报告院系光电与信息工程学院专业电子信息工程姓名学号电话2011级 2班 2013年4月20日1．实验题目实验4 .对列的基本操作2．需求分析（1）编写链接队列的基本操作函数，调用上述函数实现下列操作，操作步骤如下：调用进队函数建立一个队列。

读取队列中的第一个元素。

从队列中删除元素。

输出队列中的所有元素。

（2）编写环型队列的基本操作函数。

调用上述函数实现下列操作，操作步骤如下:调用进队函数建立一个队列。

读取队列中的第一个元素。

从队列中删除元素。

输出队列中的所有元素。

链接队列：①进队操作 EnQueue(LinkQueue *Q, QElemType e)②出队操作，队空 DeQueue(LinkQueue *Q, QElemType *e)③输出队列中元素 0utputQueue(LinkQueue Q)环型队列：①进队操作，返回1为队满 EnQueue(SqQueue *Q, QElemType e)②出队操作，返回1为队空 DeQueue(SqQueue *Q, QElemType *e)③输出队列中元素 outPutQMeue(SqQueue Q)输入形式：整型数。

3．概要设计（1）链接队列ADT QNode{数据对象：D={a i|a i∈IntegerSet,i=0,1,2,…,n,n≥0}结构关系：R={<a i,a i+1>|a i,a i+1 ∈D}基本操作：InitQueue(LinkQueue *Q)操作前提：Q是一个未初始化的链接队列操作结果：将Q初始化为一个空的链接队列EnQueue(LinkQueue *Q, QElemType e)操作前提：链接队列Q已存在操作结果：将元素e插入到链接队列中DeQueue(LinkQueue *Q, QElemType *e)操作前提：链接队列Q已存在操作结果：将链接队列Q中队头元素删除，删除的元素值通过e返回0utputQueue(LinkQueue Q)操作前提：链接队列Q已存在操作结果：将链接队列Q中的元素显示到屏幕上}本程序包含5个函数：主函数main()初始化链接队列函数 InitQueue()进队函数EnQueue()出队函数DeQueue()输出队列中元素函数 OutputStack()各函数调用关系：主函数main调用其他四个函数主函数的伪码main(){定义变量i，n，m；定义一个LinkQueue 变量Lq初始化 Lq；输入队列元素的个数；For循环（i=1;i<=n;i++）｛调用EnQueue函数；｝输出队列中元素；调用DeQueue函数；显示删除的队头元素；显示Lq；｝（2）环形队列ADT SqQueue{数据对象：D={a i|a i∈IntegerSet,i=0,1,2,…,n,n≥0}结构关系：R={<a i,a i+1>|a i,a i+1 ∈D}基本操作：InitQueue(SqQueue &Q)操作前提：Q是一个未初始化的环型队列操作结果：将Q初始化为一个空的环型队列EnQueue(SqQueue *Q,int e)操作前提：环型队列Q已存在操作结果：将元素e插入到队列中DeQueue(SqQueue *Q,int *e)操作前提：环型队列Q已存在操作结果：将环型队列Q中队头元素删除，删除的元素值通过e返回 outPutQMeue(SqQueue *Q)操作前提：环型队列Q已存在操作结果：将环型队列Q中的元素显示到屏幕上}本程序包含5个函数：主函数main()初始化链接队列函数 InitQueue()进队函数EnQueue()出队函数DeQueue()输出队列中元素函数 OutputStack()各函数调用关系：主函数main调用其他四个函数函数的伪码main（）｛定义SqQueue 变量sq;定义整型变量n,i,m;构造空的环型队列；输入队列的长度；For循环（i=1;i<=n;i++）｛调用EnQueue函数；｝输出队列元素；删除对头元素；输出队列元素；｝4．详细设计（1）链接队列（1）类型定义typedef struct QNode{int data;struct QNode *next;}QNode,*QueuePtr;typedef struct {QueuePtr front;QueuePtr rear;}LinkQueue;基本操作的伪码算法（1）初始化void InitQueue(LinkQueue *Q){Q->front=Q->rear==申请新结点;Q->front->next=NULL;}（2）进队void Push(SqStack &S,int e){定义QueuePtr变量 p；p=申请新的空间；如果申请失败，结束程序p->data=e;p->next=NULL;如果是第一个元素则{Q->front->next=p;}Q->rear->next=p;Q->rear=p;｝(3)出队int Pop(SqStack *S,int e)｛定义QueuePtr变量 p；如果队空则返回0；p=Q->front->next;*e=p->data;Q->front->next=p->next;如果Q->rear==p则Q->rear=Q->front;；释放p的空间；返回1；}（4）输出元素int OutputQueue(LinkQueue Q) {定义QueuePtr变量 p；如果队空则返回0；p=>next;while(p){printf("%d ",p->data);p=p->next;}printf("\n");返回1;}（2）环形队列类型定义typedef struct{int *base;int front;int rear;}SqQueue;基本操作的伪码算法（1）初始化void InitQueue(SqQueue &Q){=申请新的空间；如果申请失败，结束程序；==0;}（2）进队int EnQueue(SqQueue *Q,int e){ 如果队满了则返回1；Q->base[Q->rear]=e;Q->rear=(Q->rear+1)%MAXQSIZE;返回0；｝出队int DeQueue(SqQueue *Q,int *e)DeQueue(SqQueue *Q,int *e)｛如果队空则返回1；*e=Q->base[Q->front];Q->front=(Q->front+1)%MAXQSIZE;返回0；}（4）输出元素void outPutQMeue(SqQueue *Q){定义整型变量i；For循环（i=Q->front;i<Q->rear;i++){输出Q->base[i]；}换行；}5．调试分析链接队列：调试是出现错误，经过检查发现在某些地方分号用中文表示，出现空指针问题。

数据结构实验队列的基本操作《数据结构》是计算机相关专业的一门核心基础课程，也是很多高校研究生入学考试专业课必考课程之一。

它主要介绍线性结构、树型结构、图形结构三种逻辑结构元素的存储实现，在此基础上介绍一些典型算法及时、空效率分析。

这门课程的主要任务是培养学生的算法分析、设计能力及良好的程序设计习惯。

通过学习，要求学生能够掌握典型算法的设计思想及程序实现，能够根据实际问题选取合适的存储方案，设计出简洁、高效、实用的算法，为后续课程的学习及软件开发打下良好的基础。

学习这门课程，习题和实验是两个关键环节。

学生理解算法的最佳途径是上机实验。

因此，实验环节的好坏是学生能否学好《数据结构》的关键。

为了更好地配合学生实验，特编写该实验指导书。

一、实验目的、要求和任务计算机编程中加工处理的对象是数据，而数据具有一定的组织结构，所以学习编写计算机程序仅仅了解计算机语言是不够的，还必须掌握数据组织、存储和运算的一般方法，这是数据结构课程中学习和研究的内容。

由于数据结构的原理和算法较抽象，而该课程一般在本科低年级开设，对于计算机程序设计知识的初学者，理解和掌握其中的原理就显得较为困难。

1.熟练掌握C语言的编辑、编译、调试程序。

2.会书写类C语言的算法，并将算法转变为程序实现。

3.正确理解各种数据结构的逻辑特性和存储表示和基本操作的算法实现。

4.有较强的逻辑分析能力。

5.针对问题的不同选择合适的数据结构，提高算法设计的能力和动手实验的技能。

6.学会分析研究计算机加工的数据结构的特性，以便为应用设计的数据选择适当的逻辑结构、存储结构及其相应的算法，并初步掌握算法的时间分析和空间分析的技术。

7.本课程的学习过程也是复杂程序设计的训练过程，要求学生编写的程序结构清楚、正确易读，符合软件过程的规范，从而培养学生的数据抽象能力。

8.通过若干数据结构应用实例，引导学生学习数据类型的使用，为今后学习面向对象的程序做一些铺垫。

二、实验基本内容及学时分配为了达到实验目的，本课程安排了4个实验单元，训练的重点在于基本的数据结构，而不是强调面面俱到。

队列的操作方法是什么队列（Queue）是一种特殊的线性数据结构，它遵循先进先出（First-In-First-Out，FIFO）的原则。

在队列中，新元素插入的一端称为队尾（rear），已有元素删除的一端称为队头（front）。

队列的插入操作叫做入队（Enqueue），删除操作叫做出队（Dequeue），并且只能在队头和队尾进行。

队列的操作方法主要包括初始化队列、入队、出队、获取队头元素、获取队列长度、判断队列是否为空等。

1. 初始化队列：队列的初始化是为队列申请内存空间，并对队列进行一些必要的初始化操作，例如设置队头和队尾指针。

2. 入队：入队操作是将一个元素插入到队列的队尾，即将队尾指针往后移动，并将元素存储到队尾的位置。

如果队列已满，则无法进行入队操作。

3. 出队：出队操作是删除队列的队头元素，即将队头指针往后移动，同时释放原队头元素的内存空间。

如果队列为空，则无法进行出队操作。

4. 获取队头元素：获取队头元素可以通过访问队头指针所指向的位置来实现，但并不会将该元素从队列中删除。

5. 获取队列长度：获取队列的长度可以通过记录入队和出队的次数来实现，即队列内元素的数量。

6. 判断队列是否为空：通过判断队头和队尾指针是否相等，即判断队列是否为空。

如果相等，则队列为空；否则，队列不为空。

除了以上基本操作，队列还可以实现一些其他的辅助操作，例如清空队列、销毁队列、遍历队列等。

7. 清空队列：清空队列即将队列中的所有元素出队，释放对应的内存空间。

8. 销毁队列：销毁队列是释放队列所占用的内存空间，同时将队头和队尾指针置为NULL。

9. 遍历队列：遍历队列是按照队列中元素的顺序，依次访问并处理队列中的每个元素。

这些操作方法可以通过数组、链表或循环队列等数据结构来实现。

对于数组实现的队列，入队和出队操作的时间复杂度为O(1)，获取队列长度、判断队列是否为空的操作时间复杂度也为O(1)。

但是数组实现的队列长度固定，当队列容量不够时，无法继续进行入队操作。