2016聚焦中考数学(辽宁省)考点聚焦课件 第20讲 锐角三角函数和解直角三角形
- 格式:ppt
- 大小:1.41 MB
- 文档页数:33





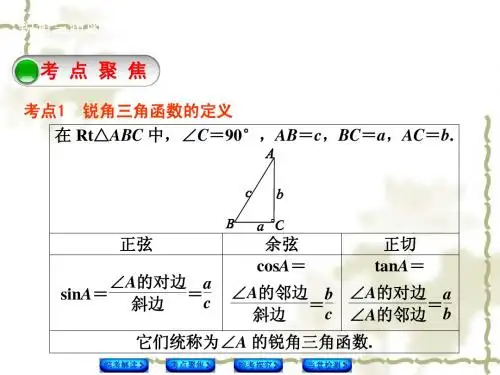

锐角三角函数与解直角三角形【考纲要求】1. 理解锐角三角函数的定义、性质及应用,特殊角三角函数值的求法,运用锐角三角函数解决与直 角三角形有关的实际问题•题型有选择题、填空题、解答题,多以中、低档题出现;2. 命题的热点为根据题中给出的信息构建图形,建立数学模型,然后用解直角三角形的知识解决问 题. 【知识网络】L 两股克理] ________________广I 石四边觀喇-_他鬲一漓形]~T 与相似形结用要点诠释:(1) 正弦、余弦、正切函数是在直角三角形中定义的,反映了直角三角形边与角的关系,是两条 线段的比值.角的度数确定时,其比值不变,角的度数变化时,比值也随之变化.(2) s i nA , cosA , tanA 分别是一个完整的数学符号,是一个整体,不能写成【考点梳理】 考点一、锐角三角函数的概念如图所示,在 Rt △ ABC 中,/ C = 90°,/ A 所对的边的邻边,/ B 所对的边AC 记为b ,叫做/ B 的对边,也是/ 叫做斜边.BC 记为a ,叫做/ A 的对边,也叫做/ B A 的邻边, 直角C 所对的边AB 记为c ,锐角 锐角 锐角 A 的对边与斜边的比叫做/A 的邻边与斜边的比叫做/A 的对边与邻边的比叫做/ A 的正弦,记作 A 的余弦,记作 A 的正切,记作 sinA , cosA , tanA , 即 sin A即 cos A即 tan A同理sinBB 的对边b ; cosB B 的邻边旦;tanB 斜边 c ; 斜边 c ;A 的对边 a 斜边c A 的邻边 b;斜边 ;c A 的对边 a A 的邻边 b . B 的对边 b B 的邻边 a乘积•书写时习惯上省略/ A 的角的记号“/”,但对三个大写字母表示成的角 应写成“ tan / AEF ,不能写成“tanAEF ” ;另外,,不能理解成 sin 与/ A , cos与/ A , tan 与/ A 的(如/ AEF ),其正切(3) 任何一个锐角都有相应的锐角三角函数值,不因这个角不在某个三角形中而不存在.(4) 由锐角三角函数的定义知:当角度在0° v /Av 90°之间变化时,,tanA > 0.考点二、特殊角的三角函数值利用三角函数的定义,可求出0°、30°、45°、60°、90°角的各三角函数值,归纳如下:要点诠释:(1)通过该表可以方便地知道0 °、30°、45°、60°、90°角的各三角函数值,它的另一个应用就是:如果知道了一个锐角的三角函数值,就可以求出这个锐角的度数,例如:若⑵仔细研究表中数值的规律会发现:sinOsin90 的值依次为0、i.cosOcos90 的值的顺序正好相反值依次增大,其变化规律可以总结为:当角度在0°<Z A v90°之间变化时,①正弦、正切值随锐角度数的增大(或减小)而增大(或减小)②余弦值随锐角度数的增大(或减小)而减小(或增大). 考点三、锐角三角函数之间的关系如图所示,在Rt△ ABC中,/ C=90°.⑴互余关系(2)平方关系:⑶ 倒数关系(4)商数关系:要点诠释:锐角三角函数之间的关系式可由锐角三角函数的意义推导得出,常应用在三角函数的计算中, 计算时巧用这些关系式可使运算简便.考点四、解直角三角形在直角三角形中,由已知元素(直角除外)求未知元素的过程,叫做解直角三角形•在直角三角形中,除直角外,一共有5个元素,即三条边和两个锐角•设在Rt△ ABC中,/ C=90°,Z A、/ B、/ C所对的边分别为a、b、c,则有:①三边之间的关系:a2+b2=c2(勾股定理).②锐角之间的关系:/ A+/ B=90° .③边角之间的关系:,h为斜边上的高要点诠释:(1) 直角三角形中有一个元素为定值(直角为90° ),是已知的值.(2) 这里讲的直角三角形的边角关系指的是等式,没有包括其他关系(如不等关系).(3) 对这些式子的理解和记忆要结合图形,可以更加清楚、直观地理解要点诠释:1在遇到解直角三角形的实际问题时,最好是先画出一个直角三角形的草图,按题意标明哪些元素是已知的,哪些元素是未知的,然后按先确定锐角、再确定它的对边和邻边的顺序进行计算2•若题中无特殊说明,“解直角三角形”即要求出所有的未知元素,已知条件中至少有一个条件为边•考点六、解直角三角形的应用解直角三角形的知识应用很广泛,关键是把实际问题转化为数学模型,善于将某些实际问题中的数量关系化归为直角三角形中的边角关系是解决实际应用问题的关键解这类问题的一般过程是:(1) 弄清题中名词、术语的意义,如仰角、俯角、坡度、坡角、方向角等概念,然后根据题意画出几何图形,建立数学模型•(2) 将已知条件转化为几何图形中的边、角或它们之间的关系,把实际问题转化为解直角三角形的问题•(3) 根据直角三角形(或通过作垂线构造直角三角形)元素(边、角)之间的关系解有关的直角三角形•⑷得出数学问题的答案并检验答案是否符合实际意义,得出实际问题的解拓展:在用直角三角形知识解决实际问题时,经常会用到以下概念:(1)坡角:坡面与水平面的夹角叫做坡角,用字母表示.坡度(坡比):坡面的铅直高度h和水平距离的比叫做坡度,用字母坡度通常写成的形式•(2)仰角、俯角:视线与水平线所成的角中,视线中水平线上方的叫做仰角,在水平线下方的叫做俯角,如图•(3)方位角:从某点的指北方向线按顺时针转到目标方向的水平角叫做方位角,如图①中,目标方向PA PB, PC的方位角分别为是40°, 135°, 245° .⑷方向角:指北或指南方向线与目标方向线所成的小于90°的水平角,叫做方向角,如图②中的目标方向线OA OB OC 0D的方向角分别表示北偏东30°,南偏东45°,南偏西80°,北偏西60° .特别如:东南方向指的是南偏东45°,东北方向指的是北偏东45°,西南方向指的是南偏西45°,西北方向指的是北偏西45° .要点诠释:1解直角三角形实际是用三角知识,通过数值计算,去求出图形中的某些边的长或角的大小,最好画出它的示意图.2.非直接解直角三角形的问题,要观察图形特点,恰当引辅助线,使其转化为直角三角形或矩形来解.例如:3•解直角三角形的应用题时,首先弄清题意(关键弄清其中名词术语的意义),然后正确画出示意图,进而根据条件选择合适的方法求解.【典型例题】类型一、锐角三角函数的概念与性质1 . (1)如图所示,在△ ABC中,若/ C= 90°,/ B= 50°, AB= 10,则BC的长为()tan50 ° B . 10 • cos50 ° C . 10 • sin50 ° D 10 sin3ABC 中,/ C= 90 °, si nA = -,求cosA+ta nB 的值.5⑶ 如图所示的半圆中, AD 是直径,且 AD= 3, AC = 2,贝U sinB 的值等于 _________(1)在直角三角形中,根据锐角三角函数的定义, 可以用某个锐角的三角函数值和一条边表示其他边. (2) 直角三角形中,某个内角的三角函数值即为该三角形中两边之比.知道某个锐角的三角函数值就知道了该角的大小,可以用比例系数k 表示各边.(3)要求sinB 的值,可以将/ B 转化到一个直角三角形中.【总结升华】已知一个角的某个三角函数值,求同角或余角的其他三角函数值时,常用的方法是:禾U 用定义,根 据三角函数值,用比例系数表示三角形的边长;(2) 题求cosA 时,还可以直接利用同角三角函数之间的关系式 sin 2 A+cos 2 A = 1,读者可自己尝试完成. 举一反三:类型二、特殊角的三角函数值2 .解答下列各题:【总结升华】【变式】Rt △ ABC 中,/ C=90°, a 、b 、c 分别是/ A 、/ B 、/ C 的对边,那么 c 等于()(A) acosA bsin B (B) (C)a sin Ab sin B(D)asin A bsin B ab cosA sin B(1)化简求值:tan60° ta n45° sin 60° cos30°sin 45 cos45sin30°;在厶ABC 中,/ C = 90°,化简,1 2sin AcosA .由第(2)题可得到今后常用的一个关系式: 21 ± 2sin a cos a =(sin a± cos a ).例如,若设 sin a +cos a = t ,贝U sin cos»21).(1)如图所示,在△ ABC 中,/ ACB= 105°,/ A = 30°, AC= 8,求 AB 和 BC 的长; (2) 在厶 ABC 中,/ ABC= 135°,/ A = 30°, AC= 8,如何求 AB 和 BC 的长?⑶ 在厶ABC 中,AO 17, AB= 26,锐角A 满足si nA,如何求BC 的长及△ ABC 的面积?13第(1)题的条件是“两角一夹边”.由已知条件和三角形内角和定理,可知/ B = 45°;过点C 作CD丄AB 于D,贝U Rt △ ACD 是可解三角形,可求出 CD 的长,从而 Rt △ CDB 可解,由此得解;第(2)题的 条件是“两角一对边”;第(3)题的条件是“两边一夹角”,均可用类似的方法解决. 类型三、解直角三角形及应用4 •如图所示,D 是 AB 上一点,且 CDL AC 于 C , S ^ ACD : S ^ CDB 2:3 , cos DCB举一反三:【变式】若sin 2仝,cos2.'sin , (2 a,为锐角),求吨)的值.AC+CD= 18,求tanA 的值和AB 的长.专题总结及应用一、知识性专题专题1锐角三角函数的定义专题2特殊角的三角函数值【专题解读】要熟记特殊角的三角函数值.例 4 计算—3|+ 2cos 45°— (.3 — 1)0.1 _例 5 计算一 —+9 + (— 1)2007 — cos 60°2例 6 计算—.2 |+ (cos 60 °— tan 30° )0+8 .1 1-—(n — 3.14)0— |1 — tan 60° —2 .3 2专题3锐角三角函数与相关知识的综合运用【专题解读】 例1 如图28- 123所示, 则下列结论正确的是 ( A . sin A =2C . cosB = -^2锐角三角函数定义的考查多以选择题、填空题为主. 在 Rt △ ABC 中,/ ACB = 90°, )1B . tan A = 一2 D . tan B = J 3例2 在厶ABC 中,/ C = 90°3,cosA =-,则 tan A 等于 (53一4c计算 BC = 1 ,【专题解读】锐角三角函数常与其他知识综合起来运用,考查综合运用知识解决问题的能力AC 例8 如图28 —124所示,在△ ABC中,AD是BC边上的高,E为边的中点,BC= 14, AD = 12, sin B=-.5(1)求线段DC的长;⑵求tan/ EDC的值.例9 如图28- 125所示,在△ ABC中,AD是BC边上的高, ⑴求证AC = BD ;⑵若sin C= 1- , BC= 12,求AD 的长.13例10 如图28- 126所示,在△ ABC中,/ B= 45 + 303,求AB的长. tan B= cos/ DAC . AIS '肽吃£,/ C = 30专题4用锐角三角函数解决实际问题【专题解读】加强数学与实际生活的联系,提高数学的应用意识,培养应用数学的能力是当今数学改革的方向,围绕本章内容,纵观近几年各地的中考试题,与解直角三角形有关的应用问题逐步成为命题的热点,其主要类型有轮船定位问题、堤坝工程问题、建筑测量问题、高度测量问题等,解决各类应用问题时要注意把握各类图形的特征及解法.例13如图28- 131所示,我市某中学数学课外活动小组的同学利用所学知识去测量沱江流经我市某段的河宽. 小凡同学在点A处观测到对岸C点,测得/ CAD=45 °,又在距A处60米远的B处测得/ CBA= 30 °,请你根据这些数据算出河宽是多少?(结果保留小数点后两位)例14如图28 - 132所示,某边防巡逻队在一个海滨浴场岸边的A点处发现海中的B点有人求救,便立即派三名救生员前去营救. 1号救生员从A点直接跳入海中;2号救生员沿岸边(岸边可以看成是直线)向前跑到C点再跳入海中;3号救生员沿岸边向前跑300米到离B点最近的D点,再跳入海中,救生员在岸上跑的速度都是6米/秒,在水中游泳的速度都是2米/秒.若/ BAD = 45°, / BCD = 60 ° ,三名救生员同时从A点出发,请说明谁先到达营救地点 B.(参考数据2衣1.4, 3〜1.7)例15如图28- 133所示,某货船以24海里/时的速度将一批重要物资从A处 -■’运往正东方向的M处,在点A处测得某岛C在它的北偏东60°方向上,该货船航'行30分钟后到达B处,此时再测得该岛在它的北偏东30°方向上;已知在C岛周…围9海里的区域内有暗礁,若货船继续向正东方向航行,该货船有无触礁危险?试说'明理由. 氐纹“ 1呼例16如图28- 134所示,某幢大楼顶部有一块广告牌在相距8米的A,B两处测得D点和C点的仰角分别为45° 和60°,且A,B, FCD,甲、乙两人分别三点在一条直线上,若BE = 15米,求这块广告牌的高度.(..3疋1.73,结果保留ffi 28 - 134整数)例17如图28- 135所示,某水库大坝的横断面是梯形,坝顶宽AD = 2.5m, 坝高4m,背水坡的坡度是1 : 1,迎水坡的坡度是1: 1.5,求坝底宽BC.例18如图28 - 136所示,山顶建有一座铁塔,塔高CD = 30m,某人在点A处测得塔底C的仰角为20°,塔顶D的仰角为23°,求此人距CD的水平距离AB.(参考数据:sin 20°~ 0.342, cos 20°~ 0.940, tan 20°~ 0.364, sin 23°~ 0.391, cos23°^ 0.921, tan 23°^ 0.424)图2K 136二、规律方法专题专题5公式法【专题解读】本章的公式很多,熟练掌握公式是解决问题的关键.例19 当0°< a V90°时,求」Sin的值.cos三、思想方法专题专题6类比思想【专题解读】求方程中未知数的过程叫做解方程,求直角三角形中未知元素的过程叫做解直角三角形,因此对解直角三角形的概念的理解可类比解方程的概念. 我们可以像解方程(组)一样求直角三角形中的未知元素.例20 在Rt△ ABC 中,/ C = 90°,/ A,/ B,Z C 的对边分别为a, b, c,已知 a = 5, b2 =』,解这个直角三角形.2专题7数形结合思想【专题解读】由“数”思“形”,由“形”想“数”,两者巧妙结合,起到互通、互译的作用, 是解决几何问题常用的方法之一.3 x+ -,贝y cos a等于( )33A . 丄 2B .22C. 迈3 D. 一23例21 如图28- 137所示,已知/ a的终边OP丄AB,直线AB的方程为y=—专题8分类讨论思想【专题解读】当结果不能确定,且有多种情况时,对每一种可能的情况都要进行讨论.例22 一条东西走向的高速公路上有两个加油站A,B,在A的北偏东45°方向上还有一个加油站C,C到高速公路的最短距离是30 km,B, C间的距离是60 km .要经过C修一条笔直的公路与高速公路相交,使两路交叉口P到B, C的距离相等,求交叉口P与加油站A的距离.(结果可保留根号)专题9转化思想例24 如图28- 140所示,A, B两城市相距100 km.现计划在这两座城市中间修筑一条高速公路(即线段AB),经测量,森林保护中心P在A城市的北偏东30° 和B城市的北偏西45°的方向上.已知森林保护区的范围在以P点为圆心,50 km为半径的圆形区域内.请问计划修筑的这条高速公路会不会穿越保护区. 为什么?(参考数据:・3 ~ 1.732, 2 〜1.414)例25小鹃学完解直角三角形知识后,给同桌小艳出了一道题:“如图28-141所示,把一张长方形卡片ABCD放在每格宽度为12 mm的横格纸中,恰好四个顶点都在横格线上.已知a = 36°求长方形卡片的周长.”请你帮小艳解答这道题.(结果保留整数;参考数据:sin 36° - 0.6,cos 36° 〜0. 8, tan 36°~ 0.7)例26如图28- 142所示,某居民楼I高20米,窗户朝南•该楼内一楼住户的A C H倒甜• 140图- 14128 - 142窗台离地面距离CM为2米,窗户CD高1 . 8米.现计划在I楼的正南方距1楼30米处新建一居民楼H.当正午时刻太阳光线与地面成30 °角时,要使n楼的影子不影响I楼所有住户的采光,新建n楼最高只能盖多少米32。



