2016年全国高考导数压轴题汇编

2016年高考数学文试题分类汇编：导数及其应用D二、填空题1、（2016年天津高考）已知函数()(2+1),()xf x x e f x '=为()f x 的导函数，则(0)f '的值为__________.2、（2016年全国III 卷高考）已知()f x 为偶函数，当0x ≤ 时，1()x f x e x --=-，则曲线()y f x =在点(1,2)处的切线方程式_____________________________.三、解答题1、（2016年北京高考）设函数()32.f x x ax bx c =+++（I ）求曲线().y f x =在点()()0,0f 处的切线方程；（II ）设4a b ==，若函数()f x 有三个不同零点，求c 的取值范围；（III ）求证：230ab -＞是().f x 有三个不同零点的必要而不充分条件.2、（2016年江苏省高考）已知函数()(0,0,1,1)x x f x a b a b a b =+>>≠≠. （1） 设a =2,b =12.① 求方程()f x =2的根;②若对任意x R ∈,不等式(2)f()6f x m x ≥-恒成立，求实数m 的最大值；（2）若01,1<<＞，函数()()2a b=-有且只有1个零点，g x f x求ab的值.3、（2016年山东高考）设f(x)=x ln x–ax2+(2a–1)x，a ∈R.(Ⅰ)令g(x)=f'(x)，求g(x)的单调区间；(Ⅱ)已知f(x)在x=1处取得极大值.求实数a的取值范围.4、（2016年四川高考）设函数f(x)=a x 2－a －lnx ，g(x)=1x －e e x ，其中a ∈R ，e=2.718…为自然对数的底数。

（Ⅰ）讨论f(x)的单调性；（Ⅱ）证明：当x ＞1时，g(x)＞0；（Ⅲ）确定a 的所有可能取值，使得f(x)＞g(x)在区间（1，+∞）内恒成立。

2016年高考数学理试题分类汇编导数及其应用一、选择题1、（2016年四川高考）设直线l 1，l 2分别是函数f (x )= ln ,01,ln ,1,x x x x -<<⎧⎨>⎩图象上点P 1，P 2处的切线，l 1与l 2垂直相交于点P ，且l 1，l 2分别与y 轴相交于点A ，B ，则△PAB 的面积的取值范围是（A ）(0,1) （B ）(0,2) （C ）(0,+∞) （D ）(1,+∞) 【答案】A2、（2016年全国I 高考）函数y =2x 2–e |x |在[–2,2]的图像大致为【答案】D二、填空题1、（2016年全国II 高考）若直线y kx b =+是曲线ln 2y x =+的切线，也是曲线ln(1)y x =+的切线，则b = ．【答案】1ln 2-2、（2016年全国III 高考）已知()f x 为偶函数，当0x <时，()ln()3f x x x =-+，则曲线()y f x =在点(1,3)-处的切线方程 是_______________。

【答案】21y x =--三、解答题1、（2016年北京高考） 设函数()a x f x xe bx -=+，曲线()y f x =在点(2,(2))f 处的切线方程为(1)4y e x =-+， （1）求a ，b 的值； （2）求()f x 的单调区间.【解析】 （I ）()e a x f x x bx -=+∴()e e (1)e a x a x a x f x x b x b ---'=-+=-+∵曲线()y f x =在点(2,(2))f 处的切线方程为(e 1)4y x =-+ ∴(2)2(e 1)4f =-+，(2)e 1f '=- 即2(2)2e 22(e 1)4a f b -=+=-+①2(2)(12)e e 1a f b -'=-+=- ②由①②解得：2a =，e b =（II ）由（I ）可知：2()e e x f x x x -=+，2()(1)e e x f x x -'=-+令2()(1)e x g x x -=-，∴222()e (1)e (2)e x x x g x x x ---'=---=-∴g 的最小值是(2)(12)e 1g =-=-∴()f x '的最小值为(2)(2)e e 10f g '=+=-> 即()0f x '>对x ∀∈R 恒成立 ∴()f x 在(),-∞+∞上单调递增，无减区间.2、（2016年山东高考）已知()221()ln ,R x f x a x x a x -=-+∈. （I ）讨论()f x 的单调性；（II ）当1a =时，证明()3()'2f x f x +＞对于任意的[]1,2x ∈成立. 【解析】(Ⅰ) 求导数322)11(=)(′x x x a x f －－－ 322)(1(=x ax x )－－当0≤a 时，(0,1)∈x ，0>)(′x f ，)(x f 单调递增， )(1,∈+∞x ，0<)(′x f ，)(x f 单调递减；当0>a 时，3322+(2)(1(=2)(1(=)(′x ax a x x a x ax x x f ))－－)－－（1） 当＜２＜a 0时，1>2a， (0,1)∈x 或),(∈+∞2a x ，0>)(′x f ，)(x f 单调递增， )(1,∈ax 2，0<)(′x f ，)(x f 单调递减； (2) 当２=a 时，1=2a， )(0,∈+∞x ，0≥)(′x f ，)(x f 单调递增， (3) 当２>a 时，1<2<0a， )(0,∈ax 2或∞)(1,∈+x ，0>)(′x f ，)(x f 单调递增， ,1)(∈ax 2，0<)(′x f ，)(x f 单调递减； (Ⅱ) 当1=a 时，212+ln =)(x x x x x f －－，32322+11=2)(1(=)(′xx x x x x x f 2－－)－－于是)2+1112+ln =)(′)(322xx x x x x x x f x f 2－－－(－－－，－1－1－322+3+ln =xx x x x ，]2,1[∈x令x x x ln =)g(－ ，322+3+=)h(xx x x －1－1，]2,1[∈x ， 于是)(+(g =)(′)(x h x x f x f ）－， 0≥1=1=)(g ′xx x x －1－，)g(x 的最小值为1=g(1)；又42432+=+=)(h ′x x x x x x x 6－2－362－3－设6+23=)(θ2x x x －－，]2,1[∈x ，因为1=)1(θ，10=)2(θ－， 所以必有]2,1[0∈x ，使得0=)(θ0x ，且0<<1x x 时，0>)(θx ，)(x h 单调递增； 2<<0x x 时，0<)(θx ，)(x h 单调递减；又1=)1(h ，21=)2(h ，所以)(x h 的最小值为21=)2(h ． 所以23=21+1=)2(+1(g >)(+(g =)(′)(h x h x x f x f ））－． 即23)()(+'>x f x f 对于任意的]2,1[∈x 成立．3、（2016年四川高考）设函数f (x )=ax 2-a -ln x ，其中a ∈R. （I ）讨论f (x )的单调性；（II ）确定a 的所有可能取值，使得f (x ) ＞-e 1-x+在区间（1，+∞）内恒成立(e=2.718…为自然对数的底数)。

2016 全国各地导数压轴题汇编1、（ 2016 年全国卷Ｉ理数）已知函数f ( x) (x 2)e x a( x 1) 2有两个零点（I ）求 a 的取值范围（II ）设 x1, x2是 f ( x) 的两个零点，求证：x1x2 22、（ 2016 年全国卷Ｉ文数）已知函数f ( x)(x2)e x a( x 1)2（I ）讨论 f (x) 的单调性（II ）若 f ( x) 有两个零点，求 a 的取值范围3、（ 2016 年全国卷II 理数）(I )讨论函数 f (x) x 2 e x的单调性，并证明当x >0 时，( x 2)e x x 2 0;x 2(II ) 证明：当a [0,1)时，函数g（ x）=e x ax a ( x0)有最小值设（）的最小值为h(a) ，x2. g x求函数 h(a) 的值域 .4、（ 2016 年全国卷II 文数）已知函数 f ( x) ( x 1)lnx a(x 1) .（I ）当a 4 时，求曲线yf ( x) 在 1, f (1) 处的切线方程；(II) 若当x 1, 时，f( x)＞0，求 a 的取值范围 .5、（ 2016 年全国卷 III 理数）设函数 f ( x) a cos2x (a 1)(cos x 1) 其中 a＞ 0，记 | f ( x) |的最大值为 A （Ⅰ）求f ( x) ；（Ⅱ）求 A ；（Ⅲ）证明f ( x) 2 A6、（ 2016 年全国卷 III 文数） 设函数 f ( x) ln x x 1. （Ⅰ）讨论 f ( x) 的单调性；（Ⅱ）证明当x 1x ；x (1, ) 时， 1ln x（Ⅲ）设 c 1，证明当 x (0,1)时，1(c 1)x c x.7、（ 2016 年天津理数）设函数 f ( x) (x 1)3ax b, x R 其中 a, b R (Ⅰ )求 f ( x) 的单调区间；(Ⅱ )若 f ( x) 存在极点 x0，且f ( x1) f ( x0 ) 其中 x1x0，求证： x1 2x0 3；(Ⅲ )设 a 0 ，函数 g (x) | f (x) |,求证： g(x) 在区间 [ 0,2] 上的最大值不小于14．．．8、（ 2016 年四川理数）设函数f ( x) ax2a ln x 其中a R（Ⅰ）讨论f( x)的单调性；（Ⅱ）确定a 的所有可能取值，使得f (x)1 e1 x 在区间（1，+∞）内恒成立( e=2.718 ⋯x为自然对数的底数)。

2021年高考数学压轴卷及答案解析——导数目录2021年高考数学导数压轴卷............. 错误!未定义书签。

一．解答题（共30小题）............ 错误!未定义书签。

2021年高考数学导数压轴卷答案解析 ..... 错误!未定义书签。

一．解答题（共30小题）............ 错误!未定义书签。

2021年高考数学导数压轴卷一．解答题（共30小题）1．（2021•株洲一模）已知函数f（x）=alnx﹣ax﹣3（a∈R）．（Ⅰ）求函数f（x）的单调区间；（Ⅱ）假设函数y=f（x）的图象在点（2，f（2））处的切线的倾斜角为45°，关于任意的t∈[1，2]，函数在区间（t，3）上总不是单调函数，求m的取值范围；（Ⅲ）求证：．2．（2021•北京校级模拟）已知函数f（x）=x2+ax﹣lnx，a∈R．（1）假设函数f（x）在[1，2]上是减函数，求实数a的取值范围；（2）令g（x）=f（x）﹣x2，是不是存在实数a，当x∈（0，e]（e是自然常数）时，函数g（x）的最小值是3，假设存在，求出a的值；假设不存在，说明理由；（3）当x∈（0，e]时，证明：．3．（2021•菏泽一模）设函数f（x）=lnx﹣﹣bx（Ⅰ）当a=b=时，求函数f（x）的单调区间；（Ⅱ）令F（x）=f（x）+＜x≤3），其图象上任意一点P（x0，y0）处切线的斜率k≤恒成立，求实数a的取值范围；（Ⅲ）当a=0，b=﹣1时，方程f（x）=mx在区间[1，e2]内有唯一实数解，求实数m的取值范围．4．（2021•秦州区校级一模）设函数f（x）=（1+x）2﹣2ln（1+x）（1）假设关于x的不等式f（x）﹣m≥0在[0，e﹣1]有实数解，求实数m的取值范围．（2）设g（x）=f（x）﹣x2﹣1，假设关于x的方程g（x）=p至少有一个解，求p的最小值．（3）证明不等式：（n∈N*）．5．（2021•陕西校级二模）关于函数f（x）和g（x），假设存在常数k，m，关于任意x∈R，不等式f（x）≥kx+m≥g（x）都成立，那么称直线y=kx+m是函数f（x），g（x）的分界限．已知函数f（x）=e x（ax+1）（e为自然对数的底，a∈R 为常数）．（Ⅰ）讨论函数f（x）的单调性；（Ⅱ）设a=1，试探讨函数f（x）与函数g（x）=﹣x2+2x+1是不是存在“分界限”？假设存在，求出分界限方程；假设不存在，试说明理由．6．（2021•安徽模拟）已知函数（a为实常数）．（Ⅰ）当a=1时，求函数g（x）=f（x）﹣2x的单调区间；（Ⅱ）假设函数f（x）在区间（0，2）上无极值，求a的取值范围；（Ⅲ）已知n∈N*且n≥3，求证：．7．（2021•黄冈模拟）已知函数f（x）=ax，g（x）=lnx，其中a∈R．（Ⅰ）假设函数F（x）=f（x）﹣g（x）有极值点1，求a的值；（Ⅱ）假设函数G（x）=f[sin（1﹣x）]+g（x）在区间（0，1）上为增函数，求a的取值范围；（Ⅲ）证明：．8．（2021•衡水三模）已知函数f（x）=x﹣alnx，g（x）=﹣，（a∈R）．（Ⅰ）假设a=1，求函数f（x）的极值；（Ⅱ）设函数h（x）=f（x）﹣g（x），求函数h（x）的单调区间；（Ⅲ）假设在[1，e]（e=…）上存在一点x0，使得f（x0）＜g（x0）成立，求a的取值范围．9．（2021•陕西模拟）已知函数．（a为常数，a＞0）（Ⅰ）假设是函数f（x）的一个极值点，求a的值；（Ⅱ）求证：当0＜a≤2时，f（x）在上是增函数；（Ⅲ）假设对任意的a∈（1，2），总存在，使不等式f（x0）＞m（1﹣a2）成立，求实数m的取值范围．10．（2021•横峰县校级一模）已知函数f（x）=alnx﹣ax﹣3（a∈R，a≠0）．（Ⅰ）求函数f（x）的单调区间；（Ⅱ）假设函数y=f（x）的图象在点（2，f（2））处的切线的倾斜角为，问：m在什么范围取值时，关于任意的t∈[1，2]，函数在区间[t，3]上总存在极值？（Ⅲ）当a=2时，设函数，假设在区间[1，e]上至少存在一个x0，使得h（x0）＞f（x0）成立，试求实数p的取值范围．11．（2021•凤凰县校级模拟）已知函数f（x）=x3﹣ax2﹣3x（1）假设f（x）在区间[1，+∞）上是增函数，求实数a的取值范围；（2）假设x=﹣是f（x）的一个极值点，求f（x）在[1，a]上的最大值；（3）在（2）的条件下，是不是存在实数b，使得函数g（x）=bx的图象与函数f（x）的图象恰有3个交点，假设存在，请求出实数b的取值范围；假设不存在，试说明理由．12．（2021•路南区校级模拟）已知函数f（x）=x3﹣（2a+1）x2+（a2+a）x．（Ⅰ）假设f（x）在x=1处取得极大值，求实数a的值；（Ⅱ）假设∀m∈R，直线y=kx+m都不是曲线y=f（x）的切线，求k的取值范围；（Ⅲ）假设a＞﹣1，求f（x）在区间[0，1]上的最大值．13．（2021•张家港市校级模拟）已知函数f（x）=x3+bx2+cx+d，设曲线y=f（x）在与x轴交点处的切线为y=4x﹣12，f′（x）为f（x）的导函数，知足f′（2﹣x）=f′（x）．（Ⅰ）设g（x）=x，m＞0，求函数g（x）在[0，m]上的最大值；（Ⅱ）设h（x）=lnf′（x），假设对一切x∈[0，1]，不等式h（x+1﹣t）＜h（2x+2）恒成立，求实数t的取值范围．14．（2021•安徽三模）已知函数在点（﹣1，f（﹣1））的切线方程为x+y+3=0．（Ⅰ）求函数f（x）的解析式；（Ⅱ）设g（x）=lnx，求证：g（x）≥f（x）在x∈[1，+∞）上恒成立；（Ⅲ）已知0＜a＜b，求证：．15．（2021秋•仙游县校级期中）已知函数f（x）=x+，h（x）=．（Ⅰ）设函数F（x）=f（x）﹣h（x），求F（x）的单调区间与极值；（Ⅱ）设a∈R，解关于x的方程log4[f（x﹣1）﹣]=log2h（a﹣x）﹣log2h（4﹣x）；（Ⅲ）试比较f（100）h（100）﹣与的大小．16．（2021•遵义二模）设函数f（x）=x2+aln（1+x）有两个极值点x1、x2，且x1＜x2，（Ⅰ）求a的取值范围，并讨论f（x）的单调性；（Ⅱ）证明：f（x2）＞．17．（2021秋•大兴区校级月考）已知函数f（x）=e x﹣e﹣x﹣2x．（Ⅰ）讨论f（x）的单调性；（Ⅱ）设g（x）=f（2x）﹣4bf（x），当x＞0时，g（x）＞0，求b的最大值；（Ⅲ）已知＜＜，估量ln2的近似值（精准到）．18．（2021•武汉模拟）己知函数f（x）=x2e﹣x（Ⅰ）求f（x）的极小值和极大值；（Ⅱ）当曲线y=f（x）的切线l的斜率为负数时，求l在x轴上截距的取值范围．19．（2021•马山县校级模拟）已知函数f（x）=x3+3ax2+（3﹣6a）x+12a﹣4（a∈R）（Ⅰ）证明：曲线y=f（x）在x=0的切线过点（2，2）；（Ⅱ）假设f（x）在x=x0处取得极小值，x0∈（1，3），求a的取值范围．20．（2021春•丰润区期中）已知函数f（x）=x3+3ax2+3x+1．（Ⅰ）求a=时，讨论f（x）的单调性；（Ⅱ）假设x∈[2，+∞）时，f（x）≥0，求a的取值范围．21．（2021•浙江）已知函数f（x）=x3+3|x﹣a|（a∈R）．（Ⅰ）假设f（x）在[﹣1，1]上的最大值和最小值别离记为M（a），m（a），求M（a）﹣m （a）；（Ⅱ）设b∈R，假设[f（x）+b]2≤4对x∈[﹣1，1]恒成立，求3a+b的取值范围．22．（2021•河西区三模）已知函数f（x）=+cx+d（a，c，d∈R）知足f（0）=0，f′（1）=0，且f′（x）≥0在R上恒成立．（1）求a，c，d的值；（2）假设，解不等式f′（x）+h（x）＜0；（3）是不是存在实数m，使函数g（x）=f′（x）﹣mx在区间[m，m+2]上有最小值﹣5？假设存在，请求出实数m的值；假设不存在，请说明理由．23．（2021•四川模拟）已知函数f（x）=lnx+x2．（Ⅰ）假设函数g（x）=f（x）﹣ax在其概念域内为增函数，求实数a的取值范围；（Ⅱ）在（Ⅰ）的条件下，假设a＞1，h（x）=e3x﹣3ae x x∈[0，ln2]，求h（x）的极小值；（Ⅲ）设F（x）=2f（x）﹣3x2﹣kx（k∈R），假设函数F（x）存在两个零点m，n（0＜m＜n），且2x0=m+n．问：函数F（x）在点（x0，F（x0））处的切线可否平行于x轴？假设能，求出该切线方程；假设不能，请说明理由．24．（2021•天津三模）已知函数f（x）=（2﹣a）（x﹣1）﹣2lnx，g（x）=xe1﹣x．（a∈R，e为自然对数的底数）（Ⅰ）当a=1时，求f（x）的单调区间；（Ⅱ）假设函数f（x）在上无零点，求a的最小值；（Ⅲ）假设对任意给定的x0∈（0，e]，在（0，e]上总存在两个不同的x i（i=1，2），使得f（x i）=g（x0）成立，求a的取值范围．25．（2021•河西区一模）已知函数g（x）=，f（x）=g（x）﹣ax．（1）求函数g（x）的单调区间；（2）假设函数f（x）在（1，+∞）上是减函数，求实数a的最小值；（3）假设存在x1，x2∈[e，e2]，使f（x1）≤f′（x2）+a，求实数a的取值范围．26．（2021•凉州区二模）已知函数f（x）=plnx+（p﹣1）x2+1．（1）讨论函数f（x）的单调性；（2）当P=1时，f（x）≤kx恒成立，求实数k的取值范围；（3）证明：1n（n+1）＜1+…+（n∈N+）．27．（2021•蚌埠二模）已知函数为大于零的常数．（1）假设函数f（x）在区间[1，+∞）内调递增，求a的取值范围；（2）求函数f（x）在区间[1，2]上的最小值；（3）求证：关于任意的成立．28．（2021•高州市模拟）设函数f（x）=（x﹣1）2+blnx，其中b为常数．（1）当时，判定函数f（x）在概念域上的单调性；（2）假设函数f（x）的有极值点，求b的取值范围及f（x）的极值点；（3）求证对任意不小于3的正整数n，不等式都成立．29．（2021•甘肃二模）已知函数f（x）=+lnx﹣2，g（x）=lnx+2x．（Ⅰ）求函数f（x）的单调区间；（Ⅱ）试问过点（2，5）可作多少条直线与曲线y=g（x）相切？请说明理由．30．（2021•吉林三模）已知函数f（x）=lnx﹣，g（x）=f（x）+ax﹣6lnx，其中a∈R（1）当a=1时，判定f（x）的单调性；（2）假设g（x）在其概念域内为增函数，求正实数a的取值范围；（3）设函数h（x）=x2﹣mx+4，当a=2时，假设∃x1∈（0，1），∀x2∈[1，2]，总有g（x1）≥h （x2）成立，求实数m的取值范围．2021年高考数学导数压轴卷答案解析一．解答题（共30小题）1．（2021•株洲一模）已知函数f（x）=alnx﹣ax﹣3（a∈R）．（Ⅰ）求函数f（x）的单调区间；（Ⅱ）假设函数y=f（x）的图象在点（2，f（2））处的切线的倾斜角为45°，关于任意的t∈[1，2]，函数在区间（t，3）上总不是单调函数，求m的取值范围；（Ⅲ）求证：．考点：利用导数研究函数的单调性；利用导数研究曲线上某点切线方程．专题：压轴题．分析：利用导数求函数的单调区间的步骤是①求导函数f′（x）；②解f′（x）＞0（或＜0）；③得到函数的增区间（或减区间），对于本题的（1）在求单调区间时要注意函数的定义域以及对参数a的讨论情况；（2）点（2，f（2））处的切线的倾斜角为45°，即切线斜率为1，即f'（2）=1，可求a 值，代入得g（x）的解析式，由t∈[1，2]，且g（x）在区间（t，3）上总不是单调函数可知：，于是可求m的范围．（3）是近年来高考考查的热点问题，即与函数结合证明不等式问题，常用的解题思路是利用前面的结论构造函数，利用函数的单调性，对于函数取单调区间上的正整数自变量n 有某些结论成立，进而解答出这类不等式问题的解．解答：解：（Ⅰ）（2分）当a＞0时，f（x）的单调增区间为（0，1]，减区间为[1，+∞）；当a＜0时，f（x）的单调增区间为[1，+∞），减区间为（0，1]；当a=0时，f（x）不是单调函数（4分）（Ⅱ）得a=﹣2，f（x）=﹣2lnx+2x﹣3∴，∴g'（x）=3x2+（m+4）x﹣2（6分）∵g（x）在区间（t，3）上总不是单调函数，且g′（0）=﹣2 ∴由题意知：对于任意的t∈[1，2]，g′（t）＜0恒成立，所以有：，∴（10分）（Ⅲ）令a=﹣1此时f（x）=﹣lnx+x﹣3，所以f（1）=﹣2，由（Ⅰ）知f（x）=﹣lnx+x﹣3在（1，+∞）上单调递增，∴当x∈（1，+∞）时f（x）＞f（1），即﹣lnx+x﹣1＞0，∴lnx＜x﹣1对一切x∈（1，+∞）成立，（12分）∵n≥2，n∈N*，则有0＜lnn＜n﹣1，∴∴点评：本题考查利用函数的导数来求函数的单调区间，已知函数曲线上一点求曲线的切线方程即对函数导数的几何意义的考查，考查求导公式的掌握情况．含参数的数学问题的处理，构造函数求解证明不等式问题．2．（2021•北京校级模拟）已知函数f（x）=x2+ax﹣lnx，a∈R．（1）假设函数f（x）在[1，2]上是减函数，求实数a的取值范围；（2）令g（x）=f（x）﹣x2，是不是存在实数a，当x∈（0，e]（e是自然常数）时，函数g（x）的最小值是3，假设存在，求出a的值；假设不存在，说明理由；（3）当x∈（0，e]时，证明：．考点：利用导数研究函数的单调性；利用导数求闭区间上函数的最值．专题：计算题；综合题；压轴题．分析：（1）先对函数f（x）进行求导，根据函数f（x）在[1，2]上是减函数可得到其导函数在[1，2]上小于等于0应该恒成立，再结合二次函数的性质可求得a的范围．（2）先假设存在，然后对函数g（x）进行求导，再对a的值分情况讨论函数g（x）在（0，e]上的单调性和最小值取得，可知当a=e2能够保证当x∈（0，e]时g（x）有最小值3．（3）令F（x）=e2x﹣lnx结合（2）中知F（x）的最小值为3，再令并求导，再由导函数在0＜x≤e大于等于0可判断出函数ϕ（x）在（0，e]上单调递增，从而可求得最大值也为3，即有成立，即成立．解答：解：（1）在[1，2]上恒成立，令h（x）=2x2+ax﹣1，有得，得（2）假设存在实数a，使g（x）=ax﹣lnx（x∈（0，e]）有最小值3，=①当a≤0时，g（x）在（0，e]上单调递减，g（x）min=g（e）=ae﹣1=3，（舍去），②当时，g（x）在上单调递减，在上单调递增∴，a=e2，满足条件．③当时，g（x）在（0，e]上单调递减，g（x）min=g（e）=ae﹣1=3，（舍去），综上，存在实数a=e2，使得当x∈（0，e]时g（x）有最小值3．（3）令F（x）=e2x﹣lnx，由（2）知，F（x）min=3．令，，当0＜x≤e时，ϕ'（x）≥0，φ（x）在（0，e]上单调递增∴∴，即＞（x+1）lnx．点评：本题主要考查导数的运算和函数的单调性与其导函数的正负之间的关系，当导函数大于0时原函数单调递增，当导函数小于0时原函数单调递减．3．（2021•菏泽一模）设函数f（x）=lnx﹣﹣bx（Ⅰ）当a=b=时，求函数f（x）的单调区间；（Ⅱ）令F（x）=f（x）+＜x≤3），其图象上任意一点P（x0，y0）处切线的斜率k≤恒成立，求实数a的取值范围；（Ⅲ）当a=0，b=﹣1时，方程f（x）=mx在区间[1，e2]内有唯一实数解，求实数m的取值范围．考利用导数研究函数的单调性；根的存在性及根的个数判断；利用导数研究曲线上某点切点：线方程．专题：计算题；压轴题．分析：（I）先求导数fˊ（x）然后在函数的定义域内解不等式fˊ（x）＞0和fˊ（x）＜0，fˊ（x）＞0的区间为单调增区间，fˊ（x）＜0的区间为单调减区间．（II）先构造函数F（x）再由以其图象上任意一点P（x0，y0）为切点的切线的斜率k≤恒成立，知导函数≤恒成立，再转化为所以a≥（﹣，x02+x0）max求解．（III）先把程f（x）=mx有唯一实数解，转化为有唯一实数解，再利用单调函数求解．解答：解：（Ⅰ）依题意，知f（x）的定义域为（0，+∞）．（1分）当a=b=时，f（x）=lnx﹣x2﹣x，f′（x）=﹣x﹣=．（2分）令f′（x）=0，解得x=1．当0＜x＜1时，f′（x）＞0，此时f（x）单调递增；当x＞1时，f′（x）＜0，此时f（x）单调递减．（3分）所以函数f（x）的单调增区间（0，1），函数f（x）的单调减区间（1，+∞）．（4分）（Ⅱ）F（x）=lnx+，x∈（0，3]，所以k=F′（x0）=≤，在x0∈（0，3]上恒成立，（6分）所以a≥（﹣x02+x0）max，x0∈（0，3]（7分）当x0=1时，﹣x02+x0取得最大值．所以a≥．（9分）（Ⅲ）当a=0，b=﹣1时，f（x）=lnx+x，因为方程f（x）=mx在区间[1，e2]内有唯一实数解，所以lnx+x=mx有唯一实数解．∴，设g（x）=，则g′（x）=．令g′（x）＞0，得0＜x＜e；g′（x）＜0，得x＞e，∴g（x）在区间[1，e]上是增函数，在区间[e，e2]上是减函数，g（1）=1，g（e2）=1+=1+，g（e）=1+，所以m=1+，或1≤m＜1+．点评：本题主要考查函数的单调性、极值、不等式、方程的解等基本知识，同时考查运用导数研究函数性质的方法，分类与整合及化归与转化等数学思想．4．（2021•秦州区校级一模）设函数f（x）=（1+x）2﹣2ln（1+x）（1）假设关于x的不等式f（x）﹣m≥0在[0，e﹣1]有实数解，求实数m的取值范围．（2）设g（x）=f（x）﹣x2﹣1，假设关于x的方程g（x）=p至少有一个解，求p的最小值．（3）证明不等式：（n∈N*）．考点：利用导数研究函数的单调性；函数恒成立问题．专题：综合题；压轴题；导数的概念及应用．分析：（1）依题意得f（x）max≥m，x∈[0，e﹣1]，求导数，求得函数的单调性，从而可得函数的最大值；（2）求导函数，求得函数的单调性与最值，从而可得p的最小值；（3）先证明ln（1+x）≤x，令，则x∈（0，1）代入上面不等式得：，从而可得．利用叠加法可得结论．解答：（1）解：依题意得f（x）max≥m，x∈[0，e﹣1]∵，而函数f（x）的定义域为（﹣1，+∞）∴f（x）在（﹣1，0）上为减函数，在（0，+∞）上为增函数，∴f（x）在[0，e﹣1]上为增函数，∴∴实数m的取值范围为m≤e2﹣2（2）解：g（x）=f（x）﹣x2﹣1=2x﹣2ln（1+x）=2[x﹣ln（1+x）]，∴显然，函数g（x）在（﹣1，0）上为减函数，在（0，+∞）上为增函数∴函数g（x）的最小值为g（0）=0∴要使方程g（x）=p至少有一个解，则p≥0，即p的最小值为0（3）证明：由（2）可知：g（x）=2[x﹣ln（1+x）]≥0在（﹣1，+∞）上恒成立所以ln（1+x）≤x，当且仅当x=0时等号成立令，则x∈（0，1）代入上面不等式得：即，即所以ln2﹣ln1＜1，，，…，将以上n个等式相加即可得到：点评：本题考查导数知识的运用，考查函数的单调性与最值，考查不等式的证明，考查恒成立问题，属于中档题．5．（2021•陕西校级二模）关于函数f（x）和g（x），假设存在常数k，m，关于任意x∈R，不等式f（x）≥kx+m≥g（x）都成立，那么称直线y=kx+m是函数f（x），g（x）的分界限．已知函数f（x）=e x（ax+1）（e为自然对数的底，a∈R 为常数）．（Ⅰ）讨论函数f（x）的单调性；（Ⅱ）设a=1，试探讨函数f（x）与函数g（x）=﹣x2+2x+1是不是存在“分界限”？假设存在，求出分界限方程；假设不存在，试说明理由．考点：利用导数研究函数的单调性；函数单调性的判断与证明．专题：计算题；压轴题；新定义．分析：（Ⅰ）f′（x）=e x（ax+1+a），当a＞0时，f′（x）＞0⇔函数f（x）在区间（﹣1﹣，+∞）上是增函数，在区间（﹣∞，﹣1﹣）上是减函数；a=0时，f′（x）＞0，函数f（x）是区间（﹣∞，+∞）上的增函数；当a＜0时，f′（x）＞0⇔ax＞﹣a﹣1，函数f（x）在区间（﹣∞，﹣1﹣）上是增函数，在区间（﹣1﹣，+∞）上是减函数．（Ⅱ）若存在，则e x（x+1）≥kx+m≥﹣x2+2x+1恒成立，令x=0，得m=1，因此x2+（k ﹣2）x≥0恒成立，由此及彼能推导出函数f（x）与函数g（x）=﹣x2+2x+1存在“分界线”．解答：解：（Ⅰ）f′（x）=e x（ax+1+a），（2分）当a＞0时，f′（x）＞0⇔ax＞﹣a﹣1，即x＞﹣1﹣，函数f（x）在区间（﹣1﹣，+∞）上是增函数，在区间（﹣∞，﹣1﹣）上是减函数；（3分）当a=0时，f′（x）＞0，函数f（x）是区间（﹣∞，+∞）上的增函数；（5分）当a＜0时，f′（x）＞0⇔ax＞﹣a﹣1，即x＜﹣1﹣，函数f（x）在区间（﹣∞，﹣1﹣）上是增函数，在区间（﹣1﹣，+∞）上是减函数．（7分）（Ⅱ）若存在，则e x（x+1）≥kx+m≥﹣x2+2x+1恒成立，令x=0，则1≥m≥1，所以m=1，（9分）因此：kx+1≥﹣x2+2x+1恒成立，即x2+（k﹣2）x≥0恒成立，由△≤0得到：k=2，现在只要判断e x（x+1）≥2x+1是否恒成立，（11分）设∅（x）=e x（x+1）﹣（2x+1），因为：∅′（x）=e x（x+2）﹣2，当x＞0时，e x＞1，x+2＞2，∅′（x）＞0，当x＜0时，e x（x+2）＜2e x＜2，∅′（x）＜0，所以∅（x）≥∅（0）=0，即e x（x+1）≥2x+1恒成立，所以函数f（x）与函数g（x）=﹣x2+2x+1存在“分界线”．方程为y=2x+1．（14分）点评：本题考查导数函数单调性中的应用，解题时要认真审题，注意挖掘题设中的隐含条件，合理地运用导数的性质进行求解．6．（2021•安徽模拟）已知函数（a为实常数）．（Ⅰ）当a=1时，求函数g（x）=f（x）﹣2x的单调区间；（Ⅱ）假设函数f（x）在区间（0，2）上无极值，求a的取值范围；（Ⅲ）已知n∈N*且n≥3，求证：．考点：函数在某点取得极值的条件；利用导数研究函数的单调性；数列与不等式的综合．专题：综合题；压轴题；导数的综合应用．分析：（Ⅰ）求出函数定义域，当a=1时求出g′（x），只需解不等式g′（x）＞0，g′（x）＜0即可．（Ⅱ）函数f（x）在区间（0，2）上无极值，则f′（x）≥0或f′（x）≤0，由此即可求出a 的取值范围．（Ⅲ）由（Ⅱ）知，当a=1时，f（x）在（0，+∞）上的最大值为f（1）=0，得f（x）=≤0，即ln，令x=适当变形即可证明．解答：解：（I）当a=1时，，其定义域为（0，+∞），g′（x）=﹣2+=，，令g′（x）＞0，并结合定义域知；令g′（x）＜0，并结合定义域知；故g（x）的单调增区间为（0，）；单调减区间为．（II），（1）当f′（x）≤0即a≤x在x∈（0，2）上恒成立时，a≤0，此时f（x）在（0，2）上单调递减，无极值；（2）当f′（x）≥0即a≥x在x∈（0，2）上恒成立时，a≥2，此时f（x）在（0，2）上单调递增，无极值．综上所述，a的取值范围为（﹣∞，0]∪[2，+∞）．（Ⅲ）由（Ⅱ）知，当a=1时，f′（x）=，当x∈（0，1）时，f′（x）＞0，f（x）单调递增；当x∈（1，+∞）时，f′（x）＜0，f（x）单调递减，∴f（x）=在x=1处取得最大值0．即f（x）=1﹣，∴，令x=（0＜x＜1），则，即ln（n+1）﹣lnn，∴ln=ln（n+1）﹣ln3=[ln（n+1）﹣lnn]+[lnn﹣ln（n﹣1）]+…+（ln4﹣ln3）＜．故．点评：本题考查了利用导数研究函数的单调性、利用导数求函数最值问题，考查了运用知识解决问题的能力．7．（2021•黄冈模拟）已知函数f（x）=ax，g（x）=lnx，其中a∈R．（Ⅰ）假设函数F（x）=f（x）﹣g（x）有极值点1，求a的值；（Ⅱ）假设函数G（x）=f[sin（1﹣x）]+g（x）在区间（0，1）上为增函数，求a的取值范围；（Ⅲ）证明：．考点：函数在某点取得极值的条件；利用导数求闭区间上函数的最值．专题：计算题；压轴题；导数的综合应用．分析：（Ⅰ）根据已知条件函数F（x）=f（x）﹣g（x）有极值点1，可得F′（1）=0，得出等式，求出a值；（Ⅱ）因为函数G（x）=f[sin（1﹣x）]+g（x）在区间（0，1）上为增函数，可以对其进行转化，可以转化为G′（x）＞0在（0，1）上恒成立，利用常数分离法进行求解；（Ⅲ）这个证明题可以利用一个恒等式，sinx＜x，然后对从第三项开始进行放缩，然后进行证明；解答：解：（Ⅰ）∵函数f（x）=ax，g（x）=lnx，其中a∈R．∴F（x）=ax﹣lnx，则F′（x）=a﹣，∵函数F（x）=f（x）﹣g（x）有极值点1，∴F′（1）=0，∴a﹣1=0，解得a=1；（Ⅱ）∵函数G（x）=f[sin（1﹣x）]+g（x）=asin（1﹣x）+lnx，∴G′（x）=acos（1﹣x）×（﹣1）+，只要G′（x）在区间（0，1）上大于等于0，∴G′（x）=acos（1﹣x）×（﹣1）+≥0，∴a≤，求的最小值即可，求h（x）=xcos（1﹣x）的最大值即可，0＜1﹣x＜1，∵h′（x）=cos（1﹣x）+xsin（1﹣x）＞0，∴h（x）在（0，1）增函数，h（x）＜h（1）=1，∴的最小值为1，∴a≤1；（Ⅲ）∵0＜＜1，∵sinx＜x在x∈（0，1）上恒成立，∴=sin+sin+…+sin≤++…+＜+++++…+=﹣＜＜ln2，∴＜ln2；点评：第一问利用导数可以很容易解决，第二问利用了常数分离法进行证明，第三问需要进行放缩证明，主要利用sinx＜x进行证明，此题难度比较大，计算量比较大；8．（2021•衡水三模）已知函数f（x）=x﹣alnx，g（x）=﹣，（a∈R）．（Ⅰ）假设a=1，求函数f（x）的极值；（Ⅱ）设函数h（x）=f（x）﹣g（x），求函数h（x）的单调区间；（Ⅲ）假设在[1，e]（e=…）上存在一点x0，使得f（x0）＜g（x0）成立，求a的取值范围．考点：利用导数研究函数的极值；利用导数研究函数的单调性；利用导数求闭区间上函数的最值．专题：计算题；压轴题；分类讨论；转化思想．分析：（Ⅰ）先求出其导函数，让其大于0求出增区间，小于0求出减区间即可得到函数的单调区间进而求出函数f（x）的极值；（Ⅱ）先求出函数h（x）的导函数，分情况讨论让其大于0求出增区间，小于0求出减区间即可得到函数的单调区间；（Ⅲ）先把f（x0）＜g（x0）成立转化为h（x0）＜0，即函数在[1，e]上的最小值小于零；再结合（Ⅱ）的结论分情况讨论求出其最小值即可求出a的取值范围．解答：解：（Ⅰ）f（x）的定义域为（0，+∞），（1分）当a=1时，f（x）=x﹣lnx，，（2分）x （0，1） 1 （1，+∞）f'（x）﹣0 +f（x）极小（3分）所以f（x）在x=1处取得极小值1．（4分）（Ⅱ），（6分）①当a+1＞0时，即a＞﹣1时，在（0，1+a）上h'（x）＜0，在（1+a，+∞）上h'（x）＞0，所以h（x）在（0，1+a）上单调递减，在（1+a，+∞）上单调递增；（7分）②当1+a≤0，即a≤﹣1时，在（0，+∞）上h'（x）＞0，所以，函数h（x）在（0，+∞）上单调递增．（8分）（III）在[1，e]上存在一点x0，使得f（x0）＜g（x0）成立，即在[1，e]上存在一点x0，使得h（x0）＜0，即函数在[1，e]上的最小值小于零．（9分）由（Ⅱ）可知①即1+a≥e，即a≥e﹣1时，h（x）在[1，e]上单调递减，所以h（x）的最小值为h（e），由可得，因为，所以；（10分）②当1+a≤1，即a≤0时，h（x）在[1，e]上单调递增，所以h（x）最小值为h（1），由h（1）=1+1+a＜0可得a＜﹣2；（11分）③当1＜1+a＜e，即0＜a＜e﹣1时，可得h（x）最小值为h（1+a），因为0＜ln（1+a）＜1，所以，0＜aln（1+a）＜a故h（1+a）=2+a﹣aln（1+a）＞2此时，h（1+a）＜0不成立．（12分）综上讨论可得所求a的范围是：或a＜﹣2．（13分）点评：本题第一问考查利用导函数来研究函数的极值．在利用导函数来研究函数的极值时，分三步①求导函数，②求导函数为0的根，③判断根左右两侧的符号，若左正右负，原函数取极大值；若左负右正，原函数取极小值．9．（2021•陕西模拟）已知函数．（a为常数，a＞0）（Ⅰ）假设是函数f（x）的一个极值点，求a的值；（Ⅱ）求证：当0＜a≤2时，f（x）在上是增函数；（Ⅲ）假设对任意的a∈（1，2），总存在，使不等式f（x0）＞m（1﹣a2）成立，求实数m的取值范围．考点：利用导数研究函数的极值；导数在最大值、最小值问题中的应用．专题：计算题；压轴题；分类讨论；转化思想．分析：（Ⅰ）先求出其导函数：，利用是函数f（x）的一个极值点对应的结论f'（）=0即可求a的值；（Ⅱ）利用：，在0＜a≤2时，分析出因式中的每一项都大于等于0即可证明结论；（Ⅲ）先由（Ⅱ）知，f（x）在上的最大值为，把问题转化为对任意的a∈（1，2），不等式恒成立；然后再利用导函数研究不等式左边的最小值看是否符合要求即可求实数m的取值范围．解答：解：由题得：．（Ⅰ）由已知，得且，∴a2﹣a﹣2=0，∵a＞0，∴a=2．（2分）（Ⅱ）当0＜a≤2时，∵，∴，∴当时，．又，∴f'（x）≥0，故f（x）在上是增函数．（5分）（Ⅲ）a∈（1，2）时，由（Ⅱ）知，f（x）在上的最大值为，于是问题等价于：对任意的a∈（1，2），不等式恒成立．记，（1＜a＜2）则，当m=0时，，∴g（a）在区间（1，2）上递减，此时，g（a）＜g（1）=0，由于a2﹣1＞0，∴m≤0时不可能使g（a）＞0恒成立，故必有m＞0，∴．若，可知g（a）在区间上递减，在此区间上，有g（a）＜g（1）=0，与g（a）＞0恒成立矛盾，故，这时，g'（a）＞0，g（a）在（1，2）上递增，恒有g（a）＞g（1）=0，满足题设要求，∴，即，所以，实数m的取值范围为．（14分）点评：本题第一问主要考查利用极值求对应变量的值．可导函数的极值点一定是导数为0的点，但导数为0的点不一定是极值点．10．（2021•横峰县校级一模）已知函数f（x）=alnx﹣ax﹣3（a∈R，a≠0）．（Ⅰ）求函数f（x）的单调区间；（Ⅱ）假设函数y=f（x）的图象在点（2，f（2））处的切线的倾斜角为，问：m在什么范围取值时，关于任意的t∈[1，2]，函数在区间[t，3]上总存在极值？（Ⅲ）当a=2时，设函数，假设在区间[1，e]上至少存在一个x0，使得h（x0）＞f（x0）成立，试求实数p的取值范围．考点：利用导数研究函数的极值；利用导数研究函数的单调性．专题：计算题；综合题；压轴题．分析：（Ⅰ）求出f′（x）对a分类讨论，由f′（x）＞0时，得到函数的递增区间；令f′（x）＜0时，得到函数的递减区间；（Ⅱ）因为函数y=f（x）的图象在点（2，f（2））处的切线的倾斜角为45°，得到f′（2）=1求出a的值代入到g（x）=中化简，求出导函数，因为函数在[t，3]上总存在极值得到g′（t）＜0，g′（3）＞0 解出m的范围记即可；（Ⅲ）F（x由题意构建新函数F（x））=f（x）﹣g（x），这样问题转化为使函数F（x）在[1，e]上至少有一解的判断．解答：解：（Ⅰ）∵f′（x）=﹣a=a（）（x＞0），∴（1）当a＞0时，令f′（x）＞0时，解得0＜x＜1，所以f（x）在（0，1）递增；令f′（x）＜0时，解得x＞1，所以f（x）在（1，+∞）递减．当a＜0时，f′（x）=﹣a（），令f′（x）＞0时，解得x＞1，所以f（x）在（1，+∞）递增；令f′（x）＜0时，解得0＜x＜1，所以f（x）在（0，1）递减；（Ⅱ）因为函数y=f（x）的图象在点（2，f（2））处的切线的倾斜角为45°，所以f′（2）=1，所以a=﹣2，f′（x）=﹣+2，g（x）=x3+x2[+f′（x）]=x3+x2[+2﹣]=x3+（2+）•x2﹣2x，∴g′（x）=3x2+（4+m）x﹣2，因为对于任意的t∈[1，2]，函数g（x）=x3+x2[+f′（x）]在区间[t，3]上总存在极值，所以只需g′（2）＜0 g′（3）＞0，解得﹣＜m＜﹣9；（Ⅲ）∴令F（x）=h（x）﹣f（x）=（p﹣2）x﹣﹣3﹣2lnx+2x+3=px﹣﹣﹣2lnx，①当p≤0时，由x∈[1，e]得px﹣≤0，﹣﹣2lnx＜0．所以，在[1，e]上不存在x0，使得h（x0）＞f（x0）成立；②当p＞0时，F′（x）=，∵x∈[1，e]，∴2e﹣2x≥0，px2+p＞0，F′（x）＞0在[1，e]上恒成立，故F（x）在[1，e]上单调递增．∴F（x）max=F（e）=pe﹣﹣4．故只要pe﹣﹣4＞0，解得p＞．所以p的取值范围是[，+∞）．点评：（Ⅰ）考查学生利用导数研究函数单调性的能力，（Ⅱ）利用导数研究曲线上某点切线方程的能力，会根据直线的倾斜角求直线的斜率，（Ⅲ）此处重点考查了等价转化的思想，把问题转化为构建一新函数，并考查了函数F（x）在定义域下恒成立问题数式中含字母系数，需分类讨论，属于难题．11．（2021•凤凰县校级模拟）已知函数f（x）=x3﹣ax2﹣3x（1）假设f（x）在区间[1，+∞）上是增函数，求实数a的取值范围；（2）假设x=﹣是f（x）的一个极值点，求f（x）在[1，a]上的最大值；（3）在（2）的条件下，是不是存在实数b，使得函数g（x）=bx的图象与函数f（x）的图象恰有3个交点，假设存在，请求出实数b的取值范围；假设不存在，试说明理由．考点：利用导数求闭区间上函数的最值；函数的单调性与导数的关系；利用导数研究函数的极值．专题：综合题；压轴题．分（1）求导函数，可得f′（x）=3x2﹣2ax﹣3，利用f（x）在区间[1，+∞）上是增函数，可析：得3x2﹣2ax﹣3≥0在区间[1，+∞）上恒成立，从而可求实数a的取值范围；（2）依题意x=﹣是f（x）的一个极值点，所以，从而可得f（x）=x3﹣4x2﹣3x，利用导数确定函数的单调性与极值，从而可求f（x）在[1，4]上的最大值；（3）函数g（x）=bx的图象与函数f（x）的图象恰有3个交点，即方程x3﹣4x2﹣3x=bx 恰有3个不等实根，即方程x2﹣4x﹣3﹣b=0有两个非零不等实根，从而可求实数b的取值范围解答：解：（1）求导函数，可得f′（x）=3x2﹣2ax﹣3∵f（x）在区间[1，+∞）上是增函数，∴f′（x）≥0在区间[1，+∞）上恒成立，即3x2﹣2ax﹣3≥0在区间[1，+∞）上恒成立，则必有且f′（1）=﹣2a≥0，∴a≤0（5分）（2）依题意x=﹣是f（x）的一个极值点，∴即∴a=4，∴f（x）=x3﹣4x2﹣3x（6分）令f′（x）=3x2﹣8x﹣3=0，得则当x变化时，f′（x），f（x）的变化情况如下表：x 1 （1，3） 3 （3，4） 4 f′（x）﹣0 +f（x）﹣6 ﹣18 ﹣12 ∴f（x）在[1，4]上的最大值是f（1）=﹣6（10分）（3）函数g（x）=bx的图象与函数f（x）的图象恰有3个交点，即方程x3﹣4x2﹣3x=bx恰有3个不等实根（12分）∴x3﹣4x2﹣3x﹣bx=0恰有3个不等实根∵x=0是其中一个根，∴方程x2﹣4x﹣3﹣b=0有两个非零不等实根，∴∴b＞﹣7，且b≠﹣3（14分）点评：本题考查导数知识的运用，考查函数的单调性与最值，考查函数图象的交点问题，解题的关键是将函数g（x）=bx的图象与函数f（x）的图象恰有3个交点，转化为方程x3﹣4x2﹣3x=bx恰有3个不等实根．12．（2021•路南区校级模拟）已知函数f（x）=x3﹣（2a+1）x2+（a2+a）x．（Ⅰ）假设f（x）在x=1处取得极大值，求实数a的值；（Ⅱ）假设∀m∈R，直线y=kx+m都不是曲线y=f（x）的切线，求k的取值范围；（Ⅲ）假设a＞﹣1，求f（x）在区间[0，1]上的最大值．考点：利用导数求闭区间上函数的最值；利用导数研究函数的极值；利用导数研究曲线上某点切线方程．专题：综合题；压轴题；导数的概念及应用．分析：（Ⅰ）求导数，确定函数的单调性，利用f（x）在x=1处取得极大值，可求实数a的值；（II）求导数，根据∀m∈R，直线y=kx+m都不是曲线y=f（x）的切线，可得对x∈R成立，即使f'（x）的最小值大于k；（III）分类讨论，确定函数在区间[0，1]上的单调性，从而可求函数的最大值．解答：解：（Ⅰ）因为f'（x）=x2﹣（2a+1）x+（a2+a）=（x﹣a）[x﹣（a+1）]…（2分）令f'（x）=0，得x1=（a+1），x2=a所以f'（x），f（x）随x的变化情况如下表：x （﹣∞，a） a （a，a+1）a+1 （a+1，+∞）f'（x）+ 0 ﹣0 +f（x）极大值极小值…（4分）因为f（x）在x=1处取得极大值，所以a=1…（5分）（II）求导数可得…（6分）因为∀m∈R，直线y=kx+m都不是曲线y=f（x）的切线，所以对x∈R成立…（7分）所以只要f'（x）的最小值大于k，所以…（8分）（III）因为a＞﹣1，所以a+1＞0，当a≥1时，f'（x）≥0对x∈[0，1]成立，所以当x=1时，f（x）取得最大值…（9分）当0＜a＜1时，在x∈（0，a）时，f'（x）＞0，f（x）单调递增，在x∈（a，1）时，f'（x）＜0，f（x）单调递减，所以当x=a时，f（x）取得最大值…（10分）当a=0时，在x∈（0，1）时，f'（x）＜0，f（x）单调递减，所以当x=0时，f（x）取得最大值f（0）=0…（11分）当﹣1＜a＜0时，在x∈（0，a+1）时，f'（x）＜0，f（x）单调递减，在x∈（a+1，1）时，f'（x）＞0，f（x）单调递增，又，当时，f（x）在x=1取得最大值当时，f（x）在x=0取得最大值f（0）=0当时，f（x）在x=0，x=1处都取得最大值0．…（14分）综上所述，当a≥1或时，f（x）取得最大值；当0＜a ＜1时，f（x）取得最大值；当时，f（x）在x=0，x=1处都取得最大值0；当时，f（x）在x=0取得最大值f（0）=0．点评：本题考查导数知识的运用，考查函数的单调性与极值，考查导数的几何意义，考查分类讨论的数学思想，属于中档题．13．（2021•张家港市校级模拟）已知函数f（x）=x3+bx2+cx+d，设曲线y=f（x）在与x轴交点处的切线为y=4x﹣12，f′（x）为f（x）的导函数，知足f′（2﹣x）=f′（x）．（Ⅰ）设g（x）=x，m＞0，求函数g（x）在[0，m]上的最大值；（Ⅱ）设h（x）=lnf′（x），假设对一切x∈[0，1]，不等式h（x+1﹣t）＜h（2x+2）恒成立，求实数t的取值范围．考点：利用导数求闭区间上函数的最值；函数恒成立问题．专题：综合题；压轴题．分析：（Ⅰ）f′（x）=x2+2bx+c，由f′（2﹣x）=f′（x），解得b=﹣1．由直线y=4x﹣12与x轴的交点为（3，0），解得c=1，d=﹣3．由此能求出函数g（x）在[0，m]上的最大值．（Ⅱ）h（x）=ln（x﹣1）2=2ln|x﹣1|，则h（x+1﹣t）=2ln|x﹣t|，h（2x+2）=2ln|2x+1|，由当x∈[0，1]时，|2x+1|=2x+1，知不等式2ln|x﹣t|＜2ln|2x+1|恒成立等价于|x﹣t|＜2x+1，且x≠t恒成立，由此能求出实数t的取值范围．解答：（本小题满分14分）解：（Ⅰ）f′（x）=x2+2bx+c，∵f′（2﹣x）=f′（x），∴函数y=f′（x）的图象关于直线x=1对称，则b=﹣1．∵直线y=4x﹣12与x轴的交点为（3，0），∴f（3）=0，且f′（x）=4，即9+9b+3c+d=0，且9+6b+c=4，解得c=1，d=﹣3．则．故f′（x）=x2﹣2x+1=（x﹣1）2，g（x）=x=x|x﹣1|=，如图所示．当时，x=，根据图象得：（ⅰ）当x＜m时，g（x）最大值为m﹣m2；。

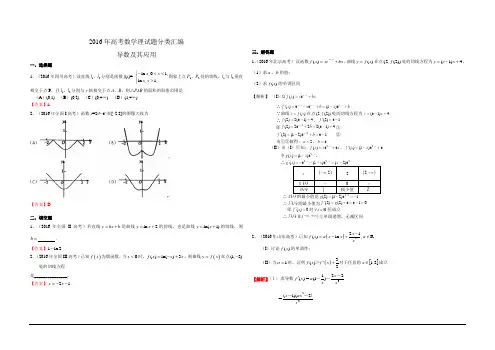
1.已知函数d x b a c bx ax x f +--++=)23()(23的图象如图所示． （I ）求d c ,的值；（II ）若函数)(x f 在2=x 处的切线方程为0113=-+y x ，求函数)(x f 的解析式； （III ）在（II ）的条件下，函数)(x f y =与m x x f y ++'=5)(31的图象有三个不同的交点，求m 的取值范围．2.已知函数)(3ln )(R a ax x a x f ∈--=． （I ）求函数)(x f 的单调区间；（II ）函数)(x f 的图象的在4=x 处切线的斜率为,23若函数]2)('[31)(23m x f x x x g ++=在区间（1，3）上不是单调函数，求m 的取值范围．3.已知函数c bx ax x x f +++=23)(的图象经过坐标原点，且在1=x 处取得极大值．（I ）求实数a 的取值范围；（II ）若方程9)32()(2+-=a x f 恰好有两个不同的根，求)(x f 的解析式； （III ）对于（II ）中的函数)(x f ，对任意R ∈βα、，求证：81|)sin 2()sin 2(|≤-βαf f ．4.已知常数0>a ，e 为自然对数的底数，函数x e x f x -=)(，x a x x g ln )(2-=． （I ）写出)(x f 的单调递增区间，并证明a e a >； （II ）讨论函数)(x g y =在区间),1(a e 上零点的个数．5.已知函数()ln(1)(1)1=---+．f x x k x（I）当1k=时，求函数()f x的最大值；（II）若函数()f x没有零点，求实数k的取值范围6.已知函数.1,ln )1(21)(2>-+-=a x a ax x x f （I ）讨论函数)(x f 的单调性； （II ）证明：若.1)()(,),,0(,,521212121->--≠+∞∈<x x x f x f x x x x a 有则对任意7.设曲线C ：()ln f x x ex =-（ 2.71828e =⋅⋅⋅），()f x '表示()f x 导函数． （I ）求函数()f x 的极值； （II ）对于曲线C 上的不同两点11(,)A x y ，22(,)B x y ，12x x <，求证：存在唯一的0x 12(,)x x ∈，使直线AB 的斜率等于0()f x '．8.定义),0(,,)1(),(+∞∈+=y x x y x F y ，（I ）令函数22()(3,log (24))f x F x x =-+，写出函数()f x 的定义域；（II ）令函数322()(1,log (1))g x F x ax bx =+++的图象为曲线C ，若存在实数b 使得曲线C 在)14(00-<<-x x 处有斜率为－8的切线，求实数a 的取值范围；（III ）当,*x y ∈N 且x y <时，求证(,)(,)F x y F y x >．9.（全国卷22）（本小题满分14分）已知函数f(x)=ln(1+x)-x,g(x)=xlnx,(i)求函数f(x)的最大值；(ii)设0<a<b,证明0<g(a)+g(b)-2g(2ba )<(b-a)ln2.10.（2009全国卷Ⅱ理）(本小题满分12分)设函数()()21f x x aIn x =++有两个极值点12x x 、，且12x x <（I ）求a 的取值范围，并讨论()f x 的单调性；（II ）证明：()21224In f x ->11.（1）已知：)0(∞+∈x ，求证xx x x 11ln 11<+<+； （2）已知：2≥∈n N n 且，求证：11211ln 13121-+++<<+++n n n 。

2016江苏高考数学压轴题（含答案）2016江苏高考压轴卷数学注意事项：1．本试卷共4页，包括填空题（第1题~第14题）、解答题（第15题~第20题）两部分．本试卷满分为160分，考试时间为120分钟．2．答题前，请务必将自己的姓名、学校、班级、学号写在答题纸的密封线内．试题的答案写在答题纸上对应题目的答案空格内．考试结束后，交回答题纸．参考公式：锥体的体积公式：V＝13Sh，其中S为锥体的底面积，h 为锥体的高．一、填空题（本大题共14小题，每小题5分，计70分．不需写出解答过程，请把答案写在题中横线上）1.若集合，，则．2.若复数（i为虚数单位）为纯虚数，则实数．3.若原点和点在直线的异侧，则的取值范围是．4.某射击选手连续射击5枪命中的环数分别为：9.7，9.9，10.1，10.2，10.1，则这组数据的方差为.5.右图是一个算法流程图，则输出的的值为．6.从2个红球，2个黄球，1个白球中随机取出两个球，则两球颜色不同的概率是.7.若且是第二象限角，则.8.正四棱锥的底面边长为，侧面积为，则它的体积为.9.已知双曲线的一条渐近线的方程为，则该双曲线的离心率为.10.不等式组所表示的区域的面积为.11.已知外接圆的半径为2，圆心为，且，，则的值等于．12.如图所示，三个边长为2的等边三角形有一条边在同一直线上，边上有10个不同的点，，…，，记（1，2，…，10），则．13.在等差数列中，首项，公差，若某学生对其中连续10项进行求和，在遗漏掉一项的情况下，求得余下9项的和为185，则此连续10项的和为．14.设关于的实系数不等式对任意恒成立，则．二、解答题15.（本小题满分14分）（本大题满分14分）如图，在△中，点在边上，，，，．（1）求的长；（2）求△的面积．16.（本小题满分14分）如图，在四棱锥P－ABCD中，底面ABCD为平行四边形，E 为侧棱PA的中点．（1）求证：PC//平面BDE；（2）若PC⊥PA，PD＝AD，求证：平面BDE⊥平面PAB．17.（本大题满分14分）如图，，是海岸线，上的两个码头，海中小岛有码头到海岸线，的距离分别为，．测得，．以点为坐标原点，射线为轴的正半轴，建立如图所示的直角坐标系．一艘游轮以小时的平均速度在水上旅游线航行（将航线看作直线，码头在第一象限，航线经过）．（1）问游轮自码头沿方向开往码头共需多少分钟？（2）海中有一处景点（设点在平面内，，且），游轮无法靠近．求游轮在水上旅游线航行时离景点最近的点的坐标．18.（本大题满分16分）已知椭圆的右焦点为，且点在椭圆上．（1）求椭圆的标准方程；（2）过椭圆上异于其顶点的任意一点作圆的两条切线，切点分别为，（，不在坐标轴上），若直线在轴，轴上的截距分别为，，证明：为定值；（3）若，是椭圆上不同的两点，轴，圆过，，且椭圆上任意一点都不在圆内，则称圆为该椭圆的一个内切圆．试问：椭圆是否存在过左焦点的内切圆？若存在，求出圆心的坐标；若不存在，请说明理由．19.已知函数．（1）当时，求的单调减区间；（2）若存在m0，方程恰好有一个正根和一个负根，求实数的最大值．20.（本大题满分16分）已知数列的通项公式为，其中，，．（1）试写出一组，的值，使得数列中的各项均为正数；（2）若，，数列满足，且对任意的()，均有，写出所有满足条件的的值；（3）若，数列满足，其前项和为，且使(，，)的和有且仅有4组，，，…，中有至少个连续项的值相等，其它项的值均不相等，求，的最小值．数学附加题注意事项：1．附加题供选修物理的考生使用．2．本试卷共40分，考试时间30分钟．3．答题前，考生务必将自己的姓名、学校、班级、学号写在答题纸的密封线内．试题的答案写在答题纸上对应题目的答案空格内．考试结束后，交回答题纸．21．【选做题】在A、B、C、D四小题中只能选做2题，每小题10分，共计20分．请在答卷纸指定区域内作答．解答应写出文字说明、证明过程或演算步骤．A．选修4—1：几何证明选讲（本小题满分10分）如图，在Rt△ABC中，AB＝BC．以AB为直径的⊙O交AC 于点D，过D作DE&#61534;BC，垂足为E，连接AE交⊙O 于点F．求证：BE&#61655;CE＝EF&#61655;EA．B．[选修4—2：矩阵与变换]（本小题满分10分）已知矩阵，求矩阵的特征值和特征向量．C．选修4—4：坐标系与参数方程（本小题满分10分）在极坐标系中，曲线C的极坐标方程为，以极点为坐标原点，极轴为轴的正半轴建立平面直角坐标系，直线的参数方程为(为参数)，求直线被曲线所截得的弦长．D．选修4—5：不等式选讲（本小题满分10分）设均为正数，且，求证：．【必做题】第22题、第23题，每题10分，共计20分．请在答卷卡指定区域内作答．解答应写出文字说明、证明过程或演算步骤．22．（本小题满分10分）甲、乙两人投篮命中的概率分别为23与12，各自相互独立．现两人做投篮游戏，共比赛3局，每局每人各投一球．（1）求比赛结束后甲的进球数比乙的进球数多1个的概率；（2）设ξ表示比赛结束后甲、乙两人进球数的差的绝对值，求ξ的概率分布和数学期望E(ξ)．23.（本小题满分10分）若存在个不同的正整数，对任意，都有，则称这个不同的正整数为“个好数”．（1）请分别对，构造一组“好数”；（2）证明：对任意正整数，均存在“个好数”．答案与提示一、填空题1.2.3.4.0.0325.6.457.8.49.510.161.1212.18013.2001 4.9解析：11.如图，取BC中点D，联结AD，则，又因为，所以O为BC的中点，因为，所以是等边三角形，，因为ABC外接圆的半径为2，所以，，所以，故答案为12.12.延长，，则，又，所以，即，则，则，故答案为180.13.等差数列中的连续10项为，遗漏的项为且则，化简得，所以，，则连续10项的和为，故答案为200.14.令，在同一坐标系下作出两函数的图像：①如图(1)，当的在轴上方时，，，但对却不恒成立；②如图(2)，，令得，令得，要使得不等式在上恒成立，只需，，.综上，，故答案为9．二、解答题15.解：（1）在△中，因为，设，则．在△中，因为，，，所以．在△中，因为，，，由余弦定理得．因为，所以，即．解得．所以的长为5.（2）由（Ⅰ）求得，．所以，从而．所以．16.证明：（1）连结AC，交BD于O，连结OE．因为ABCD是平行四边形，所以OA＝OC．因为E为侧棱PA的中点，所以OE∥PC．因为PC/&#61644;平面BDE，OE&#61644;平面BDE，所以PC//平面BDE．（2）因为E为PA中点，PD＝AD，所以PA⊥DE．因为PC⊥PA，OE∥PC，所以PA⊥OE．因为OE&#61644;平面BDE，DE&#61644;平面BDE，OE∩DE ＝E，所以PA⊥平面BDE．因为PA&#61644;平面PAB，所以平面BDE⊥平面PAB．17.解：（1）由已知得，直线的方程为，设，由及图得，，直线的方程为，即，由得即，，即水上旅游线的长为．游轮在水上旅游线自码头沿方向开往码头共航行30分钟时间．（2）解法一：点到直线的垂直距离最近，则垂足为.由（1）知直线的方程为，，则直线的方程为，所以解直线和直线的方程组，得点的坐标为（1，5）．解法2：设游轮在线段上的点处，则，，．，，，当时，离景点最近，代入得离景点最近的点的坐标为(1，5).18.解：（1）由题意得，，所以又点在椭圆上，所以解得所以椭圆的标准方程为（2）由（1）知，设点则直线的方程为①直线的方程为②把点的坐标代入①②得所以直线的方程为令得令得所以又点在椭圆上，所以即为定值．（3）由椭圆的对称性，不妨设由题意知，点在轴上，设点则圆的方程为由椭圆的内切圆的定义知，椭圆上的点到点的距离的最小值是设点是椭圆上任意一点，则当时，最小，所以①假设椭圆存在过左焦点的内切圆，则②又点在椭圆上，所以③由①②③得或当时，不合题意，舍去，且经验证，符合题意. 综上，椭圆存在过左焦点的内切圆，圆心的坐标是19.解：（1）当时，当时，，由，解得，所以的单调减区间为，当时，，由，解得或，所以的单调减区间为，综上：的单调减区间为，．（2）当时，，则，令，得或，x+0－0+↗极大值↘极小值↗所以有极大值，极小值，当时，同（1）的讨论可得，在上增，在上减，在上增，在上减，在上增，且函数有两个极大值点，，，且当时，，所以若方程恰好有正根，则（否则至少有二个正根）．又方程恰好有一个负根，则．令，则，所以在时单调减，即，等号当且仅当时取到．所以，等号当且仅当时取到．且此时，即，所以要使方程恰好有一个正根和一个负根，的最大值为．20.解：（1）、（答案不唯一）．（2）由题设，．当，时，均单调递增，不合题意，因此，．当时，对于，当时，单调递减；当时，单调递增．由题设，有，．于是由及，可解得．因此，的值为7，8，9，10，11．（4）因为，且，所以因为（，，），所以、．于是由，可得，进一步得，此时，的四个值为，，，，因此，的最小值为．又，，…，中有至少个连续项的值相等，其它项的值均不相等，不妨设，于是有，因为当时，，所以，因此，，即的最小值为．21．【选做题】A．选修4—1：几何证明选讲证明：连接BD．因为AB为直径，所以BD⊥AC．因为AB＝BC，所以AD＝DC．因为DE&#61534;BC，AB&#61534;BC，所以DE∥AB，所以CE＝EB．因为AB是直径，AB&#61534;BC，所以BC是圆O的切线，所以BE2＝EF&#61655;EA，即BE&#61655;CE＝EF&#61655;EA．B．选修4—2：矩阵与变换解：矩阵的特征多项式为，由，解得，．当时，特征方程组为故属于特征值的一个特征向量.当时，特征方程组为故属于特征值的一个特征向量．C．选修4—4：坐标系与参数方程解：曲线C的直角坐标方程为，圆心为，半径为，直线的直角坐标方程为，所以圆心到直线的距离为，所以弦长．D．选修4—5：不等式选讲因为x＞0，y＞0，x－y＞0，，=，所以．22．（本小题满分10分）解：（1）比赛结束后甲的进球数比乙的进球数多1个有以下几种情况：甲进1球，乙进0球；甲进2球，乙进1球；甲进3球，乙进2球．所以比赛结束后甲的进球数比乙的进球数多1个的概率P＝C1323(13)2(12)3＋C23(23)2(13)C13(12)3＋C33(23)3C23(12)3＝1136．（2）ξ的取值为0，1，2，3，所以ξ的概率分布列为ξ0123P7241124524124所以数学期望E(ξ)＝0×724＋1×1124＋2×524＋3×124＝1．分23.（本小题满分10分）解：（1）当时，取数，，因为，当时，取数，，，则，，，即，，可构成三个好数．（2）证：①由（1）知当时均存在，②假设命题当时，存在个不同的正整数，其中，使得对任意，都有成立，则当时，构造个数，，（*）其中，若在（*）中取到的是和，则，所以成立，若取到的是和，且，则，由归纳假设得，又，所以是A的一个因子，即，所以，所以当时也成立．所以对任意正整数，均存在“个好数”.。

高考数学压轴题100题汇总(含答案)1. 设函数f(x) = x^3 3x + 1，求f(x)的极值点和极值。

答案：f(x)的极值点为x = 1和x = 1，极值分别为f(1) = 1和f(1) = 3。

2. 已知等差数列{an}的前n项和为Sn = n^2 + n，求该数列的通项公式。

答案：an = 2n + 1。

3. 已知三角形ABC中，AB = AC = 5，BC = 8，求三角形ABC的面积。

答案：三角形ABC的面积为12。

4. 设直线y = kx + b与圆x^2 + y^2 = 1相切，求k和b的值。

答案：k = ±√3/3，b = ±√6/3。

5. 已知函数f(x) = log2(x^2 + 1)，求f(x)的导数。

答案：f'(x) = 2x/(x^2 + 1)ln2。

6. 已知向量a = (2, 3)，向量b = (1, 4)，求向量a和向量b的夹角。

答案：向量a和向量b的夹角为arccos(1/√5)。

7. 已知矩阵A = [1 2; 3 4]，求矩阵A的逆矩阵。

答案：矩阵A的逆矩阵为[4 2; 3 1]。

8. 已知函数f(x) = x^3 6x^2 + 9x + 1，求f(x)的零点。

答案：f(x)的零点为x = 1和x = 3。

9. 已知函数f(x) = sin(x) cos(x)，求f(x)在区间[0, π/2]上的最大值。

答案：f(x)在区间[0, π/2]上的最大值为√2。

10. 已知函数f(x) = x^2 + 4x + 4，求f(x)的顶点坐标。

答案：f(x)的顶点坐标为(2, 0)。

高考数学压轴题100题汇总(含答案)11. 已知函数f(x) = e^x 2x，求f(x)的导数。

答案：f'(x) = e^x 2。

12. 已知函数f(x) = x^2 4x + 4，求f(x)的极值点和极值。

答案：f(x)的极值点为x = 2，极值为f(2) = 0。

2016年全国各地高考数学试题及解答分类汇编大全（04导数及其应用）一、选择题1.（2016全国Ⅰ文）若函数1()sin 2sin 3f x x -x a x =+在(),-∞+∞单调递增,则a 的取值范围是（ ）（A ）[]1,1- （B ）11,3⎡⎤-⎢⎥⎣⎦（C ）11,33⎡⎤-⎢⎥⎣⎦ （D ）11,3⎡⎤--⎢⎥⎣⎦ 【答案】C考点：三角变换及导数的应用【名师点睛】本题把导数与三角函数结合在一起进行考查,有所创新,求解关键是把函数单调性转化为不等式恒成立,再进一步转化为二次函数在闭区间上的最值问题,注意与三角函数值域或最值有关的问题,要注意弦函数的有界性.2.（2016山东文、理）若函数()y f x =的图象上存在两点，使得函数的图象在这两点处的切线互相垂直，则称()y f x =具有T 性质.下列函数中具有T 性质的是（ ） （A ）sin y x = （B ）ln y x = （C ）e x y =（D ）3y x =【答案】A 【解析】试题分析：由函数的图象在两点处的切线互相垂直可知，存在两点处的切线斜率的积，即导函数值的乘积为负一.当sin y x =时，cos y x '=，有co s0c o s 1π⋅=-，所以在函数sin y x =图象存在两点0,x x π==使条件成立，故A 正确；函数3ln ,,x y x y e y x ===的导数值均非负，不符合题意，故选A.考点：1.导数的计算；2.导数的几何意义.【名师点睛】本题主要考查导数的计算、导数的几何意义及两直线的位置关系，本题给出常见的三角函数、指数函数、对数函数、幂函数，突出了高考命题注重基础的原则.解答本题，关键在于将直线的位置关系与直线的斜率、切点处的导数值相联系，使问题加以转化，利用特殊化思想解题，降低难度.本题能较好的考查考生分析问题解决问题的能力、基本计算能力及转化与化归思想的应用等.3. （2016四川文）已知a 函数3()12f x x x =-的极小值点，则a =（ ） (A)-4 (B) -2 (C)4 (D)2 【答案】D【解析】试题分析：()()()2312322f x x x x '=-=+-，令()0f x '=得2x =-或2x =，易得()f x 在()2,2-上单调递减，在()2,+∞上单调递增，故()f x 极小值为()2f ，由已知得2a =，故选D.考点：函数导数与极值.【名师点睛】本题考查函数的极值．在可导函数中函数的极值点0x 是方程'()0f x =的解，但0x 是极大值点还是极小值点，需要通过这点两边的导数的正负性来判断，在0x 附近，如果0x x <时，'()0f x <，0x x >时'()0f x >，则0x 是极小值点，如果0x x <时，'()0f x >，0x x >时，'()0f x <，则0x 是极大值点，4.（2016四川文、理）设直线l 1，l 2分别是函数f (x )= ln ,01,ln ,1,x x x x -<<⎧⎨>⎩图象上点P 1，P 2处的切线，l 1与l 2垂直相交于点P ，且l 1，l 2分别与y 轴相交于点A ，B ，则△P AB 的面积的取值范围是（ ） （A ）(0,1) （B ）(0,2) （C ）(0,+∞) （D ）(1,+∞) 【答案】A考点：1.导数的几何意义；2.两直线垂直关系；3.直线方程的应用；4.三角形面积取值范围. 【名师点睛】本题首先考查导数的几何意义，其次考查最值问题，解题时可设出切点坐标，利用切线垂直求出这两点的关系，同时得出切线方程，从而得点,A B 坐标，由两直线相交得出P 点坐标，从而求得面积，题中把面积用1x 表示后，可得它的取值范围．解决本题可以是根据题意按部就班一步一步解得结论．这也是我们解决问题的一种基本方法，朴实而基础，简单而实用．二、填空1.（2016全国Ⅱ理）若直线y kx b =+是曲线ln 2y x =+的切线，也是曲线ln(1)y x =+的切线，则b = ． 【答案】1ln 2-考点： 导数的几何意义.【名师点睛】函数f (x )在点x 0处的导数f ′(x 0)的几何意义是在曲线y ＝f (x )上点P (x 0，y 0)处的切线的斜率．相应地，切线方程为y －y 0＝f ′(x 0)(x －x 0)．注意：求曲线切线时，要分清在点P 处的切线与过P 点的切线的不同．2.（2016全国Ⅲ文）已知()f x 为偶函数，当0x ≤ 时，1()x f x e x --=-，则曲线()y f x =在点(1,2)处的切线方程式_____________________________. 【答案】2y x =考点：1、函数的奇偶性；2、解析式；3、导数的几何意义．【知识拓展】本题题型可归纳为“已知当0x >时，函数()y f x =，则当0x <时，求函数的解析式”．有如下结论：若函数()f x 为偶函数，则当0x <时，函数的解析式为()y f x =-；若()f x 为奇函数，则函数的解析式为()y f x =--．3.（2016全国Ⅲ理）已知()f x 为偶函数，当0x <时，()ln()3f x x x =-+，则曲线()y f x =在点(1,3)-处的切线方程是_______________．【答案】21y x =--【解析】试题分析：当0x >时，0x -<，则()ln 3f x x x -=-．又因为()f x 为偶函数，所以()()ln 3f x f x x x =-=-，所以1()3f x x '=-，则切线斜率为(1)2f '=-，所以切线方程为32(1)y x +=--，即21y x =--．考点：1、函数的奇偶性与解析式；2、导数的几何意义．【知识拓展】本题题型可归纳为“已知当0x >时，函数()y f x =，则当0x <时，求函数的解析式”．有如下结论：若函数()f x 为偶函数，则当0x <时，函数的解析式为()y f x =-；若()f x 为奇函数，则函数的解析式为()y f x =--．4.（2016天津文）已知函数()(2+1),()x f x x e f x '=为()f x 的导函数，则(0)f '的值为__________. 【答案】3 【解析】试题分析：()(2+3),(0) 3.x f x x e f ''=∴=考点：导数【名师点睛】求函数的导数的方法(1)连乘积的形式：先展开化为多项式的形式，再求导； (2)根式形式：先化为分数指数幂，再求导；(3)复杂公式：通过分子上凑分母，化为简单分式的和、差，再求导； (4)复合函数：确定复合关系，由外向内逐层求导；(5)不能直接求导的：适当恒等变形，转化为能求导的形式再求导．5. （2016浙江理）如图，在△ABC 中，AB =BC =2，∠ABC =120°.若平面ABC 外的点P 和线段AC 上的点D ，满足PD =DA ，PB =BA ，则四面体PBCD 的体积的最大值是.【答案】12由余弦定理可得222cos 2PD PB BD BPD PD PB +-∠===⋅， 所以30BPD ∠=.EDCBA P过P 作直线BD 的垂线，垂足为O .设PO d = 则11sin 22PBD S BD d PD PB BPD ∆=⨯=⋅∠，12sin 302d x =⋅，解得d =.而BCD ∆的面积111sin )2sin 30)222S CD BC BCD x x =⋅∠=⋅=.（2x ≤|x x ==故x =此时，V =21414()66t t t t-=⋅=-. 由（1）可知，函数()V t 在(1,2]单调递减，故141()(1)(1)612V t V <=-=. 综上，四面体PBCD 的体积的最大值为12. 考点：1、空间几何体的体积；2、用导数研究函数的最值．【思路点睛】先根据已知条件求出四面体的体积，再对x 的取值范围讨论，用导数研究函数的单调性，进而可得四面体的体积的最大值．三、解答题1. （2016北京文）设函数()32.f x x ax bx c =+++（I ）求曲线().y f x =在点()()0,0f 处的切线方程；（II ）设4a b ==，若函数()f x 有三个不同零点，求c 的取值范围；（III ）求证：230a b -＞是().f x 有三个不同零点的必要而不充分条件.【答案】（Ⅰ）y bx c =+;（Ⅱ）320,27c ⎛⎫∈ ⎪⎝⎭;（III ）见解析.（II ）当4a b ==时，()3244f x x x x c =+++，所以()2384f x x x '=++．令()0f x '=，得23840x x ++=，解得2x =-或23x =-． ()f x 与()f x '在区间(),-∞+∞上的情况如下：所以，当0c >且027c -<时，存在()14,2x ∈--，22,3x ⎛⎫∈-- ⎪⎝⎭， 32,03x ⎛⎫∈- ⎪⎝⎭，使得()()()1230f x f x f x ===．考点：利用导数研究曲线的切线；函数的零点 【名师点睛】1．证明不等式问题可通过作差或作商构造函数，然后用导数证明． 2．求参数范围问题的常用方法：(1)分离变量；(2)运用最值．3．方程根的问题：可化为研究相应函数的图象，而图象又归结为极值点和单调区间的讨论． 4．高考中一些不等式的证明需要通过构造函数，转化为利用导数研究函数的单调性或求最值，从而证得不等式，而如何根据不等式的结构特征构造一个可导函数是用导数证明不等式2. （2016北京理）设函数()a x f x xe bx -=+，曲线()y f x =在点(2,(2))f 处的切线方程为(1)4y e x =-+， （1）求a ，b 的值； （2）求()f x 的单调区间.【答案】（Ⅰ）2a =，b e =；（2）)(x f 的单调递增区间为(,)-∞+∞.从而),(,0)(+∞-∞∈>x x g .综上可知，0)(>'x f ，),(+∞-∞∈x ，故)(x f 的单调递增区间为),(+∞-∞. 考点：导数的应用.【名师点睛】用导数判断函数的单调性时，首先应确定函数的定义域，然后在函数的定义域内，通过讨论导数的符号，来判断函数的单调区间．在对函数划分单调区间时，除了必须确定使导数等于0的点外，还要注意定义区间内的间断点．3.（2016全国Ⅰ文）已知函数()()()22e 1xf x x a x =-+-．(I)讨论()f x 的单调性；(II)若()f x 有两个零点,求a 的取值范围. 【答案】见解析(II) ()0,+∞【解析】试题分析：(I)先求得()()()'12.xf x x e a =-+再根据1,0,2a 的大小进行分类确定()f x 的单调性；(II)借助第一问的结论,通过分类讨论函数单调性,确定零点个数,从而可得a 的取值范围为()0,+∞.试题解析： (I)()()()()()'12112.x xf x x e a x x e a =-+-=-+(i)设0a ≥,则当(),1x ∈-∞时,()'0f x <；当()1,x ∈+∞时,()'0f x >. 所以在(),1-∞单调递减,在()1,+∞单调递增. (ii)设0a <,由()'0f x =得x =1或x =ln(-2a). ①若2e a =-,则()()()'1xf x x e e =--,所以()f x 在(),-∞+∞单调递增. ②若2ea >-,则ln(-2a)<1,故当()()(),ln 21,x a ∈-∞-+∞时,()'0f x >；当()()ln 2,1x a ∈-时,()'0f x <,所以()f x 在()()(),ln 2,1,a -∞-+∞单调递增,在()()ln 2,1a -单调递减.③若2ea <-,则()21ln a ->,故当()()(),1ln 2,x a ∈-∞-+∞时,()'0f x >,当()()1,ln 2x a ∈-时,()'0f x <,所以()f x 在()()(),1,ln 2,a -∞-+∞单调递增,在()()1,ln 2a -单调递减.考点：函数单调性,导数应用【名师点睛】本题第一问是用导数研究函数单调性,对含有参数的函数单调性的确定,通常要根据参数进行分类讨论,要注意分类讨论的原则：互斥、无漏、最简；第二问是求参数取值范围,由于这类问题常涉及到导数、函数、不等式等知识,越来越受到高考命题者的青睐,解决此类问题的思路是构造适当的函数,利用导数研究函数的单调性或极值破解.4. （2016江苏）已知函数()(0,0,1,1)x x f x a b a b a b =+>>≠≠.设12,2a b ==. （1）求方程()2f x =的根;（2）若对任意x R ∈,不等式(2)f()6f x m x ≥-恒成立，求实数m 的最大值；（3）若01,1a b <<＞，函数()()2g x f x =-有且只有1个零点，求ab 的值。