金融工程案例分析(同济大学)

数学与应用数学专业培养方案
数学与应用数学专业培养方案
一、专业历史沿革
同济大学数学系始建于1945年，程其襄、杨武之、朱言钧、樊映川、张国隆、陆振邦等一大批知名专家曾在此任教。

解放后，几经国家调整，本系时有间断。

于1980年，（应用）数学系正式恢复，陆续引进一批国内外培养的具有博士学位的青年教师，原有师资队伍的结构有了变化，充实了教学与科研力量。

从20世纪90年代开始，学校又先后引进国内知名数学家、博土生导师陈志华、陆洪文、姜礼尚教授等来数学系工作，教学和科研整体实力有很大提高。

数学与应用数学专业在建系后就已设立，文革期间中断了招生，1978年恢复高考后数学与应用数学专业也随之恢复了招生。

至今本专业已培养了毕业生3000多人，数学系的学生遍布国内外的许多国家,有的继续从事做数学的教学及科学研究工作，有的在大型国企和外企，特别是银行、金融、计算机等行业工作，很多毕业生已成为杰出科学家和行业精英。

二、学制与授予学位
四年制本科。

本专业所授学位为理学学士。

三、基本学分要求
四、专业培养目标
本专业培养具备扎实数学基础，并具备运用数学知识和计算机解决实际问题的能力，受到科学研究的初步训练，能在科技、教育、信息、金融保险等部门及企事业单位从事研究、教学、管理及计算机软件开发等具有国际视野的复合型高级专门人才，或能继续在国内外攻读研究生学位的高级专门人才。

五、专业培养标准
表 1 ：专业标准。

金融工程案例之套利分析在对这三个案例做完逐个分析之后我们不难看出，三个案例中套利的总体思路是十分相似的，尤其是前两个案例都是利用两个内部收益率较高的债券组合成与另一个较低内部收益率的债券具有相同现金流的套利组合，再利用低买高卖最终实现套利的目的。

至于可口可乐公司安全债务认购凭证这一案例中则是利用了在债券回购日之前提前转化为对购买者有利的另一种债券。

下面就是对这三个案例套利的具体的分析计算。

在RJR纳斯比斯克控股资本公司一案中，RJR纳比斯克发行了三种债券分别是信用债券13.5%、贴息信用债券、信用债券15%PIK,通过现金流分析及利用excel计算出而这三种债券的内部收益率分别为6.6353%、8.9178%、10.1194%，易见信用债券13.5%的价值明显被低估,可以通过买卖一个债券组合来获利。

我们有两种组合可以选择：一是利用借助内部收益率为4.4880%的国债STRIPS构建{信用债券15%PIK、国债STRIPS}；另一种则是构建{贴息信用债券、国债STRIPS }于是这里我们又面临一个问题，到底以何种方式进行套利。

但是考虑到15%PIK信用债券在1994年之前公司可以选择以现金还是以PIK债券形式支付利息。

1994年5月15日之后，公司才以每半年现金支付利息。

考虑到公司总是希望以PIK债券形式来支付利息的，这样投资者可能就会面临债券价格下降和流动性的问题。

所以如果选择套利，可以选择第二种组合投资方法。

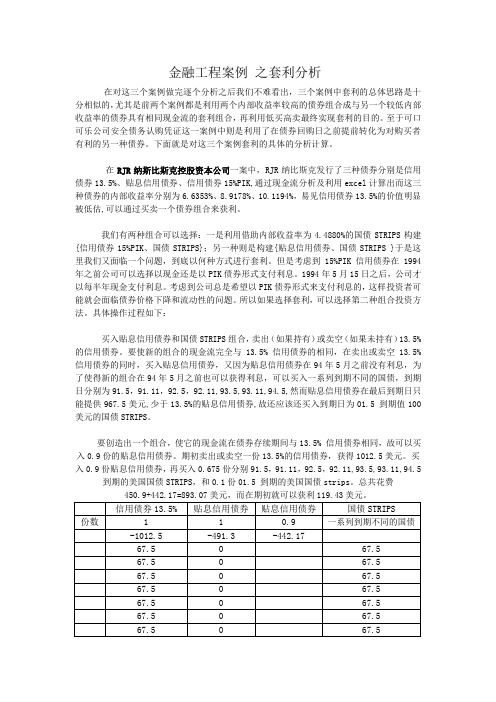
具体操作过程如下：买入贴息信用债券和国债STRIPS组合，卖出（如果持有）或卖空（如果未持有）13.5%的信用债券。

要使新的组合的现金流完全与13.5% 信用债券的相同，在卖出或卖空13.5%信用债券的同时，买入贴息信用债券，又因为贴息信用债券在94年5月之前没有利息，为了使得新的组合在94年5月之前也可以获得利息，可以买入一系列到期不同的国债，到期日分别为91.5，91.11，92.5，92.11,93.5,93.11,94.5,然而贴息信用债券在最后到期日只能提供967.5美元,少于13.5%的贴息信用债券,故还应该还买入到期日为01.5 到期值100美元的国债STRIPS。

金融数学课程体系、教材建设及人才培养的探索摘要：针对国内金融数学教学的实际情况，本文从金融数学课程的指导思想、课程体系的建立、教材建设、人才培养、科研与教学的良性互动等几方面阐述了近几年的教学探索与实践，强调数学建模与数值计算在解决实际金融问题中的重要性。

并将金融数学的教学改革总结为：以人才培养为目标、以教学改革为指导、以教材创新为核心、以科学研究为基础。

以适应国内快速发展的金融行业对金融数学人才的要求。

关键词：金融数学；教材建设；人才培养一、课程改革的指导思想学习金融数学的根本目的在于应用数学工具去解决金融业界提出的有关风险管理、风险度量、衍生产品定价以及投资效益优化等各种问题。

这里应用是目的，建模是关键，随机分析与偏微分方程是基础，计算数学是工具。

根据我们多年来的教学实践和对人才市场需求的了解，为了全面提升学生学习金融数学的积极性，提高学生解决实际问题的能力，适应金融业界对金融工程和风险管理人才的需要，要着重培养学生的数学建模能力和数值计算的能力。

数学建模就是“建桥”，把金融实际与数学科学联系起来，把金融问题转化为数学问题。

为人们应用数学方法去解决实际问题提供了前提。

因此我们认为建模是解决金融问题的关键和起始点。

为了培养学生具有这方面的能力，应该在加强学生对现代数学方法的学习和运用，提高数学基本功的同时，必须要逐步加深学生对现代金融市场基本概念的理解，以提高对金融实际的“感觉”和直观能力。

数值计算能力就是利用计算机解决金融实际问题的能力。

众所周知，由于大型计算机的出现，使得海量数据的处理和实际问题的数值模拟成为可能。

利用计算机解决实际金融问题已成为不争的事实。

随机算法与确定性算法在金融问题中得到了广泛的应用。

学生是否具备这方面的素质已愈来愈成为实际部门招聘人才的一个重要考核标准。

我们感到“金融数学的课程体系”的改革和建设应该围绕这两个能力的培养来进行。

为此我们构建了一个“从原理一方法一应用(毕业论文)”的金融数学课程体系。

金融工程案例分析金融工程是指利用数学、统计学和计算机科学等技术手段，对金融产品、金融市场和金融机构进行分析、设计和管理的学科领域。

金融工程的发展，为金融市场的创新和金融产品的多样化提供了技术支持，也为风险管理和资产定价提供了新的思路和方法。

本文将通过一个具体的金融工程案例，来分析金融工程在实际应用中的作用和意义。

案例背景。

某公司计划发行一款新的金融衍生产品，以对冲市场波动风险。

该产品的设计需要考虑到市场情况、利率变动、资产价格等多种因素，因此需要进行金融工程分析和定价。

分析过程。

首先，我们需要对市场情况进行调研和分析。

通过收集历史数据和市场预测，我们可以对市场的波动情况和未来走势有一个大致的了解。

其次，需要对利率变动进行模拟和预测。

利率的变动对金融产品的定价和风险管理有着重要影响，因此需要对利率进行多种情景下的模拟，以确定产品的敏感度和风险暴露。

再者，需要对资产价格进行建模和分析。

不同类型的资产价格波动对产品的风险敞口有着不同的影响，因此需要对资产价格进行多种情景下的模拟和分析。

定价和风险管理。

通过以上的分析，我们可以得到产品的风险敞口和预期收益。

在实际定价过程中，需要考虑到市场的流动性、投资者的需求和产品的竞争情况。

同时，也需要对产品的风险进行有效的管理，以确保投资者的利益和产品的稳健性。

在这个过程中，金融工程提供了多种定价模型和风险管理工具，可以帮助我们更好地进行产品设计和定价。

结论。

通过以上案例分析，我们可以看到金融工程在金融产品设计和风险管理中的重要作用。

金融工程不仅提供了多种定价和风险管理工具，也为金融创新和市场发展提供了技术支持。

在未来，随着金融市场的不断发展和金融产品的不断创新，金融工程将继续发挥重要作用，为金融行业的稳健发展提供支持和保障。

数学与应用数学专业培养方案一、专业历史沿革同济大学数学系始建于1945年，程其襄、杨武之、朱言钧、樊映川、张国隆、陆振邦等一大批知名专家曾在此任教。

解放后，几经国家调整，本系时有间断。

于1980年，（应用）数学系正式恢复，陆续引进一批国内外培养的具有博士学位的青年教师，原有师资队伍的结构有了变化，充实了教学与科研力量。

从20世纪90年代开始，学校又先后引进国内知名数学家、博土生导师陈志华、陆洪文、姜礼尚教授等来数学系工作，教学和科研整体实力有很大提高。

数学与应用数学专业在建系后就已设立，文革期间中断了招生，1978年恢复高考后数学与应用数学专业也随之恢复了招生。

至今本专业已培养了毕业生3000多人，数学系的学生遍布国内外的许多国家,有的继续从事做数学的教学及科学研究工作，有的在大型国企和外企，特别是银行、金融、计算机等行业工作，很多毕业生已成为杰出科学家和行业精英。

二、学制与授予学位四年制本科。

本专业所授学位为理学学士。

三、四、专业培养目标本专业培养具备扎实数学基础，并具备运用数学知识和计算机解决实际问题的能力，受到科学研究的初步训练，能在科技、教育、信息、金融保险等部门及企事业单位从事研究、教学、管理及计算机软件开发等具有国际视野的复合型高级专门人才，或能继续在国内外攻读研究生学位的高级专门人才。

五、专业培养标准座来增强，也鼓励学生与国外院校进行交流。

六、主干学科数学。

七、核心课程数学分析、高等代数、解析几何、常微分方程、复变函数、实变函数、概率论(理)、数值分析(理)、数理方程(理)等。

八、教学安排一览表见附表一。

九、实践环节安排表见附表二。

十、课外安排一览表见附表三。

十一、有关说明1. 公共基础课中的有3门计算机课程，其中在硬件技术基础、数据库技术基础、多媒体技术基础、Web技术基础和软件开发技术基础5门课程中应至少选修1门。

2.培养方案中打*的课程为研究生阶段设置的课程，供要求较高的学生选修。