第2章非线性方程求解
- 格式:pdf
- 大小:298.46 KB
- 文档页数:23


第2章 非线性方程的求根方法2.1 二分法设()0f x =在区间[,]a b 中只有一个根*x ,且满足()()0f a f b <,则二分法求根过程为: 记0[,]I a b =,取0I 的中点00.5()x a b =+,若0()0f x =,则*0x x =; 若0()()0f x f a <,则*0[,]x a x ∈,取10[,]I a x =; 若0()()0f x f a >,则*0[,]x x b ∈,取10[,]I x b=. 记111[,]I a b =,取1I 的中点1110.5()x a b =+,若1()0f x =,则*1x x =;若11()()0f x f a <,则*11[,]x a x ∈,取211[,]I a x =;若11()()0f x f a >,则*11[,]x x b ∈,取211[,]I x b =. 记222[,]I a b =⋅⋅⋅这样获得近似根序列01,,,,,k x x x ⋅⋅⋅⋅⋅⋅满足于是当k →∞时,由11()02k b a +-→得到*k x x →.二分法算法简单,收敛,但收敛速度较慢.2.2 简单迭代法将方程()0f x =等价变形为()x x ϕ=,获得 迭代计算公式1()k k x x ϕ+=取定一个初值0x ,由迭代公式算出数列()() ,,1201x x x x ϕϕ==,若*lim k k x x →∞=,则足够靠后的k x 可作为根的近似值.由上述得出{}k x 称为迭代数列,函数()x ϕ为迭代函数,如上求根方法称为简单迭代法.对根*x ,有**()x x ϕ=,点*x 称为()x ϕ的不动点,称方程()x x ϕ=为不动点方程.例1 求方程01)(3=--=x x x f 在5.10=x 附近的根.定理1 设迭代函数()[,]x C a b ϕ∈满足条件 1.当[,]x a b ∈时,有()[,]x a b ϕ∈;2.存在正常数1L <,使对任意 12,[,]x x a b ∈都有1212()()x x L x x ϕϕ∣-∣≤∣-∣则()x ϕ在[,]a b 中有唯一的不动点*x ,迭代公式1()k k x x ϕ+=对任取0[,]x a b ∈,产生的数列{}k x 都收敛于*x .证明 作辅助函数()()x x x ψϕ=-显然()[,]x C a b ψ∈.由条件1知()()0a b ψψ≤由中值定理,至少存在一个[,]a b ξ∈,使()0ψξ=,即()ξϕξ=,这说明()x ϕ在[,]a b 上有不动点ξ. 如果()x ϕ在[,]a b 上还有一个不动点η,有()ηϕη=,利用条件2,有()()L ξηϕξϕηξηξη∣-∣=∣-∣≤∣-∣<∣-∣矛盾,这就证明了满足定理条件的()x ϕ在[,]a b 中有唯一的不动点,记为*x .由*x 是不动点、迭代格式及条件2,有***112**20()()k k k k k x x x x L x x L x x L x x ϕϕ---∣-∣=∣-∣≤∣-∣≤∣-∣≤≤∣-∣注意到01L <<,在上式中令k→∞,可得0kL →,有 *lim 0kk x x →∞∣-∣=,因而有 *lim k k x x →∞=定理得证.定理2 设定理1的条件成立,则有如下误差估计式证明 只证1.由迭代公式和定理2.1的条件,有()1k k k k x x x x ϕ+∣-∣=-**()()()k k x x x x ϕϕϕ=∣-+-∣ ****()()()()k k k k x x x x x x x x ϕϕϕϕ=-+-≥---***L L)k k k x x x x x x ≥∣-∣-∣-∣=(1-∣-∣因为01L <<,所以有*111k k k x x x x L+-≤--另一方面111()()k k k k k k x x x x L x x ϕϕ+--∣-∣=∣-∣≤∣-∣代入上式得结论1.定理2.1的条件2对任意12,[,]x x a b ∈,存在正常数1L <满足1212()()x x L x x ϕϕ∣-∣≤∣-∣不易使用。
第二章 方程求根在许多实际问题中,常常会遇到方程f(x)=0求解的问题。
当f(x)为一次多项式时,f(x)=0称为线性方程,否则称为非线性方程。
对于非线性方程,由于f(x)的多样性,求其根尚无一般的解析方法可以使用,因此研究非线性方程的数值解法是十分必要的。
法、迭代法、牛顿法及割线法。
这些方法均是知道根的初始近似值后,进一步把根精确化,直到达到所要求的 精度为止。
也即求非线性方程根的数值方法。
第一节 第一节 增值寻根法与二分法2.1.1 增值寻根法设非线性方程f(x)=0的根为*x ,增值寻根法的基本思想是,从初始值0x 开始,按规定 的一个初始步长h 来增值。
令 1n x +=n x +h(n=0,1,2,…),同时计算f(1n x +)。
在增值的计算过程中可能遇到三种情形:(1) f(1n x +)=0,此时1n x +即为方 程的根*x 。
(2) f(n x )和f(1n x +)同符号。
这说明区间[n x , 1n x +]内无根。
(3) f(n x )和f(1n x +)异号,f(n x )·f(1n x +)<0此时当f(x)在区间[n x , 1n x +]上连续时,方程f(x)=0在[n x , 1n x +] 一定有根。
也即我们用增值寻根法找到了方程根的存在区间,n x 或1n x +均可以视为根的近似值。
下一步就是设法在该区间内寻找根 *x 更精确的近似值,为此再用增值寻根法 把n x 作为新的初始近似值,同时把步长缩小,例如选新步长1100h h =,这 样会得到区间长度更小的有根区间,从而也得到使f(x)n x ,作为*x 更 精确的近似值,若精度不够,可重复使用增值寻根法,直到有根区间的长度|1n x +-n x |<ε(ε为所要求的精度)为止。
此时f(n x )或f(1n x +)就可近似认为是零。
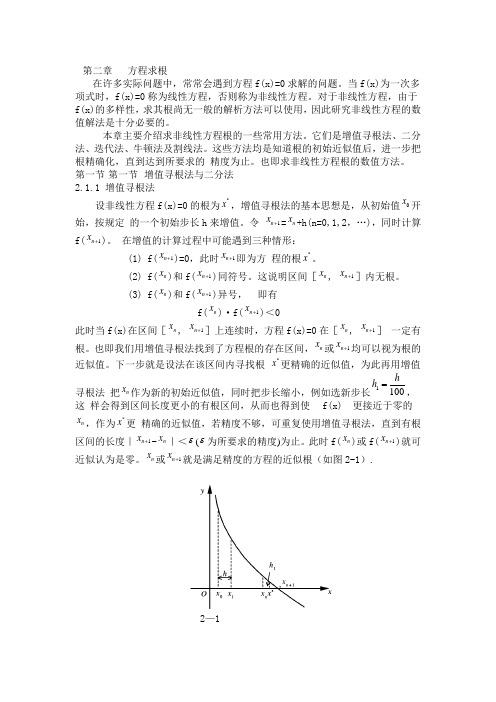
n x 或1n x +就是满足精度的方程的近似根(如图2-1).2—1例1 用增值寻根法求方程f(x)=324x x +-10=0的有根区间。



高等代数中的非线性方程组求解方法与案例高等代数中的非线性方程组求解方法与案例一、引言非线性方程组在数学和科学工程领域中具有重要的理论和实际应用价值。
本文将介绍一些常用的非线性方程组求解方法,并通过案例来展示这些方法的应用。
二、牛顿法牛顿法是一种经典的非线性方程组求解方法。
该方法利用函数的导数信息进行迭代,通过不断逼近方程组的解。
其迭代公式如下:假设方程组为 F(x) = 0,初始解为 x_0,则迭代公式为:x_{n+1} = x_n - J_F(x_n)^{-1} * F(x_n)其中,J_F(x_n) 表示 F(x_n) 的雅可比矩阵。
三、割线法割线法是一种迭代求解非线性方程组的方法。
该方法使用方程组中两个初始解点之间的割线来逼近方程组的解。
其迭代公式如下:假设方程组为 F(x) = 0,初始解为 x_0 和 x_1,则迭代公式为:x_{n+1} = x_n - \frac{F(x_n) * (x_n - x_{n-1})}{F(x_n) - F(x_{n-1})}四、二分法二分法是一种简单且可靠的非线性方程组求解方法。
该方法利用方程组在区间两端点函数值异号的性质,在区间内部寻找解。
其迭代公式如下:假设方程组为 F(x) = 0,在区间 [a, b] 内满足 F(a) * F(b) < 0,迭代公式为:x_{n+1} = \frac{a_n + b_n}{2}五、案例分析假设有如下非线性方程组:x^2 + y^2 = 10x + y = 5我们将使用上述介绍的三种方法来求解该方程组。
1. 牛顿法求解:首先,我们需要计算方程组的雅可比矩阵:J_F(x, y) = [[2x, 2y],[1, 1]]给定初始解 x_0 = (1, 4),按照牛顿法的迭代公式进行迭代计算,直到满足收敛条件。
2. 割线法求解:给定初始解 x_0 = (1, 4) 和 x_1 = (2, 3),按照割线法的迭代公式进行迭代计算,直到满足收敛条件。