2007年四川高考文科数学含答案详解解析版_免费

. . 。

..洞察2007年四川高考数学作者：北大附中成都实验学校刘永芳关键词: 考试情况、试题特点、命题趋势、教学建议、数学思想 2007年的高考已经结束了，笔者有幸聘请参加高考数学阅卷工作，掌握了部分第一手资料。

笔者通过自己的思考与专家组的点评，对2007年四川高考数学试题作了一些简要的分析。

一、总体评价今年高考试题的总体特点可以用两句话来概括：基础中有能力，稳定中有创新。

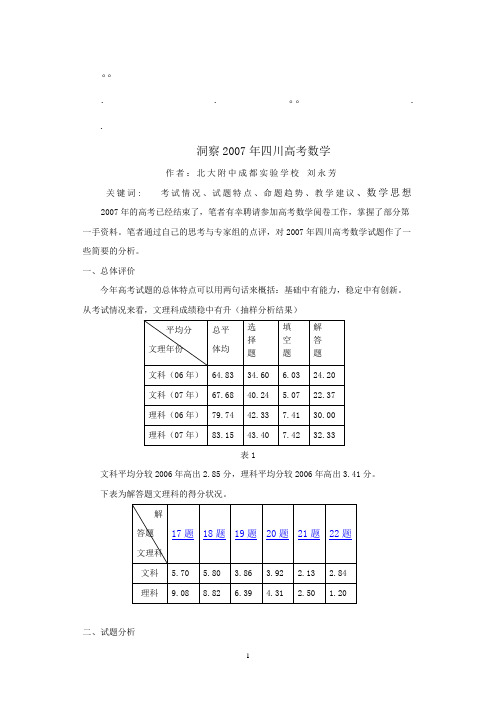
从考试情况来看，文理科成绩稳中有升（抽样分析结果）表1文科平均分较2006年高出2.85分，理科平均分较2006年高出3.41分。

下表为解答题文理科的得分状况。

二、试题分析今年是我省自主命题的第二年，与去年高考试卷相比，2007年高考数学四川卷试题具有“基础中有能力、稳定中有创新”的特点。

具体的说，今年的数学高考题起点降低，梯度分明，循序渐进，在全面考查“三基”的同时，注重考查学生的数学能力、数学思想方法、应用数学的意识和创新能力；绝大部分题目较为常规，普遍受到考生和教师的欢迎，为中学数学教学起到了良好的导向的作用。

1.“稳定”表现今年试卷在去年的基础上总体保持平稳，表现在：（1）选择题、填空题和解答题三种题型结构、排列次序仍然保持不变。

初步感觉试题总体难度适中，与去年相比文理科难度略有下降，文理差异较明显。

在去年的基础上，今年继续体现文理各自特点与要求，在考查要求与难度方面，其差异性依然十分明显。

（2）内容所占比基本没有大的起伏变化。

以理科试卷为例，具体见下表：（3）试题层次分明。

继续坚持多角度、多层次的考查方式，延续了去年分步设问、分散难点的做法，进一步体现了多题把关的命题特点。

如：理科的17题第Ⅰ问就是同角关系和二倍角关系的直接应用，18题第Ⅰ问概率题也是最基本的相互独立事件、互斥事件这些重点知识的直接应用，包括19题立体几何第Ⅰ问甚至是21题的入手，最后一题（22题）的第Ⅰ问都不难。

学生在刚学完相应的知识的前提下都能较顺利的完成第Ⅰ问，但要将每道大题全部答对，那则必须具有相当强的数学能力。

章贡区水西镇第一保育院2011—2012学年
第二学期小二班庆“三八”活动家长感言
3月8日下午，在小二班的教室里小朋友齐声唱起“世上只有妈妈好”，唱完后小朋友在老师的带领下用他们粉嫩的小手给妈妈捶捶背，做了手工项链作为礼物送给妈妈们，让我沉醉其中，想一想幼儿园里孩子们在老师的教育下从呀呀学语到如今这么乖巧懂事，真是辛苦这些勤劳的园丁了。

非常感谢小二班的老师们为我们家长提供了“三八节”与自己的孩子在幼儿园里亲密接触的机会，让我们家长能够通过这次有意义的活动进一步了解孩子的园内生活，并且对培养孩子与家长之间的亲子关系起到了很积极的作用，这些都让我深深体会到幼儿园对孩子成长和教育的高度重视以及为此做出的各种努力，我对此深为感动和感激。

我们都知道，幼儿园的教育对孩子的成长影响深远，是良好性格的形成和培育的关键时期。

现在看到孩子在幼儿园期间变得越来越懂事了，这种体贴人、关心人的品格其实比学到的书本知识更有意义。

真的希望这样的活动能举办的更多一些。

真的希望对孩子的感恩教育能一如继往的坚持下去。

先学做人，再学知识。

小二班：钟自清妈妈。

2023年普通高等学校招生全国统一考试（四川卷）数学（理科）试卷参考解析一、选择题:本题考察基础知识和基本运算,每小题5分,满分60分（1） A （2） C （3） D （4） D （5） A （6） C （7） A （8） C （9） B （10） B （11） D （12） B二、填空题:本题考察基础知识和基本运算,每小题4分,满分16分（13）1 （14）6π（15）32x =（16）① ④三、解答题:（17）本题考察三角恒等变形地主要基本公式、三角函数值地符号,已知三角函数值求角以及计算能力。

解:（Ⅰ）由1cos ,072παα=<<,得sin α==∴sin 7tan cos 1ααα===于是22tan tan 21tan ααα===-（Ⅱ）由02παβ<<<,得02παβ<-<又∵()13cos 14αβ-=,∴()sin αβ-===由()βααβ=--得:()cos cos βααβ=--⎡⎤⎣⎦()()cos cos sin sin ααβααβ=-+-11317142=⨯+=所以3πβ=（18）本题考察相互独立事件、互斥事件等地概率计算,考察随机事件地分布列,数学期望等,考察运用所学知识与方法解决实际问题地能力。

解:（Ⅰ）记"厂家任取4件产品检验,其中至少有1件是合格品"为事件A 用对立事件A 来算,有()()4110.20.9984P A P A =-=-=（Ⅱ）ξ可能地取值为0,1,2()2172201360190C P C ξ===,()11317220511190C C P C ξ===,()2322032190C P C ξ===136513301219019019010E ξ=⨯+⨯+⨯=记"商家任取2件产品检验,都合格"为事件B,则商家拒收这批产品地概率()136271119095P P B =-=-=所以商家拒收这批产品地概率为2795（19）本题主要考察异面直线所成地角、平面与平面垂直、二面角、三棱锥体积等有关知识,考察思维能力和空间想象能力、应用向量知识解决数学问题地能力、化归转化能力和推理运算能力。

目录一、专业工程概况与特点二、工程监理依据三、监理过程的控制四、质量控制流程图五、监理方法和手段六、土方工程的质量检查和评定一、工程概况：1、建设单位：宁波东部新城开发投资有限公司2、设计单位：宁波中鼎建筑设计研究院3、勘察单位（围护设计）：浙江省工程勘察院3、监理单位：宁波市天正工程咨询有限公司4、施工单位：宁波建工股份有限公司5、工程名称：东部新城邱隘安置房C1-2-1地块工程6、质量要求：一次性合格本工程位于宁波市鄞州区邱隘镇（宁波东部新城内），地块东至陈郎桥江，南至C1-2-2地块，西至规划支路，北至通途路。

总建筑面积约110907平方米，地下室开挖面积约26500平方米，基坑周长约729米，开挖深度6.1～7米为主，局部坑边电梯井深度8.5～9.4米，地质情况以淤泥粘土为主。

二、工程监理依据：1、国家、宁波市市有关法律法规、条例和规章；2、国家及有关部门颁布的工程施工技术标准、规程、规范和工程质量检验评定标准；3、上级主管部门批准的设计文件和批文；4、经审查的施工图纸、资料及说明；5、工程施工承包合同及有关文件、附件；6、监理合同及有关文件、附件；7、招标人提供的其它文件和资料。

三、监理过程的控制：1、事前控制：（1）掌握施工单位人员素质的基本情况，重点核实施工单位的主要技术负责人的技术状况，了解其完成同类项目的土方工程质量情况；（2）做好施工图会审技术交底，熟悉施工方案，使设计技术要求及施工范围具体化，保证土方施工方案准确无误；（3）了解施工单位的施工进度；（4）核定施工单位施工机械设备的进场计划；（5）检验并审核进场机械设备的相关资料；（6）掌握土方施工质量的控制要求；（7）掌握项目特定内容的施工验收规范。

2、事中控制：（1）控制好土方工程的施工质量控制要点、部位；（2）旁站监理土方工程挖土、回填土工作，严禁擅自超挖；（3）慎重处理工程变更和设计修改工作，做好工程费用的控制；（4）严格质量检验，报验制度，不合格不得进行下道工序施工；（5）定期对照工程施工总进度计划，当实际施工进度与总进度计划不符时，要求施工单位及时对进度计划进行调整，并将调整后的进度计划方案报送监理部备查；3、事后控制：（1）对于相关的工程索赔，要认真分析责任单位，正确处理有关索赔问题；（2）及时填写好验收报告、隐蔽记录，对不符合要求的部位及时要求施工单位进行返工；（3）认真审查竣工验收资料；（4）及时进行监理阶段的小结和分析。

2007年普通高等学校招生全国统一考试(四川卷)理科数学全解全析一、选择题：本大题共12小题，每小题5分，共60分． 1、复数311i i i++-的值是（ ） （A ）0（B ）1（C ）1-（D ）i解析：选A ．23331(1)201(1)(1)2i i ii i i i i i i i +++=+=+=-=--+．本题考查复数的代数运算．2、函数2()1log f x x =+与1()2x g x -+=在同一直角坐标系下的图象大致是（ ）解析：选C ．注意 1(1)()22x x g x -+--==的图象是由2x y -=的图象右移1而得．本题考查函数图象的平移法则．3、2211lim 21x x x x →-=--（ ） （A ）0 （B ）1 （C ）12 （D ）23解析：选D ．本题考查00型的极限．原式11(1)(1)12limlim (1)(21)213x x x x x x x x →→+-+===-++或原式122lim413x x x →==-．4、如图，1111ABCD A BC D -为正方体，下面结论错误．．的是（ ） （A ）//BD 平面11CB D （B ）1AC BD ⊥ （C ）1AC ⊥平面11CB D（D ）异面直线AD 与1CB 所成的角为60︒解析：选D ．显然异面直线AD 与1CB 所成的角为45︒．5、如果双曲线22142x y -=上一点P 到双曲线右焦点的距离是2，那么点P 到y 轴的距离是（ ）（A ）463 （B ）263（C ）26 （D ）23 解析：选A ．由点P 到双曲线右焦点(6,0)的距离是2知P 在双曲线右支上．又由双曲线的第二定义知点P 到双曲线右准线的距离是263，双曲线的右准线方程是263x =，故点P 到y 轴的距离是463． 6、设球O 的半径是1，A 、B 、C 是球面上三点，已知A 到B 、C 两点的球面距离都是2π，且二面角B OA C --的大小是3π，则从A 点沿球面经B 、C 两点再回到A 点的最短距离是（ ）（A ）76π （B ）54π （C ）43π （D ）32π解析：选C ．42323d AB BC CA ππππ=++=++=．本题考查球面距离． 7、设(,1)A a ，(2,)B b ，(4,5)C 为坐标平面上三点，O 为坐标原点，若OA 与OB 在OC方向上的投影相同，则a 与b 满足的关系式为（ ）（A ）453a b -= （B ）543a b -= （C ）4514a b += （D ）5414a b +=解析：选A ．由OA 与OB 在OC 方向上的投影相同，可得：OA OC OB OC ⋅=⋅即4585a b +=+，453a b -=．8、已知抛物线23y x =-+上存在关于直线0x y +=对称的相异两点A 、B ，则AB 等于（ ）（A ）3 （B ）4 （C ）32 （D ）42 解析：选C ．设直线AB 的方程为y x b =+，由22123301y x x x b x x y x b⎧=-+⇒++-=⇒+=-⎨=+⎩，进而可求出AB 的中点11(,)22M b --+，又由11(,)22M b --+在直线0x y +=上可求出1b =，∴220x x +-=，由弦长公式可求出221114(2)32AB =+-⨯-=．本题考查直线与圆锥曲线的位置关系．自本题起运算量增大．9、某公司有60万元资金，计划投资甲、乙两个项目，按要求对项目甲的投资不小于对项目乙投资的32倍，且对每个项目的投资不能低于5万元，对项目甲每投资1万元可获得0.4万元的利润，对项目乙每投资1万元可获得0.6万元的利润，该公司正确规划投资后，在这两个项目上共可获得的最大利润为（ ）（A ）36万元 （B ）31.2万元 （C ）30.4万元 （D ）24万元 解析：选B ．对甲项目投资24万元，对乙项目投资36万元，可获最大利润31.2万元．因为对乙项目投资获利较大，故在投资规划要求内（对项目甲的投资不小于对项目乙投资的32倍）尽可能多地安排资金投资于乙项目，即对项目甲的投资等于对项目乙投资的32倍时可获最大利润．这是最优解法．也可用线性规划的通法求解．注意线性规划在高考中以应用题型的形式出现． 10、用数字0，1，2，3，4，5可以组成没有重复数字，并且比20000大的五位偶数共有（ ）（A ）288个 （B ）240个 （C ）144个 （D ）126个 解析：选B ．对个位是0和个位不是0两类情形分类计数；对每一类情形按“个位－最高位－中间三位”分步计数：①个位是0并且比20000大的五位偶数有341496A ⨯⨯=个；②个位不是0并且比20000大的五位偶数有3423144A ⨯⨯=个；故共有96144240+=个．本题考查两个基本原理，是典型的源于教材的题目．11、如图，1l 、2l 、3l 是同一平面内的三条平行直线，1l 与2l 间的距离是1，2l 与3l 间的距离是2，正三角形ABC 的三顶点分别在1l 、2l 、3l 上，则⊿ABC 的边长是（ ）（A ）23 （B ）364 （C ）3174 （D ）2213解析：选D ．过点Ｃ作2l 的垂线4l ，以2l 、4l 为x 轴、y 轴建立平面直角坐标系．设(,1)A a 、(,0)B b 、(0,2)C -，由AB BC AC ==知2222()149a b b a -+=+=+=边长，检验A ：222()14912a b b a -+=+=+=，无解；检验B ：22232()1493a b b a -+=+=+=，无解；检验D ：22228()1493a b b a -+=+=+=，正确．本题是把关题．在基础中考能力，在综合中考能力，在应用中考能力，在新型题中考能力全占全了．是一道精彩的好题．可惜区分度太小．12、已知一组抛物线2112y ax bx =++，其中a 为2、4、6、8中任取的一个数，b 为1、3、5、7中任取的一个数，从这些抛物线中任意抽取两条，它们在与直线1x =交点处的切线相互平行的概率是（ ）（A ）112 （B ）760 （C ）625 （D ）516解析：选B ．这一组抛物线共4416⨯=条，从中任意抽取两条，共有216120C =种不同的方法．它们在与直线1x =交点处的切线的斜率1'|x k y a b ===+．若5a b +=，有两种情形，从中取出两条，有22C 种取法；若7a b +=，有三种情形，从中取出两条，有23C 种取法；若9a b +=，有四种情形，从中取出两条，有24C 种取法；若11a b +=，有三种情形，从中取出两条，有23C 种取法；若13a b +=，有两种情形，从中取出两条，有22C 种取法．由分类计数原理知任取两条切线平行的情形共有222222343214C C C C C ++++=种，故所求概率为760．本题是把关题．二、填空题：本大题共4小题，每小题4分，共16分；把答案填在题中的横线上． 13、若函数2()()x f x e μ--=（e 是自然对数的底数）的最大值是m ，且()f x 是偶函数，则m μ+=________．解析：1m =，0n =，∴1m μ+=．14、在正三棱柱111ABC A B C -中，侧棱长为2，底面三角形的边长为1，则1BC 与侧面11ACC A 所成的角是____________解析：13BC =，点B 到平面11ACC A 的距离为32，∴1sin 2θ=，30θ=︒．15、已知O 的方程是2220x y +-=，'O 的方程是228100x y x +-+=，由动点P 向O 和'O 所引的切线长相等，则动点P 的轨迹方程是__________________解析：O ：圆心(0,0)O ，半径2r =；'O ：圆心'(4,0)O ，半径'6r =．设(,)P x y ，由切线长相等得222x y +-=22810x y x +-+，32x =． 16、下面有5个命题：①函数44sin cos y x x =-的最小正周期是π．②终边在y 轴上的角的集合是{|,}2k k Z παα=∈． ③在同一坐标系中，函数sin y x =的图象和函数y x =的图象有3个公共点． ④把函数3sin(2)3y x π=+的图象向右平移6π得到3sin 2y x =的图象． ⑤函数sin()2y x π=-在[0,]π上是减函数．其中，真命题的编号是___________（写出所有真命题的编号）解析：①4422sin cos sin cos 2y x x x x cos x =-=-=-，正确；②错误；③sin y x =，tan y x =和y x =在第一象限无交点，错误；④正确；⑤错误．故选①④．三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤. （17）（本小题满分12分）已知0,1413)cos(,71cos 且=β-α=α<β<α<2π,(Ⅰ)求α2tan 的值. （Ⅱ）求β.（17）本题考察三角恒等变形的主要基本公式、三角函数值的符号，已知三角函数值求角以及计算能力。

2007年普通高等学校招生全国统一考试（四川卷）理科数学参考答案一．选择题：本题考察基础知识和基本运算，每小题5分，满分60分（1） A （2） C （3） D （4） D （5） A （6） C （7） A （8） C （9） B （10） B （11） D （12） B 二．填空题：本题考察基础知识和基本运算，每小题4分，满分16分 （13）1 （14）6π （15）32x =（16）① ④三．解答题：（17）本题考察三角恒等变形的主要基本公式、三角函数值的符号，已知三角函数值求角以及计算能力。

解：（Ⅰ）由1cos ,072παα=<<，得sin 7α==∴sin 7tan co s 71ααα===(22tan tan 21tan 471ααα===---（Ⅱ）由02παβ<<<，得02παβ<-<又∵()13co s 14αβ-=，∴()sin 14αβ-===由()βααβ=--得：()co s co s βααβ=--⎡⎤⎣⎦()()cos cos sin sin ααβααβ=-+-11317147142=⨯+=所以3πβ=（18）本题考察相互独立事件、互斥事件等的概率计算，考察随机事件的分布列，数学期望等，考察运用所学知识与方法解决实际问题的能力。

解：（Ⅰ）记“厂家任取4件产品检验，其中至少有1件是合格品”为事件A 用对立事件A 来算，有()()4110.20.9984P A P A =-=-=（Ⅱ）ξ可能的取值为0,1,2()2172201360190C P C ξ===，()11317220511190C C P C ξ===，()2322032190C P C ξ===136513301219019019010E ξ=⨯+⨯+⨯=记“商家任取2件产品检验，都合格”为事件B ，则商家拒收这批产品的概率()136271119095P P B =-=-=所以商家拒收这批产品的概率为2795（19）本题主要考察异面直线所成的角、平面与平面垂直、二面角、三棱锥体积等有关知识，考察思维能力和空间想象能力、应用向量知识解决数学问题的能力、化归转化能力和推理运算能力。

2007年高考数学试题汇编——排列、组合、二项式1．（全国Ⅰ卷理科第10题）的展开式中，常数项为15，则n= （ D ）A．3 B．4 C．5 D．6【解答】的展开式中，常数项为15，则，所以n可以被3整除，当n=3时，，当n=6时，，选D。

2．（全国Ⅰ卷文科第5题）甲、乙、丙3位同学选修课程，从4门课程中，甲选修2门，乙、丙各选修3门，则不同的选修方案共有（ C ）A．36种 B．48种 C．96种 D．192种【解答】甲、乙、丙3位同学选修课程，从4门课程中，甲选修2门，乙、丙各选修3门，则不同的选修方案共有种，选C。

3．（全国Ⅱ卷理科第10题）从5位同学中选派4位同学在星期五、星期六、星期日参加公益活动，每人一天，要求星期五有2人参加，星期六、星期日各有1人参加，则不同的选派方法共有（ B）A．40种 B．60种 C．100种 D．120种【解答】从5位同学中选派4位同学在星期五、星期六、星期日参加公益活动，每人一天，要求星期五有2人参加，星期六、星期日各有1人参加，则不同的选派方法共有种，选B。

4．（全国Ⅱ卷文科第10题）5位同学报名参加两个课外活动小组，每位同学限报其中的一个小组，则不同的报名方法共有（ D）A．10种 B．20种 C．25种 D．32种【解答】5位同学报名参加两个课外活动小组，每位同学限报其中的一个小组，则不同的报名方法共有25=32种，选D。

5．（北京理科第5题）记者要为5名志愿都和他们帮助的2位老人拍照，要求排成一排，2位老人相邻但不排在两端，不同的排法共有（ B ）Ａ．1440种Ｂ．960种Ｃ．720种Ｄ．480种【解答】5名志愿者先排成一排，有种方法，2位老人作一组插入其中，且两位老人有左右顺序，共有=960种不同的排法，选B。

6．（北京文科第5题）某城市的汽车牌照号码由2个英文字母后接4个数字组成，其中4个数字互不相同的牌照号码共有（ A ）Ａ．个Ｂ．个Ｃ．个Ｄ．个【解答】某城市的汽车牌照号码由2个英文字母后接4个数字组成，其中4个数字互不相同的牌照号码共有个，选A。

2007年四川省高考数学试卷（文科）一、选择题（共12小题，每小题5分，满分60分）1. 设集合M={4, 5, 6, 8}，集合N={3, 5, 7, 8}，那么M∪N=()A.{3, 4, 5, 6, 7, 8}B.{5, 8}C.{3, 5, 7, 8}D.{4, 5, 6, 8}2. 函数f(x)=1+log2x与g(x)=2−x+1在同一直角坐标系下的图象大致是（）A. B.C. D.3. 某商场买来一车苹果，从中随机抽取了10个苹果，其重量（单位：克）分别为：150，152，153，149，148，146，151，150，152，147，由此估计这车苹果单个重量的期望值是（）A.150.2克B.149.8克C.149.4克D.147.8克4. 如图，ABCD−A1B1C1D1为正方体，下面结论错误的是（）A.BD // 平面CB1D1B.AC1⊥BDC.AC1⊥平面CB1D1D.异面直线AD与CB1所成的角为60∘5. 如果双曲线x24−y22=1上一点P到双曲线右焦点的距离是2，那么点P到y轴的距离是（）A.4√63B.2√63C.2√6D.2√36. 设球O的半径是1，A、B、C是球面上三点，已知A到B、C两点的球面距离都是π2，且二面角B−OA−C的大小是π3，则从A点沿球面经B、C两点再回到A点的最短距离是（）A.7π6B.5π4C.4π3D.3π27. 等差数列{a n}中，a1=1，a3+a5=14，其前n项和S n=100，则n=()A.9B.10C.11D.128. 设A(a, 1)，B(2, b)，C(4, 5)为坐标平面上三点，O为坐标原点，若OA→与OB→在OC→方向上的投影相同，则a与b满足的关系式为（）A.4a−5b=3B.5a−4b=3C.4a+5b=14D.5a+4b=149. 用数字0，1，2，3，4，5可以组成没有重复数字，并且比20000大的五位偶数共有（）A.288个B.240个C.144个D.126个10. 已知抛物线y=−x2+3上存在关于直线x+y=0对称的相异两点A、B，则|AB|等于（）A.3B.4C.3√2D.4√21 / 8。

2007年普通高等学校招生全国统一考试（四川卷）理科数学本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

第Ⅰ卷1至2页。

第Ⅱ卷3到10页。

考试结束后，将本试卷和答题卡一并交回。

第Ⅰ卷注意事项：1．答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。

2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其它答案标号。

不能答在试题卷上。

3．本卷共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

参考公式：如果事件A 、B 互斥，那么 球是表面积公式)()()(B P A P B A P +=+ 24R S π=如果事件A 、B 相互独立，那么 其中R 表示球的半径)()()(B P A P B A P ⋅=⋅ 球的体积公式如果事件A 在一次试验中发生的概率是P ，那么334R V π=n 次独立重复试验中恰好发生k 次的概率 其中R 表示球的半径k n k kn n P P C k P --=)1()(一．选择题： (1)复数211i ii +-+的值是 （A ）0 (B)1 (C)-1 (D)1 (2)函数f (x )=1+log 2x 与g(x )= 12x -+在同一直角坐标系下的图象大致是(3)2211lim 21x x x x --=-- （A ）0 (B)1 (C)21 (D)32 (4)如图，ABCD －A 1B 1C 1D 1为正方体，下面结论错误．．的是 （A ）BD ∥平面CB 1D 1 （B ）AC 1⊥BD（C ）AC 1⊥平面CB 1D 1 （D ）异面直线AD 与CB 1角为60°（5）如果双曲线12422=-y x 上一点P 到双曲线右焦点的距离是2，那么点P 到y 轴的距离是（A ）364 （B ）362 （C ）62 （D ）32（6）设球O 的半径是1，A 、B 、C 是球面上三点，已知A 到B 、C 两点的球面距离都是2π，且二面角B －OA －C 的大小为3π，则从A 点沿球面经B 、C 两点再回到A 点的最短距离是 （A ）67π （B ）45π （C ）34π （D ）23π（7）设A (a ,1)，B (2，b )，C (4,5)，为坐标平面上三点，O 为坐标原点，若方向在与→→→OC OB OA 上的投影相同，则a 与b 满足的关系式为(A)354=-b a (B)345=-b a (C)1454=+b a (D)1445=+b a（8）已知抛物线32+-=x y 上存在关于直线0=+y x 对称的相异两点A 、B ，则|AB |等于（A ）3 （B ）4 （C ）23 （D ）24（9）某公司有60万元资金，计划投资甲、乙两个项目，按要求对项目甲的投资不小于对项目乙投资的32倍，且对每个项目的投资不能低于5万元，对项目甲每投资1万元可获得0.4万元的利润，对项目乙每投资1万元可获得0.6万元的利润，该公司正确规划投资后，在这两个项目上共可获得的最大利润为（A ）36万元 （B ）31.2万元 （C ）30.4万元 （D ）24万元 （10）用数字0，1，2，3，4，5可以组成没有重复数字，并且比20000大的五位偶数共有（A ）288个 （B ）240个 （C ）144个 （D ）126个 （11）如图，l 1、l 2、l 3是同一平面内的三条平行直线，l 1与l 2间的距离是1， l 2与l 3间的距离是2，正三角形ABC 的三顶点分别在l 1、l 2、l 3上， 则△ABC 的边长是（A ）32（B ）364 （C ）4173 （D ）3212 （12）已知一组抛物线1212++=bx ax y ，其中a 为2,4,6,8中任取的一个数，b 为1,3,5,7中任取的一个数，从这些抛物线中任意抽取两条，它们在与直线x =1交点处的切线相互平行的概率是（A ）121 （B ）607 （C ）256 （D ）255二、填空题：本大题共4小题，每小题4分，共16分，把答案填在横线上.（13）若函数2()()x f x eμ--= (e 是自然对数的底数)的最大值是m ,且f (x )是偶函数，则m +μ= .(14)如图，在正三棱柱ABC －A 1B 1C 1中，侧棱长为2，底面三角形的边长为1， 则BC 1与侧面ACC 1A 1所成的角是 .(15)已知⊙O 的方程是x 2+y 2－2=0, ⊙O ’的方程是x 2+y 2－8x +10=0,由动点P 向⊙O 和 ⊙O ’所引的切线长相等，则动点P 的轨迹方程是 . (16)下面有五个命题：①函数y =sin 4x －cos 4x 的最小正周期是π. ②终边在y 轴上的角的集合是{a |a =Z k k ∈π,2}. ③在同一坐标系中，函数y =sin x 的图象和函数y =x 的图象有三个公共点. ④把函数.2sin 36)32sin(3的图象得到的图象向右平移x y x y =ππ+= ⑤函数.0)2sin(〕上是减函数，在〔ππ-=x y 其中真命题的序号是 （写出所有真命题的编号）三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤.（17）（本小题满分12分）已知0,1413)cos(,71cos 且=β-α=α<β<α<2π,(Ⅰ)求α2tan 的值.（Ⅱ）求β.（18）（本小题满分12分）厂家在产品出厂前，需对产品做检验，厂家将一批产品发给商家时，商家按合同规定也需随机抽取一定数量的产品做检验，以决定是否接收这批产品.（Ⅰ）若厂家库房中的每件产品合格的概率为0.8，从中任意取出4件进行检验.求至少有1件是合格品的概率; （Ⅱ）若厂家发给商家20件产品，其中有3件不合格，按合同规定该商家从中任取2件，都进行检验，只有2件都合格时才接收这批产品，否则拒收.求该商家可能检验出不合格产品数ξ的分布列及期望ξE ，并求该商家拒收这批产品的概率.（19）（本小题满分12分）如图，PCBM 是直角梯形，∠PCB ＝90°，PM ∥BC ，PM ＝1，BC ＝2，又AC ＝1，∠ACB ＝120°，AB ⊥PC ，直线AM 与直线PC 所成的角为60°. （Ⅰ）求证：平面PAC ⊥平面ABC ; （Ⅱ）求二面角B AC M --的大小; （Ⅲ）求三棱锥MAC P -的体积.（20）（本小题满分12分）设1F 、2F 分别是椭圆1422=+y x 的左、右焦点. （Ⅰ）若P 是该椭圆上的一个动点，求1PF ·2PF 的最大值和最小值;（Ⅱ）设过定点)2,0(M 的直线l 与椭圆交于不同的两点A 、B ，且∠AOB 为锐角（其中O 为坐标原点），求直线l 的斜率k 的取值范围.（21）（本小题满分12分）已知函数2()4f x x =+,设曲线)(x f y =在点(,()n n x f x )处的切线与x 轴线交点为(1n x +，0)(*)n N ∈，其中x 1为正实数， （I ）用n x 表示1n x +；（II ）求证：对于一切正整数n ，1n n x x +≤； （III ）若x 1=4，记2lg 2n n n x a x +=-，证明数列n a 成等比数列，并求数列{}n x 的通项公式。

2007年普通高等学校招生全国统一考试（四川卷）理科数学本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

第Ⅰ卷1至2页。

第Ⅱ卷3到10页。

考试结束后，将本试卷和答题卡一并交回。

第Ⅰ卷注意事项：1．答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。

2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其它答案标号。

不能答在试题卷上。

3．本卷共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

参考公式：如果事件A 、B 互斥，那么 球是表面积公式)()()(B P A P B A P +=+ 24R S π=如果事件A 、B 相互独立，那么 其中R 表示球的半径)()()(B P A P B A P ⋅=⋅ 球的体积公式如果事件A 在一次试验中发生的概率是P ，那么334R V π=n 次独立重复试验中恰好发生k 次的概率 其中R 表示球的半径k n k kn n P P C k P --=)1()(一．选择题： (1)复数211i ii +-+的值是 （A ）0 (B)1 (C)-1 (D)1(2)函数f (x )=1+log 2x 与g(x )=2-x +1在同一直角坐标系下的图象大致是(3)2211lim 21x x x x →-=-- （A ）0 (B)1 (C)21 (D)32 (4)如图，ABCD -A 1B 1C 1D 1为正方体，下面结论错误．．的是 （A ）BD ∥平面CB 1D 1 （B ）AC 1⊥BD（C ）AC 1⊥平面CB 1D 1 （D ）异面直线AD 与CB 1角为60° （5）如果双曲线12422=-y x 上一点P 到双曲线右焦点的距离是2，那么点P 到y 轴的距离是 （A ）364 （B ）362 （C ）62 （D ）32（6）设球O 的半径是1，A 、B 、C 是球面上三点，已知A 到B 、C 两点的球面距离都是2π，且三面角B -OA -C 的大小为3π，则从A 点沿球面经B 、C 两点再回到A 点的最短距离是 （A ）67π （B ）45π （C ）34π （D ）23π（7）设A ｛a ,1｝，B ｛2，b ｝，C ｛4,5｝，为坐标平面上三点，O 为坐标原点，若方向在与→→→OC OB OA 上的投影相同，则a 与b 满足的关系式为(A)354=-b a (B)345=-b a (C)1454=+b a (D)1445=+b a（8）已知抛物线32+-=x y 上存在关于直线0=+y x 对称的相异两点A 、B ，则|AB |等于（A ）3 （B ）4 （C ）23 （D ）24（9）某公司有60万元资金，计划投资甲、乙两个项目，按要求对项目甲的投资不小于对项目乙投资的32倍，且对每个项目的投资不能低于5万元，对项目甲每投资1万元可获得0.4万元的利润，对项目乙每投资1万元可获得0.6万元的利润，该公司正确规划投资后，在这两个项目上共可获得的最大利润为（A ）36万元 （B ）31.2万元 （C ）30.4万元 （D ）24万元 （10）用数字0，1，2，3，4，5可以组成没有重复数字，并且比20000大的五位偶数共有（A ）288个 （B ）240个 （C ）144个 （D ）126个 （11）如图，l 1、l 2、l 3是同一平面内的三条平行直线，l 1与l 2间的距离是1， l 2与l 3间的距离是2，正三角形ABC 的三顶点分别在l 1、l 2、l 3上， 则△ABC 的边长是（A ）32（B ）364 （C ）4173 （D ）3212 （12）已知一组抛物线1212++=bx ax y ，其中a 为2,4,6,8中任取的一个数，b 为1,3,5,7中任取的一个数，从这些抛物线中任意抽取两条，它们在与直线x =1交点处的切线相互平行的概率是（A ）121 （B ）607 （C ）256 （D ）255二、填空题：本大题共4小题，每小题4分，共16分，把答案填在横线上.（13）若函数f (x )=e -(m -u )2 (c 是自然对数的底数)的最大值是m ,且f (x )是偶函数，则m +u = .(14)如图，在正三棱柱ABC -A 1B 1C 1中，侧棱长为2，底面三角形的边长为1， 则BC 1与侧面ACC 1A 1所成的角是 .(15)已知⊙O 的方程是x 2+y 2-2=0, ⊙O ’的方程是x 2+y 2-8x +10=0,由动点P 向⊙O 和 ⊙O ’所引的切线长相等，则动点P 的轨迹方程是 . (16)下面有五个命题：①函数y =sin 4x -cos 4x 的最小正周期是π. ②终边在y 轴上的角的集合是{a |a =Z k k ∈π,2|. ③在同一坐标系中，函数y =sin x 的图象和函数y =x 的图象有三个公共点. ④把函数.2sin 36)32sin(3的图象得到的图象向右平移x y x y =ππ+= ⑤函数.0)2sin(〕上是减函数，在〔ππ-=x y 其中真命题的序号是 （写出所言 ）三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤. （17）（本小题满分12分）已知0,1413)cos(,71cos 且=β-α=α<β<α<2π,(Ⅰ)求α2tan 的值.（Ⅱ）求β.（18）（本小题满分12分）厂家在产品出厂前，需对产品做检验，厂家将一批产品发给商家时，商家按合同规定也需随机抽取一定数量的产品做检验，以决定是否接收这批产品.（Ⅰ）若厂家库房中的每件产品合格的概率为0.8，从中任意取出4件进行检验.求至少有1件是合格品的概率; （Ⅱ）若厂家发给商家20件产品，其中有3件不合格，按合同规定该商家从中任取2件，都进行检验，只有2件都合格时才接收这批产品，否则拒收.求该商家可能检验出不合格产品数ξ的分布列及期望ξE ，并求该商家拒收这批产品的概率.（19）（本小题满分12分）如图，PCBM 是直角梯形，∠PCB ＝90°，PM ∥BC ，PM ＝1，BC ＝2，又AC ＝1，∠ACB ＝120°，AB ⊥PC ，直线AM 与直线PC 所成的角为60°. （Ⅰ）求证：平面PAC ⊥平面ABC ; （Ⅱ）求二面角B AC M --的大小; （Ⅲ）求三棱锥MAC P -的体积.（20）（本小题满分12分）设1F 、2F 分别是椭圆1422=+y x 的左、右焦点. （Ⅰ）若P 是该椭圆上的一个动点，求1PF ·2PF 的最大值和最小值;（Ⅱ）设过定点)2,0(M 的直线l 与椭圆交于不同的两点A 、B ，且∠AOB 为锐角（其中O 为坐标原点），求直线l 的斜率k 的取值范围.已知函数42)(+=x x f ,设曲线)(x f y =在点()处的切线与x 轴线发点()()其中xn 为实数（21）（本小题满分12分）(22)(本小题满分14分)设函数),1,(11)(N x n N n n x f n∈∈⎪⎭⎫⎝⎛+= 且.(Ⅰ)当x =6时,求nn ⎪⎭⎫⎝⎛+11的展开式中二项式系数最大的项;(Ⅱ)对任意的实数x ,证明2)2()2(f x f +＞);)()()((的导函数是x f x f x f ''(Ⅲ)是否存在N a ∈,使得an ＜∑-⎪⎭⎫ ⎝⎛+nk k 111＜n a )1(+恒成立?若存在,试证明你的结论并求出a 的值;若不存在,请说明理由.2007年普通高等学校招生全国统一考试（四川卷）理科数学参考答案一．选择题：本题考察基础知识和基本运算，每小题5分，满分60分（1） A （2） C （3） D （4） D （5） A （6） C （7） A （8） C （9） B （10） B （11） D （12） B 二．填空题：本题考察基础知识和基本运算，每小题4分，满分16分 （13）1 （14）6π（15）32x = （16）① ④三．解答题：（17）本题考察三角恒等变形的主要基本公式、三角函数值的符号，已知三角函数值求角以及计算能力。