当前位置：文档之家 › 最新空间几何体的体积(1)ppt课件

最新空间几何体的体积(1)ppt课件

  • 格式：ppt
  • 大小：1.55 MB
  • 文档页数：34

下载文档原格式

  / 34

合集下载

高中数学必修2第1章132空间几何体的体积课件(38张)1

高中数学必修2第1章132空间几何体的体积课件(38张)1

方法归纳 根据球的截面面积来求球的表面积和体积问题，关键是利 用重要的直角三角形建立关于半径R的方程．求出R，然后 代入球的表面积公式和体积公式进行求解．
4．本例中 ，若截面不过球的半径的中点，而是过半径 上与球心距离为1的点，且截面与此半径垂直，若此截面 的面积为π，试求此球的表面积和体积．
解：如图，由题意可知：OO1＝1，设截面圆的 半径为 r， 则 π＝πr2，∴r＝1， 即 O1A＝1. 在 Rt△OO1A 中， 球半径 R＝OA＝ O1O2＋O1A2＝ 12＋12＝ 2， ∴球的表面积 S 球＝4πR2＝8π，
＝ 23a，所以 CH＝EH·tan130°＝32a.
在 Rt△CDH 中，CD＝ CH2－DH2＝ 32a2－12a2＝ 2a，
所以
S
△
CDF＝12CD·AD＝
1 2
×
2a×a＝ 22a2，所以 VE－CDF＝
13·EH·S△CDF＝13× 23a× 22a2＝ 126a3.
(2)在 Rt△AFE 中，由 AE＝a，AF＝12CD＝ 22a，
43πr31∶43πr23＝rr213＝233＝8∶27.
3．如图在所有棱长均为2的正三棱柱ABC－A1B1C1中，三棱 23
锥B－A1C1C的体积是__3______．
解析：∵三棱锥 B－A1C1C 与三棱锥 B－A1AC 等底同高， 故 VB—A1C1C＝VB－A1AC，又 VB－A1AC＝VA1－ABC， ∴VB－A1C1C＝VA1－ABC， 而三棱锥 A1－ABC 的底面就是正三棱柱的底面，它的高就是 正三棱柱的高，
∴DE＝
3 4 a.
[感悟提高] (1)在三棱锥 A－BCD 中，若求点 A 到平面 BCD 的距离 h，可以先求 VA－BCD.则 因为 V＝13hS△BCD，所以 h＝S△3BVCD.这种方法就 是用等积法求点到平面的距离，其中 V 的求法 一般用换顶点法求解，可利用 VA－BCD＝VB－ACD＝VC－ABD＝VD－ ABC 求解，求解的原则是 V 易求，且△BCD 的面积易求． (2)等体积法主要用于求点面距离，且常用于三棱锥，通过选取 不同的底面建立体积等式．

空间几何体的表面积和体积1(共82张1)PPT课件

空间几何体的表面积和体积1(共82张1)PPT课件
①直棱柱：设棱柱的高为h，底面多边形的周长为c， 则
S直棱柱侧＝ ch.（类比矩形的面积）
②圆柱：如果圆柱的底面半径为r，母线长为l，那么
S圆柱侧＝ 2πr.（l 类比矩形的面积）
把直三棱柱侧面沿一条侧棱展开，得到什么图形？ 侧面积怎么求？
h
cb
a
h
h
a
bc
S 直 棱 ＝ 拄 a （ 侧 bc)hch
r1
l
r2
扇环
S 圆＝ 台 S 扇 侧 ＝ 环 （ r1 r2)l
精选PPT课件
24
S(r'2r2r'lrl)
r' x
r xl
x 2r'
r 'O’
2r
l
rxr'xr'l
rO
S 侧 r ( l x ) r 'x ( r l r x r 'x )
(r'l rl)
圆柱、圆锥、圆台三者的表面积公式之间有什么关系？
有什么关系？
扇形
R扇＝ l
l扇＝
nl
180
l
r
S圆 精选P锥 P＝ T课S 件侧 扇 ＝ n 3l6 20 11 2 8 l扇 lrl
2r
l
圆锥的侧面展开图是扇形
rO
S r2 r l r(r l)
(3)台体的侧面积
①正棱台：设正n棱台的上底面、棱台的侧面积公
别是3cm和6cm，高是3/2cm，求三棱台
的侧面积.
分析：关键是 求出斜高，注
A1 O1 C1 B1 D1 C
意图中的直角 梯形
A
O ED
B
精选PPT课件
28

专题：空间几何体的体积优秀课件

专题：空间几何体的体积优秀课件
则该平行六面体 ABCD A1B1C1D1 的
体积V Sh
[变式 1] 已知斜三棱柱 ABC A1B1C1 中，
点 A1到面 BB1C1C 的距离为 h ， 四边形 BB1C1C 面积为 S ，
则该三棱柱的体积=
方法1： 补成平行六面体
方法2： 一柱分两锥
一柱分三锥，
C1
B1 C1
A1
C
BC
A
B1 A1
B A
一柱分两锥，
方法1： 补成平行六面体
ห้องสมุดไป่ตู้
方法2： 一柱分两锥
[变式 2] 如图三棱柱 ABC A1B1C1 中，
若VABC A1B1C1 30,VM ABC 6,
则V

M A1B1C1
[变式 3] 如图三棱柱 ABC A1B1C1 中，
点 A1到面 BB1C1C 的距离为 h ， 四边形 BB1C1C 面积为 S ，
方法1：分割法
方法2：补形法
（类型二）将线段EF位置特殊化
方案3：让点D待在墙角，三条棱DA、
DC、DE两两垂直
方法1：分割法
方法2：补形法
则三棱锥 B1 A1BC 的体积=
[变式 4] 如图三棱柱 ABC A1B1C1 中，
点 A1到面 BB1C1C 的距离为 h ， 四边形 BB1C1C 面积为 S ， 取 A1B1 中点 M ，
则三棱锥 B MB1C 的体积=
方法1
M N
方法1
方法2
[例 2] 如图，在多面体 ABCDEF 中， 四边形 ABCD 是边长为 3 的正方形，
一、复习回顾——体积公式
名称
体积（V ）
柱体

空间几何体的表面积与体积PPT教学课件

空间几何体的表面积与体积PPT教学课件

单的几何体，研究空间几何体的表面积
和体积，应以柱、锥、台、球的表面积
和体积为基础.那么如何求柱、锥、台、
球2的020/12表/12 面积和体积呢？
2
2020/12/12
3
知识探究（一）柱体、锥体、台体的表面积
思考1:面积是相对于平面图形而言的， 体积是相对于空间几何体而言的.你知道 面积和体积的含义吗？
2020/12/12
21
2020/12/12
22
知识探究（一）:球的体积
思考1:从球的结构特征分析，球的大小 由哪个量所确定？
思考2:底面半径和高都为R的圆柱和圆锥 的体积分别是什么？
V柱 R3
V锥
1
3
R3
2020/12/12
23
思考3:如图，对一个半径为R的半球，其 体积与上述圆柱和圆锥的体积有何大小 关系？
思考4:圆柱的侧面展开图的形状有哪些 特征？如果圆柱的底面半径为r，母线长 为l，那么圆柱的表面积公式是什么？
S2r(rl)
2020/12/12
6
思考5:圆锥的侧面展开图的形状有哪些 特征？如果圆锥的底面半径为r，母线长 为l，那么圆锥的表面积公式是什么？
Sr(rl)
2020/12/12
7
思考6:圆台的侧面展开图的形状有哪些 特征？如果圆台的上、下底面半径分别 为r′、r，母线长为l，那么圆台的表面 积公式是什么？
17
例3 有一堆规格相同的铁制六角螺帽 共重5.8kg（铁的密度是7.8g/cm3），已 知螺帽的底面是正六边形，边长为12mm， 内孔直径为10mm，，高为10mm，问这堆 螺帽大约有多少个？
V≈2956（mm3） =2.956（cm3）

空间几何体的表面积与体积ppt课件

空间几何体的表面积与体积ppt课件

尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,
米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5
尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为
1.62立方尺,圆周率约为3,估算出堆放的米约有 ( )
A.14斛
B.22斛
C.36斛
D.66斛
【答案】 B
如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,
A.26π
B.27π
C.24π
D.32π
【 答 案 】 B 【 解 析 】 设 球 的 直 径 为 d,则 d232323227. S球4πR2πd227π.
9.(2011新课标Ⅱ卷)已知两个圆锥有公共底面,且两圆锥的顶点和
底面的圆周都在同一个球面上.若圆锥底面面积是这个球面面积
的 3 ,则这两个圆锥中,体积较小者的高与体积较大者的高的比值 16
OC1 R 2 r12 R 2 5, OC2 R 2 r22 R 2 8,
R 2 5 R 2 8 1.解这个方程得R 2 9, S球 4πR 2 36π(cm2 ).
球的表面积是36πcm2.
13.(2015新课标Ⅰ卷)《九章算术》是我国古代内容极为丰富的
数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五
1、我们是青年团，不是畸人，也不是愚人，应当给自己把幸福争过来。——屠格涅夫 19、使这个世界灿烂的不是阳光，而是女生的微笑。——俞敏洪
11、.教人法经：不问住题千教言学【 ，法树、解 经材不料析 住分千析】 斧法。、 合作圆 探究柱 法 侧 面 积 S 2 π r l 2 π 1 1 2 π .
D. 2
.3 3

空间几何体的体积课件(共26张PPT)

空间几何体的体积课件(共26张PPT)
解 因此剩余部分的体积是
5 V V1 6 V ,
所以棱锥C-A'DD'的体积与剩余部分的体积之比为1:5. 想一想
如图7-52所示，三棱锥C-A'DD'的体积是三棱柱 B'CC'-A'DD'的体积的几分之几？三棱柱 B'CC'-A'DD '的体积是长方体ABCD-A'B'C'D'的体积的几分之几？
解则
V 122 2 4 2 .
3
3即该Leabharlann 锥的体积是 4 2 .3活动 3 巩固练习，提升素养
运用祖暅原理我们还能得出这样一个结论：一个 底面半径和高都等于 R 的圆柱，挖去一个以上底面为 底面、下底面圆心为顶点的圆锥后，所得几何体的体 积与一个半径为 R 的半球的体积相等. 试一试
运用祖暅原理推导球体体积公式？
式V柱体=Sh，可得底面积为S、高为h的锥体（棱锥、圆锥） 的体积计算公式：
V锥体
1 3
Sh.
巩固练习，提升素养 在活初动中3，我们用过“自然数集”“有理数集”等表述，这里的“集”就是集合的简称，那么什么是集合呢？
例2 已知正四棱锥S-ABCD的棱长都是2，求该棱 锥的体积．
巩固练习，提升素养 在活初动中3，我们用过“自然数集”“有理数集”等表述，这里的“集”就是集合的简称，那么什么是集合呢？
活动 3 巩固练习，提升素养
解 将该长方体看成四棱柱ADD'A'-BCC'B'，设它的
底面ADD'A'的面积为S，高为h,则它的体积
V=Sh.
棱锥C-A'DD'的底面积为 1 S，高为h，因此棱锥C-

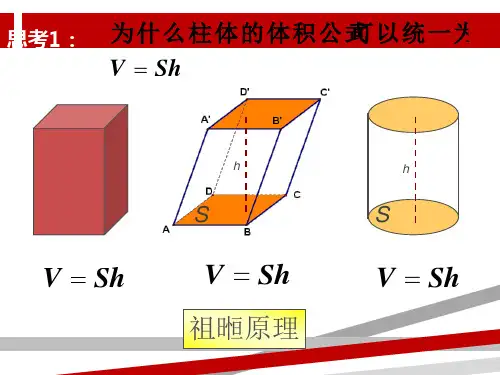
空间几何体的体积.ppt课件

空间几何体的体积.ppt课件

2．特点 (1)近代中国交通业逐渐开始近代化的进程，铁路、水运和 航空都获得了一定程度的发展。 (2)近代中国交通业受到西方列强的控制和操纵。 (3)地域之间的发展不平衡。 3．影响 (1)积极影响：促进了经济发展，改变了人们的出行方式， 一定程度上转变了人们的思想观念；加强了中国与世界各地的 联系，丰富了人们的生活。 (2)消极影响：有利于西方列强的政治侵略和经济掠夺。
时
代潮流
图说历史
主旨句归纳
(1)20世纪初，孙中山提出“民族、民权、
民生”三民主义，成为以后辛亥革命
的
指导思想。
(2)三民主义没有明确提出反帝要求，也
没
有提出废除封建土地制度，是一个
ቤተ መጻሕፍቲ ባይዱ
不彻
底的资产阶级革命纲领。
()
A．江南制造总局的汽车
B．洋人发明的火车
C．轮船招商局的轮船
D．福州船政局的军舰
[解析] 由材料信息“19世纪七十年代，由江苏沿江居民 到上海”可判断最有可能是轮船招商局的轮船。
[答案] C
[题组冲关]
1．中国近代史上首次打破列强垄断局面的交通行业是 ( )
A．公路运输
B．铁路运输
C．轮船运输
[合作探究·提认知] 电视剧《闯关东》讲述了济南章丘朱家峪人朱开山一家， 从清末到九一八事变爆发闯关东的前尘往事。下图是朱开山 一家从山东辗转逃亡到东北途中可能用到的四种交通工具。
依据材料概括晚清中国交通方式的特点，并分析其成因。 提示：特点：新旧交通工具并存(或：传统的帆船、独轮车， 近代的小火轮、火车同时使用)。 原因：近代西方列强的侵略加剧了中国的贫困，阻碍社会发 展；西方工业文明的冲击与示范；中国民族工业的兴起与发展； 政府及各阶层人士的提倡与推动。

空间几何体的体积(1)

空间几何体的体积(1)
的体积的差，再由比重算出一个六角螺帽毛坯的体积即可． 的体积的差，再由比重算出一个六角螺帽毛坯的体积即可．
3 解. V正六棱柱= 122 6 10 ≈ 3.74 × 103 (mm3 ) 4 2 3 3 V圆柱= π 5 10 ≈ 0.785 ×10 (mm )
一个毛坯的体积为 V=3.74×103-0.785×103 × × ≈2.96×103（mm3）=2.96cm3 × 约有毛坯 5.8×103÷（2.96×7.8)≈251(个) × × 个 这堆毛坯约有251个. 答．这堆毛坯约有 个
1 V锥体= sh 3
s
s
绘图05.gsp
三.台体的体积 台体的体积 上下底面积分别是s 高是 高是h， 上下底面积分别是 /,s,高是 ，则
1 V台体= h(s + ss' + s') 3
x s/ h s s s/
想 一 想 ？
上一节中，我们知道正棱柱、 上一节中，我们知道正棱柱、正棱 正棱台的侧面积之间有一定的关系。 锥、正棱台的侧面积之间有一定的关系。 那么，这里柱体、锥体、 那么，这里柱体、锥体、台体的体积公 式之间有没有类似的关系？ 式之间有没有类似的关系？ s/
数学运用
用截面截下一个棱锥C-A1DD1，求 例2． 在长方体 1中,用截面截下一个棱锥 ． 在长方体AC 用截面截下一个棱锥 C-A1DD1的体积与剩余部分的体积之比． 的体积与剩余部分的体积之比．
D1 C1 B1 D A B C A1
课堂练习
1、在△ABC中，AB=2，AC=1.5，∠BAC=1200.若将 、 中 ， ， 若将 绕直线AC旋转一周 △ABC绕直线 旋转一周，求形成的旋转体的体积． 绕直线 旋转一周，求形成的旋转体的体积．

空间几何体的体积PPT课件

空间几何体的体积PPT课件
割为3个三棱锥.
A’
C’ A’
A’
A’
C’
B’
B’
B’
1
2
3
A
CA
C
C
C
B
B
B
其中三棱锥1、2的底面积SA'AB SA'B'B , 高也相等；
三棱锥2、3的底面积SB'BC SB'C 'C , 高也相等；
因20此19/9三/22 个三棱锥的体积相等，V1 V2 V3
1 3
Sh.13
经探究得知，棱锥(圆锥)是同底等高的棱柱(圆柱) 的 1，即棱锥(圆锥)的体积：
3
V 1 Sh（其中S为底面面积，h为高）
3
由此可知，棱柱与圆柱的体积公式类似，都是底面面积乘高；棱 锥与圆锥的体积公式类似，都是等于底面面积乘高的 ．1
3
2019/9/22
14
对于任意一个底面积为S，高为h的锥体
组成的矩形（如图），底边为直四棱柱的底面周长
1
2
2
5
1
c 1 2 2 5 5 5,
D1
C1
可知直四棱柱的侧面积为
A1
B1
S侧 cl 5 5.
1 2D
2
C
两个底面面积为
S底
=2

1
2
2

2=6.
A
1
B
故2其019全/9/22面积为：11 5 .
4
练习1 . 若一个圆柱的侧面展开图是一个正方形，则
圆锥的侧面积展开图----扇形的圆心角为_1_8_0_ 度
解：设圆锥的底面圆半径为 由r 题意 S全 3S底

《空间几何体的体积》课件

《空间几何体的体积》课件
立方体的体积公式为 V = 边 长³；圆柱体的体积公式为 V = πr²h；球体的体积公式为 V = (4/3)πr³。
参考文献
• 张宇高等数学教材 • 数学分析习题集
圆锥体
பைடு நூலகம்
圆锥体的体积可以通过公式 V = (1/3)πr²h 来计算。
2
球体
球体的体积可以通过公式 V = (4/3)πr³ 来计算。
总结
定义
空间几何体是三维空间中的 实体物体，具有长度、宽度 和高度。
计算方法
空间几何体的体积可以通过 直接计算公式、剖法计算公 式或定积分计算公式来获得。
常见空间几何体体 积公式
定积分计算公式
某些几何体的体积计算需要使用定积分计算公式，比如球体。
常见空间几何体的体积计算
1
立方体
立方体的体积可以通过公式 V = 边长³来计算。
2
正方体
正方体的体积可以通过公式 V = 边长³来计算。
3
圆柱体
圆柱体的体积可以通过公式 V = πr²h 来计算。
常见空间几何体的体积计算（续）
1
《空间几何体的体积》PPT课 件
什么是空间几何体？
在数学中，空间几何体是三维空间中的实体物体，具有长度、宽度和高度。常见的空间几何体包括：立 方体、正方体、圆柱体、圆锥体和球体。
如何计算空间几何体的体积？
直接计算公式
某些几何体可以通过直接计算公式来获得体积，如立方体和正方体。
剖法计算公式
某些几何体可以通过剖法计算公式来获得体积，比如圆柱体和圆锥体。

空间几何体的体积PPT课件

空间几何体的体积PPT课件

类似地，底面积相等、高也相等的两个锥体，它
们的体积也相等。
由圆锥体积公式可知 V锥体=Sh/3
h
2020年9月28日
h
S
S
4
台体（棱台、圆台）的体积可以转化为锥体的体积来 计算。如果台体的上、下底面面积分别为S‘， S，高是h， 可以推得它的体积是
1 V台体 3h(S
SSS)
h
2020年9月28日
空间几何体的体积
2020年9月28日
1
类似于用单位正方形的面积度量平面图形的面积，我 们可以用单位正方体（棱长为1个长度单位的正方体）的 体积来度量几何体的体积。
一个几何体的体积是单位正方体体积的多少倍，那 么这个几何体的体积的数值就是多少。
长方体的长、宽、高分别为a，b，c，那么它的体积为
V长方体=abc 或 V长方体=Sh
h
S
S
5
想 一 想 ？
上一节中，我们知道正棱柱、正 棱锥、正棱台的侧面积之间有一定 的关系。那么，这里柱体、锥体、 台体的体积公式之间有没有类似的
关系？
柱体、锥体、台体的体积公式之间的 关系如下：
S’=S
V柱体 Sh
2020年9月28日
V台 体1 3h(S SSS`) S’=0
V锥体
1 3
Sh
6
感谢阅读！为了方便学习和使用，本文档的内容可以在下载后随意修改，调整和打印。欢迎下载！
2020年9月28日
汇报人：云博图文 日期：20XX年10月10日
8
例 有一堆相同规格的六角螺帽毛坯共重 5.8kg．已知底面六边形的边长是12mm， 高是10mm，内孔直径是10mm．那么约有 毛坯多少个？
分析：六角螺帽毛坯的体积是一个 正六棱柱的体积与一个圆柱的体积 的差，再由比重算出一个六角螺帽 毛坯的体积即可．

新人教A版必修二 空间几何体的表面积与体积 课件(11张)

新人教A版必修二 空间几何体的表面积与体积 课件(11张)

,其中S为底面面积,h为高.
3.圆台的体积公式为V= 1 π(r'2+r'r+r2)h,棱台的体积公式为V=1 (S'+ S 'S +
3
3
S)h,圆台和棱台的体积公式可以统一为V台= 1 (S'+ S 'S +S)h,其中S'、S分
3
别为上、下底面的面积,h为高.
4
4.半径为R的球的体积公式为V球=④ 3 πR3 .
方法 2 几何体体积的求解方法
1.割补法 求一个几何体的体积可以将这个几何体分割成几个柱体、锥体等(或 补形成柱体、锥体等),分别求出柱体、锥体等的体积,从而得出几何体 的体积. 2.等体积变换法 (1)利用三棱锥的“等积性”可以把任意一个面作为三棱锥的底面. (i)求体积时,可选择容易计算的方式来计算; (ii)利用“等积性”可求点到面的距离,关键是在面中选取三个点,与已 知点构成三棱锥. (2)此种方法充分体现了转化的数学思想,在运用过程中要充分注意距 离之间的等价转化.
A.5 000立方尺 C.6 000立方尺
B.5 立方尺 D.6 500立方尺
解题导引
解析 该楔体的直观图如图中的几何体ABCDEF.取AB的中点G,CD的
中点H,连接FG,GH,HF,则该几何体的体积为四棱锥F-GBCH与三棱柱
ADE-GHF的体积之和.又可以将三棱柱ADE-GHF割补成高为EF,底面
考点二 几何体的体积
1.长方体的体积公式是V=abc,正方体的体积公式是V=a3,圆柱的体
积公式是V=πr2h.所有棱柱和圆柱的体积公式可以统一为V柱=Sh,其中S
为底面面积,h为高.
2.圆锥的体积公式是V= 1 πr2h,棱锥的体积公式是V= 1Sh.圆锥和棱锥的

《空间几何体的体积》课件

《空间几何体的体积》课件

03 空间几何体的体积公式推导
球体体积公式的推导
球体体积公式
V=4/3πr^3
推导过程
通过将球体切割为无数个小的锥体，利用锥体体积公式V=1/3πr^2h求和，再 利用极限思想求得球体体积公式。
圆柱体体积公式的推导
圆柱体体积公式：V=πr^2h
推导过程：将圆柱体切割为无数个小的长方体，利用长方体体积公式V=lwh求和 ，再利用极限思想求得圆柱体体积公式。
深入研究空间几何体的性质
除了体积之外，空间几何体还有许多其他的性质和规律，如表面积、重心、转动惯量等， 对这些性质的研究将有助于更深入地理解空间几何体的本质。
应用空间几何体的体积公式解决实际问题
空间几何体的体积公式在许多领域都有广泛的应用，如物理学、工程学、经济学等，未来 可以通过更深入的研究，将这些公式应用到更多的实际问题中去。
圆台体体积公式的推导
圆台体体积公式
V=πh(R^2+Rr+r^2)/3
推导过程
将圆台体切割为无数个小的锥体，利用锥体体积公式 V=1/3πr^2h求和，再利用极限思想求得圆台体体积公式。
04 空间几何体的体积应用实例
球体在生活中的应用实例
球体体积公式
V = (4/3)πr³
篮球
篮球是球体形状的典型代表，其体积可以通过球 体体积公式计算得出。
地球
地球是一个近似于球体的天体，其体积可以通过 球体体积公式进行估算。
圆柱体在生活中的应用实例
圆柱体体积公式：V = πr²h 水桶：常见的水桶是圆柱体形状，其体积可以通过圆柱体体积公式计算得出。
饮料瓶：饮料瓶的形状通常是圆柱体，其体积也可以通过圆柱体体积公式计算。
圆锥体在生活中的应用实例
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

例3. 一个几何体的三视图如图所示，求这个几 何体的表面积.
解：由三个视图可知该几何体 是底面为直角梯形的直四棱柱( 即棱柱的侧棱垂直于底面，如 下图). 易知四个侧面都是矩形, 过点B作BE⊥CD于点E，在直 角梯形ABCD中，
A B 1 ,A D C D B E 2 ,CE 1,
BC 2212 5.
空间几何体的体积(1)
复习回顾：
圆柱、圆锥、圆台
名 圆柱 称
圆锥
圆台
侧
面
展
开
l
图
r
c
c l
r
,
r
c/
lc
r
侧
面 S侧=cl=2πrl
积
S侧
1cl 2
rl
S侧=
1 2
(c
c
/
)l
=π(r+r/)l
表 面
S2r22rl
S r2 rl
积
r(r l)
S (r'2 r2 ) (r' r)l
解：六角螺帽的体积是六棱柱的体积与 圆柱体积之差，即:
V31226103.14(10)210
4
2
2956(mm3)2.956(cm3)
所以螺帽的个数为
5 .8 1 0 0 0 ( 7 .8 2 .9 5 6 ) 2 5 2 （个）
答：这堆螺帽大约有252个．
课后作业： 习题1.3A组3、4题 课后练习： 完成本节的模块测评及课时作业
割为3个三棱锥.
A’
C’
B’
1
2
3
A
C
B
设三棱柱ABC-A’B’C’的底面积为S,高为h，则它的 体积为 Sh. 沿平面A’BC和平面A’B’C，将这个三棱柱分
割为3个三棱锥.
A’
C’ A’
A’
A’
C’
B’ 1
B’
B’
2
3
A
CA
C
C
C
B
B
B
其中三棱锥1、2的底面积SA'ABSA'B'B, 高也相等；
高血压的鉴别诊断（一）
❖ 原发性高血压 ❖ 继发性高血压
❖肾原性高血压
❖ 肾脏疾病：1.急性和慢性肾炎；2.慢性肾盂肾炎；3.放射 性肾炎；4.先天性多囊肾；5.肾结核；6.巨大肾积水；7. 肾肿瘤；8.肾结石；9.肾淀粉样变性
❖ 肾动脉疾病：先天性或后天性，也可分为血管内或血管 外病变。血管内病变包括：动脉内膜纤维组织增生、动 脉粥样硬化、肾动脉炎、肾动脉血栓形成或栓塞、肾动 脉瘤、先天性肾动脉畸形（缺如、狭窄、囊性动脉瘤）、 肾动静脉瘘、以及肾动脉外伤。肾动脉周围粘连、肾蒂 扭转，也可引起肾动脉狭窄。
D1
C1
S 1 1 1 2 2 1 1 5
A1
B1
2 1 2 2 11 5. 2
1 2D
2E
C
A1B
练习3.现有一棱长为1的正方体盒子AC′，一只蚂 蚁从A点出发经侧面一周到达A′点，问这只蚂蚁 走的最短路程是多少？
解:将正方体沿AA′展开，
D′
C′
A′
B′

A′
D C
A
❖ 病因鉴别诊断常较复杂，有赖于详细的病史采集、 体检和必要的实验室检查。 ❖要详细了解药物应用史、饮食情况、大小便情 况、有无引起高血压和或低血钾的相关疾病
❖还应注意完成下列步骤：1.是否存在转移性低 钾血症；2.是否存在摄入不足和肾外丢失过多； 3.是否存在肾脏失钾（尿钾测定）；4.血浆肾 素、ALD（血K+3mmol/L以上）、酸碱平衡状 态、阴离子间隙测定
高血压、低血钾的诊断和鉴别诊断
高血压、低血钾的诊断与鉴别诊断
❖ 明确高血压和低钾血症的诊断 ❖ 对高血压和钾缺乏程度及其临床危险性
进行判断，有无合并因素加重高血压和 低血钾危险 ❖ 病因诊断
❖一种疾病：同一种疾病两方面的表现 ❖两种疾病或情况：两种独立的疾病或情况的
临床表现
高血压、低血钾的病因鉴别诊断
3
对于任意一个底面积为S，高为h的锥体
由祖暅原理得：V锥体=V三棱锥=
1 3
Sh.
V1(S' S'SS)h
P
3
根据台体的特征，如何求台体的体积？A
x
D
圆台(棱台)是由圆锥(棱锥)截成的
S
C
B
hD
V
V大
V小
1S(h 3
x)
1 3
S'x
A
S
C
1[Sh(SS')x] 3
B
S'
x 2 S' x x S'h
高血压的鉴别诊断（二）
❖ 全身性疾病累及肾脏：1.结节性多动脉炎：发热、 WBC增多或兼有嗜酸性粒细胞增多、中度贫血、进 行性消瘦、肾功能损害。高血压是由肾小球肾炎、 或栓塞性肾炎、或多发性肾梗塞所致；2.SLE：912%，多在疾病后期，常伴有氮质血症；3.硬皮病： 在有肾损害时，可有高血压；4.多发性大动脉炎： 常引起大动脉任何部位或其分支的狭窄及闭塞，如 侵犯肾动脉，可发生肾血管性高血压，腹部或肾区 可闻及血管杂音，但通常本病以无脉征为主要临床 表现；4.糖尿病：毛细血管间肾小球硬化、肾小动 脉硬化；5.痛风；6.过敏性紫癜；7.急性肾衰；8.慢 性铅中毒
由祖暅原理得： V柱体= sh
设三棱柱ABC-A’B’C’的底面积为S,高为h，则它的 体积为 Sh. 沿平面A’BC和平面A’B’C，将这个三棱 柱分
割为3个三棱锥.
A’
C’
B’
A
C
B
设三棱柱ABC-A’B’C’的底面积为S,高为h，则它的 体积为 Sh. 沿平面A’BC和平面A’B’C，将这个三棱柱分
B
由图可知这只蚂蚁走的最短路程是 A'A 4212 1.7
夹在两个平行平面之间的两个几何体，被平 行于这两个平面的任意平面所截，如果截得的 两个截面的面积总相等，那么这两个几何体的 体积相等．
问题：两个底面积相等、高也相等的棱柱（圆柱） 的体积如何？
设有底面积都等于S，高都等于h的任意一个 棱柱、一个圆柱、和一个长方体，使它们的下 底面在同一平面内.
三棱锥2、3的底面积SB'BCSB'C'C, 高也相等；
因此三个三棱锥的体积相等，V1 V2 V3
1 3
Sh.
经探究得知，棱锥(圆锥)是同底等高的棱柱(圆柱) 的 1 ，即棱锥(圆锥)的体积：
3
V 1 S h（其中S为底面面积，h为高）
3
由此可知，棱柱与圆柱的体积公式类似，都是底面面积乘高；棱 锥与圆锥的体积公式类似，都是等于底面面积乘高的 ．1
S (h x )2 S hx
S S'
V1h[S(SS') S' ] 1[S SS' S']h
3
S S' 3
柱体、锥体、台体的体积公式之间有什么关系？
上底扩大
上底缩小
VSh
S' S V1(S' S'SS)h S ' 0
V
1 Sh
3
3
例3．有一堆规格相同的铁制（铁的密度是 7.8g/)c六m3角螺 帽共重5.8kg，已知底面是正六边形，边长为12mm,内 孔直径为10mm，高为10mm，问这堆螺帽大约有多少 个（ 取3.14，可用计算器）？