(推荐)6-随机振动分析

随机结构激励模型及随机振动反应分析结构在服役期间，必将受到各种荷载的作用。

对于建筑结构，在服役期间不可避免的会受到风力的作用，而且甚至会受到地震的作用；海洋上的结构，如海上风力发电高塔，海洋平台等，会受到海洋波浪的作用；行驶在路面上的车辆，由于路面的不平顺使得车辆受到动力作用；飞机在飞行中由于大气的自由流动也会受到扰动。

这些作用在结构上的荷载，不仅随着时间发生变化，而且具有明显的随机性。

而对于随机动力荷载下结构响应的问题，确定性的动力分析无法考虑随机性，随机振动理论应运而生。

随机振动的物理数学基础早在30年代已基本奠定。

1827年Brown对悬浮在水中微小花粉粒子杂乱运动的观察，为最早的系统对随机激励响应的实验研究。

19世纪后期Maxwell和Boltzmann用统计方法描述系统可能状态和达到的概率，但没有考虑统计随时间的演化。

1919年Rayleigh用“随机振动”一词描述一等价于平面随机行走的声学问题。

用随机方法研究动力学行为始于1905年，Ein stein从理论上解释了Brown运动，1915年Smoluchowski扩展了Einstein的结果并进行实验研究。

1908年Langevin导出含有随机项的微分方程，成为随机微分方程的第一个例子，Fokker于1915年、Plank于1917年、Колмогоров于1931年、伊藤于1946年都对随机微分方程的研究作出贡献。

1933年Андронов等应用随机微分方程讨论随机扰动下一般动力系统的运动。

1920年Taylor引入相关函数概念，Wiener于1930年和Хинчин于1934年分别建立了谱的理论，这些数学工具首先应用于通讯和控制系统而不是结构和机械的强度分析，因为工程技术尚无此要求。

随机振动的研究始于50年代中期。

由于喷气和火箭技术的发展在航空和航天工程中提出一系列问题，如大气湍流引起的飞机颤振，喷气噪音导致的飞行器表面结构声疲劳，传动系统中滚动件不光滑而啮合不完善的损伤积累，火箭推进中运载工具有效负载可靠性等，都促使研究者运用已有数学工具，并借鉴这些工具在通讯等学科中的应用以解决面临的工程问题。

随机振动系统的建模与分析随机振动是指振动的激励力和/或系统自身的固有参数具有不确定性的振动。

随机振动系统普遍存在于许多领域，如航空航天、土木结构、能源、环境和生物医药等。

因此，研究随机振动现象具有重要的理论和实际意义。

本文将介绍随机振动系统的建模与分析方法。

一、随机振动系统的特点随机振动系统相比于确定性振动系统而言，其具有以下几个显著的特点：1. 激励力的随机性。

激励力通常是噪声、风、地震、电磁干扰等不稳定因素，其具有随机性和不可预测性。

2. 系统特性参数的随机性。

振动系统的特性参数，如质量、刚度、阻尼等都有可能受到制造和安装误差的影响而产生随机性。

3. 振动响应的随机性。

由于振动系统存在着上述两种随机因素的影响，其振动响应也具有随机性。

二、建模方法随机振动系统建模的主要方法有两种，即时域方法和频域方法。

1. 时域方法时域是指由时间t表示的振动信号的域。

时域方法是指通过时间t和振动响应x(t)或速度v(t)、加速度a(t)等时域信号进行随机振动系统的建模和分析。

其中常用的时域方法包括统计时域分析、偏微分方程映射（PDE）方法和随机分析方法等。

2. 频域方法频域是指通过频率f表示的振动信号的域。

频域方法是指通过频率f和振动响应X(f)、速度V(f)、加速度A(f)等频域信号进行随机振动系统的建模和分析。

其中常用的频域方法包括功率谱密度（PSD）分析、阻尼比分析和极值理论等。

不同的振动系统建模方法适用于不同的振动系统类型，选择适当的方法进行建模和分析非常重要。

三、分析方法1. 单自由度（SDOF）系统SDOF系统是指具有一个自由度的振动系统，例如简谐振子、单摆等。

对于SDOF系统，可通过阻尼比和显著性水平等简易参数来描述其振动响应特性。

SDOF系统的分析可以采用传递函数、相关函数、频率响应函数等方法。

2. 多自由度（MDOF）系统MDOF系统是指具有多个自由度的振动系统，例如桥梁、建筑物等。

由于振动系统的振动响应受到多种因素的影响，其分析复杂度较高。

Alex-dreamer制作PSD：（可以相互传阅学习，但是鄙视那些拿着别人成果随意买卖！）PSD随机振动应用领域很广，比如雷达天线，飞机，桥梁，天平，地面，等等行业。

虽然现在对这方面公开资料很少，但是我相信以后会越来越多，发展的越来越成熟。

学术的浪潮总体是向前的，不会因为几个大牛保密自己的成果就会阻止我们对PSD研究，因此结合我的经验和爱好，我研究了一下两种PSD加载分析。

我标价的原则是含金量大小和花费我的时间以及我的经验值，如果你觉得值，就买；不值就不要下了。

因为我始终认为：士为知己者死，女为悦己者容。

算是互相尊重。

如果你得到这份资料，那就祝你好运！Good luck!-Alex-dreamer(南理工)一：目的：根据abaqus爱好者提出的PSD随机振动分析，提出功率谱如何定义及如何加载？如果功率谱是加速度的平方，如何加载？如果在输入点施加载荷功率谱如何定义？本文将给出详细的分析过程。

二：随机振动基本概念1. 随机振动的输入量和输出量都是概率统计值，因此存在不确定性。

输入量为PSD （功率谱密度）曲线，分为加速度、速度、位移或者力的PSD曲线；最常见的是加速度PSD，常用语BASE MOTION基础约束加载。

2. 随机振动的响应符合正态分布，PSD实际上是随机变量的能量分布，也就是在不同频率上的方差值，反映不同频率处的振动能量，PSD曲线所围成的面积是随机变量总响应的方差值；3. RMS为随机变量的标准方差，将PSD曲线包络面积开平方即为RMS。

4. 随机振动输出的位移、应力、应变等值都是对应不同频率的方差值（即PSD值），量纲为x^2，当然也可以输出这些变量的均方根值（即RMS值）；abaqus6.10以上版本可以直接在场变量里面输出设置。

见下文。

5. 如果是单个激励源，定义为非相关性分析，如是多个激励源，则需要定义相关性参数。

因此出现type=uncorrelated。

三：模型简介：1）该模型很简单，是hypermesh中一个双孔模型。

机械工程中的随机振动分析方法摘要随机振动分析方法是机械工程领域中重要的分析方法之一。

本文通过分析机械系统中的随机振动问题，介绍了随机振动相关的概念和分析方法，包括概率分布、功率谱密度、相关函数、自相关函数等。

同时，本文还介绍了随机振动分析方法的具体应用，例如在机械系统的设计、运动控制、故障诊断和损伤检测中的应用。

通过本文的阅读，读者将了解到随机振动分析方法在机械工程中的应用，以及如何通过这些方法更好地解决机械系统中的随机振动问题。

1.引言机械系统中的随机振动问题是机械工程中常见的问题之一。

对于机械系统而言，振动是不可避免的，然而，振动如果过于剧烈或者频率过高，就会引起机械系统的不稳定甚至毁坏。

因此，机械工程师需要对机械系统中的随机振动进行分析和处理。

随机振动分析方法是一种重要的机械工程分析方法。

本文将通过分析机械系统中的随机振动问题，介绍随机振动相关的概念和分析方法，并且将展示如何通过这些分析方法更好地解决机械系统中的随机振动问题。

2.随机振动的概念随机振动是指振动信号在时间域和频率域上都是随机的。

在机械系统中产生随机振动的原因很多，例如系统的结构松散、摩擦、失衡等。

对于机械系统而言，随机振动是不稳定的，因此需要进行分析和处理。

在进行随机振动分析时，我们需要了解以下几个概念：概率分布：指在一定范围内，每个随机事件发生的可能性大小。

在随机振动分析中，常用的概率分布包括正态分布、均匀分布等。

功率谱密度：指一个信号在频率域上的能量分布。

功率谱密度可以通过傅里叶变换将信号从时间域转换到频率域上进行计算。

相关函数：指在时间域上两个信号之间的相关性。

相关函数可以用来描述振动信号的相似程度。

自相关函数：指一个信号与自己的相关性。

自相关函数可以用来描述信号的周期性和重复性。

3.随机振动分析方法3.1 概率分布分析法在机械系统中，常用的随机振动分析方法之一是概率分布分析法。

概率分布分析法通过对信号的统计特性进行分析，得出信号的概率分布。

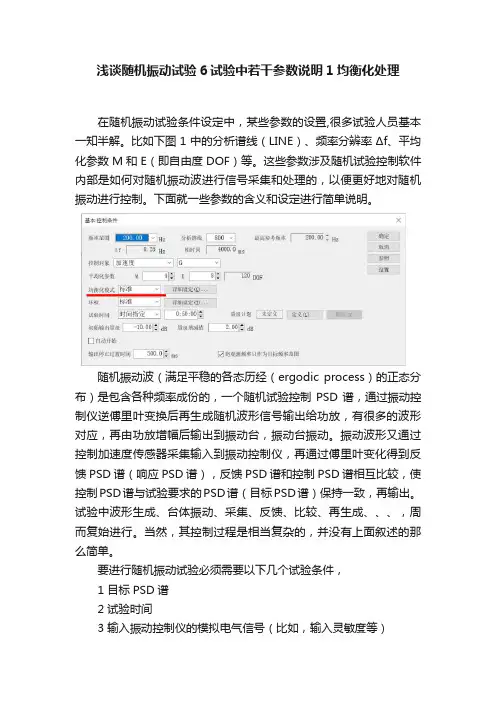
浅谈随机振动试验6试验中若干参数说明1均衡化处理在随机振动试验条件设定中，某些参数的设置,很多试验人员基本一知半解。

比如下图1中的分析谱线（LINE）、频率分辨率Δf、平均化参数M和E（即自由度DOF）等。

这些参数涉及随机试验控制软件内部是如何对随机振动波进行信号采集和处理的，以便更好地对随机振动进行控制。

下面就一些参数的含义和设定进行简单说明。

随机振动波（满足平稳的各态历经（ergodic process）的正态分布）是包含各种频率成份的，一个随机试验控制PSD谱，通过振动控制仪逆傅里叶变换后再生成随机波形信号输出给功放，有很多的波形对应，再由功放增幅后输出到振动台，振动台振动。

振动波形又通过控制加速度传感器采集输入到振动控制仪，再通过傅里叶变化得到反馈PSD谱（响应PSD谱），反馈PSD谱和控制PSD谱相互比较，使控制PSD谱与试验要求的PSD谱（目标PSD谱）保持一致，再输出。

试验中波形生成、台体振动、采集、反馈、比较、再生成、、、，周而复始进行。

当然，其控制过程是相当复杂的，并没有上面叙述的那么简单。

要进行随机振动试验必须需要以下几个试验条件，1 目标PSD谱2 试验时间3 输入振动控制仪的模拟电气信号（比如，输入灵敏度等）1和2是随机振动试验直接的要求，3是力学量和电气量转换需要的变换器。

有了这三个条件，随机振动控制仪便可动作。

为了防止损坏试验体和振动台，随机试验一开始并不是直接100%量级进行试验的，而是先发出一个白噪音谱来进行低量级的驱动，即在进行随机振动试验前，控制仪会先进行均衡化处理（equalization）。

因为试验体传递特性的差异，振动控制仪需要对此传递特性进行均衡处理，使输出的驱动信号能够满足目标谱，并使功放满足输出。

图2是均衡的示意图，振动系的传递特性H(f)，为了使控制点R处的响应谱φ(f)和目标谱Ref(f)一致，控制仪的输出信号谱Drive(f)需满足H(f)的相反曲线形状。

随机振动分析(PSD分析)随机振动分析Training ManualWor 主题:定义的rkbench •定义和目的•WorkBench 分析功能概述h-Simul •分析步骤lation D D ynamic c sA.定义和目的Training ManualWor 什么是随机振动分析(PSD——Power Spectrum Density 功率谱密度)?rkbench –功率谱密度谱是基于概率统计学的一个谱分析技术，是对随机变量均方值的度量一般用于随机振动分析。

连续瞬态响应只能通过概率分布函数进行描述h-Simul ,，即出现某水平响应所对应的概率。

功率谱密度是结构在随机动态载荷激励下响应的统计结果是一条功率谱密lation D –功率谱密度是结构在随机动态载荷激励下响应的统计结果，是条功率谱密度值——频率值的关系曲线，功率谱密度可以位移、速度、加速度、力功率谱密度形式。

Dynamic –例如火箭在每次发射中由载荷（例如加速度载荷等）产生的不同时间历程cs… 定义和目的Training ManualWor 什么PSD?激励响应的均值频率的关系此条功率谱密rkbench •PSD记录了激励和响应的均方值同频率的关系，因此PSD 是一条功率谱密度值－频率值的关系曲线–PSD曲线下的面积就是方差，即响应标准偏差的平方值h-Simul 曲线下的面积就是方差即响应标准偏差的平方值–PSD 的单位是mean square/Hz （如加速度PSD 单位G 2/Hz ）–PSD 可以是位移、速度、加速度、力或者压力lation D D ynamic c s…定义和目的Training ManualWor •典型的应用包括：飞机电子封装rkbench ––大气载荷作用下的飞机部件–爆破导流片h-Simul –激光制导系统–光学望远镜平台lation D –大型结构的地震载荷Dynamic c s…定义和目的Training ManualWor •由于时间历程不是确定的，所以瞬态分析不是可选的。

随机振动分析在统计学中的应用随机振动是指在时间上无规律变化的振动，其幅值、频率和相位均为随机变量。

随机振动分析是一种研究随机振动特性的方法，广泛应用于工程、物理、生物等领域。

然而，人们往往忽视了随机振动分析在统计学中的重要应用。

本文将探讨随机振动分析在统计学中的应用，并介绍其在统计学研究中的意义和方法。

一、随机振动在统计学中的意义统计学是研究数据收集、整理、分析和解释的科学，而随机振动分析是一种研究随机性的方法。

在统计学中，我们经常需要处理大量的数据，这些数据往往受到各种随机因素的影响。

随机振动分析可以帮助我们理解数据背后的随机性特征，从而更好地进行统计推断和决策。

二、随机振动分析的方法1. 随机振动的模型随机振动的模型是研究随机振动特性的基础。

常见的随机振动模型包括白噪声模型、布朗运动模型、随机游走模型等。

这些模型可以描述随机振动的统计特性，如均值、方差、自相关函数等。

2. 随机振动的频谱分析频谱分析是研究振动信号频率特性的方法，也是随机振动分析的重要内容之一。

通过对振动信号进行频谱分析，可以得到振动信号的频率分布情况，进而了解其频率特性和谱密度函数。

频谱分析在统计学中常用于研究时间序列数据的周期性和趋势性，例如经济指标的季节变动和长期趋势等。

3. 随机振动的概率分布随机振动的概率分布是研究振动信号幅值特性的方法。

常见的概率分布包括正态分布、指数分布、泊松分布等。

通过对振动信号进行概率分布分析，可以得到振动信号的概率密度函数和累积分布函数，从而了解其幅值分布情况和极值特性。

概率分布分析在统计学中常用于研究随机变量的概率特性和极值分布，例如极端气候事件的频率和强度等。

三、随机振动分析在统计学研究中的应用1. 时间序列分析时间序列分析是研究随机变量随时间变化规律的方法，也是统计学中的重要分析方法之一。

随机振动分析可以帮助我们理解时间序列数据的随机性特征，如趋势、周期、季节性等。

通过对时间序列数据进行随机振动分析，可以得到数据的自相关函数和偏自相关函数，从而了解数据的相关性和预测性。