数字信号处理_吴镇扬_第二版_第二章习题答案

习题一 (离散信号与系统)1.1周期序列，最小周期长度为5。

1.2 (1) 周期序列，最小周期长度为14。

(2) 周期序列，最小周期长度为56。

1.5()()()()()()()11s a s s s a n s s a s n X j x t p t X j ΩP j Ω2n τn τj sin j Ωjn e X 2n π2n n τj Sa X j jn e 2T 2πττ∞=-∞∞=-∞Ω==*⎡⎤⎣⎦ΩΩ⎛⎫-=-Ω ⎪⎝⎭ΩΩ⎛⎫-=Ω-Ω ⎪⎝⎭∑∑F 1.6 (1) )(ωj e kX (2) )(0ωωj n j e X e (3) )(21)(2122ωωj j e X e X -+ (4) )(2ωj e X1.7 (1)0n z -(2)5.0||,5.0111>--z z(3)5.0||,5.0111<--z z(4)0||,5.01)5.0(11101>----z zz1.8 (1) 0,)11()(211>--=---z z z z z X N (2) a z az az z X >-=--,)1()(211(3)a z az z a az z X >-+=---,)1()(311211.9 1.10(1))1(2)(1----+n u n u n (2))1(24)()5.0(6--⋅--n u n u n n (3))()sin sin cos 1(cos 000n u n n ωωωω++(4) )()()(1n u a a a n a n ---+-δ1.11 (1) )(1z c X - (2) )(2z X (3) )()1(21z X z -+ (4) -+<<x x R z R z X /1/1),/1(1.12 (1)1,11<-ab ab(2) 1 (3) 00n a n1.13 (1) 该系统不是线性系统；该系统是时不变系统。

根据零、 极点分布可定性画幅频特性。 当频率由0到2π 变化时， 观察零点矢量长度和极点矢量长度的变化， 在极点 附近会形成峰。 极点愈靠进单位圆， 峰值愈高； 零点附近形 成谷， 零点愈靠进单位圆， 谷值愈低， 零点在单位圆上则 形成幅频特性的零点。 当然， 峰值频率就在最靠近单位圆的 极点附近， 谷值频率就在最靠近单位圆的零点附近。
故
X (z)z 1zN z 1 N (z 1 1 )zN z 1 N (z 1 1 )z2 1 N 1 zz N 1 1 2
［例2.4.4］ 时域离散线性非移变系统的系统函数H(z)为
H(z) 1 , a和b为常数 (za)(zb)
（1） 要求系统稳定， 确定a和b的取值域。 （2） 要求系统因果稳定， 重复（1）。 解： （1） H(z)的极点为a、 b， 系统稳定的条件是收敛 域包含单位圆， 即单位圆上不能有极点。 因此， 只要满足 |a|≠1, |b|≠1即可使系统稳定， 或者说a和b的取值域为除单位圆 以的整个z平面。 （2） 系统因果稳定的条件是所有极点全在单位圆内， 所以a和b
采样间隔T=0.25 s， 得到 xˆ ( t ) ， 再让 xˆ ( t ) 通过理想低通
滤波器G(jΩ)， G(jΩ)用下式表示:
G(j)0.025
≤ 4π 4π
(1) 写出xˆ ( t )的表达式;
(2) 求出理想低通滤波器的输出信号y(t)。
解：(1)
x ˆ(t) [c2 o πn s)T (co 5πs n()T ](tn)T n
（3） 若y(n)=x(n)h(n), 则
Y(ej)1H(ej)X(ej) 2π
这是频域卷积定理或者称复卷积定理。
（4）
xe(n)12[x(n)x(n)]

2－1 试求如下序列的傅里叶变换： （1）)()(01n n n x -=δ （2）)1(21)()1(21)(2--++=n n n n x δδδ （3）),2()(3+=n u a n x n10<<a（4）)4()3()(4--+=n u n u n x（5）∑∞=-⎪⎭⎫⎝⎛=05)3(41)(k nk n n x δ（6）()6cos ,14()0,n n x n π⎧-≤≤=⎨⎩其他解： （1） 010()()j n j j nn X e n n ee ωωωδ∞--=-∞=-=∑（2） 2211()()122j j nj j n X e x n e e e ωωωω∞--=-∞==+-∑ωsin 1j +=（3） 2232()(2)1j j nj nn j nj n n a e X e a u n ea eaeωωωωω-∞∞---=-∞=-=+==-∑∑， 10<<a（4） []4()(3)(4)j j nn X e u n u n eωω∞-=-∞=+--∑∑-=-=33n nj e ω∑∑==-+=313n n j n nj e eωω（等比数列求解）ωωωωωj j j j j e e e e e --+--=--111134=⎪⎭⎫ ⎝⎛⎪⎭⎫⎝⎛=----ωωωωω21sin 27sin 1137j j j e ee ((1-e^a)提出e^(0.5a))（5） 3350011()(3)44nkj jn j k n k k X e n k e e ωωωδ∞∞+∞--=-∞==⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭∑∑∑∑∞+=--⎪⎭⎫⎝⎛-=⎪⎭⎫⎝⎛=033411141k j kj e e ωω（6） 44336441()cos 32j j j jn jn n n X e nee e e ππωωωπ---=-=-⎛⎫==+ ⎪⎝⎭∑∑994()()4()()3333001122j j n j j n n n e e e e ππππωωωω--++===+∑∑ ()9()9334()4()33()()3311112211j j j j j j e e e e e e ππωωππωωππωω-+-+-+⎡⎤⎡⎤--⎢⎥⎢⎥=+⎢⎥⎢⎥++⎢⎥⎢⎥⎣⎦⎣⎦2－2 设信号}1,2,3,2,1{)(---=n x ，它的傅里叶变换为)(ωj e X ，试计算(1)0()j X e （２）()j X ed πωπω-⎰（３）2()j X e d πωπω-⎰。

第二章习题解答1、求下列序列的z 变换()X z ，并标明收敛域，绘出()X z 的零极点图。

(1) 1()()2nu n (2) 1()()4nu n - (3) (0.5)(1)nu n --- (4) (1)n δ+(5) 1()[()(10)]2nu n u n -- (6) ,01na a <<解：(1) 00.5()0.50.5nn n n zZ u n z z ∞-=⎡⎤==⎣⎦-∑，收敛域为0.5z >，零极点图如题1解图(1)。

(2) ()()014()1414n nn n z Z u n z z ∞-=⎡⎤-=-=⎣⎦+∑，收敛域为14z >，零极点图如题1解图(2)。

(3) ()1(0.5)(1)0.50.5nnn n zZ u n z z --=-∞-⎡⎤---=-=⎣⎦+∑，收敛域为0.5z <，零极点图如题1解图(3)。

(4) [](1Z n z δ+=，收敛域为z <∞，零极点图如题1解图(4)。

(5) 由题可知，101010910109(0.5)[()(10)](0.5)()(0.5)(10)0.50.50.50.50.50.5(0.5)n n nZ u n u n Z u n Z u n z z z z z z z z z z z --⎡⎤⎡⎤⎡⎤--=--⎣⎦⎣⎦⎣⎦⋅=-----==--收敛域为0z >，零极点图如题1解图(5)。

(6) 由于()(1)nn n a a u n a u n -=+--那么，111()(1)()()()nn n Z a Z a u n Z a u n z z z a z a z a a z a z a ----⎡⎤⎡⎤⎡⎤=---⎣⎦⎣⎦⎣⎦=----=-- 收敛域为1a z a <<，零极点图如题1解图(6)。

(1) (2) (3)(4) (5) (6)题1解图2、求下列)(z X 的反变换。

jw0 n
u (n)] e jw0n z n
n 0
1 1 (e jw0 z 1 )
(1) 解：令 y (n) RN (n)
由题意可知，所求序列等效为 x (n 1) y (n) y (n) 。
Z [ y (n)] z n
n 0
N 1
1 zN z N 1 , 1 z 1 z N 1 ( z 1)
1
A B 1 2 1 1 1 1 z 1 2z 1 z 1 2 z 1 B 1 | 1 2 1 z 1 z 1 2
1 | 1 1 1 2 z 1 z 1
x(n) u (n) 2 2 n u ( n 1) u (n) 2 n 1u ( n 1)
n0
若n0 0时，收敛域为：0 z ;
(2) 解： Z [0.5 u (n)]
n
若n0 0 时，收敛域为： z 0 z 0.5
0.5
n 0

n
z n
1
1 , 1 0.5 z 1
n
(3) 解： Z [ 0.5 u ( n 1)]
n
n
j j 1 1 (3) X (e 2 ) X ( e 2 ) 2 2 j
(2) e
j n0
X (e j ) （移位特性）


2
数字信号处理习题指导

G ( z ) ZT [ x (2n)] G( z)
n
g ( n )e

jwn
令n' 2n, 则
n ' 取偶数
( z 5) z n |z 0.5 (1 0.5 z)

n n
(4) h(n)=( (5) h(n)=
1 n ) u(n) 2
1 u(n) n
n
(6) h(n)= 2 R n u(n)
解 （1）因为在 n<0 时，h(n)= 2 ≠0,故该系统不是因果系统。
n
因为 S=
n =−∞
∑
∞
|h(n)|=
∑
n =0
∞
|2 |=1< ∞ ，故该系统是稳定系统。
n
(2) 因为在 n<O 时，h(n) ≠0，故该系统不是因果系统。 因为 S=
n =−∞
n =−∞
(4) 因为在 n<O 时，h(n)=0，故该系统是因果系统 。 因为 S= |h(n)|=
n =−∞
∑
n=0
|(
1 n ) |< ∞ ，故该系统是稳定系统。 2
(5) 因为在 n<O 时，h(n)=
1 u(n)=0，故该系统是因果系统 。 n
因为 S=
n =−∞
∑ ∑
∞
∞
|h(n)|=
第二章
2.1 判断下列序列是否是周期序列。若是，请确定它的最小周期。 （1）x(n)=Acos( （2）x(n)= e (
j
π 5π n+ ) 8 6
n −π) 8 π 3π （3）x(n)=Asin( n+ ) 4 3
(1)对照正弦型序列的一般公式 x(n)=Acos( ωn + ϕ )，得出 ω =
∞
=
k =0
∑ u(k )u(n − k ) =(n+1),n≥0
即 y(n)=(n+1)u(n) (2) y(n)= ∑ λ k u (k )u (n − k )

x ( m) x1 (m) = 0
或
m = 0,± M ,±2M ,⋯
其它
∞
(6.2a)
(6.2b .2b) x1 (m) = x(m) p(m) = x(m) ∑ δ (m − Mi) (6.2b)
i =−∞
是一脉冲串序列， 式中 p(m) 是一脉冲串序列， 它在 M 的整数倍处的值 其余皆为零。 表示将采样率减少 为 1，其余皆为零。令 ↓M 表示将采样率减少 M 倍 的抽取， 6.1.1） 6.1.2 式的含意如图 6.1.1 （6.1.1 和 .2） 6.1. 的抽取， 6.1.1） （6.1.2） （ 所示， M=3。 所示，图中 M=3。
1 p( n ) = M 数展开。 数展开。
M −1 k =0
e j 2πnk / M 为周期序列 p(n) 的付里叶级 p(n)的付里叶级 ∑
所以
1 M −1 j (ω − 2πk ) / M ′(e ) = X ) （6.4） .4） ∑ X (e M k =0
jω
′(e jω ) ， X (e jω ) 分 别 是 x ′(n) 和 x (n) 的 式中 X DTFT。这样， DTFT。这样， X ′(e jω ) 是原信号频谱 X (e jω ) 先作 的移位叠加 位叠加， M 倍的扩展再在 ω 轴上每隔 2π / M 的移位叠加，
而 X 1 (e ) =
jω n = −∞
∞
∑ x ( n ) p ( n)e
− jωn
1 M −1 j 2πnk / M − jωn = ∑ [ x ( n) ]e ∑e n = −∞ M k =0 1 M −1 = X (e j (ω − 2πk / M ) ) (6.3b (6.3b) ∑ M k =0

部分练习题参考答案第二章2.1 )1(2)(3)1()2(2)(-+++-+=n n n n n x δδδδ)6()4(2)3()2(-+-+-+-+n n n n δδδδ2.2 其卷积过程如下图所示)5(5.0)4()3()2(5.2)1(5)(2)(-------+-+=n n n n n n n y δδδδδδ2.3 （1）3142,73==ωππω这是有理数，因此是周期序列。

周期N =14。

（2）k kp ππ168/12==，k 取任何整数时，p 都不为整数，因此为非周期序列。

（3）k kp k k p 45.02,5126/5221====ππππ，当p 1，p 2 同时为整数时k =5,x (n )为周期序列,周期N =60。

（4）k kp πππ25.16.12==，取k =4，得到p =6，因此是周期序列。

周期N =6。

2.4 （1） ∑∞-∞=-=*=m m n R m R n h n x n y )()()()()(45(a) 当n <0 时，y (n )=0-0.5 -1 2.55h (m ) x (m ) 00 mm-121 0.51 2 h (0-m)m-121 h (-1-m)m-12 1h (1-m) 0m-121y (n )n-12(b) 当30≤≤n 时，11)(0+==∑=n n y nm(c) 当74≤≤n 时，n n y n m -==∑-=81)(34(d) 当n>7时，y (n )=0所以743070810)(≤≤≤≤><⎪⎩⎪⎨⎧-+=n n n n n n n y 或 （2）)2(2)(2)]2()([)(2)(444--=--*=n R n R n n n R n y δδ)]5()4()1()([2-----+=n n n n δδδδ（3）∑∞-∞=--=*=m mn m n u m R n y n x n y )(5.0)()()()(5∑∞-∞=--=m mnm n u m R )(5.0)(5.05(a) 当n <0 时，y (n )=0 (b) 当40≤≤n 时，n n nnm mn n y 5.0221215.05.05.0)(1-=--==+=-∑(c) 当5≥n 时，n nm mn n y 5.03121215.05.05.0)(540⨯=--==∑=- 最后写成统一表达式：)5(5.031)()5.02()(5-⨯+-=n u n R n y nn（4）∑∞-∞=-=*=m mn m R n h n x n y 5.0)()()()(3(a) 当n ≤0 时，y (n )=0(b) 当31≤≤n 时，n nnn m mnn y 5.0121215.05.05.0)(1-=--==∑-=-(c) 当54≤≤n 时，25.05.01621)21(25.05.05.0)(6232-⨯=--==---=-∑n n n nn m mnn y(d) 当n ≥6时，y (n )=0)5(25.0)4(75.0)3(875.0)2(75.0)1(5.0)(-+-+-+-+-=n n n n n n y δδδδδ2.6 （1）非线性、移不变系统（2）线性、移不变系统 （3）线性、移变系统 （4）非线性、移不变系统 （5）线性、移变系统2.7 （1）若∞<)(n g ，则稳定，因果，线性，时变（2）不稳定，0n n ≥时因果，0n n <时非因果，线性，时不变 （3）线性，时变，因果，不稳定 2.8 （1）因果，不稳定（2）因果，稳定（3）因果，稳定 （4）因果，稳定 （5）因果，不稳定 （6）非因果，稳定 （7）因果，稳定 （8）非因果，不稳定 （9）非因果，稳定 （10）因果，稳定2.9 因为系统是因果的，所以0)(,0=<n h n令)()(n n x δ=，)1(5.0)()1(5.0)()(-++-==n x n x n h n h n y 1)1(5.0)0()1(5.0)0(=-++-=x x h h15.05.0)0(5.0)1()0(5.0)1(=+=++=x x h h 5.0)1(5.0)2()1(5.0)2(=++=x x h h 25.0)2(5.0)3()2(5.0)3(=++=x x h h 15.0)1(5.0)()1(5.0)(-=-++-=n n x n x n h n h所以系统的单位脉冲响应为)1(5.0)()(1-+=-n u n n h n δ2.10 （1）初始条件为n <0时，y (n )=0设)()(n n x δ=，输出)(n y 就是)(n h 上式可变为)()1(5.0)(n n h n h δ+-=可得 11)1(5.0)0(=+-=h h 依次迭代求得5.00)0(5.0)1(=+=h h25.00)1(5.0)2(=+=h hn n h n h 5.00)1(5.0)(=+-=故系统的单位脉冲响应为)(5.0)(n u n h n= （2）初始条件为n ≥0时，y (n )=0)]()([2)1(n x n y n y -=-0,0)(≥=n n h2)]0()0([2)1(-=-=-x h h 22)]1()1([2)2(-=---=-x h h 32)]2()2([2)3(-=---=-x h hn n h n h 2)1(2)(-=+=所以)1(2)(---=n u n h n2.11 证明（1）因为∑∞-∞=-=*m m n h m x n h n x )()()()(令m n m -='，则)()()'()'()()('n x n h m h m n x n h n x m *=-=*∑∞-∞=（2）利用（1）证明的结果有)]()([)()]()([)(1221n h n h n x n h n h n x **=**∑∞-∞=-*-=m m n h m n h m x )]()()[(12∑∑∞-∞=∞-∞=--=m k k m n h k h m x )()()(12交换求和的次序有∑∑∞-∞=∞-∞=--=**k m k m n h m x k h n h n h n x )()()()]()([)(1221∑∞-∞=-*-=k k n h k n x k h )]()()[(12)]()([)(12n h n x n h **= )()]()([21n h n h n x **=（3）∑∞-∞=-+-=+*m m n h m n h m x n h n h n x )]()()[()]()([)(2121∑∑∞-∞=∞-∞=-+-=m m m n h m x m n h m x )()()()(21)()()()(21n h n x n h n x *+*=2.12 ∑∞-∞=--=*=m m n Nm n u a m Rn y n x n y )()()()()(∑∞-∞=--=m m Nnm n u a m Ra)()((a) 当n <0 时，y (n )=0(b) 当10-≤≤N n 时，11/11)/1(1)(110--=--==++=-∑a a a a a aan y n n nnm mn(c) 当N n ≥时，1)/1(1)/1(1)(111--=--==+-+-=-∑a a a a a a aan y N n n N nN m mn最后写成统一表达式：)(1)(11)(111N n u a a a n R a a n y N n n N n ---+--=+-++ 2.13 )]4()([*)()()()(11--=*=n n n u n h n x n y δδ)()4()(4n R n u n u =--=)()()()()(421n u a n R n h n y n y n *=*=)4(1)(113141---+--=-++n u a a a n R a a n n n2.14 （1）采样间隔为005.0200/1==T)()82sin()(ˆ0nT t nT f t xn a -+=∑∞-∞=δππ)()8100sin(nT t nT n -+=∑∞-∞=δππ（2）)85.0sin()(ππ+=n n x数字频率πω5.0=，42=ωπ，周期N =42.15 （1）0)()(0n j n n j j e e nn eX ωωωδ-∞-∞=-=-=∑ （2）∑∑∞=-+-∞-∞=-==0)(0)()(n n j n j n nj j e e en x eX ωωαωω∑∞=--=0)(0n nj eeωωα)(01ωωα---=j ee （3）∑∑∑∞=+-∞=--∞-∞=-===)(0)()(n n j n nj nn nj j e eeen x eX ωαωαωω)(11ωαj e +--=（4）∑∑∞=--∞-∞=-==0cos )()(n n j n n nj j ne e en x eX ωαωωω∑∑∞=----+---∞=-+=+=0)()(0][21)(210000n n j j n j j nj n j n j n ne e e e e e ωωαωωαωωωααωαωαωωωαωωαωω2200)()(cos 21cos 111112100------+----+--=⎥⎦⎤⎢⎣⎡-+-=e e e e e e e e e e j j j j j （5）nj N N n n nj j e n N en x eX ωωωπ--=∞-∞=-∑∑⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+==12cos 1)()( ∑∑-=---=-++=1212)(21N N n n j n N j nN j N Nn nj e e e eωππω ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--+--+--=+-+-+-------)()()()()()(1)1(1)1(211)1(ωπωπωπωπωπωπωωωN j N N j N N j N j N N j N N j j Nj Nj e e e e e e e e e-0.92-0.380.920.38x (n ) 0nωωωωωωπωN j j j j N j e N e e Ne N e N 232)123()2cos(cos 21cos 12sin )2sin(------+--+=2.16 （1）⎰⎰⎰-==--πωπωππωωωπωπωπ002121)(21)(d je d je d e e H n h n j nj n j j ⎪⎩⎪⎨⎧=--=为奇数为偶数n n n n n ππ20)1(1 （2）)sin()()()(011n n h n x n y ω=*=)cos()()()(022n n h n x n y ω-=*=2.17 （1）)(ωj eX -*（2）)]()([21ωωj j e X eX -*+（3）)]()([2122ωωj j e X e X -+（4）)(2ωj e X2.18采样间隔为25.0=T ，采样频率π8=Ωs)(1t y a 没有失真，因为输入信号的频率π21=Ω小于π42=Ωs)(2t y a 失真，因为输入信号频率π52=Ω大于π42=Ωs第三章3．1 设)(ωj eX 和)(ωj e Y 分别是)(n x 和)(n y 的傅里叶变换，试求下列序列的傅里叶变换：（1）)(0n n x - （2） )(*n x （3） )(n x - （4） )(*)(n y n x （5） )()(n y n x ∙ （6） )(n nx （7） )2(n x （8）)(2n x （9）⎩⎨⎧===奇数，偶数n n n x n x 0),2()(9解：（1） FT[)(0n n x -]=∑∞-∞=--n n j e nn x ω)(0令0n n n -='，0n n n +'=，则FT[)(0n n x -]=)()(00)(ωωωj n j n n n j e X e e n x -∞-∞=+''-='∑ （2） FT[)(*n x ]=)(*])([)(**ωωωj n n j n nj e X e n x en x-∞-∞=-∞-∞=-∑∑==（3） FT[)(n x -]=∑∞-∞=--n nj en x ω)(令n n -='，则FT[)(n x -]=∑∞-∞=''n n j e n x ω)()(ωj e X -=（4） FT[)(*)(n y n x ]=)(ωj eX )(ωj e Y证明 )(*)(n y n x =∑∞-∞=-m m n y m x )()(FT[)(*)(n y n x ]=∑∑∞-∞=-∞-∞=-n nj m em n y m x ω)]()([令m n k -=，则FT[)(*)(n y n x ]=m j k kj m e ek y m x ωω-∞-∞=-∞-∞=∑∑)]()([=mj k m kj em x ek y ωω-∞-∞=∞-∞=-∑∑)()(=)(ωj eX )(ωj e Y（5） FT[)()(n y n x ∙] =∑∞-∞=-n nj en y n x ω)()(=∑⎰∞-∞=-'-''n n j n j j e d e eY n x ωωππωωπ])(21)[(=ωπωωππω'∑⎰∞-∞='---'d e n x eY n n j j )()()(21=ωπωωππω''--'⎰d e X e Y j j )()(21)( 或者 FT[)()(n y n x ]=)(*)(21ωωπj j e Y e X（6） 因为∑∞-∞=-=n nj j en x eX ωω)()(，对该式两边对ω求导，得到j e n nx j d e dX n n j j -=-=∑∞-∞=-ωωω)()(FT[)(n nx ] 因此 FT[)(n nx ]=ωωd e dX j j )(（7） FT[)2(n x ]=∑∞-∞=-n nj en x ω)2(令n n 2='，则FT[)2(n x ]=∑''-'取偶数n n j en x 2)(ω=n j nn e n x n x ω21)]()1()([21-∞-∞=-+∑=])()([212121n j n n j n j n e n x e en x ωπω-∞-∞=-∞-∞=∑∑+ =)]()([21)21(21πωω-+j j e X e X 或者FT[)2(n x ]=)()]()([21212121ωωωj j j e X e X eX =+ （8） FT[)(2n x ]=∑∞-∞=-n n j e n xω)(2利用（5）题结果，令)()(n y n x =，则FT[)(2n x ]=)(*)(21ωωπj j e X e X =ωπωωππω''--'⎰d e X e X j j )()(21)( （9） FT[)(9n x ]=∑∞-∞=-取偶数n n n j e nx ω)2(令∞≤'≤∞-='n n n ,2，则FT[)(9n x ]=)()(22ωωj n n n j e X en x ='∑∞-∞='-取偶数3．2 已知⎩⎨⎧≤<<=πωωωωω||,0||,1)(00j e X求)(ωj eX 的傅里叶反变换)(n x 。

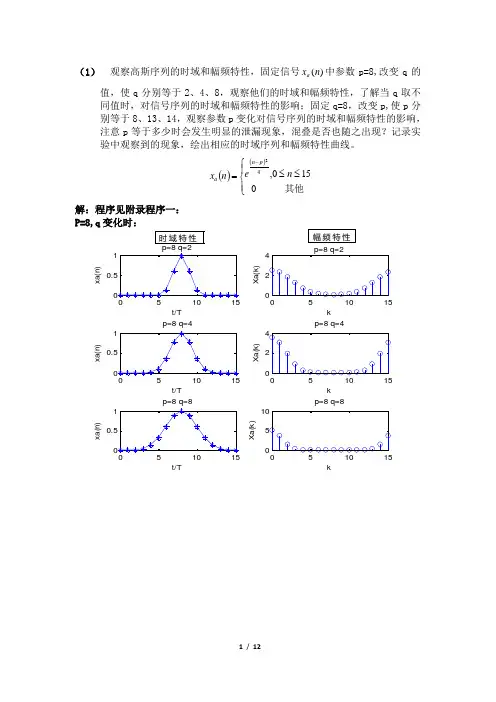
（1） 观察高斯序列的时域和幅频特性，固定信号)(n x a 中参数p=8,改变q 的值，使q 分别等于2、4、8，观察他们的时域和幅频特性，了解当q 取不同值时，对信号序列的时域和幅频特性的影响；固定q=8，改变p,使p 分别等于8、13、14，观察参数p 变化对信号序列的时域和幅频特性的影响，注意p 等于多少时会发生明显的泄漏现象，混叠是否也随之出现？记录实验中观察到的现象，绘出相应的时域序列和幅频特性曲线。

()()⎪⎩⎪⎨⎧≤≤=-其他0150,2n e n x q p n a解：程序见附录程序一：P=8,q 变化时：t/T x a (n )k X a (k )t/T x a (n )p=8 q=4k X a (k )p=8 q=4t/Tx a (n )p=8 q=8kX a (k )p=8 q=8幅频特性时域特性t/T x a (n )p=8 q=8k X a (k )p=8 q=8t/T x a (n )51015k X a (k )p=13 q=8t/Tx a (n )p=14 q=851015kX a (k )p=14 q=8时域特性幅频特性分析：由高斯序列表达式知n=p 为期对称轴； 当p 取固定值时，时域图都关于n=8对称截取长度为周期的整数倍，没有发生明显的泄漏现象；但存在混叠，当q 由2增加至8过程中，时域图形变化越来越平缓，中间包络越来越大，可能函数周期开始增加，频率降低，渐渐小于fs/2,混叠减弱；当q 值固定不变，p 变化时，时域对称中轴右移，截取的时域长度渐渐地不再是周期的整数倍，开始无法代表一个周期，泄漏现象也来越明显，因而图形越来越偏离真实值，p=14时的泄漏现象最为明显，混叠可能也随之出现；（2） 观察衰减正弦序列 的时域和幅频特性，a=0.1,f=0.0625,检查谱峰出现的位置是否正确，注意频谱的形状，绘出幅频特性曲线，改变f ，使f 分别等于0.4375和0.5625，观察这两种情况下，频谱的形状和谱峰出现的位置，有无混叠和泄漏现象？说明产生现象的原因。

＝
系统的零点为z=0， 极点为z=0.9， 零点在z平面的原点，
不影响频率特性， 而惟一的极点在实轴的0.9处， 因此滤波 器的通带中心在ω=0处。 毫无疑问， 这是一个低通滤波器。

［例2.4.2］假设x(n)=xr(n)+jxi(n)， xr(n)和xj(n)为实序列， X(z)=ZT［x(n)］在单位圆的下半部分为零。 已知
N 1
( z 1)
z
1
2 N 1
z 1 z 1
N
2
［例2.4.4］
时域离散线性非移变系统的系统函数H(z)为
1 ( z a )( z b )
H (z)
,
a 和 b 为常数
第２章
时域离散信号和系统的频域分析
（1） 要求系统稳定， 确定a和b的取值域。
第２章
时域离散信号和系统的频域分析
2.3 分析信号和系统的频率特性
求信号与系统的频域特性要用傅里叶变换。 但分析频 率特性使用Z变换却更方便。 我们已经知道系统函数的极、
零点分布完全决定了系统的频率特性， 因此可以用分析极、
零点分布的方法分析系统的频率特性， 包括定性地画幅频 特性， 估计峰值频率或者谷值频率， 判定滤波器是高通、 低通等滤波特性， 以及设计简单的滤波器（内容在教材第5 章）等。
Re［X(ejω)］=X(ejω) Im［X(ejω)］=0 ［例2.4.3］ 已知 0≤n≤N N+1≤n≤2N n<0, 2N<n
n x(n) 2 N n 0
求x(n)的Z变换。
第２章
时域离散信号和系统的频域分析
解： 题中x(n)是一个三角序列， 可以看做两个相同的矩

————第一章———— 时域离散信号与系统理论分析基础本章1.1节“学习要点”和1.2节“例题”部分的内容对应教材第一、二章内容。

为了便于归纳总结，我们将《数字信号处理（第二版）》教材中第一章和第二章的内容合并在一起叙述，这样使读者对时域离散线性时不变系统的描述与分析方法建立一个完整的概念，以便在分析和解决问题时，能全面考虑各种有效的途径，选择最好的解决方案。

1.1 学 习 要 点1.1.1 时域离散信号——序列时域离散信号（以下简称序列）是时域离散系统处理的对象，研究时域离散系统离不开序列。

例如，在时域离散线性时不变系统的时域描述中，系统的单位脉冲响应()n h 就是系统对单位脉冲响应()n δ的响应输出序列。

掌握()n δ的时域和频域特征，对分析讨论系统的时域特性描述函数()n h 和频域特性描述函数()ωj e H 和()z H 是必不可少的。

1. 序列的概念在数字信号处理中，一般用()n x 表示时域离散信号（序列）。

()n x 可看作对模拟信号()t x a 的采样，即()()nT x n x a =，也可以看作一组有序的数据集合。

要点 在数字信号处理中，序列()n x 是一个离散函数，n 为整数，如图1.1所示。

当≠n 整数时，()n x 无定义，但不能理解为零。

当()()nT x n x a =时，这一点容易理解。

当=n 整数时，()()nT x n x a =，为()t x a 在nT t =时刻的采样值，非整数T 时刻未采样，而并非为零。

在学习连续信号的采样与恢复时会看到，()n x 经过低通滤波器后，相邻的()T n nT 1~+之间的()t x a 的值就得到恢复。

例如，()n x 为一序列，取()()2n x n y =，n 为整数是不正确的，因为当=n 奇数时，()n y 无定义（无确切的值）。

2. 常用序列常用序列有六种：①单位脉冲序列()n δ，②矩形序列()n R N ，③指数序列()n u a n，④正弦序列()n ωcos 、()n ωsin ，⑤复指数序列nj eω，⑥周期序列。

习题1.设X（e"。

）和r（e JC0）分别是印7）和）仞的傅里叶变换，试求下面序列的傅里叶变换:(1) x("-"o) (3) x(-n) (5) x(")y(")(7) x(2n)⑵ x*(〃)(4) x(") * v(«) (6) nx(n) (8) /(〃)解：⑴00 FT[X(/7-Z70)] = £x(〃一〃o)e—S令n r = n-n0,即〃=n' + n Q,贝!J00FT[x(n-n o y\=工》(〃')以"''*""="初。

乂(烈)00 00(2)FT[x («)] = £ x* (n)e*= [ £ 戏〃)攻以]* = X* (e「W=—00 w=—00(3)00FT[x(—")]= 〃)e*"令=一〃,则00FT[x(—”)]= Zx(〃')e" =X(e—〃")”'=—00(4)00 x(〃) *'(〃)= ^\x(jrT)y(n -m)W=-0000 00FT[x(n) * v(w)] = Z【Z x("y("-初)]e""' n=-<x> w=-oo k = n-m,贝U00 00FT[x(ri)*y(ri)]= £[ £x(初) k=—CD W=-0000 00k=-<x> m=—cc= X(e5(em)_00 00 1时[x(M)贝〃)]= Z》(〃)贝〃)e「9 = Zx(〃)[-Lf/(em'"'"d 渺]e-加""=—00 〃=—00 2l "1 00=—£ Y(e j0)')2l " n=—<x>1 伙=一L "口")*?®"、技或者FT[x{n)y{ny\ = —「171 »兀oo(6)因为X(e，")= »("初,对该式两边口求导，得到叫、)=-J £仗"如=-jFT[nx(n)]因此矶孙(〃)]=j至@3)dco00⑺ FT\x(2ri)\=加n=-(x)令n' = 2n ,则FT[X(2W)]= £x(z/)e 7 %W--00,且取偶数00 1 r r・l 八1°0 . 1 00 . 1£?kO + (T)“x(")厂=| 广伽+£ef ("广伽〃=—oo 匕匕〃=—oo 〃=—00=L「xa*+x(/*E)F7[x(2z?)] = | X(e‘2") + X(—e'尸)(8) F7[X2(»)]= J X2(77)6^»=-OO利用(5)题结果，令x{n) = y{n),则F巾2(”)] = _£x(em)*X(eS) = —「X®。

•pp 35： 1.11 (3)
判断系统
yn
n
xm
是否为线性系统?时不变系统
m
解：线性性判断 令x(n)=ax1(n)+bx2(n)
n
n
yn xm ax1 m bx2 m
m
m
n
n
n
n
ax1m bx2 m a x1m b x2 m
y(n) 4 (n 1) 4 (n 1) (n 3) 2 (n 5) (n 7)
•pp 35： 1.12 (3)
利用卷积性质
y(n) x1(n) x2 (n)
(n) 2 (n 2) (n 4)2 (n 1) (n 3)
(n) 2 (n 2) (n 4) 2 (n 1) 2(n()n21) (n42()n1)(n24)(n 5(n) 3)
• 解：
a nu n

1
1 aZ
1
,
Z a

n
a nu n

Z

d 1
1 aZ
1

,
dZ

Z

1 1 aZ 1
2

d
1 aZ dZ
1
,

Z

1 1 aZ 1
2



a
d
Z 1 dZ
,

Z
1 1 aZ 1
2



a

Z
2

,

数字信号处理（吴镇扬）课后习题答案（比较详细的解答过程）第二章测试训练题解1.DFT和DTFT之间的关系是2.DFT和DFS之间的关系是3.对于一个128点的DFT，最先4个DFT相应于数字频率4.某滤波器的频响为H(ω) = 0.3cos2ω- 0.2cosω+ 0.05，相应于6点的DFT的H[k]为5.采样频率为22.05kHz的1024点DFT所对应的频率分辨率为6.采样率为8kHz的信号的256点DFT的第一个周期覆盖的频率范围是从0Hz至7.信号[ 1 0 2 ]的DFT每隔3个样点值重复，为8.以1600Hz对一220Hz的信号采样，进行64点DFT，最接近的DFT频率为9.以12kHz的信号对一4.25kHz的信号抽样，其256点DFT幅谱图的基带最大峰值点所对应的下标为10.采样频率为6kHz，1kHz信号的频率分辨率要达到50Hz，需11.采样频率为16kHz，1024点DFT的窗口长度为12.关于谱泄漏与窗口长度的关系是13.频谱图是展现信号的什么14.周期性方波的频谱图15.在FFT中的乘数因子是16.与512点的DFT相比，512点的FFT只需约几分之一的计算量17、一个长度为N的有限长序列可否用N个频域的采样值唯一地确定？18、计算两个Ｎ点序列的线性卷积，至少要做多少点的ＤＦＴ？19、x(2n)与x(n)的关系20、对于高斯序列x(n)=exp[-(n-p)2/q]，取16点作FFT，其幅度谱中低频分量最多的是21、一般地说按时间抽取基二FFT的_______序列是按位反转重新排列的。

22、信号x（n）＝sin(nπ/4) - cos(nπ/7)的数字周期为23、Ｎ＝２Ｌ点基二ＦＦＴ，共有______列蝶形，每列有____个蝶形。

24、信号s(t)=sin(4000πt)+sin(600πt)，则采样频率至少应为25、用按时间抽取法计算256点的FFT时，n=233的二进制位反转值是26、FFT之所以能减少DFT的运算量，是因为：，FFT减少DFT 运算量的基本处理思想是。

【最新整理，下载后即可编辑】习题一 (离散信号与系统)1.1周期序列，最小周期长度为5。

1.2 (1) 周期序列，最小周期长度为14。

(2) 周期序列，最小周期长度为56。

1.5()()()()()()()11s a s s s a n s s a s n X j x t p t X j ΩP j Ω2n τn τj sin j Ωjn e X 2n π2n n τj Sa X j jn e 2T 2πττ∞=-∞∞=-∞Ω==*⎡⎤⎣⎦ΩΩ⎛⎫-=-Ω ⎪⎝⎭ΩΩ⎛⎫-=Ω-Ω ⎪⎝⎭∑∑ 1.6 (1) )(ωj e kX (2) )(0ωωj n j e X e (3) )(21)(2122ωωj j e X e X -+ (4) )(2ωj e X1.7 (1) 0n z -(2) 5.0||,5.0111>--z z (3) 5.0||,5.0111<--z z (4)0||,5.01)5.0(11101>----z z z1.8 (1) 0,)11()(211>--=---z zz z z X N(2) a z az az z X >-=--,)1()(211 (3) a z az z a az z X >-+=---,)1()(311211.91.10 (1))1(2)(1----+n u n u n (2))1(24)()5.0(6--⋅--n u n u n n (3))()sin sin cos 1(cos 000n u n n ωωωω++(4) )()()(1n u a a a n a n ---+-δ 1.11(1))(1z c X - (2) )(2z X (3))()1(21z X z -+ (4)-+<<x x R z R z X /1/1),/1(1.12 (1) 1,11<-ab ab(2) 1 (3)00n a n1.13 (1) 该系统不是线性系统；该系统是时不变系统。

(4)h(n) = 0.5n u(n)
解答:
1
（1） 不能用令 x(n)=δ(n)来求 h(n)，然后确定稳定性，因为该系统并非线性时不变系统。
实际上，因 g(n)有界，所以，当 x(n)有界时，y(n)= x(n) g(n)<= |x(n)| |g(n)|<∞, 所以系统稳定，y(n) 只与 x(n)的当前值有关，显然是因果的。 （2）
=
N −1
kn
x(n)WN2
+
(−1)k
N −1
kn
x(n)WN2
n=0
n=0
∑N −1
当k为偶数时,上式=2
n=0
kn
x(n)WN2
=
2X
( k ); 2
当k为奇数时,上式=0.
2-9 有限长为 N = 10 的两序列
x(n)
=
⎧1, 0 ≤ ⎨⎩0,5 ≤
n n
≤ ≤
4 9
y(n)
=
⎧1, 0 ⎨⎩−1,
DFS,试利用 X1(k ) 确定 X 2 (k) . 解答:
N −1
∑ X1(k) = x(n)WNkn n=0
2 N −1
N −1
N −1
∑ ∑ ∑ X 2 (k) = x(n)W2kNn = x(n)W2kNn + x(n + N )W2kN(n+N )
N =0
n=0
n=0
注:W2kNn
− j 2π kn
,式中 a 为实数
(1) 对于什么样的 a 值范围系统是稳定的? (2) 如果 0<a<1,画出零点-极点图,并标出收敛区域; (3) 在 z 平面上用图解证明该系统是一个全通系统,即频率响应的幅度为一常数. 解答:

1. 解丗由题意可知 N=5
则周期为丗其中为整数丆且满足使N为最小整数。

2. •i1•j解丗由题意可知 N=14
则周期为丗
•i2•j解丗由题意可知 N= 8
则
则所求周期 N=14
最小公倍数丆即为丗56
3.19 (1)周期卷积的主值序列为丗f(n)R(n) ={6,3, 6,10,14,12,9};
(2)循环卷积f (n) ={6,3, 6,10,14,12,9};
•i3•j线性卷积为f(n) ={1,3, 6,10,14,12,9,5, 0, 0, 0, 0}
2.21 •i 第二种方法乯按频率抽取算法丗输入顺
序丆
输出倒序(0,8,4,12,2,10,6,14,1,9,5,13,3,11,7, 15);
4
共有4(16=2*2*2*2 )节
第一节丗数据点间距、蝶形类型均是8•C
0 1 2 3 4 5 6 7
所乘因子丗W ,W ,W ,W ,W ,W ,
W ,W ;
N N N N N N N N N
第二节丗数据点间距、蝶形类型均是4 •C
0 2 4 6
所乘因子丗W ,W ,W ,W ;
N N N N
0 4
第三节丗数据点间距、蝶形类型均是2 •C所乘因
子丗W ,W ;
N N
第四节丗数据点间距、蝶形类型均是1 •C所乘因
子丗W ;
N。